随着信息科技的迅速发展,数据规模的爆炸式增长成为了大数据时代的主要特征之一。在此时代背景下,数据通常具有维数高和稀疏性等特点,为数据挖掘带来了空前的挑战。特征提取作为处理高维数据的有效手段,通过提取数据的低维特性,可以将高维特征空间映射到低维特征空间中进行数据的分析和处理,通常分为线性特征提取和非线性特征提取2种方式。非线性特征提取不依赖于线性假设,对于处理非线性结构的数据效果较好,成为当前数据挖掘的热门方向之一。流形学习[1-6]作为一种非线性特征提取方法,应用了流形在局部结构上与欧氏空间同胚的性质。通过对高维数据样本的分析来挖掘隐藏的本质结构,从而提取有效的低维特征。然而,流形学习方法仍然存在一些不足,例如:流形学习方法忽略了数据的类别标记信息,提取的特征并不是分类上的最优特征。因此,忽略标记信息而提取到的特征在进行数据聚类或分类时,结果往往与实际存在较大差异。所以希望可以使用半监督[7-14]的方法进行学习,即少量标记信息来指导特征提取,同时又使用大量无标记信息的数据点来刻画并保持样本的局部或全局几何、线性等结构。
局部线性嵌入(LLE)[15]是一种无监督[16]的流形学习方法,直接用它提取的特征进行数据挖掘如聚类或分类得到的结果并不是很理想。因此我们希望将数据集的标记信息引入到LLE方法中用以提高特征提取效果。而已有的一些半监督方法,例如半监督局部线性嵌入方法(semi-supervised locally linear embedding, SSLLE)虽然利用了标记信息对特征提取进行一定的改进,但它只考虑了近邻点的标记信息做局部调整,因此当整体标记信息较低时每个近邻中将有可能出现没有标记点的情况。这时SSLLE将失去作用并且由于它只考虑近邻的这种调整,当标记信息很多时它们整体的区分度也不大。本文在LLE的基础上利用近邻伪标签赋予得到的标记信息作局部调整,同时从全局[17]角度对同类数据点和异类数据点进行全局调整,使得重构数据低维特征空间时,既保持局部线性结构,又能使提取后的数据在低维特征空间中可以实现具有相同标记信息的数据点互相靠近,而标记不同的数据点彼此分离,从而达到更好的特征提取结果。最后通过聚类分析及可视化证明本文方法的有效性。
1 局部线性嵌入由Roweis等提出的LLE是一个经典的保持局部线性特性的流形学习方法,可以有效提取高维数据的低维特征。其基本原理为:假设数据是分布在一个流形上的,任一点均可用它的近邻点经由线性重构而得到。基于局部线性表示系数,构造优化问题使得数据在高维原始空间到低维特征空间的过程中局部线性重构权值不发生变化,获得高维数据的低维特征。
假设数据集
对于每个数据点,计算每一个数据点
假设任一点
| $\begin{array}{l} \min \varepsilon ({{w}}) = {\displaystyle\sum\limits_{i = 1}^n {\left\| {{x_i} - \displaystyle\sum\limits_{j = 1}^k {{w_{ij}}{x_j}} } \right\|} ^2} \\ \;\;\;\;\;\;\;\;\;\;\;{\rm{s.t.}}\;\;\;\displaystyle\sum\limits_{j = 1}^k {{w_{ij}} = 1} \\ \end{array} $ | (1) |
容易获得优化问题式(1)的最优解:
| ${{{w}}_i} = \frac{{{{{\varGamma}} ^{\rm{T}}}{{G}}_i^{ - 1}}}{{{{{\varGamma}} ^{\rm{T}}}{{G}}_i^{ - 1}{{\varGamma}} }}$ | (2) |
式中:
基于局部线性重构矩阵式(2),构造优化问题:
| $\begin{array}{l} \min \sigma ({{Y}}) = {\displaystyle\sum\limits_{i = 1}^n {\left\| {{{{y}}_i} - \displaystyle\sum\limits_{j = 1}^k {{w_{ij}}{{{y}}_j}} } \right\|} ^2} \\ \;\;\;\;{\rm{s.t.}}\;\displaystyle\sum\limits_{i = 1}^n {{{y}}_i^{\rm{T}}{{{y}}_i}} = {{I}},\;\;\;\displaystyle\sum\limits_{i = 1}^n {{{{{y}}}_i} = {{0}}} \\ \end{array} $ | (3) |
获得高维数据X的低维嵌入
根据样本的邻域点分布将k维行向量
采用拉格朗日乘子法求解优化问题式(3),可得
在数据挖掘任务中,监督信息为用户提供强有力的数据分析基础。然而,众多实际问题只能获得少量样本的监督标记。半监督机器学习方法应运而生。
LLE是一种经典的无监督高维数据特征提取方法。本文在LLE基础上提出一种半监督类保持局部线性嵌入方法(SSCLLE)。该方法不仅利用近邻伪标签赋予得到的标记信息调整近邻数据间的距离,而且从全局角度加入了同类数据点和异类数据点的全局约束,使提取后的数据在低维特征空间中可以实现具有相同标记信息的数据点互相靠近,而标号不同的数据点彼此分离,达到更好的特征提取效果。
假设
一般情况下,
将所有标记样本
|
Download:
|
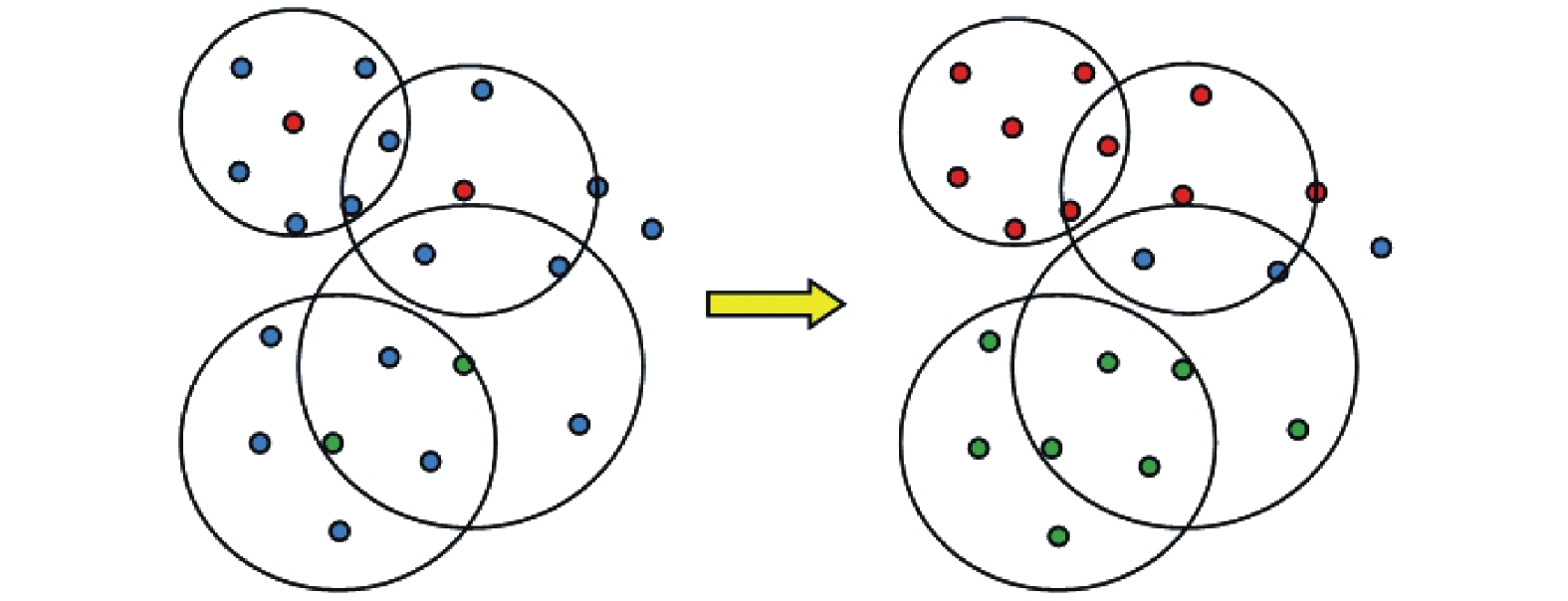
| 图 1 近邻伪标签赋值方法示意 Fig. 1 Schematic diagram of nearest neighbor pseudo label assignment method | |
在图1的左图中,红色和绿色的点分别代表标记点(2类),蓝色是无标签的点。经过上述近邻伪标签赋值方法后,只有一类标记信息的近邻点保留赋予的标签(右图新增加的红色点和绿色点),而有2种(或多种)标记的近邻点则依旧标为无标记点,保持其蓝色不变(右图大圆中的2个蓝色点)。得到的新标签数据为
新增加的伪标签虽然不是真实的标签,但由于其与被标注样本具有很好的近邻关系,通过这样的扩充可增加标记信息的量,有利于更好地描述数据的内在结构,发现样本中隐藏的鉴别能力。
为了构造出利用全局信息进行调整的优化问题,首先定义同类数据点对集合:
| ${\rm{ML}} = \left\{ {({x_i},{x_j})|i \ne j,l({x_i}) = l({x_j})} \right\}$ |
和异类数据点对集合:
| ${\rm{CL}} = \left\{ {({x_i},{x_j})|i \ne j,l({x_i}) \ne l({x_j})} \right\}$ |
分别构造同类样本项偏差和异类样本项偏差:
| ${J_{{\rm{ML}}}} = \sum\nolimits_{({x_i},{x_j}) \in {\rm{ML}}} {{d^2}({{{y}}_i},{{{y}}_j})} = {\left\| {{{{y}}_i} - {{{y}}_j}} \right\|^2}$ |
| ${J_{{\rm{CL}}}} = \sum\nolimits_{({x_i},{x_j}) \in {\rm{CL}}} {{d^2}({{{y}}_i},{{{y}}_j})} = {\left\| {{{{y}}_i} - {{{y}}_j}} \right\|^2}$ |
式中
本文的目的是要求同类样本项偏差尽量小,同时确保异类样本项偏差尽可能的大。
构造半监督数据集
| $ {{{g}}_{ij}}' = \left\{ \begin{array}{l} (1 - r){{{g}}_{ij}},\quad l({x_i}) = l({x_j})\\ (1 + r){{{g}}_{ij}},\quad l({x_i}) \ne l({x_j})\;\\ {{{g}}_{ij}},\quad {x_i}{\text{和}}{x_j}{\text{至少一个无标号}} \end{array} \right. $ | (4) |
式中0<r<1。
从式(4)可以看出,如果2个样本有相同的类标,则将其距离缩小。如果2个样本有不同的类标,则将其距离扩大。在其他情况下,样本点间的距离保持不变。
重置式(2)中的距离矩阵为
再由(2)计算样本点的邻域局部线性重构权矩阵由此利用标记信息得到改进后的新重构权矩阵
基于以上分析,构造如下优化问题:
| $\begin{array}{l} \min \rho ({{Y}}) = \beta {\displaystyle\sum\limits_{i = 1}^n {\left\| {{{{y}}_i} - \displaystyle\sum\limits_{j = 1}^n {{w_{ij}}{{{y}}_j}} } \right\|} ^2} + \\ \quad \quad \quad \alpha \displaystyle\sum\limits_{({x_i},{x_j}) \in {\rm{ML}}} {{d^2}({{{y}}_i},{{{y}}_j})} - \\ {\kern 1pt} {\kern 1pt} \quad \quad (1 - \alpha )\displaystyle\sum\limits_{({x_i},{x_j}) \in {\rm{CL}}} {{d^2}({{{y}}_i},{{{y}}_j})} \\ \;\;\;\;{\kern 1pt} {\rm{s.t.}}\;\;\displaystyle\sum\limits_{i = 1}^n {{{{y}}_i}} = {{0}}\;,\;\sum\limits_{i = 1}^n {{{y}}_i^{\rm{T}}{{{y}}_i}} = {{I}} \\ \end{array} $ | (5) |
该优化问题式(5)的目标函数由3部分组成。第1项形式上虽然和LLE相同,但其中的重构权矩阵包含了样本点的半监督信息,能够确保提取出的特征既保持数据的局部线性结构不变,又能在局部上使类内(同类)数据更紧密,并对类间(异类)数据进行分离的效果。第2项和第3项分别是全局同类样本偏差和全局异类样本偏差,目的是确保同类样本偏差最小,同时确保全局异类样本偏差最大,参数
式(5)的约束条件与LLE相同,确保提取出的特征在低维空间中旋转平移伸缩都具有平移和缩放不变性,其中I为d阶单位矩阵。
简记式(5)的目标函数为
| $\rho ({{Y}}) = \beta \sigma ({{Y}}) + \alpha {{{J}}_{{\rm{ML}}}} - (1 - \alpha ){{{J}}_{{\rm{CL}}}}$ | (6) |
这样,式(6)的第1部分形式上与LLE相同,仍可表示为
| $\sigma ({{Y}}) = {\sum\limits_{i = 1}^n {\left\| {{{{y}}_i} - \sum\limits_{j = 1}^n {{W_{ij}}{{{y}}_j}} } \right\|} ^2} = {\rm{tr}}({{{Y}}^{\rm{T}}}{{MY}})$ |
式中的M由式(2)、(4)确定。
为了简化第2部分和第3部分,给定矩阵[10]
| ${({{{y}}_i} - {{{y}}_j})^{\rm{T}}}({{{z}}_i} - {{{z}}_j}) = \sum\limits_{l = 1}^d {({y_{il}} - {y_{jl}})({{\text{z}}_{il}} - {{\text{z}}_{jl}})} = {\rm{tr}}({{{Y}}^{\rm{T}}}{{{A}}^{ij}}{{Z}})$ |
其中
| $ {({{A}}^{ij})_{pq}} = \left\{ \begin{array}{l} 1,\quad p = i,q = i\\ 1,\quad p = j,q = j\\ - 1,\quad p = i,q = j\\ - 1,\quad p = j,q = i\\ 0,\quad {\text{其他}} \end{array} \right. $ |
令
| $ w_{ij}^{{\rm{ML}}} = \left\{ {\begin{array}{*{20}{l}} {1,\quad ({x_i},{x_j}) \in {\rm{ML}}}\\ {0, \quad{\text{其他}} } \end{array}} \right. $ |
| $ w_{ij}^{{\rm{CL}}} = \left\{ {\begin{array}{*{20}{l}} {1,\quad ({x_i},{x_j}) \in {\rm{CL}}}\\ {0,\quad{\text{其他}} } \end{array}} \right. $ |
则有:
| $ \begin{array}{l} {J_{{\rm{ML}}}} = \displaystyle\sum\nolimits_{({x_i},{x_j}) \in {\rm{ML}}} {{d^2}({{{y}}_i},{{{y}}_j})}= \displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{ML}}}{d^2}({{{y}}_i},{{{y}}_j})} = \\ \;\;\displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{ML}}}{\rm{tr}}({{{Y}}^{\rm{T}}}{{{A}}^{ij}}{{Y}})} = {\rm{tr}}\left( {{{{Y}}^{\rm{T}}}(\displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{ML}}}{{{A}}^{ij}}} ){{Y}}} \right)= \\ \quad\quad\quad\quad\quad\quad\quad{\rm{tr}}({{{Y}}^{\rm{T}}}{{{V}}_{{\rm{ML}}}}{{Y}}) \\ \end{array} $ |
和
| $\begin{array}{l} {J_{{\rm{CL}}}} = \displaystyle\sum\nolimits_{({x_i},{x_j}) \in {\rm{CL}}} {{d^2}({{{y}}_i},{{{y}}_j})}=\displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{CL}}}{d^2}({{{y}}_i},{{{y}}_j})}= \\ \;\;\displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{CL}}}{\rm{tr}}({{{Y}}^{\rm{T}}}{{{A}}^{ij}}{{Y}})} = {\rm{tr}}\left( {{Y^{\rm{T}}}(\displaystyle\sum\limits_{i,j = 1}^n {w_{ij}^{{\rm{CL}}}{{{A}}^{ij}}} ){{Y}}} \right) =\\ \quad\quad\quad\quad\quad\quad\quad{\rm{tr}}({{{Y}}^{\rm{T}}}{{{V}}_{{\rm{CL}}}}{{Y}}) \\ \end{array} $ | (7) |
因此,优化问题(5)的矩阵表示形式为
| $\begin{array}{l} \min \rho (Y) = {\rm{tr}}({{{Y}}^{\rm{T}}}{{HY}}) \\ \;\;{\kern 1pt} {\rm{s}}.{\rm{t}}.\;\;{{{Y}}^{\rm{T}}}{{Y}} = {{I}},\;\;{{\bf{1}}^{\rm{T}}}{{Y}} = {\bf{0}} \\ \end{array} $ |
式中:
计算矩阵H的前d个最小非零特征值(
为了证明本文提出的SSCLLE的性能,在加州大学欧文分校(university of california irvine, UCI)数据集、实物数据集coil_20和手写数字MNIST数据集上进行实验。实验结果分别与经典的无监督流形学习方法LLE、半监督SSLLE[18]方法,半监督拉普拉斯特征映射(semi-supervised laplacian eigenmap, SSLE)[19]和分类约束降维方法(classification constrained dimensionality reduction, CCDR)[20]进行实验对比。从聚类精度和数据可视化角度对它们进行实验比较和分析。
在这里简单介绍3种半监督方法。基于LLE提出的SSLLE,它的思想是结合数据拥有的部分标记信息调整近邻样本点之间的距离,再利用调整后的距离来重构权值矩阵。虽然SSLLE可以利用部分标签信息使得近邻中同类数据点距离更近,异类数据点更远从而实现更好的分类以及聚类效果。但由于 SSLLE 方法仅对近邻点之间的距离做调整,缺乏对全局同类异类点的考虑。当标记点较少时近邻中可能出现没有同类或异类的点的情况,这时 SSLLE 将失去作用。而且由于它只考虑近邻的调整,当标记信息很多时它们整体的区分度也不大。
SSLE和CCDR都是在拉普拉斯特征映射(laplacian eigenmap,LE)的基础上提出的半监督方法。在这里SSLE也是一种利用信息在局部做调整的方法,缺点和SSLLE类似。而CCDR是一种全局的调整,相较于SSLE有较好的提取效果。
本文SSCLLE方法在保持局部线性结构的同时,不仅利用标记信息对局部做调整,同时利用全局项对全局做调整。使类内数据更紧密,而对类间数据进行分离。从而达到更好的特征提取效果,以下是相关的实验验证。
统一对各方法设定参数,进行特征提取。这里用聚类精度作为评判方法有效性的指标之一,利用模糊C均值(fuzzy c-means,FCM)聚类方法进行聚类分析。关于样本标签个数做以下设置:从数据集的每类样本中随机抽取
实验中从UCI数据库里选3个数据集,分别为Wine数据集、Seeds数据集和WDBC(wisconsin diagnostic breast cancer)。
然后,分别用5种方法进行实验比较和分析。根据特征提取的维数d做3组实验,分别设置d的值为2、3和4。每类数据随机标记5%,每组实验进行20次,求聚类精度的平均值来评判5种方法的特征提取效果。表1~3分别是d值为2、3和4时,各方法对3个数据集进行特征提取后得到的平均聚类精度。实验中,将参数设置为:
| 表 1 数据集信息 Tab.1 Data set information |
| 表 2 |
| 表 3 |
由表2~4数据可知:当特征空间的维数d为3和4时,在3个数据集上SSCLLE方法的聚类精度都比其他4种方法高,其他方法在不同数据集之间聚类精度各有高低。而当d为2时,虽然SSCLLE方法在Seeds数据集的实验中的聚类精度并不是全部保持最高,当标记比例为5%时SSLLE方法仅仅略高于本文方法,在标记比例为15%以及另外2个数据集时SSCLLE的聚类精度最高。总体实验分析可知,本文提出的半监督流形学习方法SSCLLE相比无监督方法LLE与其他3种半监督方法聚类精度最高,体现出本文方法的优势。
| 表 4 |
对于半监督方法来说标记信息的多少会影响聚类的结果。这里把3组UCI数据中的每一个类标记信息比例设置为5%、20%和40%,提取特征维数d=2。图2为3个数据集在4种半监督方法下的实验结果。

|
Download:
|
| 图 2 标记样本的比例对聚类精度的影响,d=2 Fig. 2 Influence of proportion of labeled samples on clustering accuracy, d=2 | |
由图2的实验结果可以看出:3个数据集的柱状分析图,随着数据的标记比例的增加,各个半监督方法的聚类精度也在增加,符合半监督方法利用越多标记信息就会提高聚类精度的设想。但明显可以看出2种基于局部标记信息进行调整的方法SSLLE和SSLE,随着标记信息的增加聚类精度提升,相对考虑全局信息的SSCLLE与CCDR不明显。而SSCLLE方法的聚类精度已经达到了一个很高的值,明显高于CCDR,所以相对没有CCDR提升比率那么高。总体实验分析中可以看到,在每组实验里SSCLLE方法的聚类精度基本都能保持最高,证明了本方法在UCI数据上的优势。
3.2 实物数据集COIL _20这里采用哥伦比亚大学(COIL-20) 数据集中第2种(背景被丢弃,图像由包含物体的最小正方形组成),数据集共有20种不同的物体,每种有72张图片。每个图片都是50×50的灰度图像,在实验中将每张图片以行拉成一个2500的向量。最后以向量集的形式进行处理与分析。
从数据集中按顺序选取6组数据,每组3类不同的物体。分组分别是{1,2,3},{4,5,6},{7,8,9},{10,11,12},{13,14,15}和{16,17,18},然后再随机选取3组不同的数据{9,7,10},{7,3,5},{4,10,1},每组运行20次计算聚类精度。其中Group1~Group9分别对应以上9组数据,用不同方法做实验得到聚类精度。参数设置为:
由表5实验结果可以看到,在这9组数据中由于SSLLE和本文方法SSCLLE都是在LLE方法上进行的一种改进,所以它们的聚类精度都高于LLE。且本方法利用了全局标记信息进行调整,聚类精度明显高于SSLLE。SSLE与CCDR都是一种在LE基础上做的改进,分析数据可以看出整体上它们略低于LLE的改进。且由于CCDR也是一种基于全局考虑标记信息的方法,基本上聚类精度都高于SSLE。由此体现出基于全局角度考虑标记信息的方法较局部效果要好,充分说明SSCLLE方法基于全局考虑的正确性。除在第6组数据中SSLLE方法的聚类精度最高外,其它组中都是本文中提出的SSCLLE方法精度最高。
| 表 5 COIL_20数据集在不同方法下的平均聚类精度 Tab.5 Average clustering accuracy of COIL_20 dataset under different methods |
接下来随机选出一组数据为{7,3,9},来做在不同标签比例下不同方法聚类精度的折线图,参数设置为:
|
Download:
|
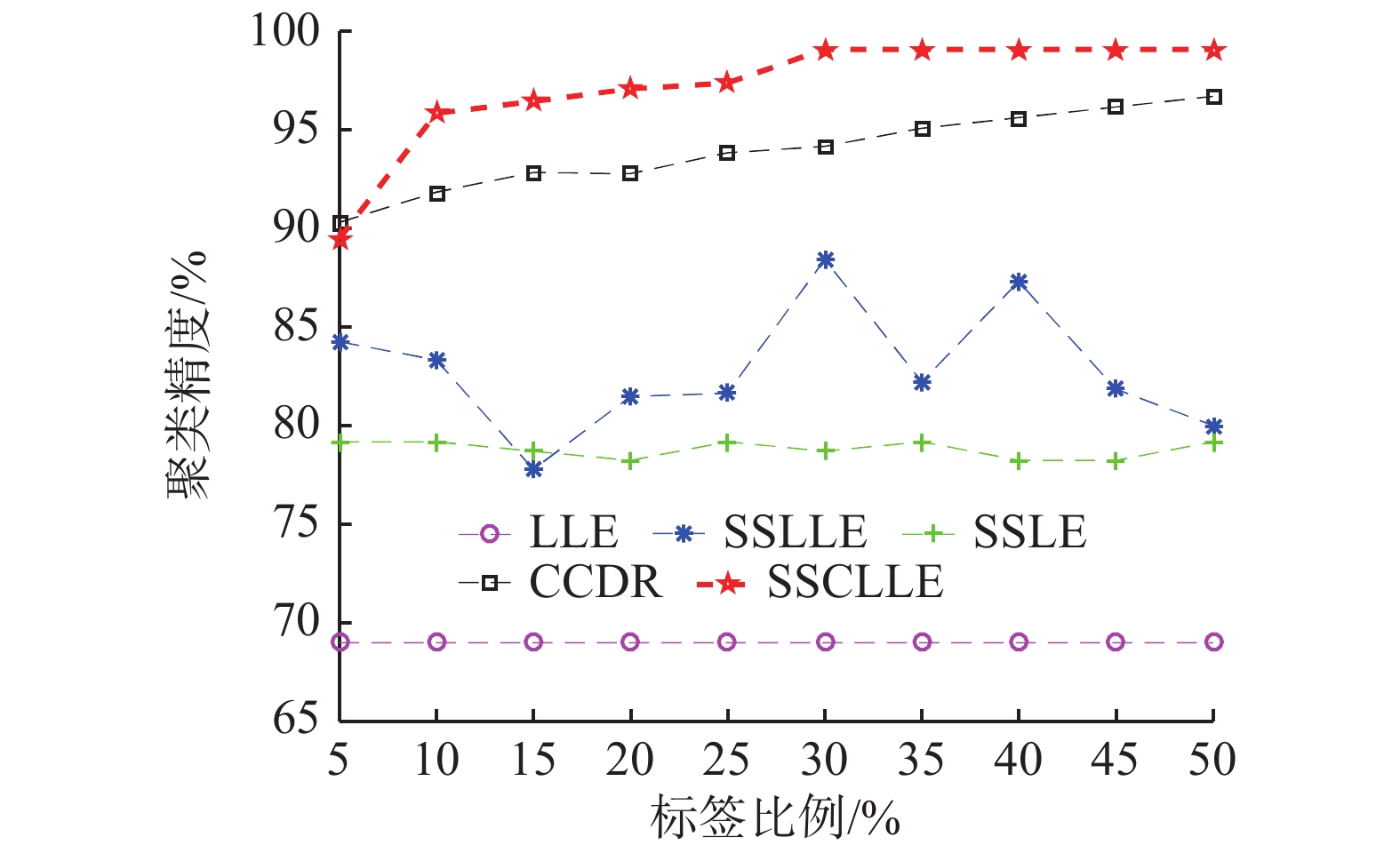
| 图 3 不同标记比例COIL_20数据集聚类精度 Fig. 3 The clustering accuracy of COIL_20 dataset under different labeling ratios | |
由图3可看出在这组数据中随着标记比例的增加无监督LLE方法精度保持不变,而SSLLE与SSLE方法的聚类精度随着标记比例的增加只发生了波动,基本没有体现出上升趋势,说明这2种利用类信息只调节近邻关系的方法对一些数据提取到的特征不能很好地提高可分性。而SSCLLE和CCDR方法都是考虑全局的调整,可看到聚类精度呈上升趋势,且高于其他方法,除在5%的情况下略低于CCDR方法外,其余比例下均高于其他方法。体现出SSCLLE方法对近邻及全局做调整的优势。
3.3 数据可视化数据可视化作为一种重要的数据分析方式,相对于单纯的数据表格等,可更加直观、形象地感知或理解高维数据集的结构分布。为验证SSCLLE方法在可视化上的优势,下面随机选取MNIST数据集中的3个手写数字做可视化实验。分别用LLE方法、半监督:SSLLE、SSLE和CCDR方法,将选取的手写数据集中3个数字提取至2维特征空间中,利用MATLAB画图工具进行画图,同类数据点的颜色和形状一样,分别观察5种不同的方法提取数据点的低维特征分布情况。手写数字选取的是{5,6,8}每类500个点分别将标记比例设为15%,参数设置为:

|
Download:
|
| 图 4 手写数字可视化 Fig. 4 Visualization of Handwritten digital | |
在图4中手写数字的5个可视化图可以看到,无监督的LLE中有2类数据重合部分较大区分度小,因而不利于数据的聚类分析。而基于标记信息局部调整的SSLLE和SSLE的方法相对LLE的分离度明显有所提升,不过依然存在重叠区域。而基于标记信息全局调整的CCDR和本文方法SSCLLE明显3类区分开了,SSCLLE相比CCDR的区分度更高重叠区域最小,可明显区分出3类数据的分布。通过实验可视化的分析,半监督方法在数据可视化方面较无监督方法优势明显,而本文方法的可视化效果相对其他半监督方法效果最好,证明了本文方法的优势。
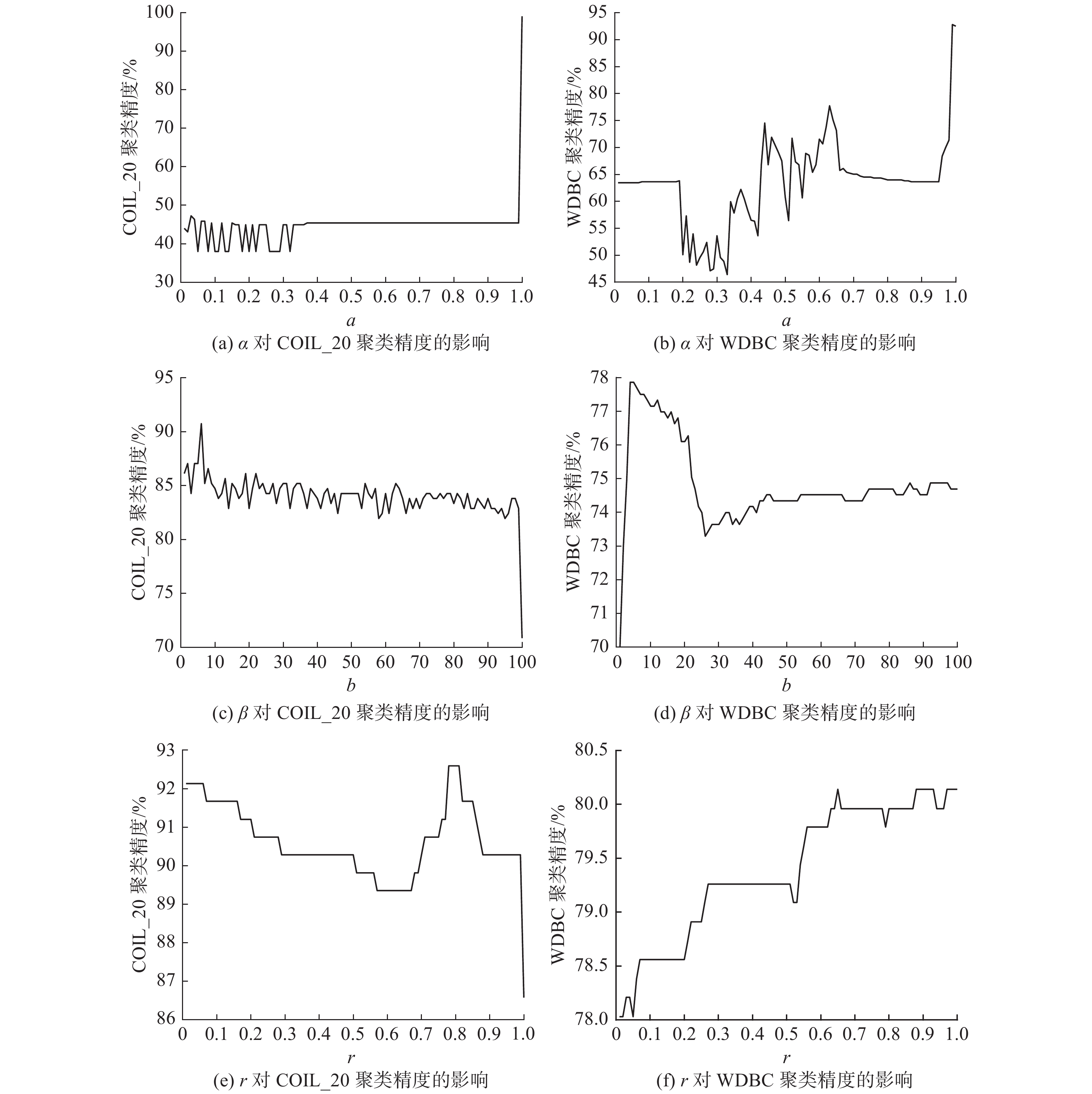
4 参数影响分析本方法中参数k、d、
从图5可以看出,同类数据样本项比异类样本项对聚类精度起到的作用更大。标记比例越高,异类标记的作用会逐渐增加。在一定的标记比例下,
|
Download:
|
|
图 5 参数
|
|
从手写数字中选取30组不同的数据,每组由3个不同的数字组成。对这30组数据分别用5种方法进行特征提取得到相应的聚类精度。
为了对比SSCLLE与其他方法的优劣,利用SPSS工具对SSCLLE方法得到的聚类精度与其他方法得到的聚类精度做成对t检验,得到以下结果如表6~8所示。
| 表 6 配对样本统计 Tab.6 Paired sample statistics |
| 表 7 配对样本相关性 Tab.7 Correlation of paired samples |
通过表8可以看到SSCLLE与其他4种方法的显著性均小于0.05,说明各对比组聚类精度有显著差异。再对比均值,可见本文SSCLLE方法相对其他方法能够有效地提高特征提取的效果。
| 表 8 配对样本检验 Tab.8 Paired sample test |
本文在LLE基础上,提出了一种半监督类保持局部线性嵌入方法(SSCLLE)。方法中不单考虑了利用近邻伪标签赋予的标记信息对局部近邻做调整,还对样本的全局距离做进一步约束,使其达到既能保持数据的局部线性结构又能使类内数据更紧密,类间数据进行分离,得到很好的特征提取效果。在UCI数据集、实物数据集COIL_20和手写数据集MNIST上对各方法进行实验对比,得到SSCLLE方法在聚类精度以及可视化上的结果均高于无监督学习LLE方法和半监督学习SSLLE、SSLE、CCDR方法。
| [1] |
LIU Feng, ZHANG Weijie, GU Suicheng. Local linear laplacian eigenmaps: a direct extension of LLE[J]. Pattern recognition letters, 2016, 75: 30-35. DOI:10.1016/j.patrec.2016.03.003 ( 0) 0)
|
| [2] |
JIANG Bo, DING C, LUO Bin. Robust data representation using locally linear embedding guided PCA[J]. Neurocomputing, 2018, 275: 523-532. DOI:10.1016/j.neucom.2017.08.053 ( 0) 0)
|
| [3] |
WANG Qian, WANG Weiguo, NIAN Rui, et al. Manifold learning in local tangent space via extreme learning machine[J]. Neurocomputing, 2016, 174: 18-30. DOI:10.1016/j.neucom.2015.03.116 ( 0) 0)
|
| [4] |
TANG Z, LAO H. Robust image hashing via DCT and LLE[J]. Computers and security, 2016, 62: 133-148. DOI:10.1016/j.neucom.2017.08.053 ( 0) 0)
|
| [5] |
ZHANG Yan, ZHANG Zhao, QIN Jie, et al. Semi-supervised local multi-manifold Isomap by linear embedding for feature extraction[J]. Pattern recognition, 2018, 76: 622-678. ( 0) 0)
|
| [6] |
LIU Zhonghua, WANG Xiaohong, PU Jiexin, et a. Nonnegative low-rank representation based manifold embedding for semi-supervised learning[J]. Knowledge-based systems, 2017, 136: 121-129. DOI:10.1016/j.knosys.2017.09.003 ( 0) 0)
|
| [7] |
CHEN Lin, YANG Meng. Semi-supervised dictionary learning with label propagation for image classification[J]. Computational visual media, 2017, 3(1): 83-94. DOI:10.1007/s41095-016-0073-1 ( 0) 0)
|
| [8] |
MIKALSEN K O, SOGUERO-RUIZ C, BIANCHI F M, et al. Noisy multi-label semi-supervised dimensionality reduction[J]. Pattern recognition, 2019, 90: 257-270. DOI:10.1016/j.patcog.2019.01.033 ( 0) 0)
|
| [9] |
PARK S H, KIM S B. Active semi-supervised learning with multiple complementary information[J]. Expert systems with applications, 2019, 126: 30-40. DOI:10.1016/j.eswa.2019.02.017 ( 0) 0)
|
| [10] |
ZHENG Feng, SONG Zhan, SHAO Ling, et al. A semi-supervised approach for dimensionality reduction with distributional similarity[J]. Neurocomputing, 2013, 103: 210-221. DOI:10.1016/j.neucom.2012.09.023 ( 0) 0)
|
| [11] |
SUN Shiliang, HUSSAIN Z, SHAWE-TAYLOR J. Manifold-preserving graph reduction for sparse semi-supervised learning[J]. Neurocomputing, 2014, 124: 13–21.
( 0) 0)
|
| [12] |
KIM K. An improved semi-supervised dimensionality reduction using feature weighting: application to sentiment analysis[J]. Expert systems with applications, 2018, 109: 49-65. DOI:10.1016/j.eswa.2018.05.023 ( 0) 0)
|
| [13] |
ROWEIS S T, SAUL L J. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326. DOI:10.1126/science.290.5500.2323 ( 0) 0)
|
| [14] |
LANGLEY P, PAZZANI M J, FISHER D H. Concept formation: knowledge and experience in unsupervised learning[M]. San Mateo: Morgan Kaufmann Publishers, 1991.
( 0) 0)
|
| [15] |
YANG Bo, XIANG Ming, ZHANG Yupei. Multi-manifold discriminant isomap for visualization and classification[J]. Pattern recognition, 2016: 215-230. DOI:10.1016/j.patcog.2016.02.001 ( 0) 0)
|
| [16] |
张长帅, 周大可, 杨欣. 一种基于核的半监督局部线性嵌入方法[J]. 计算机工程, 2011, 37(20): 157-159. ZHANG Changshuai, ZHOU Dake, YANG Xin. Method of kernel-based semi-supervised local linear embedding[J]. Computer engineering, 2011, 37(20): 157-159. DOI:10.3969/j.issn.1000-3428.2011.20.054 (  0) 0)
|
| [17] |
KIM K, LEE J. Sentiment visualization and classification via semi-supervised nonlinear dimensionality reduction[J]. Pattern recognition, 2014, 47(2): 758-768. DOI:10.1016/j.patcog.2013.07.022 ( 0) 0)
|
| [18] |
COSTA J A, HERO III A O. Classification constrained dimensionality reduction[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Philadelphia, USA, 2005: 1077–1080.
( 0) 0)
|
| [19] |
MARCILLA A, REYES-LABARTA J A, OLAYA M M. Should we trust all the published LLE correlation parameters in phase equilibria? Necessity of their assessment prior to publication[J]. Fluid phase equilibria, 2017, 433: 243-252. DOI:10.1016/j.fluid.2016.11.009 ( 0) 0)
|
| [20] |
BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum, 1981: 35–36.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


