由于人体运动学信息在教学^[1]、医疗^[2]、运动康复^[3-4]、人体外骨骼^[5-7]等领域的广泛应用，人体关节力矩的求解方法一直受到学者的广泛关注。目前对于关节力矩的求解方法根据原理主要分为两种：1)采取人体表面肌电信号(surface ectromyography)结和人体肌肉骨骼模型求解相应的关节力矩^[8-9]；2)运用惯性测量元件测量人体运动学信息，通过构建人体逆动力学模型来解算关节力矩。在人体逆动力学模型方面，哈尔滨工业大学的郭伟等^[10]将单腿支撑相的人体建立为刚体模型，通过光学动捕系统测量人体运动学信息，对人体下肢关节力矩进行解算；韩国科学技术院结合人体上肢质心的运动规律，建立了弹簧单摆模型进而解算了人体踝关节的关节力矩^[11]。由于对动力学模型精确度的依赖较高，上述方法难以提供准确度较高的关节力矩求解结果。与之相比，以表面肌电信号作为输入的人体肌肉骨骼模型，由于肌肉相对于关节的高度冗余，具有能够预测肌肉出力、体现拮抗肌肉驱动、反算肌肉激活等方面的优势，能够体现出更丰富的人体运动及肌肉激活的信息。因此近些年来，很多学者提出了使用肌电信号求解关节力矩的方法。该方法主要分为4个过程：1)从肌电信号(sEMG)求解肌肉激活(Muscle activation)；2)根据神经肌肉骨骼模型求解肌肉力；3)求解关节力臂；4)参数辨识。现阶段所使用的模型例如Zajac在1989年提出的模型^[12]或Huxley的更复杂的生物物理模型^[13-14]，又如Zahalak的模型^[15-16](Zahalak，1986，2000年)是基于Hill的经典著作^[17]。本文主要总结了近年来使用肌电信号以及相关生理学模型对关节力矩的求解方法，并阐述了利用神经肌肉骨骼模型对关节力矩求解的基本原理及过程，给出了模型中涉及的一些参数的生理学统计数据。又给出了以求解关节划分的该研究的主要应用，最后总结了这一求解方法目前所存在的问题和之后发展的方向。

1 基本原理

人体运动过程中，骨骼肌的收缩是由我们的神经系统进行控制的，当我们的大脑产生的运动指令经过脊柱中枢神经传递到骨骼肌时，骨骼肌开始收缩，与此同时，骨骼肌会产生一定的动作电位，该电位在皮肤表面表现即为肌电信号。

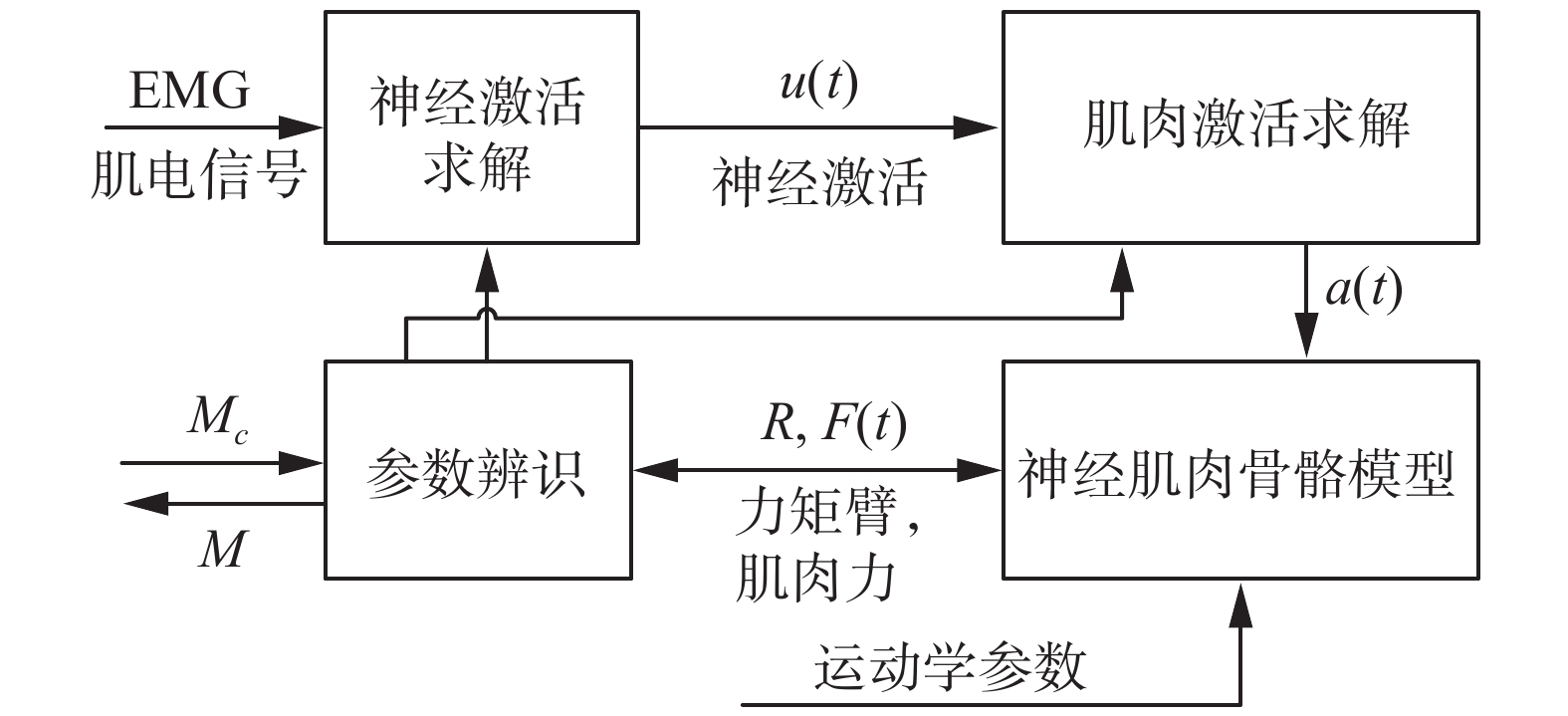
我们将通过表面电极获取的肌电信号进行一定的处理。之后利用神经激活模型求解神经激活u(t)。将u(t)代入到肌肉激活模型来求解肌肉受到神经信号后的肌肉激活程度a(t)，将其代入神经肌肉骨骼模型进而来计算肌肉力和关节力矩臂，进一步得到关节力矩M，之后根据实际测量关节力矩M_c，对整体肌肉骨骼模型的参数进行优化，最终得到准确的关节力矩。整个流程如图1所示。

2 神经激活求解

从对于肌肉骨骼模型的叙述可知，肌电信号是由神经信号刺激肌肉激活所产生的，因此肌电信号可以用来衡量肌肉激活及神经激活。然而其间的映射关系是高度非线性的，同时肌电信号的幅度也受诸多因素影响^[18]，(例如放大器的增益、所选用的电极类型、电极相对于肌肉运动点的位置、肌肉与电极之间的组织关系等)，所以很难直接利用肌电信号精准的计算和预测肌肉激活以及肌肉力。

为了从肌电信号中获取有效信息以求解关节力矩，必须滤除噪声，量化神经及肌肉的激活程度。为此，在求解肌肉激活和肌肉力之前，先要对肌电信号进行预处理，再将预处理后的肌电信号转化为神经激活u(t)。预处理过程可以描述为：1) 5~30 Hz高通滤波：由于放大器的精度不足或者电极相对肌肉发生串动会导致采集到的肌电信号的平均值产生时变的漂移，而这部分信号并不属于肌电信号，因此要消除这些由于采集误差导致的直流偏移或低频噪声。2)全波整流和归一化(除以最大自主收缩期间获得的峰值整流EMG值)处理^[19-20]。3)低通滤波：肌肉的电信号的频率成分超过了100 Hz，但是肌肉力的频率要比这低得多，因此为了使肌电信号和肌肉力量相关，滤除高频成分是非常重要的^{[12, 18, 21]}。4)求解神经激活：求取神经激活u的方法如下：

$u(t) = \alpha \times e\Bigg(t - \frac{d}{{{T_E}}}\Bigg) - {\beta _1} \times u(t - 1) - {\beta _2} \times u(t - 2)$

(1)

式中：u(t)为第t个采样点的神经激活；e为肌电信号； $\alpha{\text{、}}{\beta _1}{\text{、}}{\beta _2}$ 分别为神经激活系数；d为时间延迟； ${T_E}$ 为采样时间间隔。其中上述神经激活系数满足：

${\beta _1} = {\gamma _1} + {\gamma _2}(\left| {{\gamma _1}} \right| < 1;\left| {{\gamma _2}} \right| < 1)$

(2)

${\beta _2} = {\gamma _1} \cdot {\gamma _2}\left( {\left| {{\gamma _1}} \right| < 1;\left| {{\gamma _2}} \right| < 1} \right)$

(3)

$\alpha - {\beta _1} - {\beta _2} = 1$

(4)

3 肌肉激活求解

从肌电信号得到神经激活后，便可以对肌肉激活进行计算和估计。其具体过程为

$\left\{ \begin{array}{l} a(t) = d\ln (cu(t) + 1) ,\;\;\;\;\;0 \leqslant u(t) < 0.3\\ a(t) = mu(t) + b,\;\;\;\;\;\;\;\;\;\;\;\;0.3 \leqslant u(t) < 1 \end{array} \right.$

(5)

式中：u(t)是神经激活；a(t)是肌肉激活。肌肉激活系数c、d、m和b可以根据曲线过渡点及导数关系同时求解。一些学者又将进行了一定的化简^{[8, 22-23]}：

$a(t) = \frac{{{{\rm{e}}^{Au(t) - 1}}}}{{{{\rm{e}}^A} - 1}}$

(6)

其中，A(−3，0)是非线性因子。对于肌肉激活的求解还有一些方法主要如表1所示^[24]。

表1中列举的公式中Manal在文献[23]中提出的方法相对简便，求解的肌肉激活准确性较高，受到广泛的使用。Cavallaro在文献[25]中提出的方法是对Manal方法的简化，其中参数A₁是Manal方法中指数常数项的估计，这里会进一步引入误差，因此准确性较Manal方法低，至于Manal在文献[26]中提出的方法是针对于特定肌肉激活求解所提出的方法，该方法进一步提高了计算精度，但是相对比较繁琐，适用广泛性不强。至于Chadwich、Rengifo、Chadwick、Telen提出的方法为常微分方程，求解比其他方法繁琐，使用相对较少。

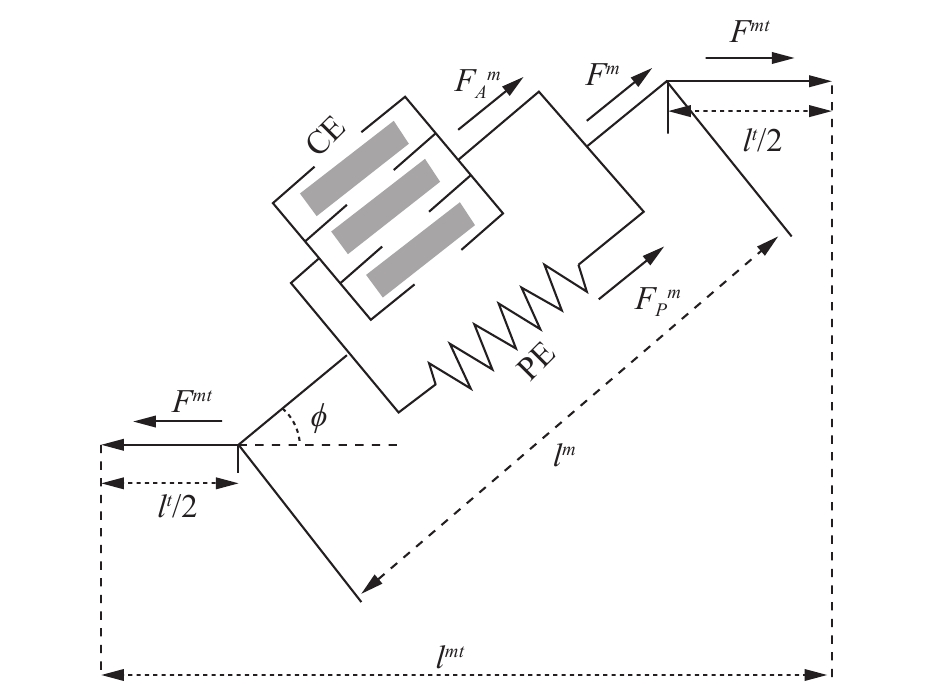
4 神经肌肉骨骼模型

在获得肌肉激活及相关人体运动学信息后，便可以利用肌肉骨骼模型对肌肉力以及关节力矩进行求解。肌肉骨骼模型如图2所示，其描述了肌肉肌腱的力的作用关系，其中用一个主动收缩单元CE和一个被动收缩单元PE来近似骨骼肌的工作情况。

整个模型对于骨骼肌力量的求解可以由式(7)进行表示：

$\begin{array}{c} \;\;{F^{mt}}(\theta,t) = {F^t} = [F_A^m + F_P^m]\cos\; \phi= \\ \;[{f_A}(l)f(v)a(t)F_o^m + {f_P}(l)F_o^m]\cos\; \phi \end{array}$

(7)

式中： ${F^t}$ 为肌腱力； $F_o^m$ 为最优肌肉纤维下肌肉力； ${f_A}(l)$ 为肌肉主动力−长度关系； ${f_P}(l)$ 为肌肉被动力−肌肉长度关系^[31]； $f(v)$ 为肌肉主动力−速度关系^{[12-13, 32]}。

4.1 肌肉力与肌肉纤维长度关系

根据肌肉骨骼模型来看，肌肉力的大小和肌肉纤维长度是有一定关系的，这里将这种关系分别描述为 ${f_A}(l)$ 和 ${f_P}(l)$ 。对于这两种肌肉力同肌肉纤维长度关系是非线性的，相关学者给出了这两种关系的描述形式。根据相关文献[18, 20, 32-34]主动收缩力同肌肉纤维长度的关系可以描述为

$\begin{array}{c} {f_A}(l) = \sin ({b_1} {l^2} + {b_2}l + {b_3})\\ ({b_1} = - 1.317,{b_2} = - 0.403,{b_3} = 2.454) \end{array}$

(8)

另外一种求解方式为

${f_A}(l) = \left\{ {\begin{array}{*{20}{l}} {{\delta _0} + {\delta _1}l + {\delta _2}{l^2}}&{0.5 \leqslant l \leqslant 1.5}\\ 0&{\text{其他}} \end{array}} \right.$

(9)

被动收缩力同肌肉纤维长度之间的关系可以表述为^{[32, 35]}

$\begin{array}{l} {f_P}(l) = {A_P} \cdot [{{\rm{e}}^{{K_{pe}}\frac{{{l^m} - l_o^m}}{{l_o^m}}}} - 1] \\ {A_P} = 0.129,{K_{pe}} = 4.525 \\ \end{array} $

(10)

可以简化为

${f_P}(l) = \frac{{{{\rm{e}}^{10(l - 1)}}}}{{{{\rm{e}}^5}}} = {{\rm{e}}^{10l - 15}}$

(11)

这里所提到的l即肌肉纤维长度是经过归一化之后的长度，即 $l = {{{l^m}} / {l_o^m}}$ ，式中的 ${l^m}$ 是指肌肉纤维长度， $l_o^m$ 是指最佳肌肉纤维长度，最佳纤维长度同肌肉激活度具有一定的关系，该关系可以描述为

$l_o^m(t) = {l_o}(\lambda (1 - a(t)) + 1)$

(12)

式中： $\lambda $ 为相关系数； ${l_o}$ 为在最大肌肉激活程度时的最佳肌肉纤维长度。

4.2 肌肉力与肌肉纤维收缩速度关系

肌肉力量的大小除了和肌肉纤维长度有关系外，它还受到肌肉纤维收缩速度的影响^{[12, 35-36]}。Hill在1938年建立肌肉骨骼模型最初是为了研究肌肉收缩和热量之间的关系^[17]，Hill通过实验发现，当肌肉缩短一个距离x时，伴随肌肉释放出一个收缩热量(H)，因此有

$H = ax$

(13)

式中：a是与肌肉横截面相关的热常数。同时Hill还推测 ${a / {F_o^m}}$ 是一个近似于0.25的常值， $F_o^m$ 是指在最佳纤维长度下的最大肌肉力。从能量守恒的角度考虑，总的能量消耗E等于肌肉耗散的热量和肌肉所做功的总和，即

$E = {F^m}x + H = ({F^m} + a)x$

(14)

等式右边对时间求导得

$({F^m} + a)\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = ({F^m} + a){v^m}$

(15)

式中： ${v^m}$ 为肌肉纤维收缩速度，之后Hill提出能量的消耗应当与力的变化成正比，于是有

$({F^m} + a){v^m} = b(F_o^m - {F^m})$

整理得

${F^m} = \frac{{F_o^mb - a{v^m}}}{{b + {v^m}}}$

(16)

到这里肌肉力和肌肉纤维收缩速度的关系是建立在最佳纤维长度的情况下的，没有考虑到纤维长度变化所带来的影响。下面给出变纤维长度的肌肉力和肌肉收缩速度之间的关系：

${F^m} = \Bigg(\frac{{F_o^mb - a{v^m}}}{{b + {v^m}}}\Bigg){f_A}(l)$

(17)

对于肌肉的舒张时的情况为

${F^m} = \Bigg(F_{{\rm{Ecc}}}^mF_o^m - (F_{{\rm{Ecc}}}^m - 1)\dfrac{{F_o^mb' + a'{v^m}}}{{b' - {v^m}}}\Bigg){f_A}(l)$

(18)

式中： $a'$ 和 $b'$ 是变心系数； $F_{Ecc}^m$ 是肌肉力的乘数，Epstein和Herzog在1998年提出其值在1.1~1.8之间^[37]。对上述肌肉力同速度的关系进行简化可得：

$\left\{ {\begin{array}{*{20}{l}} {f(v) = \dfrac{{0.3\Bigg[\dfrac{{{v^m}}}{{v_{\max }^m}} + 1\Bigg]}}{{ - \dfrac{{{v^m}}}{{v_{\max }^m}} + 0.3}}},&{\dfrac{{{v^m}}}{{v_{\max }^m}} < 0}\\ {f(v) = \dfrac{{2.34\dfrac{{{v^m}}}{{v_{\max }^m}} + 0.039}}{{1.3\dfrac{{{v^m}}}{{v_{\max }^m}} + 0.039}}},&{\dfrac{{{v^m}}}{{v_{\max }^m}} \geqslant 0} \end{array}} \right.$

(19)

其中 $v_{\max }^m$ 为最大肌肉收缩力。

4.3 肌腱力求解

求得肌肉激活之后，便可以利用肌肉激活对肌肉力 $F_i^m$ (i代表肌肉个数)进行求解。肌肉产生力量的同时，和它相连的肌腱也开始产生承载负荷，并将力从肌肉传递到骨骼，这个力称为肌腱力 ${F^t}$ 。因为肌腱与肌肉是串联的，所以任何通过肌肉的力也必须通过肌腱，反之亦然。肌腱是具有弹性的被动元件。在肌腱松弛长度 $l_s^t$ 以下，肌腱不承载任何负荷。然而，当肌腱束长度超过松弛长度时，它产生的力与拉伸距离成比例。当肌肉产生最大等距力 $F_o^m$ 时，肌腱的应变为3.3%，当力为3.5 $F_o^m$ 时，肌腱的应变为10%。肌腱束应变可定义为

$ {\varepsilon ^t} = \frac{{{l^t} - l_s^t}}{{l_s^t}} $

(20)

式中： $\varepsilon^t$ 为肌腱应变； $ {l^t} $ 为肌腱长度； $ l_s^t $ 为肌腱松弛长度

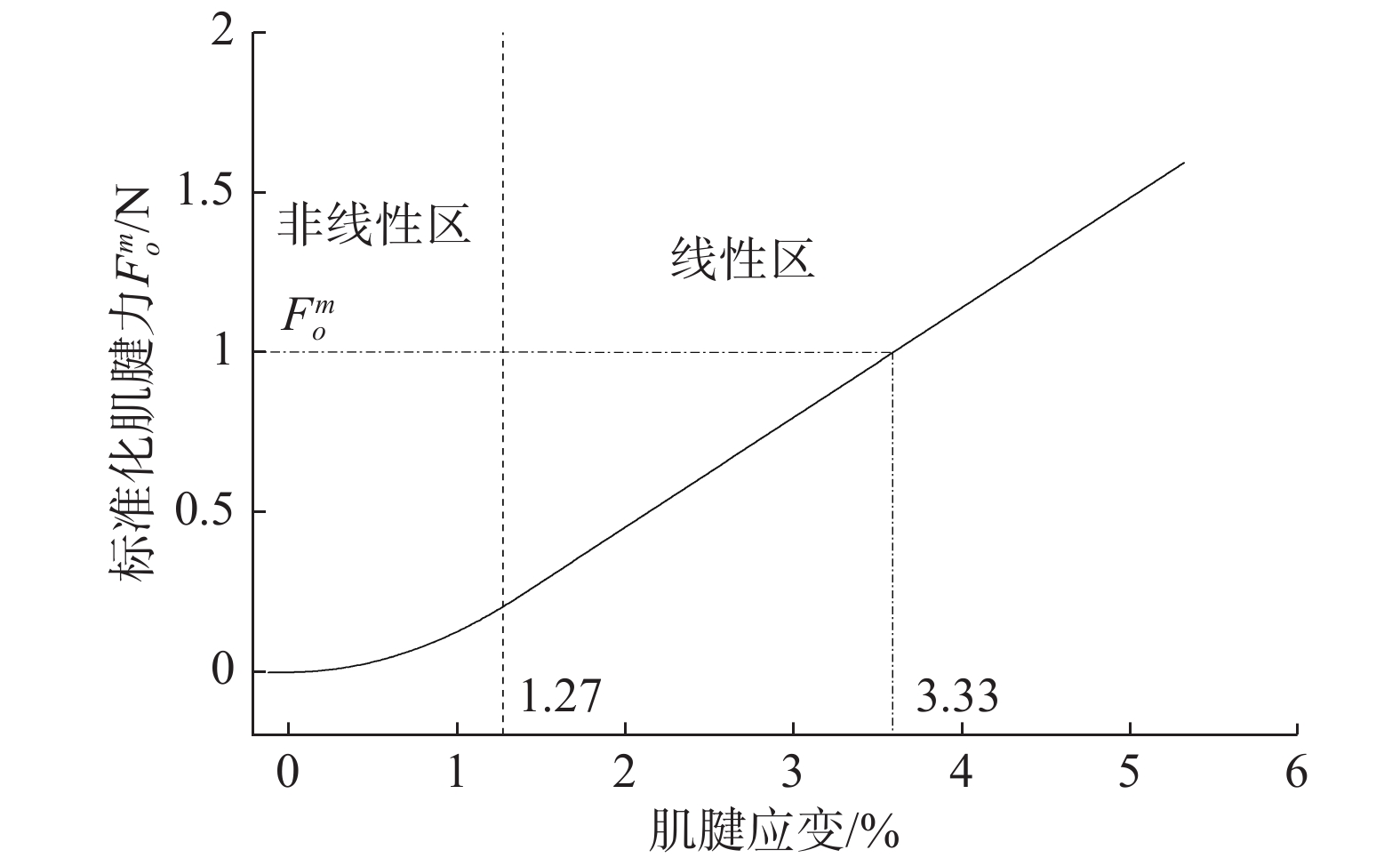
这里值得注意的是，肌腱应变不会为负值，由式(20)可以看到，只有当肌腱束长度大于肌腱束松弛长度时，力才会随应变变化，否则肌腱束力为零。肌腱应变与肌腱力的变化关系由式(21)及图3所示。

${F^t} = \left\{ {\begin{array}{*{20}{l}} 0,\qquad {\varepsilon \leqslant 0}\\ {1\;480.3{\varepsilon ^2}},&{0 < \varepsilon < 0.012\;7}\\ {37.5\varepsilon - 0.237\;5},&{\varepsilon \geqslant 0.012\;7} \end{array}} \right.$

(21)

4.4 羽状角求解

如图2所示，由于肌腱与肌肉纤维串联，肌腱力F^t和肌肉力F^m存在下述关系：

$ {F^t} = {F^m}\cos \;\phi $

(22)

其中， $\phi $ 是羽状角，即肌腱和肌肉纤维之间的角度，对于大多数的肌肉，羽状角对于肌肉力的影响是可以忽略不计的，但是对于一些转动角度大的关节骨骼肌，羽状角对其力的大小还是有很大影响的。

羽状角的大小随关节的活动及肌肉的收缩而变化。KAWAKAMI Y等^[38]在1998年利用超声波发现，内侧腓肠肌羽状角可根据关节角度和肌肉激活量从22°变为67°。虽然有一些简单的模型描述了羽状角随肌肉激活的变化，但很少有人通过体内成像研究(如超声)来证实这些变化。通过对动物肌肉的研究，一些研究人员已经提出了相对比较复杂的模型^[39](如Woittiez等)和一些简化的模型^[40](Scott&Winter)。为便于计算，利用简化模型来预测收缩肌肉的摆动角度，记采样点为t时的羽状角为 $\phi (t)$ ，其求解方程为

$\phi (t) = {\sin ^{ - 1}}\Bigg(\frac{{l_o^m\sin {\phi _0}}}{{{l^m}(t)}}\Bigg)$

(23)

式中 ${\phi _o}$ 为肌肉最佳纤维长度时的羽状角。

4.5 肌肉肌腱长度

从上文对于肌肉肌腱力的论述来看，对于肌肉力的求解来说，肌腱长度的大小的求解是至关重要的，其值可以根据式(24)得到：

${l^{mt}} = {l^t} + {l^m}\cos \;\phi $

(24)

即

${l^t} = {l^{mt}} - {l^m}\cos \;\phi $

(25)

从式(21)和式(25)可以看出，肌肉肌腱长度对于求解肌腱长度和肌腱力是必不可少的，但是肌肉肌腱长度属于人体生物参数，求解较为困难。Menegaldo等^[41]在2004年提出了一种用于计算下肢肌肉肌腱长度和关键力矩臂的方法。其研究参照了Delp等^[42-43]提出的生理模型所求出的生理学参数。其具体的计算方法如下：

$\begin{array}{c} L({Q_1},{Q_2},{Q_3},{Q_4}) = {a_1} + {a_2}{f_1}({Q_1},{Q_2},{Q_3},{Q_4}) +\\ {a_3}{f_2}({Q_1},{Q_2},{Q_3},{Q_4}) + \cdots + {a_n}{f_{n - 1}}({Q_1},{Q_2},{Q_3},{Q_4}) \end{array}$

(26)

式中：L表示肌肉肌腱长度；a_i表示为待定系数；f_i是指泛型非线性系数，根据拟合曲面的形状进行选择。而 ${Q_1}{\text{、}}{Q_2}{\text{、}}{Q_3}{\text{、}}{Q_4} $ 等则是根据Delp模型所假设的关节角度数。之后利用测定的关节角度信息，进行拟合求解的方式即可求出相应的肌肉肌腱长度。另一种较为简便的拟合求解方式为

${l^{mt}} = {b_0} + {b_1} \theta $

(27)

式中：b₀和b₁是待定参数；θ为关节角度，可以使用惯性传感器或光学动捕等方式进行测得。

4.6 肌肉力整合求解

通过对整个过程的论述，在这里重新讨论最初给定的式(7)，这时式中的大部分未知量已经在上述内容给出了求解方法，然而现在依然不能依靠式(7)直接给出对于肌肉力量的一个估计，因为肌肉纤维长度的大小并不知道。

$\begin{gathered} {F^{mt}}(\theta ,t) = {F^t} = [F_A^m + F_P^m]\cos \phi = \hfill \\ [{f_A}(l)f(v)a(t)F_o^m + {f_P}(l)F_o^m]\cos \;\phi \hfill \\ \end{gathered} $

对于肌肉纤维长度的求解需要用到数值积分的方法，因此这里首先根据上述方程(7)进行对肌肉力−肌肉收缩速度关系进行求解：

$f(v) = \frac{{{F^t} - f_p^lF_o^m\cos \;\phi }}{{{f_A}(l)a(t)F_o^m\cos \;\phi }}$

(28)

在设定一个初始的肌肉纤维长度后，便可根据式(8)~(11)求出肌肉力和肌肉纤维长度的关系；根据式(12)和(23)可以对羽状角进行相应的估计，又可以根据式(28)求出肌肉力−肌肉收缩速度关系，之后根据式(19)得到肌肉纤维速度，这时候利用数值积分的方法可以推出下一采样点的肌肉纤维长度。将该时刻的肌肉纤维长度以及关节角度代入到式(24)和(26)后，可以求得此时的肌腱长度，再利用式(20)和(21)未求出该时刻的F^t，再代入到式(7)，进行下一步的计算，不断重复此过程，最终得到测试时间段的肌肉力。

4.7 关节力矩求解

${M^j}(\theta,t) = \sum\limits_{i = 1}^m {({r_i}(\theta ) \cdot F_i^{mt}(\theta,t))} $

(29)

式中： ${M^j}\left( {\theta,t} \right)$ 代表关节j在关节角度为θ，采样时刻为t时的关节力矩， ${r_i}\left( \theta \right)$ 为第i块骨骼肌对关节j在关节角度为θ时的关节力矩臂， $F_i^{mt}\left( {\theta,t} \right)$ 为第i块骨骼肌对关节j在关节角度为θ时的肌肉力，其中对于力矩臂的求解可见式(30)：

$r(\theta ) = \frac{{\partial {l^{mt}}(\theta )}}{{\partial \theta }}$

(30)

5 参数辨识

如上所述，d、γ₁、γ₂、A是求解肌肉激活的4个主要参数，假设所有参与的肌肉都具有相同的肌肉激活求解过程。因此，只需要调整4个激活参数。在肌肉肌腱力求解过程中， $F_o^m$ 、 $l_o^m$ 、 $l_s^t$ 、 $v_{{\rm{max}}}^m$ 、 $\phi$ 是5个反映肌肉力大小的生理学参数，而在这些参数中 $F_o^m$ 、 $l_o^m$ 、 $l_s^t$ 对肌肉力的影响更为显著^[44-45]，由于 $v_{{\rm{max}}}^m$ 对整体肌肉力的影响较小，可以近似表示为 $v_{{\rm{max}}}^m = 10l_o^m$ 。由于不同肌肉的这3个参数差别较大，因此每增加一块肌肉就需要求解3个参数，诸多的参数使得整个过程变得更加繁琐，因此对参数进行优化和化简的工作就显得尤为重要。

Ai等^[46]进行了两组优化，第1组根据受试者特定的肌肉骨骼几何模型进行估计；第2组采用通用的肌肉骨骼模型。之后将两组原始肌电信号和运动学数据都输入到优化模型(非线性最小二乘和levenberg-marquardt算法)中，使得估计力矩和参考力矩差值最小。Menegaldo等^[47]采用式(31)对参数进行优化评价指标：

${\rm{RMSE}} = \dfrac{1}{{{\rm{T}}{{\rm{M}}_{{\rm{MAX}}}}}}\sqrt {\frac{{\displaystyle\sum\limits_{t = 1}^N {{{({\rm{TM}}(t) - {\rm{TS}}(t))}^2}} }}{N}} \times 100{{\% }}$

(31)

式中： ${\rm{TM}}\left( t \right)$ 是用CybexTM测量的力矩；TS(t)是预测力矩。Qashqai等^[48]也使用了类似的目标函数对模型进行了优化。

Li等^[49]采用遗传算法对未知生理参数进行优化，优化目标函数为

$\min \sum\limits_{i = 1}^n {{{({\theta _{ci}} - {\theta _{mi}})}^2}} $

式中：θ_ci为实际测量关节角度；θ_mi为模型预测关节角度,这里其使用正向动力学方法，利用预测的关节力矩进一步地求解运动学信息。遗传算法初始种群在优化过程中进化，其参考了文献[50-51]中的结果，减少了搜索空间，提高了优化速度，并通过模型参数辨识，得到最接近实际关节角的最优模型参数值，再通过实验结果得到均方根误差进而提高精度。Son等^[52]采用混合正逆动力学方法对参数进行调整，即假设肌电驱动模型估计的关节力矩近似等于测试得到的关节力矩：

$\min \sum\limits_{t = 1}^n {\Bigg({M_t} - \sum\limits_{j = 1}^m {{r_{tj}} \cdot {F_{kj}}} \Bigg)} $

式中：M_k为采样点k时的测定力矩；r_kj为j肌肉在k采样点时刻的力矩臂；F_kj为j肌肉在k采样点时的肌肉力。Buongiorno D等^[53]做了关于遗传算法(基于Genocop Ⅲ的有约束和无约束算法^[54])和线性优化方法(线性最小二乘)的对比研究工作。

为了能够为之后的相关研究提供一些帮助，这里根据文献[20, 51, 53-61]列出了一些常用肌肉的生理参数，如表2。

6 主要应用

表面肌电信号和肌肉骨骼模型主要应用于医学和运动学等方面，这种方法能够帮助人们更好地理解人体运动和人体在进行运动时力矩信息^[62-63]。现阶段基于EMG的神经肌肉骨骼模型已经被用于估计人体多处关节的力矩，神经肌肉骨骼模型的应用如表3所示。

随着其他学科的不断发展和人们对于进一步理解人类运动意图的需要，该方法又在一些机械运动控制、外骨骼控制等方面得到了应用^{[23, 64-66]}。同时，在体育运动中对运动员的肌肉力量进行分析^[67-68]、康复医学中使用该方法对一些瘫痪患者进行肌肉康复训练^{[46, 69]}、人体假肢依靠肌电信号进行控制，使得假肢能够根据人类意图去辅助患者，以及关节疾病等领域也广泛应用了这种方法^[70]。在未来，由于人机合作的需求不断加大，这种分析人体运动内力的方法将会得到更加广泛的应用。

7 结束语

肌电信号作为一种可方便获取的人体信号，受到了越来越多学者的关注，利用其对关节力矩进行求解可以充分了解人体运动时肌肉骨骼力学特性。本文结合了大量文献给出了利用肌电信号对关节力矩进行求解的方法和基础模型的综合性论述。目前该方法依然存在着一些问题。

肌电信号方面：1)作为模型的输入信号，肌电信号具有高变异性；2)测得的信号为多肌肉信号融合信号，受噪声干扰严重；3)在利用其求解肌肉激活的过程中，映射关系难以得到正确性的评价；4)目前这种映射关系并没有考虑到运动过程中肌肉疲劳对于肌肉活性的影响；5)肌电信号采集设备相对复杂，对应用环境依赖性较强，难以得到广泛的实际应用。

神经肌肉骨骼模型方面：1)生理参数较多，优化求解过程繁琐，求解过程复杂，难以评价中间变量的求解正确性，误差会随着过程不断积累；2)利用神经肌肉骨骼模型控制相关人机交互设备，难以实现实时控制的目标，且不易解决个体差异性问题；3)模型中神经激活和肌肉激活的时间序列以及时间延迟难以准确估计。

在未来对于使用肌电信号求解关节力矩技术研究时，需关注以下可实现技术突破的研究点。

1)提升肌电信号采集设备准确性和稳定性。肌电信号作为整体的输入信号，其获取精度的提升会在大程度上提高估计的关节力矩的准确性。减少肌电信号融合对于最终结果的影响，提高肌电传感器采集位置的容错性。

2)简化模型计算过程及优化参数，提高整体计算模型的鲁棒性。给出对于确定模型参数最为有利的矫正动作，同时寻找一种能够实现实时计算的方法，对于利用肌电信号求解关节力矩这一方法的实时应用以及减小计算内存和累计误差十分重要。提高模型参数的泛化能力，减少优化过程，进而解决个体差异问题对于人机交互设备的发展具有深远意义。

3)给出单肌肉对于肌肉关节力矩的影响关系，减少测量肌肉数量，可以减少整体模型的参数。同时给出肌肉疲劳对于整个模型的计算结果的影响，可以更加深层次地理解肌电信号同肌肉力之间的关系。