近年来，以深度学习(deep learning，DL)为核心的智能技术取得了长足的进步^[1]，特别是以深度强化学习(deep reinforcement learning，DRL)为代表的智能方法在解决雅达利游戏、棋类博弈对抗、即时策略游戏(real-time strategy, RTS)等决策问题上取得了众多超越人类水平的成果^[2-6]，使得面向自主认知的智能决策有望得到进一步发展，并取得关键性突破。强化学习(reinforcement learning，RL)作为解决序贯决策问题的重要方法^[5]，其通过与环境的交互试错来学习策略，恰好契合了人类的经验学习和决策思维方式，可以有效解决样本数据获取难等问题。而单Agent系统无法实现多个决策者之间的相互协作或竞争关系，往往需要多智能体通过协作来求解。多智能体系统(multi-agent system, MAS)是当前分布式AI领域的研究热点，其主要是通过研究Agent之间的协同和交互问题，用以解决复杂实时动态多智能体环境下的任务调度、资源分配、行为协调以及冲突消解等协同问题，但是多智能体会导致动作空间和状态空间呈指数级增长，带来维度灾难问题^[7]。分层强化学习(hierarchical reinforcement learning，HRL)采用问题分解并分而治之的思想，是解决大规模强化学习的潜在有效途径^[8]。因此，研究基于三者相结合的多智能体分层强化学习(multi-agent hierarchical reinforcement learning，MAHRL)使解决未知大规模复杂环境下的智能决策问题成为可能。

作为解决复杂空间下协同决策的重要途径，目前MAHRL技术已经在机器人控制、博弈决策、任务规划等领域中得到了大量的研究。本文对MAHRL的研究现状和相关应用进行了阐述和探讨。

1 预备知识 1.1 强化学习

关于机器学习的研究可以分为3个方向，即有监督学习、无监督学习和强化学习^[9]。其中强化学习的核心思想是通过Agent与环境的不断交互，以最大化累计回报为目标来选择合理的行动，这与人类智能中经验知识获取和决策过程不谋而合^[10]。特别是近年来深度强化学习在以AlphaGo、AlphaZero、AlphaStar等为代表的机器智能领域的突破^[11]，进一步展现了强化学习在解决复杂决策问题的能力，成为人工智能研究领域的热点。

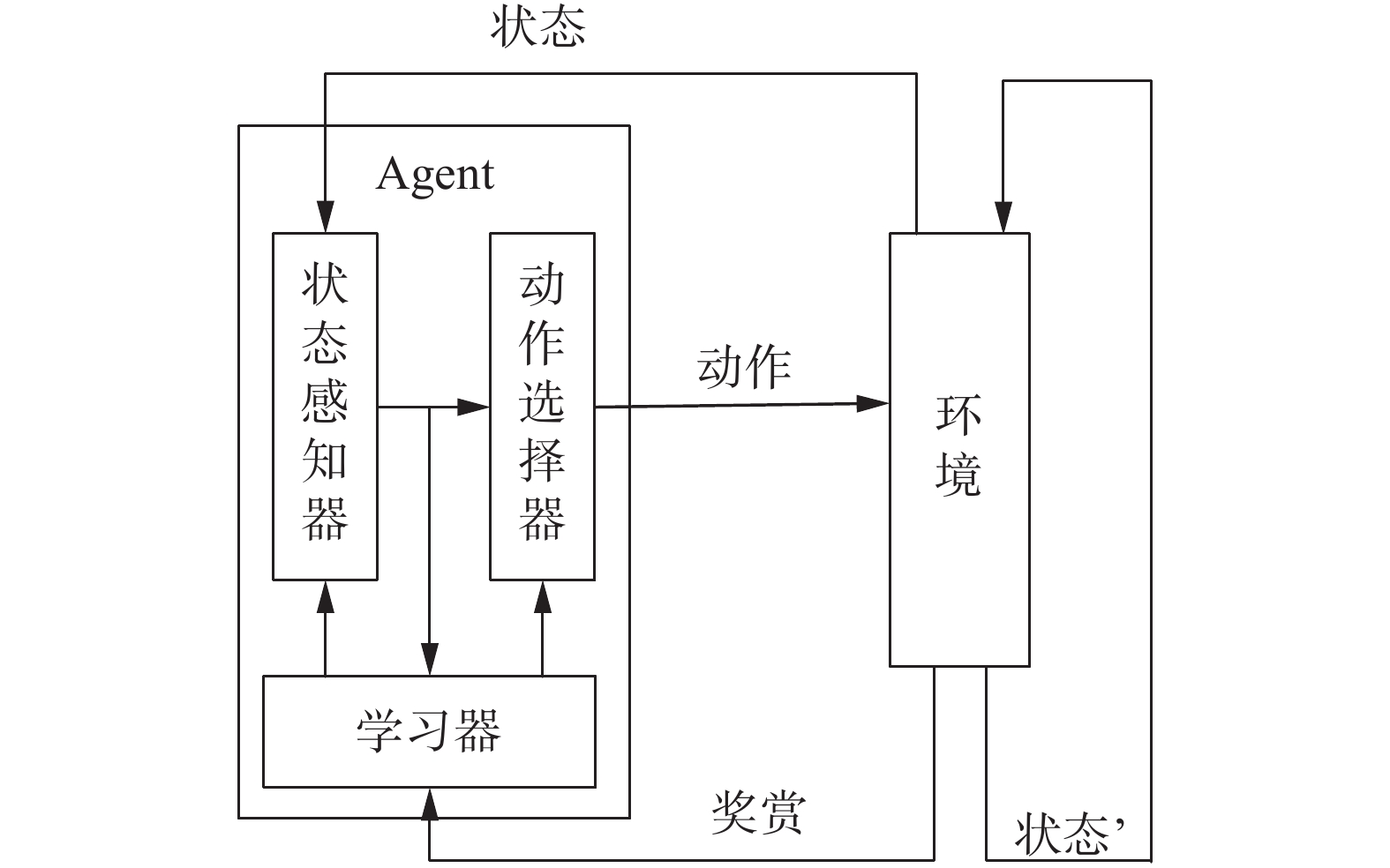
如图1所示，强化学习的架构主要包括Agent和环境两部分，Agent首先对环境状态进行感知，然后决定选择采取的动作。

Agent的动作会对环境产生影响，其环境状态也会发生变化，此时Agent会收到来自环境的反馈信号，分别用正负反馈表示这个动作对学习目标是否有益^[12]。Agent则通过不断地试错和反馈来不断优化动作选择策略，最终学习到一个有目标导向的策略。

根据环境模型是否已知，强化学习可分为有模型强化学习和无模型强化学习^[5]。若已知环境状态在智能体动作影响之下的转移规律和反馈，即状态转移概率函数和奖赏函数已知，则称为有模型强化学习，否则便是无模型强化学习。

有模型强化学习主要基于动态规划的思想，采用Bellman方程和Bellman最优方程进行策略迭代和值迭代。无模型强化学习则是基于采样的方式与环境进行交互学习，当前主要研究的方法可以分为3类：基于值函数的强化学习方法、基于策略搜索的强化学习方法和基于环境建模的强化学习方法。

1)基于值函数的强化学习。其核心思想是采用函数近似的方法将强化学习模型中的状态值函数、状态动作值函数或策略函数用一个显性的函数来表示，常用的近似函数有线性函数近似、决策树近似、核函数近似和神经网络等。其中深度神经网络是近年来在强化学习值函数近似方面应用最为广泛和成功的函数。其中,最为典型的应用开始于2013年DeepMind团队在NIPS上提出的DQN(deep Q-networks)算法^[6]，其基于值函数的泛化逼近方法，有效解决了强化学习的“维数灾难问题”，但在Q函数逼近过程中存在不稳定的现象。为解决部分可观察的马尔可夫决策问题，Hausknecht等^[13]提出了基于循环神经网络与强化学习相结合的DRQN算法，在实验环境中取得了远优于DQN算法的效果。典型的值函数近似方法还有DDQN^[14]、Sarsa^[15]、Q-learning^[16]等时序差分的强化学习算法，它们虽然在某些实际问题中取得了不错的效果，但其难以求解动作空间比较大和随机性策略问题，以及无法对连续动作空间问题进行建模等。

2)基于策略搜索的强化学习。其核心思想是将策略参数化，通过不断修正策略的参数求解最优策略。Silver等^[17]结合Actor-Critic框架和Q-learning算法提出了确定性策略梯度算法(deterministic policy gradient algorithms, DPG)，其将策略定义为一个确定性的策略函数，这样在训练模型时，就不需要考虑动作空间的大小或是否连续，能够提升连续动作空间问题求解中对于梯度的估计效率和准确性。针对经验回放的深度强化学习方法存在对内存和计算能力要求较高的问题，Mnih等^[18]提出了异步梯度下降的深度Actor-Critic框架，用于并行执行多个智能体用于神经网络控制器的优化，并与单步Q-learning、Sarsa、多步Q-learning和Actor-Critic等强化学习算法结合实现了对深度神经网络的训练，并取得了更好的效果。除此之外还有可信赖域策略搜索算法TRPO^[19] 、价值梯度SVG^[20]、引导策略搜索算法GPS^[21]、近端策略优化算法PPO^[22]和广义优势估计算法GAE^[23]随机等几种典型的基于策略梯度的方法。

3)基于环境建模的强化学习。其核心思想是通过建立环境模型来产生模拟经验样本。对于某些智能体与环境的交互成本较高的情况，而基于环境建模的强化学习通过建立环境模型来模拟经验样本，可以减少采样次数，或者无需在真实环境中进行采样。Sutton^[24]提出的Dyna框架是一种典型的基于环境建模的强化学习。其基本思想是利用与真实环境产生的经验样本来进行环境模型的学习，而值函数或者策略函数的学习与更新则基于真实样本和环境模型产生的虚拟样本。虽然Dyna框架能基于真实样本来进行环境模型学习，并取得了不错的效果，但其环境模型的建立和真实经验样本和虚拟样本的权衡仍然是制约该方法发展的关键难点。

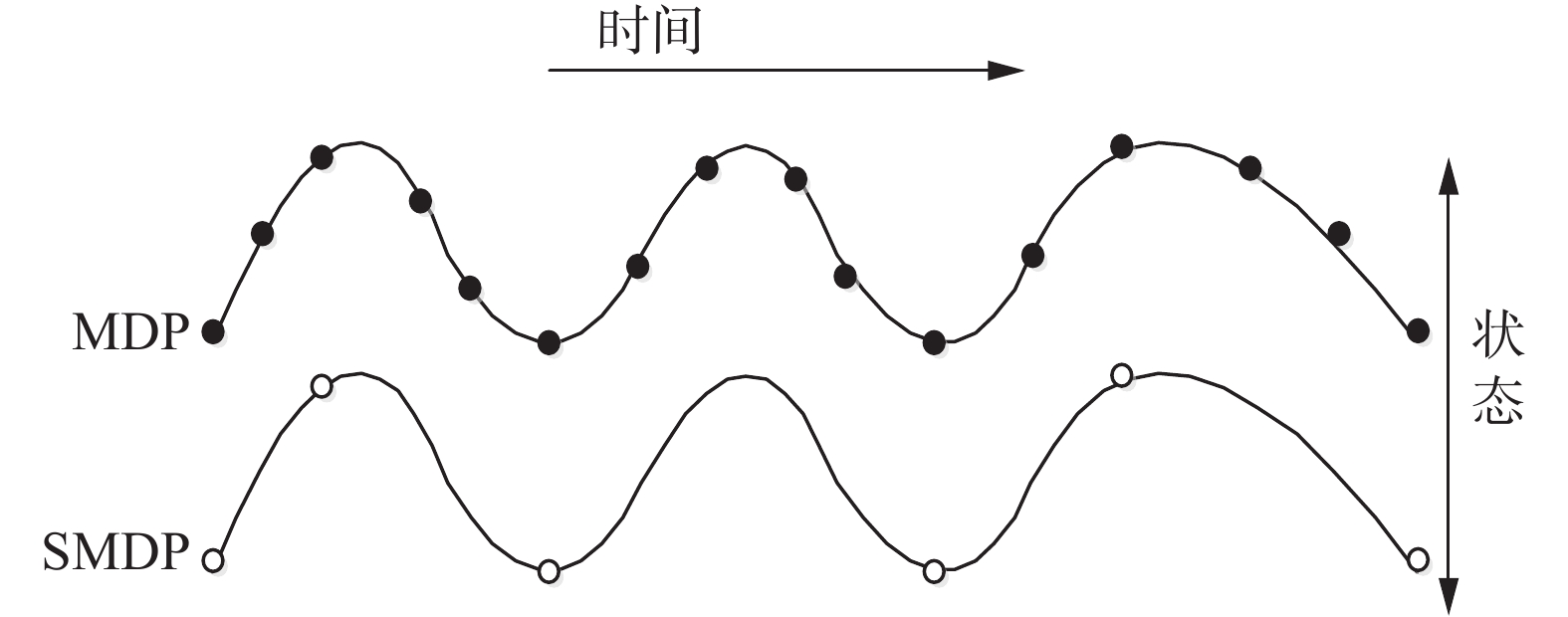
1.2 半马尔可夫决策过程

分层强化学习采用策略分层并分而治之的思想，可以有效解决维度灾难问题。策略分层的本质是基于不同的时间抽象尺度扩展动作集，即基本动作和宏动作，而Agent通过在不同程度的时间抽象尺度上进行学习，进而实现分层控制。而在马尔可夫决策过程(Markov decision process, MDP)中，每个动作都是假设在单个时间步完成，并没有考虑决策的时间间隔，所以基于MDP的强化学习无法解决需要多个时间步完成的动作^[25]，此时就需要引入半马尔可夫决策过程(semi Markov decision process, SMDP)模型，如图2所示。

图2中离散的SMDP其实是MDP的一般化过程，即MDP中在状态 $ s $ 下执行一个动作需要花费的时间步长为固定的单位时间，而在SMDP中为变量^[26]。设N表示时间步长，则标准MDP的概率转移函数和期望报酬可以被扩展为 $ P\left({s}',N|s,a\right) $ 和 $ R\left({s}',N|s,a\right) $ 。根据Bellman方程，可以得到确定策略 $ \pi $ 下的值函数为Agent执行动作 $ a $ 的立即报酬与转移到后续状态 $ {s}' $ 的折扣累积期望之和，如式(1)所示：

$\begin{array}{c} {V^\pi }\left( s \right) = \bar R\left( {s,\pi \left( s \right)} \right) + \\ \displaystyle\sum \nolimits_{s',N} P(s',N|s,\pi \left( s \right)){\gamma ^N}{V^\pi }\left( {s'} \right) \end{array}$

(1)

式中： $\bar R\left( {s,\pi \left( s \right)} \right)$ 是Agent在状态 $ s $ 下执行动作 $ \pi \left(s\right) $ 后的期望报酬，不难看出，其整体期望报酬与 $ {s}'{\text{、}}N $ 均相关。

1.3 多智能体强化学习

面对大规模复杂背景下决策问题时，单Agent系统无法实现多个决策者之间存在相互协作或竞争的关系。因此，在DRL模型基础上扩展为多个Agent之间相互合作、通信及竞争的多Agent系统，即多智能体强化学习(multi-agent reinforcement learning, MARL)。多智能体强化学习示意如图3。

目前关于MARL的研究可以包括2个方面。

1)多智能体系统研究。当前多智能体系统研究主要从体系结构、Agent信息交互方式和Agent冲突消解机制3个方面展开。①体系结构研究：主要围绕集中式和分散式2种展开研究。其中分散式又可以区分为层面式(distributed)与分层式(hierarchical)^[7]。除了基本的分层方式，多智能体体系结构研究还包括智能体协同和任务分配机制等。②智能体之间信息交互方式研究：目前主要有Agent直接通信、信道广播方式、信息黑板模式等方法。③智能体间冲突消解研究：多智能体系统中冲突矛盾主要包括空间冲突、信息冲突和任务冲突等。当前消解矛盾方法主要包括集中控制模块法和主从控制法2种。集中控制模块法通过构建模块来集中规划所有Agent的行动策略，但是会带来通信阻塞问题。主从控制法是指通过一个中心智能体来统一进行任务分配和行为规划来解决智能体之间的矛盾问题，但由于实时性和灾难空间等问题，其适应性和鲁棒性有待提升。

2)多智能体强化学习策略研究。目前MARL的学习策略主要可以分为3类：基于共享、基于对策和基于最佳响应的多智能体强化学习。①基于共享的MARL：其主要思想是研究动作选择前Agent之间的相互交互、信息共享以及值函数更新方法，基于分布式强化学习提高学习速度，典型算法有状态共享、经验共享、策略共享和建议共享等。②基于对策的MARL：其主要思想是以对策论为基础，综合考虑所有Agent的值函数，寻求某种对策下的平衡来选择动作，代表算法有Minimax-Q、Nash-Q、WoLF、CE-Q等。③基于最佳响应的MARL：其主要思想是在其他Agent无论采取何种策略情况下寻求最优策略，算法主要依赖于收敛准则和无憾准则，典型算法有PHC、IGA、GIGA、GIGA-WoLF等。

2 多智能体分层强化学习方法

基于强化学习的智能决策面临的瓶颈之一是奖赏延时，如果以最终目标为导向来优化策略，其带来的维数灾难问题会使算法效率非常低^[27]。同时由于单Agent系统无法实现多个决策者之间存在相互协作或竞争关系，这就需要引入多智能体，然而多智能体的参与又会带来维度灾难等问题。HRL基于任务分层来学习每个子任务的策略，并将多个子任务的策略组合形成有效的全局策略，可以有效解决维数灾难问题^[28]。

MAHRL是MARL和HRL相结合的结果。二者结合有两种思路：一是基于分层来解决MARL问题，二是采用多智能体解决HRL问题，所以现有MAHRL可根据采用的HRL方法或者MARL方法等不同角度进行分类。由于目前的研究多集中于前者，本文从分层强化学习的角度对多智能体分层强化学习方法进行探讨，即基于选项(option)、基于分层抽象机(hierarchical of abstract machines，HAM)、基于值函数分解(MaxQ value function decomposition)和基于端到端的(end to end)多智能体分层强化学习。

2.1 基于选项的多智能体分层强化学习

基于选项的多智能体分层强化学习主要是采用Option分层强化学习方法来解决多智能体强化学习问题。Option是一种典型的分层强化学习方法，其最早由Sutton提出^[28]，主要思想是基于选项(Option)的学习任务抽象，其中Option本质上为在某状态子空间里完成相应子任务的动作序列。其中Option本身也视作为一种特殊的动作，并与基本动作共同构成动作集，通过上下层Option间的调用形成分层控制结构。其中Option根据先验知识提前确定或者通过学习获得。根据是基于马尔可夫或者是半马尔可夫，Option方法又可以分为两类：基于马尔可夫决策过程的Markov-Option和基于半马尔可夫决策过程的Semi-Markov-Option。

Markov-Option $ <\varphi ,\pi ,\beta > $ 三元组分别代表Option的入口状态集、内部策略和终止条件。Option开始执行的前提条件是当前状态属于入口状态集，即 $ s\subseteq \varphi $ ，其中入口状态集 $ \varphi \subseteq S $ 。内部策略 $ \pi $ 一般表示为 $ \pi :\varphi \times {A}_{\varphi }\to \left[\mathrm{0,1}\right] $ ，其中 $ {A}_{\varphi } $ 为在入口状态集 $ \varphi $ 上能够执行的基本动作集。终止条件 $ \beta $ 为基于状态 $ {s}' $ 终止的概率集合 $ \beta \left({s}'\right) $ ，一般表示为 $ \beta :S\to \left[\mathrm{0,1}\right] $ 。因此 $ \; \beta \left({s}_{G}\right)=1 $ 一般作为Option任务的子目标状态点 $ {s}_{G} $ 的终止条件，同时 $ {A}_{\varphi } $ 可以视为Markov-Option的一种特例。

Semi-Markov-Option $ <\varphi ,\mu ,\beta > $ 三元组含义类似。同样其Option开始执行的前提条件 $ s\subseteq \varphi $ ，其中入口状态集 $ \varphi \subseteq S $ ，且其只能包含该Option可能探索到的所有状态。内部策略为 $ \mu :\varphi \times {O}_{\varphi }\to \left[\mathrm{0,1}\right] $ ，其中 $ {O}_{\varphi } $ 为在入口状态集 $ \varphi $ 上能够执行的基本动作集。终止条件 $ \beta $ 为基于状态 $ {s}' $ 终止的概率集合 $ \beta \left({s}'\right) $ ，而 $ \beta \left({s}_{G}\right)=1 $ 通常也是Option任务的子目标状态点 $ {s}_{G} $ 的终止条件。

针对Option强化学习问题，Precup等^[29]提出了一种基于多时间步模型的单步模型泛化方法。对于任意Option o，设 $ \varepsilon (o,s,t) $ 表示在t时刻、状态s下o被启动，则状态s下Option o获得的累计奖赏 $ R(s,o) $ 和状态转移概率 $ P\left({s}'\right|s,o) $ 可重新定义为

$\begin{array}{c} \;\;\;\;\;\;\;\;\;\;\;R\left( {s,o} \right) = \\ E\left\{ {{r_t} + \gamma {r_{t + 1}} + \cdots + {\gamma ^{\tau - 1}}{r_{t + \tau - 1}}|\varepsilon (o,s,t)} \right\} \end{array}$

(2)

和

$P\left( {s'|s,o} \right) = \sum\limits_{\tau = 1}^\infty {{\gamma ^\tau }} P(s',\tau )$

(3)

式中： $ \tau $ 为Option o持续的总时间步，对于所有状态 $ s\in S $ ， $ P({s}',\tau ) $ 为Option o从状态 $ s $ 开始经过 $ \tau $ 个时间步后终止于状态 $ {s}' $ 的概率。

此时Q-Learning的值函数迭代公式为

$\begin{array}{l} {Q_{k + 1}}\left( {s,o} \right) = \left( {1 - {\alpha _k}} \right){Q_k}\left( {s,o} \right) + \\ \;\;\;\;{\alpha _k}\left[ {r + {\gamma ^\tau }{\rm{ma}}{{\rm{x}}_{o' \in {O_{s'}}}}{Q_k}(s',o')} \right] \end{array}$

(4)

Agent的每次学习执行都是以一个Option终止为前提，故造成其利用率不高，为此Precup^[30]基于Markov-Option提出了一种面向单时间步Q-Learning的Option方法，并证明了其收敛性。Tang等^[31]则针对StarCraft游戏问题，根据作战规则不同，作战要素和动作空间组合不同设计101种输入特征向量选项，实现了订单生产的强化学习。

综上可知，基于选项的MAHRL本质上是基于状态空间，不断寻找子目标的学习过程，其可执行时态拓展动作的特点对强化学习摆动期的缩短和效率提高均有一定的促进作用，但是由于其是基于先验知识确定学习与任务之间的转移，所以基于选项的分层强化学习在未知环境中的适用性还有待提高。

2.2 基于分层抽象的多智能体分层强化学习

基于分层抽象的多智能体分层强化学习主要采用HAM^[32]分层强化学习方法来解决多智能体强化学习问题。其核心思想是将每个子任务抽象为一个基于MDP的随机有限状态机，综合考虑当前所在状态和有限状态机的状态来选择不同的策略。令 $ M=<S,A,R,P> $ 为一个有限MDP，S和A分别为状态集合和动作集合, $ R:S\times A\to r $ 为奖赏函数， $ P:S\times A\to P\left(S\right) $ 为状态转移函数。 $ \left\{{H}_{i}\right\} $ 为一个随机有限状态机的集合，其中 $ {H}_{i}=<{S}_{i},{\delta }_{i},{\varphi }_{i}> $ , $ {S}_{i} $ 、 $ {\delta }_{i} $ 、 $ {\varphi }_{i} $ 分别为 $ {H}_{i} $ 的状态集、随机转移函数和用于确定 $ {H}_{i} $ 初始状态的随机函数。

对于每个状态机，其均包含4种状态类型，即动作(action)、调用(cal1)、选择(choice)以及停止(stop)。其中在action状态时，会根据状态机的当前状态执行一个MDP中的动作；在call类型的状态时，会暂停当前的状态机 $ {H}_{i} $ ，并启动执行另一个状态机 $ {H}_{j} $ ，即把 $ {H}_{j} $ 的状态设置为 $ {\varphi }_{i}\left({s}_{t}\right) $ ，其中 $ j $ 的值由第i个状态机在时刻t时的状态确定。而choice状态是在当前状态机下随机选择下个状态，并在学习过程中不断进行策略优化。stop状态则是停止当前状态机的活动并返回调用它的状态机，同时Agent基于选择的动作进行状态转移并得到相应的奖赏。在整个运行过程中M若没有选择动作，则保持状态不变。

执行学习时，首先人为确定有限状态机集合，然后Agent从一个随机的初始有限状态机开始，按照一定的策略对其他有限状态机进行依次调用并执行。若 $ {S}_{H} $ 为随机有限状态机集合 $ H $ 的状态集，则 $ {S}_{H} $ 包含Agent从初始有限状态机开始可到达的所有状态机。为确保在MDP中可持续获得基本动作，初始状态机中不应含有无action的确定性无限环和stop类。

设HoM为基于有限马尔可夫决策过程M和上述随机有限状态机的集合 $ H $ 组合产生的MDP，则其状态集可表示为 $ {S\times S}_{H} $ ， $ H $ 和M的状态转移概率函数共同确定HoM的状态转移概率函数，将HoM中的选择点集合记为reduce(HoM)，则reduce(HoM)与HoM的优化策略相同。其中M的基本动作仅依赖于 $ H $ 的action状态，reduce(HoM)的立即奖赏也基于M的立即奖赏来确定。当M的状态不发生变化时，Agent时间步内获得的立即奖赏为0，所以立即奖赏也可以理解为Agent时间步内的累积奖赏。由此可见，HAM方法是依赖于设计者的先验知识，从而为有限马尔可夫决策过程M提供一个受约束的策略集。

其中reduce(HoM)的最优策略可使用SMDP Q-learning方法进行迭代逼近。设Agent在t时刻进入选择点 $ \left[{s}_{c},{m}_{c}\right] $ ， $ t+\tau $ 时刻到达选择点 $ \left[{s}_{c}',{m}_{c}'\right] $ ，则Q-learning算法的迭代更新公式为

$\begin{array}{l} {Q_{k + 1}}\left( {\left[ {{s_c},{m_c}} \right],{a_c}} \right) = \left( {1 - {\alpha _k}} \right){Q_k}\left( {\left[ {{s_c},{m_c}} \right],{a_c}} \right) + \\ \;\;\;\;\;\;{\alpha _k}[{r_t} + \gamma {r_{t + 1}} + \cdots + {\gamma ^{\tau - 1}}{r_{t + \tau - 1}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\gamma ^\tau }{\rm{max}}{Q_k}(\left[ {{s_{c'}},{m_{c'}}} \right],a')] \end{array}$

(5)

式中Parr等^[32]证明了式(5)以概率1收敛到reduce(HoM)的最优值函数 $ {Q}^{*} $ ，且与标准Q-learning算法的收敛条件一致。Kulkarni等^[33]提出了一种分层Q值方法，其通过构造两个层级的算法，顶层用于决策，确定下一步的目标，底层用于具体行动决策，在Montezuma’s Revenge游戏中取得了较好的效果。

综上可知，基于分层抽象的多智能体分层强化学习由于对学习类型进行了限定，在一定程度上可以简化MDP和提高学习效率，而且由于其只需要部分状态即可确定有限状态机的转移，因此对于环境部分可观测领域，基于分层抽象的MAHRL同样适用。

2.3 基于值函数分解的多智能体分层强化学习

基于值函数分解的多智能体分层强化学习主要是采用Dietterich提出的MaxQ^[34]分层强化学习方法来解决多智能体强化学习问题。其主要思想是将一个马尔可夫决策过程 $ M $ 分解为子任务集 $ \left\{{M}_{0},{M}_{1},\cdots ,{M}_{n}\right\} $ ,相应的策略 $ \pi $ 也可分解子策略集合 $ \left\{{\pi }_{0},{\pi }_{1},\cdots ,{\pi }_{n}\right\} $ ,其中 $ {\pi }_{i} $ 即为对应 $ {M}_{i} $ 的策略，而所有子任务形成以 $ {M}_{0} $ 为根节点的分层任务结构。在此分层任务结构中，解决 $ {M}_{0} $ 所采取的动作包括两种情况，即执行基本动作和执行其他子任务，执行子任务又依次执行其所需的动作，解决了根任务 $ {M}_{0} $ 也就解决了任务 $ M $ 。其中每个子任务 $ {M}_{i} $ 均由三元组 $ <{\pi }_{i},{T}_{i},{R}_{i}> $ 组成： $ {\pi }_{i} $ 为子任务策略，用于从 $ {M}_{i} $ 的子节点中选择子任务(基本动作)； $ {T}_{i} $ 为终止谓词，用于将 $ M $ 的状态集合 $ S $ 划分为 $ {M}_{i} $ 策略的活动状态集 $ {S}_{i} $ 和终止状态集 $ {F}_{i} $ ； $ {R}_{i} $ 为伪奖赏函数，其仅在学习过程中状态集 $ {F}_{i} $ 的奖赏函数分配时调用。

与分层Option方法的值函数类似，分层策略 $ \pi $ 基于在子任务上的投影值函数即可确定每个状态的期望回报值 $ {V}^{\pi }(i,s) $ 。对于每个子任务 $ {M}_{i} $ ，其均为离散时间SMDP，设状态集为 $ {S}_{i} $ ，动作集则为每个 $ {M}_{i} $ 的所有子节点，而转移概率 $ {P}_{i}({s}',\tau |s,a) $ 代表对于任意状态 $ s\in {S}_{i} $ 和 $ {M}_{i} $ 所有子节点 $ {M}_{a} $ ，执行动作 $ a $ 获得的立即奖赏为 $ {R}_{i}\left(s,a\right)={V}^{\pi }(a,s) $ ，则每个子任务 $ {M}_{i} $ 对应的Bellman方程为

$\begin{array}{l} \;\;\;\;{V^\pi }\left( {i,s} \right) = {V^\pi }\left( {a,s} \right) + \\ \displaystyle\sum\nolimits_{s',\tau } {P_i^\pi } (s',\tau |s,a){\gamma ^\tau }{V^\pi }(i,s') \end{array}$

(6)

式中： $ a={\pi }_{i}\left(s\right) $ ， $ {V}^{\pi }(i,{s}') $ 则是从子任务 $ a $ 结束时的状态 $ {s}' $ 开始，直到子任务 $ {M}_{i} $ 完成时的回报值期望。其中状态−动作值函数如式(7)所示：

$\begin{array}{l} \;\;\;\;{Q^\pi }\left( {i,s,a} \right) = {V^\pi }\left( {a,s} \right) + \\ \displaystyle\sum\nolimits_{s',\tau } {P_i^\pi } (s',\tau |s,a){\gamma ^\tau }{\rm{max}}{Q^\pi }(i,s',\pi \left( {s'} \right)) \end{array}$

(7)

式中右侧第2项称为完成函数：

$ {C^\pi }\left( {i,s,a} \right) = \sum\nolimits_{s',\tau } {P_i^\pi } (s',\tau |s,a){\gamma ^\tau }{\rm{max}}{Q^\pi }(i,s',\pi \left( {s'} \right)) $

即子任务 $ {M}_{a} $ 终止后完成子任务 $ {M}_{i} $ 的期望回报值。因此，状态−动作值函数可以分解成立即奖赏 $ {V}^{\pi }\left(a,s\right) $ 和完成函数 $ {C}^{\pi }\left(i,s,a\right) $ 两部分，即：

$ {Q}^{\pi }\left(i,s,a\right)={V}^{\pi }\left(a,s\right)+{C}^{\pi }\left(i,s,a\right) $

(8)

设MDP的分层策略 $ \pi $ 为已知，则执行任务 $ {M}_{0} $ 时会向下选择执行子任务 $ {M}_{{a}_{1}} $ ，而执行子任务 $ {M}_{{a}_{1}} $ 时又会继续向下选择执行子任务 $ {M}_{{a}_{2}} $ ，不断迭代直到最后选择基本动作 $ {a}_{n} $ ，此时根任务 $ {M}_{0} $ 中状态 $ s $ 的投影值 $ {V}^{\pi }\left(0,s\right) $ 可分解为

$\begin{array}{l} {V^\pi }\left( {0,s} \right) = {V^\pi }\left( {{a_n},s} \right) + {C^\pi }\left( {{a_{n - 1}},s,{a_n}} \right) + \cdots + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{C^\pi }\left( {{a_1},s,{a_2}} \right) + {C^\pi }\left( {0,s,{a_1}} \right) \end{array}$

(9)

式中 ${V^\pi }\left( {{a_n},s} \right) = {\displaystyle\sum _{s'}}P(s'|s,{a_n})R(s'|s,{a_n})$ ，是MaxQ算法的基础。

在Dietterich设计的MaxQ-Q学习算法中，若每个子任务 $ {M}_{i} $ 的子策略 $ {\pi }_{i} $ 都为最优，即可确定任务 $ M $ 的递归最优策略为 $ \pi =\{{\pi }_{0},{\pi }_{1},\cdots ,{\pi }_{n}\} $ 。同时，Dietterich也证明了算法在Agent奖赏有界且执行有序贪婪策略的情况下能稳定收敛。

综上可知，与Option、HAM采用单个SMDP来收敛到最优策略不同，基于MaxQ函数分解的多智能体分层强化学习通过建立多个可以同步学习的分层SMDP，利用策略分层结构来缩小每个Agent的搜索空间，可以有效提高学习效率，同时其微、宏观策略均不需要事先确定，都可以在线学习，具有较强的灵活性。但是其同样存在需要提前依靠先验知识进行任务层次划分的问题，对于环境未知的情况依然具有很大的挑战。

2.4 基于端到端的多智能体分层强化学习

基于端到端的多智能体分层强化学习主要思想是通过Agent自学实现分层抽象，即任务自动分层，而不是像前面3类是基于人为划分和指定，典型算法有瓶颈和路标状态法、共用子空间法、多维状态法、马氏空间法和基于神经网络自动分层抽象学习等。

瓶颈和路标状态法的主要思想是在问题求解过程中不断寻找中间点，并将其视为子目标从而实现任务的分解和分层。Menache等^[35]提出了一种基于状态空间分割的瓶颈状态法，其主要基于计算状态空间割集来寻找状态转移图中的最小流量边集，并将其视为状态瓶颈(子目标)，然后Agent学习子策略和策略复用来加速分层学习。瓶颈和路标状态法使用的前提是该任务具有中间点或中间阶段，所以其对于任务分段不明显或空间较大的情况并不适用。

共用子空间法的主要思想是通过寻找策略或行动地公共区域实现策略自动分层。Drunnond等^[36]提出了一种基于值函数梯度的子空间发现方法，该方法首先基于值函数梯度将相邻状态划分成不同的子空间，然后根据梯度值的高低确定该区域是否存在障碍物，以及根据其是否为局部最大、最小值判断为子空间的出入口点，然后将相关顶点和对应子空间值函数存储起来，最后Agent基于匹配与比较的形式实现相似情形的快速学习。共用子空间法使用的前提是该任务的策略或行动空间存在公共区域，同时由于其子空间的发现与更新是一个不断进行的过程，所以会带来较大的计算量。

多维状态法的主要思想是基于特征向量和特征子集对策略进行划分。HEXQ^[37]方法是一种基于因子状态表达的多维状态法，其基于变化快慢将状态变量表示成有序的因子状态表，其中每个状态变量为一个包含简单MDP的任务层，MDP之间则通过瓶颈状态集连通。多维状态法的核心思想是基于特征向量，所以对于特征向量无法表示的情况并不适用。

马氏空间法的主要思想是采用逐步分解的形式将状态空间划分成一系列都具有Markov特性的子空间。Uther等^[38]提出了一种基于树结构的TTree方法，其通过树结构来增加抽象状态的解析度和层次性，在抽象层中对采用缺省策略或由用户提供确定策略进行明确，从而通过逐层提高子空间解析度来获取模型的Markov特性。马氏空间法的缺点是对空间分解的解析度要求较高，解析度不合适会导致分层失败。

基于神经网络的自动分层抽象学习，其核心思想是利用深度神经网络的学习能力实现策略自动分层。Pierre等^[39]提出了一种Option-Critic学习方法，其通过深度神经网络来寻找任务之间的边界，并在游戏策略学习领域获得了比普通Deep Q Network方法更好的效果。还有研究者按照任务分层和策略学习两项工作分别设计神经网络，提出了一种Manager-Worker学习方法^[40]，也取得了不错的效果。对于复杂的决策问题，人工分层和抽象不仅费时费力，而且结果难免主观，因此采用基于端到端分层强化学习必然是将来研究的一个热点方向。

3 多智能体分层强化学习的应用 3.1 多智能体分层强化学习在机器人控制领域的应用

多智能体分层强化学习在机器人控制领域开展了大量研究与应用，其中最为典型的应用是足球机器人比赛^[41-43]。足球机器人系统是一个典型的多智能体系统^[44]，每个机器人球员可以看作一个Agent，其需要综合考虑自身当前状态、其他球员状态以及动作来做出决策，即需要基于组合状态和组合动作来选择动作，是多智能体分层强化学习方法适用的典型情况。LIU等^[45]针对足球机器人问题，提出了一种基于投票的多智能体强化学习方法，其采用投票的方式来综合所有Agent的策略，通过对综合策略的学习实现Agent之间的协作。DUAN等^[46]研究了基于智能体动作预测的多智能体强化学习算法并应用在足球机器人角色分配问题中，其核心思想是利用贝叶斯分类器实现其他Agent动作的预测^[47]，然后基于策略共享机制实现多智能体之间的交互，加速协作策略的学习速度，从而实现多机器人的动态角色分配和分工协作。

3.2 多智能体分层强化学习在博弈决策领域的应用

求解博弈决策问题一直是人工智能领域的难题，基于知识与规则的求解方法可以有效解决状态规模不大的博弈决策问题^[48-50]。然而对于类似于作战等复杂博弈决策问题，其巨大的状态和决策空间，同时还有战争迷雾等不确定性问题，基于人工的状态抽象和解析求解是相当困难和不现实的^[51-53]。多智能体分层强化学习的不断发展为求此类问题开辟了一条新的道路。目前比较典型的研究是针对星际争霸、王者荣耀等RTS游戏AI开展研究^[54-60]。其中我国阿里巴巴认知计算实验室提出的多智能体双向协调网络(BiCNet)方法^[61]，其通过采用actor-critic表达的向量化扩展，即使在博弈双方的Agent数量都为任意、不同地形以及不同战斗类型的情况下都能实现智能自主决策；其次，即使在没有任何人类经验数据或标签数据的情况下，BiCNet同样能学到一些与人类玩家相似的团队策略。中科院自动化所针对星际争霸中微观操作存在的状态、行动空间复杂和合作策略学习困难等问题，提出了一种基于参数共享的多智能体梯度下降Sara(λ)强化学习算法(PS-MAGDS)算法^[62]，用以解决星际争霸微观操作中的多智能体决策问题；2019年，DeepMind在《Science》中介绍了一种新型的多智能体分层强化学习策略^[3]，其在《雷神之锤》游戏中不仅学会了如何夺旗，同时也能学到一些不同于人类的团队协作策略。

3.3 多智能体分层强化学习在任务规划领域的应用

任务规划是一项多领域相关、多层面运用以及多系统集成的技术，其核心思想是基于模型和数据对要素进行全面分析，从而实现各类资源的优化配置以及各类实体行动计划的协调等^[63-64]。传统的军事运筹学、专家系统、启发式算法虽然能很好解决局部规划问题，但仍存在易陷入局部最优、数据规模大、收敛速度慢以及规则和样本获取难等问题^[65-66]。Zheng等^[67]为解决传统算法收敛速度慢、效率低等问题，提出了一种基于分层强化学习及人工势场的多Agent路径规划方法，并基于出租车问题对该算法进行了仿真实验。针对多星协同任务规划问题，Wang等^[68]引入约束惩罚算子和多星联合惩罚算子对卫星Agent原始的效用值增益函数进行改进，提出了一种基于多Agent强化学习的多星协同任务规划算法。为降低由Agent之间交互所引起的通信代价，该算法使用了基于黑板结构的多星交互方式，仿真结果显示该方法在解决多星协同任务规划问题上取得了较好的效果。

虽然MAHRL在解决复杂决策问题上有着巨大的潜力，并且也已有很多研究者对其展开了研究和在诸多领域中实现了应用，但依然存在很多问题和瓶颈值得进一步探索和研究。一是方法的可扩展性方面。当前对MAHRL的研究主要集中在以RTS游戏为代表的博弈决策问题，聚焦具体的离散动作和状态空间背景，其游戏智能决策、战略决策尚未真正意义实现，在机械制造、资源配置、自动驾驶等具体应用领域更是处于探索阶段。因此研究面向海量智能体、复杂环境应用的MAHRL方法是未来研究的重要方向。二是策略分层的自主性方面。现在的MAHRL方法普遍基于马尔可夫决策框架，环境是已知或可预测的情况，同时现有的策略分层大部分是基于一定的先验知识，而现实中许多决策问题存在不可预测、迷雾等问题，所以如何建立一种端到端和具有较强鲁棒性的自动策略分层方法是需要进一步研究的。三是与其他方法的结合方面。MAHRL本身就是多智能体和分层强化学习两种方法的结合，但由于其自身原理所限，MAHRL在探索的有效性、样本的利用率、模型的鲁棒性等方面仍不够理想。因此，针对性地研究监督学习、元学习、模仿学习、迁移学习以及增量式学习等其他方法在MAHRL中的应用与结合，将是MAHRL研究和发展的一个重要方向。

4 结束语

本文对多智能体分层强化学习进行了回顾，首先对强化学习、半马尔可夫决策过程、多智能体技术等相关研究现状进行了介绍，然后基于分层的角度，对多智能体分层强化学习进行了综述，阐述了基于选项、基于分层抽象机、基于值函数分解和基于端到端等4种多智能体分层强化学习方法的算法原理和研究现状。介绍了MAHRL在机器人控制、博弈决策以及任务规划等领域的应用现状。作为解决大规模复杂背景下协同决策的一种潜在途径，MAHRL虽然现在仍有许多问题尚未解决，但可以预见的是，随着研究的不断深入，多智能体分层强化学习将成为解决智能决策问题的重要方法。