2. 安徽农业大学 信息与计算机学院,安徽 合肥 230036
2. School of Information and Computer, Anhui Agricultural University, Hefei 230036, China
图神经网络(graph neural network, GNN)作为一种从卷积神经网络(convolutional neural networks, CNN)和图嵌入思想启发而来的新型拓展神经网络[1],可以在图领域对数据进行特征提取和表示,是一种高效、易扩展的新型的神经网络结构,在学习图数据方面表现出了强大的功能。与传统的深度学习方法相比,GNN可以通过构建的图模型来反映实体及其之间的联系。目前,国内外对GNN的研究都取得了一定的进展,如自然语言处理[2]、文本分类[3]、特征关系提取[4]、图片分类[5]、疾病预测[6]等。在推荐系统中,实体间的关系有用户与用户、用户与物品、物品与物品之间关系,传统的推荐方法主要关注用户与物品间的关系,很少关注用户相互间及物品相互间的关系。图神经网络GNN的发展,为人们进一步分析推荐系统实体及其相互间的关系提供了更好的表示方式,近年来,基于GNN推荐的相关研究越来越受到广大学者关注,并取得了一定的成果。本文分析了GNN推荐的主要过程及其研究进展,提出了GNN推荐当前存在的难点,并指出未来GNN推荐的主要研究方向。
1 图神经网络图神经网络是利用一定的方法对节点进行描述,并经过不断的节点状态更新,得到具有包含邻居节点信息和图形拓扑结构特点的状态[7],最终将这些节点通过特定方法进行输出,得到需要的结果。式(1)表示节点状态的更新方式,式(2)表示对更新完的节点状态进行输出:
| ${{{h}}_{{v}}} = f\left( {{{{X}}_{{v}}},{{{X}}_{{\rm{CO}}\left[ {{v}} \right]}},{{{h}}_{{\rm{ne}}\left[ {{v}} \right]}},{{{X}}_{{\rm{ne}}\left[ {{v}} \right]}}} \right)$ | (1) |
| ${{{o}}_{{v}}} = g\left( {{{{h}}_{{v}}},{{{X}}_{{v}}}} \right)$ | (2) |
式中:
式(1)、(2)均表示以一个节点为单位进行操作,当对所有的节点进行上述运算的时候,可以更加简洁的用式(3)、式(4)进行描述:
| $H = F(H,X)$ | (3) |
| $ O = G(H,{X_N}) $ | (4) |
式中:H表示所有节点的状态;O表示对所有的节点进行输出之后的结果;X表示边的特征;
| ${{{H}}^{{{t}} + 1}} = {{F}}\left( {{{{H}}^{{t}}},{{X}}} \right)$ | (5) |
GNN有多种变体,如根据训练方法的差异有GraphSAGE[8]、FastGCN[9]、ControlVariate[10]、Co-training GCN[11]和Self-training GCN[11]等;根据信息传播计算方式的不同有Spectral Network[12]、MoNet[13]、DCNN[14]、Gate Graph Neural Networks[15]、Sentence LSTM[16]等。
图神经网络GNN按照其构成拓扑结构边的类型,分为有向图GNN和无向图GNN,对于不同的边类型,对应的局部转换函数f的计算方法也有所差异。
1)有向图GNN
实际上有向图比无向图可以反映更多的信息,比如某种次序或者逻辑关系,在文献[17]中,Kampffmeyer等通过使用两个权值矩阵Wp,Wc来进行协同获得更加精确的处理结果,如式(6):
| ${{{H}}^t} = {\rm{\sigma }}({{D}}_p^{ - 1}{{{A}}_p} \cdot {\rm{\sigma }}({{D}}_c^{ - 1}{{{A}}_c}{{{H}}^{t - 1}}{{{W}}_c}){{{W}}_p})$ | (6) |
式中:p代表父节点(指向它的节点);c代表子节点(它指向的节点);D−1pAp、D−1cAc分别代表对父节点和子节点邻接矩阵的标准化矩阵;
2)无向图GNN
没有次序关系的节点就构成无向图,图神经网络GNN对于无向图的处理只需要将其视为两个有向图的叠加即可。实际上,无向图的计算相比有向图更为简单,对其进行更新时,只需一个权重矩阵W正常经过加权,通过激活函数更新即可。
本文将图神经网络GNN按照构成它的节点是否表示相同的实体,分为单元图GNN,二元图GNN与多元图GNN。单元图GNN中节点仅表示1种实体类型,即节点的类型唯一,在推荐系统中常常体现在用户社交关系图,如根据用户的朋友关系构建对应的GNN模型;二元图GNN中的节点所表示的实体类型为2种,诸如用户−物品购买关系图,用户−项目标签图等;图中节点所表示实体类型超过2种的为多元图GNN,在实体种类及其关系较复杂的时候可以使用这种类型的GNN模型。
2 推荐系统推荐系统就是通过分析用户的历史行为对用户的兴趣建模,从而主动给用户推荐能够满足其兴趣和需求的物品(或信息)。常见的推荐模型有基于用户行为的推荐,如协同过滤(collaborative filtering, CF)[18],隐语义模型(latent factor model, LFM)[19];基于内容的推荐,如标签推荐[20];混合推荐[21],即通过多种不同的推荐模型相互协作,如在推荐系统的不同时期分别使用不同的模型或者使用多个模型的推荐结果再进行决策。协同过滤分为基于用户的协同过滤[22]和基于物品的协同过滤[23],基于用户行为的推荐算法往往存在着冷启动问题[24]和数据稀疏性问题[25]。
随着深度学习的发展,基于深度学习的推荐研究也很多,Elkahky等[26]提出了一种多视图深度神经网络模型(Multi-View deep neural network, Multi-ViewDNN),通过用户和物品(项目)两种信息实体的语义匹配来实现用户的物品推荐;Zheng等[27]提出了一种深度协作神经网络模型(deep cooperative neural network, DeepCoNN),利用两个并行的神经网络模型学习用户和项目的隐特征,然后在两个神经网络上构建一个交互层来预测用户对项目的评分;Liu等[28]研究了位置社交网络中的行为预测问题,通过利用循环神经网络抓住序列行为之间的依赖关系,从而基于用户的历史行为序列,帮助预测下一时刻的行为。
3 GNN推荐主要过程一般说来,GNN推荐主要过程分为3个步骤:1)根据推荐系统实体及其相互关系构建对应的GNN模型。主要考虑如何将推荐系统中不同实体映射为GNN中图节点,不同实体间的联系映射为GNN图中对应的边,如何用的神经网络函数去拟合GNN中不同的节点。在GNN推荐模型中,不论是用户节点还是物品节点,都可以根据相关信息做嵌入化处理,得到对应节点的向量化描述。如对一个物品节点,可以根据不同用户对其评论或评分信息做嵌入化处理;对一个用户节点,可以根据其社交关系或物品购买记录做嵌入化处理。边作为反映GNN推荐模型中实体之间的联系,通常有两种处理方式:一是根据联系的类型及强弱程度不同,进行嵌入化操作;二是对边不进行任何处理,仅仅当成GNN推荐模型中,用于信息传播算法作用的媒介。2)决定GNN模型的信息传播与更新方法。GNN模型的变体很多,不同变体之间,信息的聚集和更新方式也不同。文献[29]指出了在不同的GNN变体中,出现的相关聚集过程。如GCN模型,通常选择mean聚集函数;GraphSAGE模型,通常采用max函数;GIN模型,通常使用的sum函数等。不同的聚集函数适合于不同的图结构,mean函数可以反映图中节点的分布情况,max函数可以反映主要特征,sum可以考虑到比较全面的图形结构特征等。信息更新过程,主要是将信息聚集之后的结果,与中心节点进行特定的运算,并作为下一层节点的初始状态。这方面,不同的模型差异也很大,如GCN模型进行信息更新时,不会考虑中心节点的信息;GraphSAGE则会将聚集结果和中心节点的向量进行连接操作;GIN模型会将两者进行直接相加等。充分考虑推荐系统实体间关系,及对应GNN模型的结构特征,选择最合适的信息传播算法,进行信息更新,往往可以取得更好的推荐效果。3)提取出更新后的节点(边、子图)特征,并用相关算法实现推荐。将GNN模型完成更新之后的节点取出,作为该节点对应的实体特征,采用相关算法进行推荐。如文献[30]中,使用协同过滤推荐的方法;文献[31]中,将GNN提取的物品特征和节点特征,通过MLP进行评分预测推荐;文献[32]中,通过两种不同的神经网络,进行试验结果预测与推荐。
4 GNN推荐相关研究由于有向图GNN推荐时,需要两个权值矩阵来实现聚集与更新操作,相对无向图GNN推荐,只需一个权重矩阵来说,就变得更为复杂。因此,在现有图神经网络GNN推荐的相关研究中,主要集中在无向图GNN推荐方面。以下重点从无向单元图GNN推荐、无向二元图GNN推荐以及无向多元图GNN推荐3个方面探讨GNN推荐相关研究。
4.1 无向单元图GNN推荐这种GNN推荐模型节点类型单一,操作比较简单。主要是将推荐系统中的实体映射到一个无向单元图GNN,图中所有节点都表示为一种实体类型。如Cui[33]等将GNN用于服装推荐,服装的类别作为节点,各个类别之间的关系作为边,各类服装放入对应的节点之中形成子图,构成了一个无向单元图GNN推荐模型,推荐与指定服装匹配度较高的目标服装实现套装搭配,取得了较好的效果。
文献[30]中,考虑到用户的行为往往受到自己当前兴趣、朋友兴趣等多种因素影响,通过构建用户—朋友的无向单元图GNN,分别对用户节点、朋友节点进行描述,并使用相关传播算法更新用户信息节点,最后和物品嵌入化得到的结果进行运算,输出用户对物品可能的喜爱程度,如图1所示。具体步骤如下:
1)将用户近期的浏览内容,通过循环神经网络(RNN)得到表示用户兴趣的hn,并用hn描述用户的节点信息;
2)将朋友的近期行为记录,通过RNN得到sks,用来表示该朋友的短期兴趣;
3)将朋友长期行为向量化,得skl,见式(7):
| ${{s}}_{{k}}^{{l}} = {W_u}\left[ {k,:} \right]$ | (7) |
式中:
4)将上述两个向量联合起来,构成代表目标节点用户的嵌入化向量
| ${{{s}}_{{k}}} = {\rm{ReLU}}\left( {{W_1}\left[ {{{s}}_{{k}}^{{s}},{{s}}_{{k}}^{{l}}} \right]} \right)$ | (8) |
式中:ReLU为非线性激活函数,
5)目标节点的初始状态选取为
| ${\rm{\alpha }}_{uk}^{\left( {\rm{l}} \right)} = \frac{{{\rm{exp}}\left( {f\left( {{{h}}_{{u}}^{\left( {{l}} \right)},{{h}}_{{k}}^{\left( {{l}} \right)}} \right)} \right)}}{{\displaystyle \sum \nolimits_{j \in N\left( u \right) \cup \left\{ u \right\}} {\rm{\alpha }}_{uk}^{\left( l \right)}{{h}}_{{k}}^{\left( {{l}} \right)}}}$ | (9) |
式中:l表示当前的更新次数,f(hlu,hlk)表示目标节点与他的第k个邻居的相似度计算结果。
6)将所有的邻居节点信息通过注意力系数相加后,得到表示目标节点所有邻居节点的信息向量
| ${{{\hat h}}_{{u}}} = \sum\nolimits_{k \in N\left( u \right) \cup \left\{ u \right\}} {{\rm{\alpha }}_{uk}^{\left( l \right)}{{h}}_{{k}}^{\left( {{l}} \right)}} $ | (10) |
| $h_{{u}}^{\left( {{{l}} + 1} \right)} = {\rm{ReLU}}\left( {{{{W}}^{\left( {{l}} \right)}}{{\hat h}}_{{u}}^{\left( {{l}} \right)}} \right)$ | (11) |
式中:W是可训练的权值矩阵,l、l+1表示当前更新的次数。
7)将节点的特征与嵌入化得到的物品特征进行相似度运算,通过softmax进行输出,此时输出的结果就是某用户对物品可能的感兴趣程度。

|
Download:
|
| 图 1 无向单元图GNN推荐模型 Fig. 1 Single-unit undirected graph GNN model | |
该模型充分考虑到社会关系与用户本人的当前兴趣,但对物品特征的提取比较粗糙,没有考虑到用户与物品之间的互动关系,同时不同的朋友对用户的影响程度也是不一样的,此模型也没有加以区分。
4.2 无向二元图GNN推荐在实际推荐中,最常见的关系就是用户与项目(物品)的交互记录,这两种实体关系就可以构成一个完整的二元拓扑图。Fan等[31]通过构建用户−物品关系二元图(用户购买的所有物品)、用户−朋友关系单元图(用户的社交关系)、物品−用户关系二元图(物品被用户购买的记录)这3个无向图用于对物品进行评分预测。同样考虑到对用户可能的行为,不仅与他自己曾经购买的物品有关,也和他的社交关系有关,该文献提出了一种新型图神经网络GNN推荐系统框架GraphRec,如图2。
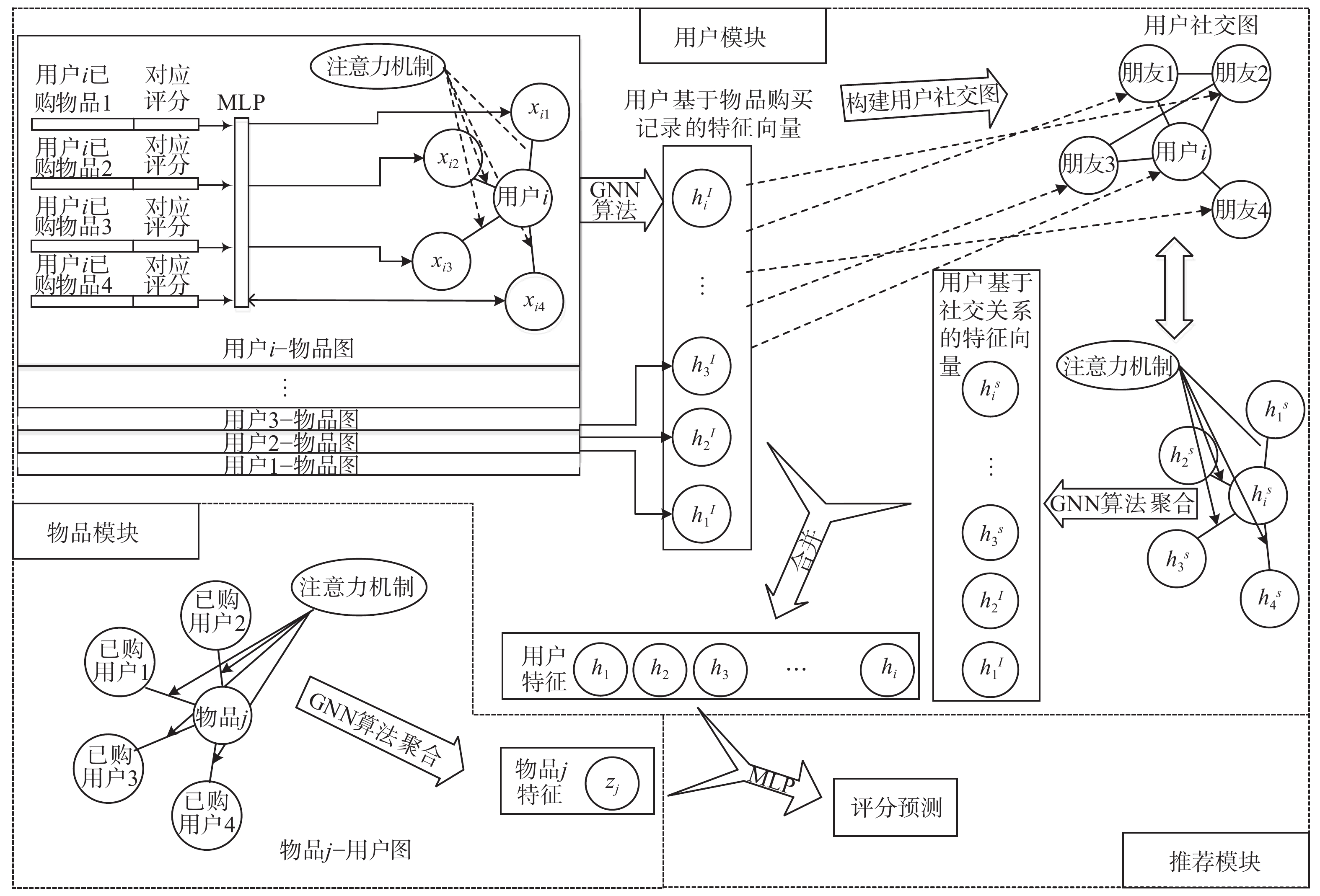
|
Download:
|
| 图 2 基于社交关系的GraphRec模型 Fig. 2 Social-based recommendation model-GraphRec | |
该框架主要由3个模块组成,分别是用户−物品关系和用户—朋友关系构成用户模块,物品−用户关系构成物品模块和由一个多层感知器(MLP)所构成的推荐模块。通过信息传播更新算法,对这3个图中的节点进行计算,根据结果进行评分预测。具体过程如下:
首先根据用户购买不同物品行为以及用户之间的社交关系构建相应的户—物品关系图和用户−朋友关系图,再在图上分别对用户i 和物品j进行嵌入化处理,得到代表用户信息的pi向量,代表物品信息的qj向量。同时每一个特定的用户对于他所购买的物品对应的评分,用独热编码向量化成er。
用户模块分为两部分,第1部分是对某用户的购买行为进行特征刻画,第2部分是对该用户的社交关系进行刻画,将两个特征结合起来通过一个多层感知器,就得到代表该用户的特征。用户模块的实现方法如下:
1)对所提取的物品qa向量和对应的评分er向量连接处理,通过一个多层感知器得到xia向量(其中a表示用户购买的相关物品,i表示某一个用户),见式(12):
| ${{{x}}_{{{ia}}}} = {{{g}}_{{v}}}\left( {\left[ {{{{q}}_a} \oplus {{{e}}_r}} \right]} \right)$ | (12) |
2)将计算出的xia和用户pi通过一个两层的神经网络得到该用户对物品的注意力系数α*,见式(13):
| $\alpha _{ia}^* = {{W}}_2^{{\rm{T}}} \cdot \sigma \left( {{{{W}}_1} \cdot \left[ {{{{x}}_{{{ia}}}} \oplus {{{p}}_{{i}}}} \right] + {{{b}}_1}} \right) + {{{b}}_2}$ | (13) |
其中,
3)对
| ${{{\alpha}} _{{{ia}}}} = \frac{{{\rm{exp}}\left( {{{\alpha}} _{{{ia}}}^*} \right)}}{{\displaystyle\sum \nolimits_{{{a}} \in {{C}}\left( {{i}} \right)} {\rm{exp}}\left( {{{\alpha}} _{{{ia}}}^*} \right)}}$ | (14) |
4)用αia对之前得到的xia向量进行加权,并且通过一个多层感知器(GNN的简单聚合函数)得到用户−物品特征hi,见式(15):
| ${{h}}_{{i}}^{{I}} = {\rm{\sigma}} ({{w}} \cdot \left\{ {\left. {\sum\nolimits_{a \in c(i)} {{a_{ia}}{x_{ia}}} } \right\}} \right. + b)$ | (15) |
5)用同样的方法对该用户的好友进行处理,得到对应hio(o表示用户好友集i的一个好友);
6)使用2)中的方法对
| $\beta _{io}^* = {{W}}_2^{\rm{T}} \cdot \sigma \left( {{{{W}}_1} \cdot \left[ {{{h}}_{{o}}^{\rm{I}} \oplus {{{p}}_{{i}}}} \right] + {{{b}}_1}} \right) + {{{b}}_2}$ | (16) |
| ${\beta _{io}} = \frac{{{\rm{exp}}\left( {\beta _{i0}^*} \right)}}{{\displaystyle\sum \nolimits_{o \in N\left( i \right)} {\rm{exp}}\left( {\beta _{io}^*} \right)}}$ | (17) |
7)将得到的β对hi进行加权并通过一个多层感知器,最后得到具有刻画用户i社交关系的向量
| ${{h}}_i^S = {\rm{\sigma}} ({{w}} \cdot \left\{ {\left. {\sum\nolimits_{o \in N(i)} {{\beta _{io}}h_o^I} } \right\}} \right.{{ + b)}}$ | (18) |
其中,b是偏置项,σ(∙)是非线性函数。将hs和hi连接起来通过多层感知器得到代表用户的向量h。
物品模块使用类似的方法对用户向量pt和评分向量er进行连接,获得zjt向量(j表示物品,t表示某用户),然后对z向量使用上述步骤2)中的方法提取出注意力系数,并且对周围的用户向量使用该系数加权后,结果通过一个多层感知器就得到代表物品j特征的向量zj。
预测模块是将上述两个模块得到的h向量,通过一个多层感知器,最终输出预测评分。
损失函数定义为均方误差,见式(19):
| ${\rm{Loss}} = \frac{1}{{2\left| O \right|}}\mathop \sum \limits_{i,j \in O} {\left( {{{r'}_{ij}} - {r_{ij}}} \right)^2}$ | (19) |
其中i、j表示用户i、物品j,r表示实际评分,r'表示预测评分,
该方法将用户的社交关系融入神经网络,同时对于用户和物品的特征刻画都相互关联起来,并且引入了注意力机制,取得了不错的效果,但是在用户模块中两个GNN模型无法并行计算,增加了模型的时间复杂度。
在文献[32]中,Rex构建了用户−标签无向二元图,通过PinSage算法(随机游走和图卷积结合)成功应用于超大规模的网页内容推荐。Wang等[34]构建用户—物品图,不同之处在于GNN算法中使用目标节点及其邻居节点的点积进行更新,并且通过协同过滤的方法进行推荐。文献[35]为了解决推荐系统的冷启动问题,利用知识图谱为推荐提供更多的辅助信息,针对不同用户将知识图谱转换为多个用户的个性加权图,并且通过GCN学习出每个物品的表示向量,然后根据用户特征向量计算出用户与物品有交互的概率。
4.3 无向多元图GNN推荐多元图GNN会大大增加模型的复杂度,同时计算复杂性和刻画节点的难度也随之增加,但多元图GNN往往更加贴近现实,可以得到更加客观的结果。文献[36]中,考虑到在一家医院的病患进行就诊时,需要进行项目测试以及根据其具体情况开出不同的药方,一般基于经验进行诊断,可能会出现误差,而且数据难以全面收集。Mao将图神经网络GNN推荐运用在诊疗研究中,如图3所示。通过一个无向多元图GNN构建病患、医疗科室、药方以及测试结果之间的关系,其中医院的各个科室作为核心节点,进行几轮信息的迭代计算之后,根据计算出的节点信息通过两种不同的神经网络,推荐可能的药方,以及某项诊疗测试的可能结果。

|
Download:
|
| 图 3 患者医疗诊断关系和医疗测试结果 Fig. 3 The graph of patients’ consults relation and laboratory testing results | |
该研究中,节点之间的关系通过3个邻接矩阵进行表示,如图4,分别是AE×P、AE×M、AE×L,其中E为医疗科室,P为患者,M为药方,L为医疗测试结果;AE×P表示医疗科室与病人之间的关系,如果病人在该医疗科室进行过就诊,则为1,否则为0。假设一个病人可以对应多个医疗科室,但是一个医疗科室只能对应一个病人,也就是说,一行最多只有一个1。AE×M表示医疗科室与药方之间的关系,如果该科室可以开出对应的药方,则该值为1,反之为0。AE×L表示医疗科室和医疗测试结果之间的关系,如果某个医疗科室有该实验测试则该两点之间有权重,选择的值是平时测试的平均值,为了对一些测试结果是0的项目进行区别,作者额外增加了一个ME×L矩阵,对于存在的项目则对应数字为1,否则为0。最后一个矩阵表示医疗科室和药方之间的关系,如果该医疗科室有对应的药方则该点为1,否则为0。

|
Download:
|
| 图 4 病患、医疗科室、药方以及医疗测试结果关系矩阵 Fig. 4 Relation matrix between patients encounters medications and laboratory test data | |
在式(20)中,f1、f2分别表示两种激活函数,N(v) 表示v节点的所有邻居,k表示第k轮运算。
| ${{{H}}^{\left( {{{k}} + 1} \right)}}\left( {{v}} \right) = f_1^{{{W}}_1^{\left( {{k}} \right)}}\left( {{{{H}}^{\left( {{k}} \right)}}\left( {{v}} \right),f_2^{{{W}}_2^{\left( {{k}} \right)}}\left( {\left\{ {{{{H}}^{\left( {{k}} \right)}}\left( w \right)|w \in N\left( v \right)} \right\}} \right)} \right)$ | (20) |
Mao对激活函数
| ${{H}}_{{i}}^{\left( {{{k}} + 1} \right)} = \phi \left( { \mathop \sum \limits_{j = 0}^n {{{A}}_{{{ij}}}} \cdot {{H}}_{{j}}^{\left( {{k}} \right)} \cdot {{W}}_{{j}}^{\left( {{k}} \right)}} \right)$ | (21) |
经过k轮计算之后,将计算的节点结果输入两种神经网络,分别进行药方和医疗测试结果的推荐。
在式(22)中,损失函数表示为两项之和,第1项Lm为药方预测的误差,见式(23),第2项LL表示使用交叉熵的方式表示医疗测试结果的预测误差,见式(24),λ是系数通过这种引入的混合误差,很有效地避免了过拟合问题。
| $L = {L_m}\left( {{{P}},{{{A}}_{{{E}} \times {{M}}}}} \right) + \lambda {L_L}\left( {{{V}},{{{A}}_{{{E}} \times {{L}}}}} \right)$ | (22) |
| ${L_M}\left( {P,A} \right) = - \frac{1}{{{N_E}}}\mathop \sum \limits_i^{{N_E}} \mathop \sum \limits_j^{{N_M}} \frac{{{N_n}}}{{{N_p}}}{a_{ij}}\log {p_{ij}} + \left( {1 - {a_{ij}}} \right)\log \left( {1 - {p_{ij}}} \right)$ | (23) |
| ${L_L}\left( {V,A} \right) = - \frac{1}{{{N_E}}}\mathop \sum \limits_i^{{N_E}} \mathop \sum \limits_j^{{N_L}} {m_{ij}}{\left( {{v_{ij}} - {a_{ij}}} \right)^2}$ | (24) |
该模型较单元图与二元图神经网络,结构更加复杂,但能更有效地对不同类型的数据信息进行充分使用。同时,通过将模型中的对象进行节点再划分,成功处理了一些实验过程中的数据缺失值问题;使用新的正则化规则,避免了过拟合情况,取得了不错效果。不足之处在于实验相关数据仅采用一家医院,对于规模更大的数据集,GNN图形结构将更复杂,实际应用有一定困难。
5 现有GNN推荐研究难点 5.1 多源多模态信息的GNN推荐问题在一个系统中,数据来源与数据结构往往呈现多源异构性。以电子商务系统为例,数据来源有商家提供的商品描述与分类信息,消费者与系统交互的点击、浏览、收藏、交易信息,消费者的评分及评论信息等;数据形式有文本信息,图像信息、数值评分与标签信息等,甚至还有语音及视频信息等。现有推荐模型对于这些多源多模态数据很难同时进行有效处理,导致数据利用不充分或数据对象之间的关系表示不明显。同样的,现有GNN推荐模型,对节点向量化的方式比较单一,如一般只能对用户留下的评论数据或者评分加以处理,难以将多源多模态信息进行融合表示以达到最佳效果。如何充分集成使用多源多模态数据信息是GNN推荐有待解决的一个问题。
5.2 GNN的有向图推荐问题目前GNN推荐模型主要是无向图GNN推荐,其中无向图的边用来反映节点之间的互动关系。但是有向图比无向图可以反映更多的信息,比如某种次序或者逻辑关系,有向图的推荐结果往往可以取得更好的效果。推荐系统中也存在着对应的有向关系,如信任关系、关注关系等。与无向图GNN推荐相比,基于有向图GNN的推荐更具有挑战性,也更为复杂。
5.3 GNN的动态推荐问题对于数据规模往往很大的图形结构,很难进行实时的图模型更新,而且图神经网络GNN迭代过程中往往需要根据整个图的信息向量化才能完成计算,对于不断更新的数据每次进行重新计算,需要花费很高的成本,如何在较低成本下完成动态的GNN更新,现有GNN推荐研究并没有考虑。如文献[30]中,用户的社交情况可能会实时发生变化,新朋友可能会对用户的兴趣造成很大影响,如果可以实时更新用户的社交图谱,就可以完成对GNN动态推荐。
5.4 GNN网络更新层数问题标准的深度神经网络推荐研究中,网络层数可以达到成百上千层,由于更深的结构,可以显著提高网络的表达能力。在GNN推荐过程中,一般层数仅仅为个位数。因为堆叠多个GNN层将会导致过度平滑,所有顶点将收敛到相同的值。如何选择GNN更新的层数以及其他相关的参数,以缓解堆叠多层GNN推荐造成的平滑问题,是GNN推荐难点所在。
5.5 数据稀疏问题GNN推荐中,通过构建节点和边,将各个对象用边“连接”起来,在缓解数据稀疏性方面相比传统的推荐模型会有提升。但GNN推荐模型在面临数据稀疏的时候,往往会出现两个问题:1)如果节点对应的对象没有任何相关记录时,相关推荐算法将难以实现,如文献[36]中,如果有新来的病人或者病人的就诊记录很少,如仅为一条记录,GNN推荐模型会难以得到可以代表用户特征的最终结果;2)节点属性维度缺失问题。一个向量化的多维节点,每一个维度都反映一个对应的属性,如果该属性的值是未知的,在向量化的过程中就无法写入相应的数值,将会影响到推荐的效果。在文献[36]中就出现了病人未参加部分医疗测试的情况,作者通过重新构建测试结果,解决这个问题,但模型的复杂度也随之增加。
6 GNN推荐未来研究方向1)基于上下文的GNN推荐
用户的兴趣和行为往往是随着时间、空间等因素动态发生变化的,在目前的推荐系统中,很多学者对基于时间上下文的个性化推荐[37],基于情景上下文的推荐[38]都有一定的研究,通过联系上下文往往会获得更加精确的推荐效果。现有GNN推荐研究不论是构建用户−用户关系图还是用户−物品(项目)关系图,都只是单纯的将用户(物品)相关信息进行处理。时间与空间上下文信息,都没有考虑在内。如在文献[31]中,作者没有考虑到用户兴趣会随着时间变化对浏览的记录产生的影响,文献[36]中,没有考虑到患者就诊记录的时间问题,但在不同时期同一个患者情况会存在很大差异。如何在GNN推荐模型中引入时间、内容以及位置等不同的上下文信息,以提高推荐性能是值得研究的重要课题之一。
2)基于GNN的跨领域推荐
跨领域推荐[39]对解决推荐系统的冷启动和数据稀疏性问题有很大的帮助,通过从辅助域到目标域的推荐可以取得良好的推荐效果。在传统的推荐研究中,跨领域推荐取得了一定成效,如基于标签的跨领域推荐[40],基于共享知识的跨领域推荐[41]等。现有GNN推荐研究中,往往只是对“一张”图进行“加工”,停留在一个单一的层面上,如何从一张图过渡到另一张图,实现不同GNN图模型间信息的有效迁移,是一个值得研究的课题。如文献[36]中,作者仅仅考虑到病人在一家医院的就诊情况,如果考虑到病人的更多信息,如生活习惯、职业、年龄等将这些作为辅助域的信息充分利用,就可以获得更加精确的推荐效果。
3)基于GNN的群组推荐
推荐系统的应用越来越广泛,推荐的对象从单个用户的个性化推荐发展为面向多个用户的群组推荐。现有GNN推荐研究中,主要是个性化推荐,很少涉及GNN群组推荐,如何通过GNN进行群组推荐未来值得研究的问题。
4)基于GNN的套餐推荐
当前的推荐系统大多推荐内容单一,仅能满足用户的部分需求,现实生活中,用户需求往往是多方面的。如对旅游的用户进行推荐时,如果能通过GNN的高度归纳性将路线规划、住宿环境、交通方式、特产商铺、消费价格等多个因素进行综合考虑,为用户推荐最适合的套餐服务,这将会给用户带来更好的旅游体验。
5) GNN推荐与其他推荐方法融合
深度学习发展迅猛,在不同领域的研究都取得了突破性进展,而 GNN推荐实质上只是获取节点的状态之后再用函数进行输出,可以考虑融合其他推荐算法或者传统深度学习技术,减少模型的时间复杂度,同时提高推荐的效果。
6) GNN推荐的可解释性研究
GNN的应用范围很广泛,比如文献[42]利用GNN模拟各个物理系统间的关系,进行演绎来预测整个系统的下一个状态,这说明GNN具有一定的因果推理能力。现有GNN推荐研究中,尽管取得了不错的推荐效果,但是推荐结果往往很难给出一个令用户信服的科学解释。如在文献[31]中,作者使用多个GNN模型得出特征后,通过MLP进行评分预测,仍然缺乏一定的可解释性。
7 结束语图神经网络(GNN)推荐方法可以通过节点、边及对应的拓扑结构直接反映推荐系统中实体及其相互间关系,直接在图上对相关信息进行不断更新计算,具有很强的归纳性,有效避免了传统推荐方法中信息利用不完全带来诸多问题,越来越受到学术界和产业界的关注。本文深入分析了GNN推荐及其过程,对现有GNN推荐相关研究从无向单元图推荐、无向二元图推荐、无向多元图推荐3个方面进行详细探讨,对各自的优点与不足进行了分析,指出了GNN推荐面临的难点及未来的研究方向,对基于图的深度推荐系统进一步研究具有一定的借鉴意义。
| [1] |
ZHOU J, CUI G, ZHANG Z, et al. Graph neural networks: a review of methods and applications[J]. arXiv: 1812.08434, 2018.
( 0) 0)
|
| [2] |
BASTINGS J, TITOV I, AZIZ W, et al. Graph convolutional encoders for syntax-aware neural machine translation[C]//Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Copenhagen, Denmark, 2017: 1957−1967.
( 0) 0)
|
| [3] |
HENAFF M, BRUNA J, LECUN Y. Deep convolutional networks on graph-structured data[J]. arXiv:1506.05163, 2015.
( 0) 0)
|
| [4] |
ZHANG Yuhao, QI Peng, MANNING C D. Graph convolution over pruned dependency trees improves relation extraction[C]//Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Brussels, Belgium, 2018: 2205−2215.
( 0) 0)
|
| [5] |
WANG Xiaolong, YE Yufei, GUPTA A. Zero-shot recognition via semantic embeddings and knowledge graphs[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018: 6857−6866.
( 0) 0)
|
| [6] |
RHEE S,SEO S, KIM S.Hybrid approach of relation network and localized graph convolutional filtering for breast cancer subtype classification[J].arXiv: 1711.05859,2017.
( 0) 0)
|
| [7] |
KAWAMOTO T, TSUBAKI M, OBUCHI T. Mean-field theory of graph neural networks in graph partitioning[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook, USA, 2018: 4361−4371.
( 0) 0)
|
| [8] |
HAMILTON W, YING Zhotao, LESKOVEC J. Inductive representation learning on large graphs[C]//Advances in Neural Information Processing Systems. Long Beach, US, 2017: 1024−1034.
( 0) 0)
|
| [9] |
CHEN J, MA T, XIAO C. Fastgcn: fast learning with graph convolutional networks via importance sampling[J]. arXiv:1801.10247, 2018.
( 0) 0)
|
| [10] |
CHEN Jianfei, ZHU Jun, SONG Le. Stochastic training of graph convolutional networks with variance reduction[C]//Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden, 2018: 941−949.
( 0) 0)
|
| [11] |
LI Q, HAN Z, WU X M. Deeper insights into graph convolutional networks for semi-supervised learning[C]//Thirty-Second AAAI Conference on Artificial Intelligence. New Orleans, USA,2018.
( 0) 0)
|
| [12] |
BRUNA J, ZAREMBA W, SZLAM A, et al. Spectral networks and locally connected networks on graphs[C]//International Conference on Learning Representations (ICLR2014). Banff, Canada, 2014: 1−14.
( 0) 0)
|
| [13] |
MONTI F, BOSCAINI D, MASCI J, et al. Geometric deep learning on graphs and manifolds using mixture model CNNs[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 5115−5124.
( 0) 0)
|
| [14] |
ATWOOD J, TOWSLEY D. Diffusion-convolutional neural networks[C]//Advances in Neural Information Processing Systems. Barcelona, Spain, 2016: 1993−2001.
( 0) 0)
|
| [15] |
LI Y, ZEMEL R, BROCKSCHMIDT M, et al. Gated graph sequence neural networks [J]. arXiv:1511.05493, 2015.
( 0) 0)
|
| [16] |
ZHANG Yue, LIU Qi, SONG Linfeng. Sentence-state LSTM for text representation[C]//Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics. Melbourne, Australia, 2018: 317−327.
( 0) 0)
|
| [17] |
KAMPFFMEYER M, CHEN Yinbo, LIANG Xiaodan, et al. Rethinking knowledge graph propagation for zero-shot learning[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA, 2019: 11487−11496.
( 0) 0)
|
| [18] |
黄璐, 林川杰, 何军, 等. 融合主题模型和协同过滤的多样化移动应用推荐[J]. 软件学报, 2017, 28(3): 708-720. HUANG Lu, LIN Chuanjie, HE Jun, et al. Diversified mobile app recommendation combining topic model and collaborative filtering[J]. Journal of software, 2017, 28(3): 708-720. (  0) 0)
|
| [19] |
胡堰, 彭启民, 胡晓惠. 一种基于隐语义概率模型的个性化Web服务推荐方法[J]. 计算机研究与发展, 2014, 51(8): 1781-1793. HU Yan, PENG Qimin, HU Xiaohui. A personalized Web service recommendation method based on latent semantic probabilistic model[J]. Journal of computer research and development, 2014, 51(8): 1781-1793. DOI:10.7544/issn1000-1239.2014.20130024 (  0) 0)
|
| [20] |
刘建勋, 石敏, 周栋, 等. 基于主题模型的Mashup标签推荐方法[J]. 计算机学报, 2017, 40(2): 520-534. LIU Jianxun, SHI Min, ZHOU Dong, et al. Topic model based tag recommendation method for Mashups[J]. Chinese journal of computers, 2017, 40(2): 520-534. DOI:10.11897/SP.J.1016.2017.00520 (  0) 0)
|
| [21] |
曹俊豪, 李泽河, 江龙, 等. 一种融合协同过滤和用户属性过滤的混合推荐算法[J]. 电子设计工程, 2018, 26(9): 60-63. CAO Junhao, LI Zehe, JIANG Long, et al. A hybrid recommendation algorithm based on collaborative filtering and user attribute filtering[J]. Electronic design engineering, 2018, 26(9): 60-63. DOI:10.3969/j.issn.1674-6236.2018.09.014 (  0) 0)
|
| [22] |
张双庆. 一种基于用户的协同过滤推荐算法[J]. 电脑知识与技术, 2019, 15(1): 19-21. ZHANG Shuangqing. User-based collaborative filtering recommendation algorithm[J]. Computer knowledge and technology, 2019, 15(1): 19-21. (  0) 0)
|
| [23] |
邓园园, 吴美香, 潘家辉. 基于物品的改进协同过滤算法及应用[J]. 计算机系统应用, 2019, 28(1): 182-187. DENG Yuanyuan, WU Meixiang, PAN Jiahui. Improved item-based collaborative filtering algorithm and its application[J]. Computer systems & applications, 2019, 28(1): 182-187. DOI:10.15888/j.cnki.csa.006726 (  0) 0)
|
| [24] |
高玉凯, 王新华, 郭磊, 等. 一种基于协同矩阵分解的用户冷启动推荐算法[J]. 计算机研究与发展, 2017, 54(8): 1813-1823. GAO Yukai, WANG Xinhua, GUO Lei, et al. Learning to recommend with collaborative matrix factorization for new users[J]. Journal of computer research and development, 2017, 54(8): 1813-1823. DOI:10.7544/issn1000-1239.2017.20170188 (  0) 0)
|
| [25] |
王伟, 陈伟, 祝效国, 等. 众筹项目的个性化推荐: 面向稀疏数据的二分图模型[J]. 系统工程理论与实践, 2017, 37(4): 1011-1023. WANG Wei, CHEN Wei, ZHU K, et al. Personalized recommendation of crowd-funding campaigns: a bipartite graph approach for sparse data[J]. Systems engineering–theory & practice, 2017, 37(4): 1011-1023. DOI:10.12011/1000-6788(2017)04-1011-13 (  0) 0)
|
| [26] |
ELKAHKY A M, SONG Yang, HE Xiaodong. A multi-view deep learning approach for cross domain user modeling in recommendation systems[C]//Proceedings of the 24th International Conference on World Wide Web. Florence, Italy, 2015: 278−288.
( 0) 0)
|
| [27] |
ZHENG Lei, NOROOZI V, YU P S. Joint deep modeling of users and items using reviews for recommendation[C]//Proceedings of the Tenth ACM International Conference on Web Search and Data Mining. New York, USA, 2017: 425−434.
( 0) 0)
|
| [28] |
LIU Q, WU S, WANG L, et al. Predicting the next location: a recurrent model with spatial and temporal contexts[C]//Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. Arizona, USA ,2016: 194−200.
( 0) 0)
|
| [29] |
XU,KEYULU,et al.How powerful are graph neural networks [J]. arXiv:1810.00826, 2018.
( 0) 0)
|
| [30] |
SONG Weiping, XIAO Zhiping, WANG Yifan, et al. Session-based social recommendation via dynamic graph attention networks[C]//Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining. New York, United States, 2019: 555−563.
( 0) 0)
|
| [31] |
FAN Wenqi, MA Yao, LI Qing, et al. Graph neural networks for social recommendation[C]//The World Wide Web Conference. New York, USA, 2019: 417−426.
( 0) 0)
|
| [32] |
YING R, HE Ruining, CHEN Kaifeng, et al. Graph convolutional neural networks for web-scale recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, USA, 2018: 974−983.
( 0) 0)
|
| [33] |
CUI Zeyu, LI Zekun, WU Shu, et al. Dressing as a whole: outfit compatibility learning based on node-wise graph neural networks[C]//The World Wide Web Conference. New York, USA, 2019: 307−317.
( 0) 0)
|
| [34] |
WANG X, HE X, WANG M, et al. Neural graph collaborative filtering[J]. arXiv:1905.08108, 2019.
( 0) 0)
|
| [35] |
WANG Hongwei, ZHAO Miao, XIE Xing, et al. Knowledge graph convolutional networks for recommender systems[C]//The World Wide Web Conference. San Francisco, USA, 2019: 3307−3313.
( 0) 0)
|
| [36] |
MAO C, YAO L, LUO Y. MedGCN: Graph convolutional networks for multiple medical tasks[J]. arXiv: 1904.00326, 2019.
( 0) 0)
|
| [37] |
刘云, 王颖, 亓国涛, 等. 时间上下文的协同过滤Top-N推荐算法[J]. 计算机技术与发展, 2017, 27(7): 79-82. LIU Yun, WANG Ying, QI Guotao, et al. Collaborative filtering top-N recommendation algorithm based on time context[J]. Computer technology and development, 2017, 27(7): 79-82. DOI:10.3969/j.issn.1673-629X.2017.07.019 (  0) 0)
|
| [38] |
沈记全, 王磊, 侯占伟, 等. 基于情景上下文与信任关系的旅游景点推荐算法[J]. 计算机应用研究, 2018, 35(12): 3640-3643. SHEN Jiquan, WANG Lei, HOU Zhanwei, et al. Attractions recommendation algorithm based on situational context and trust relationship[J]. Application research of computers, 2018, 35(12): 3640-3643. DOI:10.3969/j.issn.1001-3695.2018.12.026 (  0) 0)
|
| [39] |
李林峰, 刘真, 魏港明, 等. 基于共享知识模型的跨领域推荐算法[J]. 电子学报, 2018, 46(8): 1947-1953. LI Linfeng, LIU Zhen, WEI Gangming, et al. Cross-domain recommendation algorithm based on sharing knowledge pattern[J]. Acta electronica sinica, 2018, 46(8): 1947-1953. DOI:10.3969/j.issn.0372-2112.2018.08.020 (  0) 0)
|
| [40] |
邢长征, 杨晓婷. 基于SVD++与标签的跨域推荐模型[J]. 计算机工程, 2018, 44(4): 225-230. XING Changzheng, YANG Xiaoting. Cross-domain recommendation model based on SVD++ and tag[J]. Computer engineering, 2018, 44(4): 225-230. DOI:10.3969/j.issn.1000-3428.2018.04.036 (  0) 0)
|
| [41] |
李林峰, 刘真, 魏港明, 等. 基于共享知识模型的跨领域推荐算法[J]. 电子学报, 2018, 46(8): 1947-1953. LI Linfeng, LIU Zhen, WEI Gangming, et al. Cross-domain recommendation algorithm based on sharing knowledge pattern[J]. Acta electronica sinica, 2018, 46(8): 1947-1953. DOI:10.3969/j.issn.0372-2112.2018.08.020 (  0) 0)
|
| [42] |
BATTAGLIA P, PASCANU R, LAI M, et al. Interaction networks for learning about objects, relations and physics[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook, USA, 2016: 4502−4510.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


