自然界里存在着许多生物聚集的现象，比如候鸟迁徙、鱼群逆流、蚁群迁徙等，通过对自然界各种群集现象的研究以及对现有的网络模型结构的理解，学者们提出了多智能体系统(multi-agent systems，MAS)的概念^[1]。多智能体系统中各智能体间相互协同合作的基础就是一致性问题；文献[2]给出了多智能体系统一致性问题的系统基础结构，同时对一致性问题提出了标准化的数学表达。

在多智能体系统实际应用中，为解决如机器人的避障问题、两组无人机在保持其编队的同时向相反方向飞行问题等。文献[3]研究了存在敌对关系的多智能体系统的一致性问题，提出了二分一致性的概念，其中将智能体划分为两个不同的集合，这两个集合中的智能体分别收敛到两个大小相同但符号相反的期望值并保持一致。文献[4]分析给出了存在敌对关系的含常数时滞多智能体系统达到二分一致性的充分必要条件，证明了具有无向拓扑结构的多智能体系统可行的最大时滞仅仅和拉普拉斯矩阵的最大特征值有关。此外，文献[5-8]在多智能系统二分一致性方面也做了重要研究。在智能体系统应用中，由于通信设备发展水平限制各个体之间客观存在通信时延，这一问题严重地影响系统的稳定性。因此，研究含通信时延的多智能体系统的稳定性在实际工程中有着至关重要的意义。文献[9-10]通过对系统进行了频域的分析，同时还利用线性矩阵不等式的定理给出了系统在所提出的控制协议中，允许的时滞上界。文献[11-12]中分别给出了具有常数时延的二阶多智能体系统达成一致的充分必要条件。文献[13]利用线性矩阵不等式理论，对通信时延为常数的二阶多智能体系统给出实现一致性收敛的充分条件。对于一般时延线性系统，文献[14]研究了一种基于观测器的多智能体系统控制策略，利用系统转换方法，建立了多智能体系统一致性的等价条件。文献[15-16]通过适当的线性变换，证明了含时变时延的离散线性多智能体系统的一致性理论。文献[17-18]针对通信资源受限的情况，设计分析分布式异步控制算法，解决了结构不平衡有向图中多智能体系统环形编队问题。同时，文献[19-22]进一步对考虑时滞约束条件下的多智能系统进行稳定性问题分析。

综合所述，本文研究了具有固定时延和时变时延的多智能体系统二分一致性控制。在固定时延系统下，利用广义Nyquist准则的方法，分析并得到系统实现二分一致的充分条件。在时变时延下，利用Lyapunov稳定性理论和线性矩阵不等式理论，分析得到相较于文献[16]保守性更小的系统实现二分一致性的充分条件。

文中 $ {{R}} $ 表示一个实数， $ {{ R}}^{n\times n} $ 表示一个 $ n\times n $ 的实数矩阵， $ {{ x}}^{n} $ 表示一个 $ n $ 维实数向量， $ { I}\in {{ R}}^{n\times n} $ 为 $ n $ 阶单位阵； $ {{\bf{1}}}_{{ n}} $ 表示向量 $\left[\mathrm{1\;\;1}\;\; \cdots \;\;1\right]\in {{ R}}^{n}$ ， $ {{\bf{0}}}_{n} $ 表示向量 $ \left[\mathrm{0\;\;0}\;\;\cdots \;\;0\right]\in {{ R}}^{n} $ ； ${\rm{diag}}\left\{{\lambda }_{1}\;{\lambda }_{2}\;\cdots \;{\lambda }_{n}\right\}$ 表示 $ n $ 阶对角阵。

1 预备知识 1.1 图论与数学基础

考虑权重符号图，用三元组 $ { G}=\left({ V},{ E},{ A}\right) $ 来表示；其中 $ { V}=\left\{{v}_{1},{v}_{2},\cdots ,{v}_{n}\right\} $ 表示由一组节点组成的集合， $ { E}\subseteq { V}\times { V} $ 表示边的集合，节点的下标集合 $ { N}=\left\{\mathrm{1,2},\cdots ,n\right\} $ ，同时 $ { A}=\left[{a}_{ij}\right]\in {{ R}}^{n\times n} $ 是带权重的符号图 $ { G} $ 所对应的邻接矩阵， $ {a}_{ij} $ 表示权重。如果智能体 $ i $ 和智能体 $ j $ 之间存在信息交互，对应邻接矩阵 $ { A} $ 中的元素 $ {a}_{ij} $ 非零。边集可以表示为 $ { E}= {{ E}}^{+}\cup {{ E}}^{-} $ ， $ {{ E}}^{+} $ 和 $ {{ E}}^{-} $ 分别为边集合中的正边集合和负边集合，即 $ {{ E}}^{+}=\left\{\left(i,j\right)\left|{a}_{ij}>0\right.\right\} $ 和 $ {{ E}}^{-}=\left\{\left(i,j\right)\left|{a}_{ij}<0\right.\right\} $ 。若 $ {a}_{ij}\ne 0 $ ，称节点 $ {v}_{j} $ 为节点 $ {v}_{i} $ 的邻居，节点 $ {v}_{i} $ 的所有邻居组成的集合称节点 $ {v}_{i} $ 的邻集，记该集合为 $ {N}_{i} $ ，即 $ {N}_{i}=\left\{j\in V\left|\left(i,j\right)\in E,i\ne j\right.\right\} $ 。带权重符号图的邻接矩阵 $ { A}=\left[{a}_{ij}\right]\in {{ R}}^{n\times n} $ ，其中元素定义为：

${a_{ij}} = \left\{ {\begin{array}{*{20}{l}} { {\text{非}} 0,}\quad{\left( {{v_j},{v_i}} \right) \in E}\\ {0,}\quad{\text{其他}} \end{array}} \right.$

本文不考虑带自环的图，即 $ {a}_{ii}=0,\forall i= \mathrm{1,2},\cdots , n $ 。节点 $ {v}_{i} $ 到节点 $ {v}_{j} $ 的一组边用路径 $\left\{ {\left( {{v_{{i_1}}},{v_{{i_2}}}} \right),} \right. \left. {\left( {{v_{{i_2}}},{v_{{i_3}}}} \right), \cdots ,( {{v_{{i_{p - 1}}}},{v_{{i_p}}}} )} \right\}$ 来表示，其中 $ {v}_{{i}_{m}} $ 是不同的节点， $ m=\mathrm{1,2},\cdots ,p $ ， $ i\ne j $ 。如果任意两个节点都存在路径，则无向符号图 $ { G} $ 是连通的。

考虑正负混合连接权重矩阵 $ { A} $ ，若令矩阵 $ { L}={ C}-{ A}=\left[{l}_{ij}\right]\in {{ R}}^{n\times n} $ 表示无向符号图 $ { G} $ 的拉普拉斯矩阵，则其元素 $ {l}_{ij} $ 可定义为

${l_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\displaystyle\sum \limits_{j \in {N_i}} \left| {{a_{ij}}} \right|{\rm{,}}}\quad{j = i}\\ { - {a_{ij}}{\rm{,}}}\quad{j \ne i} \end{array}} \right.$

其中 ${ C}={\rm{diag}}\left\{\displaystyle\sum \limits_{j\in {N}_{1}}\left|{a}_{1j}\right|,\displaystyle\sum \limits_{j\in {N}_{2}}\left|{a}_{2j}\right|,\cdots ,\displaystyle\sum \limits_{j\in {N}_{n}}\left|{a}_{nj}\right|\right\}$ 为图 $ { G} $ 的度矩阵。

定义1^[23] 　对于符号图 $ { G} $ ，如果节点集 $ { V} $ 可以分为两个集合 $ {{ V}}_{1} $ 和 $ {{ V}}_{2} $ ，其中， $ {{ V}}_{1}\cup {{ V}}_{2}={ V},{{ V}}_{1}\cap {{ V}}_{2}=\mathrm{\varnothing } $ ，且满足以下２个条件：

1)若 $ \forall {v}_{i},{v}_{j}\in {{ V}}_{l}\left(l\in \left\{\mathrm{1,2}\right\}\right) $ ，则所有权重 ${a}_{ij} \geqslant 0$ ；

2)若 $ \forall {v}_{i}\in {{ V}}_{l},{v}_{j}\in {{ V}}_{q},l\ne q\left(l,q\in \left\{\mathrm{1,2}\right\}\right) $ ，则所有权重 ${a}_{ij}\leqslant 0$ 。

则称该符号图 $ { G} $ 为结构平衡；否则称该符号图为结构不平衡。

引理1^[24] 　若图 $ { G} $ 为结构平衡时，则存在正交矩阵 $ { D} $ 使得 $ {{ L}}_{{ D}}={ D}{ L}{ D} $ 为图 $ { G} $ 的拉普拉斯矩阵，存在单一特征值0。对应的矩阵 $ { D} $ 称为规范变换(gauge transformation)。

引理2^[25] 　对于任意 $ \gamma \in \left[\mathrm{0,1}\right) $ ，当 $\omega \in [-{\text{π}},{\text{π}}]$ 时，凸包 $\gamma {\rm{C}}\mathrm{o}({E}_{i}\left(\mathrm{j}\omega \right),i\in { N})$ 不包含 $ (-1,\mathrm{j}0) $ 点，其中 ${E}_{i}\left(\mathrm{j}\omega \right)=\dfrac{\text{π}}{2\tau }\times \dfrac{{\mathrm{e}}^{-\tau \mathrm{j}\omega }}{\mathrm{j}\omega }$ ， $ \tau $ 为系统的时延。

引理3^[18] 　对于 $\omega \in \left[-{\text{π}},{\text{π}}\right]$ ，凸包 ${\rm{C}}\mathrm{o}(0\cup \{{W}_{i}\left(\mathrm{j}\omega \right), i\in { N}\left)\right\})$ 包含圆盘集合 $ {\cup }_{i\in { N}}{G}_{i} $ 。

1.2 问题描述

假设系统由 $ n $ 个一阶积分器智能体系统组成，该系统中每个智能体的动力学方程可以描述为

$ {\dot{x}}_{i}\left(t\right)={u}_{i}\left(t\right),i=\mathrm{1,2},\cdots ,n $

(1)

其中 $ {x}_{i}\left(t\right)\in R $ 和 $ {u}_{i}\left(t\right)\in R $ 分别表示智能体 $ i $ 的状态和控制输入。在上述系统式(1)中考虑含固定时延和时变时延多智能体系统的二分一致性控制协议 $ {u}_{i}\left(t\right) $ 分别为

$ \begin{array}{l} {u_i}\left( t \right) = - \displaystyle\sum\limits_{j \in {N_i}} {\left| {{a_{ij}}} \right|} ({x_i}\left( {t - {\tau _0}} \right) - {\rm{sgn}}\left( {{a_{ij}}} \right){x_j}(t - {\tau _0})) \end{array}$

(2)

和

$ \begin{array}{l} {u}_{i}\left(t\right)=-\displaystyle\sum \limits_{j\in {N}_{i}}\left|{a}_{ij}\right|({x}_{i}\left(t-\tau \left(t\right)\right)- \mathrm{sgn}\left({a}_{ij}\right){x}_{j}(t-\tau (t\left)\right) \end{array} $

(3)

其中 $ {\tau }_{0} $ 为系统固定时延； $ \tau \left(t\right) $ 为系统时变时延，且 $0 \leqslant \tau \left(t\right) \leqslant {h}$ , ${h}$ 为时延上界。

定义向量 ${ x}\left(t\right)={\left[{x}_{1}\left(t\right)\quad{x}_{2}\left(t\right) \quad \cdots \quad {x}_{n}\left(t\right)\right]}^{\mathrm{T}}$ ，将二分一致性控制协议式(2)或式(3)分别作用于系统式(1)，得到

$ \dot{{ x}}\left(t\right)=-{ L}{ x}\left(t-{\tau }_{0}\right) $

(4)

和

$ \dot{{ x}}\left(t\right)=-{ L}{ x}(t-\tau (t\left)\right) $

(5)

其中 $ { L} $ 为拉普拉斯矩阵。

2 二分一致性分析 2.1 含固定时延的二分一致性

为便于进行二分一致性分析，引入中间变量对原系统进行规范状态变换。定义矩阵 ${ D}= {\rm{diag}} \left({\sigma }_{1},{\sigma }_{2},\cdots ,{\sigma }_{{n}}\right),{\sigma }_{{i}}\in \{\pm 1\}$ 是在 $ R $ 中进行的坐标变换。对给定系统式(4)做如下变换：

定义 $ {Y}_{i}\left(t\right)={\sigma }_{i}{x}_{i}\left(t\right) $ ，由于 ${\sigma }_{{i}}\in \{\pm 1\}$ ，所以 $ {x}_{i}\left(t\right)= {\sigma }_{i}{Y}_{i}\left(t\right) $ ；其中 $ {\sigma }_{i} $ 由引理1给出，则进而定义向量 ${ Y}\left(t\right)={\left[{Y}_{1}\left(t\right)\quad{Y}_{2}\left(t\right)\quad \cdots \quad{Y}_{n}\left(t\right)\right]}^{\mathrm{T}}$ ，则有 $ { Y}\left(t\right)={ D}x\left(t\right) $ ，代入式(4)可得

$ \begin{array}{c} \dot{{ Y}}\left(t\right)={ D}\dot{{ x}}\left(t\right)={ D}\left(-{ L}{ x}\left(t-{\tau }_{0}\right)\right)= \\ { D}\left(-{ L}{{ D}}^{-1}{ Y}\left(t-{\tau }_{0}\right)\right)= -{{ L}}_{{ D}}{ Y}\left(t-{\tau }_{0}\right) \end{array} $

(6)

其中

$ \begin{array}{l} {{ L}}_{{ D}}={ D}{ L}{ D}={ C}-{ D}{ A}{ D}= \\ \left\{ {\begin{array}{*{20}{l}} { - |{a_{ij}}|,}\quad{{v_j}\in {N_i}}\\ {\displaystyle \sum \limits_{{v_j}\in {N_i}} \left| {{a_{ij}}} \right|,}\quad{j = i}\\ {0,}\quad{\text{其他}} \end{array}} \right. \end{array} $

可知系统式(4)的二分一致性问题等价于系统式(6)的稳定性问题。

定理1　给定包含 $ n $ 个智能体的一阶系统式(1)的结构平衡符号图 $ G $ ，应用含固定时延的二分一致性控制协议式(2)，对于通信时延 $ {\tau }_{0} $ 满足条件：对于 $ \forall i\in { N} $ ，如果 $\varepsilon {\tau }_{0} < \dfrac{\text{π}}{4}$ ，其中 $\varepsilon = \mathrm{m}\mathrm{a}\mathrm{x} \left(\displaystyle\sum \limits_{{v}_{j}\epsilon {N}_{i}}\left|{a}_{ij}\right|\right)$ ，则系统可实现二分一致性。

证明　对系统(6)进行拉氏变换，得到特征方程：

$ \mathrm{det}\left(s{ I}+{{ L}}_{{ D}}\left(s\right)\right)=0 $

其中

$\begin{array}{l} {{ L}}_{{ D}}\left(s\right)={\mathrm{e}}^{-{\tau }_{0}s}\left({ C}-{ D}{ A}{ D}\right)= \\ \left\{ {\begin{array}{*{20}{l}} { - |{a_{ij}}|{{\rm{e}}^{ - {\tau _0}s}},}\quad{{v_j} \in {N_i}}\\ {\displaystyle \sum \limits_{{v_j}\in {N_i}} \left| {{a_{ij}}} \right|{{\rm{e}}^{ - {\tau _0}s}},}\quad{j = i}\\ {0,}\quad{\text{其他}} \end{array}} \right. \end{array}$

令

$ F\left(s\right)=\mathrm{det}\left({s}{ I}+{{ L}}_{{ D}}\left(s\right)\right) $

(7)

根据线性系统稳定性条件和判定规则可知，系统式(6)要实现稳定性等价于 $ F\left(s\right) $ 的零点具有负实部或者 $ s=0 $ ，接下来分两点进行分析。

1)当 $ s=0 $ 时， $ F\left(0\right)=\mathrm{d}\mathrm{e}\mathrm{t}(0{ I}+{{ L}}_{{ D}}\left(0\right)) $ ，根据引理1可得 $ {{ L}}_{{ D}} $ 存在单一特征根0，因此当 $ s=\;0 $ 时， $ F\left(s\right) $ 只有一个零点。

2)当 $ s\ne 0 $ 时，令

$ {F}^{*}\left(s\right)=\mathrm{d}\mathrm{e}\mathrm{t}({ I}+{ G}(s\left)\right) $

(8)

其中

$ { G}\left(s\right)={\mathrm{e}}^{-{\tau }_{0}s}\frac{{ C}-{ D}{ A}{ D}}{s} $

(9)

若使式(7)的零点都具有负实部，则式(8)的零点需都具有负实部。令 $ s=\mathrm{j}\omega $ ，代入式(9)得到

$ { G}\left(\mathrm{j}\omega \right)={\mathrm{e}}^{-{\tau }_{0}\mathrm{j}\omega }\frac{{ C}-{ D}{ A}{ D}}{s} $

(10)

根据广义Nyquist准则，当式(10)特征值 $\lambda \left({{G}}\left(\mathrm{j}\omega \right)\right)$ 不包含点 $ (-1,\mathrm{j}0) $ , $\omega \in [-{\text{π}},{\text{π}}]$ 时式(8)的零点都具有负实部。进一步对式(10)的特征值 $\lambda \left({{G}}\left(\mathrm{j}\omega \right)\right)$ 进行分析，利用Gerschgorin圆盘定理，可得：

$ \lambda \left({{G}}\left(\mathrm{j}\omega \right)\right)\in {\cup }_{i\in { N}}{G}_{i} $

(11)

$ \begin{array}{c} {G}_{i}=\left\{\zeta \epsilon C,|\zeta -\displaystyle\sum \limits_{{v}_{j}\epsilon {{ N}}_{i}}\left|{a}_{ij}\right|\dfrac{{\mathrm{e}}^{-{\tau }_{0}\mathrm{j}\omega }}{\mathrm{j}\omega } \leqslant \left|\displaystyle\sum \limits_{{v}_{j}\epsilon {{ N}}_{i}}\left|{a}_{ij}\right|\dfrac{{\mathrm{e}}^{-{\tau }_{0}\mathrm{j}\omega }}{\mathrm{j}\omega }\right|\right\} \end{array} $

(12)

其中， $ \zeta $ 为任意特征值， $ C $ 为复数域，令 ${\varepsilon }_{i}= \displaystyle\sum \limits_{{v}_{j}\epsilon {{ N}}_{i}}\left|{a}_{ij}\right|$ ，则圆盘中心为

$ {G}_{i0}\left(\mathrm{j}\omega \right)={\varepsilon }_{i}\frac{{\mathrm{e}}^{-{\tau }_{0}\mathrm{j}\omega }}{\mathrm{j}\omega } $

定义复平面原点为0点，则过0点和圆盘中心 $ {G}_{i0} $ 的直线与圆盘 $ {G}_{i} $ 的交点为 $ {W}_{i} $ ，其轨迹为

$ {W}_{i}\left(\mathrm{j}\omega \right)=2{\varepsilon }_{i}\frac{{\mathrm{e}}^{-{\tau }_{0}\mathrm{j}\omega }}{\mathrm{j}\omega } $

由引理2 ，令 $ {W}_{i}\left(\mathrm{j}\omega \right)={\gamma }_{i}{E}_{i}\left(\mathrm{j}\omega \right) $ 。当 ${\gamma }_{i}=\dfrac{4{\varepsilon }_{i}{\tau }_{0}}{\text{π}} < 1$ 时，得到 ${\varepsilon }_{i}{\tau }_{0} < \dfrac{\text{π}}{4}$ 。令 $ \gamma =\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\gamma }_{i},i\in { N}\right\} $ ，显然当 $ \gamma <1 $ ，对于任意的 $ i\in { N} $ ，下式成立：

$ \begin{array}{c} \gamma {\rm{C}}\mathrm{o}({0\cup \{E}_{i}\left(\mathrm{j}\omega \right),i\in { N}\})\ni \\ {\gamma }_{i}{\rm{C}}\mathrm{o}({0\cup \{E}_{i}\left(\mathrm{j}\omega \right),i\in { N}\})={\rm{C}}\mathrm{o}({W}_{i}\left(\mathrm{j}\omega \right),i\in { N}\left\}\right) \end{array}$

可知, $(-1,\mathrm{j}0)\notin \gamma {\rm{C}}\mathrm{o}({0\cup \{E}_{i}\left(\mathrm{j}\omega \right),i\in { N}\})$ ，则 $(-1,\mathrm{j}0)\notin {\rm{C}}\mathrm{o}({0\cup \{W}_{i}\left(\mathrm{j}\omega \right),i\in { N}\})$ 。由引理3，得 ${\rm{C}}\mathrm{o} (0\cup \left\{{W}_{i}\left(\mathrm{j}\omega \right),i\in { N})\right\})\supseteq {\cup }_{i\in { N}}{G}_{i}$ ，因此 $ (-1,\mathrm{j}0)\notin {\cup }_{i\in { N}}{G}_{i} $ 。进而代入式(12)可知 $\lambda \left({{G}}\left(\mathrm{j}\omega \right)\right)$ 不包含 $ (-1,\mathrm{j}0) $ 。根据广义Nyquist准则，式(8)的零点都具有负实部，所以系统式(6)可实现渐近稳定，则可说明系统式(4)可实现二分一致性。

2.2 含时变时延的二分一致性

在实际工程中多智能系统所含时延并不是固定不变的，因此在本节中将考虑系统中含有时变时延的一阶系统进行二分一致性分析，针对系统式(5)引入中间变量对其进行规范状态变换，过程同式(4)变换：

$ \dot{{ Y}}\left(t\right)=-{{ L}}_{{ D}}{ Y}\left(t-\tau \left(t\right)\right) $

(13)

易得知式(13)的稳定性问题等价于系统式(5)的二分一致性问题。因此，可以借助系统式(13)的稳定性分析扩展到二分一致性分析。

下面通过构造Lyapunov-Krasovskii函数，给出了含时变时延系统式(5)实现二分一致性的充分条件。

定理2　假设系统式(1)的拓扑是连通且结构平衡的，如果存在对称矩阵： $ {{ P}}_{11} $ 、 ${{ P}}_{12}{\text{、}}{{ P}}_{13}{\text{、}}{{ P}}_{22}{\text{、}} {{ P}}_{23}{\text{、}}$ ${{ P}}_{33}{\text{、}}{{ Q}}_{11}{\text{、}}{{ Q}}_{12}{\text{、}}{{ Q}}_{22}{\text{、}}{{ W}}_{11}{\text{、}}{{ W}}_{12}{\text{、}}{{ W}}_{22}{\text{、}}{ Z}$ ，且都为非负矩阵，则系统式(1)在控制协议式(3)作用下可以达到二分一致性，从而给定时变时延上界 $ h>0 $ 满足条件式(14)和式(15)：

$ {{\psi = }}\left[ {\begin{array}{*{20}{c}} {{{{\Lambda }}_{11}}}&{{{{\Lambda }}_{12}}}&{{{{\Lambda }}_{13}}}&{{{{P}}_{12}}}&{ - \dfrac{1}{h}{{W}}_{11}^{\rm{T}} + \dfrac{1}{h}{{Z}}}\\ * &{{{{\Lambda }}_{22}}}&{ - {{L}}_{{D}}^{\rm{T}}}&0&{ - {{L}}_{{D}}^{\rm{T}}{{{P}}_{13}}}\\ * & * &{{{{\Lambda }}_{33}}}&{{{{P}}_{22}}}&{ - {{{P}}_{33}} + \dfrac{1}{h}{{W}}_{12}^{\rm{T}}}\\ * & * & * &{ - {{{Q}}_{22}}}&{{{{P}}_{23}}}\\ * & * & * & * &{ - \dfrac{1}{h}{{{W}}_{11}} - \dfrac{1}{{{h^2}}}{{Z}}} \end{array}} \right] < 0 $

(14)

$\begin{array}{c} { P}=\left[\begin{array}{c}{{ P}}_{11}\; {{ P}}_{12}\; {{ P}}_{13}\\ {{{ P}}^{\mathrm{T}}_{12}}\; {{ P}}_{22} \;{{ P}}_{23}\\ {{{ P}}^{\mathrm{T}}_{13}}\; {{{ P}}^{\mathrm{T}}_{23}}\; {{ P}}_{33}\end{array}\right]>0;{ Q}=\left[\begin{array}{c}{{ Q}}_{11} \;{{ Q}}_{12}\\ {{{ Q}}^{\mathrm{T}}_{12}}\; {{ Q}}_{22}\end{array}\right]>0 \; \\ { W}=\left[\begin{array}{c}{{ W}}_{11} \;{{ W}}_{12}\\ {{{ W}}^{\mathrm{T}}_{12}} \;{{ W}}_{22}\end{array}\right]>0 ;\; { Z}>0 \end{array}$

(15)

式中：*表示对称的值，且

$ \begin{array}{c} {{ \varLambda }}_{11}={{ P}}_{13}+{{{ P}}_{13}}+{{ Q}}^{\mathrm{T}}_{11}+h{{ W}}_{11} \\ {{ \varLambda }}_{12}=-{{ P}}_{11}{{ L}}_{{ D}}-{{ Q}}_{12}{{ L}}_{{ D}}-h{{ W}}_{11}{{ L}}_{{ D}} \\ {{ \varLambda }}_{13}=-{{ P}}_{13}+{{{ P}}^{\mathrm{T}}_{23}}+\dfrac{1}{h}{{ W}}_{22} \\ {{ \varLambda }}_{22}={{ Q}}_{22}-{h}{{{ L}}^{\mathrm{T}}_{{ D}}}{{ W}}_{22}{{ L}}_{{ D}}+\dfrac{{{h}}^{2}}{2}{{{ L}}^{\mathrm{T}}_{{ D}}}{ Z}{{ L}}_{{ D}} \\ {{ \varLambda }}_{33}=-{{ P}}_{23}-{{{ P}}^{\mathrm{T}}_{23}}-{{ Q}}_{11}-\dfrac{1}{h}{{ W}}_{22} \end{array} $

证明　构造如下Lyapunov-Krasovskii函数：

$ { V}\left(t\right)={{ V}}_{1}\left(t\right)+{{ V}}_{2}\left(t\right)+{{ V}}_{3}\left(t\right)+{{ V}}_{4}\left(t\right) $

(16)

其中

$\begin{array}{c} {{ V}}_{1}\left(t\right)={{ \varsigma }\left(t\right)}^{\mathrm{T}}{ P}{ \varsigma }\left(t\right) \\ {{ V}}_{2}\left(t\right)=\displaystyle\int_{t-\tau \left(t\right)}^{t}{{ \rho }\left(s\right)}^{\mathrm{T}}{ Q}{ \rho }\left(s\right)\mathrm{d}s \\ {{ V}}_{3}\left(t\right)=\displaystyle\int_{-h}^{0}\int_{t+\theta }^{t}{{ \rho }\left(s\right)}^{\mathrm{T}}{ W}{ \rho }\left(s\right)\mathrm{d}s\mathrm{d}\theta \\ {{ V}}_{4}\left(t\right)=\displaystyle\int_{-h}^{0}\int_{\theta }^{0}\int_{t+\lambda }^{t}{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}{ R}\dot{{ Y}}\left(s\right)\mathrm{d}s\mathrm{d}\lambda \mathrm{d}\theta \\ { \varsigma }\left(t\right)={\left[{{ Y}\left(t\right)}^{\mathrm{T}}\quad{{ Y}\left(t-h\right)}^{\mathrm{T}}\quad\displaystyle\int_{t-h}^{t}{{ Y}\left(s\right)}^{\mathrm{T}}{\rm{d}}s\right]}^{\mathrm{T}} \\ { \rho }\left(s\right)={\left[{{ Y}\left(s\right)}^{\mathrm{T}}\quad{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}\right]}^{\mathrm{T}} \end{array} $

根据Newton-Leibniz公式，则有式（17）和（18）：

$ { Y}\left(t-h\right)={ Y}\left(t\right)-\int_{t - h}^t \dot{{ Y}}\left(s\right){\rm{d}}s $

(21)

$ \begin{array}{c} \displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}\dot{{ Y}}\left(\mathrm{s}\right)\mathrm{d}s\mathrm{d}\theta =\displaystyle\int_{-h}^{0}\left[{ Y}\left(t\right)-{ Y}\left(t-\theta \right)\right]\mathrm{d}\theta = \\ h{ Y}\left(t\right)-\displaystyle\int_{t-h}^{t}{ Y}\left(s\right){\rm{d}}s \end{array} $

(22)

有如下积分不等式：

$ \begin{array}{c} -\displaystyle\int_{t-h}^{t}{{ \rho }\left(s\right)}^{\mathrm{T}}{ W}{ \rho }\left(s\right)\mathrm{d}s\leqslant \\ -\dfrac{1}{h}\displaystyle\int_{t-h}^{t}{{ \rho }\left(s\right)}^{\mathrm{T}}\mathrm{d}s{ W}\displaystyle\int_{t-h}^{t}{ \rho }\left(s\right)\mathrm{d}s \end{array} $

(23)

$ \begin{array}{c} \displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}{ R}\dot{{ Y}}\left(s\right)\mathrm{d}s\mathrm{d}\theta \leqslant \\ -\dfrac{2}{{h}^{2}}\displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}\mathrm{d}s\mathrm{d}\theta { R}\displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}\dot{{ Y}}\left(s\right)\mathrm{d}s\mathrm{d}\theta \end{array} $

(24)

对式(17)~(20)沿系统式(5)轨迹的时间导数，考虑式(21)~(24)则有

$ \begin{array}{c} {\dot{{ V}}}_{1}\left(t\right)={\dot{{ \varsigma }}\left(t\right)}^{\mathrm{T}}{ P}{ \varsigma }\left(t\right)+{{ \varsigma }\left(t\right)}^{\mathrm{T}}{ P}\dot{{ \varsigma }}\left(t\right)= \\ \left[{{ Y}\left(t\right)}^{\mathrm{T}}\;\;\;{{ Y}\left(t-h\right)\;}^{\mathrm{T}}\;\;\;\displaystyle\int_{t-h}^{t}{{ Y}\left(s\right)}^{\mathrm{T}}{\rm{d}}s\right].\\ \left[\begin{array}{ccc}{{ P}}_{11}& {{ P}}_{12}& {{ P}}_{13}\\ *& {{ P}}_{22}& {{ P}}_{23}\\ *& *& {{ P}}_{33}\end{array}\right]\left[\begin{array}{c}{ Y}\left(t\right)\\ { Y}\left(t-h\right)\\ \displaystyle\int_{t-h}^{t}{ Y}\left(s\right){\rm{d}}s\end{array}\right] \end{array} $

(25)

$ \begin{array}{c} {\dot{{ V}}}_{2}\left(t\right)={{ \rho }\left(t\right)}^{\mathrm{T}}{ Q}{ \rho }\left(t\right)-{{ \rho }\left(t-h\right)}^{\mathrm{T}}{ Q}{ \rho }\left(t-h\right)= \\ \left[{{ Y}\left(t\right)}^{\mathrm{T}}\quad{\dot{{ Y}}\left(t\right)}^{\mathrm{T}}\right]\left[\begin{array}{cc}{{ Q}}_{11}& {{ Q}}_{12}\\ *& {{ Q}}_{22}\end{array}\right]\left[\begin{array}{c}{ Y}\left(t\right)\\ \dot{{ Y}}\left(t\right)\end{array}\right]- \\ {\left[\begin{array}{c}{ Y}\left(t-h\right)\\ \dot{{ Y}}\left(t-h\right)\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{{ Q}}_{11}& {{ Q}}_{12}\\ *& {{ Q}}_{22}\end{array}\right]\left[\begin{array}{c}{ Y}\left(t-h\right)\\ \dot{{ Y}}\left(t-h\right)\end{array}\right] \end{array} $

(26)

$ \begin{array}{c} {\dot{{ V}}}_{3}\left(t\right)=h{{ \rho }\left(t\right)}^{\mathrm{T}}{ W}{ \rho }\left(t\right)-\displaystyle\int_{t-h}^{t}{{ \rho }\left(s\right)}^{\mathrm{T}}{ W}{ \rho }\left(s\right)\mathrm{d}s \leqslant \\ h\left[{{ Y}\left(t\right)}^{\mathrm{T}}{\dot{{ Y}}\left(t\right)}^{\mathrm{T}}\right]\left[\begin{array}{cc}{{ W}}_{11}& {{ W}}_{12}\\ *& {{ W}}_{22}\end{array}\right]\left[\begin{array}{c}{ Y}\left(t\right)\\ \dot{{ Y}}\left(t\right)\end{array}\right]- \\ \dfrac{1}{h}\displaystyle\int_{t-h}^{t}{\left[\begin{array}{c}{ Y}\left(s\right)\\ \dot{{ Y}}\left(s\right)\end{array}\right]}^{\mathrm{T}}\mathrm{d}s\left[\begin{array}{cc}{{ W}}_{11}& {{ W}}_{12}\\ *& {{ W}}_{22}\end{array}\right]\displaystyle\int_{t-h}^{t}\left[\begin{array}{c}{ Y}\left(s\right)\\ \dot{{ Y}}\left(s\right)\end{array}\right]\mathrm{d}s \end{array} $

(27)

$ \begin{array}{c} {\dot{{ V}}}_{4}\left(t\right)=\dfrac{{h}^{2}}{2}{\dot{{ Y}}\left(t\right)}^{\mathrm{T}}{ Z}\dot{{ Y}}\left(t\right)-\displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}{ Z}\dot{{ Y}}\left(s\right)\mathrm{d}s\mathrm{d}\theta - \\ \displaystyle\int_{-h}^{0}\displaystyle\int_{t+\theta }^{t}{\dot{{ Y}}\left(s\right)}^{\mathrm{T}}{ Z}\dot{{ Y}}\left(s\right)\mathrm{d}s\mathrm{d}\theta \leqslant \\ \dfrac{{h}^{2}}{2}{{ Y}\left(t-\tau \left(t\right)\right)}^{\mathrm{T}}{{{ L}}_{{ D}}}^{\mathrm{T}}{ Z}{{ L}}_{{ D}}{ Y}\left(t-\tau \left(t\right)\right)- \\ \dfrac{2}{{h}^{2}}\left\{\left[h{{ Y}\left(t\right)}^{\mathrm{T}}-\displaystyle\int_{t-h}^{t}{{ Y}\left(s\right)}^{\mathrm{T}}\mathrm{d}s\right]{ Z}\left[h{ Y}\left(t\right)-\displaystyle\int_{t-h}^{t}{ Y}\left(s\right)\mathrm{d}s\right]\right\} \end{array} $

(28)

结合式(21)~(24)整理得：

$ \dot{{ V}}\left(t\right)\leqslant {{ \xi }\left(t\right)}^{\mathrm{T}}{ \psi }{ \xi }\left(t\right) $

其中

$ { \xi }\left(t\right)=[{{ Y}\left(t\right)}^{\mathrm{T}}\quad{{ Y}\left(t-\tau \left(t\right)\right)}^{\mathrm{T}}\quad{{ Y}\left(t-h\right)}^{\rm{T}}{\begin{array}{c}\\ \end{array}} $

$ {\dot{{ Y}}\left(t-h\right)}^{\mathrm{T}}\quad\int_{t-h}^{t}{{ Y}\left(s\right)}^{\mathrm{T}}\mathrm{d}s{]}^{\mathrm{T}} $

若式(14)、(15)成立，则有 $ \dot{{ V}}\left(t\right)<0 $ ，这意味着系统式(13)是渐近稳定的，即系统式(1)可以在控制协议式(3)下达到二分一致性。

3 数值仿真分析

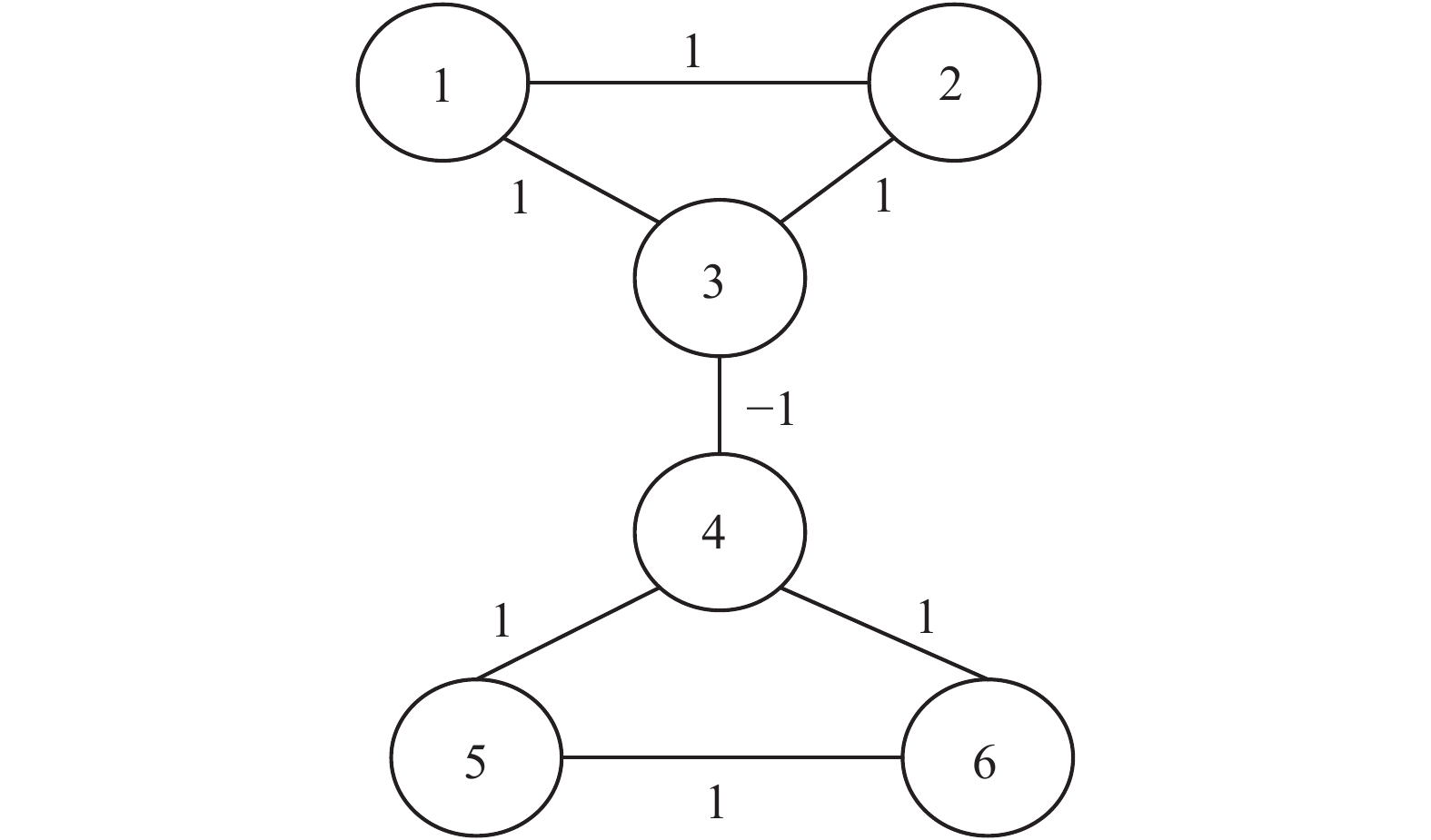
本文考虑有6个智能体，且其通信拓扑如图1所示。且 $ {{ V}}_{1}=\left\{{v}_{1},{v}_{2},{v}_{3}\right\} $ ， $ {{ V}}_{2}=\left\{{v}_{4},{v}_{5},{v}_{6}\right\} $ ，满足结构平衡。

由图1可写出拉普拉斯矩阵 $ { L} $ ：

$ {{L}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 2\\ { - 1}\\ { - 1} \end{array}}&{\begin{array}{*{20}{c}} { - 1}\\ 2\\ { - 1} \end{array}}&{\begin{array}{*{20}{c}} { - 1}\\ { - 1}\\ 3 \end{array}}&{\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}}\\ 0&0&1&3\\ 0&0&0&{ - 1}\\ 0&0&0&{ - 1} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}}\\ { - 1}\\ 2\\ { - 1} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}}\\ { - 1}\\ { - 1}\\ 2 \end{array}} \right]$

3.1 含固定时延的系统

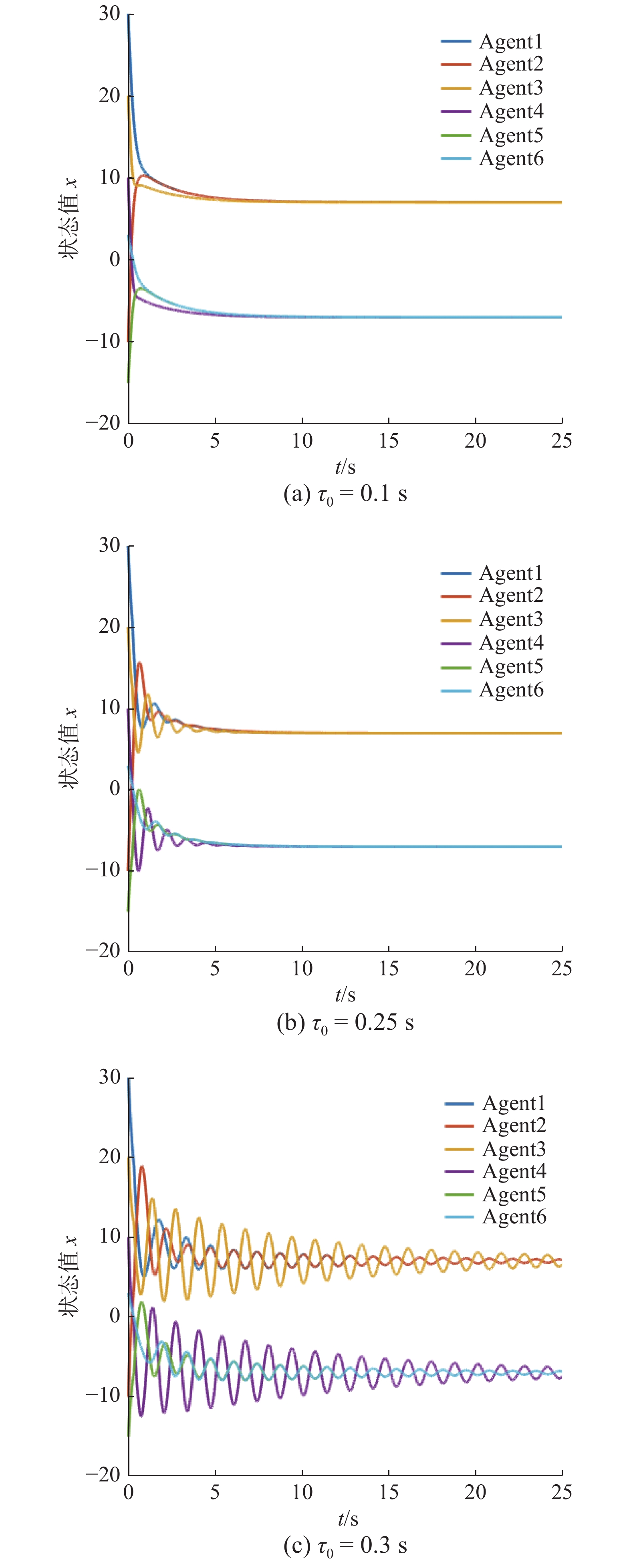
假设智能体初始状态 ${{x}}\left(0\right)=[30\quad-10\quad0\;\;10 \;\; -15\;\;\;3{]}^{{\rm{T}}}$ ，智能体系统的连接权重如图1。 ${{ E}}= \mathrm{max} \left(\displaystyle\sum \limits_{{v}_{j}\epsilon {N}_{i}}\left|{a}_{ij}\right|\right)=3$ ，则根据定理1可得 $ {\tau }_{0}<0.26 $ s，分别取时延 $ {\tau }_{0}=0.1 $ s、 $ {\tau }_{0}=0.25 $ s、 $ {\tau }_{0}=0.3 $ s进行仿真，如图2所示。

由图2可看出，多智能体系统在连通无向拓扑下，当其能够达到结构平衡时，若系统时延满足定理1中给出的条件，则智能体能实现二分一致性；反之，当系统时延 $ {\tau }_{0}>0.26\;\mathrm{s} $ 时系统不收敛，无法实现二分一致性。

3.2 含时变时延的系统

假设智能体初始状态 $ x\left(0\right)=[30\;-10\;\;20\;\;10\; -15\;\;\; 3{]}^{\mathrm{T}} $ ，系统中6个智能体间的连接权重如图1所示。根据定理2利用线性矩阵不等式工具箱，求解线性矩阵不等式可得到时延上界 $ h=1.58\;\mathrm{s} $ ，相较文献[16]中的时延 $1.46\;\mathrm{s}$ ，本文结论表明可以使得系统具有更小的保守性。假设系统存在时变时延 $\tau \left(t\right)=1.5 \left|\mathrm{sin}\left(t\right)\right|$ 进行仿真，得到仿真结果如图3所示。

由图3可看出，多智能体系统在连通无向拓扑下，且其结构平衡，同时满足定理2中给出的条件，在时变时延 $\tau \left(t\right)=1.5 \left|\mathrm{sin}\left(t\right)\right|$ 约束情况下，智能体系统仍能够实现二分一致性。

4 结束语

本文针对一阶多智能体系统，研究了在无向符号图拓扑结构并考虑通信网络含时延约束下的二分一致性问题。利用规范状态变换将多智能体系统的二分一致问题转换成一个相应的系统稳定性问题。考虑系统含固定时延约束时，利用广义Nyquist准则的方法分析并得到含固定时延系统实现二分一致性的充分条件。进一步考虑系统存在时变时延约束时，通过引入包含三积重分项的Lyapunov函数，利用线性矩阵不等式理论得到满足系统稳定的充分条件。最后，数值仿真验证了所给出定理的正确性。在后续工作中，将针对基于事件触发的量化多智能体系统时延二分一致性等问题展开深入研究。