移动机器人利用传感器和感知算法来了解周围的环境，因此越来越多地应用于人类有限、不可能或危险的环境中，帮助人类解决环境监测、搜救、寻源、主动感知等问题^[1-3]。尽管通过改善机器人感知方式来提高信息收集质量的方法已经被研究了近30年，然而大多数的机器人系统的任务执行方式是被动的^[4]。虽然单机器人系统具有相对较强的性能，但有些任务本身可能过于复杂，甚至不可能完成，例如空间上相互独立的任务^[5]。在多机器人系统中，异构机器人可以针对不同层次的任务进行专门化设计，可以应用于复杂的感知任务中。

现有的主动感知方法是反应性的，不受历史状态的影响，是一个马尔可夫过程。状态感知的质量会影响算法性能，可以通过选择最优感知位置来改进^[2，6]。这通常是一个短视问题，从控制策略上来说是贪婪的^[7]。最近，研究者们把主动感知问题从主动视觉扩展到了更为复杂的场景和任务：1)主动的目标识别、检测与跟踪；2)广阔的环境，如农场；3)具有丰富的社会知识、求知能力和非近视性的规划方法。但是这些感知任务大都是单机器人系统^[8]，且很少应用在多目标场景。

为了弥补这一差距，本文提出了一个基于自组织映射网络(self-organizing map,SOM) 的分散式异构机器人的框架来解决多目标主动感知的任务。在发现多目标的位置后，自组织映射算法为无人机团队规划出一条时间最短的路径，从而执行监视、拍照等任务。

1 相关工作 1.1 主动感知

被动感知与主动感知的区别在于环境状态量是否与智能体有交互。在被动感知中，智能体使用一组被动观察量来分类、估计、预测或推断与环境相关的一些信息^[9]。在主动感知中，智能体通过采取行动并观察环境如何变化，以动态的方式与环境交互更改状态^[6]。在此过程中，通过环境状态的变化，观察变得依赖于行动。

文献[3-4]证明了主动感知系统的性能高度依赖于机器人所选择的观测位置，但是其目标函数为机器人团队的观测奖励，且不同位置的观测奖励值是预先设定的^[3]。本文的研究目的是让机器人团队最小化旅行时间同时遍历所有目标，在这个过程中无人机团队的路径点是SOM算法规划出来的而不是从提前设定的一系列路径点序列中进行选择。

1.2 带邻域的多旅行商问题

图1给出了本文的研究场景，这是一个带邻域的多旅行商问题 (multiple traveling salesman problem with k-neighbourhood, k-MTSP)^[10]。k-MTSP是典型的NP-hard问题，不能在多项式时间内求出最优解。对于n个目标来说，存在着[(n−1)!]/2条可能的路径。可行解的数目随着n的增加呈指数倍增长，同时可行解以及路径长度的计算量将正比于n!/2。现有的方法在目标数量较少时有着不错的效果，但是当目标较多时会出现计算量大耗时长且不能得到较好的结果^[11]。因此，本文提出使用SOM来解决这一难题。

1.3 自组织映射特征网络

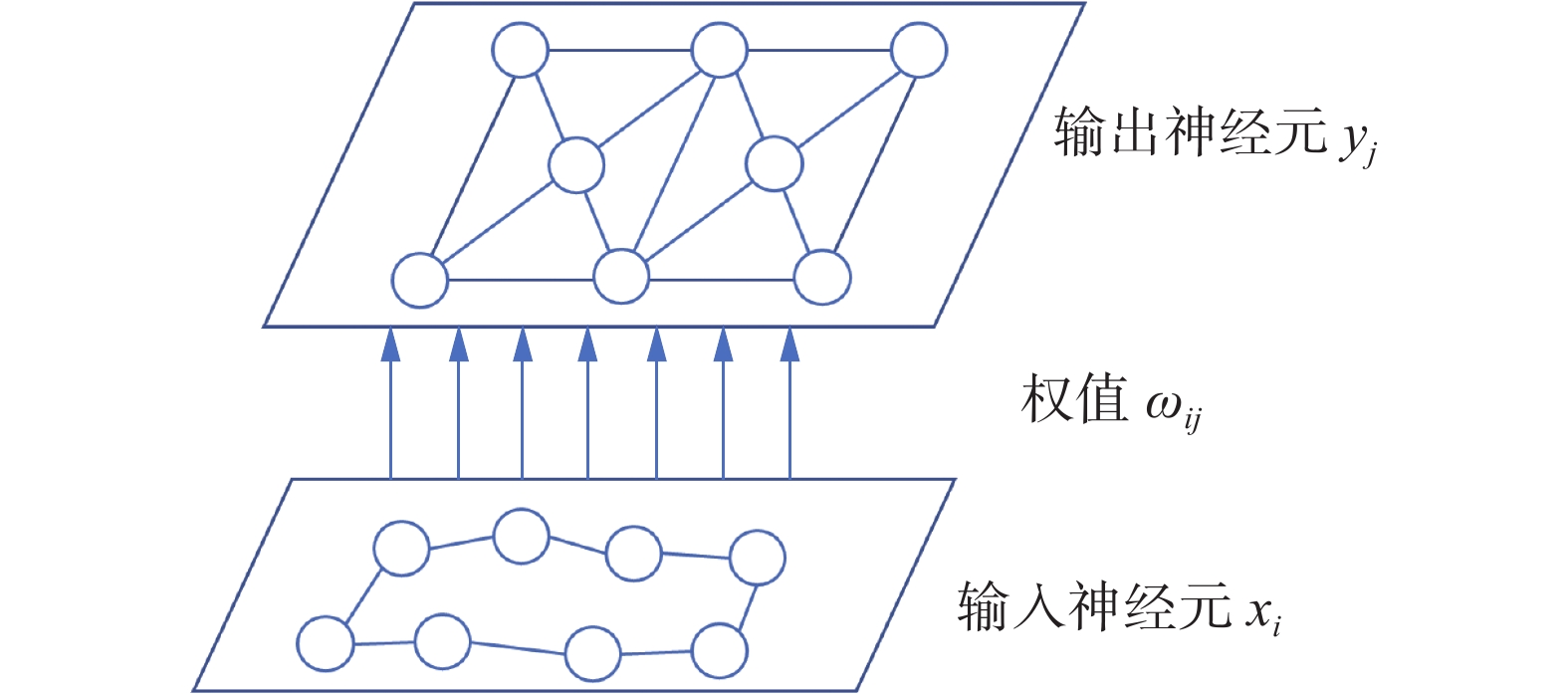
如图2所示，SOM是一种竞争性的双层神经网络且在输出层的样本空间中形成新的拓扑结构^[12-16]。在SOM的训练过程中，多个神经元通过竞争协作完成对输入样本的模式分类。网络中的输入神经元 ${x_i}$ 与输出神经元 ${y_j}$ 通过权值 ${\omega _{ij}}$ 相连，同时，近邻的输出神经元之间也通过权值相连^[3]。SOM的输出结果保持自组织的拓扑结构，映射到多维的向量空间中。

2 问题建模

图1中给出了异构机器人的主动感知框架。无人机团队中一部分通过搭载的传感器设备搜索区域的目标，另一部分执行快速遍历的主动感知任务^[17]。任务目标是在满足旅行预算的前提下为机器人团队 $R = \left\{ {{r_1},{r_2}, \cdot \cdot \cdot ,{r_R}} \right\}$ 规划一个由路径点序列 $X = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_i}} \right\}$ 组成的平滑路径，使其能够监视环境中的每一个目标 $N = \left\{ {{n_1},{n_2},} \right. \left.{ \cdot \cdot \cdot ,{n_N}} \right\}$ ，并使得团队的旅行时间 ${T_{\rm{sum}}} = {t_{{r_1}}} + {t_{{r_2}}} + {t_{{r_3}}} + \cdot \cdot \cdot + {t_{{r_R}}}$ 最短。考虑到实际环境中，被感知目标并非无体积的质点，而且机器人上一般搭载有感知设备，如雷达、深度相机等。因此目标n_N是一个圆形的感知区域 ${s_N} \in {R}$ ，其感知半径为k。无人机只需要访问到感知区域的任意位置，即可执行捕获任务 $\left\| {{x_i} - {n_N}} \right\| \leqslant k$ 。这是一个k-MTSP问题，目标函数为最小化旅行时间，即

$ \min {\rm{mize}} T(X)=\displaystyle \sum\limits_{i=1}^{n} T\left(X_{i}\right) $

SOM规划出的平滑路径都有旅行消耗 ${c_i} \geqslant 0$ ，定义为无人机在路径 ${X_i}$ 上的时间。机器人团队有总的旅行预算时间 ${b_i} \geqslant 0$ 。当SOM为机器人团队规划出一次路径时，会计算出当前轮次的旅行消耗，选择获胜机器人 ${R}_{r}$ ，即

$ R_{r} \leftarrow \arg \min \left(\dfrac{c_{q}}{b_{q}}\right), \quad c_{i} \leqslant b_{i}。$

3 感知路径生成

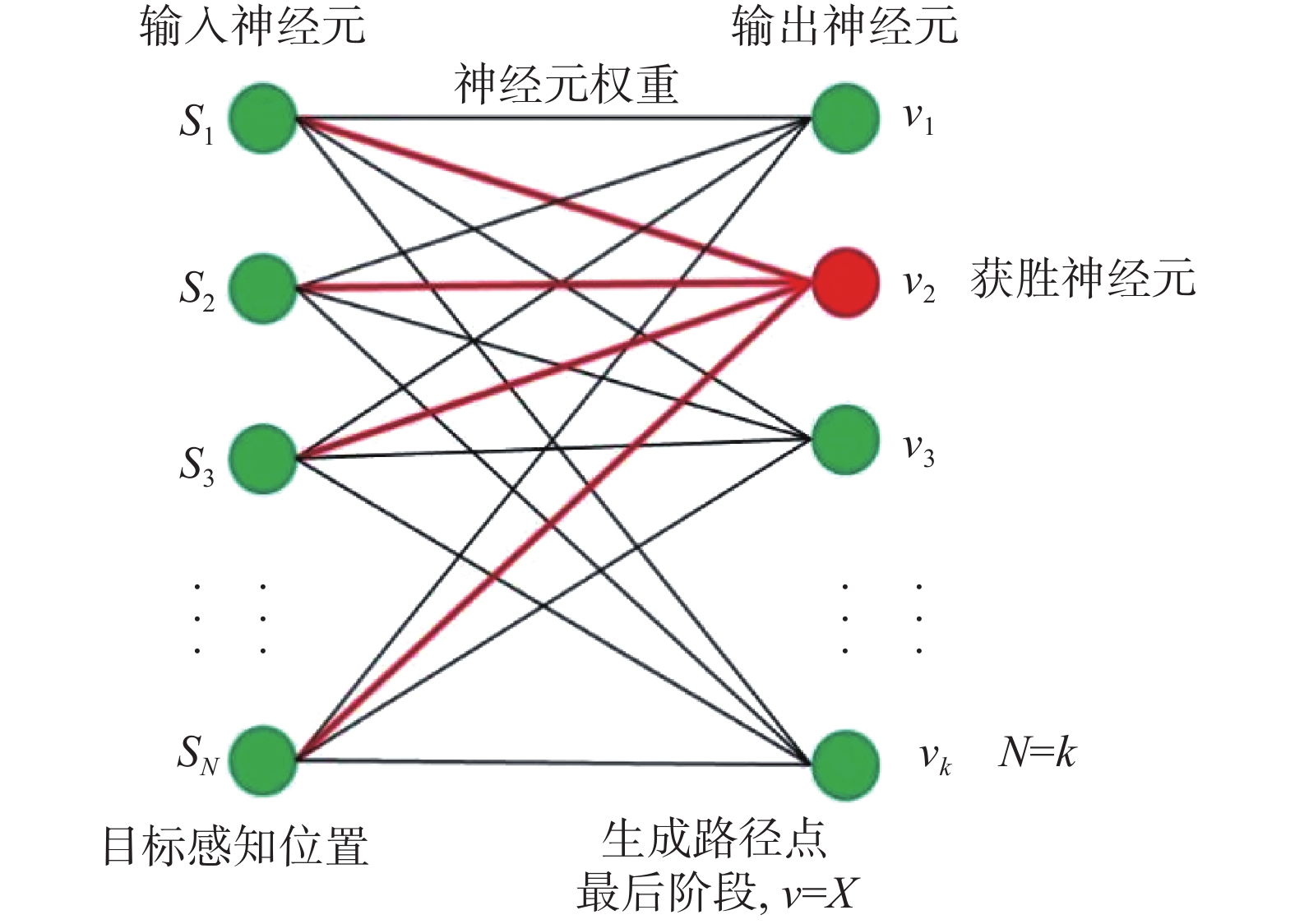
图3给出了应用于大规模场景多目标感知的SOM训练结构。

定义SOM输入层的兴奋神经元邻域为

$ {T_{j,I(x)}} = \exp \left( - \dfrac{{S_{j,I(x)}^2}}{{2{\sigma ^2}}}\right) $

(1)

式中I(x)是获胜神经元的索引^[18]。学习增益 $ \mathrm{\sigma } $ 随着时间的推移而减少，即

$ \sigma(t)=\sigma_{0} \exp \left(-t / \tau_{\sigma}\right) $

(2)

拓扑邻域更新了获胜神经元的权重，同时邻域内的其他神经元权重也进行了更新，但幅度较小，以此保障具有输入空间映射结构的训练样本向目标逼近。权重更新方式为

$ \Delta \omega_{j i}=\eta(t) \cdot T_{j, I(x)}(t) \cdot\left(x_{i}-\omega_{j i}\right) $

(3)

式中： $\eta(t) $ 为依赖于时间的学习率 ， $\eta(t)= \eta_{0} \exp \left(-t / \tau_{\eta}\right)$ 。

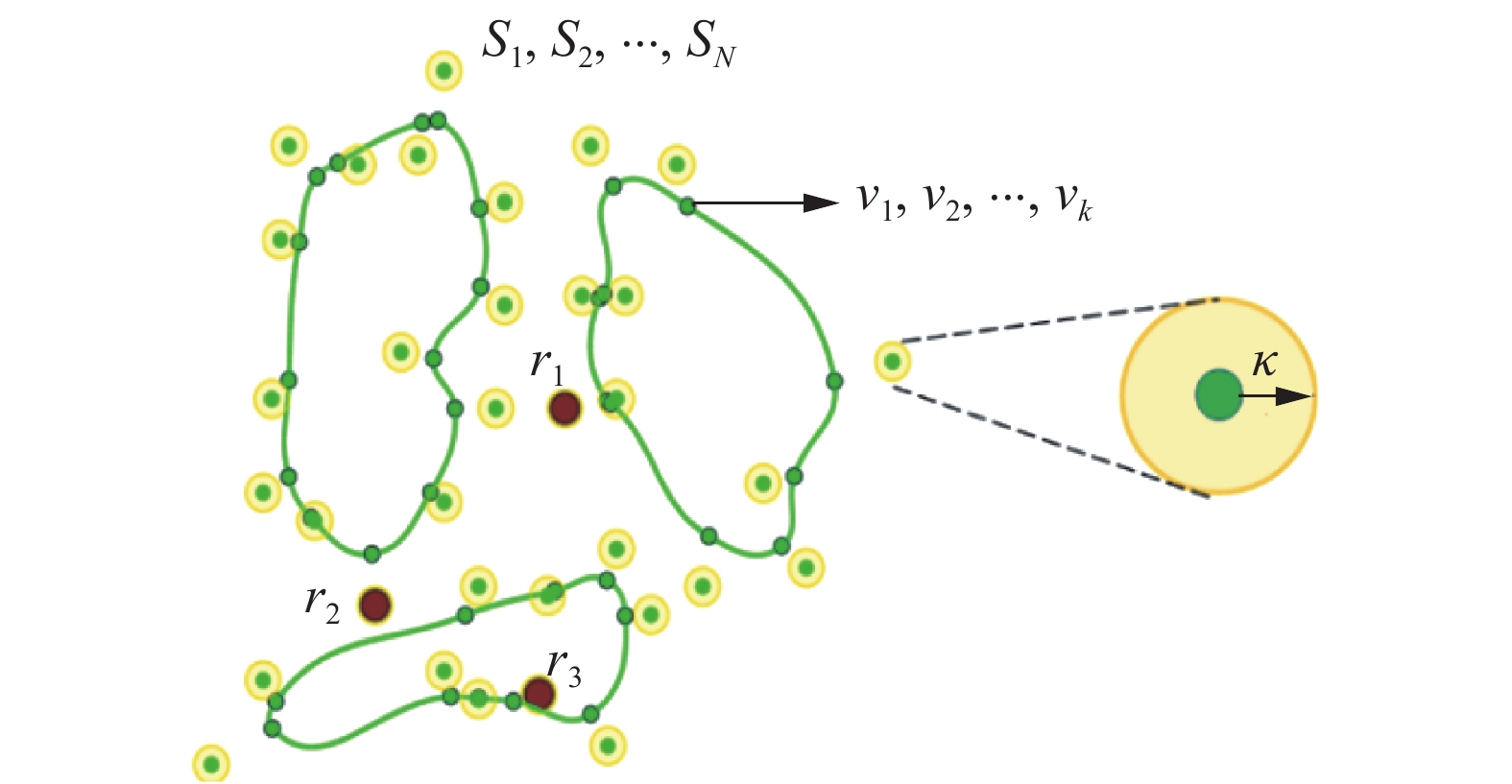
图4给出了某训练阶段示意图。本文SOM的输入样本是群体目标的感应位置 ${s_N} \in {R}$ ，输出结果是经过训练后的路径点 $ v=\{{v}_{1},{v}_{2},\dots {v}_{k}\} $ ，其中k是当前网络中神经元的数量，多轮迭代后即为无人机团队的路径点序列 $ {X}_{i} $ 。为了避免网络训练的结果陷入局部最优，感应位置组成的样本空间以随机的顺序输入给SOM，每一轮的迭代都是SOM对输入空间的一个自适应过程^[19]。

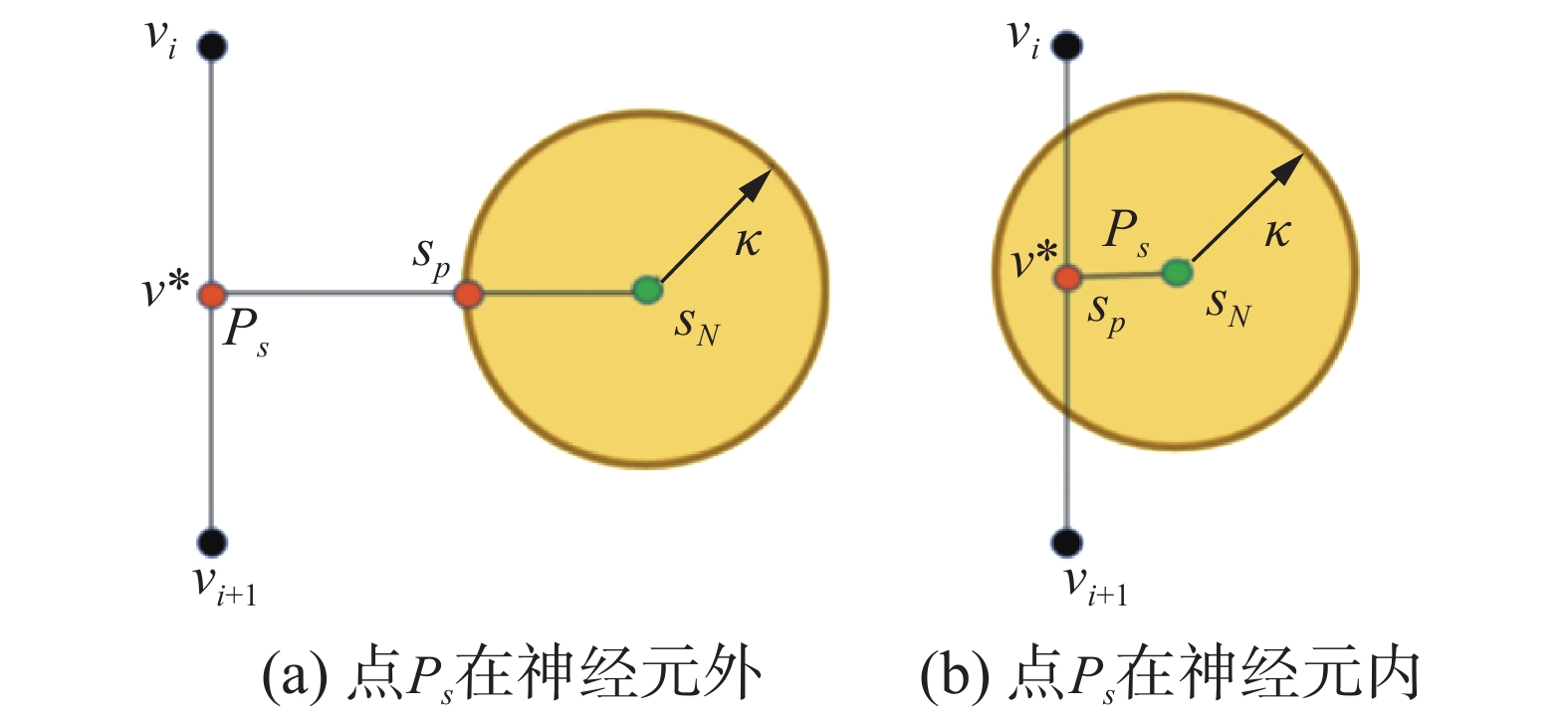
如图5所示，SOM输出的拓扑结构中，与目标位置s最佳匹配的神经元是拓扑结构中距离目标欧氏距离最近的点。然后在点 $ {p}_{s} $ 处创建获胜神经元 $ {v}^{*} $ 。

可行的迭代方法是线段(p_s，s_n)中的某一个点逐渐趋近于邻域长度k。该几何迭代过程有两种情况：1）如果 $ {p}_{s} $ 已经位于领域内，那么只需要在 $ {p}_{s} $ 处创建获胜神经元，网络不需要进行自适应的过程；2）如果 $ {p}_{s} $ 位于感知区域外部，那么需要按照标准SOM的方法进行迭代。标准的SOM学习可以看作神经元朝向 $ {s}_{p} $ 的移动同时产生一个新的神经元使v变为 $ {v}' $ , 即

$ v^{\prime}=v+\mu f(\sigma, d)\left(v^{*} s_{p}-v\right) $

(4)

式中： $ \mu $ 为学习率； $ f\left(\sigma ,d\right) $ 是邻域函数； $ \sigma $ 是网络的学习增益； $ d $ 是 $ \nu $ 到 $ {\nu }^{*} $ 的欧氏距离。邻域函数定义了周围被调整的竞争性神经元，并且具有SOM中针对 TSP 进行调整的标准形式：

$ f(\sigma ,d) = \left\{ \begin{array}{l} \operatorname{e} ^\frac{{ - {d^2}}}{{{\sigma ^2}}},\;\quad d < 0.2M \\ 0,\;\quad {\text{其他}} \\ \end{array} \right. $

(5)

在每轮训练结束后，学习率根据

$ \sigma {\rm{ = }}\left( {{\rm{1 - }}\alpha } \right)\sigma $

(6)

逐渐减少， $ \alpha $ 是增益减少比率。此外，在每一个学习阶段之后，都会进行一个环再生，以去除所有竞争失败的神经元。

如果所有获胜神经元都明显接近各自的，从而使其在每个神经元的k邻域内，则SOM的迭代过程将终止。然后，连接获胜神经元的光滑曲线序列是主动感知问题的可行解决方案。如果网络收敛速度不够快，可以在最大迭代轮次之后终止学习过程，并且可以通过遍历环并使用与获胜神经元关联的 $ {s}_{p} $ 来构建可行的解决方案。对于已用的学习速率 $ \mu =0.5 $ ,网络收敛的同时对SOM的初始学习增益按照 $ \sigma =12.41n+0.6 $ ,增益递减率 $ \alpha =0.1 $ ，网络在不到100 个学习轮次内稳定。

为了避免无人机飞行过程中大角度转弯带来的不稳定性，对SOM生成的路径进行三阶分段贝塞尔平滑处理^[20]：

$ {X\left(\tau \right)=B}_{0}{(1-\tau )}^{3}+3{B}_{1}\tau {(1-\tau )}^{2}+\\ 3{B}_{2}{\tau }^{2}\left(1-\tau \right)+{B}_{3}{\tau }^{3} $

(7)

式中： $ \tau \in \left[0,1\right] $ ； ${{B}_{0}{\text{、}}B}_{3}$ 为每段分段Bezier曲线的起点和终点的位置； $ {B}_{1}$ 、 ${B}_{2} $ 决定了每段分段Bezier曲线起点和终点处的切线。无人机的闭环轨迹曲线由多个分段Bezier曲线组成，为保证轨迹连续，无人机闭环轨迹中相邻两个分段贝塞尔曲线 ${X}_{i-1}{\text{、}}{X}_{i}$ 的路径点需满足 $ {B}_{3}^{i-1}={B}_{0}^{i} $ 。闭环轨迹中第i-1个分段Bezier曲线起点的切线 $ {t}_{a}^{i-1} $ 和第i个分段Bezier曲线终点的切线 $ {t}_{b}^{i} $ ，切线 $ {t}_{a}^{i-1} $ 的长度 $ {l}_{a}^{i-1} $ 和切线 $ {t}_{b}^{i} $ 的长度 $ {l}_{b}^{i} $ 分别为

$ t_a^{i - 1} = B_1^{i - 1} - B_0^{i - 1},\quad t_b^i = B_3^i - B_2^i\\ $

(8)

$ l_a^{i - 1} = \left\| {t_a^{i - 1}} \right\|,\quad l_b^i = \left\| {t_b^i} \right\| $

(9)

无人机群体轨迹平滑满足:

$ l_a^{i - 1}t_b^i = l_b^it_a^{i - 1} $

(10)

4 实验结果及分析

本文进行了一系列仿真实验来验证提出的算法效果。所有实验均使用C++编程，并在装有2.5 Hz频率下i5-7300HQ中央处理器的操作系统上进行仿真，仿真结果数据用MATLAB2016b进行处理。由于单次实验结果不具有代表性，本文在相同条件下进行了20次实验，以此来分析SOM在大规模场景下多目标主动感知任务的效果。无人机的水平初始速度 $v = 5\;{\rm{m }}/ {\rm{s}}$ ，目标数为31，竖直与水平方向的加速度为0，无人机近似地认为是在二维平面内匀速运动。场景中群体目标的感知邻域半径k为5 m，SOM的训练次数为100，学习率为0.5。

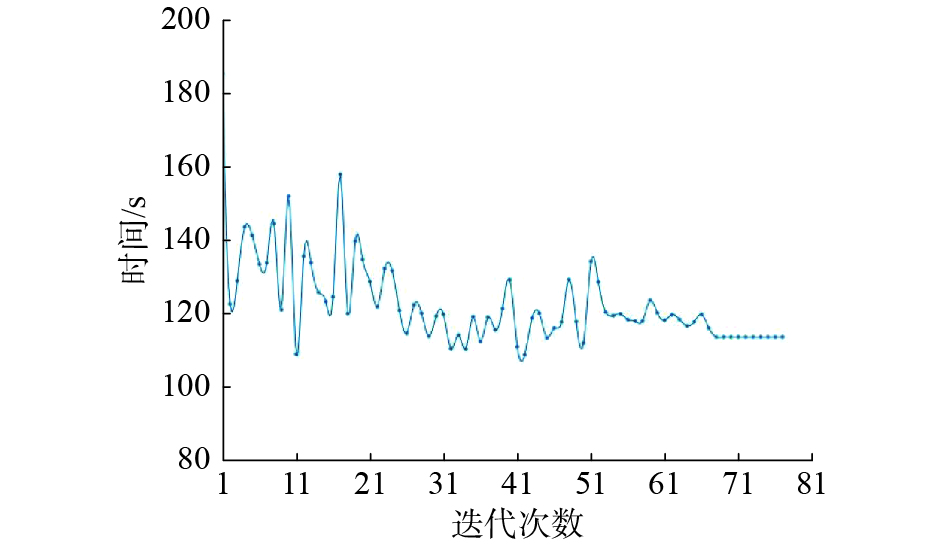
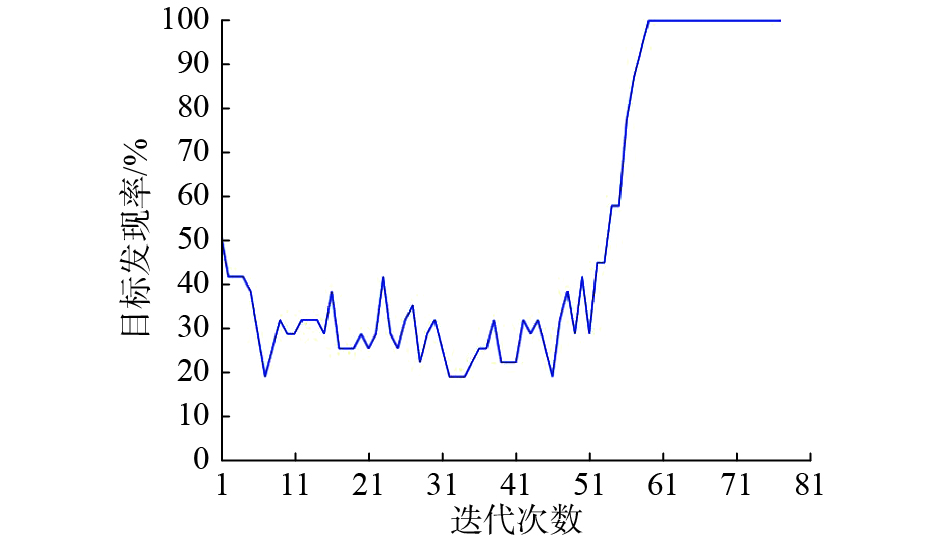
图6展示了SOM算法的迭代过程。初始阶段，把异构无人机团队测得的目标位置坐标作为初始样本输入到SOM网络中进行训练，最终经过70～80次的迭代，算法收敛，得出最终结果。由于SOM是一种竞争性神经网络，所以不同轮次的获胜神经元及兴奋神经元邻域是不同的，这就造成了目标覆盖率并不是线性单调函数，如图7所示。相对应的每一轮迭代结果的无人机旅行时间也不是迭代轮次的单调函数，自适应过程的旅行时间会产生随机振荡，但是在过程中会趋于稳定，如图8所示。

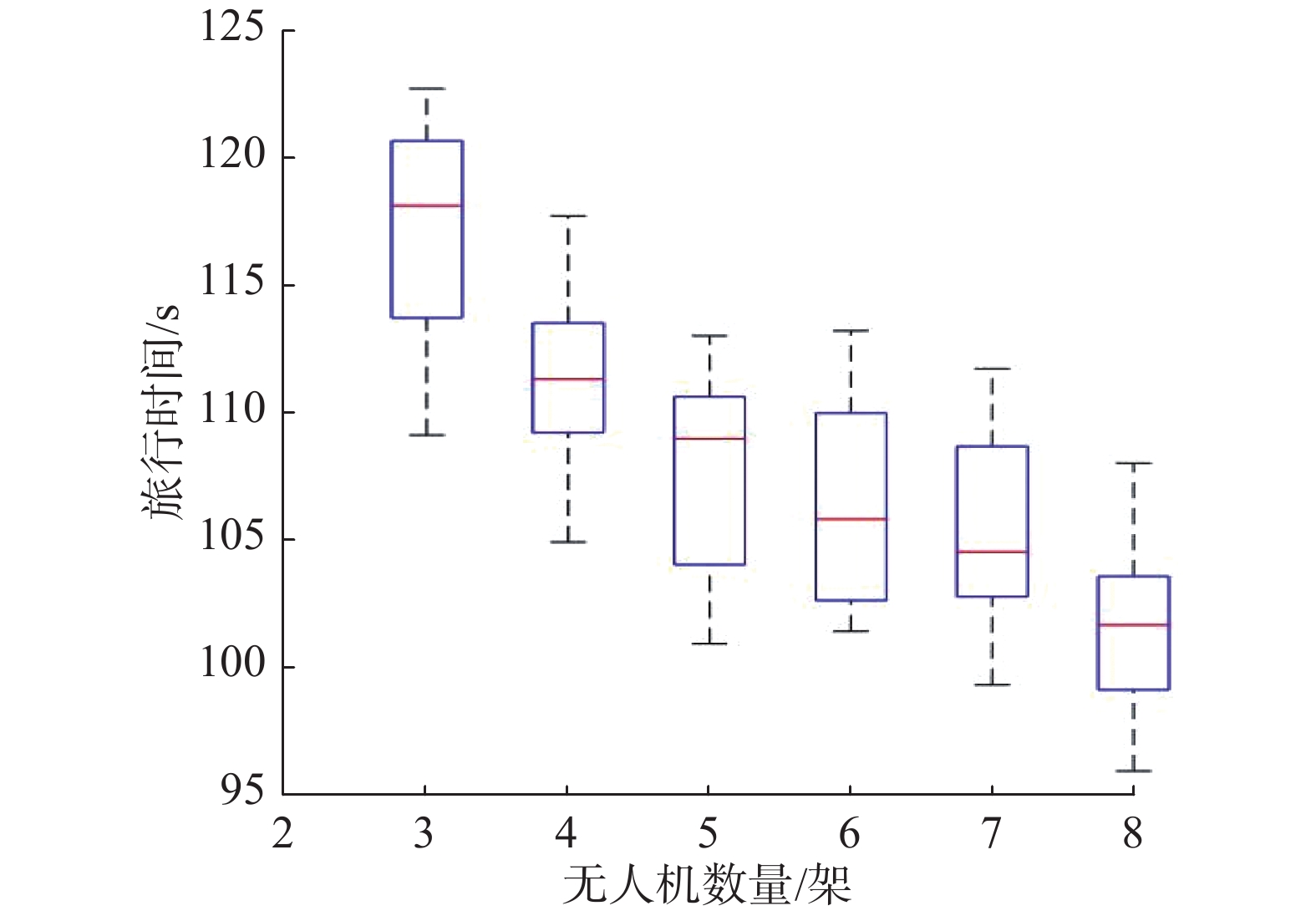
为了验证无人机数量对结果的影响，本文在相同的实验条件下改变无人机数量进行测试。实验结果表明，有限增加无人机数量可以减少总旅行时间，如图9所示。

为了评估本文提出的方法，在相同的场景条件下使用遗传算法、蚁群算法、粒子群优化算法^[15]进行对比实验，取20次实验的平均值，如表1所示。实验结果表明，本文的方法得出的无人机团队旅行时间较短，可以应用于大规模场景下多目标群体智能的主动感知问题。

本文在gazebo中搭建了仿真环境，进一步评估提出算法的可行性。如图10所示，黑色物体代表四旋翼无人机。彩色立方体代表真实世界中的物体，把模型点云数据处理为八叉树结构，方便数理分析，不同颜色代表物体在三维空间中具有不同的高度，红色最低紫色最高。无人机的初始位置和目标点随机给出，算法根据环境数据和目标点的三维坐标规划出最短的路径。在gazebo中的仿真结果如图11所示，底部栅格代表仿真模型的分辨率，在给定目标点后，算法为无人机在三维空间中规划出了一条时间最短的路径，由图中的灰色空心立方体表示。仿真结果进一步验证了算法结果。

5 结束语

本文使用SOM完成了海域多目标主动感知任务。仿真实验表明，本文使用的方法为无人机团队规划出了一条时间最短的平滑路径。通过与其他算法对比，本文使用的SOM算法在解决带邻域的多旅行商问题时耗时较短。随着最优化理论在机器学习领域的进一步发展，将会进一步降低旅行商问题的复杂度。