支持向量机(support vector machine, SVM)^[1]是由Vapnik提出的基于结构风险最小化原理的二分类分类器。其基本思想是在2个平行支持超平面之间找到最大化边界。与此同时，对于非线性分类问题，内核技巧也可以应用到SVM中。然而，SVM的计算复杂度却很高。

2007年，Jayadeva等^[2]提出了孪生支持向量机(twin support vector machine, TWSVM)，它为每一类构造一个超平面，使每一类样本尽可能距离本类的超平面近，而尽可能地远离另一类的超平面。TWSVM的2个非平行的超平面是通过求解2个二次规划问题(quadratic programming problems,QPPs)得到的，每个QPP的约束条件都只与一类样本有关。TWSVM不但保持了SVM的优点，而且训练速度比传统SVM要快4倍。为了进一步提升TWSVM的性能，学者们已经提出了不少改进算法，例如：孪生有界支持向量机^[3](twin bounded support vector machine, TBSVM)、最小二乘孪生支持向量机^[4](least square twin support vector machine, LSTWSVM)、非平行支持向量机^[5](nonparallel support vector machine，NPSVM)。具体来说，LSTWSVM使用平方损失函数将TWSVM中的凸二次规划问题转化为解线性方程组，从而实现极快的训练速度。但是，LSTWSVM对噪声很敏感，因为它要求超平面与其他类的点距离恰好为1。近些年来出现了许多改进的算法。Nasiri等^[6]提出了一种基于能量的LSTWSVM(energy-based least square twin support vector machine, ELS-TWSVM)模型，该模型为每一类引入一个能量因子以减少噪声的影响。马跃峰等^[7]提出了一种基于全局代表点的快速最小二乘支持向量机稀疏化算法(global-representation-based sparse least squares support vector machine, GRS-LSSVM)，利用数据全局代表性指标，在全部数据中，一次性地选择出其中最具有全局代表性的数据并构成稀疏化后的支持向量集，然后在此基础上求解决策超平面。吴青等^[8]提出了一种最小二乘大间隔孪生支持向量机(least squares large margin twin support vector machine, LSLMTSVM)，该方法在TWSVM的目标函数中引入间隔均值和间隔方差，通过优化间隔分布来获得具有更强泛化能力的模型。

实际上，在大多数分类问题中，不同的类可能有不同的结构信息。然而，传统的SVM和TWSVM都没有完全应用类中样本的分布信息。最流行的方法之一是基于假设的聚类算法^[9]，利用聚类算法提取类中的结构信息。例如，结构化最大边缘机(structured large margin machine, SLMM)^[10]、最小最大概率机(minimax probability machine，MPM)^[11]和最大最小边缘机(maxi-min margin machine，M⁴)^[12]。但是，这些方法的计算复杂度高于经典的SVM。因此，Xue等^[13]提出了一种结构正则化支持向量机(structural regularized SVM，SRSVM)。此方法将集群粒度导入到获得数据结构的正则化项。遵循SLMM和SRSVM的策略，Qi等^[14]提出了一种新的结构化的TWSVM(structural twin support vector machine, S-TWSVM)。与SRSVM类似，S-TWSVM使用聚类算法提取每个类的结构信息，并将得到的结构信息引入到S-TWSVM模型中。

在本文中，受文献[6]的启发，首先对结构化的最小二乘孪生支持向量机(structural least square twin support vector machine, S-LSTWSVM)进行改进，提出了一种基于能量的结构最小二乘孪生支持向量机(energy-based structural least square twin support vector machin, ES-LSTWSVM)。为每个超平面引入能量因子，将等式约束条件转换为基于能量的形式。最后采用“多对一”的策略^[15]解决多分类问题。

本文的主要贡献如下：

1) 提出了一种基于能量的结构化最小二乘孪生支持向量机；

2) 采用“多对一”的策略将提出的算法扩展到多分类问题中；

3) 选择几种有代表性的相关算法进行对比实验，在UCI数据集上的实验结果表明提出的算法具有良好的分类性能。

1 相关工作

本节介绍TWSVM和S-TWSVM的数学模型。假设在 ${{\bf{R}}^n}$ 空间中训练数据集定义为 $T = \left\{ {({x_i},{y_i})|i = 1,2, \cdots ,m} \right\}$ ，其中 ${x_i}$ 是输入， ${y_i} \in \left\{ { + 1, - 1} \right\}$ 是对应的输出。它们共有 $m$ 个训练样本，每个样本有 $n$ 个属性，其中有 ${m_1}$ 个样本属于正类， ${m_2}$ 个样本属于负类，分别用矩阵 ${{A}}$ 、 ${{B}}$ 来表示。

1.1 TWSVM

TWSVM通过训练数据集寻找2个不平行的分离超平面：

${{{x}}^{\rm{T}}}{{{w}}_1}{\rm{ + }}{b_1} = 0,{{{x}}^{\rm{T}}}{{{w}}_2}{\rm{ + }}{b_2} = 0$

它们一般通过求解下面2个二次规划问题来得到：

$ \begin{array}{c} \min\limits_{{w_1},{b_1},{\xi _2}} \;\;\;\;\dfrac{1}{2}{({{A}}{{{w}}_1} + {{{e}}_1}{b_1})^{\rm{T}}}({{A}}{{{w}}_1} + {{{e}}_1}{b_1}) + {c_1}{{e}}_1^{\rm{T}}{\xi _2} - \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\;\; ({{B}}{{{w}}_1} + {{{e}}_2}{b_1}) \geqslant {{{e}}_2} - {\xi _2},{\xi _2} \geqslant 0 \end{array} $

$ \begin{array}{c} \min\limits_{{w_2},{b_2},{\xi _1}} \;\;\;\;\;\;\dfrac{1}{2}{({{B}}{{{w}}_2} + {{{e}}_2}{b_2})^{\rm{T}}}({{B}}{{{w}}_2} + {{{e}}_2}{b_2}) + {c_2}{{e}}_1^{\rm{T}}{\xi _1}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;({{A}}{{{w}}_2} + {{{e}}_1}{b_2}) \geqslant {{{e}}_1} - {\xi _1},{\xi _1} \geqslant 0 \end{array} $

式中：c₁、c₂>0是2个惩罚参数； ${{{e}}_1}$ 、 ${{{e}}_2}$ 是元素全为1的列向量； ${\xi _1}$ 、 ${\xi _2}$ 是松弛变量。

TWSVM通过如下的决策函数判定新样本的类别标签：

${\rm{Label}}({{x}}) = \arg\min\limits_{l = 1,2} \left| {{{{x}}^{\rm{T}}}{{{w}}_l} + {b_l}} \right|$

1.2 S-TWSVM

首先，S-TWSVM通过“沃氏链接”(ward’s linkage)聚类算法^[16]提取类内的结构信息。然后它使用2个非平行超平面来判定新数据的类别，其中每个超平面尽可能离本类数据点近，并且在目标函数中只考虑该类的结构信息，而约束条件规定该超平面要离其他类数据点至少距离为1个单位。假设通过聚类之后正类中有 ${C_P}$ 个簇，负类中有 ${C_N}$ 个簇。那么S-TWSVM的优化问题可以表述为

$ \begin{array}{c} \min\limits_{{w_ + },{b_ + },\xi } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}\left\| {{{A}}{{{w}}_ + } + {{{e}}_ + }{b_ + }} \right\|_2^2 + {c_1}{{e}}_ - ^{\rm{T}}\xi + \frac{1}{2}{c_2}(\left\| {{{{w}}_ + }} \right\|_2^2 + b_ + ^2)+ \\ \dfrac{1}{2}{c_3}{{w}}_{\rm{ + }}^{\rm{T}}{\displaystyle\sum\nolimits_ + }{{{w}}_ + } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\begin{array}{*{20}{c}} {}&{ - ({{B}}{w_ + } + {{{e}}_ - }{b_ + }) + \xi \geqslant e_ -} ,\xi \geqslant 0 \end{array} \end{array} $

$ \begin{array}{c} \min\limits_{{w_ - },{b_ - },\eta } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}\left\| {{{B}}{{{w}}_ - } + {{{e}}_ - }{b_ - }} \right\|_2^2 + {c_4}{{e}}_ + ^{\rm{T}}\eta + \frac{1}{2}{c_5}(\left\| {{{{w}}_ - }} \right\|_2^2 + b_ - ^2) + \\ \dfrac{1}{2}{c_6}{{w}}_ - ^{\rm{T}}{\displaystyle\sum\nolimits_ - }{{{w}}_ - } \\ {\rm{s}}{\rm{.t}}{\rm{.}}{\begin{array}{*{20}{c}} {}&{({{A}}{{{w}}_ - } + {{{e}}_ + }{b_ - }) + \eta \geqslant {{e}}_ +} ,\eta \geqslant 0 \end{array} } \end{array} $

式中： ${c_i} \geqslant 0(i = 1,2, \cdots ,6)$ 是惩罚参数； $\xi $ 、 $\eta $ 是松弛变量； ${{{e}}_ + }$ 、 ${{{e}}_ - }$ 是元素全为1的列向量； ${\displaystyle\sum\nolimits_ + } = {\displaystyle\sum\nolimits_{{P_1}}} + \cdots + {\displaystyle\sum\nolimits_{{P_{{C_P}}}}}$ ； ${\displaystyle\sum\nolimits_ - } = {\displaystyle\sum\nolimits_{{N_1}}} + \cdots + {\displaystyle\sum\nolimits_{{N_{{C_N}}}}}$ ； ${\displaystyle\sum\nolimits_{_{{P_i}}}}$ 和 ${\displaystyle\sum\nolimits_{{N_j}}}$ 是2类中的每一个簇的相应协方差矩阵，其中， $i = 1,2, \cdots ,{C_P},j = 1,2, \cdots ,{C_N}$ 。

新的数据点被分配给正类还是负类取决于得到的2个超平面 ${{w}}_ + ^{\rm{T}}{{x}} + {b_ + } = 0$ 和 ${{w}}_ - ^{\rm{T}}{{x}} + {b_ - } = 0$ 中它距离哪一个超平面更近，即

${\rm{Label}}({{x}}) = \arg\min\limits_{ + , - } \left\{ {\left| {{{w}}_ + ^{\rm{T}}{{x}} + {b_ + }} \right|,\left| {{{w}}_ - ^{\rm{T}}{{x}} + {b_ - }} \right|} \right\}$

2 ES-LSTWSVM

在本节中，提出了一种基于能量的结构化孪生支持向量机(ES-LSTWSVM)。该算法主要分为2步：1)用某种聚类方法提取类内的结构信息;2)最小化每个类中各个簇之间的紧密度并将其嵌入到目标函数中。此外，利用核技巧使模型能够解决非线性可分问题。在下面的小节中，将具体讨论这些步骤。

2.1 线性 ES-LSTWSVM

有很多聚类方法可被用于提取类内的结构信息，例如：k均值算法^[17]、模糊聚类和密度聚类^[18-21]。使用拐点图^[22]来确定最佳聚类数目。聚类之后，通过计算类中各个簇的协方差矩阵将结构信息引入到优化问题中。因此，聚类之后的簇应该是紧凑的并且是球形的。鉴于此，采用Ward’s linkage聚类算法，这是一种层次聚类方法，为协方差矩阵的计算提供了基础。

假设从正类和负类中分别得到了 ${C_p}$ 和 ${C_n}$ 个簇，即 $A = {P_1} \cup \cdots\cup {P_i} \cup \cdots \cup{P_{{C_p}}}$ ， $B = {N_1} \cup \cdots \cup{N_i} \cup \cdots \cup{N_{{C_n}}}$ 。对于线性可分的二分类问题，ES-LSTWSVM模型可表示为

$\begin{array}{c} \min\limits_{{w_ + },{b_ + },\xi } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}{\left\| {{{A}}{{{w}}_ + } + {{{e}}_ + }{b_ + }} \right\|^2} + \dfrac{{{c_1}}}{2}{{{\xi }}^{\rm{T}}}{{\xi }} + \\ \dfrac{{{c_2}}}{2}(\left\| {{{{w}}_ + }} \right\|_2^2 + b_ + ^2) + \dfrac{{{c_3}}}{2}{{w}}_ + ^{\rm{T}}{\displaystyle\sum\nolimits_ + }{{{w}}_ + } \\ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&{}&{ - ({{B}}{{{w}}_ + } + {{{e}}_ - }{b_ + })} \end{array} + {{\xi }} = {{{E}}_ - } \\ \end{array} $

(1)

$\begin{array}{c} \min\limits_{{w_ - },{b_ - },\eta } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}{\left\| {{{B}}{{{w}}_ - } + {{{e}}_ - }{b_ - }} \right\|^2} + \dfrac{{{c_4}}}{2}{{{\eta }}^{\rm{T}}}{{\eta }} + \\ \dfrac{{{c_5}}}{2}(\left\| {{{{w}}_ - }} \right\|_2^2 + b_ - ^2) + \dfrac{{{c_6}}}{2}{{w}}_ - ^{\rm{T}}{\displaystyle\sum\nolimits_ - }{{{w}}_ - } \\ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&{}&{{{A}}{{{w}}_ - } + {{{e}}_ + }{b_ - }} + {{\eta }} = {{{E}}_ + } \end{array} \\ \end{array} $

(2)

式中： ${c_i}\left( {i = 1,2, \cdots ,6} \right)$ 是惩罚参数； $\xi $ 、 $\eta $ 是松弛变量； ${E_ + }$ 和 ${E_ - }$ 是超平面的能量因子； ${\displaystyle\sum\nolimits_ + } = {\displaystyle\sum\nolimits_{{P_1}}} + \cdots + {\displaystyle\sum\nolimits_{{P_{{C_P}}}}}$ ； ${\displaystyle\sum\nolimits_ - } = {\displaystyle\sum\nolimits_{{N_1}}} + \cdots + {\displaystyle\sum\nolimits_{{N_{{C_N}}}}}$ ； ${\displaystyle\sum\nolimits_{_{{P_i}}}}$ 和 ${\displaystyle\sum\nolimits_{{N_j}}}$ 分别是对应于2个类中的第i个簇和第j个簇的协方差矩阵， $i = 1,2, \cdots ,{C_P},j = 1,2, \cdots ,{C_n}$ 。

将等式约束条件代入目标函数式(1)中得到：

$\begin{array}{c} \min\limits_{{w_ + },{b_ + }} \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}{\left\| {{{A}}{{{w}}_ + } + {{{e}}_ + }{b_ + }} \right\|^2} + \dfrac{{{c_1}}}{2}{\left\| {{{B}}{{{w}}_ + } + {{{e}}_ - }{b_ + } + {{{E}}_ - }} \right\|^2} + \\ \dfrac{{{c_2}}}{2}(\left\| {{{{w}}_ + }} \right\|_2^2 + b_ + ^2) + \dfrac{{{c_3}}}{2}{{w}}_ + ^{\rm{T}}{\displaystyle\sum\nolimits_ + }{{{w}}_ + } \\ \end{array} $

(3)

分别对式(3)中 ${{{w}}_ + }$ 和 ${b_ + }$ 求导，并且由KKT条件得：

$\begin{array}{c} {{{A}}^{\rm{T}}}({{A}}{{{w}}_ + } + {{{e}}_ + }{b_ + }) + {c_1}{{{B}}^{\rm{T}}}({{B}}{{{w}}_ + } + {{{e}}_ - }{b_ + } + {{{E}}_ - }) + \\ {c_2}{{{w}}_ + } + {c_3}{\displaystyle\sum\nolimits_ + }{{{w}}_ + } = 0 \end{array} $

(4)

${{e}}_ + ^{\rm{T}}({{A}}{{{w}}_ + } + {{{e}}_ + }{b_ + }) + {c_1}{{e}}_ - ^{\rm{T}}({{B}}{{{w}}_ + } + {{{e}}_ - }{b_ + } + {{{E}}_ - }) + {c_2}{b_ + } = 0$

(5)

将式(4)、(5)整理成矩阵的形式为

$\begin{aligned} & \left[ {\begin{array}{*{20}{c}} {{{{A}}^{\rm{T}}}{{A}}}&{{{{A}}^{\rm{T}}}{{{e}}_ + }} \\ {{{e}}_ + ^{\rm{T}}{{A}}}&{{{e}}_ + ^T{{{e}}_ + }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + {c_1}\left[ {\begin{array}{*{20}{c}} {{{{B}}^{\rm{T}}}{{{B}}}}&{{{{B}}^{\rm{T}}}{{{e}}_ - }} \\ {{{e}}_ - ^{\rm{T}}{{B}}}&{{{e}}_ - ^{\rm{T}}{{{e}}_ - }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + \\ &\quad \quad {c_1}\left[ {\begin{array}{*{20}{c}} {{{{B}}^{\rm{T}}}} \\ {{{e}}_ - ^{\rm{T}}} \end{array}} \right]{E_ - } + {c_2}\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + {c_3}\left[ {\begin{array}{*{20}{c}} {{\displaystyle\sum\nolimits_ + }{{{w}}_ + }} \\ 0 \end{array}} \right] = 0 \end{aligned}$

$\begin{aligned} & \left[ {\begin{array}{*{20}{c}} {{{{A}}^{\rm{T}}}} \\ {{{e}}_ + ^{\rm{T}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A}}&{{{{e}}_ + }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + {c_1}\left[ {\begin{array}{*{20}{c}} {{{{B}}^{\rm{T}}}} \\ {{{e}}_ - ^{\rm{T}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{B}}}&{{{{e}}_ - }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + \\ & \quad \quad {c_2}\left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] + {c_3}\left[ {\begin{array}{*{20}{c}} {{\displaystyle\sum\nolimits_ + } {{{w}}_ + }} \\ 0 \end{array}} \right] = - {c_1}\left[ {\begin{array}{*{20}{c}} {{{{B}}^{\rm{T}}}} \\ {{{e}}_ - ^{\rm{T}}} \end{array}} \right]{{{E}}_ - } \end{aligned} $

使 ${{P}} = \left[ {\begin{array}{*{20}{c}} {{A}}&{{{{e}}_ + }} \end{array}} \right]$ ， ${{Q}} = \left[ {\begin{array}{*{20}{c}} {{B}}&{{{{e}}_ - }} \end{array}} \right]$ ，并且 ${\displaystyle\sum\nolimits_1} = \left[ {\begin{array}{*{20}{c}} {{\displaystyle\sum\nolimits_ + }}&0 \\ 0&0 \end{array}} \right]$ 。则解可表示为

${z_1} = \left[ {\begin{array}{*{20}{c}} {{{{w}}_ + }} \\ {{b_ + }} \end{array}} \right] = - {c_1}{({{{P}}^{\rm{T}}}{{P}} + {c_1}{{{Q}}^{\rm{T}}}{{Q}} + {c_2}I + {c_3}{\displaystyle\sum\nolimits_1})^{ - 1}}{{{Q}}^{\rm{T}}}{{{E}}_ - }$

同理，式(2)可表示为

$ {z_2} = \left[ {\begin{array}{*{20}{c}} {{{{w}}_ - }} \\ {{b_ - }} \end{array}} \right] = {c_4}{({{{Q}}^{\rm{T}}}{{Q}} + {c_4}{{{P}}^{\rm{T}}}{{P}} + {c_5}I + {c_6}{\displaystyle\sum\nolimits_2})^{ - 1}}{{{P}}^{\rm{T}}}{{{E}}_ + } $

式中： ${\displaystyle\sum\nolimits_2} = \left[ {\begin{array}{*{20}{c}} {{\displaystyle\sum\nolimits_ - }}&0 \\ 0&0 \end{array}} \right]$ ； ${{I}}$ 是适当维数的单位矩阵。

ES-LSTWSVM通过如下的决策函数判定新样本的类别标签：

${\rm{Label}}({{x}}) = \left\{ {\frac{{\left| {{{{x}}^{\rm{T}}}{{{w}}_ + } + {b_ + }} \right|}}{{\left\| {{{{w}}_ + }} \right\|}}} \right.,\left. {\frac{{\left| {{{{x}}^{\rm{T}}}{{{w}}_ - } + {b_ - }} \right|}}{{\left\| {{{{w}}_ - }} \right\|}}} \right\}$

2.2 非线性 ES-LSTWSVM

对于非线性分类问题，利用核技巧进行处理。首先将原始特征空间中的数据映射到希尔伯特空间中： $\varPhi :{{\bf{R}}^m} \to H$ 。类似于线性情形，决策函数可表示为 ${f_ + }(x) = ({{{w}}_ + }\varPhi (x)) + {b_ + }$ 和 ${f_ - }(x) = ({{{w}}_ - } \varPhi (x)) + {b_ - }$ 。

由希尔伯特空间理论^[23]知：

$ {{{w}}_ + } = \sum\limits_{i = 1}^{{m_1} + {m_2}} {{{({\lambda _ + })}_i}} \varPhi ({x_i}) = \varPhi (M){\lambda _ + } $

$ {{{w}}_ - } = \sum\limits_{i = 1}^{{m_1} + {m_2}} {{{({\lambda _ - })}_i}} \varPhi ({x_i}) = \varPhi (M){\lambda _ - } $

ES-LSTWSVM构造如下2个基于核函数的超平面：

$K({{{x}}^{\rm{T}}},{{{M}}^{\rm{T}}}){\lambda _ + } + {b_ + } = 0$ ， $K({{{x}}^{\rm{T}}},{{{M}}^{\rm{T}}}){\lambda _ - } + {b_ - } = 0$

式中： ${{M}} = \left[ {{{{A}}^{\rm{T}}}\begin{array}{*{20}{c}} {} \end{array}{{{B}}^{\rm{T}}}} \right]$ ； $K({x_i}{x_j}) = ({\mathit{\Phi}} ({x_i}){\mathit{\Phi}} ({x_j}))$ 。

在非线性情形下，ES-LSTWSVM可表示为

$\begin{array}{l} \min\limits_{{w_ + },{b_ + },\xi } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}{\left\| {K({{A}},{{{M}}^{\rm{T}}}){\lambda _ + } + {{{e}}_ + }{b_ + }} \right\|^2} + \dfrac{{{c_1}}}{2}{{{\xi }}^{\rm{T}}}{{\xi }} + \\ \dfrac{{{c_2}}}{2}(\left\| {{{{\lambda }}_ + }} \right\|_2^2 + b_ + ^2) + \dfrac{{{c_3}}}{2}{{\lambda }}_ + ^{\rm{T}}\varPhi {({{M}})^{\rm{T}}}\displaystyle\sum\nolimits_ + ^\varPhi \varPhi ({{M}}){{{\lambda }}_ + } \\ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&{}&{ - (K({{B}},{{{M}}^{\rm{T}}}){\lambda _ + } + {{{e}}_ - }{b_ + })}+ {{\xi }} = {{{E}}_ - } \end{array} \end{array} $

(6)

$\begin{array}{l} \min\limits_{{w_ - },{b_ - },\eta } \begin{array}{*{20}{c}} {}&{\dfrac{1}{2}} \end{array}{\left\| {K({{B}},{{{M}}^{\rm{T}}}){\lambda _ - } + {{{e}}_ - }{b_ - }} \right\|^2} + \dfrac{{{c_4}}}{2}{{{\eta }}^{\rm{T}}}{{\eta }} + \\ \dfrac{{{c_5}}}{2}(\left\| {{{{\lambda }}_ - }} \right\|_2^2 + b_ - ^2) + \dfrac{{{c_6}}}{2}{{\lambda }}_ - ^{\rm{T}}\varPhi {({{M}})^{\rm{T}}}\displaystyle\sum\nolimits_ - ^\varPhi \varPhi ({{M}}){{{\lambda }}_ - } \\ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}.}&{}&{(K({{A}},{{{M}}^{\rm{T}}}){{{\lambda }}_ - } + {{{e}}_ + }{b_ - })} \end{array} + {{\eta }} = {{{E}}_ + } \end{array} $

(7)

式中： $\displaystyle\sum\nolimits_ + ^\varPhi = \displaystyle\sum\nolimits_{{P_1}}^\varPhi + \cdots + \displaystyle\sum\nolimits_{{P_{{C_p}}}}^\varPhi$ ； $\displaystyle\sum\nolimits_ - ^\varPhi = \displaystyle\sum\nolimits_{{N_1}}^\varPhi + \cdots + \displaystyle\sum\nolimits_{{N_{{C_n}}}}^\varPhi$ 。 $\displaystyle\sum\nolimits_{{P_i}}^\varPhi$ 和 $\displaystyle\sum\nolimits_{{N_j}}^\varPhi$ 分别是由核Ward’s linkage聚类算法得到的2个类中第i个簇和第j个簇对应的协方差矩阵^[13-14]， $i = 1,2, \cdots ,{C_p},j = 1,2, \cdots ,{C_n}$ 。

类似于线性情形，式(6)、(7)的解可表示为

$\begin{array}{c} {z_1} = \left[ {\begin{array}{*{20}{c}} {{w_ + }} \\ {{b_ + }} \end{array}} \right] = \\ - {c_1}{\left( {{{P}}_\varPhi ^{\rm{T}}{{{P}}_\varPhi } + {c_1}{{{Q}}_\varPhi }^{\rm{T}}{{{Q}}_\varPhi } + {c_2}{{I}} + {c_3}\displaystyle\sum\nolimits_1^\varPhi } \right)^{ - 1}}{{{Q}}_\varPhi }^{\rm{T}}{{{E}}_ - } \end{array} $

(8)

$ \begin{array} {c}{z_2} = \left[ {\begin{array}{*{20}{c}} {{w_ - }} \\ {{b_ - }} \end{array}} \right]=\\ {c_4}{\left( {{{{Q}}_\varPhi }^{\rm{T}}{{{Q}}_\varPhi } + {c_4}{{{P}}_\varPhi }^{\rm{T}}{{{P}}_\varPhi } + {c_5}{{I}} + {c_6}\displaystyle\sum\nolimits_2^\varPhi } \right)^{ - 1}}{{{P}}_\varPhi }^{\rm{T}}{{{E}}_ + } \end{array} $

式中： ${{{P}}_\varPhi } = \left[ {\begin{array}{*{20}{c}} {K({{A}},{{{M}}^{\rm{T}}})}&{{{{e}}_ + }} \end{array}} \right]$ ； ${{{Q}}_\varPhi } = \left[ {\begin{array}{*{20}{c}} {K({{B}},{{{M}}^{\rm{T}}})}&{{{{e}}_ - }} \end{array}} \right]$ ，

$\displaystyle\sum\nolimits_1^\varPhi = \left[ {\begin{array}{*{20}{c}} {\varPhi {{({{M}})}^{\rm{T}}}\displaystyle\sum\nolimits_ + ^\varPhi \varPhi ({{M}})}&0 \\ 0&0 \end{array}} \right]$

$ \displaystyle\sum\nolimits_2^\varPhi = \left[ {\begin{array}{*{20}{c}} {\varPhi {{({{M}})}^{\rm{T}}}\displaystyle\sum\nolimits_ - ^\varPhi \varPhi ({{M}})}&0 \\ 0&0 \end{array}} \right]$

3 实验结果与分析

使用“多对一”的策略将ES-LSTWSVM模型扩展到多类分类中。为了证明该算法的有效性，给出了该算法在多个UCI数据集上的实验结果。在实验中，选择了“一对一” 最小二乘孪生支持向量机(1-v-1 LSTWSVM)、“一对多”最小二乘孪生支持向量机(1-v-r LSTWSVM)、改进的最小二乘孪生多分类支持向量^[24]( improvements on least squares twin multi-class classification support vector machine，ILST-KSVC)，多生最小二乘支持向量机^[25](multiple birth least squares support vector machine，MBLSSVM)与本文算法进行比较。实验结果为10折交叉验证的平均值。在非线性情形下，使用高斯核函数 $K({x_i},{x_j}) = \exp ({{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}} / {2{\sigma ^2}}})$ 。

3.1 实验结果

在本节中，使用UCI数据集中的Iris、Wine、Vowel、Balance、Vehicle、Zoo和Segment。这些数据集的特征如表1所示。

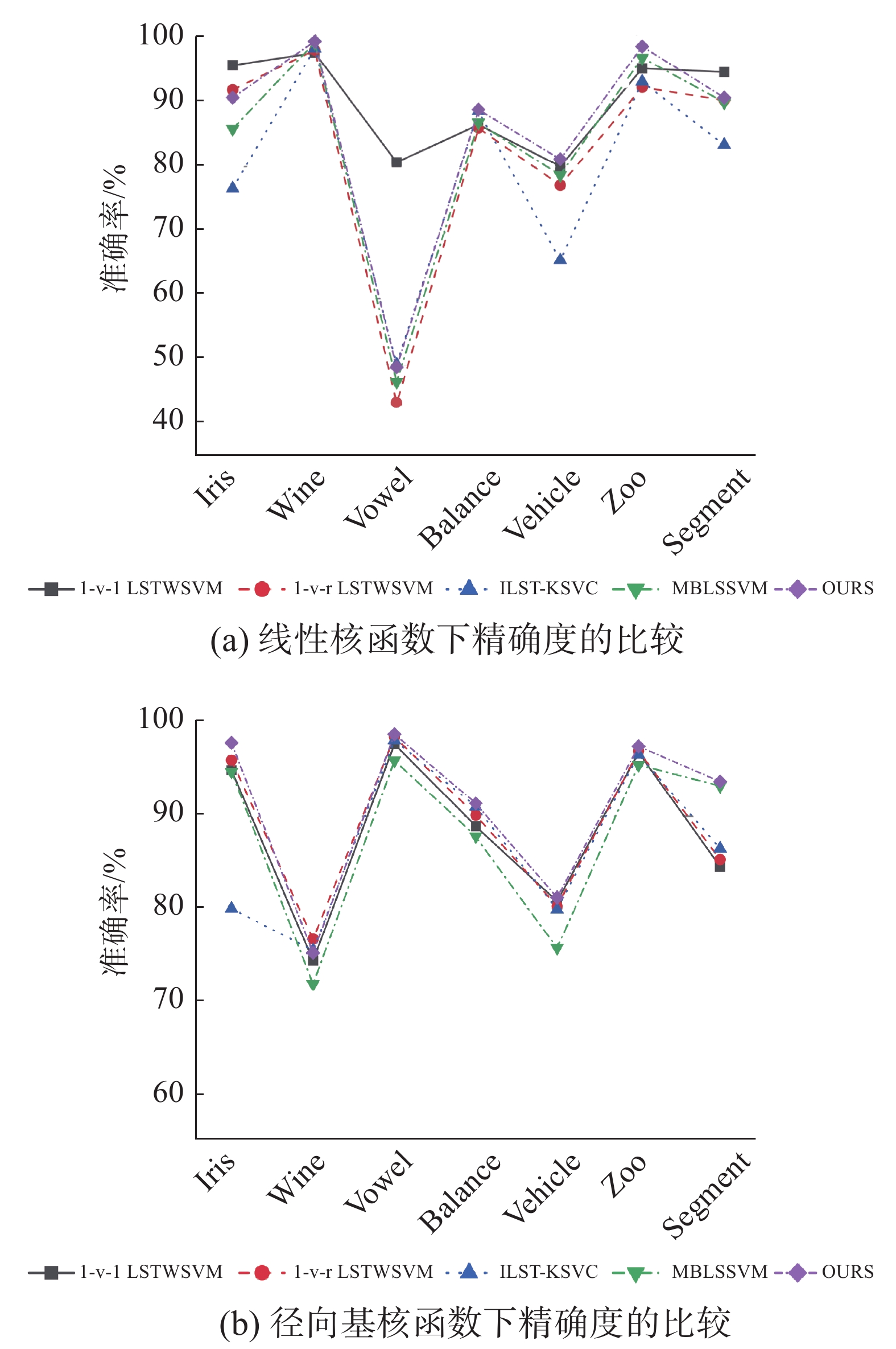
表2列出了上述算法在使用线性核的情况下的分类结果。表3给出了上述算法在使用高斯核的情况下的分类结果。从表2可以看出，提出的算法在Wine、Balance、Vehicle、Zoo 这4个数据集上有最高的分类精度，并且在其他数据集上也有不错的表现。从表3可以看出，所提出的算法在Iris、Vowel、Balance、Vehicle、Zoo、Segment这6个数据集上的分类准确率最高，并且在Wine数据集上也有较高的准确率。图1是对实验结果更直观的表示。

3.2 能量参数 ${E_ + }$ 和 ${E_ - }$ 对算法性能的影响

为了分析能量参数 ${E_ + }$ 和 ${E_ - }$ 对ES-LSTWSVM的分类性能的影响，在Heart、Liver、Breast和Ionosphere数据集上进行了实验。通过引入可变能量参数，所提出的分类器将做出相应的调整以减少噪声干扰。并使用网格搜索对参数进行选择。为了只考虑能量参数对实验结果的影响，将ES-LSTWSVM中的其他参数设置为固定值。图2显示了分类性能在Australian、Heart和Diabetes数据集上随能量参数 ${E_ + }$ 和 ${E_ - }$ 的变化而变化。图2(a)显示当 ${E_ + } = 0.7,\;{E_ - } = 1.0$ 时，算法在Heart数据集上的分类准确率高达86.96%。图2(b)显示当 ${E_ + }: {E_ - } = 4:3$ 时，算法在Liver数据集上的分类准确率高达71.15%。图2(c)显示当 ${E_ + } = 0.8,{E_ - } = 0.7$ 时，算法在Breast数据集上的分类准确率高达77.38%。图2(d)显示当 ${E_ + }:{E_ - } = 1:1$ 时，算法在Ionosphere数据集上的分类准确率高达88.68%。由此可知，可以通过寻找最优能量参数来确定最优超平面。

4 结束语

在本文中，提出了一种基于能量的结构化最小二乘孪生支持向量机，称为ES-LSTWSVM。首先使用聚类算法来获取类中的结构信息，然后为每个超平面引入能量因子，将传统TWSVM的不等式约束转换为基于能量模型的等式约束。这使得提出的ES-LSTWSVM不仅有较低的计算复杂度，而且提高了模型的泛化能力。最后，使用“多对一”策略将ES-LSTWSVM扩展到多类分类问题中。实验结果表明，所提出的算法具有良好的分类性能。