随着通信技术、计算机技术和控制技术的广泛应用，传统的电力系统已发展为与信息网紧密结合的电力信息−物理系统^[1](electrical cyber physical system，ECPS)。物理电网信息化在提升电力自动化水平的同时，也为ECPS的安全性带来了诸多隐患^[2-9]，电力网或信息网的故障可能波及对方网络，产生相互之间的连锁故障传播，从而严重影响ECPS的安全运行。因此，研究提升ECPS鲁棒性的方法具有重要的理论价值和现实意义。

电力系统鲁棒性的相关研究理论和方法中，基于还原论^[10-11]的方法难以从全局的角度辨识电网的脆弱环节，而复杂网络理论认为结构决定功能，可通过网络结构来研究其鲁棒性^[12-18]。随后，Buldyrev^[19]首次提出相依网络的概念，推动了人们利用网络理论研究ECPS的新高潮。目前主要通过加边策略和保护关键结构2个角度以提升ECPS鲁棒性。在加边策略的研究中，文献[20]讨论了电力网与信息网的相似性对网络鲁棒性的影响。文献[21]通过定义网间节点度数差提出2种加边策略以改善系统的鲁棒性，并指出双网加边策略的效果优于单网加边策略。文献[22]提出一种优先连接策略以优化已有加边策略。在保护关键结构方面，文献[23]提出一种相依节点对重要度综合指标以识别系统中的关键节点，并指出保护关键节点可改善系统的脆弱性。文献[24]提出加权介数、加权度数的概念，并指出高加权介数与高加权度数的信息节点对信息层具有关键作用。文献[25]指出电力网与信息网的耦合体是ECPS极为重要的组成部分，在信息层的预防措施中需要重点关注。上述研究对ECPS的鲁棒性优化具有一定启发意义。

但已有研究仅限于在网络中增加连边或重点保护关键结构，然而实际电网的运行与扩建中很少单一地增加输电线或仅局限于保护关键的元件，而是考虑负载容量并通过同时增设厂站及输电线以分担某厂站较大的电力负荷。

本文综合考虑上述问题，采用华中地区某省电力网的拓扑结构数据，构建电力网与信息网部分一一对应的相依网络模型，并采用非线性负载-容量模型作为系统的级联失效模型。在已有电力信息−物理相依系统鲁棒性研究成果基础上，基于增加节点的角度提出4种可能的增设电力节点及其信息设备对应的节点配置优化策略。最后通过电力负荷及系统鲁棒性的优化度2方面对华中某省电力网与IEEE118节点系统的电力信息−物理系统在4种节点配置策略下进行仿真及分析。本研究对实际电力系统在建设与规划过程中将有限资源进行较优分配具有一定的指导意义。

1 ECPS建模

ECPS包含大量的电力厂站及通信设备，分别构成物理层(P)和信息层(C)。基于复杂网络理论和相依网络理论，ECPS可抽象成一个无向网络，其拓扑关系可用邻接矩阵A表示：

${{A}} = {\left( {{a_{i,j}}} \right)_{\left( {M + N} \right) \times \left( {M + N} \right)}} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_P}}&{{{{A}}_{P - C}}} \\ {{{\left( {{{{A}}_{P - C}}} \right)}^{\rm{T}}}}&{{{{A}}_C}} \end{array}} \right]$

式中：M、N分别表示物理层、信息层的节点总数； ${{{A}}_P}$ 、 ${{{A}}_C}$ 分别表示物理层、信息层内部的连接关系； ${{{A}}_{P - C}}$ 表示物理层与信息层的相依关系； ${\left( {{{{A}}_{P - C}}} \right)^{\rm{T}}}$ 为 ${{{A}}_{P - C}}$ 的转置。

物理层为ECPS中的载流电力网。图1为华中地区某省电力网的地理接线图，其中包括220 kV和500 kV层面的变电站、开关站、牵引站以及相应的线路。为简化分析，忽略各站点的内部结构，将220 kV层面的变电站、发电厂抽象成物理节点。忽略厂站内部的连线，合并2个厂站间的多条线路得物理连边，由此得电力网邻接矩阵 ${{{A}}_P}$ 。

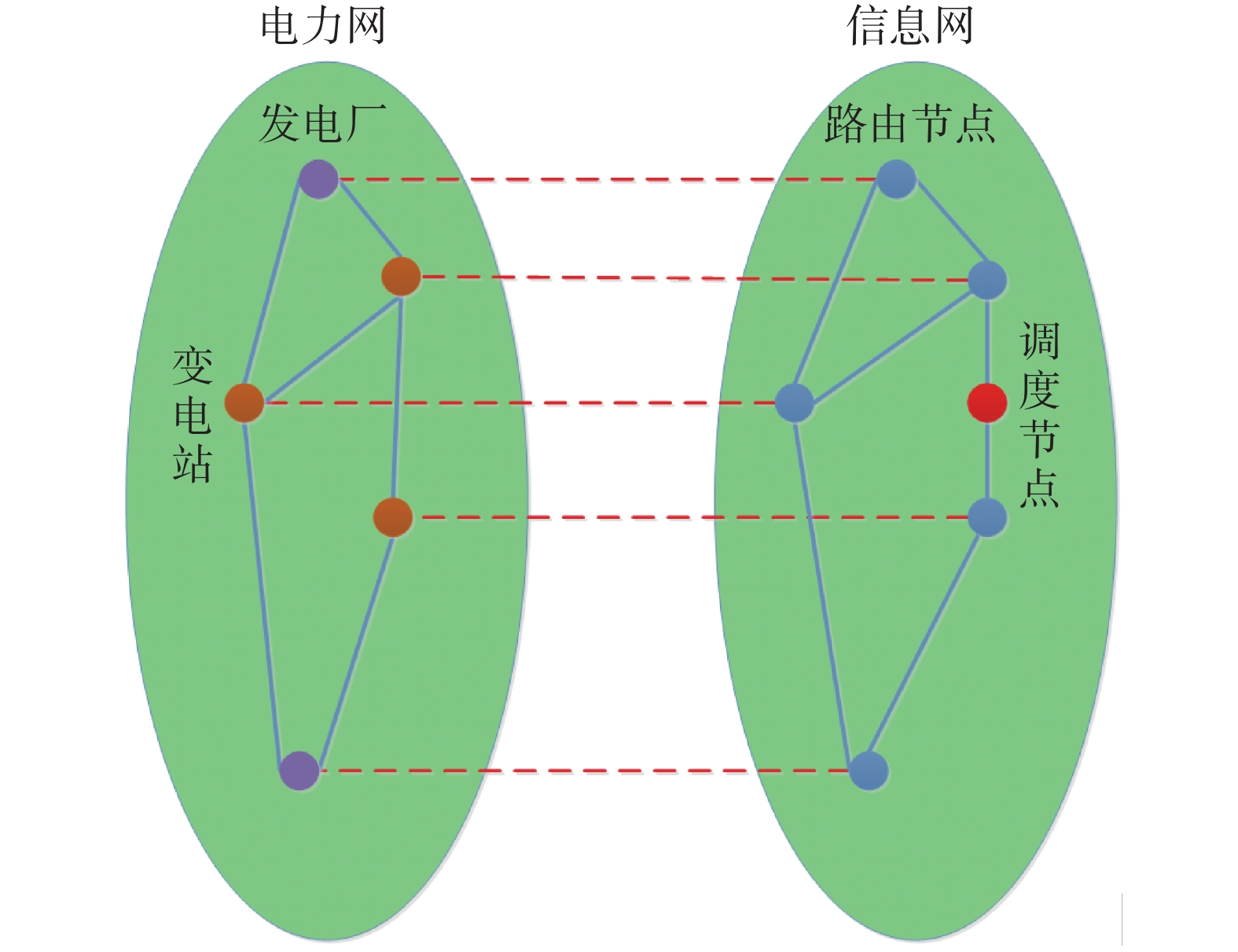
每个物理设备均配有相应的信息设备以实现信息采集、监督和控制等作用。为简化分析，可将信息设备、通信链路分别整合为信息节点、信息连边，其节点分布与物理层相同。此外信息层还存在一个(或少数几个)负责计算、决策等重要工作的调度中心，且一般都配有备用发电机组，在主供电厂失效下仍可保持正常工作^[5]，即为与电力网“解耦”的自治节点。文献[1]指出，电力通信网为复杂网络中典型的无标度网络^[26]，其高度数节点(度：与该节点连接的其他节点的数目)通常视作网络中具有某种特定功能的节点，因此本文将信息层中最高度数节点定义为调度中心，并基于BA网的生成过程构造出包含 $M + 1$ 个节点的信息层，即得信息网邻接矩阵 ${{{A}}_C}$ 。

相依边是物理层与信息层互相联系的抽象。物理设备为信息设备供电，信息设备采集物理设备的状态信息并控制物理层的安全运行。本文依据文献[1]，将物理层与信息层按介数−度方式部分一对一相依：将物理节点按介数降序排列为 ${B_P} = \{ {B_{P_1}},{B_{P_2}},\cdots,{B_{P_M}}\} $ ，将信息节点按度数降序排列后除去最高度数节点得 ${D_C} = \{ {D_{C_1}},{D_{C_2}},\cdots,{D_{C_N}}\} $ ，并按顺序依次在2个序列的节点之间增加一条相依边(即物理节点 ${B_{P_1}}$ 连接信息节点 ${D_{C_1}}$ ，物理节点 ${B_{P_2}}$ 连接信息节点 ${D_{C_2}}$ ，依次类推)，由此得电力网与信息网的相依关系矩阵 ${{{A}}_{P - C}}$ 。电力信息−物理相依系统的相依网络模型如图2所示。

为便于ECPS节点配置优化策略初期的研究分析，做如下简化与假设：

1)假设复杂网络、相依网络理论中的研究成果适用于ECPS；

2)假设物理节点或信息节点的负载一旦超过其容量上限将导致该节点失效，且电力网与信息网的节点服从负载重分配机制；

3)假设2个厂站间直接相连或通过邻居厂站进行连接可提升它们之间的连通性；

4)为便于分析节点配置优化策略的有效性，本文配置策略中增加的厂站默认为大型电力厂站；

5)鉴于实际建设电力厂站与信息系统的成本构成因素较为复杂，本文将增加节点的数量作为评估投入成本相对大小的依据，增加的节点越多表示投入的成本越大。

2 ECPS级联失效模型 2.1 非线性负载容量模型

节点的介数定义为网络的所有最短路径中经过该节点的路径数占最短路径总数的比例，表示节点作为“桥梁”的重要程度。电力系统的主要功能是将电能输送至用户，假设电能通过最短路径进行传输，则可用介数近似表征各厂站传输电能的相对大小，信息网的通信信息传输亦可以此近似。因此，本文采用非线性负载−容量模型^[27]对ECPS进行级联失效分析。

${L_{{p_i}}} = \sum\limits_{s \ne i \ne t \in {V_P}}^M {\frac{{{\sigma _{st}}(i)}}{{{\sigma _{st}}}}},\;{L_{{C_i}}} = \sum\limits_{s \ne i \ne t \in {V_C}}^N {\frac{{{\sigma _{st}}(i)}}{{{\sigma _{st}}}}} $

(1)

${C_{{P_i}}} = {L_{{P_i}}} + \beta {L_{{P_i}}^\alpha} ,\;{C_{{C_i}}} = {L_{{C_i}}} + \beta {L_{{C_i}}^\alpha} $

(2)

式中： ${L_{{P_i}}}$ 、 ${L_{{C_i}}}$ 分别表示物理层、信息层中节点 $i$ 的初始负荷； ${C_{{P_i}}}$ 、 ${C_{{C_i}}}$ 分别表示物理层、信息层中节点 $i$ 的容量； ${\sigma _{st}}$ 表示节点 $s$ 与节点 $t$ 间最短路径的条数； ${\sigma _{st}}(i)$ 表示由节点 $s$ 与节点 $t$ 间经过节点 $i$ 的最短路径条数；α、β为容忍参数，且 $\alpha \geqslant 0$ 、 $\beta \geqslant 0$ ，可根据实际情况进行灵活调节。 $\alpha $ 、 $\beta $ 越大，表示节点的容量越大，网络抵御级联失效的能力越强。

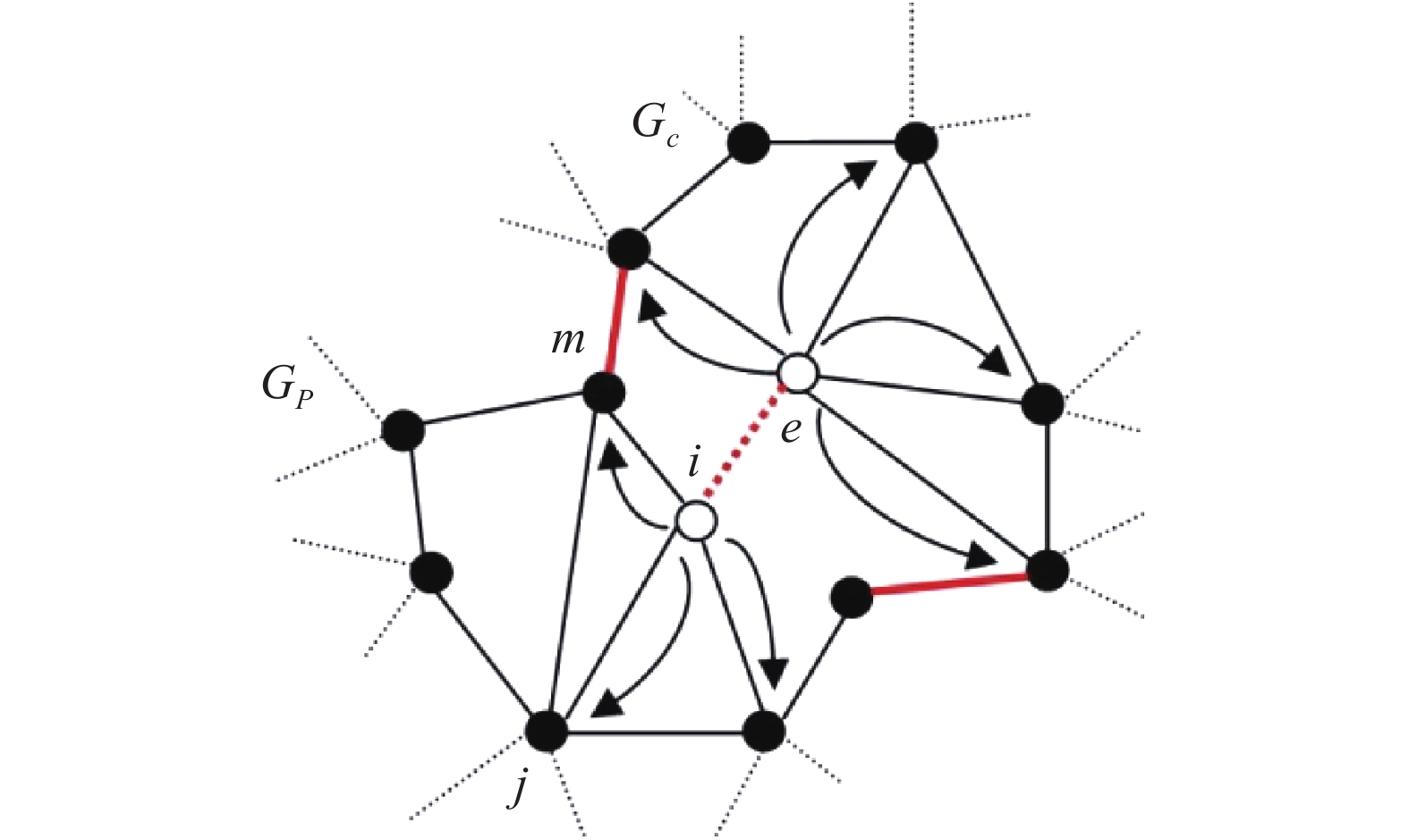
图3为简化的相依网络部分示意图，清晰地展示了负载重分配过程。假设物理节点 $i$ 失效，其负载按比例分配给其所有邻居节点，且失效节点 $i$ 的邻接节点 $j$ 获得的额外负载 $\Delta {L_{ji}}$ 的值与其负载值成比例关系。

$\Delta {L_{ji}} = \frac{{{L_i}{L_j}}}{{\displaystyle\sum\limits_{a \in {{\mathit{\Gamma}} _i}} {{L_a}} }}$

(3)

式中： ${\varGamma _i}$ 表示节点 $i$ 的邻居节点的集合； ${L_i}$ 、 ${L_j}$ 分别表示节点 $i$ 、 $j$ 的负载值。

同时，与节点 $i$ 相依的信息节点 $e$ 失效，节点 $e$ 同样按式（3）对其邻居节点进行负载重分配。任一子网络的节点负载超过其容量，均按该过程进行负载重分配，直至子网络任意节点 $m$ 的负载满足 ${L_{mi}} + \Delta {L_{mi}} \leqslant {C_m}$ 时，整个相依网的级联失效现象才会停止，达到暂时的稳定状态。

2.2 ECPS脆弱性评价指标

级联失效后拓扑结构的完整度与网络的脆弱性有非常紧密的联系：剩余的拓扑结构越完整，网络从失效状态中恢复的速度越快。本文基于文献[19]，从网络连通性的角度对ECPS的脆弱性进行分析。按攻击比例 $p$ 对物理层进行随机攻击，其中 $p$ 为攻击的物理节点总数占物理节点总数的比例。采用最大连通片 $G$ 表示网络在遭受攻击后的拓扑完整度^[28]。

$G = \frac{{{M'} + {N'}}}{{M + N}}$

式中： ${M'}$ 、 ${N'}$ 分别表示级联失效后物理层、信息层的剩余节点数。 $G$ 值越大说明网络的损坏程度越小，即网络的鲁棒性能越好。

同时定义临界值 ${P_c}$ 以表示系统能承受的相对最大攻击比例，即 $G$ 趋于0时对应的 $p$ 值。当攻击比例小于该值时，系统能维持相对稳定的状态。而当攻击比例大于该值时，系统中剩余有效节点的数目趋近于0，整个系统将彻底崩溃。 ${P_c}$ 值越大表明系统的鲁棒性越强。

3 节点配置优化策略

本文配置节点的主要目的是通过增加较少的节点达到既定的负荷及系统鲁棒性优化度，因此本节首先基于减轻电力负荷的目的对新增电力厂站的连边方式进行分析，并以此为基准研究电力网与信息网中配置相依节点对的优化策略。

3.1 节点配置比例

考虑到实际的经济成本因素，不可能无限制地增加厂站及信息设备，本文提出节点配置比例 ${f_n}$ 。

${f_n} = \frac{n}{M}$

式中 $n$ 表示在物理层与信息层配置的节点数。

3.2 连边方式分析

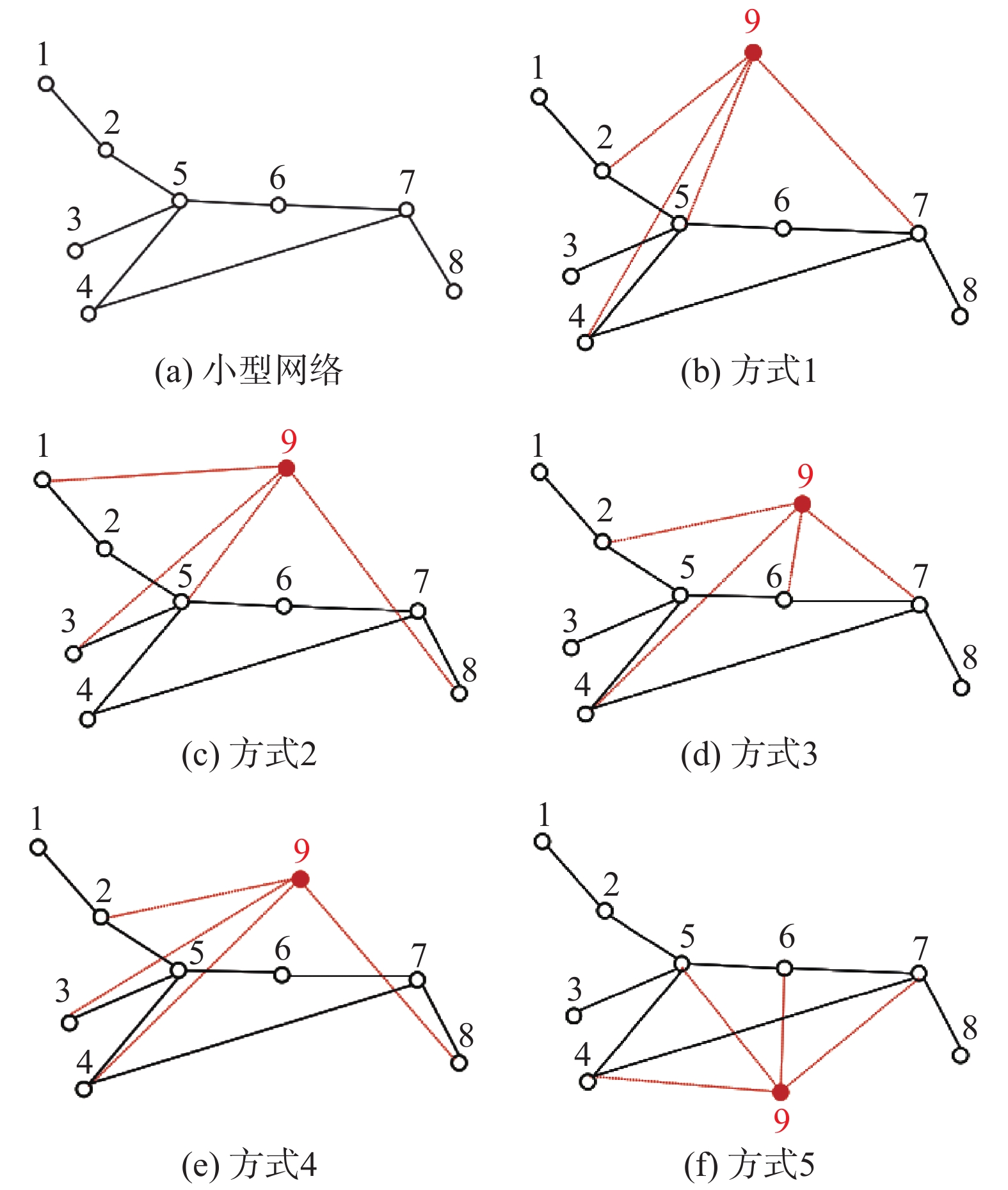
连边方式的选取在节点配置中起到至关重要的作用，合理的连边方式可通过配置较少的节点达到既定的效果。考虑到实际的大型电力厂站间应保持快速、良好的连通性以应对电力系统的结构脆弱性，因此本文根据假设3)，从复杂网络理论的角度使配置节点与待减负的目标节点或目标节点的邻居直接相连。为研究不同节点配置方式对大负载节点的减负作用，从电力网中抽取某一小块网络用以连边方式的研究与分析，如图4(a)所示。

首先根据式(1)求得网络中各节点的初始负载 ${L_0}$ 如表1所示。为达到减负目的，现以5种方式分别在网络中为目标节点(负载最大的5号节点)配置一个与其度数相同的9号节点。若连边过程中出现重边，则选择排序规则中的下一个节点。

方式1　直接连接目标节点与大负载节点。将配置节点连接目标节点及3个次负载最大节点，即节点5、7、2、4，如图4(b)所示。

方式2　直接连接目标节点与小负载节点。将配置节点连接目标节点以及负载最小的3个节点，即节点5、8、3、1，如图4(c)所示。

方式3　连接目标节点的邻居节点与大负载节点。考虑到若使配置节点连接目标节点的所有邻居，将导致配置节点的负荷过大，为避免其又形成新的负载过大节点，将配置节点一半数量的邻居节点取目标节点中负载最大的2个邻居节点，剩余数量的邻居节点取网络中除目标节点外负载最大的2个节点，即节点2、4、7、6，如图4(d)所示。

方式4　连接目标节点的邻居与小负载节点。与方式3类似，将配置节点一半的邻居节点取目标节点中负载最大的2个邻居节点，剩余数量的邻居节点取网络中负载最小的2个节点，即节点2、4、8、3，如图4(e)所示。

方式5　将配置节点与目标节点及任意3个节点相连，即节点5、4、6、7，如图4(f)所示。

由表1可知，前4种连边方式均可降低目标节点的负荷，这说明可通过配置节点来达到减负的目的。同时，4种连边方式下目标节点的负荷计算公式均发生了2类变化，下面以方式1为例做进一步说明：

1)配置节点使原网络中某2个节点之间的最短路径数变少。例如原网络中2号节点与7号节点间存在步数为3的2-5-6-7与2-5-4-7两条最短路径，且都经过5号目标节点，而配置9号节点后，仅有步数为2且不经过5号节点的2-9-7最短路径，这等同于将5号节点的负载公式中 ${{{\sigma _{27}}(5)} / {{\sigma _{27}}}}$ 项变为0，即负载变小；

2)配置节点形成了新的最短路径。例如原网络中1号节点与4号节点之间有一条步数为3的1-2-5-4最短路径，而配置9号节点后，又增加一条1-2-9-4最短路径，则5号节点负载公式中 ${{{\sigma _{14}}(5)} / {{\sigma _{14}}}}$ 项分子不变而分母增大，即负载变小。

然而在方式5下，目标节点的负载上升，显然不是所有的节点配置方式均能降低目标节点的负载，不恰当的配置方式只会起反作用，甚至降低网络的鲁棒性，因此研究配置节点的连边方式具有实际意义。

3.3 节点配置优化策略

相依网络中网间的拓扑互相似性表明：若耦合的2个单网络拓扑完全相同且对应节点间相互依存，则相依网络可映射为单层网络而不会扩大网间的交互影响^[29]。因此本文将电力网与信息网中新增的相依节点对按拓扑互相似性原则进行增边以提升系统的鲁棒性。根据小型网络的节点配置方式分析，假设不考虑电网建设中的实际距离，本文基于减轻厂站电力负荷过大的目的，提出4种可能的增设电力节点及其信息设备对应的节点配置优化策略。4种策略中，每一步新增一对相依节点，首先根据不同的节点配置策略增加物理节点以达到减负目的，然后增加信息节点并按拓扑互相似性原则进行增边。基于假设3)，每个配置节点的连边数量均为初始物理层中最大度节点的度数 ${k_{\max }}$ 。

1)策略1—连接大电力负荷节点

每一步首先对所有物理节点的电力负荷进行重新计算，并将节点按负荷从大到小进行排序，标注为 ${A_i}$ (i=1,2,…,M),即 ${L_{{A_1}}} \geqslant {L_{{A_2}}} \geqslant \cdots \geqslant {L_{{A_M}}}$ ，如果2个节点具有相同的负荷，则对它们进行随机排序。新配置的物理节点依次连接序列 ${A_i}$ 中前 ${k_{\max }}$ 个节点 ${A_1},{A_2},\cdots,{A_{{k_{\max }}}}$ ，并找出这些节点的所有相依节点作为新配置的信息节点的邻居节点，然后在2个子网络中新配置的节点间连接一条相依边。重复该步骤直至配置n个节点，且不允许出现自环或重边。

2)策略2—连接大电力负荷及小电力负荷节点

每一步首先对物理层各个节点的电力负荷进行重新计算，并将节点按负荷从大到小进行排序，标注为 ${A_i}$ (i=1,2,…,M)。新配置的物理节点连接电力负荷最大的1个节点与负荷最小的 $\left( {{k_{\max }} - 1} \right)$ 个节点，即 ${A_1},{A_{\left( {M - {k_{\max }} + 2} \right)}},{A_{\left( {M - {k_{\max }} + 3} \right)}},\cdots,{A_M}$ ，并找出这些节点的所有相依节点作为新配置的信息节点的邻居节点，然后在2个子网络中新配置的节点间连接一条相依边。重复该步骤直至配置n个节点，且不允许出现自环或重边。

3)策略3—连接大电力负荷节点的邻居及大电力负荷节点

每一步首先对所有物理节点的电力负荷进行重新计算，并将节点按负载从大到小进行排序，标注为 ${A_i}$ (i=1,2,…,M)。然后将电力负荷最大的物理节点 ${A_1}$ 的所有k个邻居节点按负荷从大到小进行排序，并标注为 ${A_{1i}}$ (i=1,2,…,k)。新配置的物理节点依次连接 ${A_{1i}}$ 中前 ${{{k_{\max }}} / 2}$ 个节点以及 ${A_i}$ 中除 ${A_1}$ 节点之外的前 ${{{k_{\max }}} / 2}$ 个节点，即 ${A_{11}},{A_{12}},\cdots,$ ${A_{1({{{k_{\max }}} / 2})}},$ ${A_2},{A_3},\cdots,{A_{({{{k_{\max }}} / 2} + 1)}}$ ，并找出这些节点的所有相依节点作为新配置的信息节点的邻居节点，然后在2个子网络中新配置的节点间连接一条相依边。重复该步骤直至配置n个节点，且不允许出现自环或重边。

4)策略4—连接大电力负荷节点的邻居及小电力负荷节点

每一步首先对所有物理节点的电力负荷进行重新计算，并将节点按负荷从小到大进行排序，标注为 ${A_i}'$ (i=1,2,…,M)。然后将负荷最大的物理节点 ${A_M}'$ 的所有k个邻居节点按负载从大到小进行排序，并标注为 ${A'_{Mi}}$ (i=1,2,…,k)。新增物理节点连接依次连接序列 ${A'_{Mi}}$ 中的前 ${{{k_{\max }}} / 2}$ 个节点以及序列 ${A'_i}$ 中的前 ${{{k_{\max }}} / 2}$ 个节点，即 ${A_{M1}}$ ${A_{M1}},{A_{M2}},\cdots$ ${A_{M({{{k_{\max }}} / 2})}}, {A'_1},{A'_2},\cdots, {A'_{{{{k_{\max }}} / 2}}}$ ，并找出这些节点的所有相依节点作为新配置的信息节点的邻居节点，然后在2个子网络中新配置的节点间连接一条相依边。重复该步骤直至配置n个节点，且不允许出现自环或重边。

4 仿真结果及分析

本节主要通过MATLAB仿真平台，针对已有华中某省电力网及IEEE118节点系统对应的电力信息−物理系统在4种节点配置策略下的电力负荷优化及系统鲁棒性进行仿真及分析。为避免随机性，每个仿真实验平均3 000次。

考虑到ECPS物理层不可能一直保持单一的新建厂站，实际还存在线路或设备老化、增加输电供电可靠性、控制短路电流、城区改造及设备升级扩容等现实因素，将导致厂站或线路的增添或撤销，使ECPS的拓扑结构发生变化，后续电力系统的超前规划相当于又在新的拓扑结构上增设厂站，本文据此将仿真实验中的节点配置比例控制在30%以内。

4.1 华中某省ECPS优化分析

本节对华中某省ECPS在4种节点配置优化策略下进行仿真实验分析，并依据文献[26]选取容忍参数 $\alpha = 0.85$ 、β ${\rm{ = }}15$ 。

4.1.1 电力负荷优化度

本文采用柱状图5以直观地展示不同配置节点比例下，4种策略对华中某省电力网初始节点负荷分布的影响。

由图5可知：

1)当 ${f_n} = 10\% $ 时，原物理层及其在4种策略下电力负荷处于900以上的物理节点比例分别为35%、34%、16%、32%、20%，且随着配置节点比例的增加，4种策略均可逐步降低900以上高电力负荷节点的比例，显然4种策略均可有效减少高电力负荷的节点比例，其中策略2、策略4较优。

2)以 ${f_n}$ =10%为例比较策略2和策略4的电力负荷分布情况：电力负荷处于0~300的节点比例分别为58%、54%，处于300~600的节点比例分别为22%、14%，处于600~900的节点比例分别为4%、12%，显然策略2能更有效地将大部分物理节点的负荷控制在较低的范围内。

3)策略4在 ${f_n}$ =30%下电力负荷由高至低的分布比例分别为：17%、5%、19%、59%，而策略2在 ${f_n}$ =10%下的分布为：16%、4%、22%、58%，显然策略2仅需配置10%的节点就能基本达到策略4配置30%节点下所能达到的电力负荷分布效果，这对于成本的控制具有积极作用。

4)综上可知，不论是出于物理层整体的电力负荷分布还是成本控制方面的考虑，策略2均优于其他3种策略。

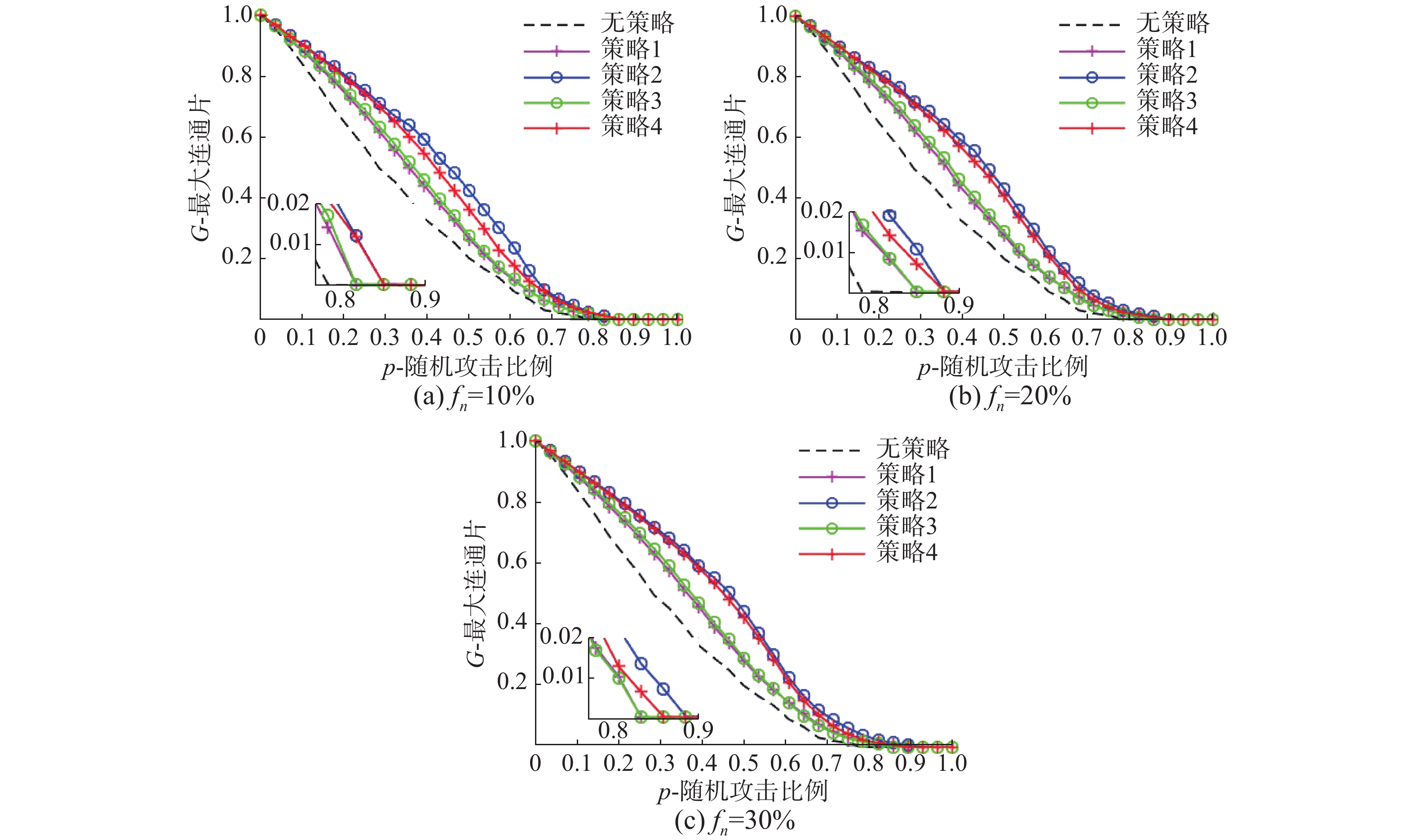
4.1.2 ECPS鲁棒性优化度

本节通过最大连通片与攻击比例的关系图6以直观地比较节点配置比例 ${f_n}$ 分别在10%、20%、30%情况下，不同策略对华中某省ECPS系统鲁棒性的影响。

由图6可知：

1)在4种策略的优化下，网络遭受攻击后的拓扑完整度均高于原网络，显然4种策略均可有效改善ECPS抵御级联失效的能力。

2)策略的效果对比：不论 ${f_n}$ 如何变化，系统在策略2与策略4下遭到攻击后的拓扑完整度均高于策略1与策略2，这说明配置的物理节点对ECPS鲁棒性优化度的影响与其邻居节点在物理层内电力负荷的相对大小有关，当配置物理节点的邻接节点中存在小电力负荷节点时，对系统的鲁棒性有更大的提升作用。

3)策略2在保持系统拓扑完整度方面效果最优：由图6可知无论配置节点比例如何设定，策略2在整个攻击过程中存活的最大连通片最高，特别地，当 ${f_n}$ =30%、 $p$ =50%时，原系统仅剩20%的有效节点，而策略2仍能保持约50%。

4) ${P_c}$ 优化方面：原系统在攻击比达到80%时 $G$ 趋于零，即 ${P_c}$ =80%，而配置节点后 ${P_c}$ 均有提升，当 ${f_n}$ =10%时，4种策略分别将 ${P_c}$ 优化至82%、86%、82%、86%。且当 ${f_n}$ 保持在20%以内时，4种策略的优化度均随着 ${f_n}$ 的增加有不同程度的提升，其中策略2的作用最显著。但在 ${f_n}$ 超过20%后，仅有策略2能够继续提升 ${P_c}$ ，且优化至90%以上，显然整个过程中策略2对 ${P_c}$ 的优化度最佳。

4.2 IEEE118节点系统优化分析

本节将验证4种策略对IEEE118节点系统的有效性。IEEE118节点系统是一个由118总线、19个发电机、35个同步电容器、177条线路、9个变压器以及91个负载组成的测试用例，代表了美国电力系统的一部分，为常用的标准测试系统。

4.2.1 电力负荷优化度

由图7可知，1) 4种策略对IEEE118节点系统的负荷优化效果与华中某省ECPS极为相似；2) 4种策略均可有效减少900以上高电力负荷的节点比例，且策略2的优化度最高，策略4次之；3)策略2仅需配置10%的节点就已基本达到策略4在配置30%节点下所能达到的电力负荷分布效果，这有益于对有限的资源进行较优的分配；4)策略2在电力负荷优化与成本控制方面均优于其他3种策略。

4.2.2 系统鲁棒性优化度

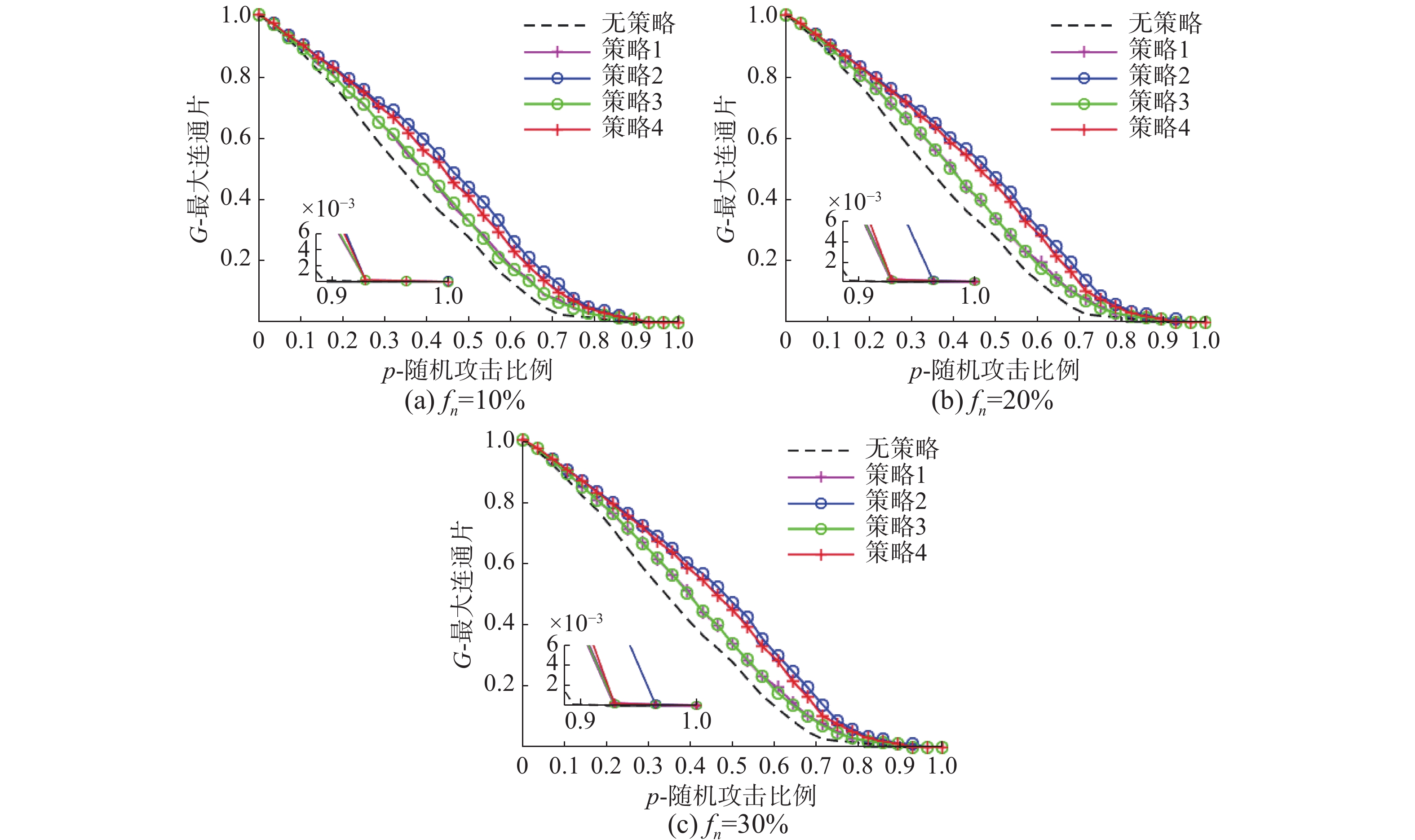
由图8可知，1) IEEE118节点系统与华中某省ECPS在各个配置节点比例及节点配置策略下的鲁棒性优化效果基本一致；2)在不同的节点配置比例下4种策略均能提升系统的拓扑完整度，且策略2的优化效果依旧为4种策略中最优；3)策略2对 ${P_c}$ 的优化效果最佳：由图8知原系统中 ${P_c}$ =89%，当 ${f_n}$ =10%时，4种策略均能将 ${P_c}$ 优化至94%，而当 ${f_n}$ 增加至20%时，只有策略2能进一步优化 ${P_c}$ 至96%，但若继续配置至30%节点， ${P_c}$ 无明显提升，这是由于此时系统 ${P_c}$ 较高，显然当攻击比例达到96%时系统中节点的损耗量巨大，难以继续维持整个系统的工作状态，所以此时继续配置节点也难以再优化 ${P_c}$ 值。

综合对华中某省电力网及美国电网的ECPS在电力负荷优化度和系统鲁棒性2方面的仿真分析可知，策略2—连接大电力负荷及小电力负荷节点时仅需配置较少的节点就能达到既定的负荷及系统鲁棒性优化效果。同时策略2在实际电网建设中具有一定的现实依据及优势：当新增设的厂站直接连接容量大及容量小的厂站时，首先能够提高线路的功率传输能力、减少因短路故障引起的跳闸事故，同时还能配合实现电能的协调调度、分担高电压等级厂站的供电压力以减少事故发生率，进而降低因事故造成的各项损失。

5 结束语

本文主要基于复杂网络理论，考虑到电力网络存在扩建等现实问题，研究受成本约束下如何增设站点从而优化负荷分布、改善系统的鲁棒性。采用华中地区某省电力网220 kV网架的拓扑结构数据，构建了电力网与信息网部分一一对应的相依网络模型，并采用非线性负载−容量模型作为系统的级联失效模型。根据实际电网中超前规划新增厂站的现实情况，在已有电力信息−物理相依系统鲁棒性研究成果基础上，以增加节点的角度提出4种可能的增设电力节点及其信息设备对应的节点配置优化策略，并验证了4种节点配置策略在华中某省电力网及IEEE118总线的电力信息−物理系统中的电力负荷优化及系统鲁棒性进行仿真及分析。仿真结果表明，在4种策略中，以配置的物理节点连接大电力负荷及小电力负荷节点为基准时，仅需配置较少的节点就能达到既定的优化度，且该策略的实施在实际电网建设中具有一定的现实依据及优势。本结论对于电力系统在建设与规划过程中将有限资源进行较优分配具有一定的指导意义。