知识图谱(knowledge graph)的概念是谷歌在2012年正式提出的，主要用于提升搜索引擎性能。随着大数据时代的到来，知识图谱规模得到了快速的增长，各种大规模知识图谱相继出现(如Freebase^[1]、WordNet^[2]、NULL^[3]等)。当前知识图谱已在数据挖掘、人工智能等领域具有至关重要的作用，促进了人工智能及其应用的发展，如智能问答^[4]、个性化旅游推荐等。

虽然现有知识图谱的规模已经相当大，但其仍是不完整的，如Freebase中75%的人不存在国籍信息，71%的人没有准确的出身地信息^[5]，因此有必要对现有知识图谱进行自动补全。这是当前知识图谱研究中最主要的任务和挑战之一。近年来，将知识图谱中实体与关系嵌入到向量空间进行知识图谱补全的方法显示出强大的可行性与鲁棒性。但是知识图谱嵌入的研究仍然面临着一个共同的问题，即在现有知识图谱嵌入模型训练时，是通过删除正例三元组(h, r, t)中的h(或t)，然后从实体集中随机选择一个实体对删除h(或t)不完整的三元组进行填充来生成负例三元组，致使获得的大量负例三元组都是低质量的。低质量的负例三元组将导致知识图谱嵌入模型训练时无法对实体向量与关系向量进行有效的更新，从而影响知识图谱的有效嵌入。

针对这一不足提出了一种通用的解决方法，基于实体相似性负采样的负例三元组生成方法来提高知识图谱嵌入的质量。该方法能够在训练中生成一个高质量的负例三元组，从而实现知识图谱嵌入模型的改进。我们将相似性负采样与TransE模型^[6]相结合得到TransE-SNS模型，并且在4个通用数据集(FB15K、FB13、WN11和WN18)上进行了实验，在链接预测与三元组分类任务中均获得了有效的提升。

1 相关研究

知识图谱嵌入(knowledge graph embedding)旨在将知识图谱中的实体与关系嵌入到连续的、稠密的、低维的和实值的向量空间，将其表示为稠密低维实值向量。然后可以通过向量之间的欧氏距离、曼哈顿距离或马氏距离计算实现对知识图谱中对象间的相似度计算。

在各类知识图谱嵌入模型中，基于翻译的表示学习^[7]模型实现了先进的性能。其中典型的翻译模型是由Bordes等^[6]于2013年提出的TransE模型。TransE模型将三元组(h, r, t)中的关系视为向量空间中头实体到尾实体的翻译操作。如果三元组(h, r, t)成立，则头实体向量 ${{h}}$ 、关系向量 ${{r}}$ 与尾实体向量 ${{t}}$ 应满足 ${{h}} + {{r}} \approx {{t}}$ 。由于TransE模型极为简单，同时在处理大规模数据方面表现出优异的性能，从而引起了基于翻译的表示学习研究热潮。在随后几年时间里，基于翻译的模型衍生出一系列的模型。Wang等^[8]提出让一个实体在不同关系下拥有不同的表示，将实体投影到关系所在超平面，然后在超平面上进行翻译操作。Lin等^[9]认为实体与关系应当处于不同的语义空间，提出了TransR/CtransR模型。TransR/CtransR通过投影矩阵将实体从实体空间投影到关系空间，然后在关系空间中建立翻译操作。Ji等^[10]认为实体从实体空间投影到关系空间是实体与关系的交互过程，提出了分别为头、尾实体提供不同的投影矩阵。TranSparse模型^[11]考虑了实体与关系的不平衡性和异质性，提出了一种根据关系的复杂程度来自适应的构造稀疏矩阵对实体进行投影，这样防止了简单关系过拟合、复杂关系欠拟合的发生。Feng等^[12]认为 ${{h}} + {{r}} \approx {{t}}$ 的翻译规则过于严格，于是建立了更加灵活的翻译规则 ${{h}} + {{r}} \approx \alpha {{t}}$ ，提高了模型的表达能力。Chang等^[13]认为FT模型的翻译规则仍过于复杂，进一步提出了 $({{h}} + {{{\alpha}}_h}) + $ $ ({{r}} + {{{\alpha}}_r}) \approx ({{t}} + {{{\alpha}}_t})$ 的翻译规则，实现了翻译模型性能的提升。Tan等^[14]考虑了不同关系空间中实体的不同状态和特征倾向，将实体的本征态与拟态进行线性组合作为实体的嵌入特征，并为每个关系都构造了一个动态关系空间，提高了关系表示的能力，减少了来自其他关系的噪声。Wang等^[15]将生成对抗网络引入表示学习模型中，利用生成器来获得高质量的负例三元组，提高了知识表示学习的能力。

2 基于相似性负采样的知识图谱嵌入 2.1 实体的相似性 2.1.1 实体局部结构的相似性

在本节中，将从两个角度对实体的相似性进行描述：1) 知识图谱中实体局部结构的相似性；2) 知识图谱通过 TransE 等翻译模型嵌入到向量空间中实体向量的相似性。

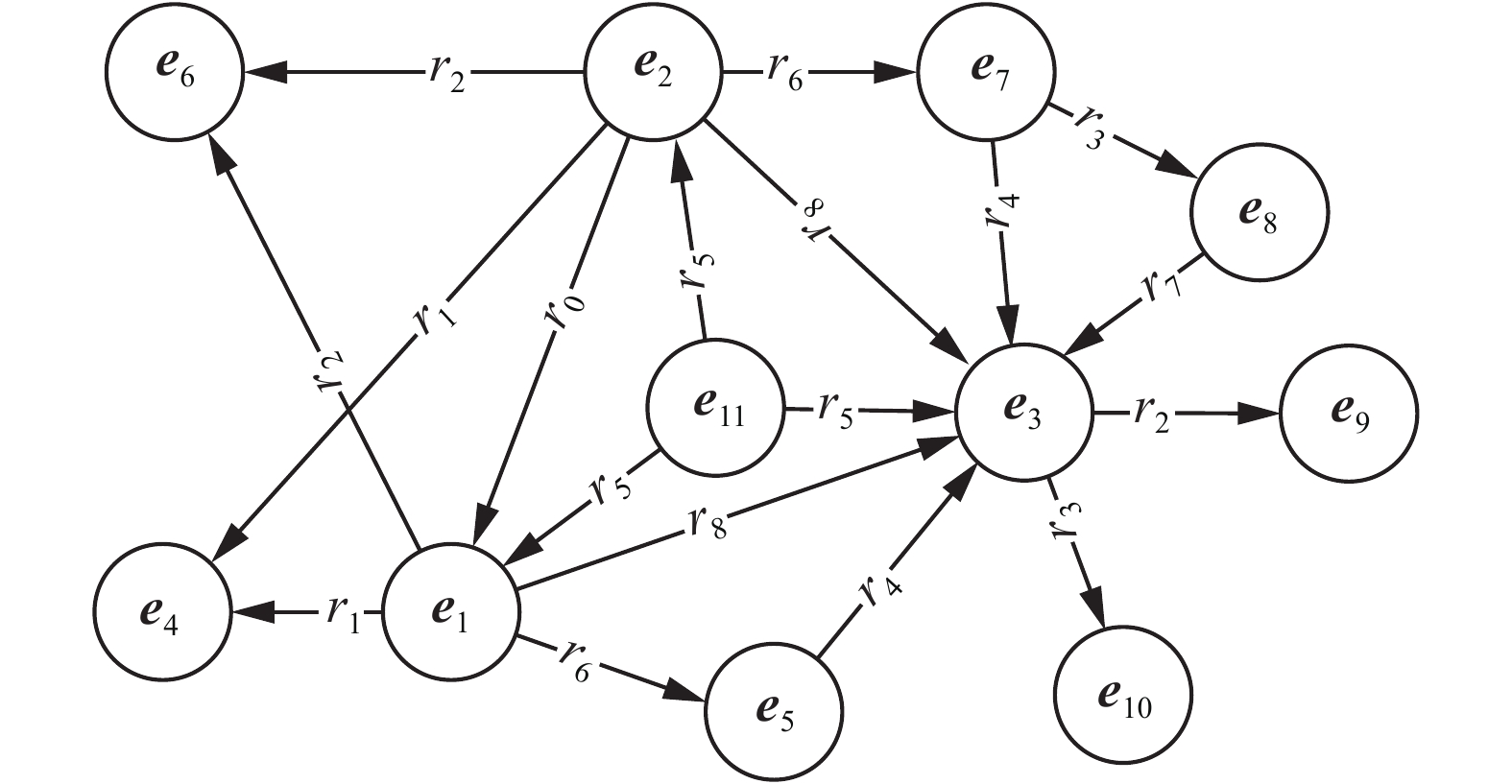
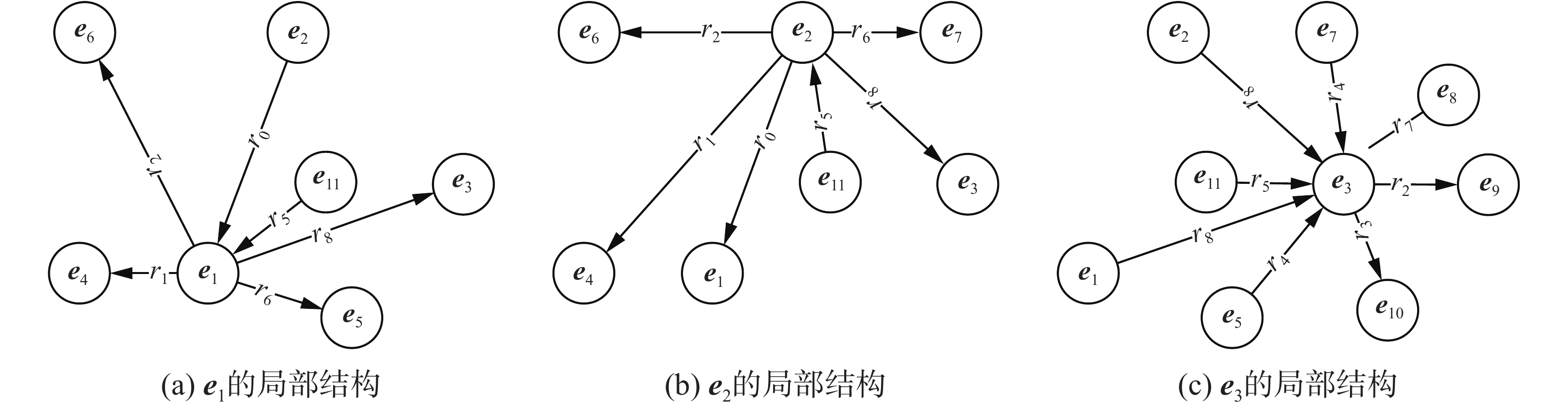
知识图谱中的每个实体间都存在着一定的联系，包括直接联系与间接联系。直接联系是2个实体之间存在直接关系。间接联系是2个实体之间存在的关系路径。例如，给定一个简单的知识图谱，如图1所示。其中，实体e₁与实体e₃之间存在着直接关系(r₈)和关系路径(r₆, r₄)；实体e₂与实体e₃之间存在着直接关系(r₈)和关系路径(r₆, r₄)、(r₆, r₃, r₇)等。本文将一个实体与其他实体的直接联系形成的结构称为该实体的局部结构，如图2所示。对于任意2个实体，如果它们的局部结构越相似，那么这2个实体也越相似。例如，e₁与e₂的局部结构中分别含有6个关系，并且这些关系均相同，其中存在4个关系构成了相似的三元组( $ * $ , r₁, e₄)、( $ * $ , r₂, e₆)、(e₁₁, r₅, $ * $ )和( $ * $ , r₈, e₃)，其中 $ * $ 可以用e₁或e₂代替，1个关系连接e₁与e₂的三元组(e₂, r₀, e₁)，1个关系连接着不同的尾实体构成2个三元组(e₁, r₆, e₅)和(e₂, r₆, e₇)。通过对比e₁与e₂的局部结构可以判定e₁与e₂的相似性较高。与此相同，通过对比e₁与e₃的局部结构，我们可以判定e₁与e₃的相似性较低。

2.1.2 实体向量的相似性

当利用TransE模型将知识图谱嵌入到向量空间中时，对于知识图谱中的每一个三元组(h, r, t)应当满足 ${{h}} + {{r}} \approx {{t}}$ 。对于头实体h而言，它在向量空间中的向量 ${{h}} \approx {{t}} - {{r}}$ ，即 ${{h}}$ 可以由 ${{t}} - {{r}}$ 得到，将 ${{t}} - {{r}}$ 称之为 ${{h}}$ 的空间约束。与此相同， ${{h}} + {{r}}$ 是 ${{t}}$ 的空间约束， ${{t}} - {{h}}$ 是 ${{r}}$ 的空间约束。因此，给定一个知识图谱，通过 ${{h}} + {{r}} \approx {{t}}$ 将知识图谱中的实体与关系嵌入到向量空间时，可以将知识图谱中实体的特征与关系的特征在向量空间中的特征表示分别称之为实体向量与关系向量。例如图2中的实体e₁与e₂，当他们嵌入到向量空间中时，需要满足4个相同的空间约束，即 $ * \approx {{{e}}_4} - {{{r}}_1}$ 、 $ * \approx {{{e}}_6} - {{{r}}_2}$ 、 $ * \approx {{{e}}_{11}} - {{{r}}_5}$ 和 $ * \approx {{{e}}_3} - {{{r}}_8}$ ，其中 $ * $ 可以用 ${{{e}}_1}$ 或 ${{{e}}_2}$ 替换，在这4个相同的空间约束下促使 ${{{e}}_1}$ 与 ${{{e}}_2}$ 趋近于相等。但与此同时， ${{{e}}_1}$ 还需满足空间约束 ${{{e}}_1} \approx {{{e}}_2} - {{{r}}_0}$ 和 ${{{e}}_1} \approx {{{e}}_5} - {{{r}}_6}$ ， ${{{e}}_2}$ 还需满足空间约束 ${{{e}}_2} \approx {{{e}}_1} - {{{r}}_0}$ 和 ${{{e}}_2} \approx {{{e}}_7} - {{{r}}_6}$ ，在这2个不同的空间约束下促使 ${{{e}}_1}$ 与 ${{{e}}_2}$ 又存在着一定的区别。因此，向量空间中的 ${{{e}}_1}$ 与 ${{{e}}_2}$ ，在相同的空间约束下驱使他们接近于相等，同时又在不同的约束下迫使他们产生一定的区别，这使得 ${{{e}}_1}$ 与 ${{{e}}_2}$ 在靠近的同时又存在一些距离。然而，对于图2中的实体e₁与e₃， ${{{e}}_1}$ 在向量空间中受到的所有空间约束均与e₃受到空间约束完全不同，这将使得 ${{{e}}_1}$ 与 ${{{e}}_3}$ 在向量空间中相距较远。综上所述，在向量空间中，对于任意两个实体，如果他们受到的相同约束越多，那么这两个实体向量之间的距离越小，即实体越相似，反之亦然。

2.2 随机抽样的局限性

现有知识图谱嵌入模型都是采用随机抽样来生成一个负例三元组，即采用相同概率从实体集中抽取一个实体替换正例三元组中的头实体(或尾实体)。然而，通过该方式生成负例三元组会存在一个问题：可能会在训练中生成大量的低质量负例三元组。导致上述问题的关键在于随机抽样忽略了实体之间的相似性。抽取的替换实体与被替换实体之间相似性可能是很低的，如图1中的实体e₁与e₃。一个低质量的负例三元组相对于正例三元组来说是极易区分的，这样的负例三元组对于学习知识图谱的有效嵌入是没有作用的。为了深入理解高质量的负例三元组与低质量负例三元组的区别，通过一个具体的例子进行阐述。

假设在知识图谱中有一个正例三元组(广西，省会，南宁)，根据随机抽样原则，选择替换尾实体南宁来生成负例三元组。首先，通过移除南宁会得到一个不完整的三元组(广西，省会，？)。然后，以相同的概率从实体集中抽取一个实体进行尾实体填充，假设抽取到一个Person类型实体马云，我们就会得到一个奇怪的负例三元组(广西，省会，马云)，这样的负例三元组就是一个低质量的负例三元组。与此相反，如果抽取到一个City类型实体桂林，将会得到一个高质量的负例三元组(广西，省会，桂林)。由于南宁与桂林的相似度远高于南宁与马云的相似度。南宁与桂林拥有许多相同或者相似的属性或者关系类型，比如，它们均属于广西，都拥有城市属性，地理位置相近，气候类型相同，地形地貌相似，历史文化也相似。与此相反，南宁与马云，一个是城市，一个是人，他们几乎没有相同的属性或者关系类型，因此他们的相似度是极低的。

在知识图谱嵌入模型中，如TransE模型使用基于边界的损失函数作为训练目标。训练过程中，当在使用相似性低的实体进行替换来生成负例三元组时，得到的是一个低质量的负例三元组，这将导致生成的负例三元组与正例三元组的得分之差大于边界值，使得损失值为0。在损失值为0时，模型将不会对实体向量与关系向量进行更新，也就是说本次训练对于实体向量与关系向量的学习无益，无法获得更多的样本特征。为了得到高质量的负例三元组，促进实体向量与关系向量的有效更新，实现知识图谱中实体与关系的有效嵌入，应该使用与被替换实体具有一定程度相似性的替换实体。因此，针对此问题我们提出了解决方案−相似性负采样。

2.3 相似性负采样

一个高质量的负例三元组可以帮助知识图谱嵌入，而得到一个高质量的负例三元组的关键是获取一个与被替换实体相似的实体。将知识图谱嵌入到向量空间中时，实体的局部结构相似性转化为2个实体向量的相似性。2个实体向量之间的距离越小，它们就越相似，反之亦然。这促使我们萌发出对实体进行聚类后获得相似实体。于是使用简单有效的K-Means算法^[16-18]对实体进行聚类，然后使得替换实体与被替换实体属于同一个簇。上述实体抽样过程，称为相似性负采样(similarity nagetive sampling, SNS)。

对于一个给定的知识图谱G = (E, R, S)，其中E = {e₁, e₂, $ \cdots ,\;{ e}_N$ }表示知识图谱中包含N个实体的实体集合，R ={r₁, r₂, $ \cdots, \; r_M$ }表示知识图谱中包含M个关系的关系集合，S $ \subseteq $ E ×R ×E表示知识图谱中的三元组集合。本文目标是将N个实体划分到K个聚类中，使得每个实体到所属聚类中心最近，即，每个实体到所属聚类中心的欧氏距离之和最小，即满足式(1)：

$\arg \min \sum\limits_{i = 1}^K {\sum\limits_{e \in {C_i}} {{{\left\| {{{e}} - {{{c}}_i}} \right\|}_{{L_2}}}}} $

(1)

式中：K表示聚类中心的数量； ${{e}}$ 是一个实体向量； ${{{c}}_i}$ 表示第i个聚类中心向量；C_i表示第i个聚类中实体e的集合；L₂是第二范数欧氏距离。

知识图谱中实体的相似性负采样详细过程：首先通过TransE模型训练50个epoch获取实体集E与关系集R的向量表示，然后利用K-Means聚类将实体集划分为K个簇{E₁, E₂, $ \cdots , \;{ E}_K$ }，每个簇中的实体之间具有较高的相似性。当给定一个被替换实体e∈E_k (k∈{1, 2, $ \cdots ,\;K$ })时，从簇E_k中选择替换实体e' 。那么，获得的替换实体e' 与被替换实体e将具有较高的相似性。

2.4 TransE-SNS模型

在本节中，详述了将实体相似性负采样与TransE模型结合得到TransE-SNS，同时给出了TransE-SNS模型完整代码的训练过程，即算法1。

TransE-SNS采用 ${{h}} + {{r}} \approx {{t}}$ 的翻译原则将实体和关系嵌入同一个向量空间。因此为TransE-SNS定义了得分函数：

${f_r}( h, t) = {\left\| {{{h}} + {{r}} - {{t}}} \right\|_{{L_2}}}$

(2)

式中： ${{h}}{\text{、}}{{r}}{\text{、}}{{t}} \in {{\rm{R}}^{{n}}}$ ；L₂是第二范数欧氏距离。

在TransE-SNS中，采用了基于边界的损失函数作为训练目标，基于边界的损失函数为

$L = \sum\limits_{({ h},{ r},{ t})} \in S {\sum\limits_{{\rm Ne}{g_{({ h},{ r},{ t})}}} \in { S}'} {\nabla {{[{f_r}({ h},{ t}) + \gamma - {f_r}({ h}',{ t}')]}_ +}} $

(3)

式中：S是正例三元组集合；S' = {(h' , r, t) | h' ∈E_h；(h' , r, t) $\notin $ S}∪{(h, r, t' ) | t' ∈E_t；(h, r, t' ) $\notin $ S}(其中，E_e表示实体e所在的簇)是负例三元组集合；Neg_{(h, r, t)}是S' 中(h, r, t)对应的一个负例三元组；[f_r (h, t) +γ−f_r (h' , t' )]₊ = max (0, f_r (h, t) +γ−f_r (h' , t' ))；γ是边界值。本文利用随机梯度下降算法(SGD)^[19]最小化基于边界的损失函数。

算法1给出了TransE-SNS模型的完整训练过程。在训练过程中，前50个epoch采用的是随机抽样来生成负例三元组进行训练，然后对实体向量进行第一次聚类。之后每完成训练50个epoch，就对训练得到的实体向量重新进行一次聚类。

算法1 　Learning TransE-SNS

输入　训练集S ={(h, r, t)}和负例三元组集S' ={(h' , r, t) | h' ∈E_h, (h' , r, t) $\notin $ S}∪{(h, r, t' ) | t' ∈E_t,(h' , r, t) $\notin $ S}，实体集E，关系集R，边界值γ，嵌入维度n，学习率α, K-Means聚类中心数k，实体聚类子集E_i (i = 1, 2, $ \cdots , k$ )。

输出　实体向量与关系向量

1)初始化：

2) ${{r}}$ ← uniform ( ${{- 6} / {\sqrt {{n}}}}$ , ${6 / {\sqrt {{n}}}}$ )对于每一个r∈R

3) ${{r}}$ ← ${{r}}/||{{r}}||$ 对于每一个r∈R

4) ${{e}}$ ← uniform ( ${{- 6} / {\sqrt {{n}}}}$ , ${6 /{\sqrt {{n}}}}$ )对于每一个e∈E

4) ${{e}}$ ← ${{e}}/||{{e}}||$ 对于每一个e∈E

5) loop

6) S_batch ← sample (S, b) //从S中抽取一个大小为b的mini-batch

7)T_batch← Ø // 初始化正负例三元组对的集合

8) for (h, r, t)∈S_batch do

9) Neg_(h,r,t) ← sample(S'_{(h, r, t)}) //抽取一个负例三元组(h' , r, t)或(h, r, t' )

10) T_batch ←T_batch∪{(h, r, t), Neg_{(h, r, t)}}

11) end for

12) 更新实体向量与关系向量

　　　 $\displaystyle\sum\limits_{({ h},{ r},{ t}) \in { S}} {\displaystyle\sum\limits_{{\rm Ne}{{\rm g}_{({ h},{ r},{ t})}} \in { S}'} {\nabla {{[{f_{ r}}({ h},{ t}) + \gamma - {f_{ r}}({ h}',{ t}')]}_ +}}} $

13) if epoch % 50 == 0 then

14) 更新E_i,// K-Means聚类

15) end if

16) end loop

3 实验与分析

为了评估方法的性能，在4个公开数据集上进行实验，通过链接预测和三元组分类任务进行评价。

3.1 数据设置

我们使用的数据集是来自于2个被广泛使用的知识图谱WordNet和Freebase。WordNet是一个大型的英语词汇知识图谱。在WordNet中，将代表某一基本词汇概念的同义词集合作为实体，并在这些同义词集合之间建立各种语义关系。在本文中，使用WordNet中的2个子集：WN18^[20]和WN11^[21]。Freebase是一个大型的人类知识的知识图谱，存储了真实世界中的一般事实。本文也使用了Freebase中的2个子集：FB15K^[20]和FB13^[21]。在表1中给出了这4种数据统计数据。

3.2 链接预测

链接预测旨在预测一个三元组(h, r, t)中缺失的h(或t)。在这项任务中，将测试三元组(h, r, t)缺失的h(或t)称为正确实体，除正确实体以外的其他实体均被视为候选实体。首先，利用候选实体替换测试三元组(h, r, t)中的h(或t)以获得候选三元组。然后，计算候选三元组与测试三元组的得分。最后，根据实体对应的三元组得分从低到高对候选实体与正确实体进行升序排列。在2个数据集WN18和FB15K上进行链接预测任务，使用2项常用的评价标准作为实验中的评价指标^[6]：正确实体排名前10的比例(Hits@10)和正确实体的平均排名(Mean Rank)。显然，对于一个好的预测应该有一个高的Hits@10和低的Mean Rank。

值得注意的是，在候选三元组集合中有一部分候选三元组可能存在于训练集、验证集和测试集中。虽然这些候选三元组不是当前测试的正确三元组，但它们应该被认为是正确的，并且它们的得分很可能比当前正确三元组的得分更低，从而影响正确实体的排名。我们将已经在训练集、验证集和测试集中出现过的候选三元组滤除。因此，在测试过程中设置了一个过滤器，并将2项评价指标中经过滤器滤除的称之为“Filt”，反之，将其称之为“Raw”。

在这项任务中，为了得到模型的最佳参数设置，尽可能多地尝试了参数的各种设置，参数主要从以下设置中选择：模型训练周期epoch∈{1 000，2 000，3 000}，学习率α∈{0.01，0.001，0.000 1}，边界值γ∈{1，2，2.5，3，3.5，4，4.5，5，5.5，6}，嵌入维度n∈{25，50，100，200}，批处理大小B∈{100，200，500，1 000}，聚类中心数K∈{16，32，64}，聚类迭代次数i∈{10，20，50}，三元组得分与聚类相似度均采用L₂第二范数进行计算。在2个数据集上，都获得了关于平均排名和排名前10的比例的最佳参数设置，如表2所示。

在WN18和FB15K上的链路预测任务实验结果，如表3所示。表中对比模型的实验结果来自于原文献，加粗的结果为表中最优结果。从表中可以看出，本文方法在大多数情况下都达到了最先进的效果。在WN18中，本文方法在Hits@10 (raw, bern)中性能略低于TranSparse-DT。在FB15K中，本文方法在Mean Rank (bern)和Hits@10 (raw, bern)未能获得所有模型中的最佳性能。我们认为TransE-SNS未能在所有的情况下达到最佳性能有以下2个原因：1)FB15K数据比较稀疏，连接的多个相同关系的实体较少，即每个实体本身对应的相似实体较少，这导致聚类后每个簇中依旧包含一定数量的相似性较低的实体。2)聚类中心K值选择比较困难，并且K值选择被限制在几个固定值中。因此，K-Means聚类不能很好地对实体进行聚类。

图3是在数据集FB15K中1 345个关系，按照4种不同的关系类别分布情况，其中1-to-1的简单关系占比为24%, 1-to-N、N-to-1和N-to-N的复杂关系分别占比23%、29%和24%。

表4显示了4种不同关系类别下Hits@10的链接预测结果。值得注意的是，TransE-SNS模型在大多数情况下都优于其他模型。特别是，头部和尾部的预测在N-to-N关系中实现了最先进的性能。本文方法在N-to-1关系中略显不足。总体来说，本文方法在处理复杂关系方面具有显著的优势。

3.3 三元组分类

三元组分类任务旨在判断一个给定的三元组(h, r, t)是否正确。在本文中，使用3个数据集(即WN11、FB13和FB15k)来验证方法在不同数据集上的有效性。Socher等^[20]提供了2个数据集(即WN11和FB13)。在WN11和FB13中，已经包含正例三元组和负例三元组。其中，每一个负例三元组都是通过破坏正例三元组来获得的。在FB15K中只存在正例三元组，于是使用与Socher等^[20]相同的原理构造负例三元组。

在实验中，为每个关系r都设置了一个阈值δ_r。在验证集上，通过最大化分类准确度来获取每一个关系所对应的δ_r。对于给定三元组(h, r, t)，如果其得分函数的得分低于δ_r，则将其归类为正例，否则为负例。使用与链接预测相同的方式来获得此任务的最佳参数设置，并得到了3个数据集上的最佳参数设置，如表5所示。

表6所示是WN11、FB13和FB15K三元组分类任务的实验结果。从表6中可知，TransE-SNS在所有数据集上的分类性能都优于TransE和TransH。在FB13上，TransE-SNS更是取得了所有模型中的最佳性能。相对于TranSparse-DT和GTans-SW，TransE-SNS在WN11与FB15K上的性能略显不足。总体来说，尽管TransE-SNS并未在所有数据集上实现最佳性能，但TransE-SNS与大多数模型相比，仍具有较大优势。

4 结束语

本文针对知识图谱嵌入模型中采用随机抽样无法很好地获取高质量的负例三元组，提出了一种相似性负采样方法用于提高负例三元组的质量。与随机抽样相比，相似性负采样在很大程度上提高了替换实体与被替换实体间的相似性，从而提高了负例三元组的质量。在训练时，相似性负采样生成的高质量负例三元组促进了模型对实体与关系特征的学习。通过将相似性负采样与TransE模型结合得到TransE-SNS模型。我们的方法能够通过高质量的负例三元组充分获取实体有效特征，同时忽略了低质量的负例三元组。实验结果表明，TransE-SNS模型在链路预测与三元组分类任务中均取得了较优的性能。特别是，相较于基础模型TransE，引入相似性负采样后对模型性能具有较大提升。并且，TransE-SNS模型与TransE一样简单且有效，具有较强的可行性与鲁棒性。但是由于K-Means聚类算法本身在K值选择以及对数据具有一定要求，造成相似性负采样对于较为稀疏的大规模知识图谱较难实现相似实体的聚类与采样，从而影响模型的整体效果。在以后将进一步探索不同聚类算法和知识图嵌入模型的组合，得到一个更加有效的知识图谱嵌入模型。