在生物界的许多种群里，个体行为都较为简单，例如蚁群、蜂群、鸟群等，然而这些生物个体一旦聚集进行沟通合作，行为上可能表现出十分复杂的特征，由此产生了群体智能。群体智能即个体借助相互合作由简单的智能行为产生复杂的智能行为，其控制方式不是集中式，而采用分布式。群体智能具有自组织性、简单性和可扩充性等特性，突出了在适当的进化机制引导下个体通过协同合作而表现出复杂行为的能力。针对这些行为现象，人们对个体简单的智能行为及协同合作智能行为等建立数学模型并深入分析，研究种群的协同合作智能行为和强大的处理问题能力的背后机理，目前已提出了许多群体智能算法，攻破了一些较为困难的优化课题。群智能优化算法将生物界的各种种群中的个体表示为搜寻空间内的点，个体的进化和觅食行为类似优化和搜索阶段；将个体对环境的适应性通过定义目标函数并进行优化求解得以实现；优化与搜寻阶段中用可行的较优解代替可行的较劣解的更新过程被类比为个体的优胜劣汰过程或觅食过程，整个群体将会逐步收敛，直至最优解。因此，构成一类以“生成+核查”为特点的迭代优化算法^[1]。

布谷鸟搜索(cuckoo search, CS)算法属于典型的具有迭代搜寻特征的群智能优化算法。作为新型的启发式搜索算法，是以布谷鸟的寄巢产卵特点及少部分生物的莱维飞行(Levy flights)模式为参照，由Yang等^[2]于2009年提出。其主要思想是通过随机行走方式产生候选鸟巢以及采用贪婪策略更新鸟巢位置，最终使鸟巢位置达到或者接近全局最优解^[3]。文献[4]针对CS算法构造了Markov链数学模型，验证了CS算法具有全局收敛特性。

布谷鸟搜索算法的优点包括简单、参数少、易实现、搜索路径优、易收敛到全局最优且收敛速度快等，自从提出后就得到人们的关注，目前已经成为一种活跃的群智能算法^[5-7]。近几年来国内外众多学者对CS算法及其应用做了较为深入的研究，但是迄今有关CS算法的综述比较少。文献[8]简单地介绍了CS算法的发展概况并比较了几种改进算法，文献[9]详述了CS算法原理，并将其与遗传算法(genetic algorithm, GA)和粒子群优化(particle swarm optimization, PSO)算法作了比较，但它们都对CS算法的发展概况论述得不够系统和全面。因此，为了进一步加快CS算法的研究与应用进程，能够更有效地解决实际问题，需要对CS算法作较全面、系统的总结和评述。本文首先阐述了CS算法的生物背景、基本模型及实现步骤；然后对当前CS算法的改进研究进行了归纳；其次总结了CS算法的应用现状；随后就优缺点及适用范围两方面对CS算法与其他群体智能算法进行了比较；最后指出了目前CS算法中尚存在的问题及有待研究的方向，以期为CS算法的研究提供指导和启迪。

1 布谷鸟搜索算法原理 1.1 生物背景

布谷鸟最特殊的习性是寄巢产卵^[10]。大自然中有一些布谷鸟会将自己的卵产在寄主鸟巢中，同时布谷鸟也会移除鸟巢中其他卵使得鸟巢中的卵数量保持相近。因为布谷鸟的卵与寄主的卵相比孵化周期更短，孵出的布谷鸟幼雏势必本能地把寄主的卵推出卵巢，以此增加自己的存活率，提高竞争性。在某些情况下，当布谷鸟寄生其卵时，寄主鸟类会攻击布谷鸟，也有可能发现鸟巢中陌生的卵。这时，寄主鸟类会丢弃布谷鸟所产的卵或直接重新筑巢。与寄主鸟类不停地争斗中，布谷鸟的卵及孵化的幼雏皆沿着仿照寄主鸟类的方式生长。

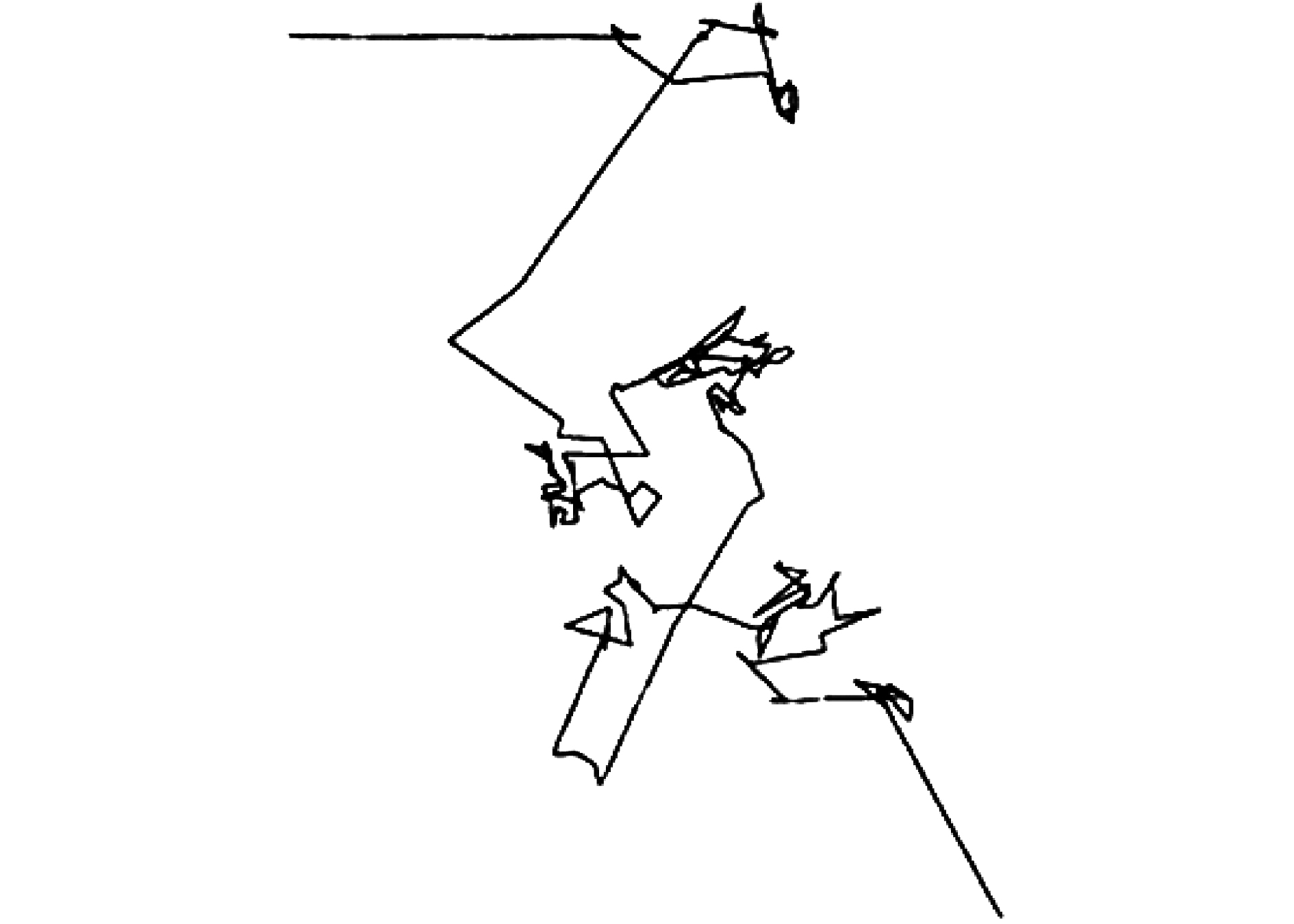
在自然界中，动物会以随机或准随机的方式寻找食物。一般来说，是根据当前的位置或状态和到下一位置的转移概率而作出下一次移动，因此动物的觅食过程实际上是随机行走，其所选取的方向可以用数学建模方法来表示。例如，大量实验表明，动物界中许多如信天翁、蜜蜂等动物的寻觅食物轨迹符合Levy飞行的典型特性^[11]。Levy飞行一词出自法国数学家Paul Pierre Levy，是一种Markov过程，其步长满足Levy分布，是一种在短程搜索中穿插长行程的游走方式^[12]，如图1所示。

从图1中可以看出，一部分解可以在当前最优值附近进行局部搜索，另一部分解则可以跳出当前最优值附近搜索，因此Levy飞行可以加大搜寻的区间，使用Levy飞行的优化算法更容易摆脱局部极值点。文献[13]在PSO优化算法中引入Levy飞行，克服了易收敛到局部最优的缺陷，取得了令人满意的效果。Levy飞行能较大地提高不确定环境下的资源搜索效率。

1.2 CS算法的基本模型

针对布谷鸟的寄巢产卵习性，CS算法假定如下3个条件：

1) 布谷鸟每次仅仅产一只卵，孵化时鸟巢的选取是随机的；

2) 在每组鸟巢中，最好的鸟巢可以被保留到下一代；

3) 可以选择的鸟巢数目一定，鸟巢主人察觉布谷鸟卵的概率为 ${P_{\alpha} }$ 。

CS算法的鸟巢坐标位置与解空间中的解一一对应，在以上3个假定基础上，CS算法利用Levy飞行随机行走方式和偏好随机行走方式更新鸟巢位置。

1) Levy飞行随机行走。利用式(1)产生新解。

$ {{x}}_i^{t + 1} = {{x}}_i^t + \alpha \oplus L(\lambda ), \quad i = 1,2, \cdot \cdot \cdot ,n $

(1)

式中： ${{x}}_i^t$ 和 ${{x}}_i^{t + 1}$ 分别表示第 $t$ 代和第 $t + 1$ 代第 $i$ 个鸟巢的位置； $\alpha $ 表示步长控制量； $ \oplus $ 为点对点乘法； $n$ 为鸟巢个数，即可行解个数； $L(\lambda )$ 为Levy随机搜索路径，且 $L(\lambda ) \sim {u^{ - \lambda }}(1 < \lambda \leqslant 3)$ ，其中 $u$ 表示由Levy飞行得到的随机步长。

由于对Levy分布进行积分运算比较困难，文献[14]提出了使用Mantegana算法来进行计算，即

$ {{x}}_i^{t + 1} = {{x}}_i^t + {\rm{stepsize}} \oplus {\rm{randn}}(),\quad i = 1,2, \cdot \cdot \cdot ,n $

(2)

式中： ${\rm{randn}}()$ 为满足高斯分布的随机函数； ${\rm{stepsize}} = \alpha \cdot S \oplus ({{x}}_i^t - {{x}}_{{\rm{best}}}^t)$ ， $\alpha $ 通常取0.01， ${{x}}_{{\rm{best}}}^t$ 为第 $t$ 代最优鸟巢位置。 $S$ 通过式(3)求得：

$ S = \frac{u}{{{{\left| v \right|}^{{1 / \beta }}}}}, \quad u \sim N(0,\sigma _u^2),v \sim N(0,\sigma _v^2) $

(3)

式中： ${\sigma _v} = 1$ ， $\;\beta = 1.5$ ， ${\sigma _u}$ 按式(4)计算：

$ {\sigma _u} = {\left\{ {\frac{{\Gamma (1 + \beta ) \cdot \sin({{{\rm{{\text{π}} }}\beta } / 2})}}{{\Gamma \left[ {{{(1 + \beta )} / 2}} \right] \cdot \beta \cdot {2^{{{(\beta - 1)} / 2}}}}}} \right\}^{{1 / \beta }}} $

(4)

2) 偏好随机行走。仿照寄主察觉布谷鸟的卵后将其丢弃的想法和原理。具体操作如下：得到一个满足 $[0,1]$ 均匀分布的随机数 $r$ ，并与发现概率 ${P_{\alpha} } \in [0,1]$ 进行比较，若 $r > {P_a}$ ，则按式(5)得到新解：

$ {{x}}_i^{t + 1} = {{x}}_i^t + r({{x}}_j^t - {{x}}_k^t), \quad i = 1,2, \cdot \cdot \cdot ,n $

(5)

式中 ${{x}}_j^t$ 与 ${{x}}_k^t$ 表示第 $t$ 代的随机解。反之，若 $r \leqslant {P_a}$ ，则保持不变，即 ${{x}}_i^{t + 1} = {{x}}_i^t$ 。

通过上述2种方式所得新解均采用贪婪选择操作，即得到新解后，将新解和原解的适应度函数值进行比较，与原解相比，如果新解较优，那么将新解取代原解，反之保持原解不变。

1.3 CS算法的实现步骤

综合CS算法上述2种更新方式，可得到CS算法的以下实现步骤：

1)初始化算法的基本参数：鸟巢数目 $n$ ，发现概率 ${P_a}$ ，搜索精度 $\varepsilon $ 或最大迭代次数 $T$ ，并以随机方式生成 $n$ 个鸟巢的初始位置 ${{{X}}_i}(i = 1,2, \cdot \cdot \cdot ,n)$ ，这里 ${{{X}}_i} = {[{x_1}\;{x_2}, \cdots \;{x_d}]^{\rm{T}}}$ ， $d$ 为待求解问题的维数，求解初始鸟巢位置的适应度函数值，并得到初始最优适应度函数值；

2)根据式(2)~(4)更新当前鸟巢位置；

3)求出当前全部鸟巢的适应度函数值，若在适应度函数值上新鸟巢优于原鸟巢，则替换原鸟巢位置；

4)根据式(5)更新鸟巢的位置，依然采用适应度函数值较好的鸟巢位置替换原鸟巢位置；

5)得到当代最优的适应度函数值，且和上一代最优适应度函数值比较，保留一组最佳适应度函数值的鸟巢位置，迭代次数加1；

6)如果未满足搜索精度要求或未达到最大迭代次数，那么回到2)，反之继续；

7)得到全局最优位置。

2 布谷鸟搜索算法研究现状

CS算法自从2009年发表后就受到许多重视，并得到大量的研究。目前关于CS算法的研究主要分为两个方面：算法的改进和算法的应用。

2.1 CS算法的改进

1) 基于 ${P_a}$ 和 $\alpha $ 的改进

在CS算法中，发现概率 ${P_a}$ 和步长控制量 $\alpha $ 作为关键的两个参数，在迭代过程中通常保持不变。但在寻优过程中，若 ${P_a}$ 一直较大， $\alpha $ 较小，会缩短算法收敛时间，但是易收敛到局部最优；而若 ${P_a}$ 较小， $\alpha $ 较大，则会使收敛速度变慢。因此可对 ${P_a}$ 和 $\alpha $ 进行调整以改进CS算法。

文献[15]使 ${P_a}$ 和 $\alpha $ 随迭代次数变化：

$ {P_a}(t) = {P_{a,\min }} + ({P_{a,\max}} - {P_{a,\min }}) \cdot {\left( {\frac{{N - t}}{N}} \right)^{{m_1}}} $

(6)

$ \alpha (t) = {\alpha _{\min }} + ({\alpha _{\max }} - {\alpha _{\min }}) \cdot {\left( {\frac{{N - t}}{N}} \right)^{{m_2}}} $

(7)

式中： $t$ 为当前迭代次数； $N$ 表示总迭代次数； ${P_{a,\max}}$ 、 ${P_{a,\min }}$ 表示 ${P_a}$ 的最大值与最小值； ${\alpha _{\max }}$ 、 ${\alpha _{\min }}$ 表示 $\alpha $ 的最大值与最小值； ${m_1}$ 和 ${m_2}$ 为非线性因子，取值大于0，用来控制 ${P_a}$ 和 $\alpha $ 的下降速率， ${m_1}$ 应小于1，相反 ${m_2}$ 应大于1。实验证明了改进的CS算法能减少时间并提升精度。

文献[16]按照Rechenberg原则，即将“所有变异的成功比例应该保持在 $1/5$ 原则”作为调整策略对 ${P_a}$ 和 $\alpha $ 修正：

$ {P_a}(t + 1) = \left\{ {\begin{array}{*{20}{l}} {{P_a}(t) \cdot {f_p},}&{R > 0.3} \\ {{P_a}(t),}&{0.2 \leqslant R \leqslant 0.3} \\ {{{{P_a}(t)} / {{f_p}}},}&{R < 0.2} \end{array}} \right. $

(8)

$ \alpha (t + 1) = \left\{ {\begin{array}{*{20}{l}} {\alpha (t) \cdot {f_{\alpha} },}&{R > 0.3} \\ {\alpha (t),}&{0.2 \leqslant R \leqslant 0.3} \\ {{{\alpha (t)} / {{f_{\alpha} }}},}&{R < 0.2} \end{array}} \right. $

(9)

式中： $R$ 为新解改善的比例； ${f_p}$ 为发现概率的学习因子； ${f_{\alpha} }$ 为步长控制量的学习因子。针对6个函数的测试结果表明该改进算法行之有效。

文献[17]采用余弦递减策略实现 ${P_a}$ 的动态变化：

$ {P_a}(t) = {P_{a,\max}}\cos \left( {\frac{{\rm{\pi }}}{2} \cdot \frac{{t - 1}}{{N + 1}}} \right) + {P_{a,\min}} $

(10)

式中： $t$ 表示当前迭代次数； $N$ 表示总迭代次数； ${P_{a,\max}}$ 与 ${P_{a,\min}}$ 分别为 ${P_a}$ 的最大值与最小值。

文献[18-19]同样将 ${P_a}$ 和 $\alpha $ 调整成关于迭代次数的自适应方程，以提高算法的准确性和收敛速度。通过自适应调整 ${P_a}$ 和 $\alpha $ 参数，加快了算法迭代后期的收敛速度，但是对于算法前期收敛速度的提升有限，有待进一步改进。

2) 基于自适应步长的改进

CS算法利用Levy飞行机制得到步长是盲目的，缺乏自适应性，无法保证快速收敛，为此依据不同搜寻阶段中所得结果，对步长大小进行自适应调整。

文献[20]提出的自适应调整步长策略为

$ {S_i} = {S_{\min }} + \left( {{S_{\max }} - {S_{\min }}} \right){d_i} $

(11)

式中： ${S_{\max }}$ 和 ${S_{\min }}$ 分别表示最大步长和最小步长。 ${d_i}$ 定义为

$ {d_i} = \frac{{\left\| {{n_i} - {n_{{\rm{best}}}}} \right\|}}{{{d_{\max }}}} $

(12)

式中： ${n_i}$ 表示第 $i$ 个鸟巢位置； ${n_{{\rm{best}}}}$ 表示此时最佳状态的鸟巢位置； ${d_{\max }}$ 表示其他鸟巢与当前的最优位置的最大距离。通过实验证明这一改进方法能快速地达到全局最优。

文献[21]结合迭代次数及鸟巢的适应度值给出了自适应选取步长的另一种模型：

$ {S_i}(t + 1) = {\left( {\frac{1}{t}} \right)^{\left| {{{\left( {{f_{{\rm{best}}}}(t) - {f_i}(t)} \right)} / {\left( {{f_{{\rm{best}}}}(t) - {f_{{\rm{worst}}}}(t)} \right)}}} \right|}} $

(13)

式中： $t$ 代表当前迭代次数； ${f_i}(t)$ 是第 $i$ 个鸟巢位置的第 $t$ 代适应度值； ${f_{{\rm{best}}}}(t)$ 为第 $t$ 代最优适应度值； ${f_{{\rm{worst}}}}(t)$ 为第 $t$ 代最差适应度值。仿真结果验证了该方法可更高效地搜寻到局部最优解或次优解。

文献[22]利用了当前解与最优解间的距离，距离较长则增加步长，距离较短则减小步长，以此实现步长的自适应动态更新，达到算法的局部性搜索与全局性搜索之间的均衡。通过实验证明改进的方法和标准CS算法比较，在迭代后期所得精度和达到的速度均有提升。文献[23]同时利用自适应调整步长与自适应发现概率来对算法进行改进，因此提升了结果的准确性。

动态地调整步长，使得CS算法具有更好的自适应性，从而算法的求解速度加快，收敛精度也有相应的提升，但是当遇到复杂多模态问题及优化高维空间时受到局限。

3) 基于混沌理论的改进

在原始CS算法中，由于采用随机行走模式，其单一性导致搜索时随机性强，将混沌理论引入CS算法中，可以使算法更容易跳出局部最优点，提升算法在迭代更新后期的收敛速度。

文献[24]应用12个混沌映射来调整原始CS算法中使用的步长，通过测试27个基准函数和一个工程案例，验证了改进的算法，进一步提高了CS算法的评价指标。

文献[25]借用混沌映射对鸟巢位置进行初始化，增加了种群的多样性，并将改进后的混沌布谷鸟算法运用于图像增强中，实验从视觉分析和定量分析两方面证明了混沌CS算法优于其他同类算法。

文献[26]采用Logistic映射生成混沌序列，将其映射到鸟巢位置的更新过程中，其次运用混沌CS算法进行高光谱影像波段选择，实验结果证明混沌CS算法的搜寻性能更优，最终的分类更为精确。

4) 与其他算法混合的改进

文献[27]组合PSO和CS两种优化方法，把PSO的解融入CS方法中鸟巢位置的迭代过程。其基本思想是：在每次进行更新迭代时，先利用PSO算法对初始位置进行更新，得到一组最优的粒子位置 ${{{P}}_i} = {[{p_1} \;{p_2} \cdot \cdot \cdot {p_i} \cdot \cdot \cdot {p_n}]^{\rm{T}}}$ 和一个全局最优位置 ${{{P}}_b}$ ，保留全局最优解 ${{{P}}_b}$ ，并将这组粒子位置的最优解 ${{{P}}_i}$ 代替CS算法里的相应位置继续更新。该方法既保留了PSO算法的搜索特性，又兼顾了CS算法在搜索全局最优解上的优点，提高了求解精度。文献[28]在偏好随机游动的鸟巢更新公式中引入全局最优导向算法，使被保留的鸟巢也向最优的方向游动，增加了鸟巢的多样性，提高了收敛速度。文献[29]将人工蜂群优化算法和CS算法相融合，达到算法的局部及全局搜索性能的均衡，使算法的精度得到提升。文献[30]在迭代过程中加入正交交叉运算，CS算法的搜寻能力有所提高，同时引入外部存档机制以此维持一段时间里的种群状况，实验表明提出的策略能提高收敛速度。

上述的改进方法有效地改善了CS算法的性能，但是对于多维问题，由于可能存在维间的干扰，统一更新解的每一维会对算法求解的准确性产生影响，使得搜寻效果不够理想。

5) 基于种群特征和种群变异的改进

文献[31]在算法框架中引入如年龄结构、变异成功率等种群特征的反馈信息，自适应地调节算法参数，提升了CS优化方法的局部搜索性能，针对8个函数的测试结果表明了它具有较好的收敛特性。文献[32]利用合作协同进化框架的思想，对种群的解向量进行平均分解，得到若干子向量，并对每个子向量利用CS算法进行更新，最后重新组合成解向量，有效地改善了CS算法的性能。但是此类改进方法会使目标函数计算的次数增多，使得算法变得复杂，寻优时间加长。

6) 结合优化策略的改进

文献[33]结合全局随机扰动策略加快算法收敛速度，引入模拟退火机制防止算法陷入局部最优，实验结果证明了该算法在精度和稳定性方面的优势。文献[34]引入均衡单进化函数评价策略，避免了多维度之间互相干扰。但是此类方法在搜索速度上有待提高。

7) 基于种群多样性的改进

文献[35]借助多策略差分操作来提高种群的多样性，并增加排队优选机制，避免陷入局部极值，加快搜索进程。文献[36]通过移民算子进行各种群间的信息交流，利用多个种群同时进行全局探索和局部开发，提高全局寻优性能。

8) 其他方法

文献[37]使用正交学习的搜寻方式以改善CS优化方法的搜索能力。文献[38]将逐维改进的思想引入CS算法中，改进了鸟巢飞行步长的调整方法，使算法收敛速度加快，求解精度有所提高。文献[39]利用模式搜索趋化机制的局部寻优能力加强局部求解，同时采用自适应竞争机制来改进CS算法，测试结果验证了其全局搜寻性能优，所求得的结果精度高。

2.2 CS算法的应用

CS算法因其需要较少的参数、实现简单、高效等优点，已经成为当下群智能算法活跃的研究分支之一。至今为止，CS算法通常应用于下列领域。

1) 水电系统

文献[40]采用CS算法确定压力调节阀的数量、最佳安装位置和最佳操作模式，建立了给水管网调压阀优化模型，结果显示，该方法更好地降低了漏损。文献[41]针对配电系统中在电容器开关约束条件下的分流电容器放置问题，利用CS算法作为优化工具，设计了最佳的电容器分配方案，结果证明该方法可以降低系统中的峰值负载损耗和容量成本。文献[42]在设计现代农场的集成电力系统中引入CS算法，对影响电力系统性能的特定部件的选择进行优化，结果表明此系统取得了很好的效果。文献[43]在多机电力系统最优稳定器(PSS)设计中，用CS算法调整PSS的参数，通过在不同的工作和干扰条件下的实验证明了CS算法在提供良好阻尼特性方面的有效性。

2) 资源分配

文献[44]利用交叉与变异操作改进离散CS算法，并将其引入敌我辨认系统的干扰资源分配问题，仿真分析表明，该方法能更好地解决干扰资源的一对一，多对少分配问题。文献[45]在解决可靠性冗余分配问题时，在多个约束条件下使用CS算法对组件或子系统的可靠性目标进行设置，仿真结果表明和现有同类方法比较，CS算法优化求得的解更为精确。文献[46]涉及具有执行器故障的分布式结构变型飞机的控制分配问题，将执行器控制分配转换成整数规划，并使用改进的CS算法来获得实际的执行器控制分配指令，实验结果表明该方法得到的分配结果更加精确。

3) 多目标优化

文献[47]针对作业车间多目标调度的问题，在CS算法中利用帕累托存档保存所有非支配解，并利用改进的算法寻找到最优解，测试结果表明CS算法相比其他方法，所求解更加有效。文献[48]在CS算法中引入交叉和选择算子，增加了种群的多样性，并将其用于板翅式换热器(PFHEs)的多目标优化设计，通过仿真实验证明CS算法拥有更精确的优化结果。文献[49]利用自适应CS算法解决多目标函数的优化问题，有效地改善了求解的性能。

4) 图像处理

最近几年，在图像处理许多领域采用了CS算法。文献[50]利用CS算法的并行寻优性能加快图像多阈值分割中最优阈值的搜索过程，取得了更好的分割结果。文献[51]采用非完全Beta函数灰度变换达到增强图像的目的，并将CS算法用于参数的自适应寻优，实验结果表明该方法效率更高，鲁棒性更强。文献[52]将Tent映射生成的混沌序列用于优化布谷鸟算法，用改进的布谷鸟算法来搜索二维Renyi灰度熵最优阈值，提高了搜索速度。文献[53]将布谷鸟搜索算法引入到图像匹配过程，通过求解全局最优解实现了在较少调节参数下的图像匹配，仿真实验验证了该方法的有效性。此外，CS算法还被用于图像配准^[54]、图像掩膜^[55]、数字水印^[56]等方面。

5) 分布式云计算

文献[57]首先依据安全强度、用户需求设置以及安全需求等级构建云计算资源调度的数学模型，然后采用改进的CS算法对云计算资源调度数学模型进行求解，得到云计算资源的最优调度方案，提高了云计算资源的利用率，均衡云计算系统各节点之间的负载。文献[58]利用CloudSim软件搭建分布式云计算仿真环境进行任务调度实验，并引入混沌理论，对CS算法每一轮迭代的中间个体解进行混沌扰动，通过混沌布谷鸟算法进行资源调度，实验证明混沌布谷鸟算法在收敛性、求解精度、执行效率和相对标准差等方面优于其他算法。

6) 其他领域

CS算法的应用还涉及函数优化^[22]、医学应用^[59]、预测问题^[60]、控制问题^[61]、人脸识别^[62]等应用领域。文献[22]利用改进CS算法对一些函数进行测试，结果证明CS算法更具竞争力。文献[59]运用CS算法优化模糊和决策树分类器，并进行心脏病预测，在数据集上进行测试，结果表明该模型能达到更高的精度。文献[60]在处理有机碳含量预测问题时加入CS算法进行优化，提高了预测精度。文献[61]将CS优化方法用于桥式起重机系统PID控制器的参数寻优，达到更好的消摆和定位控制。文献[62]将CS优化方法运用到人脸识别中，结果显示CS优化优于粒子群优化和蚁群优化(ant colony optimization, ACO)。

3 CS算法与其他群智能算法比较

CS算法与GA、ACO、PSO、人工蜂群(artificial bee colony, ABC)算法均属于群智能优化算法，它们皆为基于种群借助迭代来实现优化步骤的概率搜寻算法。依据文献[2-3, 5-8, 13-62]，总结与对比了这5种算法的优点、缺点以及适合求解的问题，结果如表1所示。

虽然GA、ACO、PSO和ABC的研究及应用比较成熟，但从表1可知，CS算法在参数数目、通用性、全局寻优能力等方面综合优势更强，可灵活地跟其他算法进行多种组合，并具有更广泛的适用性。文献[2, 26, 31]的研究结果表明：CS算法在解决复杂问题方面优于其他算法。显然，CS算法可广泛应用于实际领域，深入研究CS算法无论在理论上还是实际应用中都有着重要的作用。

4 CS算法存在的问题及展望

从上述总结中可以看出，CS算法具有诸多优点，适用性很强。然而，CS算法作为新近出现的群体智能优化算法，对其研究还处在发展阶段，仍有很多关键问题亟待解决。目前，CS算法存在的不足及有待进一步研究的方向可总结如下：

1) 在迭代期间，布谷鸟随机行走得到一个新位置，随机行走模式的单一导致其搜索时针对性不强，很难迅速寻找到解的全局最优值，搜索精度有待提升。因此，有必要对搜索方式进行改进，使每次的搜索都向有利的方向进行，比如引入非均匀变异算子或者增加选择性淘汰策略等，提高算法的搜索精度。

2) 搜寻到新的位置后，会用贪婪选择的模式保留全局最优值，但是全局优化问题多极值会导致算法容易早熟，收敛到局部最优解。将CS算法与粒子群算法、蛙跳算法等算法进行结合，利用各个智能优化算法的优势，可以得到单一的算法无法实现的结果。从而增强算法的鲁棒性、提高算法的搜索能力。

3) CS算法是以概率 ${P_{\alpha} }$ 抛弃部分解然后再产生新解，但这种方法忽略了种群内具有优势的群体知识，加大了搜寻的运算量。可考虑加入一些策略促进种群之间协作，例如：构建双层交互学习模型，双种群互相学习，合作寻优，实现种群间信息共享，学习优势经验，增加种群多样性。

4) CS算法作为新近出现的群体智能优化算法，尚有改进和提升的空间，它的应用研究仍处于初始阶段。相比PSO、ABC等智能算法来说，目前CS算法在金融、自动控制、神经网络训练、图像处理等领域的应用还较少。因此，研究CS算法更多的应用将对解决复杂的工程和控制等领域的优化问题有重要的意义，也能更好地促进CS算法的发展。

5 结束语

CS算法是一类新兴的群智能优化算法，它在许多应用领域具有广阔的前景，而其在很多方面还有待进一步研究。本文阐述了CS算法的原理和改进方法，鉴于算法仍处于快速发展阶段，因此还有一些改进方法尚未包含在本文中。此外，还归纳了CS算法在实际领域中的应用，指出了目前所存在的问题，且对进一步的研究方向进行展望。进一步加强对CS算法理论和具体应用的研究有利于拓展群体智能优化技术的研究和应用领域，从而得到更快的发展和广泛的融合，以期能有效地解决更多的实际应用问题。