2. 陕西师范大学 数学学院,陕西 西安 710062;
3. 西北工业大学 计算机学院,陕西 西安 710072;
4. 北京邮电大学 智能科学技术中心,北京 100876
2. College of Mathematics, Shannxi Normal University, Xi’an 710062, China;
3. School of Computer Science, Northwestern Polytechnical University, Xi’an 710072, China;
4. Center for Intelligent Science and Technology, Beijing University of Posts Telecommunications, Beijing 100876, China
机制主义的人工智能理论抓住并提升了目前三大流派的共性,为人工智能理论的发展构建了一个统一的平台[1]。泛逻辑理论要在不确定性演化环境下对各种非经典逻辑进行统一的柔性归纳[2]。Lukasiewiez[3]提出的多值逻辑和Zadeh[4]提出的模糊逻辑先后突破了布尔的二值逻辑,所引起反响至今还是方兴未艾。特别是,王国俊[5]提出的计量逻辑、Schweizer等[6]提出的概率逻辑、周红军[7]提升出的概率计量逻辑以及王国俊学派[8-11]和徐扬[12]在格值逻辑方面的工作。这些工作和何华灿的泛逻辑都与概率论有密切的联系,不妨统称为广义概率逻辑。概率论的出现改变了数学,广义概率逻辑的出现对逻辑发展有重要意义。
信息不同于物质,它在物理空间中不占位置,不具有不可入性。但是,“有这样一种学说:在物质世界与信息世界的对立统一中,物质在物理空间中具有不可入性和惯性,信息在可能性空间中也具有不可入性和惯性。这应当成为柔性逻辑的公理”[2]。这里提出了一个非常重要的概念“可能性空间”,究竟什么是可能性空间,它与概率论和模糊数学所提的可能性空间有什么联系与区别?什么是广义概率逻辑?广义概率逻辑的发展将面临什么问题?这些问题的深入探讨,将会对人工智能的发展带来重大的影响。本文就是要用因素空间的数学理论来把这些问题说清楚。
1 可能性空间在前面曾提到,就像物质在物理空间中具有不可入性和惯性一样,信息在可能性空间中也具有不可入性和惯性。这两句话意义重大。信息是要占“地方”的,需要有空间,这个空间不在物质世界里,在认识主体的处理架构之中。
可能性空间在概率论和模糊数学中分别出现过两次。第一次,Kolmogorov 在1936年用公理化定义把概率定义成为像面积、体积和重量一样的测度,可加性测度是不可入性的产物,测度测量“占有”这位数学家第一次把信息概念与物质概念等同起来,在可能性空间中为事件争夺地盘。三十多年以后,模糊集的创始人 Zadeh[13]也要把模糊概念放到可能性空间中来争夺地盘。
Kolmogorov的可能性空间就是他所定义的基本空间
用因素空间描述概率论叫做因素概率论。每个可描述的发生因素
对称性公理 具有可能结果数为
现代概率论的发展要归功于中心极限定理和各种概率分布的推导,但其根源是来自古典概率和样本平权公理:
样本平权公理 设
模糊数学也强调可能性空间,这种可能性空间与概率论不同,所有主观性测度都是非可加的。如果把不可入性狭义地理解为测度的可加性,那么非可加的测度是可入的。但是,非可加的测度照样是要占“地方”的,汪培庄把模糊集定义所在的论域
总之,概率论与模糊数学都特别强调可能性空间。在英文中概率与可能性是一个字probability,为了与概率相区别,Zadeh把模糊分布的可能性改称为possibility[13],不幸的是,这个词的中文翻译也是可能性。西方人对probability和possibility的理解是有分别的,probability是预测中某种结果出现的可能性,而possibility是识别中某种类别出现的可能性。随机性出现在预测过程中,当事件还没有发生的时候,大家要猜测将会是什么结果,这时就要用到概率,事情一旦发生,所占的位置马上腾空,可能性空间马上关闭而转换成另一个可能性空间。面对一个已经发生的事情,要去判断这是什么的时候,如果说不清楚,这就出现了模糊性,有多种possibility等我们去选择,这些possibility也要在这个新的可能性空间中来争夺地盘。为了避免文字上的混淆,我们最好把可能性空间改称为信息空间。概率论的可能性空间是以发生因素所组成的信息空间,模糊数学的可能性空间是由识别因素所组成的信息空间。在信息科学领域里,因素
概率论的产生是数学上的重大事件,相应的广义概率逻辑的发展将是逻辑学中的一个重大事件。为了促进这一发展,我们需要在广义概率逻辑中引用因素表现论域。
2 简化的Stone表示定理与因素表现论域在这一章里,我们需要对经典逻辑作一点反思,弄清Stone拓扑表示定理的思想实质,强调谓词变元的因素特质,用因素空间的思想对数理逻辑开拓一种新的思路。
2.1 命题演算的局限性布尔命题演算系统
这个系统对经典逻辑来说是自给自足的了。但是,命题演算在语言上存在着一个大问题:语言学上的每一句话都有主语和谓语,一个判断句的谓语是“be”, 宾语是be所连接的一个名词、代名词或形容词,它表示一个概念。要问主语是否符合这个概念,便形成一个判断。有人主张把be+概念合称为一个谓词,我们赞同并采用此说法。概念是命题的核心,主语是命题的立足点。主语不同,无法进行推理,我是中国人推不出安倍晋三是亚洲人。绕了一个大圈子,人们发现,如果把主语事先规定死了的话,则命题演算就是概念演算。在进行推理的时候,如无特别声明,参加演算的命题必须是同一个对象,不能有变!命题演算的局限性是很大的。
谓词演算的朴素思想本来是很简单的(绝不像一阶谓词逻辑定义得那么烦琐):将命题
谓词演算带给逻辑学的一项最重要的启迪就是:逻辑蕴涵的本质就是集合的被包含,三段论法就是包含关系的传递。逻辑从数学中找到了坚固的理论基础。
道理非常简单,概念的内涵与外延是逆向对合的:概念甲的内涵蕴涵乙的内涵,当且仅当概念乙的外延包含概念甲的外延。但是,直到Stone拓扑表示定理的出现,这条简单的道理才从数学上得到严格的证明。
Stone拓扑表示定理告诉我们,任何一个布尔代数都同构于由其全体极大滤子所形成的紧零维Hausdorff空间的开闭集代数[16]。简单地说,就是布尔逻辑与集合论是同构的。但要问怎样同构法,就复杂化了。为了简单,我们不妨提出一个Stone简化定理。需要介绍滤子的2种不同的定义,我们把一般格论中定义的滤子叫做强滤子。权威的格论著作[17]给出:在一个尔代数B = (B,
| $p \leqslant q \Leftrightarrow p \vee q = q \Leftrightarrow p \wedge q = p$ |
定义1 在布尔代数
在某些格论的文献中所定义的滤子只满足第一个条件。于是,滤子与强滤子是两个不同的概念,按强滤子叙述更好。称只含有限个原子命题集
命题1 在
证明 因为平凡强滤子
任给一个真强滤子
任取
显而易见,若
定义2 强滤子的最小元叫做它的滤尾。
命题2
证明 下面将提到的
定义3 记
表现论域是按照强滤子来定义的。强滤子所具有的尾敛性是拓扑学中邻域系的典型特征。在有限情形下,它保证了滤尾的存在,在无限情形下保证了强滤子向一点的收缩。它始终保证强滤子像一颗炮弹,在有限情形下有弹尖(滤尾),在无限情形下有尖口(极限点)。非强滤子由于没有尾敛性,它就不是一个弹头而是多弹头的并。不难证明,
Stone拓扑表示定理说布尔代数
Stone简化定理 任何一个
证明 命题2说明
Stone简化定理把
命题3 表现论域的构造。设
| $ U = \left \{ {x_1} \wedge {x_2} \wedge \cdots \wedge {x_n}\big|{{x_j} = {p_j} {\text{或}}\neg {p_j}(j = 1,2, \cdots ,n)\ } \big. \right \} $ | (2.2) |
证明 给定
考虑
反之,设
例1 设
| $B = \{ 0,p,\neg p,1\} $ |
B包含两个次小元
所以,
例2 设
| $ \begin{array}{c} {B} = \left\{ {0,pq,{p^\prime }q,p{q^\prime },{p^\prime }{q^\prime },pq \vee {p^\prime }q = q} \right.,\\ pq \vee pq' = p,pq \vee p'q',p'q \vee pq',\\ p'q \vee p'q' = p',pq' \vee p'q' = q',\\ pq \vee p'q \vee p'q' = pq \vee p',\\ pq \vee p'q \vee pq' = q \vee pq',\\ pq \vee p'q \vee p'q' = pq \vee p',\\ pq \vee pq' \vee pq' = pq \vee pq' \vee pq',\\ p'q \vee pq' \vee p'q' = p'q \vee q',\\ pq \vee p'q \vee p'q' \vee p'q' = 1\} \end{array} $ |
这里,
所以,B的表现论域是
一般地说,若
从二值逻辑到多值逻辑,所有新的理论都要推广Stone拓扑表现定理,这是考验新逻辑理论的一块试金石。我们需要做什么工作呢?首先, 要去掉有限布尔代数的限制,使Stone简化定理的面扩大,然后,要证明一个普适性的广义Stone简化定理。若有一个能够一劳永逸地解决Stone简化定理推广的理论,就可以加速新理论的发展。比如,抓住
在命题演算中我们曾经强调过,由我是中国人推不出安倍是亚洲人。推理句中的前后两个命题必须是同一个对象。在谓词逻辑中也应该坚持同对象推理的原则,毫无联系的两个对象之间是不能推理的。
常会遇见下面的推理句:若气温高则降雨量大
| $ {{\text{高}}^{(x)}} \to {{\text{大}}^{\left( y \right)}} $ |
这里
变元
若对象是张三,如果他的智商
我们希望搞辩证逻辑,辩证法的核心是要具体问题具体分析,什么是具体分析呢?就是要对问题的内在和外在的因素进行分析。在谓词逻辑中把变元进一步写成因素是逻辑发展的新机。
逻辑是对事物的性质进行是非判断的科学,它要离开具体事物的性质而抽象出是非判断的一般规律,但抽象离不开现实,要想使逻辑更加有效地解决实际问题,需要开辟逻辑返回世界的接口。表现论域
给定一个因素空间
定义4 在
1)它的符号集是字集
2) 它的公式集
3) 它的公理集是布尔逻辑的公理集再补充以下假设公理
4) 真值集是二值布尔代数W2:
5) 推理规则:
这个定义的意思是这样:任何逻辑系统都包含5个要素,即符号集
| $ \Gamma \vdash \phi\;\;\; {\rm{iff}}\;\;\;\Gamma | = \phi $ |
则这个子系统中的定理叫做强
背景公理
| $\begin{array}{c} I = I({f_1}) \times I({f_2}) \times \cdots \times I({f_n}) = \\ \left \{ {a_{1(1)}},{a_{1(2)}},\cdots ,{a_{n(n)}}\big| {{a_{ik}} \in I({f_i})(i = 1,2, \cdots ,n)} \big. \right \} \end{array} $ |
式中
为什么会有虚的信息组态呢?因为因素之间存在着相互联系与制约。譬如,气温与降雨量这两个因素在平面的联合分布就形成一个背景集
背景关系
考虑推理句“若气温

|
Download:
|
| 图 1 因素推理的直观模型 Fig. 1 Illustration of factorial reasoning | |
非因素的布尔代数没有背景一说,所讨论的背景
布尔逻辑可以用电路来表现,每个字代表一个电器开关。每一个
定义5 若
命题4 公式
最小化理论将语法的结构和逻辑的语义功能有效地联系起来,意义重大。但是这种联系有一个前提,表现逻辑的电路开关必须相互独立。如果开关之间存在着关联,或者,由于系统受到侵蚀,两个开关在开时连通,在变元非独立的情况下,逻辑的结构功能关系应当如何进行呢?例如,给出下面一张三变元公式
| 表 1 公式
|
3个开关,每个开关有2种状态,搭配出8种组态,形成表现论域
注意,为了简单,我们在符号上有下列等价的表示方法:
| $\begin{gathered} \left( {0,0,0} \right) = (\neg {p_1}) \wedge (\neg {p_2}) \wedge (\neg {p_3}) = , {{\underline{x} }_1} \wedge {{\underline{x} }_2} \wedge {{\underline{x} }_3} = {{\underline{x} }_1}{{\underline{x} }_2}{{\underline{x} }_3} \\ \left( {0,1,1} \right) = (\neg {p_1}) \wedge \left( {{p_2}} \right) \wedge \left( {{p_3}} \right) = , {{\underline{x} }_1} \wedge {x_2} \wedge {x_3} = {{\underline{x} }_1}{x_2}{x_3} \end{gathered}$ | (3.1) |
命题5 若字组
证明 若字组
命题6 若字组
证明 若字组
当
极小化方法(新):
1) 将赋值表中所有不属于背景
2) 将
3) 逐一检查长度
4) 字组长度
命题7 用极小化方法所得到的是
证明 首先要证明算法一定有停止的时候,亦即,正字类一定会被删尽。设
所记下的每一字或字组都被
例3 以表1为例,给定
1)将赋值表中所有不属于背景
| 表 2 表1在R上的子表 Tab.2 The sub-table of table 1 on R |
2) 将
| ${\text{正类}}=\{ {x_1}{x_2}{x_3},{x_1}{x_2}{x_3},{x_1}{x_2}{x_3}\} $ |
| ${\text{反类}}=\{ {x_1}{x_2}{x_3}\} $ |
3) 逐一检查长度
| ${\text{正类}} = \{ {x_1}{x_2}{x_3}\} $ |
继续考察单字组,
结论:
对于独立的3个开关来说,
这个例子引自文献[18], 该文最早把因素逻辑的思想应用于故障检测,说明在变化的环境中布尔逻辑是如何被辩证化地发挥其推理功能的。
机制主义人工智能强调语法、语用和语义的全信息。全信息的核心是语义,而语义是语法和语用的结合体。所以,逻辑的结构−功能分析不仅是电路实现的实践问题,更是人工智能理论的一个关键点。语法−语用的结合都是在场景多变的非独立信息系统中来实现的。没有因素逻辑的思想和框架,是很难面对这种挑战的[19]。
4 逻辑的目标驱动与逆向推理机制主义人工智能突出目标驱动,为智能服务的逻辑也应该是目标驱动的。逻辑以推理的后件为目标。我们希望生活快乐
经典的布尔逻辑只有寻找真集能钻进
定义6 如果
命题8 若
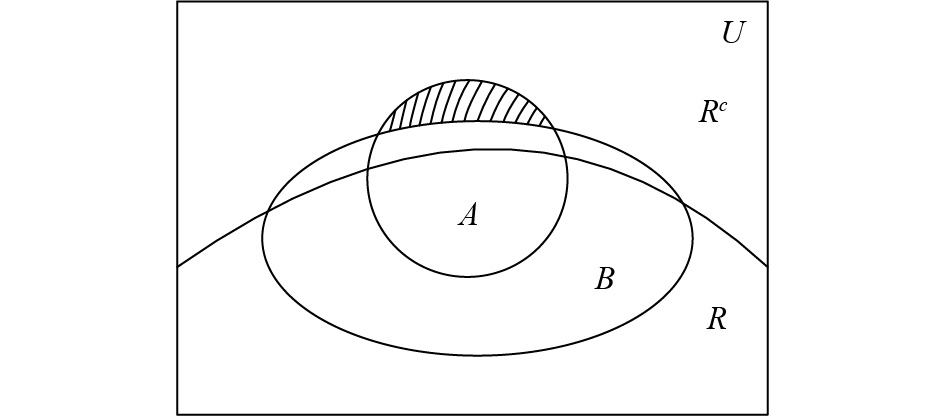
在图2 中,那个带阴影的月亮是我们的关注点。它是所有满足前件
|
Download:
|
|
图 2 |
|
我们的目标
泛逻辑把模糊数学出现以来所出现的多种连续并、交算子对的定义用带参数的方式统一归纳成为一套单一的运算。归纳的根基是4种极端的连续算子对, 其中前3对算子为:
1) Zadeh算子:
| $ \begin{array}{l} {\mu _A}_{ \cup B}\left( x \right) = {\rm{max}}\{ {\mu _A}\left( x \right),{\mu _B}\left( x \right)\} \\ {\mu _A}_{ \cap B}\left( x \right) = {\rm{min}}\{ {\mu _A}\left( x \right),{\mu _B}\left( x \right)\} \end{array} $ |
2) 概率算子:
| $ \begin{aligned} {\mu _A}_{ \cup B}\left( x \right) = & {\mu _A}\left( x \right) + {\mu _B}\left( x \right) - {\mu _A}\left( x \right){\mu _B}\left( x \right)\\ & {\mu _A}_{ \cup B}\left( x \right) = {\mu _A}\left( x \right){\mu _B}\left( x \right) \end{aligned}$ |
3) 有界和积算子:
| $ \begin{array}{l} {\mu _A}_{ \cup B}\left( x \right) = {\rm{min}}\{ {\mu _A}\left( x \right) + {\mu _B}\left( x \right), 1\} \\ {\mu _A}_{ \cap B}\left( x \right) = {\rm{max}}\{ {\mu _A}\left( x \right) + {\mu _B}\left( x \right) - 1, 0\} \end{array} $ |
这3种算子在什么情形下适用,泛逻辑都有明文规定。这3套算子的选择,是需要数学来证明的。
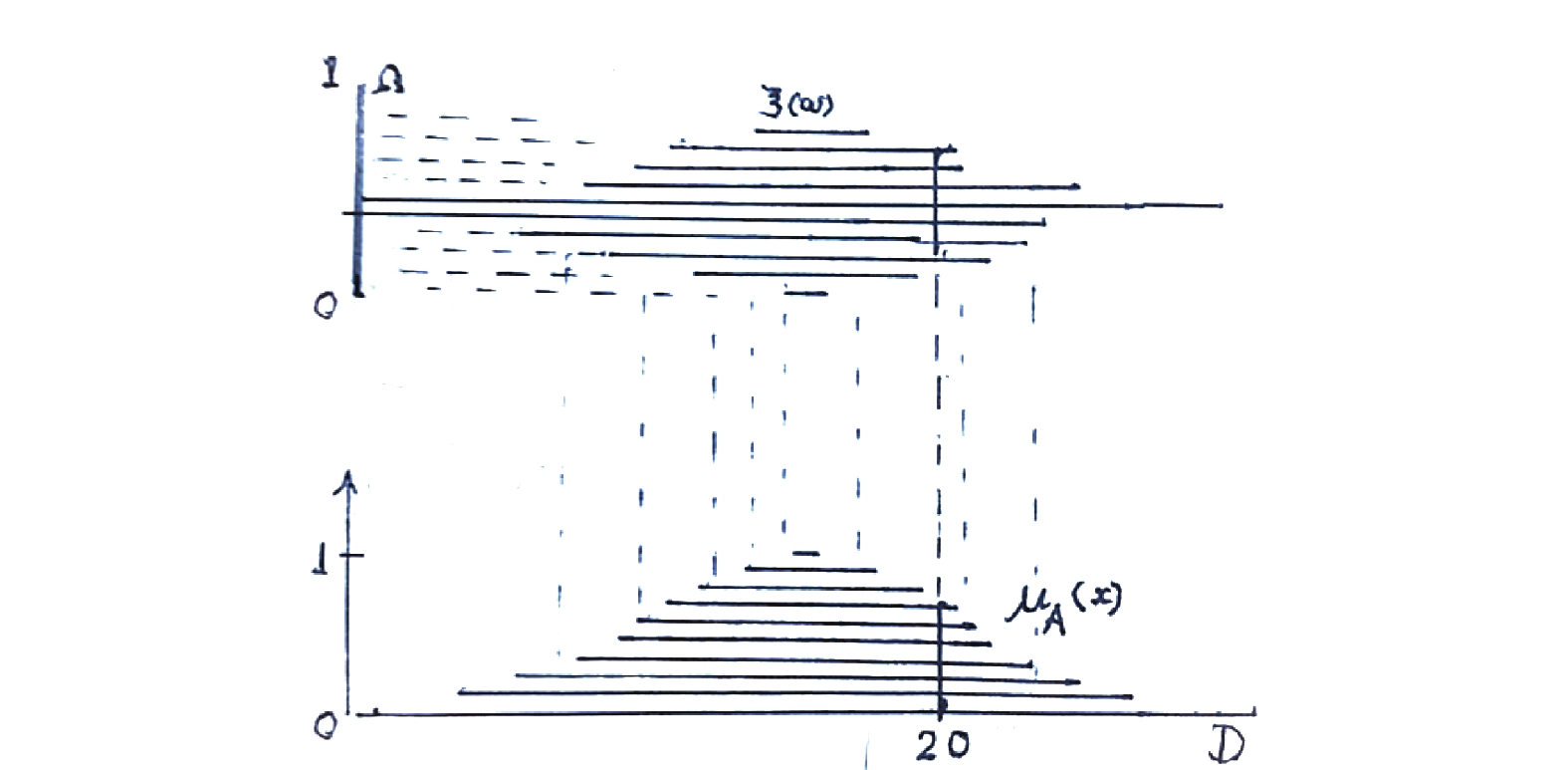
所谓模糊性,就是概念外延的不确定性,以年轻这一概念为例,不同人或同一人在不同场景下所报的年轻区间是不一样的。设有
|
Download:
|
| 图 3 模糊集是随机云的落影 Fig. 3 A fuzzy set is the falling shadow of a random cloud | |
模糊集A和B分别是截集At和Bs的落影,其中(t,s)是
|
Download:
|
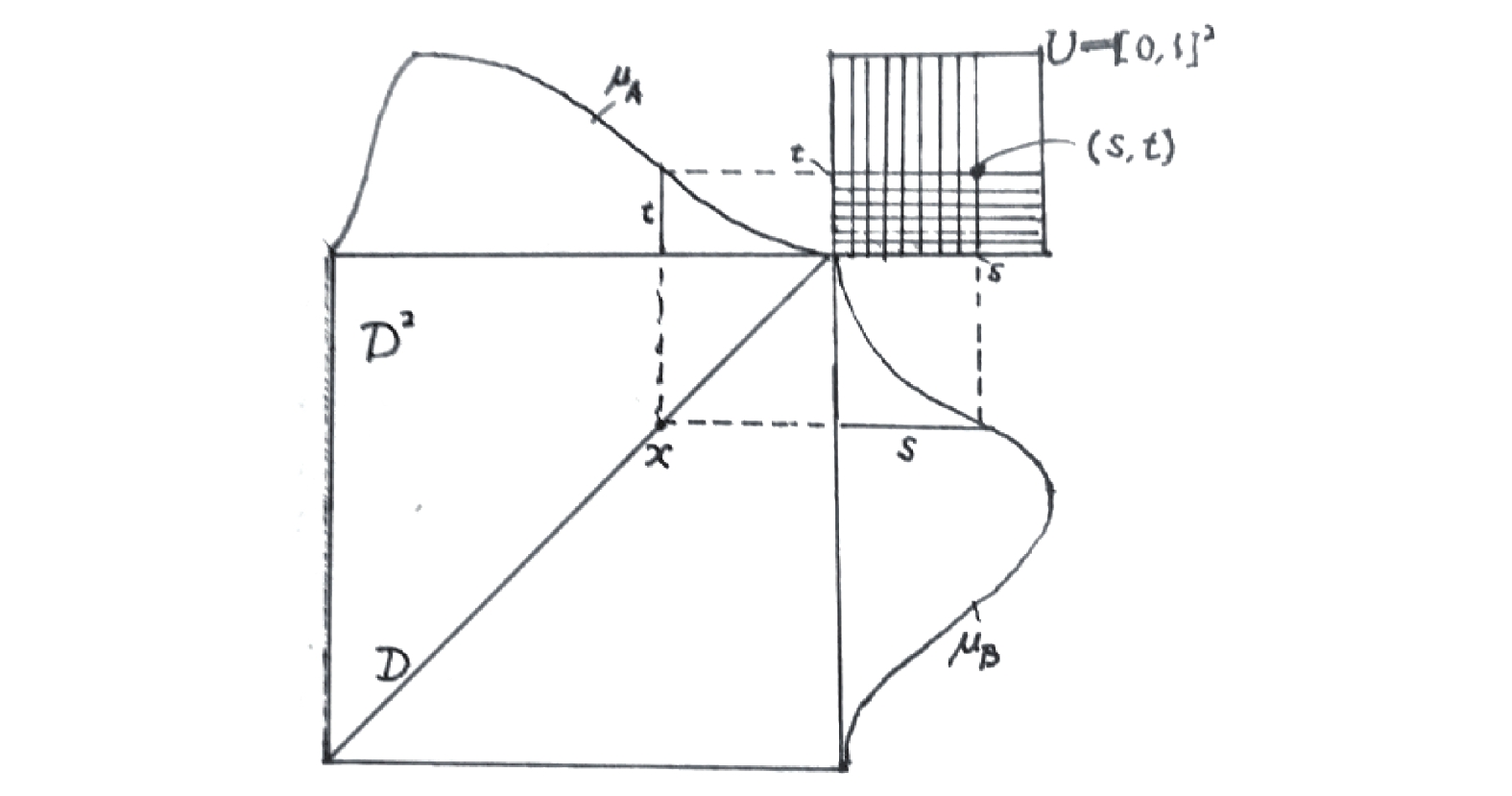
| 图 4 模糊集的并、交运算 Fig. 4 Union and intersection of fuzzy sets | |
定理1 隶属度运算的确定法则。给定
| $ \begin{split} & {\mu _A}_{ \cup B}\left( x \right) = {\mu _A}\left( x \right) \wedge {\mu _B}\left( x \right) = R({\text{交区}})\\ & {\mu _A}_{ \cap B}\left( x \right) = {\mu _A}\left( x \right) \vee {\mu _B}\left( x \right) = R({\text{并区}}) \end{split} $ | (6.1) |
这里,
证明
定理1的直观意思见图4。
定理2 当两个概念的表现因素是完全正相关时,它们之间的并、交运算必须取最大、最小概率:
| $\begin{array}{l} {\mu _A}_{ \cup B}\left( x \right) = {\rm{max}}({\mu _A}\left( x \right),{\mu _B}\left( x \right))\\ {\mu _A}_{ \cap B}\left( x \right) = {\rm{min}}({\mu _A}\left( x \right),{\mu _B}\left( x \right)) \end{array}$ |
当两个概念的表现因素相互独立时,它们之间的并、交运算必须取概率和与概率积:
| $ \begin{array}{c} {\mu _A}_{ \cup B}\left( x \right) = {\mu _A}\left( x \right) + {\mu _B}\left( x \right) - {\mu _A}\left( x \right) \times {\mu _B}\left( x \right)\\ {\mu _A}_{ \cap B}\left( x \right) = {\mu _A}\left( x \right) \times {\mu _B}\left( x \right) \end{array} $ |
当两个概念的表现因素是完全负相关时,它们之间的并、交运算必须取有界和与有界积:
| $\begin{aligned} & {\mu _A}_{ \cup B}\left( x \right) = {\rm{min}}({\mu _A}\left( x \right) + {\mu _B}\left( x \right), 1)\\ & {\mu _A}_{ \cap B}\left( x \right) = {\rm{max}}({\mu _A}\left( x \right) + {\mu _B}\left( x \right) - 1, 0) \end{aligned}$ |
定理2是因素空间对泛逻辑前3个连续逻辑算子对的证明,所叙述的条件完全符合泛逻辑的要求。定理2的证明见文献[20],这一结果曾在1991横滨国际模糊系统协会议上宣读。定理2的证明是最早也是最严格的数学证明。定理1也给出了在一般情况下隶属度的计算方法。其运算可由因素背景分布唯一确定。明确指明了解决隶属度运算的选择性困难的关键在于模糊概念背后的因素背景分布。
6 结束语因素空间是泛逻辑表现的空间和舞台,因素空间为泛逻辑连续算子对的选择提供数学依据。泛逻辑是因素空间表现的内核与指引。泛逻辑与因素空间是逻辑与数学之间互相依靠的伙伴。
机制主义人工智能−泛逻辑−因素空间三者的结合,可以为人工智能的统一机制从逻辑与数学方面提供比较全面的研究。本文着重阐述了泛逻辑与因素空间之间存在着天然的联系,这样就保证了三结合理论的内在和谐与统一。
| [1] |
钟义信. 高等人工智能原理: 观念•方法•模型•理论[M]. 北京: 科学出版社, 2014.
( 0) 0)
|
| [2] |
何华灿. 泛逻辑学原理[M]. 北京: 科学出版社, 2001.
( 0) 0)
|
| [3] |
LUKASIEWIEZ L. On three-valued logic[J]. Ruch filozifaczny, 1920, 5: 170-171. ( 0) 0)
|
| [4] |
ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [5] |
王国俊. 计量逻辑学(I)[J]. 工程数学学报, 2006, 23(2): 191-215. WANG Guojun. Quantitative logic (I)[J]. Chinese journal of engineering mathematics, 2006, 23(2): 191-215. DOI:10.3969/j.issn.1005-3085.2006.02.001 (  0) 0)
|
| [6] |
SCHWEIZER B, SKLAR A. Probabilistic metric spaces[M]. New York: North Holland, 1983.
( 0) 0)
|
| [7] |
周红军. 概率计量逻辑及其应用[M]. 北京: 科学出版社, 2015.
( 0) 0)
|
| [8] |
王国俊. 一类一阶逻辑公式中的公理化真度理论及其应用[J]. 中国科学: 信息科学, 2012, 42(5): 648-662. WANG Guojun. Axiomatic theory of truth degree for a class of first-order formulas and its application[J]. China science information, 2012, 42(5): 648-662. (  0) 0)
|
| [9] |
裴道武. 基于三角模的模糊逻辑理论及其应用[M]. 北京: 科学出版社, 2013.
( 0) 0)
|
| [10] |
张小红. 模糊逻辑及其代数分析[M]. 北京: 科学出版社, 2008.
( 0) 0)
|
| [11] |
张小红, 折延宏. 模糊量词及其积分语义[M]. 北京: 科学出版社, 2017.
( 0) 0)
|
| [12] |
XU Yang, QIN Keyun, RUAN Da, et al. Lattice-valued logic: an alternative approach to treat fuzziness and incomparability[M]. Berlin, Heidelberg: Springer, 2003.
( 0) 0)
|
| [13] |
ZADEH L A. Fuzzy sets as a basis for a theory of possibility[J]. Fuzzy sets and systems, 1978, 1(1): 3-28. DOI:10.1016/0165-0114(78)90029-5 ( 0) 0)
|
| [14] |
汪培庄, SUGENO M. 因素场与模糊集的背景结构[J]. 模糊数学, 1982(2): 45-54. WANG Peizhuang, SUGENO M. The factors field and background structure for fuzzy set[J]. Fuzzy mathematics, 1982(2): 45-54. (  0) 0)
|
| [15] |
汪培庄. 模糊集与随机集落影[M]. 北京: 北京师范大学出版社, 1985.
( 0) 0)
|
| [16] |
STONE M H. The theory of representation for Boolean algebras[J]. Transactions of the American mathematical society, 1936, 40(1): 37-111. ( 0) 0)
|
| [17] |
DAVEY B A, PRIESTLEY H A. Introduction to lattices and order[M]. Cambridge: Cambridge University Press, 1990.
( 0) 0)
|
| [18] |
崔铁军, 汪培庄, 马云东. 01型空间故障树的结构化表示方法[J]. 大连交通大学学报, 2016, 37(1): 82-87. CUE Tiejun, WANG Peizhuang, MA Yundong. Structured representation methods for 01 space fault tree[J]. Journal of Dalian Jiaotong University, 2016, 37(1): 82-87. DOI:10.11953/j.issn.1673-9590.2016.01.082 (  0) 0)
|
| [19] |
汪培庄. 因素空间理论: 机制主义人工智能理论的数学基础[J]. 智能系统学报, 2018, 13(1): 37-54. WANG Peizhuang. Factor space-mathematical basis of mechanism based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 37-54. (  0) 0)
|
| [20] |
汪培庄. 模糊数学与优化[M]. 北京: 北京师范大学出版社, 2013.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


