2. 中南大学 信息科学与工程学院,湖南 长沙 410083
2. School of Information Science and Engineering, Central South University, Changsha 410083, China
抠图是按照不透明度将感兴趣物体,从图像或视频序列中精确分离出来的一种图像处理技术[1-2]。抠图是一个高病态问题,需要用户提供一定的标注信息进行求解。目前的单帧抠图算法都要求用户输入的标注信息完全正确,并采用大数值的输入控制参数,以迫使输出值与用户标注值严格相同[3-12]。然而过强的输入约束,使得信息传播只与标注区域的边界相关,传播距离有限;在多层抠图算法中[13],通过超像素来构建不同层级的图像,虽能够提高算法运算速度,但受超像素预分割精度的影响,高层计算出的结果在向下层传递标注时也会造成错误的初始值。而视频抠图是单帧抠图在图像序列流上的扩展[14-18],帧间标注信息的传递尤为重要。目前视频抠图多数采用半自动标注的方式,通过帧间传播策略将关键帧上的标注信息依次向后续帧传递。虽有学者[15, 18]利用光流信息提高了帧间连续性,但依然采用的是硬约束的方式,因此要求传播产生的三分图对前景边界有良好的包围性并严格正确,这使得后续帧的三分图产生过程复杂,影响了算法的可扩充性和快速性。针对三分图标注的产生方法,不少学者也作了进一步的研究,但仍然是建立在初始标注完全正确的基础上[19-20]。
综上可知,传统算法采用的硬约束方式使得抠图效果严重依赖于所采用标记的准确性,对用户输入要求高。为此,本文在随机游走算法基础上,提出了软约束随机游走算法(soft-constrained random walk, SCRW),使得输入控制矩阵能够根据图像颜色分布特性进行自适应调整。
1 随机游走分割算法随机游走是一种具有马尔科夫链性质的特殊布朗运动,在给定的图和一个出发点上,信息以一定的概率随机地移动到邻居节点上。借助电势理论,Grady[21]指出图像分割过程实际上是求解带边界条件的Dirichlet问题。首先建立一张自然图像对应的无向图模型
| ${L_{ij}} = \left\{ \begin{gathered} \!\!\!\!\!\!\!\!\!\!\! \!\!\!\! \!\!\! \sum\nolimits_j {{w_{ij}}}, \;\;\; i = j \\ - {w_{ij}}, \;\;\;\;\;\; i \ne j, j \in {\varOmega _i} \\ \!\!\!\! \!\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!0, \;\;\; \;\;\; \text{其他} \\ \end{gathered} \right.$ |
式中
| $p_i^k = \left\{ \begin{array}{l} 1,\;\;\;\;\;{x_i}\text{属于第}k\text{类}\\ 0,\;\;\;\;\;\text{其他} \end{array} \right.$ |
由文献[21]知,随机游走分割算法的Dirichlet问题也可写成两顶点概率差值的加权和形式:
| $D\left[ {{ p}_{}^k} \right] = \frac{1}{2}\sum\limits_{{e_{ij}} \in E} {{w_{ij}}} {\left( {p_i^k - p_j^k} \right)^2}$ | (1) |
求解可得未标注点的首达概率
| ${{p}}_U^k = - {{L}}_U^{ - 1}{{{B}}^{\rm{T}}}{{p}}_M^k$ | (2) |
在传统双层抠图中,其求解的目标函数不但要求两近邻像素点间的
| $J = \min \frac{1}{2}\left( {\sum\limits_{i = 1}^n {{{\sum\limits_{j \in {\varOmega _i}} {{w_{ij}}\left( {{\alpha _i} - {\alpha _j}} \right)} }^2} + \lambda \sum\limits_{i \in S} {{{\left( {{\alpha _i} - {{\tilde \alpha }_i}} \right)}^2}} } } \right)$ | (3) |
式中:
结合原始的随机游走算法,将传统双层抠图算法扩展为多图层抠图,像素点到
| $D\left[ {{{{\alpha }}^k}} \right] = \frac{1}{2}\left( {\sum\limits_{i = 1}^n {{{\sum\limits_{j \in {\Omega _i}} {{w_{ij}}\left( {\alpha _i^k - \alpha _j^k} \right)} }^2} + \sum\limits_{i \in S} {{h_i}{{\left( {\alpha _i^k - \tilde \alpha _i^k} \right)}^2}} } } \right)$ | (4) |
式中:
1)标注信息从已知区域向未知区域扩散时,未知区域只能接受已标注区域的边界信息,扩散过程只依赖于局部相似关系建立的图模型,而与已知区域内部的其他信息无关。尤其是标注信息不足时,局部模型的小窗口特性限制了输入信息的传播距离。
2)为了使目标函数值最小,传统算法会迫使
针对
将式(4)写成矩阵形式,则有
| $\begin{gathered} D\left[ {{{{\alpha}} ^k}} \right] = \frac{1}{2}\left( {{{\left( {{{{\alpha}} ^k}} \right)}^{\rm{T}}}{{L}}\left( {{{{\alpha}} ^k}} \right) + {{\left( {{{{\alpha}} ^k} - {{\tilde {{\alpha}} }^k}} \right)}^{\rm{T}}}{{H}}\left( {{{{\alpha}} ^k} - {{\tilde {{\alpha}} }^k}} \right)} \right) =\\ \frac{1}{2}\left( {\left[ {{{\left( {{{\alpha}} _l^k} \right)}^{\rm{T}}} {{\left( {{{\alpha}} _u^k} \right)}^{\rm{T}}}} \right]\left[ \begin{gathered} {{{L}}_l}\quad{{B}} \\ {{{B}}^{\rm{T}}} \quad {{{L}}_u} \\ \end{gathered} \right]\left[ \begin{gathered} {{\alpha}} _l^k \\ {{\alpha}} _u^k \\ \end{gathered} \right] + } \right. \cdots \;+ \\ \left. {{{\left( {\left[ \begin{gathered} {{\alpha}} _l^k \\ {{\alpha}} _u^k \\ \end{gathered} \right] - \left[ \begin{gathered} \tilde {{\alpha}} _l^k \\ \tilde {{\alpha}} _u^k \\ \end{gathered} \right]} \right)}^{\rm{T}}}\left[ \begin{gathered} {{{H}}_l} \quad {\bf{0}} \\ {{\bf{0}}^{\rm{T}}} \quad {{{H}}_u} \\ \end{gathered} \right]\left( {\left[ \begin{gathered} {{\alpha}} _l^k \\ {{\alpha}} _u^k \\ \end{gathered} \right] - \left[ \begin{gathered} \tilde {{\alpha}} _l^k \\ \tilde {{\alpha}} _u^k \\ \end{gathered} \right]} \right)} \right) \\ \end{gathered} $ | (5) |
式中:对角矩阵
| $\begin{gathered} {{\alpha}} _u^k = {\left( {{{{L}}_u} + {{{H}}_u}} \right)^{ - 1}}\left( { - {{{B}}^{\rm{T}}}{{\alpha}} _l^k + {{{H}}_u}\tilde {{\alpha}} _u^k} \right) = \\ {\left( {{{{L}}_u} + {{{H}}_u}} \right)^{ - 1}}\left( { - {{{B}}^{\rm{T}}}{{\alpha}} _l^k} \right){\rm{ + }}{\left( {{{{L}}_u} + {{{H}}_u}} \right)^{ - 1}}{{{H}}_u}\tilde {{\alpha}} _u^k \\ \end{gathered} $ | (6) |
当
| $ \begin{array}{c} {{A}} = {\left( {{{{L}}_u} + {{{H}}_u}} \right)^{ - 1}}{{{H}}_u} = \\ {\left( {{{{L}}_u} + {{{H}}_u}} \right)^{ - 1}}\left( {{{{D}}_u} + {{{H}}_u}} \right){\left( {{{{D}}_u} + {{{H}}_u}} \right)^{ - 1}}{{{H}}_u} = \\ {\left( {{{\left( {{{{D}}_u} + {{{H}}_u}} \right)}^{ - 1}}\left( {{{{D}}_u} - {{{W}}_u} + {{{H}}_u}} \right)} \right)^{ - 1}}{\left( {{{{D}}_u} + {{{H}}_u}} \right)^{ - 1}}{{{H}}_u} = \\ {\left( {{{I}} - {{\left( {{{{D}}_u} + {{{H}}_u}} \right)}^{ - 1}}{{{W}}_u}} \right)^{ - 1}}{\left( {{{{D}}_u} + {{{H}}_u}} \right)^{ - 1}}{{{H}}_u} \end{array} $ | (7) |
式(7)等价于
| ${a_{ii}} = \frac{{{h_i}}}{{{h_i} + {d_i}}} \times 1 + \sum\limits_{j \ne i} {\frac{{{w_{ij}}}}{{{h_i} + {d_i}}}} {a_{ij}}$ | (8) |
| ${a_{ij}} = \sum\limits_{j \ne k} {\frac{{{w_{kj}}}}{{{h_i} + {d_i}}}} {a_{jk}}, \;\;\; i \ne j $ | (9) |
由文献[22]可知,式(8)、式(9)正是部分吸收随机游走算法(partial absorption random walk, PARW)的基本形式,故
结论1 由于吸收概率矩阵
结论2 自吸收概率
由于本文所提带软性约束条件的随机游走SCRW与部分吸收式随机游走算法PARW本质上是相同的,此时图中节点
| ${p_{ij}} = \left\{ \begin{gathered} \frac{{{h_i}}}{{{h_i} + {d_i}}}, \;\;\; i = j \\ \frac{{{w_{ij}}}}{{{h_i} + {d_i}}},\;\;\;i \ne j \\ \end{gathered} \right.$ | (10) |
式(10)表明,初始信息有
由上可知,节点的自吸收概率与
在非归一化图模型中,若各点的输入控制参数取为相同的值,即
而在归一化图模型中,各点的度都为
因此,在节点度
根据图像特性[23],在围绕图像点
1)线−线模型:前景和背景都是线性变化,则存在颜色常量
由于图像RGB 3通道分别符合线性关系,记3×3矩阵
| ${{Q}}\left[ \begin{gathered} {{{\alpha}} _j} \\ {\alpha _j}\beta _j^F \\ (1 - {\alpha _j})\beta _j^B \\ \end{gathered} \right] = {{{I}}_j} - {{{B}}_2}$ |
式中
| ${\alpha _j} = a_i^rI_j^r + a_i^gI_j^g + a_i^bI_j^b + {b_i}$ |
2)点−线模型:前景或是背景其中之一退化为点模型,在窗口内取值为常数,不妨设前景为常量,背景呈线性,则
| $\begin{gathered} {{{I}}_j} = {\alpha _j}{{F}} + (1 - {\alpha _j})\left( {\beta _j^B{{{B}}_1} + \left( {1 - \beta _j^B} \right){{{B}}_2}} \right)= \\ {\alpha _j}\left( {{{F}} - {{{B}}_2}} \right) + (1 - {\alpha _j})\beta _j^B\left( {{{{B}}_1} - {{{B}}_2}} \right) + {{{B}}_2} \\ \end{gathered} $ |
推导可知存在自由度为3的变换:
| ${\alpha _j} = a_i^r{{I}}_j^r + a_i^g{{I}}_j^g + a_i^b{{I}}_j^b$ |
3)点−点模型:前景和背景都取值为常数的点模型,即
| ${\alpha _j} = a_i^1\tilde I_j^1 + a_i^2\tilde I_j^2$ |
4)单点模型:前景和背景取为相同常数,即
记局部窗口内的特征矩阵为
| ${h_i} = \left\{ \begin{array}{l} {\gamma _1}, \quad G = (V,E)\text{是非归一化图}\\ {\gamma _2} \times {\rm{rank}}({{{G}}_i}) \times \displaystyle\frac{{{\sigma _i}}}{{\overline \sigma }},\quad G = (V,E) \text{是归一化图} \end{array} \right.$ | (11) |
式中:
| $\begin{gathered} {p_{ii}} = {{{h_i}} / {\left( {{h_i} + {d_i}} \right)}} = \\ {{{\gamma _2} \times {\rm{rank}}({{{G}}_i}) \times \sigma _i}/ {\left( {{\gamma _2} \times {\rm{rank}}({{{G}}_i}) \times \sigma _i + {d_0} \times \overline \sigma } \right)}} \\ \end{gathered} $ |
由于特征矩阵秩
| ${\rm{rank}}({{{G}}_i}) = \arg \mathop {\max }\limits_{k \in \{ 1,2,3,4\} } \left[ {\frac{{{\sigma _{ik}}}}{{{\sigma _i}}} > t} \right]$ | (12) |
式中:
为了提高算法的快速性,单帧抠图采用双层的形式。首先对图像进行SLIC超像素[24]分割,构建基于超像素的图模型
在高层中,图模型
| ${w_{uv}} = \exp \left( { - \frac{{\left\| {{c_u} - {c_v}} \right\|}}{{\delta _{}^2}}} \right)$ | (13) |
式中:
在低层中,图模型按照传统的CF算法[10]建立,相似度函数为
| ${w_{i,j}} = \sum\limits_{q\left| {(i,j) \in {\varOmega _q}} \right.} {\frac{1}{{\left| {{\varOmega _q}} \right|}}\left( {1 + {{({{{I}}_i} - {{{\mu}} _q})}^{\rm{T}}}{{({\sum _q} + \frac{\varepsilon }{{\left| {{\varOmega _q}} \right|}}{\Lambda _3})}^{ - 1}}({{{I}}_j} - {{{\mu}} _q})} \right)} $ |
式中:
| $\left\{ \begin{gathered} {t_f} = \frac{{{\rm{mean}}({{{\alpha}} _s}) + 1.2 \times \max ({{{\alpha}} _s})}}{2} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{t_b} = 0.5 \times {\rm{mean}}({{{\alpha}} _s}) \\ \end{gathered} \right.$ |
式中
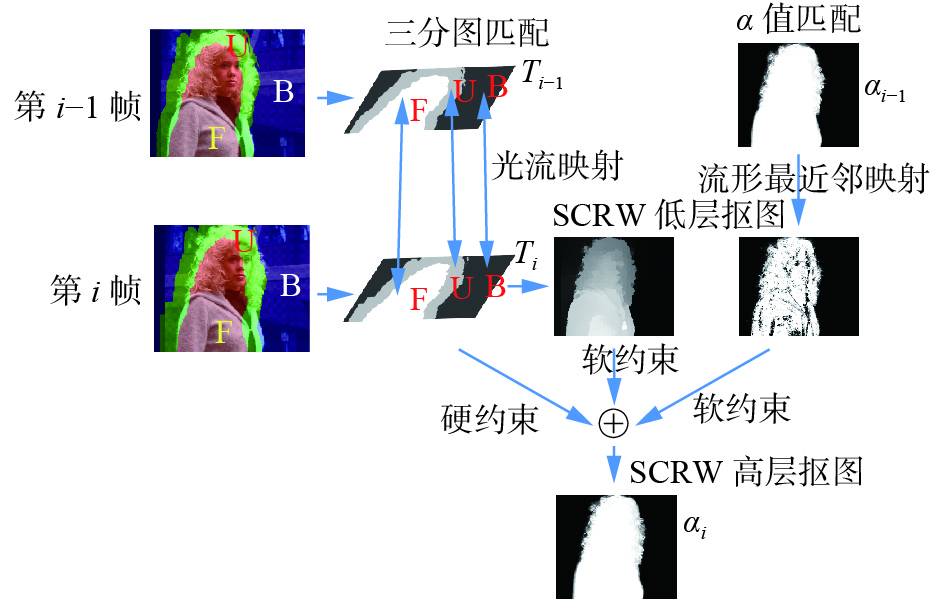
由于视频抠图处理数据量大,一般无法对每帧图像进行标注,但图像序列间具有连续性与相似性,充分利用图像的帧间信息可以获得单张图像不具备的特征。本文在单帧双层SCRW算法的基础上,采用软硬两种约束相结合的方式进行视频抠图。图1为视频抠图的示意图:左侧为输入的第
|
Download:
|
| 图 1 SCRW视频抠图示意 Fig. 1 Schematic of SCRW video matting process | |
首先计算图像的前向与后向运动向量[26-27]
| ${w_{kl}} = \exp \left( { - \frac{{\left\| {{{{F}}_k} - {{{F}}_l}} \right\|}}{{\delta _{}^2}}} \right) $ |
式中:Fk为颜色特征;Fl为运动向量特征,取值为
| ${{F}} = \left[ {l\;\;h\;\;v\;\;{\lambda _f}{u_b}\;\;{\lambda _f}{v_b}\;\;{\lambda _f}{u_f}\;\;{\lambda _f}{v_f}} \right]$ | (14) |
式中
| ${{X}} = \left[ {r\;\;g\;\;b\;\;{\lambda _s}x\;\;{\lambda _s}y} \right]$ | (15) |
上述FLANN搜索特征中未加入光流向量是因为不同帧间的光流特征不具有可比性。与传统视频抠图要求三分图密实围绕前景物体、宽度较窄不同,本文只需要勾画前景与背景的大致区域,即只需要前背景的稀疏输入,因而未知区域的范围较宽。然而未知区域通常包含复杂的图像细节,如毛发、孔洞等,且由于图像运动造成的前景物体遮挡、新增前景等原因,当前帧未知区域中的点与前一帧的流形匹配点有可能差别较大,置信度低。设
| ${h_i} = {\gamma _3} \times \left( {1 - \frac{{m_i}}{{\max ({m_i})}}} \right)$ | (16) |
式中
1)用光流法计算视频序列中每一帧的前向、后向光流运动向量
2)用前向光流
3)以
4)通过流形最近邻映射将前帧
5)综合三分图硬约束
6)将
7)判断视频是否处理完毕或到预定处理帧数,否则转到2)。
6 实验结果实验的运行环境为:Intel Core i3双核3.3 GHz CPU,编程环境为Matlab 2016。对比算法有CF[10]、LB[11]、KNN[12]抠图算法。由于CF算法在层数大于5时,程序无法正常运行,因此取层数level=1及level=5两种水平下的结果与本文算法进行对比,文中超像素数取1 000。实验中定量分析图片源于抠图标准网站
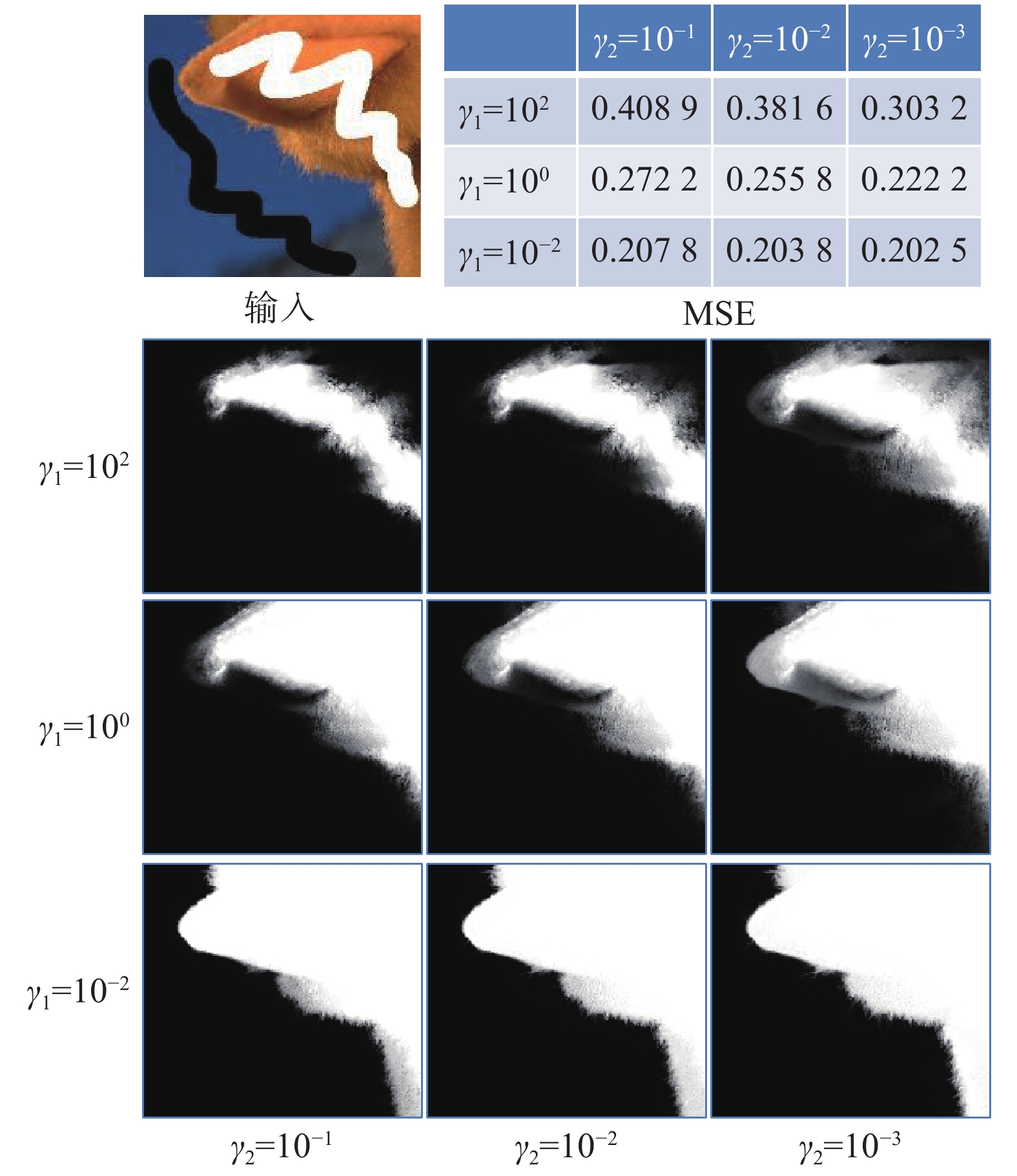
1)参数
为了验证参数
|
Download:
|
|
图 2 全局输入控制参数
|
|
2)容错性
图3是不完全正确标注情况下,传统CF算法和本文所提SCRW算法的容错性比较。在图3(b)中,白色画线为前景标注,黑色画线为背景标注,中间圆圈区域内,用户错误地将中间背景布标注为前景。图3(c)的传统CF抠图算法,因为采用

|
Download:
|
| 图 3 容错性比较 Fig. 3 Comparison of fault tolerances | |
3)定量比较
在图4(a)中,三分图1是原始三分图,三分图2~三分图5是原三分图的未知区域向外扩展10、15、20、25个像素点而得,笔画式标注则是手动标注(白色前景,黑色背景),图4(a)的用户标注信息从左至右依次减少。图4(b)、(c)为各算法在不同的用户标注下的MSE误差及运算时间。由图4(b)知,在三分图比较紧凑的情况下,未知区域中的点距离已知区域近,不需远距离的信息传播就能获得引导信息,CF、LB算法的MSE误差反而比较小;但随着用户标注区域的减少,CF、LB算法由于缺乏远距传播,未知区域中的部分点得不到引导信息,产生了较大的误差,虽然CF算法随着降采样水平的增高,也具有一定的远距传播能力,但其过强的输入控制使高层中不够准确的结果在低层中产生误扩散,故其MSE误差在高level的情况下反而更大;KNN算法虽采用非局部近邻,但其流形近邻的搜索特征包含空间信息,传播距离也有限;而本文算法的高层远距离传播及低层细节恢复能力使得算法的整体误差最小,尤其是在用户输入信息不够充分的情况下能够取得更好的结果。在图4(c)中,CF算法在level=5时的运算时间最短,但其相应的误差最大,是以牺牲准确度来降低运算时间;除此之外,随着未知区域的增加,各算法的运算时间出现不同程度的增加,但本文算法的增量最小,运算时间基本在10 s左右。

|
Download:
|
| 图 4 不同用户输入下各算法准确率及运算时间对比 Fig. 4 Comparison of algorithm accuracy and operation time with different user inputs | |
实验中特征权重参数
如图5所示,是Amira视频第79帧到第82帧的各算法运行结果。图5(b) 的三分图为前帧通过光流匹配得到的,图5(a)前背景边界线与图5(b)中的三分图对应。由图5(a)知,随着前景图像的运动,匹配的三分图虽然大致划分了前景背景区域,但并没有很好地贴近前景边界,虽然图5(d)中的高层软约束SCRW能够增加输入信息的远距传播能力,但因前景物体与背景的颜色存在一定的相似度,因此Amira图像的灰色外套及眼部没有完全地被抠选出来(图中箭头所示)。在图5(e)中,由于CF算法的局部窗口作用会使得算法在确定的前景和背景间平滑过渡,未知区域中的前景物体出现了半透明的抠图结果。本文所提出的带流形匹配的SCRW算法由于存在三分图和前帧

|
Download:
|
| 图 5 Amira视频序列抠图结果 Fig. 5 Matting results of Amira video sequence | |
本文针对抠图算法标注准确性问题,根据带约束随机游走算法信息流的传播特性,提出了一种带软性约束的随机游走算法,并将其应用到单帧图像抠图和视频抠图中。实验结果表明,输入控制参数对标注信息的扩散距离具有直接的影响,软性约束下随机游走具有更加优良的容错特性,所提算法避免了视频抠图中获取三分图标注的繁杂计算,为提高抠图算法的精度提供了新的思考方向。但本文算法在大尺寸图像和视频上运行缓慢,对边界模糊图像的处理效果不够理想,如何进一步提高算法的快速性和复杂图像的处理能力仍将是未来努力的方向。
| [1] |
YAO Guilin, ZHAO Zhijie, LIU Shaohui. A comprehensive survey on sampling-based image matting[J]. Computer graphics forum, 2017, 36(8): 613-628. DOI:10.1111/cgf.13156 ( 0) 0)
|
| [2] |
ZHU Qingsong, SHAO Ling, LI Xuelong, et al. Targeting accurate object extraction from an image: a comprehensive study of natural image matting[J]. IEEE transactions on neural networks and learning systems, 2015, 26(2): 185-207. DOI:10.1109/TNNLS.2014.2369426 ( 0) 0)
|
| [3] |
KARACAN L, ERDEM A, ERDEM E. Alpha matting with KL-divergence-based sparse sampling[J]. IEEE transactions on image processing, 2017, 26(9): 4523-4536. DOI:10.1109/TIP.2017.2718664 ( 0) 0)
|
| [4] |
XU Ning, PRICE B, COHEN S, et al. Deep image matting[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA, 2017: 311–320.
( 0) 0)
|
| [5] |
SHI Yongfang, AU O C, PANG Jiahao, et al. Color clustering matting[C]//Proceedings of 2013 IEEE International Conference on Multimedia and Expo. San Jose, USA, 2013: 1–6.
( 0) 0)
|
| [6] |
JIN Meiguang, KIM B K, SONG W J. Adaptive propagation-based color-sampling for alpha matting[J]. IEEE transactions on circuits and systems for video technology, 2014, 24(7): 1101-1110. DOI:10.1109/TCSVT.2014.2302531 ( 0) 0)
|
| [7] |
HE Bei, WANG Guijin, ZHANG Cha. Iterative transductive learning for automatic image segmentation and matting with RGB-D data[J]. Journal of visual communication and image representation, 2014, 25(5): 1031-1043. DOI:10.1016/j.jvcir.2014.03.002 ( 0) 0)
|
| [8] |
JOHNSON J, VARNOUSFADERANI E S. Sparse coding for alpha matting[J]. IEEE transactions on image processing, 2016, 25(7): 3032-3043. DOI:10.1109/TIP.2016.2555705 ( 0) 0)
|
| [9] |
LI Xuelong, LIU Kang, DONG Yongsheng, et al. Patch alignment manifold matting[J]. IEEE transactions on neural networks and learning systems, 2018, 29(7): 3214-3226. DOI:10.1109/TNNLS.2017.2727140 ( 0) 0)
|
| [10] |
LEVIN A, LISCHINSKI D, WEISS Y. A closed-form solution to natural image matting[J]. IEEE transactions on pattern analysis and machine intelligence, 2008, 30(2): 228-242. DOI:10.1109/TPAMI.2007.1177 ( 0) 0)
|
| [11] |
ZHENG Yuanjie, KAMBHAMETTU C. Learning based digital matting[C]//Proceedings of the 12th International Conference on Computer Vision (ICCV). Kyoto, Japan, 2009: 889–896.
( 0) 0)
|
| [12] |
CHEN Qifeng, LI Dingzeyu, TANG C K. KNN matting[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(9): 2175-2188. DOI:10.1109/TPAMI.2013.18 ( 0) 0)
|
| [13] |
TSENG C Y, WANG S J. Learning-based hierarchical graph for unsupervised matting and foreground estimation[J]. IEEE transactions on image processing, 2014, 23(12): 4941-4953. DOI:10.1109/TIP.2014.2323132 ( 0) 0)
|
| [14] |
GONG Minglun, QIAN Yiming, CHENG Li. Integrated foreground segmentation and boundary matting for live videos[J]. IEEE transactions on image processing, 2015, 24(4): 1356-1370. DOI:10.1109/TIP.2015.2401516 ( 0) 0)
|
| [15] |
LEE S Y, YOON J C, LEE I K. Temporally coherent video matting[J]. Graphical models, 2010, 72(3): 25-33. DOI:10.1016/j.gmod.2010.03.001 ( 0) 0)
|
| [16] |
SHAHRIAN E, PRICE B, COHEN S, et al. Temporally coherent and spatially accurate video matting[J]. Computer graphics forum, 2014, 33(2): 381-390. DOI:10.1111/cgf.12297 ( 0) 0)
|
| [17] |
LI Dingzeyu, CHEN Qifeng, TANG C K. Motion-aware KNN Laplacian for video matting[C]//Proceedings of 2013 IEEE International Conference on Computer Vision (ICCV). Sydney, Australia, 2013: 3599-3606.
( 0) 0)
|
| [18] |
SINDEEV M, KONUSHIN A, ROTHER C. Alpha-flow for video matting[C]//Proceedings of the 11th Asian Conference on Computer Vision. Daejeon, Korea, 2012: 438–452.
( 0) 0)
|
| [19] |
CHO D, KIM S, TAI Y W, et al. Automatic trimap generation and consistent matting for light-field images[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 39(8): 1504-1517. DOI:10.1109/TPAMI.2016.2606397 ( 0) 0)
|
| [20] |
CHO H W, CHO Y R, SONG W J, et al. Image matting for automatic target recognition[J]. IEEE transactions on aerospace and electronic systems, 2017, 53(5): 2233-2250. DOI:10.1109/TAES.2017.2690529 ( 0) 0)
|
| [21] |
GRADY L. Random walks for image segmentation[J]. IEEE transactions on pattern analysis and machine intelligence, 2006, 28(10): 1768-1783. ( 0) 0)
|
| [22] |
WU Xiaoming, LI Zhenguo, SO A M C, et al. Learning with partially absorbing random walks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS). Lake Tahoe, USA, 2012: 3077–3085.
( 0) 0)
|
| [23] |
SINGARAJU D, ROTHER C, RHEMANN C. New appearance models for natural image matting[C]//Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Miami Beach, USA, 2009: 659-666.
( 0) 0)
|
| [24] |
ACHANTA R, SHAJI A, SMITH K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(11): 2274-2282. DOI:10.1109/TPAMI.2012.120 ( 0) 0)
|
| [25] |
MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configuration[C]//Proceedings of the International Conference on Computer Vision Theory and Applications. Lisbon, Portugal, 2009: 331–340.
( 0) 0)
|
| [26] |
BAKER S, SCHARSTEIN D, LEWIS J P, et al. A database and evaluation methodology for optical flow[J]. International journal of computer vision, 2011, 92(1): 1-31. DOI:10.1007/s11263-010-0390-2 ( 0) 0)
|
| [27] |
BROX T, BRUHN A, PAPENBERG N, et al. High accuracy optical flow estimation based on a theory for warping[C]//Proceedings of the 8th European Conference on Computer Vision (ECCV). Prague, Czech Republic, 2004: 25–36.
( 0) 0)
|
| [28] |
RHEMANN C, ROTHER C, WANG Jue, et al. A perceptually motivated online benchmark for image matting[EB/OL].(2009-06)[2018-09-11] http://www.alphamatting.com/.
( 0) 0)
|
| [29] |
CHUANG Y Y, AGARWALA A, CURLESS B, et al. Video matting of complex scenes[EB/OL]. (2002-07)[2018-09-11] http://grail.cs.washington.edu/projects/digital-matting/video-matting/.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


