2. 清华大学 信息技术研究院,北京 100084;
3. 清华大学 生命学院,北京 100084
2. Institute of Information Technology, Tsinghua University, Beijing 100084, China;
3. School of Life Sciences, Tsinghua University, Beijing 100084, China
从现象中发现规律,是人类智能最核心的能力之一,人们也很早就开始研究如何用数学方法来分析数据中的规律。从1930年Fisher线性判别和1950年感知器算法开始,诞生了模式识别学科,研究从数据中学习分类信息的数学方法,形成了最早的机器学习研究。“机器学习”这个术语也是20世纪50年代末提出来的,最初并不专指从数据中学习,更多地包括了机器推理等经典人工智能问题,直到20世纪后期才逐渐被用来专指从数据中学习。现在,这2个术语的含义已经非常接近,模式识别专指对数据的分类,机器学习则指学习数据中的各种规律尤其是分类规律,而“深度学习”是机器学习中最新发展起来的一类方法的总称。
很多模式识别方法和统计学习方法,如线性判别、近邻法、罗杰斯特回归、决策树、支持向量机等,已经在很广泛的问题上取得了成功,如广告点击率预测[1-3]、希格斯子信号识别[4]、基于基因表达的疾病分型[5-6]等。这些统计学习方法往往直接根据特征对样本进行分类,不进行特征变换或只进行一次特征变换或选择。与深度学习方法相比,这些方法中特征变换较少,或者依赖于上游处理来对特征进行变换,所以被有些人称作“浅层模型”或“浅层学习方法”。
这些浅层模型在很多应用上取得了成功,但是也存在很大局限,即模型的效果非常依赖于上游提供的特征。一方面,构造特征的过程是很困难的,需要对问题有丰富的先验知识,对原始数据详尽地了解;另一方面,在先验知识不充分的情况下,需要人为构建的特征数目庞大,如某些广告点击率预测算法中人工构造的特征维数高达数亿维[1, 7]。
深度学习是一种深层的机器学习模型,其深度体现在对特征的多次变换上。常用的深度学习模型为多层神经网络,神经网络的每一层都将输入非线性映射,通过多层非线性映射的堆叠,可以在深层神经网络中计算出非常抽象的特征来帮助分类。比如:在用于图像分析的卷积神经网络中,将原始图像的像素值直接输入,第一层神经网络可以视作边缘的检测器,而第二层神经网络则可以检测边缘的组合,得到一些基本模块,第三层之后的一些网络会将这些基本模块进行组合,最终检测出待识别目标。深度学习的出现使得人们在很多应用中不再需要单独对特征进行选择与变换,而是将原始数据输入到模型中,由模型通过学习给出适合分类的特征表示。
当前,深度学习是机器学习领域最热门的分支,并且有多个高度集成化的方法平台可以让使用者无需对方法原理充分了解就可以搭建程序进行实验和应用。本文尝试结合笔者的理解对最典型的深度学习方法原理进行综述,对深度学习与以往机器学习方法的关系进行讨论,并对未来需要研究的问题进行展望。
1 机器学习简史深度学习的基础是人工神经网络,其发展经历了3次大的起伏。1943年,受生物神经元工作模式的启发,心理学家McCulloch和数学家Pitts发表了神经元的数学模型[8]。1949年,Hebb[9]提出神经元上连接的强度可以通过训练调整的思想。1957年,Rosenblatt[10]提出感知器(perceptron)的概念和模型,提出了用数据训练其参数的算法并用当时的电子管硬件实现,成为第一个可学习的机器。这些工作构成了后来人工神经网络的基础,当时的感知器模型只有一层,1969年Minsky等[11]指出感知器模型无法学习如异或这样的非线性关系,虽然可以通过试凑多个感知器模型的叠加来实现非线性分类,但对这种多个感知器构成的模型如何构造和如何训练其参数难以解决。而在同一时期,1956年夏天在Dartmouth召开的暑期研讨会发起了以符号主义和知识推理为核心的人工智能(AI)研究,也就是经典AI研究,伴随着这一时期经典AI的快速发展[12-13],人工神经网络尚在萌芽阶段(当时还未出现“人工神经网络”这个术语)就进入了第一次低谷。
人工神经网络(artificial neural networks,ANN)这一术语被广泛使用是在20世纪80年代,并很快被简称为神经网络(neural networks,NN)。1982年,Hopfield等[14]提出了一个具有完整理论基础的神经网络模型。20世纪80年代中期,反向传播(back-propagation,BP)算法被应用于训练神经网络[15-18],解决了多层感知器无法训练的问题,从而使神经网络具有了非线性表示能力,以BP算法训练的多层感知器(multi-layer perceptron,MLP)成为最成功的神经网络模型。同期,Kohonen[19]发展了自组织映射(self-organizing map,SOM)竞争学习神经网络模型。这些方法在很多模式识别问题上取得了很好的效果,掀起了神经网络研究真正的高潮,现在人们通常称之为神经网络研究的第二次高潮。限制性玻耳兹曼机(restrictive Boltzman machine,RBM)等非监督学习模型也是在这一时期被提出来的[20]。
但神经网络方法也存在很多问题。首先,多层感知器虽然具有极强的非线性表示能力,但也因此导致参数解空间中存在大量的局部极值,使用梯度下降法进行训练很容易产生一个并不好的局部极小值,导致多层感知器在很多问题上推广能力较差。其次,虽然神经网络在理论上可以有很多层,但多层神经网络训练速度很慢,这既是因为当时的硬件条件限制,也是因为多层神经网络存在梯度消散现象,即误差在反向传播过程中会迅速衰减,导致对深层网络权值的修正非常缓慢,因此人们实际上只使用二层或三层的神经网络。对这些问题缺乏如何解决或如何避免的理论指导,实际应用中多靠试算和经验,限制了神经网络的进一步发展,使神经网络研究走向低谷。
与此同时,基于20世纪70年代在苏联开展的统计学习理论研究基础,Vapnik等[21-22]在1992—1995年发明了支持向量机(support vector machines, SVM)方法,该方法在小样本下有较好的推广能力,几乎不需要调参,算法复杂度不依赖于样本维数,再加上有着较强的理论基础支持,迅速成为机器学习研究的主流方向[23],在机器学习研究中掀起了SVM热潮,同时人们对神经网络的研究迅速降温。
神经网络的再次崛起开始于2006年,Hinton等[24]提出了深度置信网络(deep belief network, DBN)及限制性波耳兹曼机(RBM)的训练算法,并将该方法应用于手写字符的识别,取得了很好的效果。文献[24]提出,先使用非监督学习方法逐层初始化参数,再使用监督学习方法微调整个网络的训练方法,有效解决了深层神经网络学习的问题。这样的训练方法能够将神经网络放在一个较好的初始值上,容易收敛到较好的局部极值。之后的几年中,深度神经网络蓬勃发展,并被一般化为“深度学习”,许多深度学习的训练技巧被提出来,比如参数的初始化方法、新型激活函数、Dropout(舍弃)训练方法等,这些技巧较好地解决了当结构复杂时传统神经网络存在的过拟合、训练难的问题。与此同时,计算机和互联网的发展也使得在诸如图像识别这样的问题中可以积累前所未有的大量数据对神经网络进行训练。2012年的ImageNet竞赛中,Krizhevsky等[25]使用卷积神经网络使准确率提升了10%,第一次显著地超过了手工设计特征加浅层模型进行学习的模式,在业界掀起了深度学习的热潮。2015年,Google旗下DeepMind公司研发的AlphaGo使用深度学习方法在围棋比赛中击败了欧洲围棋冠军[26],使得深度学习影响日益广泛。有人把当前深度学习的大发展称作人工智能的第3次热潮。
深度学习现在已经用来泛指各种基于多层网络结构的机器学习模型,通过多层模型可以实现更复杂的函数关系。与浅层模型相比,深度学习直接把原始观测数据作为输入,通过多层模型进行逐级特征提取与变换,实现更有效的特征表示。在此基础上,往往在最后一级连接一个浅层模型,如Softmax分类器、MLP神经网络、SVM等,实现更好的分类性能。在这个意义上,深度学习方法不能简单地看作取代了以往的浅层学习方法,而是在原有各种方法基础上的集成与发展。
从以上回顾可以看到,所谓人工智能3次浪潮的说法并不十分严格。在1957年提出人工智能(AI)这个术语的时候,其含义并非指现在人们热议的机器学习,而是以符号主义、知识工程等为核心的狭义的AI。这种狭义的AI研究在20世纪80年代走入低谷,但伴随着的是神经网络热潮的出现,而与20世纪90年代神经网络逐渐降温同时出现的是SVM热潮,这一热潮一直持续到2010年前后,深度学习掀起了新的热潮。与以往的热潮不同,这一新的热潮并没有导致传统浅层机器学习方法和狭义AI研究更加低落,而是带动了几乎所有机器学习相关的研究。同时,人们开始正式把基于数据的机器学习纳入到人工智能范畴,并使机器学习走到了人工智能的最核心。从这个意义上看,这种人工智能研究从20世纪三四十年代就已经开始了,随后陆续出现了感知器、符号主义与机器推理、神经网络、支持向量机、深度学习等多个研究热潮,并未陷入低谷,当前热潮的最大特点是业外人士对人工智能的关注达到了前所未有的程度。
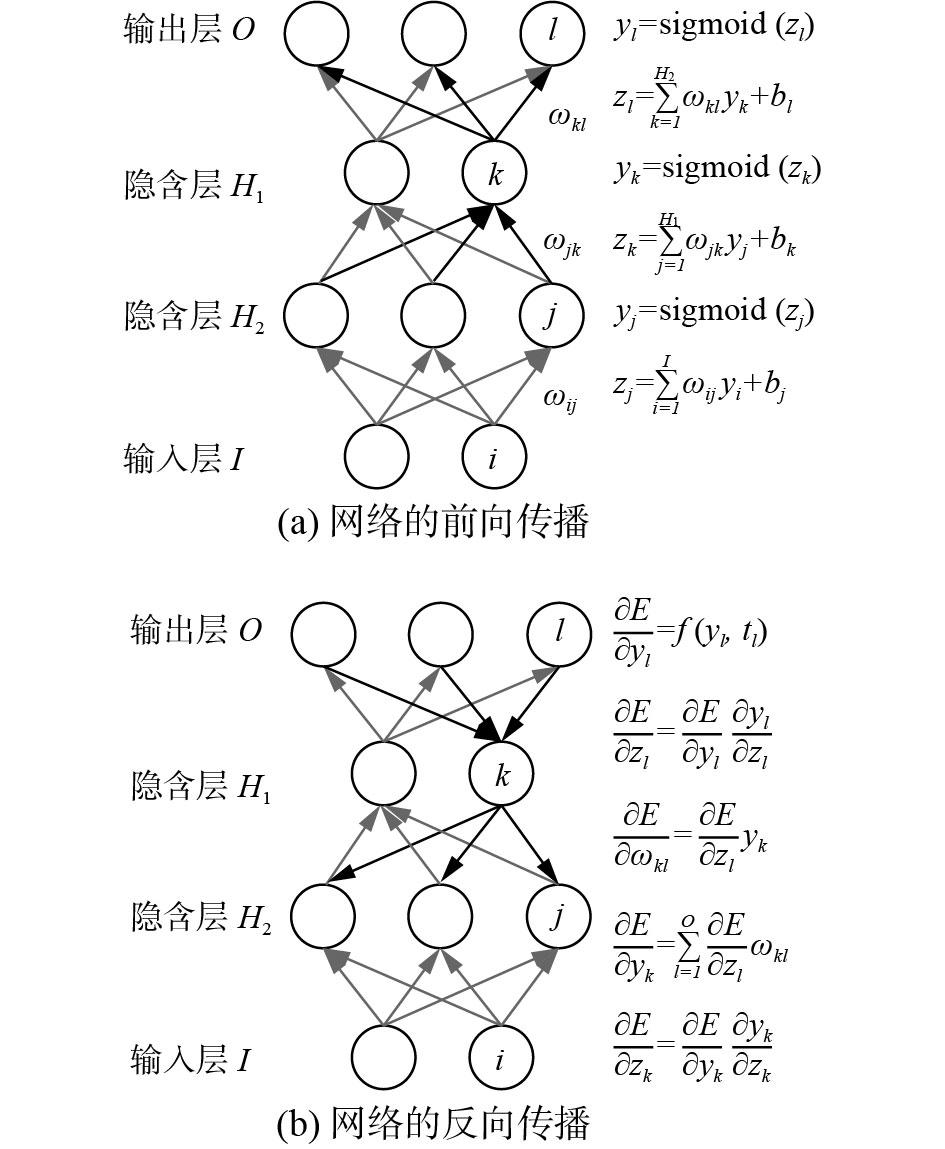
2 深度学习的核心学习算法深度学习最常用于各种监督模式识别问题,比如图像识别、自然语言识别等。在讨论深度学习的典型模型之前,我们先来讨论作为各种深度学习模型和算法共同基础的核心学习算法。一般地,深度神经网络包含输入层、多个隐含层以及输出层,传统多层感知器神经网络训练的反向传播(BP)算法仍然是深度神经网络训练的核心算法,它包括信息的前向传播过程和误差梯度的反向传播过程。
多层感知器的基本结构如图1所示,每层都包含若干节点,I是输入层节点个数,H1和H2是2个隐含层的节点个数,O是输出层的节点个数,
|
Download:
|
| 图 1 多层感知器前向传播与反向传播过程 Fig. 1 Processes of forward propagation and back propagation of multilayer perceptron | |
图1(a)示意了信号在网络中前向传播的过程,每个节点中都包含2步操作,先对上一层节点输出值进行线性组合,再对得到的中间值进行非线性变换后输出。对于1个输入样本,经过上述2步操作可以得到第1层隐含节点的输出值,隐含节点输出值就是特征的某种抽象表示,可以重复这个过程得到更深层次的隐含节点值,越深层次的隐含节点所表示的特征越抽象,对于最后一层隐含节点,可以连接到输出层中进行分类并输出。实验表明,将神经网络视作特征提取器,将最后一层特征输入到如SVM等其他分类器中,也能获得很好的分类效果[27]。网络输出的分类结果,可以与真实标签比对计算误差或损失函数值。当输出结果与真实标签相等时损失为零,二者相差越大损失函数值越大,常见的损失函数有二次损失、对数损失等。在训练样本上的总损失是监督学习中的优化目标,常用梯度下降法优化这个目标,这个过程就是机器的“学习”或用样本对机器的“训练”。
要对神经网络各层的参数进行训练,需要计算损失对网络中间各层参数的梯度,BP算法就是把损失从输出层逐层往前传递,这个过程叫做误差的反向传播,如图1(b)所示,其中E为损失函数,
对于一个或两个隐层的多层感知器网络来说,可以直接用BP算法进行训练。但对于有更多层复杂结构的深度学习模型,则需要结合深层网络结构设计采用多种训练技巧。下面就对典型深层网络结构和对应算法的核心思想进行讨论。
3 深度学习的网络结构深度学习的性能很大程度上取决于网络的结构。对于不同类型的数据和问题,人们发展了多种不同的网络结构模型。
3.1 自编码机与限制性玻耳兹曼机自编码机(auto encoder ,AE)与限制性玻耳兹曼机(RBM)是深度学习中使用较多的2种非监督学习的神经网络模型,但它们通常并不直接用于解决非监督学习问题,而是通过非监督学习找到更好体现数据内在规律的特征表示,再用到监督学习的深层神经网络模型中,常常被用于神经网络的初始化及学习,适用于下游分类的特征表示。
自编码机[28-30]是一种特殊的多层感知器,网络结构包括编码器与解码器2部分,如图2(a)所示。对于给定训练集

|
Download:
|
| 图 2 自编码机与级联的自编码机 Fig. 2 Auto-encoder and concatenated auto-encoder | |
| $ {h_{W,b}}\left( {{{{x}}^i}} \right) = g\left( {f\left( {{{{x}}^i}} \right)} \right) \approx {{{x}}^i},\quad i = 1,2, \cdots ,n $ |
式中:f代表编码器,g代表解码器,
| $ f\left( {{{x}^i}} \right) = g\left( {{{x}^i}} \right) = {{x}^i},\quad i = 1,2, \cdots ,n $ |
即可实现目标,但这样的网络仅仅是将输入复制到了隐含状态和输出,没有学到任何信息。一种有用的自编码机结构是隐含节点的数目比输入节点数目少,如图2(a)所示,这样迫使网络对数据的特征进行压缩。当各个特征相互独立时,想用少量隐含状态表示所有特征就很困难。但是如果特征之间存在一定的相关性,算法就可以发现这样的相关性并学习到特征的一种压缩表示。实际上,当网络中连接都为线性连接时,算法的压缩结果与主成分分析(PCA)相同;当网络中连接为非线性时,自编码机能学到比核主成分分析(KPCA)更灵活的数据压缩表示。自编码机作为一种特殊的多层感知器,可以用一般的BP算法训练网络参数,也可以使用recirculation方法进行训练[31]。
普通的自编码机存在一些潜在的问题,例如:当编码器和解码器的能力过强时,编码器可以直接将原始数据
| $ {\rho _{{j}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {a_j}\left( {{{x}^i}} \right) $ |
式中:
| $ {\rm{Loss}} = L\left( {x,{h_{w,b}}\left( x \right)} \right) + \beta \mathop \sum \limits_{j = 1}^s \left[ {\rho \log \frac{\rho }{{{\rho _j}}} + \left( {1 - \rho } \right){\rm log}\frac{{1 - \rho }}{{1 - {\rho _j}}}} \right] $ |
式中:s为隐含节点数目;左边第一项是衡量自编码机能否良好地恢复输入的损失函数;左边第二项是针对稀疏性的惩罚项;β是稀疏惩罚项系数,该值越大获得的稀疏性越强。训练该目标函数得到的隐含状态将是稀疏的。
另一种改进方法是去噪自编码机[34],将训练数据进行微小扰动之后输入,并试图恢复加入噪声之前的样本;而收缩自编码机[35]对
在深度学习模型中,经常把输入端设计为自编码器,在进行以上非监督训练后去掉解码器部分,用中间层的输出作为对样本的压缩表示,接入到下一层神经网络作为输入。也有些模型采用多个自编码器进行级联来构成栈式自编码机[36],逐级训练编码器,实现对样本更好的表示,如图2(b)所示。
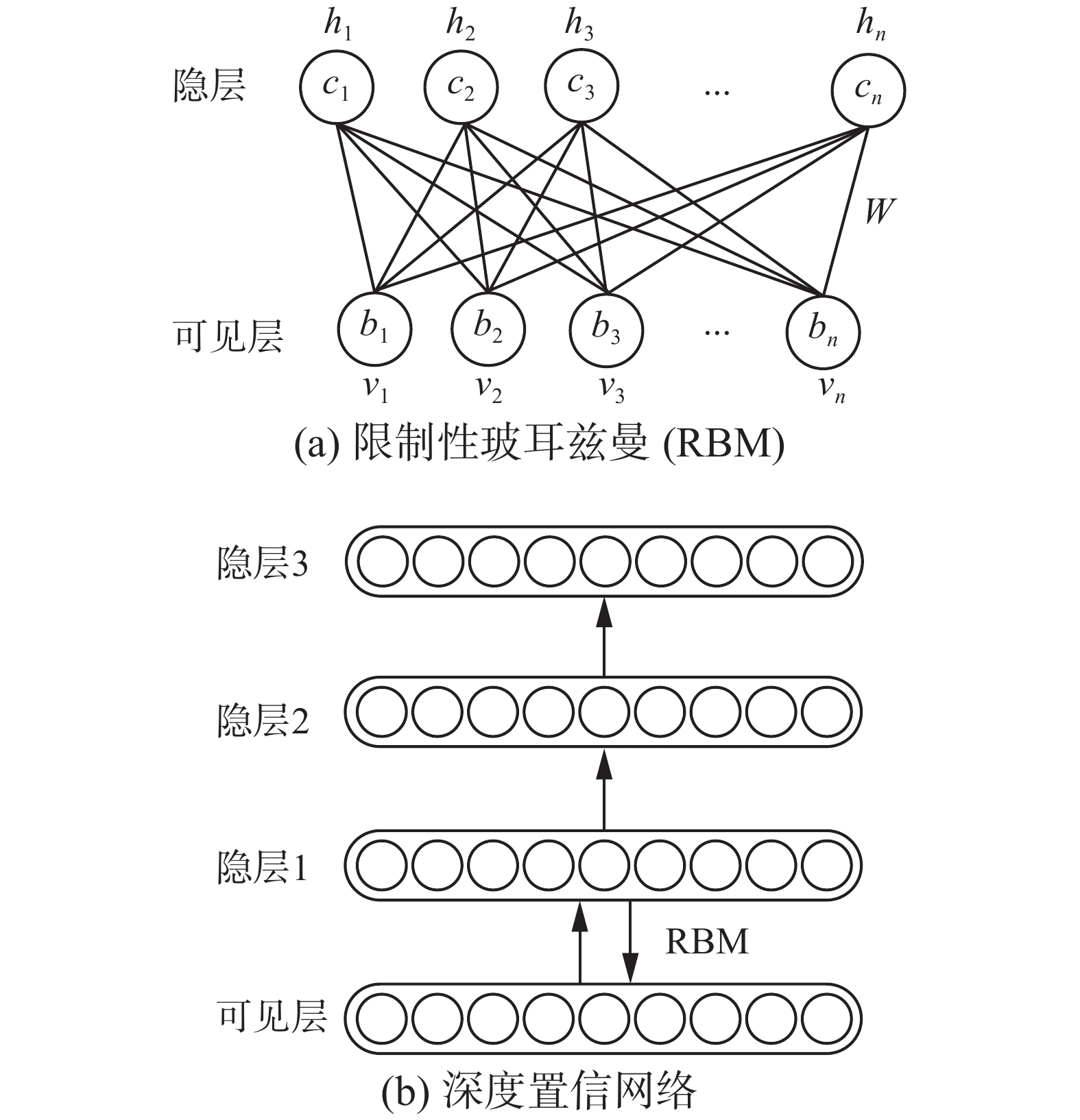
限制性玻耳兹曼机RBM[20, 37-38] 是一种能量模型,通过建立概率分布与能量函数之间的关系,求解能量函数,刻画数据内在的规律。典型的RBM网络结构如图3(a)所示。之所以使用能量模型是因为:很多时候无法直接得到数据的分布形式,根据统计力学的结论,任何概率分布都能用基于能量的模型来描述[39]。通过基于能量的模型,能对数据分布进行建模。在能量模型中,数据的概率分布可由式(1)计算得到:
|
Download:
|
| 图 3 限制性玻耳兹曼机与深度置信网络 Fig. 3 Restricted Boltzmann machine and deep belief network | |
| $ P\left( {x} \right) = \frac{{{{\rm e}^{ - E\left( x \right)}}}}{{\mathop \sum \nolimits^ {{\rm e}^{ - E\left( x \right)}}}} $ | (1) |
式中
| $ E\left( {{v},{h}} \right) = - {{v}^{\rm{T}}}W{h} - {{ b}^{\rm T}}{v} - {{ c}^{\rm{T}}}{h} $ |
式中:
为了达到刻画原数据分布的目的,希望理论的边缘分布
| $ {\rm KL}(q|{\rm{|}}p{\rm{)}} = \mathop \sum \limits_{v \in {\rm{\varOmega }}} q\left( v \right){\rm{ln}}\left( {q\left( v \right)} \right) - \mathop \sum \limits_{v \in {\rm{\varOmega }}} q\left( v \right){\rm{ln}}\left( {p\left( v \right)} \right) $ |
式中:Ω为参数空间;左边第一项表示数据的熵,为常数项;左边第二项可用样本进行估计,即
在深度学习的应用中,自编码机与限制性玻耳兹曼机常常用于参数的预训练。如图3(b)所示,可以将自编码机和限制性玻耳兹曼机堆叠起来构成深度置信网络[41-42]。该网络可以采用逐层训练的方式训练参数,即每轮训练中,输入固定不变,训练网络得到一层的参数与输出,将输出传输到下一层网络中并固定,之后训练得到下一层网络的参数,如此循环直至每一层自编码机与限制性玻耳兹曼机都训练完成。训练完成之后,可以将网络参数保留组成多层感知器进行监督学习任务,使用BP算法对预训练的参数初始值进行微调。这样初始化多层感知器的方式能够将初始值放在一个较好的地方,从而收敛到较好的局部最优解[36]。也有研究表明,预训练能够起到正则化的作用,增强模型的推广能力(泛化性能)[39]。
3.2 卷积神经网络卷积神经网络(convolutional neural network ,CNN)是一种深层前馈型神经网络,最常用于图像领域的监督学习问题,比如图像识别、计算机视觉等。早在1989年,LeCun等[43]就提出了最初的CNN模型,并在之后进行了完善[44],在AlexNet取得2012年ImageNet竞赛冠军之后[25],CNN在图像识别领域几乎成为深度学习的代名词,在其他领域中也得到越来越多的应用。
卷积神经网络通常包含卷积层、降采样层、全连接层与输出层,卷积层和降采样层可以有多个。一个经典卷积神经网络LeNet如图4(a)所示。
|
Download:
|
| 图 4 多种深度神经网络示意图 Fig. 4 Schematics of different deep neural networks structures | |
卷积层的作用是进行特征提取。对于一幅输入图像,一层卷积层中包含多个卷积核,每个卷积核都能与输入图像进行卷积运算产生新的图像,新图像上的每个像素即卷积核所覆盖的一小片区域内图像的一种特征,用多个卷积核分别对图像进行卷积即可提取不同种类的特征。比如,在图4(a)的例子中,C2层中输入为6幅特征图,包含16个卷积核,最终产生了16幅特征图的输出,本层的特征图是上一层提取到的特征图的不同组合。
这样复杂的网络构成,如果直接采用BP算法进行学习将过分复杂,需要适当的设计才能有效地进行学习。卷积层设计背后最重要的思想是稀疏连接与权值共享。稀疏连接即每一个输出特征图的像素都只与上一层特征图的小区域相关。这一方面契合了动物视觉细胞的感受野现象[45],另一方面能够保证特征具有平移不变性,这在图像识别领域是非常重要的。权值共享指每次都使用同样的卷积核遍历整幅输入图像,这可以大大减少参数的数目,起到正则化的作用。对于大多数图像识别问题,如果某一种特征特别重要的话,在全图中任意位置中出现都应该具有判别效力。
降采样层会选取输入特征图的一个小区域,比如图4(a)中S1中即每次选取
CNN最后几层通常会连接几个全连接层,在整幅图像层面进行特征组合与推断,形成利于分类的特征。全连接层中输入与输出的每个节点之间都有相互连接,因此会带来大量的待估计参数。近年来全连接层开始越来越少被使用,比如有研究发现其作用也可以用所谓的1×1卷积核的卷积层替代[46]。卷积神经网络的训练本质上仍然利用梯度的链式传递法则。
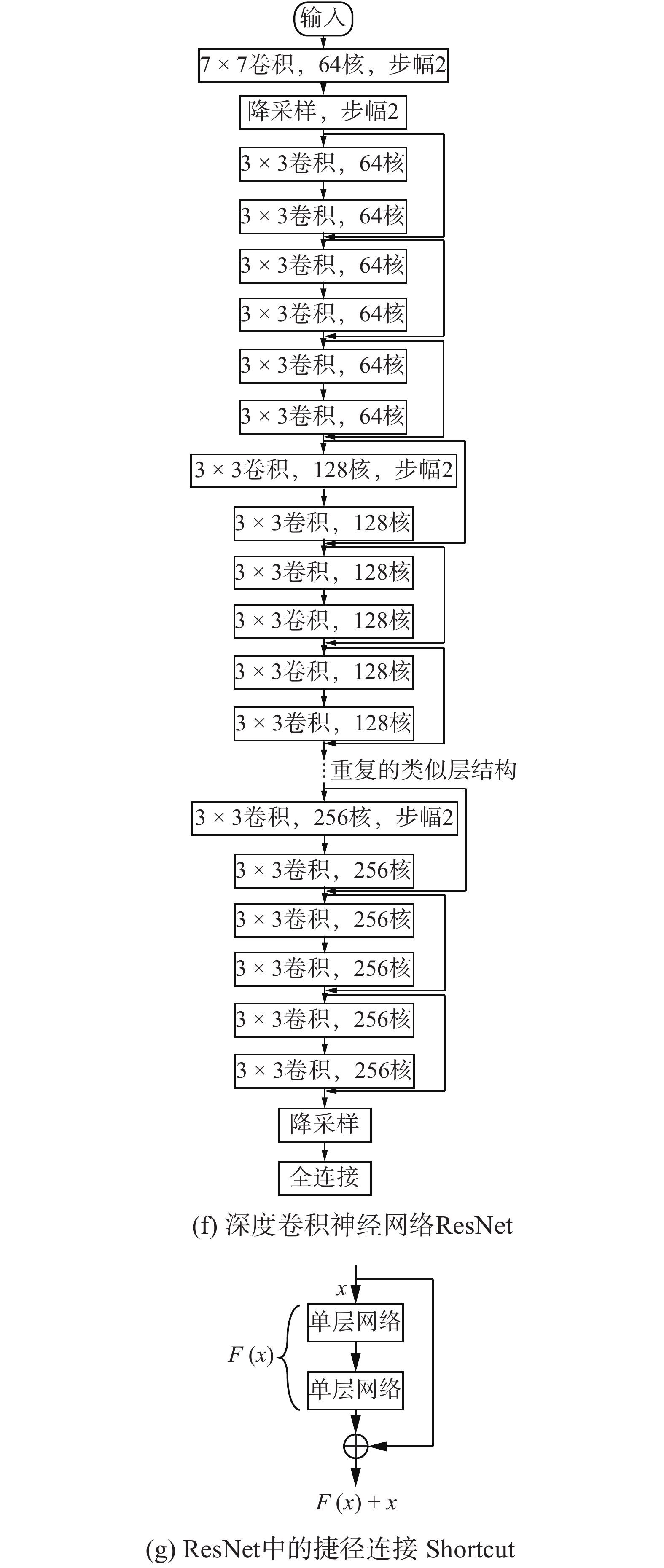
CNN在图像领域获得了极大的成功,也不断有新的发展。在网络架构方面,网络不断变深,理论上越深层的网络能够抓取图像中越抽象的特征,也就拥有更强的学习能力,当然随之而来的训练难度也会变大。2012年,Krizhevsky等[25]提出了AlextNet,包含5层卷积层与3层全连接层,如图4(b)所示。网络中采用了新型激活函数ReLU帮助模型收敛,并提出Dropout方法来减轻过拟合现象。2014年VGGNet[47]出现,如图4(c)所示,网络中只使用较小的卷积核与降采样尺寸,但将网络提升到了最多19层,验证了网络层数加深能够帮助网络取得更好的性能。同年,GoogLeNet[48]网络继承了“网络中网络”思想[49],如图4(d)所示,采用了Inception结构作为基本单元,如图4(e)所示,Inception结构中大量使用1×1的卷积核,极大地减少了参数的数目,比起AlexNet参数从6 000万减少到了500万个,使得训练速度与推广能力都有所增强。另外,网络中加入了3个辅助分类器来提供梯度,减轻梯度消散的现象。2015年,ResNet[50]中引入了输入到输出的直接连接,如图4(g)所示,认为网络学习目标值与输入值的残差比直接学习目标值更为简单,通过引入直接连接解决了深层网络的训练错误率有时反而会比浅层网络的训练错误率高的问题,网络深度最多被提升到了152层,如图4(f)所示。
除了在图像领域的应用,也有学者尝试把其他领域的问题转化为类似图像识别的问题,采用或借鉴CNN方法取得了较好的效果。最为典型的例子是在自然语言处理中的应用。我们可以通过将1个词或者1个字母表示为1个向量的方法将1句话转化为二维的矩阵,然后在二维矩阵上应用卷积神经网络。一般来说,卷积核的宽度选用词向量维数,这样对矩阵进行卷积操作可以看作是从句子中提取关键词语、词组特征,从而可以完成各类自然语言处理任务,比如文本分类[51]、机器翻译[52]、语言模型[53]等。再比如在围棋比赛中,卷积神经网络也被用于提取棋盘特征,以此描述棋盘上双方的局势[26]。总的来说,一些能够转化为二维或者多维矩阵特征,并且局部特征有较强相关性的任务,都比较适合用CNN进行建模。
3.3 循环神经网络循环神经网络(recurrent neural network,RNN)有别于前面所提到的前馈类型的神经网络,其主要目的是对序列型数据进行建模,例如语音识别、语言翻译、自然语言理解、音乐合成等序列数据。这类数据在推断过程中需要保留序列上下文的信息,所以其隐节点中存在反馈环,即当前时刻的隐含节点值不仅与当前节点的输入有关,也与前一时刻的隐含节点值有关。
循环神经网络的结构如图5(a)所示。网络的输入为序列型数据,记为

|
Download:
|
| 图 5 循环神经网络 Fig. 5 Recurrent neural network | |
| $ {h_t} = \sigma \left( {W{h_{t - 1}} + U{x_t}} \right)\; $ |
式中:σ代表非线性单元;W是历史数据对当前输出的权重;U是当前数据对输出的权重。对于不同类型的问题,循环神经网络可以采用不同种类的输出,比如:对于序列的分类问题[57],可以将所有时刻的隐含状态收集到一起作为序列特征输入到分类器中进行分类,如图5(c)所示;而对于序列生成或语言模型问题[56, 58-59],每一时刻都应有相应的输出,如图5(d)。可以将每一时刻的隐含状态作为特征进行分类,即
| $ {o_t} = {\rm{Softmax}}\left( {V{h_t}} \right)\; $ | (2) |
式(2)中Softmax就是罗杰斯特回归在多类问题上的推广形式,Softmax将多分类的输出数值转化为相对概率,使我们更容易对输出进行理解和比较。其定义为:假设有一个数组X,Xi表示X中的第i个元素,那么元素Xi的Softmax值定义为
| $ {S_i} = \frac{{{{\rm{e}}^{{X_i}}}}}{{\sum\limits_{{j}} {{{{{\rm e}}}^{{{{x}}_{{j}}}}}} }} $ |
为了在减少参数数目的同时使循环神经网络能处理不同长度的输入序列,网络中的参数针对输入序列的每个时刻都是相等的,这也使得参数的梯度计算比前馈神经网络略复杂了一些。
循环神经网络的训练,需要使用随时间的反向算法计算参数的梯度[18, 60] ,其本质上仍然利用梯度的链式传递法则。将RNN沿时间展开后,可以视为一个很深层的前馈神经网络,所以存在严重的梯度消散现象[61-63],导致RNN无法学习到数据中的长程依赖关系。
图6(a)为RNN的时间序列展开图,图6(b)为RNN的单元结构图。为了减轻RNN中的梯度消散现象,可以从单元结构与优化两方面着手改进。单元结构方面,长短时记忆模型(long short-term memory,LSTM)[64-66]添加了额外的隐含状态来记忆序列的信息,使用3个门来控制当前时刻的输入对记忆的影响,如图6(c)所示。通过这样的改造,记忆能够更加通畅地在时间序列中传递,从而记住更久远之前的信息。长短时记忆模型被发明之后,也出现了诸多变种[67-68],最实用的是门控循环单元(gated recurrent unit)[69]。门控循环单元合并了长短时记忆模型中的2种隐含状态,如图6(d)所示,将控制门的个数减少到了2个,使得收敛所需的时间有所下降,经过实验验证,门控循环单元相比长短时记忆模型几乎没有性能的损失[68, 70]。改进优化方面,研究表明在参数初始化合适的情况下,循环神经网络也能较好地学习到长程依赖关系[71]。

|
Download:
|
| 图 6 LSTM的结构示意图 Fig. 6 Schematic of LSTM structure | |
上面介绍的循环神经网络只能用于处理输出数据定长的情况。对于某些实际问题,如语言翻译[72]、问答系统[73]等,对给定输入需要给出序列的输出。针对这一类问题,人们提出了seq2seq[74]及encoder-decoder[69]模型。2种模型都使用了2个循环神经网络,一个用于收集输入序列中的信息,将输入序列的信息用向量进行表示,比如用最后1个时刻的隐状态作为输入序列的向量表示,另一个循环神经网络则用于生成序列。每一时刻都要综合输入序列的信息以及已产生序列中的信息来决定下一个单词的概率分布,利用采样决定生成的单词,然后可将生成的单词重新输入网络得到新的概率分布,如此循环即可生成整条序列。
在很多序列相关的问题中,输出往往只与输入的某些片段有较强的联系。比如:在机器翻译问题中,输出单词的最大信息量来自于与输出单词意义相同的词,如将“knowledge is power”翻译为“知识就是力量”,其中“力量”一词之所以被生成完全是从“power”中获取的信息。人们为建模这种关系引入了注意力机制[75-76],即输出序列的每个词都只将注意力放在输入序列的一个区域而不是完整的输入序列中。该机制能够大大提高循环神经网络的效果,被广泛使用于各类序列学习任务中。分级注意记忆(hierarchical attentive memory)[77]进一步将节点组织成二叉树的形式,加快了搜索效率,且能够增强训练数据与测试数据长度不一致情况下的推广能力。
在网络结构方面,双向的循环神经网络[78]使用从前向后以及从后向前2条链对时序数据建模,用于刻画序列的上下文信息而不仅仅是过去时刻的信息。深层循环神经网络[79-80]对循环神经网络进行叠加,将一层循环神经网络的隐含状态序列作为下一层循环神经网络的输入,可以学习到更深层次的特征。
4 深度学习的优化技巧各种深度神经网络已经在大量应用中展现了出色的效果,一些典型的模型和算法已经比较成型并且有一些公开的框架可以使用,这大大方便和加快了各种深度学习方法的应用。但针对一个实际的问题,深度学习的求解过程中存在大量的技巧需要摸索,有效地使用一些技巧能够改善网络的收敛性以及网络的推广能力。
深度学习的参数求解本质上是一个优化问题,不同的优化方法各有优劣[81-83]。常用的优化方法大体上可以按照其收敛性分为一阶优化算法与二阶优化算法。一阶优化算法是以目标函数相对于待优化参数的一阶导数(梯度)作为优化的依据,二阶优化算法则同时考虑了二阶导数信息。
一阶优化算法中最常用的当属以BP算法为代表的梯度下降法及其变种。梯度下降法每轮迭代中都计算参数的梯度,并将参数向负梯度方向移动一段距离来更新参数值。根据每次计算梯度时取用的样本数不同分为梯度下降、随机梯度下降、批量梯度下降等。梯度下降每轮迭代计算所有样本的梯度平均,这样可以保证每次移动都必定能优化目标函数,但梯度计算耗时长。相对地,随机梯度下降每次只选取一个样本计算梯度,速度快而且有一定的跳出局部最优的能力,但目标函数波动剧烈。为了缓解随机梯度下降梯度变化剧烈的问题,人们引入了动量(momentum)机制[84-85]。动量的引入使得计算得到的梯度起到微调参数更新方向的作用,减少了振荡,有利于目标函数的收敛。批量梯度下降法综合了随机梯度下降法与梯度下降法的优点,选取训练集中的一部分计算梯度和,以此平衡计算速度与算法稳定性。
在梯度下降类算法中,学习率(亦称步长)即每一轮学习时参数更新幅度的选择是很关键的一点,学习率过低算法收敛过慢,而学习率过高则容易不收敛。因此,人们研究出一些自适应的梯度下降法,能够在学习过程中根据历史的参数更新信息自动调节学习率,如AdaGrad[86]、RMSProp[87]、AdaDelta[88]、Adam[89]等。
二阶优化算法考虑了目标函数的二阶导数信息,也就是目标函数在当前参数附近的曲率,使得参数的更新方向估计得更加准确,在某些问题上能够求解一阶优化算法不能解决的问题。常用的二阶优化算法包括牛顿法、共轭梯度法、BFGS算法[90]、L-BFGS算法[91]等。二阶优化算法的主要差别体现在Hessian矩阵逆的计算或近似上,文献[82]指出,使用大规模集群并行化计算时,L-BFGS与共轭梯度法能够取得比随机梯度下降更快的收敛速度。文献[92-93]采用不估计Hessian矩阵的二阶优化算法,并在自编码机、循环神经网络上取得了较好的效果。
在优化问题中,参数初始值的选择是很关键的。早期的神经网络一旦结构复杂就无法保证推广性能的一大原因是初始值选取无有效方法,深度置信网络(DBN)等采用非监督学习方法进行参数初始化(即预训练)使得深度神经网络有了较好的实用性[94]。以往常用方法是用均值为0、方差较小的高斯分布或均匀分布来进行初始化,这样的初始化方法无法保证变量的方差在传播过程中相等,会导致变量值逐渐增大或逐渐减小。当变量值都很小时,都集中在sigmoid函数的线性区内,也就失去了层数增加的意义;而当变量值都很大时,变量都处于饱和区内,梯度减小不利于收敛。Glorot等[95]给出了一种方法,在使用sigmoid或是tanh作为激活函数时,能够确保证变量的方差在前向传播与反向传播的过程中都近似相等。He等[96]做了类似的推导,给出了ReLU作为激活函数时,深度神经网络的参数初始化形式。
激活函数的选择对模型的性能、收敛速度都有很大的影响[97]。早期被广泛使用的激活函数是sigmoid函数,由于其在两侧的导数趋近于0,被称为软饱和函数[98]。软饱和性会使得网络的梯度难以向回传播,当网络的后几层很快收敛到饱和区后,网络的前几层仍然停留在随机初始化的状态而得不到训练,造成网络的推广性能较差[95, 99]。tanh同样是一种软饱和的激活函数,相比sigmoid函数,由于其输出的均值比sigmoid函数更接近于0,随机梯度下降速度能够更趋近于自然梯度(natural gradient)[100],故其收敛速度更快[101]。深度神经网络直接监督式训练的主要突破点是采用了ReLU函数[25, 102],它至今仍是使用最广泛的激活函数,ReLU函数在x>0处导数恒定为1,故梯度不会衰减,从而缓解梯度消散现象,ReLU还能使神经网络具有稀疏表达的能力,可以提升网络性能。但其在x<0处梯度硬饱和,权重无法更新,存在神经元死亡现象。由于ReLU的均值恒定大于0,故会影响网络的收敛性[103-104]。为了解决神经元死亡问题,人们发展了PReLu[96]、ELU[104]等ReLU的推广算法,算法在x<0区域内也有梯度,且输出均值更接近于0,可以使网络具有更好的收敛性能。Maxout[105]使用一个小的神经网络作为非线性单元,理论上在隐含节点数目足够的情况下能够近似任意地激活函数,且其基本不存在神经元死亡现象,但为此需要付出更大的参数数目与计算量。
过拟合或过学习是影响神经网络方法推广能力的主要原因,对于深度神经网络,舍弃(Dropout)法[25]是一种常用的避免过拟合方法。Dropout是指,在每轮训练过程中,随机地让网络的部分隐含节点不工作,即以概率p将隐含节点的输出置零,这些隐含节点的参数也暂时不更新。这种舍弃训练也属于一种正则化方法。这样每轮训练的网络结构都是不同的,最终进行分类时使用整个网络进行分类,类似于取了不同分类器的平均,与集成学习中的bagging自举聚合(bootstrap aggregating)方法有异曲同工之妙。使用舍弃训练使网络避免某些神经元共同激活,削弱了神经元之间的联合适应性,可以增强推广能力[106]。也有观点认为,舍弃训练可以理解为数据增强(data augmentation)的一种形式[107],因为其易于实现,且可应用于各类不同的网络结构中,故被广泛使用。舍弃训练会降低网络的有效节点数目,因此应用时网络的宽度也需要相应增加,这使得在样本数目极少时表现不佳[108]。另外,应用舍弃训练也会使得网络的训练时间上升为原来的2~3倍。除了舍弃训练方法,还有一些类似的方法或改进方法,比如:DropConnect[109]方法随机地将隐含节点的一些输入连接置零,理论上可以获得更好的模型平均效果,自适应舍弃(adaptive dropout)[110]方法能够根据上一层的输出结果寻找最优的舍弃率,等等。
2015年,人们提出了批量归一化(batch normalization)算法[111],使用该方法可以选择较大的初始学习率使网络快速收敛,并且可以提高网络的推广性能,某种程度上可以代替舍弃训练等正则化方法。算法的核心思想很简单,机器学习的本质是学习数据的分布,归一化能够使训练数据与测试数据分布相同,从而可以提升推广性能,而且在批量梯度下降中,归一化能够使得模型不必去适应学习每轮不同的输入数据分布,从而提升训练速度。但在训练一般的深度神经网络时,只有输入层能满足分布相同的条件,经过非线性变换之后,每层隐含层的输入分布就不再稳定,会受到之前数层的参数影响。为了解决这一问题,使神经网络的每一层输入都拥有相同的分布,引入Batch Normalization方法,即
| $ \widehat {{x_i}} = \frac{{{x_i} - {\mu _x}}}{{\sqrt {\sigma _x^2} }}\; $ |
式中,均值
| $ {y_i} = \gamma \widehat {{x_i}} + \beta \; $ |
这样一次从
类似的这些优化策略与技巧,都是研究者针对不同的数据和实验情况提出的,面对一个特定的实际问题,并没有办法事先确定哪种策略是最优策略。但是,了解这些策略和技巧的思路与原理,将有利于在面对实际问题时更快找到适当的策略,或者研究出新的策略。
5 深度学习的理论分析深度学习在很多应用中取得成功,一方面离不开深度神经网络模型的设计,另一方面离不开如上所举例的一些经验技巧,虽然研究人员对其中的原理提出了一定的解释,但大都缺乏严格的理论支持。有一些理论研究对部分学习算法的收敛性质进行了证明,但对于深度学习模型的样本表示能力和学习推广能力的研究,大多停留在描述和实验说明阶段,这也是当前人们学习和研究深度学习方法遇到的一个重要困难。
与此相比,一些浅层的机器学习方法则在理论上有较多研究成果,在一定条件下它们的性能有严格的理论保障。以支持向量机为例,它可以看作是对简单的线性分类器的一种扩展,通过最大化分类间隔获得小样本情况下最佳的推广能力,通过一层核函数变换实现非线性,围绕这一方法有一套比较严格的数学理论和证明,这就是著名的“统计学习理论”[23]。而对于各种深度学习模型在很多领域取得的出色应用效果,现存的数学理论尚不能很好地给出定量解释,包括常用的复杂性理论[112-114]。
关于“对抗样本”的研究也促进了对理论可解释性的关注,图7是一个对抗样本示例[115],通过在一个熊猫图像上加入微弱噪声,形成一幅新的图像,这幅图像在人眼看来还是熊猫,但是神经网络却以99.3%的置信度认为是长臂猿。如果缺乏理论解释,人们就会担心黑盒模式下的深度学习会存在对抗样本,导致系列风险。因此对深度学习进行系统的理论分析是势在必行的,近年来投入相关研究的研究人员也开始逐渐增加。

|
Download:
|
| 图 7 对抗样本示例 Fig. 7 An adversarial example | |
一般地,要从理论上分析一个机器学习算法,通常需要考虑3个主要的问题:推广性问题、表示性问题及优化问题。推广性问题讨论的是经验风险和期望风险之间的关联性,也就是,在什么情况下,训练误差足够小就能够保证对未来测试样本的预测错误也足够小。对于神经网络,经典的分析理论及统计学习理论都给出了相似的结论[116-120]:只要样本的数量相对于网络规模足够大,就能保证神经网络具有一定的推广性。由于样本量和计算能力的限制,统计学习理论的研究重点是在有限样本下如何通过控制学习模型的容量(capacity)来达到高的推广能力。而深度学习则突破了这一限制,考虑如何通过大规模的样本来达到高的推广能力。为了达到相同的推广能力,规模越大的神经网络需要的样本量也更多。这些认识只是定性的推断,深度神经网络的结构和规模、训练样本的数量和质量、学习机器的推广能力这三者之间的关系,需要从理论上进行更系统和深入地研究。对于一些难以获得足够样本的问题,人们提出了用相关问题的样本进行迁移学习(transfer learning)的方法,为提高机器学习性能开辟了新的思路[121],这已经成为机器学习领域的一个重要研究方向,而这种引入其他数据的学习过程也使得理论分析的难度进一步加大。
为什么要采用深层神经网络,这是机器学习的表示性问题。对于多层感知器神经网络的表示性,20世纪就已经有理论研究:几乎任何函数都能够用适当规模的人工神经网络模型进行表示[122]。这个结论指出,无论多么复杂的分类或者回归模型都能够被特定的神经网络所表示,只要所用的神经网络具备足够多的非线性节点以及足够多的隐层数。随后,Barron[123]提出了一个定理,进一步证明了单隐层的非线性神经网络能够用来表示几乎任何的函数。这个定理相当于告诉人们,深度更深的神经网络并不会比浅层的神经网络具有更强的函数表示性。换言之,多隐层神经网络所能表示的函数单隐层神经网络也能表示,只要单隐层节点的数目足够多。但是,关于表示性的结论只是说明存在一定的网络结构能够实现任意复杂的函数映射,但并不意味着这样的结构能够或者容易得到。有研究指出,浅层神经网络的表示能力和深层神经网络的表示能力依然有所不同,这种不同体现在表示性和参数数目的相对关系上[124-125]。
浅层神经网络规模的扩展主要是横向的,也就是增加网络每一层的节点数量;而深层神经网络的规模扩展主要是纵向的,也就是,增加网络的层数。神经网络规模的增加必然会使网络的参数数量增加,而参数的增加同时也会提高神经网络的表示能力。但是,纵向和横向分别增加相同数量的参数对网络的表示性的提升是不同的,通常以纵向方式增加参数会获得更多的表示性提升[126],结合了对自然认知系统的理解CNN、RNN等深层神经网络,可以在提升表示性的同时减少参数数目和增加参数的可学习性。这是深层神经网络在参数的表示效率上所具有的优势,同时也是深度网络在很多应用中取得比浅层模型更优效果的一个重要原因。
优化问题的理论解释是当前深度学习面临的另一个主要问题。众多的训练技巧都能够很好地帮助提升神经网络的优化结果,但是现在仍然无法很好地从理论上来进行解释,而面对一个新的实际问题时使用什么样的技巧更奏效也往往需要大量试错。表示性问题关心的是,是否存在所要优化的目标的最优解;而优化问题关心的是,是否能学习到这样的最优解,以及如何能学习到这样的最优解。存在最优解并不代表就一定能通过优化方法找到,特别是对于非凸的优化问题。迭代优化方法的优化过程一般和初始值有关,而初始值一般都是随机生成的,因此这类优化方法找到的解也会具有一定的随机性。而训练神经网络一般采用的都是迭代的方法,为了保证能够以一个比较大的概率获得满意的优化结果,除了要应用上述的训练技巧外,还需要配合恰当的网络结构,当然具体的结构需要根据具体的问题而定。
根据上面的讨论,要获得较好的优化结果,需要从3方面入手:神经网络结构的设计、优化算法及初始化方法。近来出现了许多理论结合实验的方法来对这3方面进行分析与讨论[127-136],人们期望在深度学习展示出大量成功应用实例的同时,也能够在理论上对它们的优势和适用范围有越来越深入的认识。
6 总结与展望对传统的机器学习来说,在一些复杂问题上,构造特征的过程是很困难的,但是很多传统机器学习方法的性能在一定条件下有严格的理论保障。深度学习能够自动地提取特征,并将简单特征逐渐组合成更复杂的特征,通过这些复杂特征来解决问题,在很多领域取得了出色的应用效果。但是,现存的数学理论尚不能很好地给出定量解释,包括推广性问题、表示性问题及优化问题。未来理论研究的进步将会进一步加快深度学习的发展,更好地指引深度学习的应用。
本文是笔者结合自己工作尝试对深度学习进行的一个综述和讨论,这一领域包含的内容很多,近年来发展非常快,加之笔者水平所限,本文的讨论难免挂一漏万,望同行学者指正。由于深度学习模型的复杂度较高且需要用大量样本进行计算,对存储和计算资源的要求都很高,很多运算都需要用GPU加速等方式来实现,国内外学者和产业界也纷纷推出了多种深度学习的软硬件平台。由于篇幅限制,本文未对此方面进行介绍和讨论。
| [1] |
MCMAHAN H B, HOLT G, SCULLEY D, et al. Ad click prediction: a view from the trenches[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago, USA, 2013: 1222–1230.
( 0) 0)
|
| [2] |
GRAEPEL T, CANDELA J Q, BORCHERT T, et al. Web-scale Bayesian click-through rate prediction for sponsored search advertising in Microsoft’s bing search engine[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel, 2010: 13–20.
( 0) 0)
|
| [3] |
HE Xinran, PAN Junfeng, JIN Ou, et al. Practical lessons from predicting clicks on ads at Facebook[C]//Proceedings of the 8th International Workshop on Data Mining for Online Advertising. New York, USA, 2014: 1–9.
( 0) 0)
|
| [4] |
CHEN Tianqi, HE Tong. Higgs boson discovery with boosted trees[C]//Proceedings of the 2014 International Conference on High-Energy Physics and Machine Learning. Montreal, Canada, 2014: 69–80.
( 0) 0)
|
| [5] |
GOLUB T R, SLONIM D K, TAMAYO P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring[J]. Science, 1999, 286(5439): 531-537. DOI:10.1126/science.286.5439.531 ( 0) 0)
|
| [6] |
POON T C W, CHAN A T C, ZEE B, et al. Application of classification tree and neural network algorithms to the identification of serological liver marker profiles for the diagnosis of hepatocellular carcinoma[J]. Oncology, 2001, 61(4): 275-283. DOI:10.1159/000055334 ( 0) 0)
|
| [7] |
AGARWAL D. Computational advertising: the linkedin way[C]//Proceedings of the 22nd ACM International Conference on Information & Knowledge Management. San Francisco, USA, 2013: 1585–1586.
( 0) 0)
|
| [8] |
MCCULLOCH W S, PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. Bulletin of mathematical biology, 1990, 52(1/2): 99-115. ( 0) 0)
|
| [9] |
HEBB D O. The organization of behavior: a neuropsychological theory[M]. New York: John Wiley and Sons, 1949: 12–55.
( 0) 0)
|
| [10] |
ROSENBLATT F. The perceptron−a perceiving and recognizing automaton[R]. Ithaca, NY: Cornell Aeronautical Laboratory, 1957.
( 0) 0)
|
| [11] |
MINSKY M L, PAPERT S A. Perceptrons: an introduction to computational geometry[M]. Cambridge: MIT Press, 1969: 227−246.
( 0) 0)
|
| [12] |
HAUGELAND J. Artificial intelligence: the very idea[M]. Cambridge: MIT Press, 1989: 3–11.
( 0) 0)
|
| [13] |
MCCORDUCK P. Machines who think: a personal inquiry into the history and prospects of artificial intelligence[M]. 2nd ed. Natick: A. K. Peters/CRC Press, 2004: 2−12.
( 0) 0)
|
| [14] |
HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the national academy of sciences of the United States of America, 1982, 79(8): 2554-2558. DOI:10.1073/pnas.79.8.2554 ( 0) 0)
|
| [15] |
LE CUN Y. Learning process in an asymmetric threshold network[M]//BIENENSTOCK E, SOULIÉ F, WEISBUCH G. Disordered Systems and Biological Organization. Berlin, Heidelberg: Springer, 1986.
( 0) 0)
|
| [16] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 ( 0) 0)
|
| [17] |
PARKER D B. Learning-logic[R]. Technical Report TR-47. Cambridge, MA: Center for Computational Research in Economics and Management Science, Massachusetts Institute of Technology, 1985.
( 0) 0)
|
| [18] |
RUMELHART D E, MCCLELLAND J L. Readings in congnitive science[M]. San Francisco: Margan Kaufmann, 1988: 399−421.
( 0) 0)
|
| [19] |
KOHONEN T. Self-organization and associative memory[M]. 3rd ed. Berlin Heidelberg: Springer-Verlag, 1989: 119−155.
( 0) 0)
|
| [20] |
SMOLENSKY P. Information processing in dynamical systems: foundations of harmony theory[M]//RUMELHART D E, MCCLELLAND J L. Parallel Distributed Processing, Vol. 1. Cambridge: MIT Press, 1986: 194–281.
( 0) 0)
|
| [21] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. DOI:10.1023/A%3A1022627411411 ( 0) 0)
|
| [22] |
BOSER B E, GUYON I M, VAPNIK V N. A training algorithm for optimal margin classifiers[C]//Proceedings of the 5th Annual Workshop on Computational Learning Theory. Pittsburgh, Pennsylvania, USA, 1992: 144–152.
( 0) 0)
|
| [23] |
张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32-42. ZHANG Xuegong. Introduction to statistical learning theory and support vector machines[J]. Acta automatica sinica, 2000, 26(1): 32-42. DOI:10.3969/j.issn.1003-8930.2000.01.008 (  0) 0)
|
| [24] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 ( 0) 0)
|
| [25] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3098997 ( 0) 0)
|
| [26] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 ( 0) 0)
|
| [27] |
TANG Yichuan. Deep learning using linear support vector machines[J]. arXiv: 1306.0239, 2015.
( 0) 0)
|
| [28] |
BOURLARD H, KAMP Y. Auto-association by multilayer perceptrons and singular value decomposition[J]. Biological cybernetics, 1988, 59(4/5): 291-294. ( 0) 0)
|
| [29] |
HINTON G E, ZEMEL R S. Autoencoders, minimum description length and Helmholtz free energy[C]//Proceedings of the 6th International Conference on Neural Information Processing Systems. Denver, Colorado, USA, 1993: 3–10.
( 0) 0)
|
| [30] |
SCHWENK H, MILGRAM M. Transformation invariant autoassociation with application to handwritten character recognition[C]//Proceedings of the 7th International Conference on Neural Information Processing Systems. Denver, Colorado, USA, 1994: 991–998.
( 0) 0)
|
| [31] |
HINTON G E, MCCLELLAND J L. Learning representations by recirculation[C]//Proceedings of 1987 International Conference on Neural Information Processing Systems. Denver, USA, 1987: 3
( 0) 0)
|
| [32] |
SCHÖLKOPF B, PLATT J, HOFMANN T. Efficient learning of sparse representations with an energy-based model[C]//Proceedings of 2006 Conference Advances in Neural Information Processing Systems. Vancouver, Canada, 2007: 1137–1144.
( 0) 0)
|
| [33] |
RANZATO M, HUANG Fujie, BOUREAU Y L, et al. Unsupervised learning of invariant feature hierarchies with applications to object recognition[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA, 2007: 1–8.
( 0) 0)
|
| [34] |
VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland, 2008: 1096–1103.
( 0) 0)
|
| [35] |
RIFAI S, VINCENT P, MULLER X, et al. Contractive auto-encoders: explicit invariance during feature extraction[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue, Washington, USA, 2011: 833−840.
( 0) 0)
|
| [36] |
BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy layer-wise training of deep networks[C]//Proceedings of the 19th International Conference on Neural Information Processing Systems. Vancouver, Canada, 2006: 153–160.
( 0) 0)
|
| [37] |
SALAKHUTDINOV R, MNIH A, HINTON G. Restricted Boltzmann machines for collaborative filtering[C]//Proceedings of the 24th International Conference on Machine Learning. Corvalis, Oregon, USA, 2007: 791–798.
( 0) 0)
|
| [38] |
HINTON G E. A practical guide to training restricted Boltzmann machines[M]//MONTAVON G, ORR G B, MÜLLER K R. Neural Networks: Tricks of the Trade. 2nd ed. Berlin, Heidelberg: Springer, 2012: 599–619.
( 0) 0)
|
| [39] |
LECUN Y, CHOPRA S, HADSELL R, et al. A tutorial on energy-based learning[M]//BAKIR G, HOFMANN T, SCHÖLKOPF B, et al. Predicting Structured Data. Cambridge: MIT Press, 2006: 45−49.
( 0) 0)
|
| [40] |
LEE H, EKANADHAM C, NG A Y. Sparse deep belief net model for visual area V2[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada, 2007: 873–880.
( 0) 0)
|
| [41] |
HINTON G E. Deep belief networks[J]. Scholarpedia, 2009, 4(5): 5947. DOI:10.4249/scholarpedia.5947 ( 0) 0)
|
| [42] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 ( 0) 0)
|
| [43] |
LE CUN Y, BOSER B, DENKER J S, et al. Handwritten digit recognition with a back-propagation network[C]//Proceedings of the 2nd International Conference on Neural Information Processing Systems. Denver, USA, 1989: 396–404.
( 0) 0)
|
| [44] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 ( 0) 0)
|
| [45] |
HUBEL D H, WIESEL T N. Receptive fields and functional architecture of monkey striate cortex[J]. The journal of physiology, 1968, 195(1): 215-243. DOI:10.1113/jphysiol.1968.sp008455 ( 0) 0)
|
| [46] |
SPRINGENBERG J T, DOSOVITSKIY A, BROX T, et al. Striving for simplicity: the all convolutional net[J]. arXiv: 1412.6806, 2014.
( 0) 0)
|
| [47] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. arXiv: 1409.1556, 2014.
( 0) 0)
|
| [48] |
SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA, 2015: 1–9.
( 0) 0)
|
| [49] |
LIN Min, CHEN Qiang, YAN Shuicheng. Network in network[J]. arXiv: 1312.4400, 2013.
( 0) 0)
|
| [50] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 770–778.
( 0) 0)
|
| [51] |
ZHANG Xiang, ZHAO Junbo, LECUN Y. Character-level convolutional networks for text classification[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada, 2015: 649–657.
( 0) 0)
|
| [52] |
GEHRING J, AULI M, GRANGIER D, et al. Convolutional sequence to sequence learning[J]. arXiv: 1705.03122, 2017.
( 0) 0)
|
| [53] |
PHAM N Q, KRUSZEWSKI G, BOLEDA G. Convolutional neural network language models[C]//Proceedings of 2016 Conference on Empirical Methods in Natural Language Processing. Austin, Texas, USA, 2016: 1153–1162.
( 0) 0)
|
| [54] |
HARRIS D M, HARRIS S J. Digital design and computer architecture[M]. 2nd ed. San Francisco: Morgan Kaufmann Publishers Inc., 2013: 123−125.
( 0) 0)
|
| [55] |
MIKOLOV T, CHEN Kai, CORRADO G, et al. Efficient estimation of word representations in vector space[J]. arXiv: 1301.3781, 2013.
( 0) 0)
|
| [56] |
GOLDBERG Y, LEVY O. word2vec Explained: deriving Mikolov et al.’s negative-sampling word-embedding method[J]. Arxiv: 1402.3722, 2014.
( 0) 0)
|
| [57] |
TANG D, QIN B, LIU T. Document modeling with gated recurrent neural network for sentiment classification[C]//Conference on Empirical Methods in Natural Language Processing. Lisbon, Portugal, 2015: 1422–1432.
( 0) 0)
|
| [58] |
SUTSKEVER I, MARTENS J, HINTON G. Generating text with recurrent neural networks[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue, Washington, USA, 2011: 1017–1024.
( 0) 0)
|
| [59] |
GRAVES A. Generating sequences with recurrent neural networks[J]. arXiv: 1308.0850, 2013.
( 0) 0)
|
| [60] |
WERBOS P J. Generalization of backpropagation with application to a recurrent gas market model[J]. Neural networks, 1988, 1(4): 339-356. DOI:10.1016/0893-6080(88)90007-X ( 0) 0)
|
| [61] |
PASCANU R, MIKOLOV T, BENGIO Y. On the difficulty of training recurrent neural networks[C]//Proceedings of the 30th International Conference on Machine Learning. Atlanta, Georgia, USA, 2013: 1310−1318.
( 0) 0)
|
| [62] |
BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE transactions on neural networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181 ( 0) 0)
|
| [63] |
HOCHREITER S, BENGIO Y, FRASCONI P. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies[M]//KOLEN J F, KREMER S C. A Field Guide to Dynamical Recurrent Networks. New York: Wiley-IEEE Press, 2001: 6−8.
( 0) 0)
|
| [64] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 ( 0) 0)
|
| [65] |
GERS F A, SCHMIDHUBER J, CUMMINS F. Learning to forget: continual prediction with LSTM[J]. Neural computation, 2000, 12(10): 2451-2471. DOI:10.1162/089976600300015015 ( 0) 0)
|
| [66] |
GERS F A, SCHRAUDOLPH N N, SCHMIDHUBER J. Learning precise timing with LSTM recurrent networks[J]. The journal of machine learning research, 2003, 3: 115-143. ( 0) 0)
|
| [67] |
GERS F A, SCHMIDHUBER J. Recurrent nets that time and count[C]//Proceedings of 2000 IEEE-INNS-ENNS International Joint Conference on Neural Networks. Como, Italy, 2000: 3189.
( 0) 0)
|
| [68] |
GREFF K, SRIVASTAVA R K, KOUTNIK J, et al. LSTM: a search space odyssey[J]. IEEE transactions on neural networks and learning systems, 2017, 28(10): 2222-2232. DOI:10.1109/TNNLS.2016.2582924 ( 0) 0)
|
| [69] |
CHO K, VAN MERRIENBOER B, GULCEHRE C, ET AL. Learning phrase representations using RNN encoder-decoder for statistical machine translation[J]. arXiv: 1406.1078, 2014.
( 0) 0)
|
| [70] |
JOZEFOWICZ R, ZAREMBA W, SUTSKEVER I. An empirical exploration of recurrent network architectures[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille, France, 2015: 2342–2350.
( 0) 0)
|
| [71] |
LE Q V, JAITLY N, HINTON G E. A simple way to initialize recurrent networks of rectified linear units[J]. arXiv: 1504.00941, 2015.
( 0) 0)
|
| [72] |
WU Yonghui, SCHUSTER M, CHEN Zhifeng, et al. Google’s neural machine translation system: bridging the gap between human and machine translation[J]. arXiv: 1609.08144, 2016.
( 0) 0)
|
| [73] |
YIN Jun, JIANG Xin, LU Zhengdong, et al. Neural generative question answering[J]. arXiv: 1512.01337, 2016.
( 0) 0)
|
| [74] |
SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 3104–3112.
( 0) 0)
|
| [75] |
MNIH V, HEESS N, GRAVES A, et al. Recurrent models of visual attention[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 2204–2212.
( 0) 0)
|
| [76] |
BAHDANAU D, CHO K, BENGIO Y. Neural machine translation by jointly learning to align and translate[J]. arXiv: 1409.0473, 2016.
( 0) 0)
|
| [77] |
ANDRYCHOWICZ M, KURACH K. Learning efficient algorithms with hierarchical attentive memory[J]. arXiv: 1602.03218, 2016.
( 0) 0)
|
| [78] |
SCHUSTER M, PALIWAL K K. Bidirectional recurrent neural networks[J]. IEEE transactions on signal processing, 1997, 45(11): 2673-2681. DOI:10.1109/78.650093 ( 0) 0)
|
| [79] |
PASCANU R, GULCEHRE C, CHO K, et al. How to construct deep recurrent neural networks[J]. arXiv: 1312.6026, 2014.
( 0) 0)
|
| [80] |
HERMANS M, SCHRAUWEN B. Training and analyzing deep recurrent neural networks[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, USA, 2013: 190–198.
( 0) 0)
|
| [81] |
LE Q V, NGIAM J, COATES A, et al. On optimization methods for deep learning[C]//Proceedings of the 28th International Conference on International Conference on Machine Learning. Bellevue, Washington, USA, 2011: 265–272.
( 0) 0)
|
| [82] |
RUDER S. An overview of gradient descent optimization algorithms[J]. arXiv: 1609.04747, 2016.
( 0) 0)
|
| [83] |
YOUSOFF S N M, BAHARIN A, ABDULLAH A. A review on optimization algorithm for deep learning method in bioinformatics field[C]//Proceedings of 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences. Kuala Lumpur, Malaysia, 2016: 707–711.
( 0) 0)
|
| [84] |
QIAN Ning. On the momentum term in gradient descent learning algorithms[J]. Neural networks, 1999, 12(1): 145-151. DOI:10.1016/S0893-6080(98)00116-6 ( 0) 0)
|
| [85] |
SUTSKEVER I, MARTENS J, DAHL G, et al. On the importance of initialization and momentum in deep learning[C]//Proceedings of the 30th International Conference on International Conference on Machine Learning. Atlanta, USA, 2013: 1139−1147.
( 0) 0)
|
| [86] |
DUCHI J, HAZAN E, Singer A Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. The journal of machine learning research, 2011, 12: 2121-2159. ( 0) 0)
|
| [87] |
TIELEMAN T, HINTON G E. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude[C]//COURSERA: Neural Networks for Machine Learning. 2012.
( 0) 0)
|
| [88] |
ZEILER M D. ADADELTA: an adaptive learning rate method[J]. arXiv: 1212.5701, 2012.
( 0) 0)
|
| [89] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[J]. arXiv: 1412.6980, 2014.
( 0) 0)
|
| [90] |
FLETCHER R. Practical methods of optimization[M]. New York: John Wiley and Sons, 2013: 110−133.
( 0) 0)
|
| [91] |
NOCEDAL J. Updating quasi-Newton matrices with limited storage[J]. Mathematics of computation, 1980, 35(151): 773-782. DOI:10.1090/S0025-5718-1980-0572855-7 ( 0) 0)
|
| [92] |
MARTENS J. Deep learning via Hessian-free optimization[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel, 2010: 735–742.
( 0) 0)
|
| [93] |
KIROS R. Training neural networks with stochastic hessian-free optimization[J]. arXiv: 1301.3641, 2013.
( 0) 0)
|
| [94] |
ERHAN D, BENGIO Y, COURVILLE A, et al. Why does unsupervised pre-training help deep learning?[J]. The journal of machine learning research, 2010, 11: 625-660. ( 0) 0)
|
| [95] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. Sardinia, Italy, 2010, 9: 249–256.
( 0) 0)
|
| [96] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 1026–1034.
( 0) 0)
|
| [97] |
XU Bing, WANG Naiyan, CHEN Tianqi, et al. Empirical evaluation of rectified activations in convolutional network[J]. arXiv: 1505.00853, 2015
( 0) 0)
|
| [98] |
GULCEHRE C, MOCZULSKI M, DENIL M, et al. Noisy activation functions[C]//Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York, USA, 2016: 3059–3068.
( 0) 0)
|
| [99] |
LECUN Y, BOTTOU L, ORR G B, et al. Efficient BackProp[M]//ORR G B, MÜLLER K R. Neural Networks: Tricks of the Trade. Berlin, Heidelberg: Springer, 1998: 9–50.
( 0) 0)
|
| [100] |
AMARI S I. Natural gradient works efficiently in learning[J]. Neural computation, 1998, 10(2): 251-276. DOI:10.1162/089976698300017746 ( 0) 0)
|
| [101] |
LECUN Y, BOSER B, DENKER J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541 ( 0) 0)
|
| [102] |
NAIR V, HINTON G E. Rectified linear units improve restricted Boltzmann machines[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel, 2010: 807–814.
( 0) 0)
|
| [103] |
CLEVERT D A, UNTERTHINER T, HOCHREITER S. Fast and accurate deep network learning by exponential linear units (ELUs)[J]. arXiv: 1511.07289, 2016.
( 0) 0)
|
| [104] |
LI Yang, FAN Chunxiao, LI Yong, et al. Improving deep neural network with multiple parametric exponential linear units[J]. Neurocomputing, 2018, 301: 11-24. DOI:10.1016/j.neucom.2018.01.084 ( 0) 0)
|
| [105] |
GOODFELLOW I J, WARDE-FARLEY D, MIRZA M, et al. Maxout networks[C]//Proceedings of the 30thInternational Conference on Machine Learning. Atlanta, USA, 2013: 1319–1327.
( 0) 0)
|
| [106] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[J]. arXiv: 1207.0580, 2012.
( 0) 0)
|
| [107] |
BOUTHILLIER X, KONDA K, VINCENT P, et al. Dropout as data augmentation[J]. arXiv: 1506.08700, 2016.
( 0) 0)
|
| [108] |
SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The journal of machine learning research, 2014, 15(1): 1929-1958. ( 0) 0)
|
| [109] |
WAN Li, ZEILER M, ZHANG Sixin, et al. Regularization of neural networks using DropConnect[C]//Proceedings of the 30th International Conference on Machine Learning. Atlanta, USA, 2013: 1058–1066.
( 0) 0)
|
| [110] |
BA L J, FREY B. Adaptive dropout for training deep neural networks[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, USA, 2013: 3084–3092.
( 0) 0)
|
| [111] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[J]. arXiv: 1502.03167, 2015.
( 0) 0)
|
| [112] |
DANIELY A, LINIAL N, SHALEV-SHWARTZ S. From average case complexity to improper learning complexity[C]//Proceedings of the 46th Annual ACM Symposium on Theory of Computing. New York, USA, 2014: 441–448.
( 0) 0)
|
| [113] |
DANIELY A, SHALEV-SHWARTZ S. Complexity theoretic limitations on learning DNF’s[J]//JMLR: Workshop and Conference Proceedings. 2016: 1–16.
( 0) 0)
|
| [114] |
DANIELY A. Complexity theoretic limitations on learning halfspaces[C]//Proceedings of the 48th Annual ACM Symposium on Theory of Computing. Cambridge, USA, 2016: 105–117.
( 0) 0)
|
| [115] |
GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples[J]. arXiv: 1412.6572, 2015.
( 0) 0)
|
| [116] |
ANTHONY M, BARTLETT P L. Neural network learning: theoretical foundations[M]. New York: Cambridge University Press, 2009: 286−295.
( 0) 0)
|
| [117] |
BARTLETT P L. The sample complexity of pattern classification with neural networks: the size of the weights is more important than the size of the network[J]. IEEE transactions on information theory, 1998, 44(2): 525-536. DOI:10.1109/18.661502 ( 0) 0)
|
| [118] |
BAUM E B, HAUSSLER D. What size net gives valid generalization?[J]. Neural computation, 1989, 1(1): 151-160. DOI:10.1162/neco.1989.1.1.151 ( 0) 0)
|
| [119] |
HARDT M, RECHT B, SINGER Y. Train faster, generalize better: Stability of stochastic gradient descent[J]. arXiv: 1509.01240, 2015.
( 0) 0)
|
| [120] |
NEYSHABUR B, TOMIOKA R, SREBRO N. Norm-based capacity control in neural networks[C]//Proceedings of the 28th Conference on Learning Theory. Paris, France. 2015, 40: 1–26.
( 0) 0)
|
| [121] |
PRATT L Y. Discriminability-based transfer between neural networks[C]//Proceedings of the 5th International Conference on Neural Information Processing Systems. Denver, USA, 1992: 204–211.
( 0) 0)
|
| [122] |
HORNIK K, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366. DOI:10.1016/0893-6080(89)90020-8 ( 0) 0)
|
| [123] |
BARRON A R. Universal approximation bounds for superpositions of a sigmoidal function[J]. IEEE transactions on information theory, 1993, 39(3): 930-945. DOI:10.1109/18.256500 ( 0) 0)
|
| [124] |
DELALLEAU O, BENGIO Y. Shallow vs. deep sum-product networks[C]//Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada, Spain, 2011: 666–674.
( 0) 0)
|
| [125] |
BIANCHINI M, SCARSELLI F. On the complexity of neural network classifiers: a comparison between shallow and deep architectures[J]. IEEE transactions on neural networks and learning systems, 2014, 25(8): 1553-1565. DOI:10.1109/TNNLS.2013.2293637 ( 0) 0)
|
| [126] |
ELDAN R, SHAMIR O. The power of depth for feedforward neural networks[C]//JMLR: Workshop and Conference Proceedings. 2016: 1–34.
( 0) 0)
|
| [127] |
ANDONI A, PANIGRAHY R, VALIANT G, et al. Learning polynomials with neural networks[C]//Proceedings of the 31st International Conference on Machine Learning. Beijing, China, 2014: 1908–1916.
( 0) 0)
|
| [128] |
ARORA S, BHASKARA A, GE Rong, et al. Provable Bounds for Learning Some Deep Representations[C]//Proceedings of the 31st International Conference on Machine Learning. Beijing, China, 2014: 584–592.
( 0) 0)
|
| [129] |
BRUNA J, MALLAT S. Invariant scattering convolution networks[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(8): 1872-886. DOI:10.1109/TPAMI.2012.230 ( 0) 0)
|
| [130] |
CHOROMANSKA A, HENAFF M, MATHIEU M, et al. The loss surfaces of multilayer networks[C]//Proceedings of the 18th International Conference on Artificial Intelligence and Statistics. San Diego, USA, 2015, 38: 192–204.
( 0) 0)
|
| [131] |
GIRYES R, SAPIRO G, BRONSTEIN A M. Deep neural networks with random Gaussian weights: a universal classification strategy?[J]. IEEE transactions on signal processing, 2016, 64(13): 3444-3457. DOI:10.1109/TSP.2016.2546221 ( 0) 0)
|
| [132] |
LIVNI R, SHALEV-SHWARTZ S, SHAMIR O. On the computational efficiency of training neural networks[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 855–863.
( 0) 0)
|
| [133] |
NEYSHABUR B, SALAKHUTDINOV R, SREBRO N. Path-SGD: path-normalized optimization in deep neural networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada, 2015: 2422–2430.
( 0) 0)
|
| [134] |
SAFRAN I, SHAMIR O. On the quality of the initial basin in overspecified neural networks[C]//Proceedings of the 33rd International Conference on Machine Learning. New York, USA, 2016: 774−782.
( 0) 0)
|
| [135] |
SEDGHI H, ANANDKUMAR A. Provable methods for training neural networks with sparse connectivity[J]. arXiv: 1412.2693, 2015.
( 0) 0)
|
| [136] |
DANIELY A, FROSTIG R, SINGER Y. Toward deeper understanding of neural networks: the power of initialization and a dual view on expressivity[C]//Proceedings of the 30th Conference on Neural Information Processing Systems 29. Barcelona, Spain, 2016: 2253–2261.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


