近年来，随着人工智能的迅速发展，标记学习成为其重点的研究领域之一。其中单标记学习将每个示例由一个特征向量和一个标记来描述；而多标记学习^[1]则将一个示例同时分配给多个标记，即每个对象由一个特征向量和一个二元标记向量来表示。多标记学习的这种示例表达方式更加契合现实世界对象存在的多义性，因此多标记学习成为模式识别与标记学习的重点研究课题之一，并已成功应用于文本分类^[2-3]、图像识别^[4]、生物学习^[5]和情感分析^[6]等领域。

目前，在多标记学习问题中，诸多学者已研究并提出多种多标记学习算法，而这些方法大致可以分为2类，即问题转换法和算法适应法。其中问题转换法是将多标记学习任务转换为一个或者多个相应单标记学习任务，然后再通过传统单标记学习方法进行处理，典型算法包括BR^[4]、LP^[7]、PPT^[8]和RAKEL^[9]等。而算法适应法通过扩展特定单标记学习算法，修改其约束条件从而可以直接处理多标记学习任务，例如ML-KNN^[10]、MLNB^[11]、Rank-SVM^[12]和ML-RBF^[13]等。而这些适应型算法就是将最近邻(k-nearest neighbors，KNN)、朴素贝叶斯(naive bayes，NB)、支持向量机(support vector machine，SVM)和径向基函数(radial basis function，RBF)神经网络等算法适应于多标记数据。这些改造的算法在多标记学习中取得了不错的效果。但其中BR、LP、ML-KNN、MLNB和Rank-SVM等算法因本身特点所限，导致其时间消耗较大。

为了解决分类算法时间消耗大的问题，近年间，部分学者提出了多种基于极限学习机(extreme learning machine，ELM)的多标记学习算法。ELM是由Huang等^[14]提出的是一种单隐藏层前馈神经网络(single-hidden layer feedforward neural networks，SLFNs)算法，该算法具有模型设计简单、运行速度快和泛化性能高等特点，在多标记学习中具有良好的性能表现。为提高ELM分类模型的稳定性及鲁棒性，邓万宇等^[15]提出正则极限学习机算法(regularized extreme learning machine，RELM)，对损失函数施加L2惩罚以避免分类模型出现过拟合现象。随后，Miche等^[16]提出TROP-ELM(tikhonov-regularized optimally pruned extreme learning machine，TROP-ELM)算法，将L1和L2惩罚级联使用，对隐藏层神经元施加L1惩罚，对回归权重施加L2惩罚，以达到删减神经元个数和稳定数值的作用。但这些算法都需要随机初始化权值和偏置，使得算法对于随机值敏感，导致算法稳定性不高。为处理这一问题，Huang等^[17]提出使用核函数映射特征空间以代替传统隐藏层随机特征映射函数，使得该算法可以直接处理回归问题、单标记和多标记分类。基于ELM的多标记分类算法，ER等^[18]和Sun等^[19]利用ELM提出一种高速多标记分类器模型，将ELM适应于多标记数据集，分类效果较为理想。Zhang等^[20]提出了一种多层ELM-RBF算法，改变传统ELM算法的单隐藏层策略，使用多隐藏层来实现多标记分类，在分类精度上也取得了不错的效果。Luo等^[21]首次采用核ELM来处理多标记问题，以保证分类算法的稳定性。对于多标记学习与正则化理论结合部分。Han等^[22]提出将多标记学习作为弹性网络惩罚的最小二乘优化问题，并不使用L1惩罚进行稀疏表示。本文创作的思想来源于此，且已有研究表明在多标记数据集中特征之间存在着相关性和冗余性，此时将RELM原L2正则项用弹性网络正则代替，既保证模型稳定性也可对模型进行稀疏性表示。

结合上述ELM算法和正则化理论，本文首次将弹性网络正则结合核极限学习机(kernel extreme learning machine，KELM)应用到多标记分类中，使用弹性网络正则约束核KELM，提出基于弹性网络极限学习机的多标记学习算法(multi-label learning algorithm of elastic net kernel extreme learning machine，ML-EKELM)。该算法通过KELM映射特征空间，然后对损失函数添加弹性网络^[23]正则项，最后采用坐标下降法^[24]迭代求解多标记目标优化问题。KELM与弹性网络的结合提高了算法鲁棒性，保证了模型稀疏性，提供了一种基于ELM解决多标记问题的新途径。通过对比现有基于ELM的先进多标记算法和经典多标记算法，验证了本文算法的有效性和可靠性。

1 基本理论研究 1.1 极限学习机理论

传统神经网络算法需要较多的网络参数设置，在求解最优解时很有可能出现局部最优解，而无法得到全局最优解。而极限学习机是一种高效且具有优化学习算法的单隐层前馈神经网络，求解时只需设置隐藏层节点数，并随机初始化权值和偏置就可求解出全局最优解。ELM求解单隐层前馈神经网络，可分为2个阶段：随机特征映射和线性参数求解。

在对ELM两个阶段进行分析之前，需要做出以下形式化定义：设有N个随机样本 $ \left\{ {\left( {{{{X}}_i},{{{Y}}_i}} \right)\left| \right.} \right.$ $\left. {i = 1,2, \cdots ,N} \right\}$ ，其中特征空间与标记空间可分别表示为 $ {{{X}}_i} = {\left[ {{x_{i1}}{x_{i2}} \cdots{x_{in}}} \right]^{\rm{T}}}$ ， $ {{{Y}}_i} = {\left[ {{y_{i1}}{y_{i2}} \cdots {y_{i{\rm{m}}}}} \right]^{\rm{T}}}$ ，则对于具有L个隐藏节点的单隐藏层神经网络形式化定义为：

${f_{\rm{L}}}({{{X}}_j}) = \sum\limits_{i = 1}^L {{{{\beta}} _i}} {g_i}({{{X}}_j})$

(1)

式中： $ {{{\beta }}_i} = {\left[ {{\beta _{i1}}{\beta _{i2}} \cdots {\beta _{im}}} \right]^{\rm{T}}}$ 表示输出权值；g_i表示第i个隐藏节点的输出，实质为激活函数，并可表示为：

$ {g_i}\left( {{{{X}}_j}} \right) = g\left( {{{{w}}_i} \cdot {{{X}}_j} + {b_i}} \right) $

(2)

式中： $ {{{w}}_i} = {\left[ {{w_{i1}}{w_{i2}} \cdots {w_{im}}} \right]^{\rm{T}}}$ 为输入权值；b_i表示第i个隐藏神经元的偏置；∙表示为点积。通常式(1)用来建模回归，对于分类问题可使用sigmoid函数来限制输出值的范围，从而达到分类效果。

以上为ELM的第1阶段即随机特征映射，对于第2阶段的线性参数求解，通过最小化平方误差的近似误差来求解连接隐藏层和输出层的权值β。可表示为：

$ \mathop {\min }_{{\beta }} \left\| {{{H\beta }} - {{{Y}}}} \right\|^2 $

(3)

式中H为隐藏层输出矩阵，即

$ {{H}} = \left[ {\begin{array}{*{20}{c}} {h\left( {{{{x}}_1}} \right)}\\ {h\left( {{{{x}}_2}} \right)}\\ \vdots \\ {h\left( {{{{x}}_N}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{h_1}\left( {{{{x}}_1}} \right)}&{{h_2}\left( {{{{x}}_1}} \right)}& \cdots &{{h_L}\left( {{{{x}}_1}} \right)}\\ {{h_1}\left( {{{{x}}_2}} \right)}&{{h_2}\left( {{{{x}}_2}} \right)}& \cdots &{{h_L}\left( {{{{x}}_2}} \right)}\\ \vdots & & \vdots \\ {{h_1}\left( {{{{x}}_N}} \right)}&{{h_2}\left( {{{{x}}_N}} \right)}& \cdots &{{h_L}\left( {{{{x}}_N}} \right)} \end{array}} \right] $

(4)

Y为训练标记矩阵：

$ {{Y}} = \left[ {\begin{array}{*{20}{c}} {{{y}}_1^{\rm T}}\\ {{{y}}_2^{\rm T}}\\ \vdots \\ {{{y}}_N^{\rm T}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_{11}}}& {{y_{12}}}& \cdots &{{y_{1m}}}\\ {{y_{21}}}& {{y_{22}}}& \cdots &{{y_{2m}}}\\ \vdots & & \vdots \\ {{y_{N1}}}&{{y_{N2}}}& \cdots &{{y_{Nm}}} \end{array}} \right] $

(5)

通过式(1)、式(3)，最小二乘解为

$ {\hat {{\beta }}} = {{{H}}^{\dagger} }{{Y}} $

(6)

式中H^†表示H的Moore-Penrose广义逆矩阵，表示为

$ {\rm{s}}{\rm{.t.}}\;\;\;{{{H}}^{\dagger} } = \left\{ {\begin{array}{*{20}{c}} {{{\left( {{{{H}}^{\rm T}}{{H}}} \right)}^{ - 1}}{{{H}}^{\rm T}},\;{{{H}}^{\rm T}}{{H}}{\text{非奇异}}}\\ {{{{H}}^{\rm T}}{{\left( {{{H}}{{{H}}^{\rm T}}} \right)}^{ - 1}},\;{{H}}{{{H}}^{\rm T}}{\text{非奇异}}} \end{array}} \right. $

(7)

最终求出的 $ {\hat {{\beta }}}$ 即可以预测未知标记，表示为

$ {\hat {{Y}}} = {{H}}{{\hat {{\beta }}}} $

(8)

1.2 正则化理论

在机器学习中，偏差(bias)与方差(variance)共同影响模型的准确率。高偏差容易导致模型欠拟合(unfitting)，高方差则会导致模型过拟合(overfitting)。通常，解决高偏差可选择使用更为复杂的模型或增加模型参数来降低偏差值，但这就会导致模型过拟合情况发生。而正则化理论是解决高方差或避免训练模型过拟合的有效方法之一，在机器学习领域被广泛使用。

通过正则化方式，可以降低模型的复杂度，避免可能的过度拟合。近年来，研究者提出了多种适合机器学习的正则化方法，其中L2正则化、L1正则化和弹性网络正则化等使用较为普遍。这些正则化方法详细描述如下：

1) L2正则(Ridge Regression)

L2正则化模型(也称为岭回归)是在最小化损失函数后添加正则项 $ {\textit{λ}}\left\| {{\beta }} \right\|_2^2$ ，其中参数 $ {\textit{λ}} \in \left[ {0, + \infty } \right]$ ，起到降低权重的作用，最终得到目标函数：

$ {L_2} = \mathop {\min }_{{\beta }} \left\| {{{H\beta }} - {{Y}}} \right\|_2^2 + {\textit{λ}}\left\| {{\beta }} \right\|_2^2 $

(9)

2) L1正则(Lasso)

L1正则化模型(也称为Lasso模型)则是在最小化损失函数添加正则项 $ {\textit{λ}}{\left\| {{\beta }} \right\|_1}$ ，其中 $ {\textit{λ}} \in \left[ {0, + \infty } \right]$ ，而Lasso最大的特点在于产生稀疏权值矩阵，构造出稀疏模型已达到特征选择的作用，最终目标函数为

$ {L_1} = \mathop {\min }_{{\beta }} \left\| {{{H\beta }} - {{Y}}} \right\|_2^2 + {\textit{λ}}\left\| {{\beta }} \right\|_1 $

(10)

3) L2&L1正则(Elastic Net)

弹性网络正则化是一种结合L1正则与L2正则的各自优点的新型正则化方法，即在最小化损失函数添加正则项 $ {\textit{λ}}\left( {\alpha {{\left\| {{\beta }} \right\|}_1} + \left( {1 - \alpha } \right)\left\| {{\beta }} \right\|_2^2} \right)$ ，其中 $ {\textit{λ}} \in \left[ {0, + \infty } \right]$ ， $ \alpha \in \left[ {0,1} \right]$ ，目标函数定义为

$ \begin{array}{l} {L_{{\rm{ElasticNet}}}} = \mathop {\min }_{{\beta }} \left\| {{{H\beta }} - {{Y}}} \right\|_2^2 +\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\textit{λ}}\left( {\alpha {{\left\| {{\beta }} \right\|}_1} + \left( {1 - \alpha } \right)\left\| {{\beta }} \right\|_2^2} \right) \end{array} $

(11)

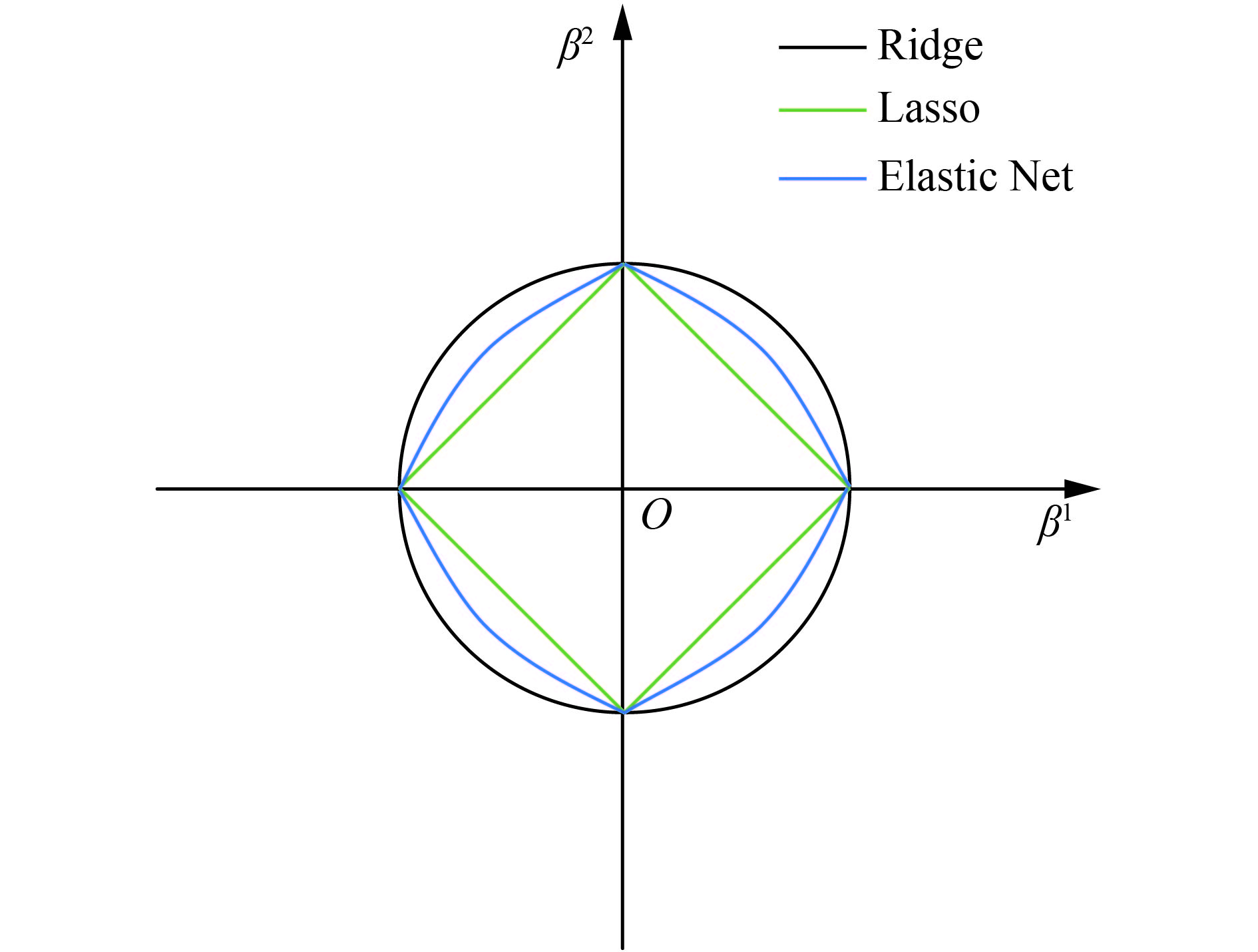
通过式(11)可知：当α=0时，Elastic Net即为L2正则；当α=1时，Elastic Net即为L1正则；当 $ \alpha \in \left( {0,1} \right)$ 时，Elastic Net将保留L2和L1正则各自特点，达到弹性2种正则的作用。根据这一特点给出3种正则化的二维图像描述，如图1所示。

2 基于弹性网络核极限学习机算法 2.1 基于ELM的多标记学习

传统单标记学习无法对于真实世界对象多语义性、概念复杂性进行有效处理，且无法满足目前机器学习的高要求，由此建立了多标记学习框架可以解决这一问题。该框架通过对任意一个对象，进行一个特征向量的描述，根据特征向量尽可能将对象进行合适的类别标记和精准分类^[25]。假定含有N个样本的多标记数据集，X为n维的示例空间Rⁿ，Y为m类标记空间，则在多标记学习中，给定数据集 $ { D} = \left\{ {\left( {{{{x}}_1},{{{Y}}_1}} \right),\left( {{{{x}}_2},{{{Y}}_2}} \right), \cdots ,\left( {{{{x}}_n},{{{Y}}_n}} \right)} \right\}$ ，其中 $ {{{x}}_i} \in {{X}}$ 是一个示例， $ {{{Y}}_i} \in {{Y}}$ 是一组标记集合 $ \left\{ {{{y}}_1^{\left( i \right)},{{y}}_2^{\left( i \right)}, \cdots ,{{y}}_m^{\left( i \right)}} \right\}$ ，且 $ {{y}}_m^{\left( i \right)} \in {{Y}}$ ，可得到映射关系 $ f:{{X}} \to {2^{{Y}}}$ 。

根据多标记学习的目标，同时结合ELM学习模型，ELM的随机映射函数 $ h\left( {{x_i}} \right)$ 将x_i从输入空间映射到L维的特征空间，Y_i∈R^m为输出标记集合。根据式(4)、(5)和(8)，可得多标记ELM的输出函数f_l(x)为：

$ {f_l}\left( {{x}} \right) = {{H\beta }} = {\left[ {\begin{array}{*{20}{c}} {h\left( {{{{x}}_1}} \right)}\\ {h\left( {{{{x}}_2}} \right)}\\ \vdots \\ {h\left( {{{{x}}_N}} \right)} \end{array}} \right]_{N \times L}}\left[ {\begin{array}{*{20}{c}} {{{\beta }}_1^{\rm{T}}}\\ {{{\beta }}_2^{\rm{T}}}\\ \vdots \\ {{{\beta }}_L^{\rm{T}}} \end{array}} \right] $

(12)

将式(9)和(12)结合即为正则ELM，即RELM算法，该算法添加L2正则来提高原始ELM算法的稳定性和泛化性能，同时有效避免过拟合，目标函数表示为：

$ \mathop {\min } _{{\beta }} {L_{{\rm{RELM}}}} = \frac{1}{2}{\left\| {{{\beta }}} \right\|^2} + \frac{C}{2}\mathop \sum _{i = 1}^N \left\| {{{{\xi }}_i}} \right\|^2 $

(13)

式中C为正则化系数；由式(6)、(7)和(13)求解目标函数，可得输出权值β：

$ {{\beta }} = {{{H}}^{\rm T}}{\left( {\frac{{{I}}}{C} + {{H}}{{{H}}^{\rm T}}} \right)^{ - 1}}{{Y}} $

(14)

式中I为L维单位矩阵。这样最终多标记学习目标函数表示为：

$ {f_l}\left( {{x}} \right) = {{H\beta }} = {{H}}{{{H}}^{\rm T}}{\left( {\frac{{{I}}}{C} + {{H}}{{{H}}^{\rm T}}} \right)^{ - 1}}{{Y}} $

(15)

通过式(14)得到训练集的输出权值，再通过随机映射函数h(x)将测试集的特征向量映射，最终多标记预测结果可由式(15)得出。这种基于正则化ELM的多标记学习算法，不仅在预测精度上取得了不错的效果，并且求解速度也具有较大优势。

2.2 弹性核极限学习机的多标记学习算法

基于L2正则能够有效控制训练模型过拟合到某个特征上，即假设参数分布服从高斯分布以达到稳定模型的作用；而基于L1正则能够约束目标方程稀疏性进而实现特征选择，即假设参数分布服从拉普拉斯分布以保证稀疏化模型。简单来说，即L2正则只能让某些参数逼近于0，而L1正则可以使得某些参数等于0。基于以上正则化特点分析，结合这2种正则的弹性网络可以实现正则和稀疏双重作用^[23]。本节将使用Elastic Net替换原有RELM中的L2正则，首次运用到多标记学习中。

设多标记数据集 $ {{D}} = \left\{ {{{{x}}_i},{{{Y}}_i}} \right\}_{i = 1}^N$ ，其中x_i∈Rⁿ是n维特征向量，Y_i∈R^m为输出标记集合。则基于L2正则RELM替换为Elastic Net，通过式(11)将式(13)改写为：

$ \begin{split} & \mathop {\min } _{{\beta }} {L_{\rm{E}}} = \frac{{\rm{C}}}{2}\mathop \sum _{i = 1}^N {\left\| {{{{\xi }}_i}} \right\|^2} +{\textit{λ}} \left( {{R_\alpha }\left( {{\beta }} \right)} \right)\\ & {R_\alpha }\left( {{\beta }} \right) = {\rm{\alpha }}{\left\| \beta \right\|_1} + \left( {1 - \alpha } \right)\left\| \beta \right\|_2^2\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{{{\xi }}_i} = {{{Y}}_i} - {f_l}\left( {{{{x}}_i}} \right),i = 1,2, \cdots ,N \end{split} $

(16)

由于传统ELM算法需设置隐藏层节点数，并且需初始随机权值和偏置，易受随机值的影响导致计算结果不稳定，采用核ELM则可以解决这一问题。根据式(4)和(12)，当映射函数h(x)未知时，即引入核矩阵(本文采用RBF核)：

$ \begin{split} & {{H}} = {{\bf{\varOmega }}_{{\rm{ELM}}}}:{{\bf{\varOmega }}_{{\rm{ELM}}\left( {i,j} \right)}} = K\left( {{{{x}}_i},{{{x}}_j}} \right)\\ & \;\;\;K\left( {{{{x}}_i},{{{x}}_j}} \right) = {\rm{exp}}\left( { - \gamma {{\left\| {{{{x}}_i} - {{{x}}_j}} \right\|}^2}} \right) \end{split} $

(17)

式中γ一般取值为1。结合式(3)、(12)和(17)，式(16)可进一步改写为带有RBF核映射的目标函数：

$ \mathop {\min } _{{\beta }} {L_{\rm{E}}} = \frac{{\rm{C}}}{2}{\left\| {{{Y}} - {{\bf{\varOmega }}_{{\rm{ELM}}}}{{\beta }}} \right\|^2} + \lambda {R_\alpha }\left( {{\beta }} \right) $

(18)

由于Elastic Net本身结构特点，具有L1正则导致存在不可导点，无法使用类似于BP神经网络(back propagation)的梯度下降法(gradient descent)或传统ELM将神经网络转化为最小二乘法。坐标下降法^[26]则可以解决这一问题，因其是一种非梯度优化算法，无需求导目标函数，只需通过坐标方向搜寻最小值，符合弹性网络求解的要求，因此本文采用坐标下降法对于弹性网络核极限学习机进行目标求解。根据式(18)求解最小化目标，即

$ \mathop {{\rm{min}}}\limits_{{\beta }} \frac{C}{2}\mathop \sum _{i = 1}^N {\left( {{{{Y}}_i} - \mathop \sum _{j = 1}^N {{\bf{\varOmega }}_{{\rm{ELM}}\left( {i,j} \right)}}{{{\beta }}_j}} \right)^2} + \lambda {{ R}_\alpha }\left( {{\beta }} \right) $

(19)

通过坐标下降法，式(19)的更新公式可表示为：

$ {{{\beta }}_j} \leftarrow \frac{{S{{\left( {\mathop \sum \limits_{i = 1}^N {{\bf{\varOmega }}_{{\rm{ELM}}\left( {i,j} \right)}}\left( {{{{Y}}_i} - {\tilde {{Y}}}_i^{\left( j \right)}} \right),{\textit{λ}} \alpha } \right)}_ + }}}{{1 + \lambda \left( {1 - \alpha } \right)}} $

(20)

式中： $ {{\tilde {{Y}}}_i^{\left( j \right)}}$ 为拟合值； $ {{{{Y}}_i}}-{{\tilde {{Y}}}_i^{\left( j \right)}}$ 为β_j的部分残差；S是软阈值算子(soft-thresholding)^[27]，用于处理L1惩罚。文献[28]给出详细求解算法，最后对于L2惩罚进行比例收缩。其中S详细定义为：

$ \begin{split} & S\left( {\delta ,\gamma } \right) \equiv {\rm{sign}}\left( \delta \right){\left( {\left| \delta \right| - \gamma } \right)_ + } = \\ & \left\{ {\begin{array}{*{20}{c}} {\delta - \gamma ,\;\;\;\delta > 0\;{\text{且}}\;\gamma < \left| \delta \right|}\\ {\delta + \gamma ,\;\;\;\delta < 0\;{\text{且}}\;\gamma < \left| \delta \right|}\\ {0,\;\;\;\;\;\;\;\gamma \geqslant \left| \delta \right|\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. \end{split} $

(21)

在训练集中通过坐标下降法求出输出权值矩阵β，设x_j^*为测试数据第j个示例的特征向量，则多标记预测结果可以表示为

$ {f_l}\left( {x_j^{*}} \right) = {{\bf{\varOmega }}_{{\rm{ELM}}\left( {i,j} \right)}}{{\beta }} $

(22)

式中： $ {{\bf{\varOmega }}_{{\rm{ELM}}\left( {i,j} \right)}}$ 表示将训练集全部特征向量与测试集特征向量共同使用式(17)的RBF核函数映射，最后提出算法具体步骤如算法1所示。

算法1　基于弹性网络核极限学习机的多标记学习算法(ML-EKELM)。

输入　训练数据集 $ { D} = \left\{ {{{{x}}_i},{{{Y}}_i}} \right\}_{i = 1}^N$ ，测试数据集 $ {{ D}^{*}} =$ $\left\{ {{{x}}_j^{*}} \right\}_{j = 1}^M$ ，RBF核参数γ，正则化参数λ、α，最大迭代次数Q；

输出　测试数据集预测标记Y^*。

训练training set D

for training set D

step 1: compute training data kernel matrix Ω_train according to Eq. (17);

step 2: calculate the output weight β;

for i =1 to Q

update output weight β according to Eq. (20) and Eq. (21)

end for

end for

测试testing set D^*

for testing set D^*

step 1: compute training and testing data kernel matrix Ω_test according to Eq. (17);

step 2: get predicted result f_l(x^*) according to Eq. (22)

end for

return predicted testing data label set Y^*= $ \left\{ {y_j^*\left| {{f_l}\left( {x_j^*} \right) > 0} \right.,} \right.$ $ \left. j = 1,2, \cdots ,M \right\}$ 。

3 实验方案及结果分析 3.1 实验数据描述

为验证本文算法的有效性，特选取了Yeast Gene^[12]、Scene^[4]、Yahoo Web Pages^[10](包含11个子数据集)等13个数据集。其中Yeast Gene包含2 417个样本，训练数据集有1 500个样本，测试数据集有917个样本，每个样本包含103个属性值，所有的样本大致有14种类别属性，每个样本对应的平均标记数为4.24。Scene数据集由2 407张图片组成，人工手动标记图片6类标记，平均每张图片有1.24±0.44个类标记，特征向量维度为294维，其中1 211个训练集和1 196个测试集。雅虎网页数据集是从雅虎网站收集，包括11个版块(“Arts”、“Business”、“Computers”等)，各数据子集特征数在400~1 100之间，各数据子集中包含2 000个训练集以及3 000个测试集，详细信息如表1所示。

3.2 多标记评价指标

对于多标记学习，传统单标记评价指标例如Accuracy、Precision和Recall都无法直接对多标记学习算法进行指标评价。为有效验证算法综合性能，本文将使用5种多标记通用评价指标进行算法评价，评价指标包括：Hamming Loss、One-Error、Coverage、Ranking Loss和Average Precision^[1]。

设多标记分类器为h(∙)，预测函数 $ f\left( { \cdot , \cdot } \right)$ ，排序函数rank_f。多标记数据集 $ {{D}} = \left\{ {\left( {{x_i},{Y_i}} \right)\left| {1 \leqslant i \leqslant n} \right.} \right\}$ 。上述5种评价指标HL、OE、CV、RL和AP形式化定义如下：

$ {\rm H{L}_{\rm{D}}}\left( h \right) = \frac{1}{n}\mathop \sum _{i = 1}^n \frac{1}{{\left| Y \right|}}\left| {h\left( {{x_i}} \right)\Delta {Y_i}} \right| $

(23)

式中： $ \Delta $ 表示两个集合之间的对称差。海明损失是评估对象标记被错误分类标记的次数情况，正确的标记被错误预测情况。当HL_D(h)=0时为最好的情况，即HL_D(h)越小，h(∙)的性能越高。

$ {\rm O{E}_{\rm{D}}}\left( f \right) = \frac{1}{n}\mathop \sum _{i = 1}^n \left[ {\left[ {\arg {\rm{ma}}{{\rm{x}}_{y \in Y}}f\left( {{x_i},y} \right)} \right] \notin {Y_i}} \right] $

(24)

1-错误率是评估对象最高排位标记并未正确标记的次数情况。当OE_D(f )=0时为最好的情况，即OE_D(f )越小，f的性能越高。

$ {\rm C{V}_{\rm{D}}}\left( f \right) = \frac{1}{n}\mathop \sum _{i = 1}^n {\rm{ma}}{{\rm{x}}_{y \in {Y_i}}}{\rm{ran{k}}}_f\left( {{x_i},y} \right) - 1 $

(25)

覆盖率是评估对象标记序列中所需标记数达到覆盖全部标记，即CV_D(f )越小，f的性能越高。

$ \begin{split} & {\rm R{L}_{\rm{D}}}\left( f \right) = \frac{1}{n}\mathop \sum _{i = 1}^n \frac{1}{{\left| {{{ Y}_i}} \right|\left| {{{\bar { Y}}_i}} \right|}}\Big|\Big\{ ({y_i},{y_2})|f({x_i},{y_1}) \leqslant \\ & \;\;\;\;\;\;\;\;\left. {\left. {f\left( {{x_i},{y_2}} \right),\left( {{y_1},{y_2}} \right) \in {{ Y}_i} \times {{\bar { Y}}_i}} \right\}} \right| \end{split} $

(26)

排序损失是评估对象非属标记的排位高于所属标记的次数情况。当RL_D(f )=0时为最好情况，即RL_D(f )越小，f的性能越高。

$ {\rm A{P}_{\rm{D}}}\left( f \right) = \frac{1}{n}\mathop \sum _{i = 1}^n \frac{1}{{\left| {{{ Y}_i}} \right|}}\mathop \sum _{y \in {{ Y}_i}} \frac{{\left| {\left\{ {{y^{'\left| {ran{k_f}\left( {{x_i},y'} \right) \leqslant ran{k_f}\left( {{x_i},y} \right),y' \in {Y_i}} \right.}}} \right\}} \right|}}{{{\rm{ran{k}}}_f\left( {{x_i},y} \right)}} $

(27)

平均精度是评估在特定标记y∈Y_i排列的正确标记的平均分数。当AP_D(f )=1时为最好情况，即AP_D(f )越大，f的性能越高。

3.3 实验环境及实验方案

对比实验代码均在Matlab2016a中运行，硬件环境Intel® Core^TM i5-7500 3.4 GHz CPU，8 GB内存；操作系统为Windows 10。为了验证算法的可靠性和有效性，算法选择多标记的5种常用评价指标，分别是：Hamming Loss、One Error、Coverage、Ranking Loss和Average Precision。通过评价指标来综合衡量各算法的性能，评估各算法的性能。实验中将5种评价指标分别简写为：HL↓、OE↓、CV↓、RL↓和AP↑。其中↑表示指标数值越高越好，↓表示指标数值越低越好。对比实验算法采用ML-KELM^[21]、RELM^[15]、ELM^[18]3种基于ELM的多标记算法，以此来验证本文提出的ML-EKELM算法较目前已提出基于ELM的多标记算法的优势，同时对比ML-RBF^[13]、ML-KNN^[10]2种经典的多标记算法。

考虑算法对比验证的可行性和准确性，减少随机误差的产生，各测试算法在一个数据集中做10次实验，最终将10次实验得到的5种评价指标求出平均值(mean)和标准差(standard deviation)。在每个评价指标数据下标注排位情况，如ML-EKELM₍₁₎表示在某个数据集ML-EKELM算法最为优秀，同时用黑体表示，并在雅虎网页数据集给出了11个子集的平均评价指标数据Average。

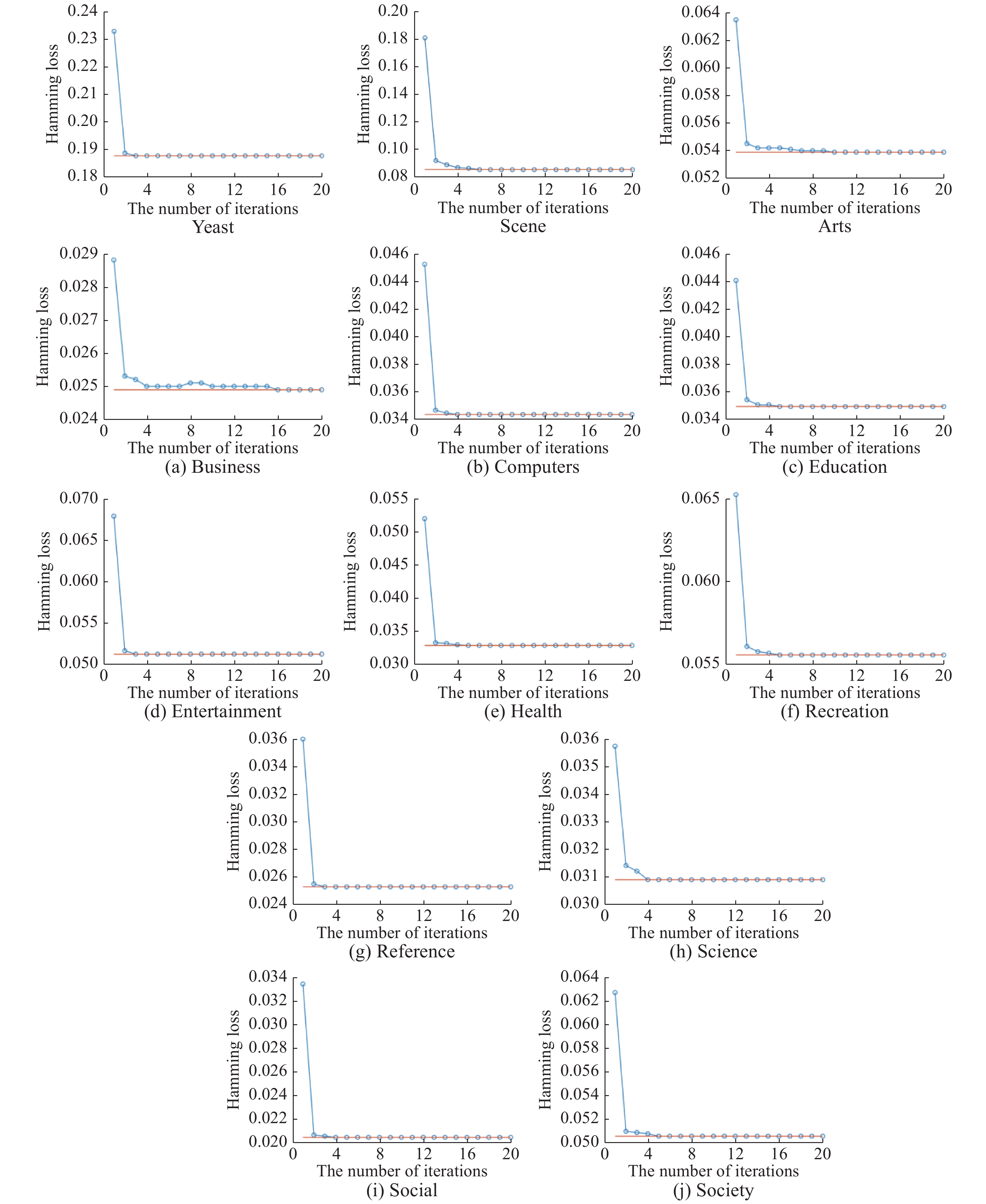
3.4 实验结果及分析

为了更直观展示本文算法收敛速度，13个数据集迭代收敛情况如图2所示。同时，在13个数据集中对比实验结果如表2~9所示，其中表2是酵母菌基因数据集对比试验结果，表3为场景数据集对比实验实验结果，表4~8则是雅虎网页数据集的实验结果，表9给出各算法在13个数据集中实验的时间消耗，并给出平均时间消耗。在此特别说明：因算法ML-EKELM、ML-KELM、ML-KNN的分类器具有稳定性，10次实验结果相同，其标准差均为0。

图2为ML-EKELM算法在13个多标记数据集中以Hamming Loss为指标的迭代次数图，最终收敛的Hamming Loss值用水平线表示。通过图2可以看出，使用坐标下降法求解弹性网络正则的ML-EKELM算法，迭代次数均小于20次，在大部分数据集中都在3次左右迭代达到收敛，在Arts和Business数据集中算法迭代收敛次数分别是10和16次。同时可以发现在13个数据集中只有Business数据集迭代收敛时出现波动，这一波动表明ML-EKELM算法在收敛过程中遇到局部最小值并成功寻找到全局最小值，这也进一步说明该算法求解弹性网络具有较强的鲁棒性，并且效率较高。

表2中，在Yeast Gene数据集上与其他算法对比，ML-EKELM算法在5种评价指标中均为第1，在HL↓指标中较第2位算法降低3.5%损失；如表3所示，在Scene数据集中，本文ML-EKELM算法同样在5种评价指标中最为优秀，在OE↓指标中比第2位算法降低11.8%错误率，同时在AP↑指标中比第2位算法提高1.7%准确率；雅虎网页数据集包含11个子数据集，其中分别对每个评价指标在各个子数据集中做出比较，如表4所示，在HL↓指标上，Arts、Business、Computers、Education、Entertainment、Health、Reference，Science和 Society等数据集中ML-EKELM性能最优，在Recreation数据集上，该算法位列第2，与第1位算法相差仅1.6%，在数据集Social上，ML-EKELM与ML-KELM性能并列第1，在HL↓的平均指标中可以看出，ML-EKELM算法性能最优。在表5中，对比了不同算法在各个数据集上的OE↓指标数值，其中在Social数据集上，ML-EKELM较ML-KELM相差仅为0.3%，排位第2，在其他数据集中该指标均为最优；11个子数据集在CV↓指标上如表6所示，ML-EKELM算法在Computers、Entertainment和Recreation数据集中指标上最优，其他数据均为第2，与平均指标性能最优的ML-KNN算法相差10.4%。

在RL↓指标上如表7所示，该算法在Arts、Computers、Entertainment、Health和Recreation等数据集上，指标性能最优，在平均性能指标位列第2位，与平均指标性能最优的ML-KNN算法仅相差1.9%；在AP↑指标上如表8所示，ML-EKELM算法在各个数据集上的性能指标均为最优。在雅虎网页数据集中，可以看出在CV↓和RL↓评价指标上，ML-KNN具有一定优势，但HL↓、OE↓和AP↑则排名靠后。而本文提出的算法在HL↓、OE↓和AP↑上都具有较大优势，在CV↓和RL↓上对比其他算法也处于优势地位。

各算法在多个数据集实验的时间消耗如表9所示，本文提出的算法ML-EKELM由于采用坐标下降法求解弹性网络，是一种迭代算法，所以在平均时间消耗上高于直接求解矩阵解析解的3种ELM算法77.5%~91.4%，但该算法平均时间消耗低于ML-RBF算法24.9%，平均时间消耗低于ML-KNN算法196.9%。从时间消耗可以看出ML-EKELM算法对比传统ELM算法有一定差距，但是对于其他多标记学习算法具有一定优势，ML-EKELM兼具准确率高与时间消耗较低的特点。

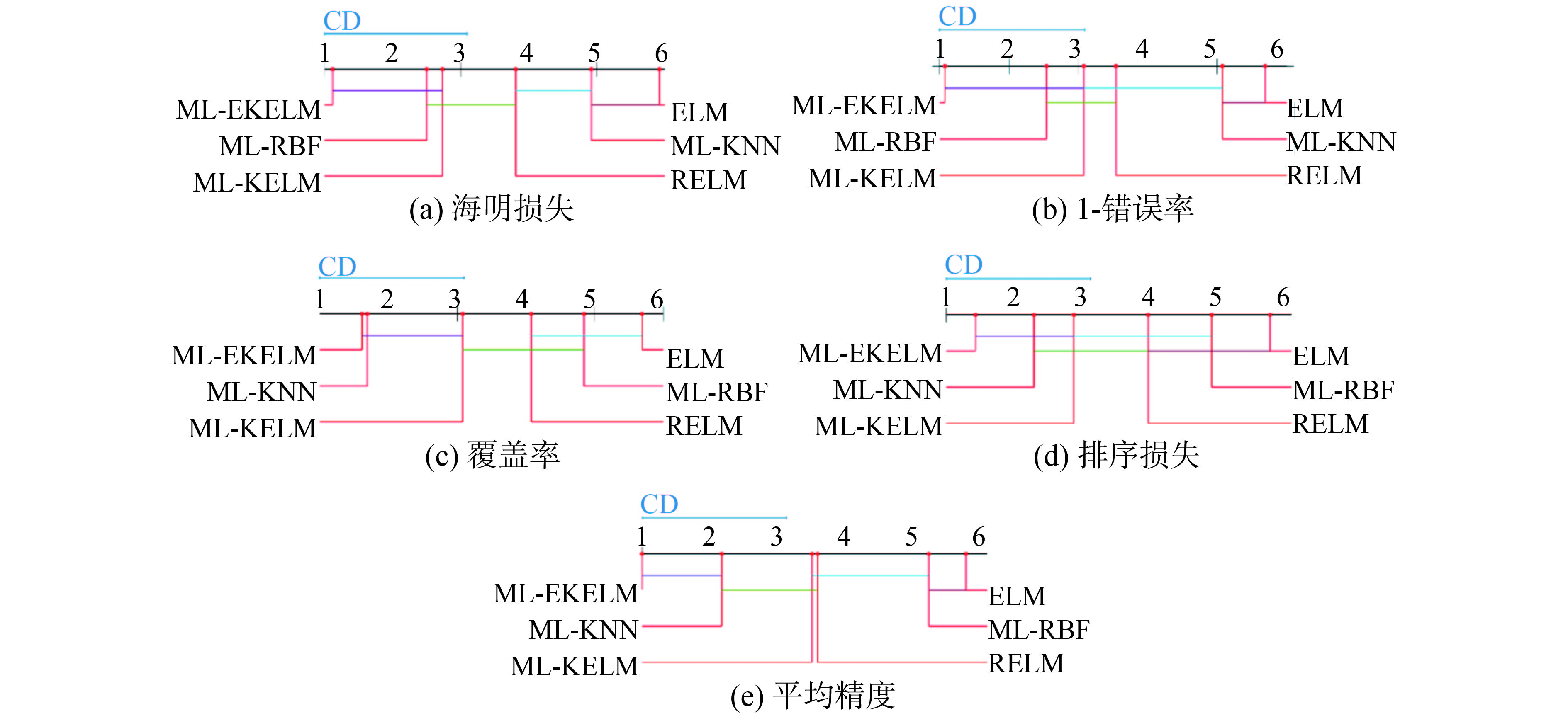
为了更清晰地展示各算法在13个数据集上的相对性能，采用显著性水平为5%的 Nemenyi检验^[29]。当两个对比算法在各数据集中的平均排序差值小于或等于临界差(critical difference，CD)，则认为这两个算法没有显著性差异；反之则2个算法有显著性差异。图3给出了在5种评价指标下各算法的性能，其CD值为2.0913，没有显著性差异的算法用实线相连，在图3评价指标子图中各算法坐标即平均排序位置，数值越小则算法性能越高。

对任意某个算法，都有25个结果作为对比(在5个评价指标上具有5个对比算法)，通过图3可以得出：

1)对于ML-EKELM算法，在5个评价指标上的性能均处于首位，除图3(c)中Coverage指标与第2位的ML-KNN相差不大，其余4个指标与第2位具有较大优势。在64%的情况下，统计上优于其它算法，如图3(a)在Hamming Loss指标上，ML-EKELM与RELM、ML-KNN和ELM有显著性差异，且优于这3种算法；如图3(b)在One-Error指标上，ML-EKELM与RELM、ELM和ML-KNN有显著性差异，且优于这3 种算法；如图3(c)在Coverage指标上，ML-EKELM与RELM、ML-RBF和ELM有显著性差异，且优于这3种算法；如图3(d)在Ranking Loss指标上，ML-EKELM与RELM、ML-RBF和ELM有显著性差异，且优于这3种算法；如图3(e)在Average Precision指标上，ML-EKELM与RELM、ML-RBF、ELM和ML-KNN有显著性差异，且优于这4种算法。在36%情况下，与其它算法性能无显著性差异。

2)对于ML-KELM算法，统计上优于其它对比算法有36%；与其它对比算法无显著性差异有64%。

3)对于ML-KNN算法，有20%的情况，在统计上优于其它对比算法；有44%的情况，与其他对比算法无显著性差异；在36%的情况性能弱于其他算法。

通过以上对于图3的分析，ML-EKELM算法综合性能最为优秀，在统计上优于其他对比算法有64%；第2位的是ML-KELM算法，在36%的情况下，在统计上优于其它对比算法，第3则是ML-KNN算法，有20%的情况优于其他对比算法。

基于以上的实验结果和分析表明提出的基于弹性网络核极限学习机的多标记学习算法(ML-EKELM)在综合性能方面有较好的表现，是对于ELM解决多标记问题的一种补充。

4 结束语

本文首次提出基于弹性网络核极限学习机的多标记学习算法，通过弹性网络正则防止数据训练时过拟合情况发生，并可对核映射后特征进行稀疏化表示，即可对特征进行选择。对比传统使用岭回归正则化ELM算法，弹性网络正则式存在不可导点，所以采用非梯度优化的坐标下降法，而无需对目标函数求导。该算法对于多标记学习任务，在运行速度和分类精度上都具有一定优势，对比试验进一步说明算法的可靠性和稳定性。

但目前本文只将弹性网络和ELM结合运用到多标记学习中，对于弹性网络如何稀疏化特征空间以及进行特征选择并未深入研究和实验，这将是今后研究的一个重要方向和目标。