2. 重庆邮电大学 计算智能重庆市重点实验室,重庆 400065
2. Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
模糊粗糙集理论是1990年由D.Dubios和H.Prade共同提出的处理数值型数据中存在的不一致性的数学理论[1]。经过多年的发展,模糊粗糙集在理论和应用方面都取得了相当丰富的研究成果,在系统控制、故障诊断、机器学习与数据挖掘等众多领域都有着广泛的应用。经典的粗糙集理论强调的是对象间的不可区分性,主要用于处理清晰、离散且有限的属性值,而在实际生活中大部分的数据集都具有多种多样的属性值,粗糙集在处理这些本身具有模糊性的数据和连续属性时存在一定的局限性[2]。粗糙集理论中的等效关系是研究模糊粗糙集理论的基础,将经典粗糙集理论中的被近似对象由清晰集转换为模糊集,并将论域上的分明等效关系弱化为模糊等效关系即可得到模糊粗糙集[3]。
超网络(hypernetworks)是受生物分子网络启发而建立的一种基于超图实现的认知学习模型,能够表示模式特征间的高阶关联关系[4]。目前,国内的研究者们主要研究演化超网络模型,探究其应用领域并在此基础上对超网络模型进行改进。王进等[5]结合OCDD算法,提出了一种能处理多值数据的细粒度超网络分类方法;王进等[6]在超网络的演化学习过程中引入遗传算法,从而得到了一种具有较高的分类准确率的模式识别方法;为了处理多类型癌症分子问题,王进等[7]提出了一种基于演化超网的多类型癌症分子分型系统。同时,在中文文本分类[8]、评分预测、道路限速标志识别[9]等方面,演化超网络模型也得到了很好的应用。超网络的研究在国内起步较晚,在许多领域都值得研究和学习。
本文结合模糊粗糙集的思想提出了一种模糊超网络(fuzzy hypernetworks,F-hypernetworks)。在模糊超网络中,对于连续型的属性不需要对其进行离散化处理,解决了传统超网络只能处理离散型属性的问题,并对传统超网络训练过程中具有很大随机性的超边替代环节进行了改进。
1 相关概念 1.1 模糊等价类定义1 给定决策表(U, A∪D),其中:U为非空有限论域;A为条件属性集合,也称特征集合;D为决策属性集合,也称类别属性集。在没有说明的情况下,属性是指条件属性。
1) 自反性,
2) 对称性,
则称P为U上的模糊相似关系[10]。
定义2 设P是U上的模糊相似关系,对于给定的
| ${\mu _P}(x,y) = \left({{\mathop \sum \limits_{a \in p} {{\mu_a(x,y)}}}}\right)\Big/{{\left| P \right|}}$ | (1) |
对于属性
| ${\mu _a}(x,y) = \exp \left( { - \frac{{{{\left( {a\left( x \right) - a\left( y \right)} \right)}^2}}}{{2{\sigma _a}^2}}} \right)$ | (2) |
式中:
| ${\mu _a}(x,y) = \left\{ {\begin{array}{l} \!\!\!\!{0, \;\;\;a\left( x \right) \ne a\left( y \right)}\\ \!\!\!\!{1, \;\;\;a\left( x \right) = a\left( y \right)} \end{array}} \right.$ | (3) |
式中
定义3 给定决策表(U, A∪D),P是U上的模糊相似关系,对于给定的
| ${[x]_{P{\textit{λ}} }} = \left\{ {\left. y \right|{\mu _P}(x,y) \geqslant {\textit{λ}} ,{\textit{λ}} \in [0,1]} \right\}$ | (4) |
式中:
定义4 设
| ${\mu _{\underline {{P_I}} X}}(x) = {\rm{in}}{{\rm{f}}_{y \in U}}I\left( {{\mu _P}(x,y),{\mu _X}(y)} \right),\;\forall x \in U$ | (5) |
| ${\mu _{\overline {{P^T}} X}}(x) = {\rm{su}}{{\rm{p}}_{y \in U}}T\left( {{\mu _P}(x,y),{\mu _X}(y)} \right),\;\forall x \in U$ | (6) |
对
| $I(x,y) = {\rm{min}}(1 - x + y , 1)$ | (7) |
| $T(x,y) = {\rm{max}}(x + y - 1 , 0)$ | (8) |
根据式(5),对象x关于模糊正域的隶属度[13]可表示为
| ${\mu _{{\rm{PO}}{{\rm{S}}_P}\left( D \right)}}\left( x \right) = \mathop {\sup }\limits_{X \in U/D} {\mu _{\underline {{P_I}} X}}\left( x \right)$ | (9) |
在模糊粗糙集条件下,决策属性D对条件属性集P的依赖度[13]为
| $k = \gamma _P'\left( D \right) = \frac{{\left| {{\mu _{{\rm{PO}}{{\rm{S}}_P}\left( D \right)}}\left( x \right)} \right|}}{{\left| U \right|}} = \frac{{\mathop \sum \limits_{x \in U} {\mu _{{\rm{PO}}{{\rm{S}}_P}\left( D \right)}}\left( x \right)}}{{\left| U \right|}}$ | (10) |
k值的大小,反映了条件属性集P的分类能力。决策属性D对属性集P的依赖程度越大,以P为依据进行分类的效果越好。以表1所示的决策信息系统为例计算各个属性的依赖度。
| 表 1 决策信息系统 Tab.1 Decision information system |
a1、a2、a3为条件属性,D为决策属性。对于所有
| $\begin{array}{c} {\mu _{a{ _1}}}\left( {x,y} \right) = \\ \left[ {\begin{array}{*{20}{c}} \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{0.109\,\,3}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{0.196\,\,6}\!\!\\ \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{0.109\,\,3}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{0.196\,\,6}\!\!\\ \!\!{0.955\,\,8}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{0.323\,\,2}\!\! & \!\!{0.323\,\,2}\!\!\\ \!\!{0.109\,\,3}\!\! & \!\!{0.109\,\,3}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{0.955\,\,8}\!\!\\ \!\!{0.196\,\,6}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{0.323\,\,2}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\!\\ \!\!{0.196\,\,6}\!\! & \!\!{0.196\,\,6}\!\! & \!\!{0.323\,\,2}\!\! & \!\!{0.955\,\,8}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! \end{array}} \right] \end{array}$ |
| $\begin{array}{c} {\mu _{{a_{ 2}}}}\left( {x,y} \right) = \\ \left( {\begin{array}{*{20}{c}} \!\!{1.000\,\,0}\!\! & \!\!{0.097\,\,4}\!\! & \!\!{0.911\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.432\,\,4}\!\! \\ \!\!{0.097\,\,4}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.034\,\,9}\!\! & \!\!{0.097\,\,4}\!\! & \!\!{0.097\,\,4}\!\! & \!\!{0.688\,\,9}\!\! \\ \!\!{0.911\,\,0}\!\! & \!\!{0.034\,\,9}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.911\,\,0}\!\! & \!\!{0.911\,\,0}\!\! & \!\!{0.225\,\,2}\!\! \\ \!\!{1.000\,\,0}\!\! & \!\!{0.097\,\,4}\!\! & \!\!{0.911\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.432\,\,4}\!\! \\ \!\!{1.000\,\,0}\!\! & \!\!{0.097\,\,4}\!\! & \!\!{0.911\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.432\,\,4}\!\! \\ \!\!{0.432\,\,4}\!\! & \!\!{0.688\,\,9}\!\! & \!\!{0.225\,\,2}\!\! & \!\!{0.432\,\,4}\!\! & \!\!{0.432\,\,4}\!\! & \!\!{1.000\,\,0}\!\! \end{array}} \right) \end{array}$ |
| $\begin{array}{c} {\mu _{a{ _3}}}\left( {x,y} \right) = \\ \left( {\begin{array}{*{20}{c}} {1.000\,\,0} & \!\!{0.155\,\,6}\!\! & \!\!{0.628\,\,1}\!\! & \!\!{0.054\,\,6}\!\! & \!\!{0.054\,\,6}\!\! & \!\!{0.054\,\,6}\!\!\\ \!\!{0.155\,\,6}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.628\,\,1}\!\! & \!\!{0.890\,\,2}\!\! & \!\!{0.890\,\,2}\!\! & \!\!{0.890\,\,2}\!\!\\ \!\!{0.628\,\,1}\!\! & \!\!{0.628\,\,1}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{0.351\,\,2}\!\! & \!\!{0.351\,\,2}\!\! & \!\!{0.351\,\,2}\!\! \\ \!\!{0.054\,\,6}\!\! & \!\!{0.890\,\,2}\!\! & \!\!{0.351\,\,2}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\!\\ \!\!{0.054\,\,6}\!\! & \!\!{0.890\,\,2}\!\! & \!\!{0.351\,\,2}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\!\\ \!\!{0.054\,\,6}\!\! & \!\!{0.890\,\,2}\!\! & \!\!{0.351\,\,2}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! & \!\!{1.000\,\,0}\!\! \end{array}} \right) \end{array}$ |
决策划分:
| $U/D = \left\{ {{\rm{\{ }}1,3,6{\rm{\} }},\{ 2,4,5\} } \right\}{\rm{ = \{ }}{X_1},{X_2}{\rm{\} }}$ |
| ${\mu _{{X_1}}}(x) = \{ 1,0,1,0,0,1\} $ |
| ${\mu _{{X_2}}}(x) = \{ 0,1,0,1,1,0\} $ |
根据式(5)可得:
| $\begin{array}{c} {\mu _{\underline {a{ _1}_I} {X_1}}}(1) = 0,\;{\mu _{\underline {{a_{ 1}}_I} {X_1}}}(2) = 0,{\mu _{\underline {a{ _1}_I} {X_1}}}(3) = 0.044\,\,2 \\ {\mu _{\underline {{a_{ 1}}_I} {X_1}}}(4) = 0,\;{\mu _{\underline {a{ _1}_I} {X_1}}}(5) = 0,\;{\mu _{\underline {a{ _1}_I} {X_1}}}(6) = 0\\ {\mu _{\underline {a{ _1}_I} {X_1}}}\left( x \right) = \{ 0,0,0.044\,\,2,0,0,0\} \end{array}$ |
同理可得:
| $\begin{array}{c} {\mu _{\underline {a{ _1}_I} {X_2}}}\left( x \right) = \{ 0,0,0,0.044\,\,2,0,0\} \\ {\mu _{{\rm{PO}}{{\rm{S}}_{{a_{ 1}}}}\left( D \right)}}\left( x \right) = \mathop {\sup }\limits_{X \in U/D} {\mu _{\underline {{a_{ 1}}_I} X}}\left( x \right) = \\ {\rm{max}}\{ {\mu _{\underline {a{ _1}_I} {X_1}}}\left( x \right),{\mu _{\underline {{a_{ 1}}_I} {X_2}}}\left( x \right)\} =\{ 0,0,0.044\,\,2,0.044\,\,2,0,0\} \\ \gamma _{a{ _1}}'\left( D \right) = 0.014\,\,7 \end{array}$ |
按上述方法分别求出a2、a3的依赖度:
| $\begin{array}{c} {{\gamma '}_{{a_2}}}\left( D \right) = 0.118\,5\\ {{\gamma '}_{{a_3}}}\left( D \right) = 0.221\,0 \end{array}$ |
由此可以计算出每个属性的依赖度,并称其为属性的重要度。
1.2 模糊超网络模型定义5 设G=<X, E, λ>是一个模糊超网络,
定义6 模糊超网络G1=<X1, E1, λ1>,模糊超网络G2=<X2, E2, λ2>,若X1=X2则λ1=λ2。
定义7 模糊超网络G=<X, E, λ>,超边的属性集为
定义8 给定模糊超网络G=<X, E, λ>,样本x在属性集
| ${[x]_{B{\textit{λ}} }} = \left\{ {e{\rm{|}}\left( {e \in E} \right) \wedge {\mu _B}\left( {x,e} \right) \geqslant {\textit{λ}} } \right\}$ | (11) |
λ-等价类样本集合为
| $[x]_B^{\textit{λ}} = \left\{ {y{\rm{|}}(y \in X) \wedge {\mu _B}(x,y) \geqslant{\textit{λ}}} \right\}$ |
定义9 给定模糊超网络G=<X, E, λ>,
| ${R_{B\lambda }}\left( e \right) = \left\{ {x{\rm{|}}e \in {{[x]}_{B\lambda }},x \in X} \right\}$ | (12) |
定义10 给定模糊超网络G=<X, E, λ>,
| ${\rm{Conf}}_{B} = \frac{{\left| {\left\{ {x{\rm{|}}x \in {R_{B{\textit{λ}} }}\left( e \right),D\left( x \right) = D\left( e \right)} \right\}} \right|}}{{\left| {\left\{ {x{\rm{|}}x \in {R_{B{\textit{λ}}}}\left( e \right)} \right\}} \right|}}$ | (13) |
定义11 给定模糊超网络G=<X, E, λ>,C为样本的条件属性集,D为样本的决策属性,对任意的样本
1) 如果
2) 如果
3) 如果
| $f\left( x \right) = \frac{{\left| {\left\{ {y{\rm{|}}{\mu _C}\left( {x,y} \right) \geqslant {\textit{λ}} ,D\left( x \right) = D\left( y \right)} \right\}} \right|}}{{\left| {\left\{ {y{\rm{|}}{\mu _C}\left( {x,y} \right) \geqslant {\textit{λ}} } \right\}} \right|}},\;y \in X$ | (14) |
如果
图1给出了4个样本的λ-等价类样本集合,由式(14)可得:
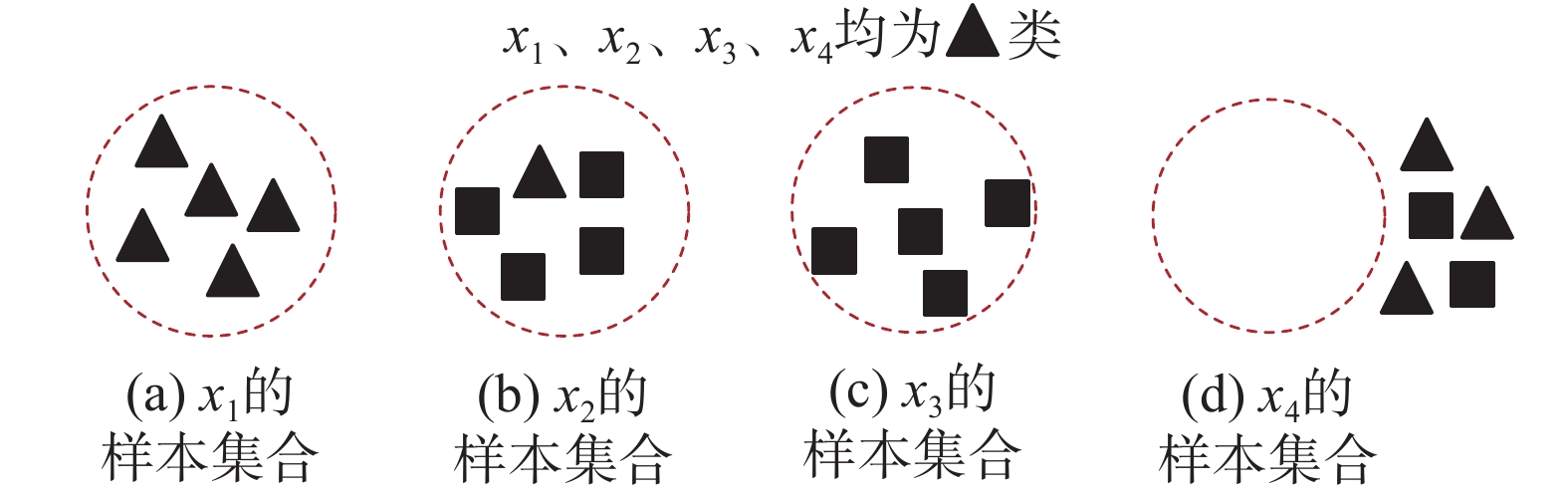
|
Download:
|
| 图 1 λ-等价类样本示例 Fig. 1 Examples of λ-equivalence class sample | |
定义12 给定模糊超网络G=<X, E, λ>,C为样本的条件属性集,D为样本的决策属性,任意超边集
| $\begin{array}{l} {\rm{POS}}\left( {E'} \right) = \{ e{\rm{|}}\mathop {\max }\limits_{D\left( x \right) \ne D\left( e \right)} \left\{ {{\mu _B}\left( {x,e} \right)} \right\} < \lambda \cap \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\max }\limits_{D\left( x \right) = D\left( e \right)} \left\{ {{\mu _B}\left( {x,e} \right)} \right\} \geqslant \lambda ,x \in X,e \in E'\} \\ {\rm{NEG}}\left( {E'} \right) = \{ e{\rm{|}}\mathop {\max }\limits_{D\left( x \right) \ne D\left( e \right)} \left\{ {{\mu _B}\left( {x,e} \right)} \right\} \geqslant {\textit{λ}} + \dfrac{{1 - {\textit{λ}} }}{2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \in X,e \in E'\} \\ {\rm{BND}}\left( {E'} \right) = E' - {\rm{POS}}\left( {E'} \right) - {\rm{NEG}}\left( {E'} \right) \end{array}$ | (15) |
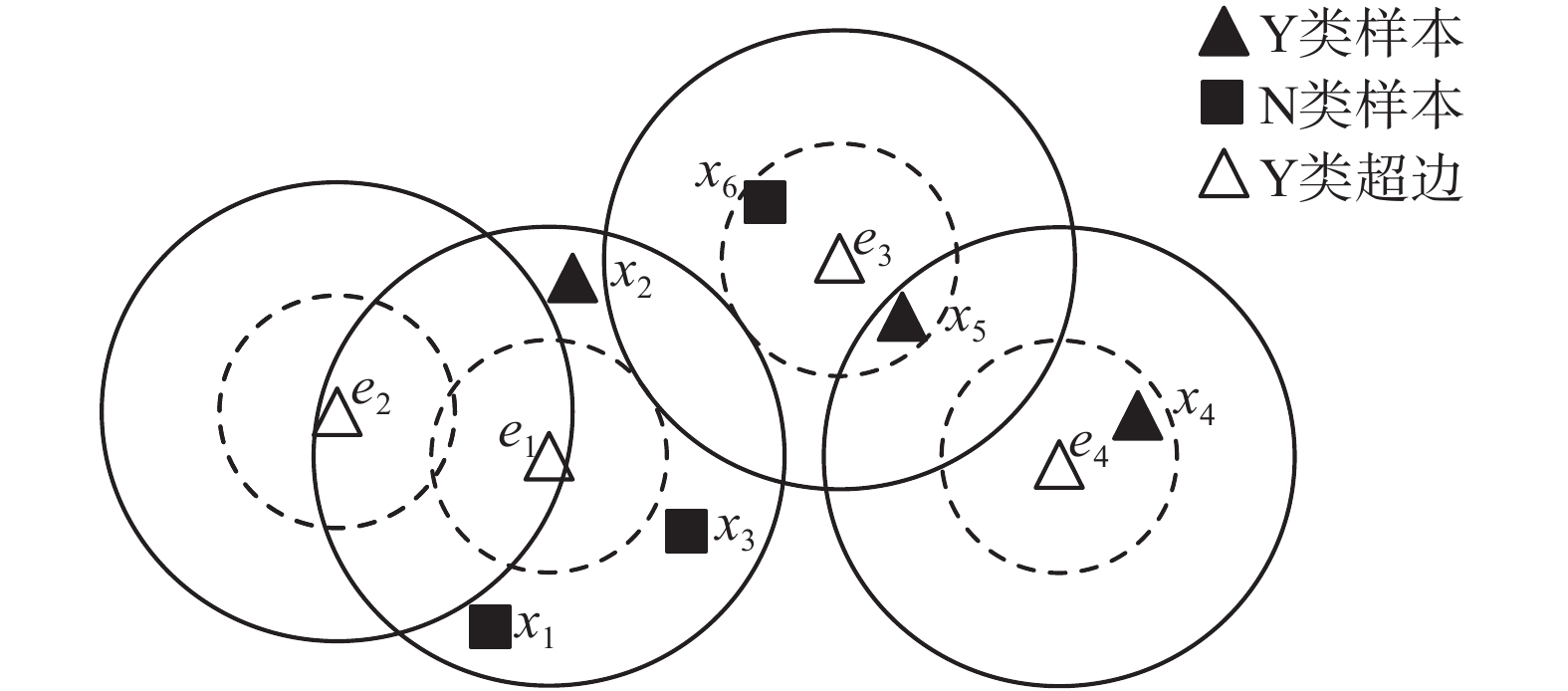
以表1的决策信息系统为例,图2是表1的一个模糊超网络模型,超边集
|
Download:
|
| 图 2 模糊超网络示例 Fig. 2 Example of a Fuzzy hypergraph | |
根据式(15)、表2与图2可知,正域超边需同时满足两个条件:
1)
2)
负域超边需满足条件:
| $\mathop {\max }\limits_{D\left( x \right) \ne D\left( e \right)} \left\{ {{\mu _B}\left( {x,e} \right)} \right\} \geqslant 0.75$ |
| 表 2 样本-超边相似度 Tab.2 Sample_Hyperedge similarity |
对于超边e1,与e1相似度最高的异类样本为x3,μ(e1, x3)=0.72<0.75,不满足负域条件,所以e1不是负域超边,μ(e1, x3)=0.72>0.5不满足正域条件1),所以e1是边界域超边。
对于超边e2,与e2相似度最高的异类样本为x1,μ(e2, x1)=0.30<0.75,不满足负域条件,所以e2不是负域超边,与e2相似度最高的同类样本为x2,μ(e2, x2)=0.35<0.5不满足正域条件2),所以e2是边界域超边。
对于超边e3,与e3相似度最高的异类样本为x6,μ(e3, x6)=0.77>0.75,满足负域条件,所以e3是负域超边。
对于超边e4,与e4相似度最高的异类样本为x3,μ(e4, x3)=0.34<0.5,与e4相似度最高的同类样本为x4,μ(e4, x4)=0.82>0.5满足正域条件,所以e4是正域超边。
综上所述,
同传统超网络一样,模糊超网络生成算法也分为三大步骤:初始化超边集,训练样本分类,超边替代。超网络通过迭代训练的方式进行演化学习,当分类正确率和迭代次数满足特定条件时,即可退出迭代,输出模型。由于传统超网络采用随机生成的方式初始化超边,增大了超边替代阶段筛选和替换分类能力差的超边的难度[14]。所以本文提出的模糊超网络对超边的初始化随机生成进行了控制,同时在超边替代过程中,对不同域中的超边进行相应的处理以提高超网络的分类效果。算法流程如图3所示。

|
Download:
|
| 图 3 分类算法流程 Fig. 3 Flow of this algorithm | |
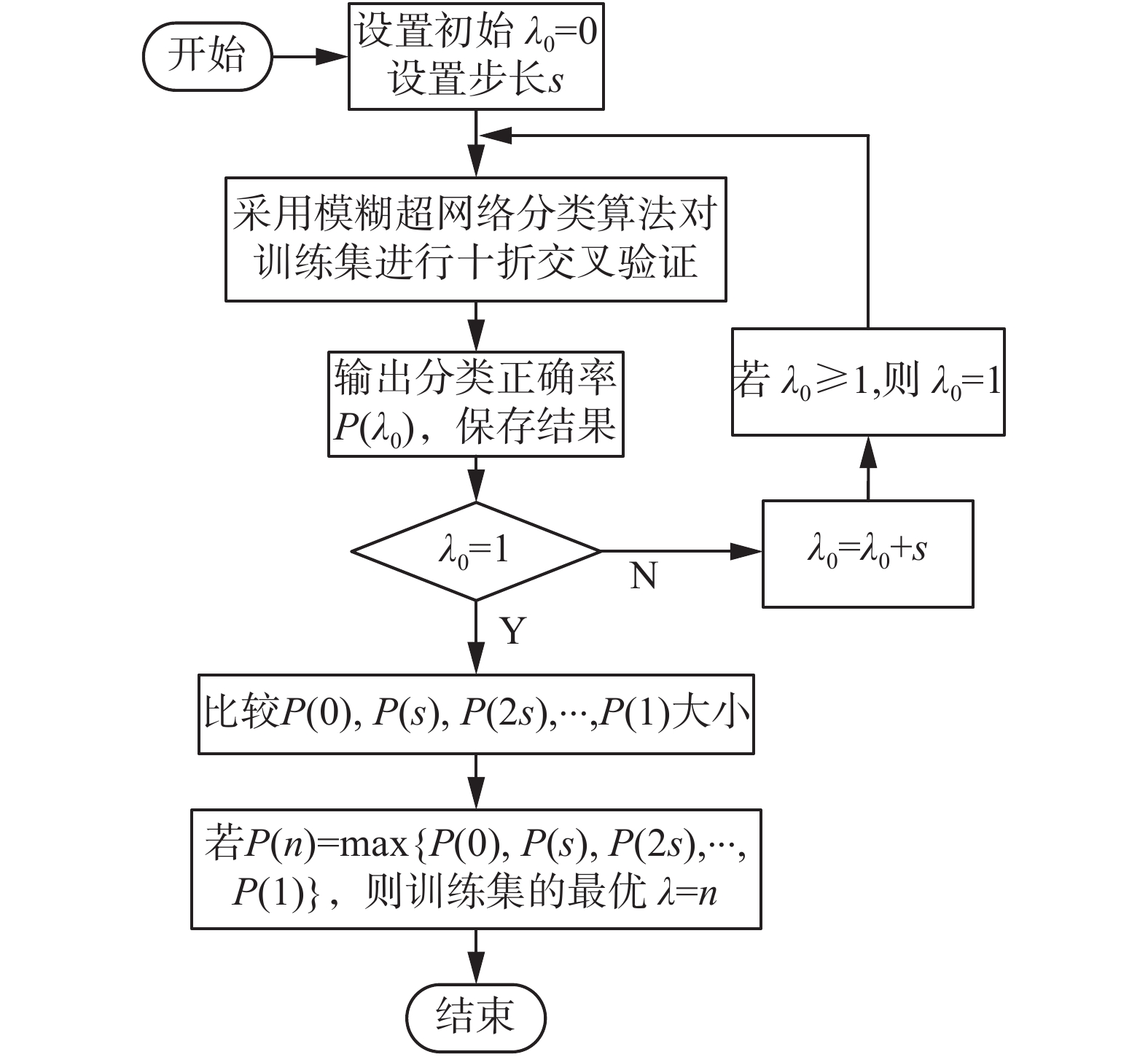
由定义6可知,每一个训练样本集都有且只有一个最优模糊相似度阈值λ,所以本文在执行分类算法前需要通过循环迭代的方法计算出最优λ,具体流程如图4所示。初始设置模糊相似度阈值λ0为0,然后通过叠加步长来改变λ0的取值,在不同的λ0值下,采用模糊超网络分类方法对训练集进行十折交叉验证[15]得到相应的分类正确率。将正确率最高的λ0值作为最优模糊相似度阈值λ执行后续的分类算法。值得注意之处在于,从理论上说,对于同一个训练集,λ是唯一的,本方法计算出的结果仅是一个接近的阈值,一般步长设置越短越接近最优模糊相似度阈值。本文所设置的步长s=0.01,足以满足实验需求。
|
Download:
|
| 图 4 计算最优λ流程图 Fig. 4 Flow chart for calculating optimal λ | |
根据训练集中的样本生成模糊超网络中的超边。本文设置每个样本直接生成5条超边,超边的属性数目与样本一致。每条超边的初始化主要由条件属性初始化和决策属性初始化两部分组成。
1) 条件属性初始化
条件属性初始化主要有两种方式:一种是随机属性继承,超边从条件属性集中随机选择十分之七的属性继承样本的属性值,即超边在这些属性上的取值与生成该超边的样本相同。剩余属性则根据训练集在该属性上的取值范围随机生成属性值。如图5所示,x为样本,e为x按照随机属性继承方式生成的超边。

|
Download:
|
| 图 5 随机属性继承示例图 Fig. 5 Example of random attribute inheritance | |
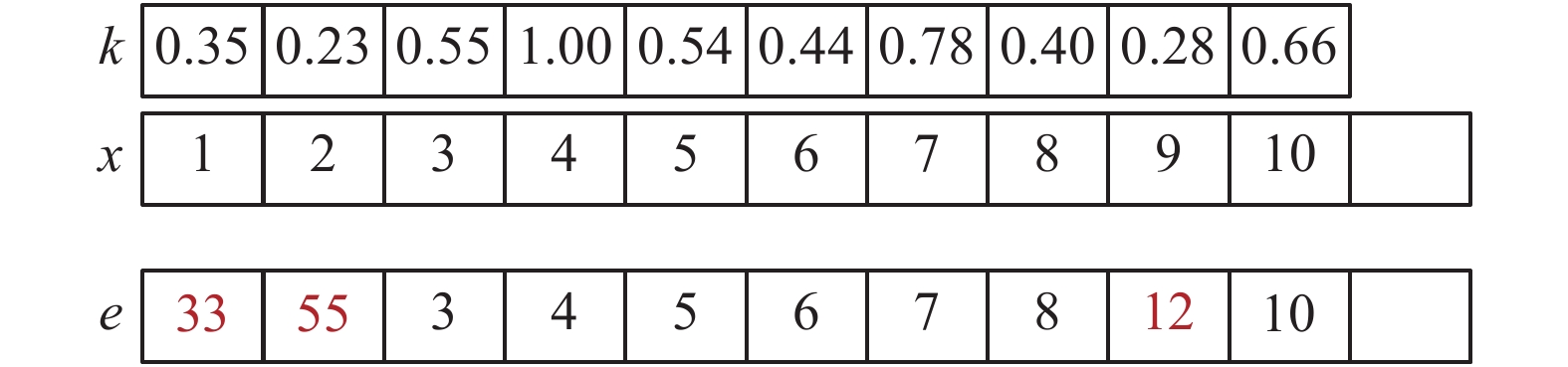
另一种是择优属性继承,超边从所有属性中选择重要度较高的前十分之七的属性继承样本的属性值,剩余属性上的取值则根据训练集中同类样本在该属性上的取值范围随机生成。如图6所示,样本x拥有10个属性,首先利用样本x的λ-等价类样本集合按照定义4所示的方法计算出各个属性的重要度k,然后重新生成重要度较低的属性1、2、9对应的属性值。
|
Download:
|
| 图 6 择优属性继承示例图 Fig. 6 Example of preferred attribute inheritance | |
2) 决策属性初始化
正域样本生成的超边,条件属性初始化采取随机属性继承方式,决策属性直接继承生成该超边的样本。边界域样本生成的超边,条件属性初始化采取择优属性继承方式,决策属性直接继承生成该超边的样本。负域样本生成的超边,同样采取随机属性继承的方式确定条件属性,因为其决策属性与原始样本相同的概率较低,所以该类超边的决策属性是根据整个数据集确定的,与关联该超边的样本集中的大类样本类别一致。
2.1.3 训练样本分类给定模糊超网络G=<X, E, λ>,决策属性的取值范围
| ${[x]_{\textit{λ}} }^j = \left\{ {e{\rm{|}}e \in {{[x]}_{\textit{λ}} }\cap {D(e) = j} } \right\}$ | (16) |
对于每一个样本x的分类过程如下:
1) 计算出样本x在λ下的模糊等价类超边
2) 将
| $\left| {{{[x]}_\lambda }} \right| = \mathop \sum \limits_{j \in V_{\rm{D}}} \left| {{{[x]}_\lambda }^j} \right|$ | (17) |
3) 计算x的类别
| $D{\rm{(}}x{\rm{)}} = {\rm{argmax}}\left( {\left| {{{[x]}_\lambda }^j} \right|} \right),\;j\in {V_D}$ |
4) 若
采用上述分类规则对训练集的每个样本进行分类,计算模糊超网络模型对训练集的分类正确率。
2.1.4 超边替代首先判断超边所在区域,然后不同的区域采取不同的措施:
若超边e是正域超边,则超边e与训练集中所有异类样本相似度较低,与同类样本相似度较高,该超边的存在有助于提高分类效果,故选择保留超边e;
若超边e是负域超边,则超边e与训练集中某一异类样本相似度较高,在分类的过程中超边e会影响其他类别的分类效果,故需要替换;
若超边e是边界域超边,在衡量超边e的分类效果时,需要通过置信度ConfB进行判断,若ConfB>γ(本文取γ=0.5),保留超边e,反之,则替换掉超边e。其中存在一种特殊情况:当关联超边e的样本数为0时,无法计算置信度ConfB。此时,需要查看超边参与分类的样本集合
| ${\rm{Conf}}_{B} = \frac{{\left\{ {x{\rm{|}}D\left( e \right) = D\left( x \right),x \in P\left( e \right)} \right\}}}{{\left| {P(e)} \right|}}$ | (18) |
算法1 初始化超边库算法
输入 训练样本集X,最优阈值λ;
输出 超边集E。
1)
2) 计算每个样本的λ-等价类样本集合,根据定义11判断样本所属区域
3) for each x in X do
4) j=0
5) while(j<5) /*设置每个样本生成的超边数*/
6) if
7) 根据样本x生成超边e,e直接继承x的决策属性,条件属性初始化采取随机属性继承方式
8) end if
9) if
10) 根据样本x生成超边e,条件属性初始化采取随机属性继承方式,决策属性根据整个数据集确定
11) end if
12) if
13) 根据x生成超边e,超边直接继承x的决策属性,计算在x的λ-等价类样本集合中各条件属性的依赖度,将条件属性按依赖度大小从大到小排序,超边e择优选择排在前7/10的属性继承样本x的属性值
14) end if
15)
16) end while
17) end for
18) return E; /*输出初始超边库*/
算法2 超边替代算法
输入 训练样本集X,最优阈值λ,超边集E;
输出 超边集E。
1) for each e in E do
2) 根据定义12判断超边e所属区域
3) if
4) end if
5) if
6) 计算e的置信度
7) if
8) 参照算法1中的生成超边方法,该超边对应的原始样本重新生成一条新超边enew,E=E−{e};E =
9) end if
10) end if
11) if
12) 参照算法1,原始样本重新生成一条新超边enew,E=E−{e};
13) end if
14) end for
15) return E; /*输出更新后的超边库*/
算法3 生成模糊超网络算法
输入 训练样本集X,最优阈值λ;
输出 超网络G。
1) 执行算法1生成初始超边集E
2) k=0,Ebest=
3) while (k<100)
/*设置最小迭代次数用以保障超网络能够得到充分的演化,可根据实际演化效果增减次数*/
4) for each x in X do
5) 计算样本x在λ下的模糊等价类超边集合
6) end for
7) 根据训练样本的实际类别,计算当前超边集对训练集的分类正确率P;k++
8) if P>Pmax then
9) Pmax = P,Ebest=E;/*保存当前最优超边集*/
10) end if
11) 执行算法2更新超边集
12) end while
13) m=0
14) while (m<10) /*退出迭代条件 */
15) for each x in X do
16) 计算样本x在λ下的模糊等价类超边集合
17) end for
18) 根据训练样本的实际类别,计算当前超边集对训练集的分类正确率P
19) if P > Pmax then
20) Pmax = P,Ebest=E,m=0
21) else m++
22) end if
23) 执行算法2更新超边集
24) end while
26) return G=<X, Ebest, λ>;/*输出模糊超网络*/
令训练集样本数目为n,样本的属性数目为m。算法1的平均时间复杂度为O(m×n2),算法2的时间复杂度为O(m×n),算法3的时间复杂度为O(m×n2),所以建模的时间复杂度为O(m×n2)。
计算最优模糊相似度阈值时循环迭代所用的时间约为建模时间的10×s-1倍,迭代步长s在(0, 1)范围内取值。s值越小,计算所用的时间越长,得到的结果越接近理论上的最优阈值。最优模糊相似度阈值是一个非常重要的参数,在部分数据集上,略微改变阈值,分类结果就会有较大的改变。对于这类数据集而言,计算最优模糊相似度阈值是非常重要的环节。但也有一些数据集,例如大部分的离散型数据集,在一定范围内改变阈值,生成的超网络的分类效果不变,处理这些数据集时,可以通过设置合理的步长和初始阈值,达到既不影响分类效果又能减少迭代时间的目的。
3 实验评价 3.1 数据集及评价指标为验证算法的有效性,本文选取机器学习数据库UCI中的15个数据集进行实验,每个数据集的详细信息如表3所示,按数据集大小从小到大排序。
| 表 3 实验数据集 Tab.3 Experimental data sets |
混合矩阵(confusion matrix)[16]是一个常用的评价指标,如表4所示。TP表示正类样本被正确预测为正类的样本数;FN、FP分别表示预测错误的实际正类和负类样本数目;TN表示负类样本被正确预测为负类的样本数。
| 表 4 混合矩阵 Tab.4 Confusion matrix |
查准率:表示被分类器预测为正类的样本中正类样本所占的比例。计算公式为
| ${\rm{Precision}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}$ |
查全率:又称召回率,表示正类样本被分类器正确预测为正类的比例。计算公式为
| ${\rm{Recall}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}$ |
F-Measure指标[17]是一种综合查全率和查准率的分类评价指标:
| ${\rm{F}} - {\rm{Measure}} = \frac{{2 \times {\rm{Precision}} \times {\rm{Recall}}}}{{{\rm{Precision}} + {\rm{Recall}}}}$ |
正确率即分类正确样本数与分类总数之比。
本文采用正确率、查准率(Precision)、查全率(Recall)、和F-Measure作为评价指标。
3.2 实验方法为了考察模糊超网络分类算法的性能,本文采用Java语言实现算法并将其与NaiveBayes、KNN、J48(C4.5) 、SMO[18] 和BP-KNN[19] 5种算法进行对比。利用Weka[20]平台,在15个数据集上对以上算法进行对比实验,BP-KNN根据文献[19]设置参数,其余分类器的参数均为Weka平台下算法的默认值。实验中模糊超网络模型所涉及的随机种子均设为seed=1 234。所有实验结果均为采用5-折交叉验证后的结果。
3.3 实验结果本次实验将模糊超网络分类算法封装成Weka平台可识别的分类器,所有的评价指标均由Weka平台的评估器计算并输出。表5~8分别给出了本算法与其他算法的正确率、查准率、查全率和F-Measure的结果。
| 表 5 正确率值 Tab.5 Accuracy |
| 表 6 查准率 Tab.6 Precision |
| 表 7 查全率 Tab.7 Recall |
| 表 8 F-Measure值 Tab.8 F-Measure |
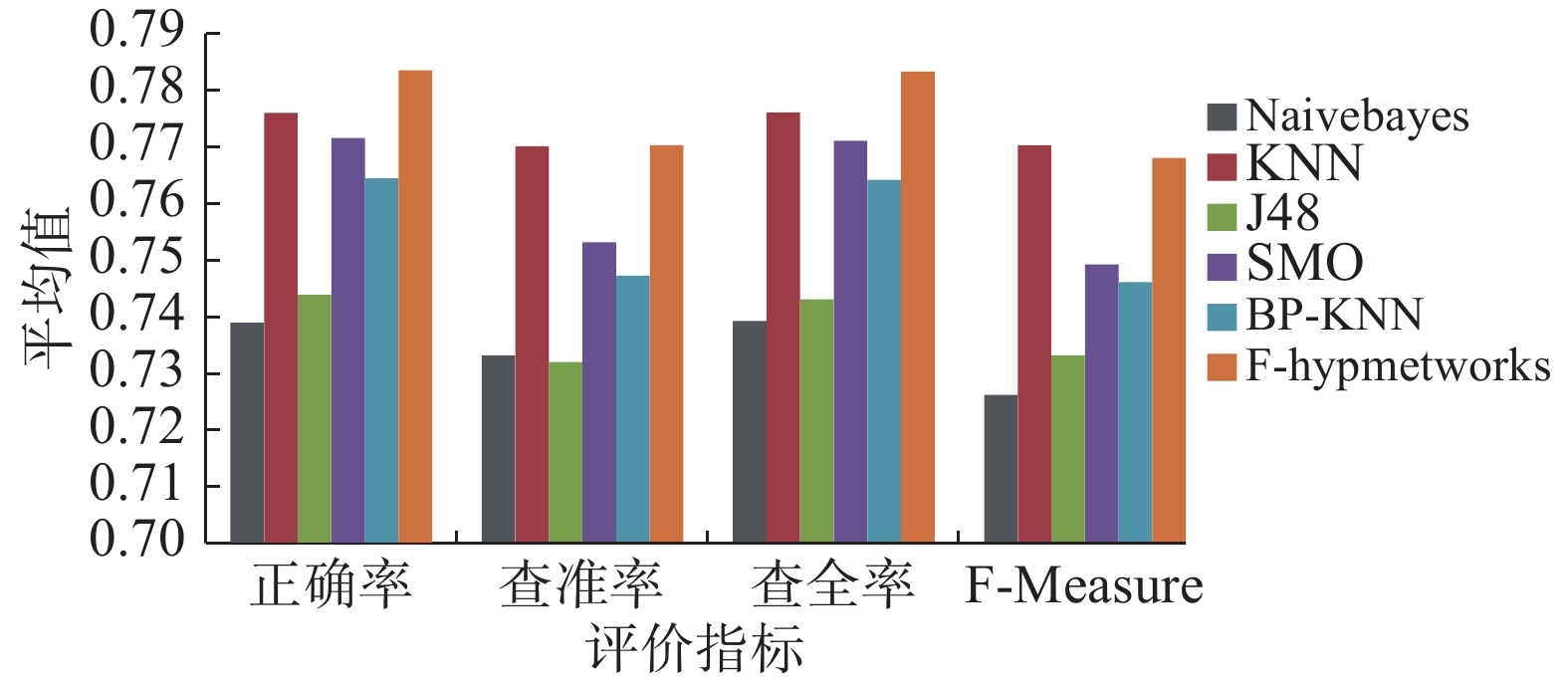
由图7可知,相较于其他5种分类算法,本文提出的模糊超网络算法在正确率、查准率、查全率上都具有一定的优势。为了进一步考查模糊超网络分类算法与对比算法之间的比较效果,本文根据这6种算法在各个评价指标上的实验结果,按照1、2、3、4、5、6的次序进行Rank排序评分,得到了如表9所示的6种算法在15个实验数据集上的各项Rank平均值。
|
Download:
|
| 图 7 各项指标平均值柱状图 Fig. 7 Average value of each indicator | |
| 表 9 不同算法在评价指标上的Rank平均值 Tab.9 Rank mean of different algorithms in evaluation index |
从表5~8可以看出,本算法在一些数据集上的分类效果并不是最好的。例如,在tic-tac-toe数据集上,与分类效果较好的3个算法相比,F-hypernetworks的正确率下降了近13%,查准率、查全率和F-Measure上的结果也相差较大。通过分析可知,在tic-tac-toe数据集中,不同类别的样本之间的相似度较高,约83%的样本与异类样本的最大模糊相似度不低于其与同类样本的最大模糊相似度。而在分类效果较好的BLOGGER数据集上,这种样本的数目只占总数的22%,在breast-cancer数据集上仅有2%。由于超边对这些样本的识别率不高,模糊超网络对其做出误判的概率较大,如果数据集中存在大量的这种样本,会导致最终的分类结果不理想。
结合图7与表9可知,模糊超网络在正确率、查准率、查全率、F-Measure的Rank平均值上均为最优。本文选取的对比算法都是应用较为广泛的分类算法,对实际生活中的大部分数据集具有较好分类效果。同这些优秀的算法相比,模糊超网络分类算法仍具有一定的优势,在Recall、Precision等指标上表现出了比较好的结果。
4 结束语本文结合模糊粗糙集和超网络的相关知识提出了一种模糊超网络模型,用于处理分类问题。首先,根据模型的最优模糊相似度阈值λ计算样本的λ-等价类样本集合;其次,根据该集合的分布情况来定义边界域样本、正域样本和负域样本,对于不同区域的样本采取不同的处理方法生成超边;然后,在超边替代阶段,同样通过划分3个区域来控制超边的替换;最后,在分类时,会根据样本的λ-等价类超边来判断样本的类别。通过在15个UCI数据集上的实验结果表明,模糊超网络具有较高的适用性,在不同的数据集上都能取得较好的分类效果。但是,随着训练样本数量的增大,模糊超网络模型在初始化阶段生成的超边越多,模型在演化训练阶段所消耗的时间越长,最终会导致算法的运行时间较长,因此提高算法处理大数据的时间效率将是接下来的研究重点。
| [1] |
RIZA L S, JANUSZ A, BERGMEIR C, et al. Implementing algorithms of rough set theory and fuzzy rough set theory in the R package " RoughSets”[J]. Information sciences, 2014, 287: 68-89. DOI:10.1016/j.ins.2014.07.029 ( 0) 0)
|
| [2] |
ZHANG Yu. Research on extension of the fuzzy rough set theory[J]. Advanced materials research, 2012, 532-533: 1472-1476. DOI:10.4028/www.scientific.net/AMR.532-533 ( 0) 0)
|
| [3] |
陈德刚. 模糊粗糙集理论与方法[M]. 北京: 科学出版社, 2013.
( 0) 0)
|
| [4] |
王进, 朱文晓, 孙开伟, 等. 基于残差超网络的DNA微阵列数据分类[J]. 重庆邮电大学学报 (自然科学版), 2015, 27(5): 647-653. WANG Jin, ZHU Wenxiao, SUN Kaiwei, et al. Using residual hypernetwork for the classification of DNA microarray data[J]. Journal of Chongqing University of Posts and Telecommunications (natural science edition), 2015, 27(5): 647-653. (  0) 0)
|
| [5] |
王进, 张军, 胡白帆. 结合最优类别信息离散的细粒度超网络微阵列数据分类[J]. 上海交通大学学报, 2013, 47(12): 1856-1862. WANG Jin, ZHANG Jun, HU Baifan. Optimal class-dependent discretization-based fine-grain hypernetworks for classification of microarray data[J]. Journal of Shanghai Jiaotong University, 2013, 47(12): 1856-1862. (  0) 0)
|
| [6] |
王进, 黄萍丽, 孙开伟, 等. 基于演化学习超网络的微阵列数据分类[J]. 江苏大学学报 (自然科学版), 2014, 35(1): 56-62. WANG Jin, HUANG Pingli, SUN Kaiwei, et al. Microarray data classification based on evolutionary learning hypernetwork[J]. Journal of Jiangsu University (natural science edition), 2014, 35(1): 56-62. (  0) 0)
|
| [7] |
王进, 丁凌, 孙开伟, 等. 演化超网络在多类型癌症分子分型中的应用[J]. 电子与信息学报, 2013, 35(10): 2425-2431. WANG Jin, DING Ling, SUN Kaiwei, et al. Applying evolutionary hypernetworks for multiclass molecular classification of cancer[J]. Journal of electronics and information technology, 2013, 35(10): 2425-2431. (  0) 0)
|
| [8] |
王进, 金理雄, 孙开伟. 基于演化超网络的中文文本分类方法[J]. 江苏大学学报 (自然科学版), 2013, 34(2): 196-201. WANG Jin, JIN Lixiong, SUN Kaiwei. Chinese text categorization based on evolutionary hypernetwork[J]. Journal of Jiangsu University (natural science edition), 2013, 34(2): 196-201. (  0) 0)
|
| [9] |
王进, 孙开伟, 李钟浩. 超网络道路限速标志识别[J]. 小型微型计算机系统, 2012, 33(12): 2709-2714. WANG Jin, SUN Kaiwei, LI Zhonghao. Hypernetworks for road speed limit sign recognition[J]. Journal of Chinese computer systems, 2012, 33(12): 2709-2714. DOI:10.3969/j.issn.1000-1220.2012.12.027 (  0) 0)
|
| [10] |
齐亚丽. 基于模糊粗糙集属性约简方法的研究[D]. 锦州: 渤海大学, 2016. QI Yali. The research of attribute reduction method based on fuzzy rough sets[D]. Jinzhou: Bohai University, 2016. (  0) 0)
|
| [11] |
LI Xingyi, LI Xueling, SHI Huaji. Case based reasoning based on fuzzy rough set[C]//Proceedings of the 2nd IEEE International Conference on Information and Financial Engineering. Chongqing, China, 2010: 778–782.
( 0) 0)
|
| [12] |
王世强, 张登福, 毕笃彦, 等. 基于模糊粗糙集和蜂群算法的属性约简[J]. 中南大学学报 (自然科学版), 2013, 44(1): 172-178. WANG Shiqiang, ZHANG Dengfu, BI Duyan, et al. Attribute reduction method based on fuzzy rough sets and artificial bee colony algorithm[J]. Journal of Central South University (science and technology), 2013, 44(1): 172-178. (  0) 0)
|
| [13] |
WANG Xueen, HAN Deqiang, HAN Chongzhao. Fuzzy-rough set based attribute reduction with a simple fuzzification method[C]//Proceedings of the 24th Chinese Control and Decision Conference. Taiyuan, China, 2012: 3793–3797.
( 0) 0)
|
| [14] |
HU Feng, SHI Jin. Neighborhood hypergraph based classification algorithm for incomplete information system[J/OL]. Mathematical problems in engineering, 2015, Article ID 735014, DOI: 10. 1155/2015/735014.
( 0) 0)
|
| [15] |
KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. San Francisco, CA, USA, 1995: 1137–1143.
( 0) 0)
|
| [16] |
HU Feng, LIU Xiao, LU Xi. A novel cost sensitive classification algorithm based on neighborhood hypergraph[J]. Journal of computational information systems, 2015, 11(1): 109-121. ( 0) 0)
|
| [17] |
HU Feng, LI Hang. A novel boundary oversampling algorithm based on neighborhood rough set model: NRSBoundary-SMOTE[J]. Mathematical problems in engineering, 2013, 2013: 694809. ( 0) 0)
|
| [18] |
LUO Yueguo, XIONG Zhongyang, XIA Shuyin, et al. Classification noise detection based SMO algorithm[J]. Optik-international journal for light and electron optics, 2016, 127(17): 7021-7029. DOI:10.1016/j.ijleo.2016.05.018 ( 0) 0)
|
| [19] |
路敦利, 宁芊, 臧军. 基于BP神经网络决策的KNN改进算法[J]. 计算机应用, 2017(S2): 65-67. LU Dunli, NING Qian, ZANG Jun. Improved KNN algorithm based on BP neural network decision making[J]. Journal of computer applications, 2017(S2): 65-67. (  0) 0)
|
| [20] |
袁梅宇. 数据挖掘与机器学习: WEKA应用技术与实践[M]. 2版. 北京: 清华大学出版社, 2014.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


