2. 诸暨市联系数学研究所,浙江 诸暨 311800
2. Institution of Zhuji connection Mathematics, Zhuji 311800, China
集对分析自赵克勤于1989年提出以来,已在包括人工智能在内的众多领域得到广泛应用。在中国知网上,用主题词“集对分析”,检索到2 000多篇文献,其中外文文献100多篇,内容涉及航空航天、军事国防、气象预报、水文水资源、生态、环境、矿山、地质、能源、交通、城市建设、社会经济、机电制造、邮电通信、物流、农业、林业、医药、卫生、教育、体育、安全与非传统安全、系统工程与管理决策、计算机与人工智能等[1],与此同时,出版集对分析专著14部[2-15]和一本论文集[16];本文在笔者早期曾经综述集对分析理论和应用研究进展的基础上[17],主要综述集对分析在人工智能中的已有应用,简介集对分析最新进展中与人工智能有关的“自然智能”“智脑”“集对人”等新理念,促进集对分析的进一步发展及其在人工智能中的进一步应用[18-19]。
1 集对分析的理论与联系数 1.1 基本原理成对原理和系统不确定性原理是集对分析的2个基本原理。
成对原理 指“事物(或概念)成对存在”,最早在文献[20]中提出。
时间与空间、物质与能量、物质与信息、信息与知识、知识与智能,以及人的2只眼睛,2只耳朵、2个鼻孔、2只手、2条腿等,都是成对存在的例子。
从哲学看,成对原理是事物普遍联系原理和对立统一的换一种说法。但成对原理为提出集对和集对分析提供了一种思想指导,也为人工智能提供了一种思想指导。例如,在成对原理指导下,当人们创建一种人工智能理论时,会考虑是否同时去创建与之成对的另一个理论;当人们发现一项新的智能技术时,会思考与之成对的另一项智能技术。其客观效果是让人们智慧地研究人工智能,智慧地发展人工智能。
事实上,人工智能可以看成由“人工”与“智能”构成的对子;“人工”是“人”与“工”构成的对子,“智能”是“智”与“能”构成的对子;即便是人工智能的英文“artificial intelligence”,也可以看成由 “artificial ”与“intelligence”构成的对子,等等。
不确定性原理 通常指由德国物理学家海森堡于1927年提出的“测不准原理”:一个微观粒子的某些物理量,例如位置和动量、方位角与动量矩、时间和能量等,不可能同时具有确定的数值,其中一个量越确定,另一个量的不确定程度就越大。测量一对共轭量的误差的乘积必然大于常数h/(2π)(h是普朗克常数)。“测不准原理”反映了物质世界中微观粒子运动的基本规律,是现代物理学的一个基本原理。
“测不准原理”对系统分析的启示在于:当分析进入到系统的微观层次时会遇到部分系统参数不能确定的问题。
问题在于,微观是一个相对的概念。例如:在人工智能中,智能科学是宏观,智能技术是微观;智能理论体系是宏观,某个理论细节是微观;智能机器是宏观,智能思维是微观;机器整机是宏观,机器零件是微观;机器硬件是宏观,机器软件是微观;在机器的信息处理中,机器的信息输入与输出是宏观,信息在机器内部处理是微观,等等。这就意味着,当把某一事物宏观表现与微观表现联系在一起作全局性的系统分析时,不可避免地存在不确定性,这种不确定性首先来自系统宏微层次划分的相对性和系统宏微边界的模糊性,其次来自系统宏微层次的相互渗透与动态迁移。因此,当对某一问题作系统性研究时,其研究过程和研究结果会不可避免地存在这种或那种不确定性。这一原理简称为“系统不确定性原理”或“全局不确定性原理”,也可以看作前述成对原理的一个派生原理:系统的确定性与不确定性成对存在。
1.2 基本理论系统不确定性理论与同异反系统理论是集对分析的2个基本理论,这2个理论的核心思想是系统中的不确定性与确定性成对存在,相互联系,相互作用,在一定条件下相互转化。当系统的不确定性趋于极限时,不确定性系统(理论)就转化为同异反系统(理论)。集对分析的这2个基本理论既是系统的,也是数学的,且具体蕴含在集对分析创建的联系数中,这两个理论的要点与联系数的对应阐述详见文献[18-21]。
1.3 联系数联系数是集对的特征函数,也是集对分析中数学建模的一个重要数学工具,最早形成于赵克勤对集合论中罗素悖论的解读。
罗素悖论也称理发师悖论:村上有一个理发师,约定为所有不能为自己理发的人理发,但遇到自己的头该由谁理的困惑,他若为自己理发,按约定他不能为自己理发;他不为自己理发,按约定他得为自己理发;罗素悖论曾引发历史上第三次数学危机。集对分析用集合
| $\mu = a + bi$ | (1) |
| $\mu = a + bi + cj$ | (2) |
| $\mu = a + bi + cj + dk$ | (3) |
| $\mu = a + bi + cj + dk + el$ | (4) |
| $\mu = a + bi + cj + dk + el + \cdots + xy$ | (5) |
| $\mu = \left[ \begin{array}{l} a{_1} + b{_1}i + c{_1}j + d{_1}l + \cdots \\ a{_2} + b{_2}i + c{_2}j + d{_2}l + \cdots \\ \quad\quad\quad\quad \vdots \\ a{_n} + b{_n}i + c{_n}j + d{_n}l + \cdots \end{array} \right]$ | (6) |
| $ \partial \mu = \partial a + \partial bi + \partial cj + \cdots $ | (7) |
| $ {\partial ^2}\mu = {\partial ^2}a + {\partial ^2}bi + {\partial ^2}cj + \cdots $ | (8) |
| $ \vdots $ |
| $ {\partial ^{n - 1}}\mu = {\partial ^{n - 1}}a + {\partial ^{n - 1}}bi + {\partial ^{n - 1}}cj + \cdots $ | (9) |
式(7)~(9)为全偏联系数,由偏正联系数与偏负联系数组成的代数和。一个
| $ \begin{array}{l} {\partial ^2}\mu = {\partial ^{2 + }}\mu + {\partial ^{2 - }}\mu =\displaystyle \frac{{\displaystyle\frac{a}{{a + b}}}}{{\displaystyle \frac{a}{{a + b}} + \displaystyle\frac{b}{{b + c}}}} +\displaystyle \frac{{\displaystyle \frac{b}{{a + b}}}}{{\displaystyle\frac{b}{{a + b}} + \displaystyle \frac{c}{{b + c}}}}j = \\ \qquad\displaystyle\frac{{\displaystyle \frac{a}{{a + b}}}}{{\displaystyle \frac{a}{{a + b}} +\displaystyle \frac{b}{{b + c}}}} - \displaystyle\frac{{\displaystyle \frac{b}{{a + b}}}}{{\displaystyle \frac{b}{{a + b}} + \displaystyle\frac{c}{{b + c}}}} \end{array} $ | (10) |
式(10)是一个没有不确定系数
式(1)~(10)蕴含着基于集对分析的不确定系统理论的全部内容,具体解释见文献[23-24]。
把基于联系数的建模和计算与针对不确定性的系统分析有机结合,是集对分析处理不确定性问题的核心技术,在人工智能研究中得到广泛应用。
2 集对分析在人工智能基础研究中的应用 2.1 智能的定义什么是智能?这是人工智能的一个基础问题。学术界对智能有多种定义。如文献[25-26]中有:“智能是一种应用知识处理环境的能力,或者是由目标准则衡量的抽象思考能力”,以及“人的智能是人类理解和学习事物的能力”,等等。
鉴于人工智能在近几十年中不断从生物行为中受到启发而开发出种种智能算法,如蚁群算法、遗传算法等,也从某种无机物的自然现象中受到启发而开发出诸如模拟退火算法等其他智能算法,特别是计算机和机器人这类无机物不仅已经有一定的智能而且还在日益增加智能。因此,从实际出发,需要从一个更为一般、更为基础的角度定义什么是智能。所以笔者在文献[15]中根据集对分析关于事物或概念成对存在原理,给出一个智能新定义:智能是系统存在和发展并与环境联系的一种能力。
根据“智能是系统存在和发展并与环境联系的一种能力”这个新定义可知:智能不仅仅是人的专利,人之外的生物,如动物和植物,也具有智能,后者如向日葵、含羞草等;智能也不仅存在于有机物和生物界中,无机物和无机界中也存在智能,例如,两物体相撞时作用力与反作用力大小相等,方向相反,分别作用在这两个物体上,说明相撞的这两个物体有“以牙还牙”这种高级智能。又如撤销外力后恢复原始状态的弹簧,具有记忆的材料等无机物具有简单智能,至于地球围绕太阳公转的同时还有自转以保持这种运动长期维持,说明人类居住的地球也具有相当智能,2017年地球人接收到13亿年前宇宙深处两个黑洞碰撞归并发出的引力波,验证了爱因斯坦“运动着的物质在告诉时空如何弯曲,弯曲的时空在告诉物质如何运动”,空间与空间中运动的物体相互传递信息、相互作用的假设;推而思之,可知自然界乃至整个宇宙,都具有某种智能,原因在于自然界中的各种物质和物体都以系统的形态而存在,都有为了自身的存在和发展与环境联系的能力,因而都具有智能。显然,应当承认这种智能,称其为系统的自然智能,或简称系统智能或自然智能,或直称智能。
2.2 自然智能的科学原理迄今为止,人们对自然智能的认识和理解,集中在以下10个科学原理的认识和应用上。
原理1 联系原理 客观事物处在相互联系之中。
原理2 对立统一原理 对立的双方共处于一个统一体中。
由于在各种各样的联系中,2个事物的联系是一种最基本的联系,再结合对立统一原理,可以引出以下的成对原理。
原理3 成对原理 事物或概念都成对存在。
原理4 系统不确定原理 组成系统的要素存在确定性关系的同时,存在不确定性关系。
原理5 相互作用原理 联系着的2个或2个以上事物存在相互作用。
相互作用原理也是哲学、物理学和其他学科公认的一个科学原理。
根据相互作用原理可知,在给定的时空中,物质和能量存在相互作用,从而使物质产生运动。在有人参与的物质运动中,人与物质运动构成事,因此事物处在运动之中,由此引出运动原理。
原理6 运动原理 客观上存在的事物总是处于运动之中。
由于具体的事物运动总是在一定的时空中展开,根据相互作用原理和时间的单向性可知,事物的运动具有方向性,对这种方向性设定适当的起点后,也称事物运动具有发展性,简称事物的发展,所以运动原理也可以称为事物的发展原理。
原理7 关联原理 联系着的2个或2个以上事物与他们在相互联系过程中因相互作用而产生的新事物存在关联。
关联原理可以看作相互作用原理的一个二级原理,也可以看作联系原理的三级原理。根据这个原理,得到以下命题。
命理1 信息是物质与能量相互作用的产物。
命理2 物质、能量、信息3者之间存在关联。
根据命题1和命题2,得到以下推论。
推论1 信息具有一定的物质与能量。
推论2 信息具有不确定性。
原理8 最小作用量原理 自然界中存在的各种系统总是通过消耗最小能量与其他系统发生联系,以利于系统自身的存在和发展。
最小作用量原理提示系统天然地具有价值意识,也就是以最小的成本获得最大收益。
原理9 能量转换与守恒原理 在自然界的各种变化中,能量既不会无中生有,也不会自行消灭,只会从一种形式转化为另一种形式,转换前后的总能量恒定。
信息作为物质与能量的一个相互作用产物,其所具有的能量,在文献[15]中称为信息能,在不同信息形式的转换中也同样守恒,包括信息转换成智能后仍然守恒。
原理10 功能原理 功能原理是能量转换与守恒原理的一个派生原理,其本质是能量在转化过程中会有能量消耗,但得到的新能量与消耗掉的能量总和不变。
随着科学发展,人们还会发现新的科学原理。但我们相信,新的科学原理与已知的科学原理都是自然智能的具体体现。
2.3 人工智能认识到自然具有智能和自然智能所依据的科学原理,就不难推出人所具有的智能本质上由自然赋予。自然借助各种联系,特别是借助地球这个具有相当智能的星球创造了人,并缓慢地、有序地、持续不断地赋予人以智能,使人得以生存和不断发展进化。如今,人又根据已知的科学原理把自然赋予的智能经过加工和制造,有目的地传递和赋予给人所创造的机器和其他有关系统,让机器和其他有关系统帮助人更好地认识自然、利用自然和开发自然,这就是人工智能,从而把人工智能看成人类进化过程中的一个必然事件。
不难认同,到目前为止,人与自然界和宇宙具有的智能相比,仅具有非常有限的一部分智能,人所不知道的远远超过所知道的。人是自然的产物,自然是人的母亲。人与自然应当和谐相处,知恩图报,知恩共存。人与宇宙相比,不过是沧海一粟,或许连沧海一粟也谈不上。人在懂得人之伟大的同时,也要懂得人之渺小。
显然,上面给出的智能和人工智能新定义有助于消除人们对人工智能不断发展引起的恐惧,也加强人对自然的敬畏,不断探索自然的秘密,感悟和学习自然智能,有利于人的智能不断成熟和人工智能的不断发展。
说到人工智能,不能不提到人工智能三大学派。
人工智能从20世纪50年代提出以来,长时期在实用价值的引导下对人工智能基础多头探索,客观上形成符号主义、联结主义、行为主义三大学派。但从前述系统自然智能的角度看,这三大学派本质上是技术型的,其科学基础仍然是前述的10个原理;但集对分析在技术层面上也可以对各个学派提供理论支撑[27]。
首先,集对分析支撑行为主义。行为主义认为,系统的智能活动是基于“感知和行动的”。从集对分析角度看,感知和行动是一个集对。一般来说,人对外界的感知和一定的行动相对应。但是在很多情况下,一定的感知可以有不同的行动与之对应;反过来也是如此,即同一行动可以有多种不同的感知与之相对应。换言之,这中间既有一定的规则可以让系统或机器遵循,同时又存在不确定性可以使系统或机器灵活地加以选择执行。对于这样的一种智能机制,可以用集对分析联系数进行描述并开展进一步的分析。
其次,集对分析支撑联结主义。联结主义认为,人脑思维的基元是神经元,神经元与神经元之间以不同的方式联结形成不同的结构,不同的结构具有以不同的方式进行信息处理和交换的功能,在此基础上形成人的智能活动;联结主义也称结构(功能主义)。从集对分析角度看,两个神经元的联结是一种基本的联结形式,这正好由“集对”这个概念来担当。而且,不管人脑的神经元结构有多么复杂,在结果处理上总不外乎同(与给定的目标一致)异(与给定的目标有差距)反(与给定的目标价值相矛盾),并可以在一定条件下对“同异反”程度展开度量。也就是,同时显示出某种数量上的简单性,类似于将集对分析联系数作了复杂的运算后,其结果仍然是一个看上去有同异反平凡结构的联系数,因此集对分析同时是对联结主义(结构功能主义)的一种支撑。
第三,集对分析支撑符号主义。符号主义认为,思维的基元是符号,思维过程是有关符号的运算和逻辑推理,符号主义也称形式主义,计算机的全部运算和推理都是借助形式上的各种特定符号进行。集对分析强烈支撑符号主义是因为:首先,有关联系数的运算就是一种符号运算,按集对分析理论,运算结果的“同异反”是什么含义,要结合具体问题背景加以理解;其次,集对分析认为,从已知两个集合的“同”可以在一定条件下得出这两个集合的“异”和“反”。反之亦然,即从两个集合的“反”也可以得出这两个集合的“同”和“异”(参见后面的7.3节);“异”中则自然地蕴含着“同”和“反”。显然,这里对条件和背景的选择有独特的意义,一切随条件和背景的改变而改变,同样的符号在不同的条件和背景下完全可以有不同的含义。再次,集对通过自身的特征函数进行集对运算,本身就是一种符号运算。
综上所述,人工智能领域中的符号主义、联结主义、行为主义都可以都得到集对分析的理论支撑和方法论支撑,原因就在于集对分析既支撑3大学派中被确定部分的公知,也支撑不确定部分的争论,进一步把确定的部分与不确定的部分联系起来。
3 集对分析在模式识别中的应用 3.1 基于集对分析的同异反模式识别技术该技术分为基于联系数的同异反定量模式识别和定性与定量相结合的同异反模式识别,前者又分为:
1) 基于联系数伴随函数的模式分类
设
2) 基于同异反距离的模式分类
白杨文于1996年给出同异反距离模式识别的择优原则和择近原则[28]。择优原则是指预先有优化准则或有优化目标时,用最优化方法寻找出最优的模式;择近原则是一一计算待需要识别的n个模式与事先给定模式的距离,按距离的由小到大次序确定与事先给定模式的“同(最接近事先给定模式)异(与事先给定模式有一定距离)反(与事先给定模式有较大距离)”。当“同异反”是相对独立和有确定的属性且不计较“异”的不确定性时,同异反模式识别结果是一个唯一确定的结果;当计及同异反中“异”的不确定性时,同异反模式识别结果需要通过不确定性分析后才能给出结论。当没有事先给定的模式时,可以在给出的n个模式中先根据某种准则(如最优指标集)找出最优模式作为标准模式,再根据择优原则和择近原则实现模式的同异反识别和聚类。
3.2 基于集对分析的指纹识别成科扬在文献[29]中基于集对分析建立了一套新型的指纹识别系统,基本思路:把模板指纹的所有特征组成集合
该识别系统的主要步骤如下:
1) 确定各个指纹特征的权系数
因为指纹特征点的类型、欧氏距、相对角、至中心所穿纹线数等几个属性在判断两枚指纹对应特征点是否匹配的决定性作用不一,所以要对各属性确定其权系数。因此用专家定权法确定指纹特征点类型、欧氏距离、相对角、至中心所穿纹数这4个属性的权重。
2) 选取待识别指纹的特征点
对于预处理过的指纹图象,可提取两类特征点:纹线的端点和分叉点。其他类型纹线特征均可以被分解成这两类加以提取,纹线中的眼、桥、剪刀形交叉均可以拆分成两个纹线分叉点,图象中的孤立点不予提取,如图1。

|
Download:
|
| 图 1 特征点提取 Fig. 1 Feature point extraction | |
3) 确定特征点的属性
任取一特征点,以此为中心,辐射状向外搜索,直至某一定值R为止。在此范围之内,记录其所搜索到的其他特征点的类型、相对角、欧氏距、至中心所穿纹线数等,如图2所示,并将此作为该中心特征点的属性。图2中,O为中心点,
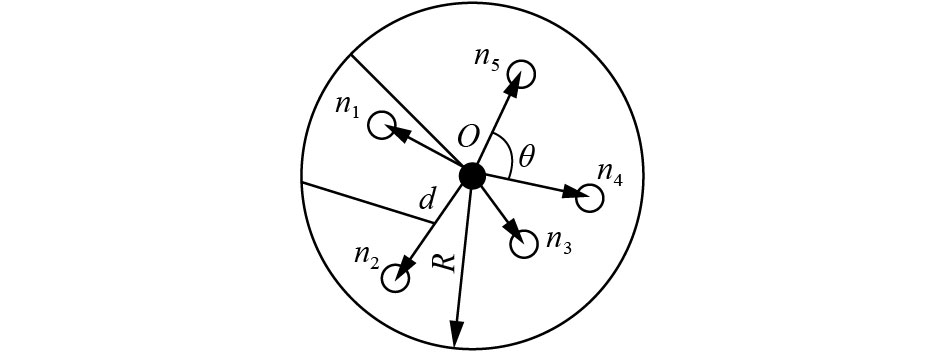
|
Download:
|
| 图 2 特征点的属性 Fig. 2 Feature points’ properties | |
4) 确定各对应特征点对的联系数
任取两个分别来自模板指纹和待识指纹的特征点,设此两中心特征点在R范围内分别有N1、N2个卫星特征点。对于类型、相对角、欧氏距、至中心所穿纹线数等属性分别求该两中心特征点在其上的联系度,即
| ${\mu _{ijk}} = {a_{ijk}} + {b_{ijk}}i + {c_{ijk}}j$ | (11) |
式中:
| ${a_{ijk}} = {N_a}/N$ | (12) |
| ${b_{ijk}} = {N_b}/N$ | (13) |
| ${c_{ijk}} = {N_c}/N$ | (14) |
式(12)~(14)中
5) 指纹图像匹配的确定
设待识指纹特征点
| ${R_{ij}} = \left| {{{\left[ {{f_1}\,\,\,\,{f_2}\,\,\,\,\cdots \,\,\,\,{f_m}} \right]}^{\rm{T}}} \times [{\mu _{ij1}}\,\,\,\,{\mu _{ij2}}\,\,\,\,\cdots \,\,\,\,{\mu _{ijm}}]} \right|$ | (15) |
当
李德顺等[30]把基于集对分析的同异反模式识别用于金属矿山地质灾害模式判断。高洁等[31]提出一种基于集对分析同异反模式识别的聚类预测法。该方法融合集对分析中的同异反模式识别的“择近原则”和聚类分析的基本思想,应用于邮电业务总量预测有较好效果。阎理等[32]给出了基于集对分析的系统相似识别方法和应用实例。刘秀梅等[33]把同异反模式识别技术用于不确定空情意图识别,改进了前人得到的结果。张秀辉等[34-35]把集对分析用于雷达信号分选和图像边缘检测。
4 集对分析在不确定性推理中的应用 4.1 基于赵森烽−克勤概率的不确定性推理文献[36]给出了一种不同于经典概率的赵森烽−克勤概率,其特点是把观察者关注的主事件概率与非主事件概率联系起来,合写在同一个概率表达式中,也称联系概率,还给出了基于这种新概率的不确定性推理示例;与基于经典概率的不确定性推理不同之处在于:推理结果中既包括了基于经典概率的推理结果(相当于主事件的推理结果),也包括了非经典概率的推理结果(相当于非主事件概率的推理结果),还包括了上述2种推理结果的相互转换机制。
4.2 基于集对分析的同异反推理同异反推理是集对分析中的同异反系统理论的具体应用,实质是不确定性趋向极限时的一种推理,其一般的推理模式图3所示。
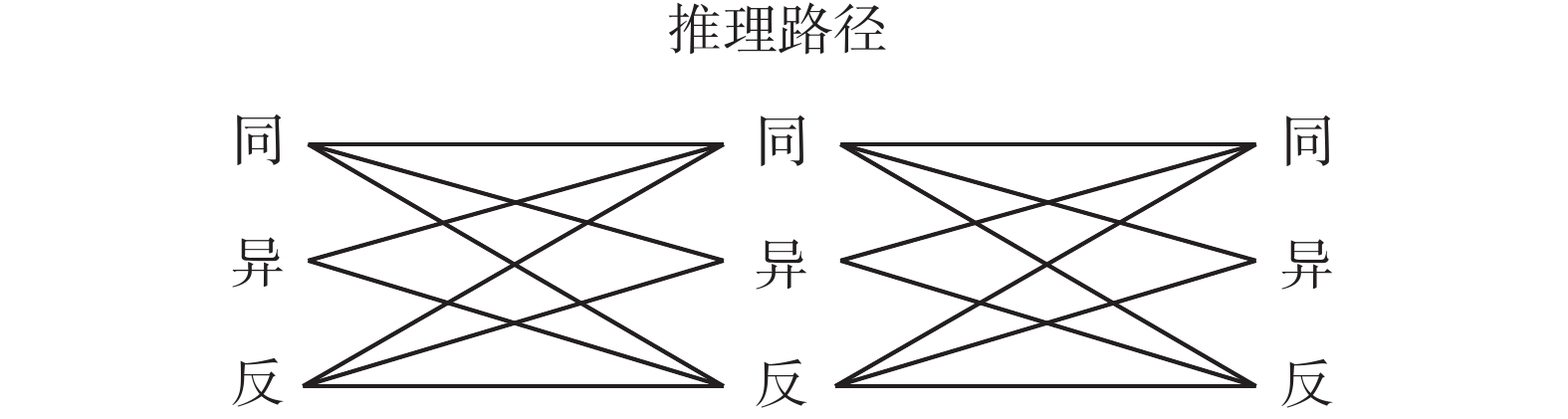
|
Download:
|
| 图 3 同异反系统推理示意 Fig. 3 Reasoning of the same difference contradiction system | |
图3的左侧同异反指已知条件系统,中间的同异反指推理路径,右侧的同异反指推理结果;其同异反含义需结合实际问题定义或赋值,详见文献[37]。
4.3 基于集对分析的推理应用实例马守明等[38]利用集对分析的同异反系统理论,提出一种利用同异反向量夹角余弦对不确定性上下文进行推理的方法,并用于智能空间场景中不确定上下文状态推理的实例分析,概念清晰、计算简明,具有较强的实用价值和较高的可靠性。
阎红灿等[39]给出了基于集对分析的案例检索模型,思路是把目标案例与案例库中源案例建立集对,利用属性重要度和联系度构建本体案例检索模型,通过本体的词义扩展解决检索词的多词同义问题,有效提高了不确定性案例的检索精度,运算量少,查全率和查准率较海明距离法高。
5 集对分析在智能决策中的应用 5.1 同异反智能决策同异反智能决策也简称同异反决策,是集对分析同异反系统理论在决策中的具体应用,同异反决策一词最早见于文献[40],之后不断发展完善,根据文献[15]所述,同异反智能决策的一般步骤如下:
1) 作系统在正常情况下的决策;
2) 作系统在异常情况下的决策;
3) 作系统在反常情况下的决策;
4) 作系统在正常情况兼有异常情况下的决策;
5) 作系统在正常情况、异常情况、反常情况依次出现、交替出现、同时出现、随机出现情况下的决策;
6) 作系统在同异反不同情况下的综合决策;
7) 作系统在多种不确定性情况下的综合决策,具体结合各种不确定性因素的分析和联系数中i的不同取值展开讨论,评价决策风险;
8) 利用同异反数据作出评价系统潜在发展趋势的判断;
9) 利用同异反数据作评价系统显在发展趋势的判断;
10) 根据同异反数据确定的联系数的其他伴随函数进行决策等。
由此可知,同异反决策具有确定性建模和不确定性系统分析集成,同异反集成、定性决策与定量决算集成等特点简称为集成决策。
5.2 同异反智能决策的应用刘秀梅等在文献[8]中介绍了把集对分析同异反决策思想用于区间数决策非集对分析建模改进,共有23个实例支持基于集对分析的同异反决策优越于其他非集对分析决策建模,其机制就在于对区间数决策作联系数建模计算的同时,作系统不确定性分析[41];赵森烽等[42]给出了基于赵森烽−克勤概率的智能风险决策模型;吴爱燕等[43]把集对分析与云模型结合,给出基于集对云的多属性群决策方法和应用实例,等等。
6 集对分析在知识生态学中的应用 6.1 知识生态集对分析的原理知识是人们认识客观世界的结晶。知识来自社会实践又被社会实践所反复证明其客观性、合理性、科学性。随着科学技术发展和社会进步,传统知识不断被新知识补充、扩展甚至替代,不同领域的知识更新呈现出类似于作物群落新陈代谢的生态学现象,由此引出的知识生态学概念被人们接受;知识工程则被看作知识生态学中的一门技术性学科;不同时空中的智脑群落在新陈代谢着的知识,构成了不同的知识生态,既相互依赖、相互补充,又相互竞争、进化。
首先,知识从发现到形成需要一个过程,这个过程可长可短,但不可能没有过程。如果把知识的发现作为一个集合,把知识的最终形成作为另一个集合,知识从发现到形成的过程就是把这2个集合联系起来的一个集对,这是知识与知识生态集对分析的第一原理,也称知识生态的过程原理,根据这个原理可以用特定的集对表示一种特定的知识。
其次,知识从发现到形成的过程中要接受社会实践的反复证明,历经由粗到精、由表到里、由浅入深、由零星到系统、由低级到高级的反复证伪证实。在这个过程中,知识的一部分被沉淀和积聚,表现出确定性;另一部分则表现为不确定性。因此,就知识的系统性、完整性、有效性看,一种特定的知识是表现为确定的知识和表现为不确定知识的对立统一体,这是知识与知识生态集对分析的第二原理,也称知识生态的确定-不确定原理。至于那些已经完全地表示为确定的知识,可以视为其中的不确定性知识已经转化为确定的知识,或者看成是确定的知识和不确定知识对立统一体中的一个相对稳定的部分。
再次,知识总是被发现、被表达、被转移、被学习、被掌握、被使用、被发展、被完善、被创新等,这说明知识是被动的,人是主动的。因此,如果把人与知识构成一个集对,则人与知识这个集对是一个有主次关系的集对,这是知识生态集对分析的第三原理,简称知识与知识生态的主次原理。
第四,知识需要传承,从知识生态学角度看,知识的传承相当于知识的播种,一定的知识被播种在适当的土壤中,会在适当的时空中生长、开花、结果;又通过对果实的筛选,存优去劣,被再度播种,代代相传并不断进化;若把上下两代知识作为2个不同的集合,则代代之间的知识传承可以作集对分析,这是知识与知识生态集对分析的第四原理,简称知识与知识生态的传承原理。
第五,历史表明,人类的知识在不断增长,新的知识不断地在替代旧的知识并快速地用于不同问题的求解,从而使不同领域的知识更新呈现出类似于作物群落新陈代谢的生态学现象。因此,如果把已有的旧知识作为一个集合,把新知识作为另一个集合,则得到由新旧知识组成的集对。新旧知识的相互联系、交互交叉、中介过渡,以及对立互补等分析,就是一个以新旧知识关系为研究内容的集对分析,这是知识与知识生态学集对分析的第五原理,也称知识与知识生态的新陈代谢原理,或简称为知识新陈代谢原理。
知识与知识生态学集对分析的上述5个原理决定了集对分析在知识生态学中的应用有丰富内容,核心技术依然是确定性的知识建模与不确定性知识的系统分析有机结合。
6.2 知识的同异反创新规律与同异反知识体系知识的同异反创新规律如图4所示。

|
Download:
|
| 图 4 同异反知识创新 Fig. 4 Innovation in the same difference contradiction knowledge | |
图4中的“S”是“Same”的第一个字母,指新的知识与已有知识“同”,“D”是“Difference”的第一个字母,指新的知识与已有知识“异”,“C”是“Contradiction”的第一个字母,指新的知识与已有知识“反(对立或矛盾)”,知识综合创新时,可把上述同异反分枝图倒过去用。由图4看出,知识创新是一个不断深入细化的过程,也是不断综合归并的过程;但从另一个侧面看,知识创新不仅是一个体系,而且是一个复杂的过程,见图5。

|
Download:
|
| 图 5 同异反知识系统展开 Fig. 5 Expansion of the same difference contradiction system | |
要说明的是,按图5给出的知识由同一性知识Ks、差异性知识Kd、对立性知识Kc 3部分组成之说,仍需明确它们之间的层次关系。按人们的认知习惯和到目前为止对知识概念的理解要求,通常把同一性知识视为知识的核心位置,其现实意义是新的知识应当与已有的知识“兼容同一”,方能被已有的知识接受;差异性知识处于核心层外面,对立性甚至是矛盾的知识则在差异性知识的外层,因此是一个洋葱模型;这符合知识创新实际;一定意义上,知识创新是一个由试错到准确、由假设到证实,由表及里、由此及彼的过程。这从一个侧面说明了知识创新过程的风险性和艰巨性,从历史唯物主义的角度看,整个人类历史都可以看作是一个知识创新的过程。人类的社会实践是在经历了无数的失败、挫折、彷徨,甚至付出一代又一代的巨大牺牲之后,才正确地认识到了客观世界中极为有限的一部分知识。
6.3 应用实例余国祥[44]把集对分析用于默会知识与显性知识的联系与转换研究,指出默会知识与显性知识之间存在中介知识,教师是这种中介知识的创造者和应用者,教学过程是教师和学生借助中介知识领会和掌握默会知识与显性知识的过程。徐忆琳[45]一般性地研究了知识创新规律,图4来自徐忆琳的工作。杜春彦等[46]基于集对分析给出了一种知识的不确定描述及其传播算法,并应用于不确定性推理。张新华等[47-48]分别把集对分析用于技术知识产权评估和武器装备知识产权评估。阮光册[49]基于知识关联思想,把集对分析用于检索结果聚类研究。
总的来说,已有的集对分析应用工作还处于知识工程这个层次上,如何在知识生态学意义上运用集对分析还有待深入研究。
7 集对分析在自然语言和人类语言理解中的应用 7.1 自然语言和人类语言顾名思义,自然语言是自然的语言,这也是基于第2章中提出的自然界本身具有智能的观点。自然语言首先应当从普适意义上理解为自然界自己的语言,是自然界中物质与物质、物质与能量、能量与能量进行相互联系的一种工具和方式,这将有助于人们对自然语言的深入研究和向自然智能不断学习。基于这样的认识,自然界中的雷鸣电闪、风雨霜雪、阳光普照、潮涌潮落、月移星走等,都是一物对他物诉说的语言,懂得这些语言的物体于是有了热涨冷缩,以便更好地保存自己;凝聚汇合,以便积蓄能量与另一类物质或物体抗衡;诞生消亡、以周期性地出现在自然界中等,我们把这类语言称为自然界中存在于无机物之间的无机语言;而对于存在于生物种群之间的花香鸟语、莺歌燕舞、人欢马叫、文本书信这类语言称为有机物之间的有机语言,无机语言和有机语言是构成自然语言的2个大类,若把它们各作成一个集合,则所谓的自然语言就是一个集对。
人是自然的产物,因此人类语言因此是自然语言中有机语言的一个子集。
人类语言包括文字性语言、口语、音乐和肢体语言。文字性语言又分为形式化语言和非形式化语言,形式化语言如数学语言、计算机语言,非形式化语言如各民族文字性语言。口语分为有声口语与无声口语(哑语),音乐也可以看成一种有声口语,哑语可以部分地看作一种肢体语言,但肢体语言并不限于哑语。非形式化语言还有旗语、图语、舞蹈等。
从现状看,人类语言有三大作用:1)满足人与人之间信息与情感的交流,以维系和发展人类社会;2)把人类的语言赋给机器,让机器明白人的意思和理解人的感情,代替人做某些工作;3)设法与地外星人展开交流,虽然目前还没有找到外星人在哪里,是以何种生命形态而存在,更不知道他们使用何种语言,但科学界对于地球外生命的存在确信无疑,找到外星人仅仅是时间问题,一旦找到,第一件事就需要和外星人有信息交流,这种交流需要的语言显然应当是地球人和外星人都能理解的自然语言。从这个意义上也可以看出,不能把当今地球上的人类语言指称为自然语言。
至此,可以给出自然语言和人类语言的以下层次结构图(见图6)。
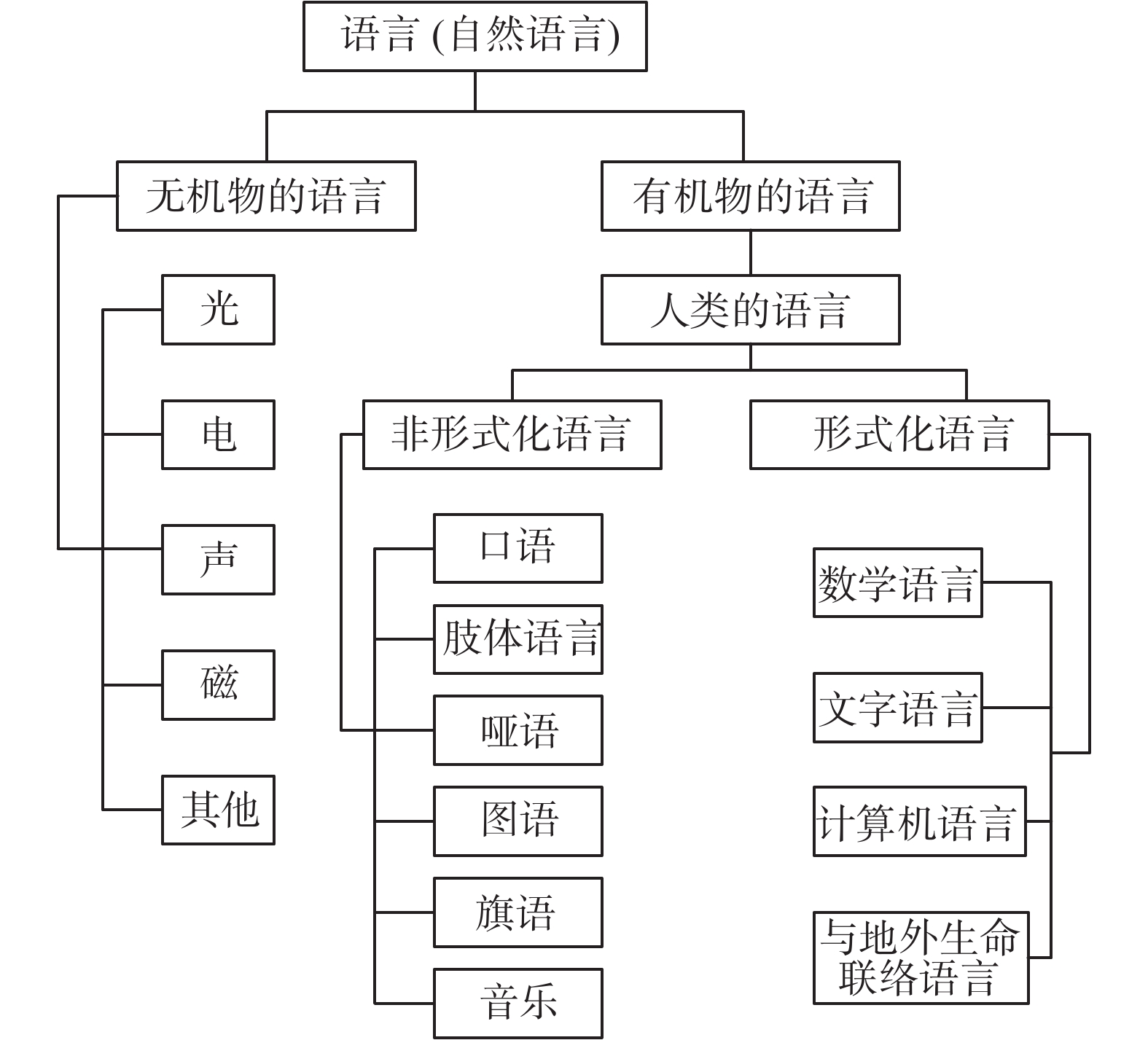
|
Download:
|
| 图 6 自然语言的层次结构 Fig. 6 Natural of languages by hierarchical structure | |
首先,把人类语言理解和人类语言处理看成2个不同的集合,根据集对理论可知这2个集合的关系具有同异反特征。相同点是:人类语言在处理前需要理解,而理解本身也可以看成一种处理,简言之,“理解=处理”。不同点是:在时间上,理解在先,处理在后;在空间上,理解一般在意识时空中进行,而处理多在实时空中进行。以文字语言为例,在实时空中的操作有字与词的分类操作、字与词性标注、字与词义界定、字与词义标注、字与词的搭配关系确定与标注、语句结构分析和标注、语法分析、语义分析和语义判定、段落分析、上下文分析、章节分析、篇目分析、语意和篇意分析等,虽然在这些具体的操作中也或多或少有理解在内,但以操作为主十分明确。特别地,语言理解所在的意识时空和语言处理所在的现实时空,是有一定对立意义的2个时空,实际语言理解和处理在这种双时空中进行的现象符合语言与语言理解的成对原理。
上述关于人类语言理解和处理概念的集对分析表明:人类语言理解贯穿人类语言处理全过程,对于理解的研究应当优先于处理的研究,因此没有对人类语言的理解就没法对人类语言处理。人类语言理解和人类语言处理在意识时空和现实时空中既有分别又可以同时进行表明:人类语言理解和人类语言处理在一定意义上依赖于对这2个时空的认知与研究。但遗憾的是,目前人们对于这2个时空的知识有不少停留在假设的基础上。虽然如此,我们借助集对分析认识到:人类语言理解和处理一般情况下达不到完全同一的境界。
7.3 应用举例1) 中文语义的相反相成
某一体育球赛场中出现了“中国队大胜韩国队”的标语,把这一句理解成中国队打胜了球而同时韩国队输了球,显然符合该语句提出者要表达中国队打胜了球而同时韩国队输了球的意思;但“中国队大败韩国队”,同样可以理解成中国队打胜了球而同时韩国队输了球。这个例子表明,意义相反的字“胜”与“败”,在与其他字和词汇组成同样语句结构的条件下可以有相同意义的理解。相反相同可以看成一种特殊的同异反。
2) 中英文翻译
把中文和英文各组成一个集合,则中文和英文构成一个集对。中英文翻译就是一种特定意义的集对分析。因为中文和英文有各自的文字形式(异),有不同甚至是相反的语法规则(反),中英文翻译要求则是让中英文对话双方能各自理解对方要表达的意思(同),所以中英文翻译是一种特定的同异反集对分析。
3) 语言的联系数刻画
汪新凡[50]还根据多属性决策需要给出了语言变量的联系数表达,如:极差=0.03+0.03i,很差=0.13+0.07i,差=0.3+0.1i,一般=0.5+0.1i,好=0.7+0.1i,很好=0.83+0.17i,极好=0.97+0.03i,
以便于构建决策模型和作出决策。
8 集对分析在专家系统中的应用 8.1 专家系统应用集对分析的原理原理1 成对原理 首先,人机成对存在。专家系统都由人设计研究而成,设计人员与已有的计算机知识有机结合产生专家系统;专家系统的实际应用也由人与机器共同完成,人机交互界面就是人机成对存在相互作用的一个机构,不少情况下由系统给出的推理结论也需要人的认可。其次,专家系统的结构在功能上也成对配制,例如:知识库既存储预先给定的知识,也储存系统在应用过程中所获得的知识;知识库与推理机成对合作完成推理,推理机与解释器成对合作完成解释等。第三,推理机也是在成对原理役使下工作,一般把基于确定性知识的推理与基于不确定性知识的推理相结合后输出推理结果,等等。
原理2 同异反原理 把专家系统中的任意2个部分结构联系起来展开分析,总会看到这两个结构为了实现系统解决同一个问题的需要,在结构上相异甚至有相反的组件;不仅如此,知识库中储存的知识也具有同异反特性;数据库中的数据从时间上可以分为历史数据、近期数据和推测数据;推理结果可能完全符合实际,也可有与实际相异(一定程度上与实际相符)、甚至相反(与实际相距太远)。
原理3 不确定性原理 专家系统依靠知识库中的知识开展工作,尽管这种知识是为解决特定类别的问题预先设置储备,但现实问题具有多样性和不确定性。这种不确定性包括对问题的描述不确切,需要推理的证据不充分,系统对于新知识的理解不准确,系统所在的工作环境不理想,等等。从严格意义上说,专家系统通常是在具有不确定性的环境下接受和处理各种不确定性问题,因此可以应用集对分析的不确定性系统理论来研究和处理专家系统面临的各种不确定性问题。
8.2 集对分析在专家系统中的应用举例例1 徐峰[53]依托“863”计划中的“网络化农业病虫害远程诊断平台与示范”和“数字畜牧业精细养殖平台技术研究与示范”课题,针对现有猪病诊断专家系统的不足,把集对分析用于新型猪病诊断专家系统的研制,解决了生猪养殖实践中猪病诊断这一难题。
例2 食品安全是关乎国计民生的重大问题。徐超[54]依托国家质检总局科技计划项目(CAIQ—20I0IK155)、湖南省科技重大专项“湖南省食品安全监控技术体系研究与示范”和宁波市重大科研项目(2011C11020),把集对分析用于进出口食品安全监管专家系统中的风险评价研究。
例3 大豆紫斑病是大豆病虫害疾病中一种常见的疾病,卞世晖[55]把集对分析的不确定性推理用于安徽省龙亢农场农科所自行研发的大豆病虫害诊断专家系统改进,提高了诊断准确率[55]。
例4 董卫华等[56]结合开发装备故障智能诊断系统,探讨了数据挖掘及其相关技术在实现知识自动获取和简化推理机设计方面应用的可能性,通过把集对分析与粗集理论相结合,从数据库中提取隐含的、未知的、对决策有潜在价值的知识规则,弥补故障诊断专家系统中知识获取和推理机方面存在的不足。
9 集对分析与神经网络的融合及应用 9.1 融合原理与途径基本原理是集对分析中的成对原理、同异反原理和不确定性原理。基于成对原理,可以把人工神经网络与人脑神经网络看作一个集对,两者虽然在功能上有相同之处,但在结构上相异,人工神经网络是无机物,人脑是有机物,这种同异反关系决定了人工神经网络处理的结果在逼近现实世界真实结果时存在不确定性。基于此认为,在人工神经网络的改进和完善过程中可以借鉴和应用集对分析“确定性计算与不确定性分析相结合”的思路;另外,社会网络化的人工神经网络可以看作大脑神经网络的一种外化,因此是一个更为重要的研究方向,不便对人脑作外科手术式研究的问题,可以通过对社会网络作切割式的研究来模拟。
9.2 应用举例例5 李佳等[57]提出一种把集对分析(SPA)与人工神经网络(ANN)相耦合的模型(SPA-ANN模型),应用此模型进行年径流预测,并与单独的人工神经网络模型和最近邻抽样回归模型预测效果进行比较分析,得到较好结果。
例6 陈晶等[58]把集对分析与径向基函数神经网络结合,提出集对分析径向基函数神经网络预测模型,简记为SPA-RBFNN,思路是将研究对象t–1时和t时的影响因子集构造为集对并计算联系度,将联系度的同一度、差异度、对立度及研究对象t–1时的值作为输入,研究对象t时的值作为输出,构建径向基函数神经网络,以年径流预测作为应用举例,模型结构清晰,计算步骤明确,预测精度较高。
例7 赵晓慎等[59]为客观和有效地定量评估BP神经网络凌汛开河日期预测模型,以黄河内蒙段三湖河口站冰凌开河日期为例,采用粒子群算法、遗传算法及小波分析理论对BP神经网络进行改进,并用集对分析对改进预测模型的数据集合建立评估模型。评估结果表明,集对分析法与平均相对误差精度法相比能更合理地反映模型预测效果。
10 集对分析在智能工程中的应用 10.1 应用的必要性与可能性智能工程是把人工智能的原理方法与技术用于各种工程的一个统称,如航天工程、智能电网、无人驾驶交通、各种智能制造、智能住宅和智能大厦等。智能工程内容包括工程中的智能系统设计、制作建造与运行管理3个层次。由于这些工程大都在开放的环境中运行,而实时环境中的各种工程及其运行都有耗能最少、产出最大、对环境负面影响最小、对各种信息处理敏捷正确以及宜人性等要求,面临各种不确定性因素干扰,包括对极端情况的适应,为此可以把集对分析中的不确定性理论、同异反系统理论和联系数用于智能工程中各层次、各环节的不确定性处置和处理,以达到工程设计施工与工程运行效用最优的目标。
10.2 应用举例例8 载人航天工程是人类从事太空探测研究,“试验”性生产和军事应用等活动,是一项复杂的系统工程。根据中国载人航天发展规划,2020年前后,中国将独立建立自己的空间站,届时载人航天器的发射及飞行任务将十分密集,型号研制及测试验证周期将大幅压缩,如何能够有效地对载人航天器执行任务前的地面综合测试工作的质量和效果进行快速评估,成为当前亟待解决的难题。中国空间技术研究院的魏邦友在文献[60]中披露:为了能够对载人航天器执行任务前的状态进行快速地评价和摸底,基于以往同类型成功型号测试数据和实际情况,以及数理统计和集对分析(SPA)等理论,提出相关系数、均方误差和联系度3个评价参量,从而全方位、多角度地对待发载人航天器的状态进行定量说明,快速判断其当前状态是否满足发射及飞行任务要求。
例9 黄德才等[61]把集对分析用于网格计算研究,给出了一种基于联系数的网格静态调度算法。
例10 蒋云良等[62]对多传感器数据融合过程中各传感器可信度估计困难和如何对不同类型传感器数据进行融合问题,提出一种基于集对分析联系数的多传感器数据融合方法。该方法首先利用同一度函数计算多个传感器的相互支持程度,然后计算观测值与传感器特性函数的同一度,最后利用最小最大法获得多传感器对目标属性的融合结果。该方法不需假定传感器特征函数服从分布。仿真实验表明,该方法能客观地识别出目标,是多传感器数据融合的一种新方法。
例11 王海颖等[63]针对先验知识未知的多传感器多次检测同一目标特征参数的情形,分析多传感器测量数据过程中产生不确定性的原因,设计了一种新的基于集对分析联系度的多传感器可靠性数据融合方法。通过利用集对分析特征函数的优势,挖掘量测数据间对立度、同一度和差异度调整数据间的联系程度,定义联系度矩阵,并利用扩维来度量不同时刻传感器测量值间的综合相近程度,然后参照在融合过程中已有的信噪比加权方法合理分配量测数据所占权重,实现传感器的加权融合。应用实例及仿真计算验证了该方法的有效性,融合结果具有更好的精确性、可靠性和稳健性。
例12 李春磊等[64]把集对分析用于最终工艺路线智能决策,为智能制造中工艺路线制订提供了新思路。
例13 刘英等[65]把集对分析用于砂轮主轴转动系统故障分析。
例14 卢凯等[66]针对城市社会车辆实际行驶速度的区间变化特点,以双向绿波带宽最大为目的,利用集对分析方法,对不同信号协调控制方案在车速不确定性情况下的控制效果进行分析、评价、选优。
例15 黑启动是指电力系统在突发故障情况下大面积停电后处于全“黑”状态,在不依赖别的网络帮助,仅通过系统中具有自启动能力的发电机组启动,带动无自启动能力的发电机组,逐渐扩大系统恢复范围,最终实现整个供电系统恢复的过程。赵玉玲等[67]把集对分析用于电力系统黑启动群决策研究。
11 集对分析在智能社会中的应用 11.1 智能社会智能社会还没有明确的定义。但我们可以认为:智能社会是指社会各个方面都实现智能化的一种社会形态,是现代科技发展到一定水平必然出现的一种社会形态。从目前情况看,智能社会是人们借助各种各样的智脑系统和互联网处理各种社会事务及个人事务,通过信息能的开发和利用,使社会物质财富极大化,同时又得到个性化满意服务的一种社会形态。由于人的欲望和本性使然,智能社会仍然存在物质财富社会分配不匀、信息能与其他能源相互转换效率不尽人意,特别是个人信息隐私、网络社区与实社区的和谐协调、地球人寻找其他宜居星球以开辟新的人类家园等新的社会问题,因此各种各样的不确定性依然存在,同异反现象普遍存在,对立统一规律仍然是各种事物和各种运动所遵循的规律,集对分析中的成对原理、不确定性原理和同异反原理在智能社会中依然有广阔的应用领域。
11.2 应用举例例16 网络的日益延伸和繁荣是智能社会的一大特点,网络计算是人工智能中的一个热点,黄德才等[68]最早研究了不确定性环境下的网格动态调度算法,朱红宁等[69]研究了基于SPA的Web服务选取算法,杨静等[70]开展了基于SPA的多数据流同异反分析。
例17 以兴趣或主题分享等为目的的兴趣型社交网络引领着社交网络的发展,张春英等[71]早在2013年把集对分析用于网络社区问题研究,陈晓等[72]则在张春英等工作的基础上,进一步把集对分析中的联系度用于主题关注网络社区发现研究,构建了一个新型社交网络模型——主题关注模型,给出了具体算法,并用实验验证了模型的合理性,与其他方法比较说明了算法的经济性。
例18 隐私保护是智能社会中每个公民特别关心的问题,晏燕等[73]把集对分析用于隐私保护度量研究。
例19 智脑与集对人。智脑是赵克勤在2014年集对分析湖州会议上提出的概念。所谓智脑,最基本、最简单、最常见的模型就是眼下比比皆是的“人脑+电脑”系统,放大地看是由人脑与网络组成的智能系统,实事求是地说是由亿万只电脑与亿万个人脑组成的超级脑系统,眼下的网络连同在线的亿万个人脑,就是这样的一个超级脑系统。基于集对的定义和集对分析理论,这个超级脑系统是一个集对系统,只要把网络中的亿万台计算机作为一个集合,把在线的亿万个人脑作为另一个集合,这个超级脑系统就是一个在实时计算和分析有关问题的在线集对,这个超级脑系统的各种实时计算和各种具体分析就是一类超级集对分析。但这个超级集对仍具有集对的一般性质,也就是集对中的2个集合具有:同一性,即网络中的计算机或多或少地具有部分人脑的功能,如对信息的感知和分类识别、记忆与理解、计算与分析,等等;差异性,即人脑与计算机存在诸多差异,例如用于大规模并行计算的神经网络与人脑内部的神经网络的差异等;对立性,即人脑对复杂事物的即刻直觉决策与计算机软件的程序性决策相对立等;这2个集合相互联系中的种种不确定性,其同异反程度可以用同异反联系数表征。由此得智脑的定义:智脑是由人脑与电脑组成的一种智能系统。网络是一类将众多电脑联结而成的网络系统,因此可简称为网络脑。这样,所谓智脑可以进一步看成由人脑+网络脑组成的一种脑集对,可称为“脑对” “双脑” “多脑” “智脑系统”等,简称“智脑”。当然,上面说的电脑也包括智能手机在内。
从时空角度看,上述智脑系统的最大潜力在于智脑的进化。智脑智能在智脑的进化中得到不断扩充、强化,不断地向完善接近。
人脑的进化已有数十万年历史,人脑的社会化合作也有几千年历史,总体上说是一种极为缓慢的进化。其进化历史不能在实验室重演,人脑思维也不能在实验室解剖条件下进行观察性地研究,以至于人们至今对人脑的认知仍然是未知超过已知。但20世纪末出现的计算机网络(脑),在空间上不断快速延伸扩展的同时,也在技术、结构、功能、机制多个维度上发生着进化,质的变化隐含在缓慢的量变之中,我们猜想,当把人脑沿时间维的进化与由计算机构成的网络脑沿空间维的进化有机结合,由此形成的智脑智能进化将会有前所未有的速度和规模,在这个过程中,人们迟早会承认网络脑在一定程度上就是人脑的一种物理映像,人脑的许多机制可以在网络脑中得到合理地诠释。而已经有2只眼睛,2只耳朵、2个鼻孔、2只手、2条腿和1个大脑的人,再加一个智脑,成为有2个脑袋的人,称为“集对人”,既形象,也是事实,也是一个有现代人意义的集对模型。至于“集对人”是否可以看成人类进化史上的一个新人种?有待人类学家研究。
12 结束语大自然创造了人类,并赋予人类智能,远古时代的原始人会制作简陋的工具摄取食物以生存繁衍,近代人通过把工具复杂化以制造出机器,引发的工业革命极大地推动和发展了人类社会,使得当代科学家梦想着把智能不断地赋予机器,让机器不仅能帮助人们高效率地创造物质财富和思想财富,还能帮助人类去寻找第2个、第3个甚至更多个宜居星球,以创造更加美好的未来。这个智能大搬迁的历史进程,无疑是确定性与不确定性相互联系、相互依存、相互纠缠、对立统一的过程。集对分析作为对不确定性“客观承认、系统描述、定量刻画、具体分析”的一种新的系统数学理论,把确定性的数学计算与不确定性的系统分析有机结合,毫无疑问可以在人工智能中得到应用,也已经在人工智能中得到不少成功的应用。我们有理由相信,随着互联网的不断发展,智能社会将不以人的意志为转移而出现在地球上,集对分析在人工智能中的应用会有一个新的进展。
| [1] |
赵克勤. 集对与集对分析——一个新的概念和一种新的系统分析方法[C]. 全国系统理论与区域规划研讨会. 包头, 中国, 1989: 8.
( 0) 0)
|
| [2] |
赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000.
( 0) 0)
|
| [3] |
王文圣, 李跃清, 金菊良, 等. 水文水资源集对分析[M]. 北京: 科学出版社, 2010.
( 0) 0)
|
| [4] |
刘保相. 粗糙集对分析理论与决策模型[M]. 北京: 科学出版社, 2010.
( 0) 0)
|
| [5] |
沈定珠. 体育用联系数学[M]. 北京: 中国教育文化出版社, 2007.
( 0) 0)
|
| [6] |
郭瑞林. 作物育种同异理论与方法[M]. 北京: 中国农业科学技术出版社, 2011.
( 0) 0)
|
| [7] |
赵克勤, 赵森烽. 奇妙的联系数[M]. 北京: 知识产权出版社, 2014.
( 0) 0)
|
| [8] |
刘秀梅, 赵克勤. 区间数决策集对分析[M]. 北京: 科学出版社, 2014.
( 0) 0)
|
| [9] |
蒋云良, 赵克勤, 刘以安, 等. 信息处理集对分析[M]. 北京: 清华大学出版社, 2015.
( 0) 0)
|
| [10] |
王万军, 晏燕. 不确定信息处理的集对分析研究与应用[M]. 兰州: 兰州大学出版社, 2015.
( 0) 0)
|
| [11] |
汪明武, 金菊良, 周玉良. 集对分析耦合方法与应用[M]. 北京: 科学出版社, 2014.
( 0) 0)
|
| [12] |
潘争伟, 吴成国, 金菊良. 水资源系统评价与预测的集对分析方法[M]. 北京: 科学出版社, 2016.
( 0) 0)
|
| [13] |
李丽红, 杨亚锋, 李言, 等. 集对推理与决策[M]. 北京: 清华大学出版社, 2016.
( 0) 0)
|
| [14] |
汪明武, 金菊良. 联系数理论与应用[M]. 北京: 科学出版社, 2017.
( 0) 0)
|
| [15] |
蒋云良, 赵克勤. 人工智能集对分析[M]. 北京: 科学出版社, 2017.
( 0) 0)
|
| [16] |
赵克勤, 米红. 非传统安全与集对分析[M]. 北京: 知识产权出版社, 2010.
( 0) 0)
|
| [17] |
蒋云良, 徐从富. 集对分析理论及其应用研究进展[J]. 计算机科学, 2006, 33(1): 205-209. JIANG Yunliang, XU Congfu. Advances in set pair analysis theory and its applications[J]. Computer science, 2006, 33(1): 205-209. DOI:10.3969/j.issn.1002-137X.2006.01.057 (  0) 0)
|
| [18] |
赵克勤. 集对分析的不确定性系统理论在AI中的应用[J]. 智能系统学报, 2006, 1(2): 16-25. ZHAO Keqin. The application of uncertainty systems theory of set pair analysis (SPU) in the artificial intelligence[J]. CAAI transactions on intelligent systems, 2006, 1(2): 16-25. (  0) 0)
|
| [19] |
赵克勤. 二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用
[J]. 智能系统学报, 2008, 3(6): 476-486. ZHAO Keqin. The theoretical basis and basic algorithm of binary connection A+Bi and its application in AI [J]. CAAI transactions on intelligent systems, 2008, 3(6): 476-486. (  0) 0)
|
| [20] |
赵克勤. 成对原理及其在集对分析(SPA)中的作用与意义[J]. 大自然探索, 1998, 17(4): 90. ZHAO Keqin. The function and meaning of pair principle in the set pair analysis[J]. Exploeratioin nature, 1998, 17(4): 90. (  0) 0)
|
| [21] |
赵克勤. SPA的同异反系统理论在人工智能研究中的应用[J]. 智能系统学报, 2007, 2(5): 20-35. ZHAO Keqin. The application of SPA-based identical-discrepancy-contrary system theory in artificial intelligence research[J]. CAAI transactions on intelligent systems, 2007, 2(5): 20-35. (  0) 0)
|
| [22] |
赵克勤. 偏联系数[M]//中国人工智能学会. 中国人工智能进展. 北京: 北京邮电大学出版社, 2005: 884–885.
( 0) 0)
|
| [23] |
赵克勤. 集对分析对不确定性的描述和处理[J]. 信息与控制, 1995, 24(3): 162-166. ZHAO Keqin. Disposal and description of uncertain ties based on the set pair analysis[J]. Information and control, 1995, 24(3): 162-166. (  0) 0)
|
| [24] |
赵克勤, 宣爱理. 集对论——一种新的不确定性理论方法与应用[J]. 系统工程, 1996, 14(1): 18-23, 72. ZHAO Keqin, XUAN Aili. Set pair theory——a new theory method of non—define and its applications[J]. Systems engineering, 1996, 14(1): 18-23, 72. DOI:10.3321/j.issn:1001-506X.1996.01.003 (  0) 0)
|
| [25] |
蔡自兴, 徐光佑. 人工智能及其应用[M]. 4版. 北京: 清华大学出版社, 2010.
( 0) 0)
|
| [26] |
钟义信. 高等人工智能原理—观念•方法•模型•理论[M]. 北京: 科学出版社, 2014:1–452.
( 0) 0)
|
| [27] |
朱其秀. 集对分析用于人工智能研究的思考[J]. 绍兴文理学院学报, 1996, 16(4): 113-118. ZHU Qixiu. Set pair annlysis for the study of artificial intelligence[J]. Journal of Shaoxing college of arts sciences, 1996, 16(4): 113-118. (  0) 0)
|
| [28] |
周志华, 曹存根. 神经网络及其应用[M]. 北京: 清华大学出版社, 2004.
( 0) 0)
|
| [29] |
成科扬. 基于集对分析的指纹识别系统研究[M]//中国人工智能学会. 中国人工智能进展. 北京: 北京邮电大学出版社, 2005: 1475–1478.
( 0) 0)
|
| [30] |
李德顺, 宫博, 许开立. 论金属矿山地质灾害模式识别模型[J]. 工业安全与环保, 2012, 38(3): 37-40. LI Deshun, GONG Bo, XU Kaili. Discussion on the geological disasters pattern recognition model of the metal mine[J]. Industrial safety and environmental protection, 2012, 38(3): 37-40. DOI:10.3969/j.issn.1001-425X.2012.03.013 (  0) 0)
|
| [31] |
高洁, 盛昭瀚. 集对分析聚类预测法及其应用[J]. 系统工程学报, 2002, 17(5): 458-462. GAO Jie, SHENG Zhaohan. Method and application of set pair analysis classified prediction[J]. Journal of systems engineering, 2002, 17(5): 458-462. DOI:10.3969/j.issn.1000-5781.2002.05.012 (  0) 0)
|
| [32] |
阎理, 阎滨. 相似系统集对分析[J]. 指挥技术学院学报, 2000, 11(3): 9-13. YAN Li, YAN Bin. The set pair analysis for similarity system[J]. Journal of institute of command and technology, 2000, 11(3): 9-13. (  0) 0)
|
| [33] |
刘秀梅, 赵克勤. 基于联系数的不确定空情意图识别[J]. 智能系统学报, 2012, 7(5): 450-456. LIU Xiumei, ZHAO Keqin. Inference method on intention with uncertain aerial information based on the connection number[J]. CAAI transactions on intelligent systems, 2012, 7(5): 450-456. DOI:10.3969/j.issn.1673-4785.201206016 (  0) 0)
|
| [34] |
张秀辉, 刘以安, 曹宁生, 等. 基于集对分析的雷达信号分选算法[J]. 现代雷达, 2010, 32(2): 35-37. ZHANG Xiuhui, LIU Yi'an, CAO Ningsheng, et al. Radar signal sorting method based on set pair analysis[J]. Modern radar, 2010, 32(2): 35-37. DOI:10.3969/j.issn.1004-7859.2010.02.008 (  0) 0)
|
| [35] |
LIU Yi’an, MONG Xianhai, WANG Shitong. Studies for image edge detection with set pair analysis[C]//DCABES. 2006: 373–76.
( 0) 0)
|
| [36] |
赵森烽, 赵克勤. 概率联系数化的原理及其在概率推理中的应用[J]. 智能系统学报, 2012, 7(3): 200-205. ZHAO Senfeng, ZHAO Keqin. The principle of a connection number in probability and its application in probabilistic reasoning[J]. CAAI transactions on intelligent systems, 2012, 7(3): 200-205. DOI:10.3969/j.issn.1673-4785.201112014 (  0) 0)
|
| [37] |
蒋云良, 张裔智, 潘云鹤, 等. 基于集对分析的定量推理初探[J]. 计算机工程, 1996, 22(3): 286-290. JIANG Yunliang, ZHANG Yizhi, PAN Yunhe, et al. First exploration of quantitative inference of identity-discrepancy-contrary based on the set pair analysis[J]. Computer engineering, 1996, 22(3): 286-290. (  0) 0)
|
| [38] |
马守明, 王汝传, 叶宁. 基于集对分析的上下文感知不确定性的推理方法[J]. 南京邮电大学学报(自然科学版), 2009, 29(1): 64-67. MA Shouming, WANG Ruchuan, YE Ning. An uncertainty reasoning approach based on set pair analysis for context awareness[J]. Journal of Nanjing university of posts and telecommunications(natural science), 2009, 29(1): 64-67. DOI:10.3969/j.issn.1673-5439.2009.01.015 (  0) 0)
|
| [39] |
阎红灿, 王会芳, 马会霞. 基于集对分析的本体案例检索模型[J]. 微型机与应用, 2014, 33(21): 75-78. YAN Hongcan, WANG Huifang, MA Huixia. Ontology case retrieval model based on SPA[J]. Microcomputer and its applications, 2014, 33(21): 75-78. DOI:10.3969/j.issn.1674-7720.2014.21.025 (  0) 0)
|
| [40] |
赵克勤. 集对分析与同异反决策[J]. 决策探索, 1992(2): 14-15. ZHAO Keqin. The same differences counter-decision and Set pair analysis[J]. Policy research and exploration, 1992(2): 14-15. (  0) 0)
|
| [41] |
刘秀梅, 赵克勤. 基于联系数不确定性分析的区间数多属性决策[J]. 模糊系统与数学, 2010, 24(5): 141-148. LIU Xiumei, ZHAO Keqin. Multiple attributes decision-making of intervals based on analysis of the uncertainty of connection number[J]. Fuzzy systems and mathematics, 2010, 24(5): 141-148. (  0) 0)
|
| [42] |
赵森烽, 赵克勤. 联系概率的由来及其在风险决策中的应用[J]. 数学的实践与认识, 2013, 43(4): 165-171. ZHAO Senfeng, ZHAO Keqin. The contact probability in risk decision-making medium application[J]. Mathematics in practice and theory, 2013, 43(4): 165-171. DOI:10.3969/j.issn.1000-0984.2013.04.024 (  0) 0)
|
| [43] |
吴爱燕, 曾广平, 涂序彦. 集对云多属性群决策方法及应用[J]. 计算机科学, 2014, 41(12): 231-233, 250. WU Aiyan, ZENG Guangping, TU Xuyan. Study on set pair cloud multi-attribute group decision method[J]. Computer science, 2014, 41(12): 231-233, 250. DOI:10.11896/j.issn.1002-137X.2014.12.050 (  0) 0)
|
| [44] |
余国祥. 默会知识和显性知识的同异反集对分析[J]. 襄樊学院学报, 2008, 29(5): 84-88. YU Guoxiang. A SPA of tacit knowledge and explicit knowledge in identity, discrepancy and contrary[J]. Journal of Xiangfan university, 2008, 29(5): 84-88. DOI:10.3969/j.issn.1009-2854.2008.05.021 (  0) 0)
|
| [45] |
徐忆琳. 用SPA同异反系统理论研究知识创新规律[J]. 科学学研究, 2002, 20(3): 327-329. XU Yilin. Research on the law of knowledge innovation using IDC-SPA theory[J]. Studies in science of science, 2002, 20(3): 327-329. DOI:10.3969/j.issn.1003-2053.2002.03.022 (  0) 0)
|
| [46] |
杜春彦, 柴春红. 基于SPA的不确定推理模型[J]. 数学的实践与认识, 2004, 34(9): 130-134. DU Chunyan, CHAI Chunhong. Uncertain reasoning model based on set pair[J]. Mathematics in practice and theory, 2004, 34(9): 130-134. DOI:10.3969/j.issn.1000-0984.2004.09.022 (  0) 0)
|
| [47] |
张新华. 技术知识产权评估模型及应用[J]. 科研管理, 1999, 20(6): 47-51. ZHANG Xinhua. Evaluation model and application in technoque knowledge of righting[J]. Science research management, 1999, 20(6): 47-51. DOI:10.3969/j.issn.1000-2995.1999.06.007 (  0) 0)
|
| [48] |
周萍, 阎理. 集对分析与武器装备知识产权管理绩效评估[J]. 军事经济研究, 2005(6): 51-52. ZHOU Ping, YAN Li. Application of SPA to the performance evaluation of the intelligent property right management of the weapon equipment[J]. Militang economic research, 2005(6): 51-52. (  0) 0)
|
| [49] |
阮光册. 基于知识关联的检索结果聚类分析研究[J]. 情报科学, 2015, 33(2): 63-66. RUAN Guangce. Search result clustering analysis based on knowledge relation[J]. Information science, 2015, 33(2): 63-66. (  0) 0)
|
| [50] |
汪新凡. 基于联系数的纯语言多属性群决策方法[J]. 重庆工商大学学报( 自然科学版), 2006, 23(6): 580-584. WANG Xinfan. Pure linguistic information multi-attribute group decision-making method based on connection number[J]. Journal of Chongqing technology and business university(natural sciences edition), 2006, 23(6): 580-584. (  0) 0)
|
| [51] |
徐改丽. 基于语言评估和集对分析的多属性决策方法[J]. 重庆工学院学报(自然科学), 2009, 23(8): 85-89. XU Gaili. Multi-attribute decision-making method based on linguistic assessments and set pair analysis[J]. Journal of Chongqing institute of technology(natural science), 2009, 23(8): 85-89. (  0) 0)
|
| [52] |
栗飞, 刘博, 徐海峰. 基于集对分析的混合型多属性目标威胁评估[J]. 海军航空工程学院学报, 2012, 27(2): 219-222. LI Fei, LIU Bo, XU Haifeng. Threat assessment of hybrid multiple attribute targets based on set pair analysis[J]. Journal of naval aeronautical and astronautical university, 2012, 27(2): 219-222. (  0) 0)
|
| [53] |
徐峰. 猪病诊断专家系统研究[D]. 北京, 中国: 中国农业大学, 2005: 1–50. XU Feng. An expert system for pig diseases diagnosis[D]. Beijing, China: Agricultural University, 2005: 1–50. (  0) 0)
|
| [54] |
徐超. 进出口食品安全监管中风险评价和专家系统的研究[D]. 杭州, 中国: 浙江大学, 2013. XU Chao. The research of risk assessment and expert system for imported and exported food safety supervision[D]. Hangzhou, China: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013185682.htm (  0) 0)
|
| [55] |
卞世晖. 专家系统中不确定性推理的研究与应用[D]. 合肥, 中国: 安徽大学, 2010. BIAN Shihui. Research and application of uncertainty reasoning in expert system[D]. Hefei, China: Anhui University, 2010. (  0) 0)
|
| [56] |
董卫华, 张政保. 数据挖掘及数据库技术在故障诊断专家系统中的应用[J]. 河北省科学院学报, 2006, 23(4): 20-23. DONG Weihua, ZHANG Zhengbao. Application of data mining and database technology in expert system for fault diagnosis[J]. Journal of the Hebei academy of sciences, 2006, 23(4): 20-23. DOI:10.3969/j.issn.1001-9383.2006.04.006 (  0) 0)
|
| [57] |
李佳, 王黎, 马光文, 等. 基于SPA-ANN耦合模型的年径流预测[J]. 水力发电学报, 2009, 28(1): 41-44. LI Jia, WANG Li, MA Guangwen, et al. Annual runoff forecasting based on SPA-ANN coupling model[J]. Journal of hydroelectric engineering, 2009, 28(1): 41-44. (  0) 0)
|
| [58] |
陈晶, 王文圣, 李跃清. 集对分析径向基函数神经网络预测模型[J]. 水文, 2011, 31(2): 11-14. CHEN Jing, WANG Wensheng, LI Yueqing. Prediction model of radial basis function neural network based on set pair analysis[J]. Journal of China hydrology, 2011, 31(2): 11-14. DOI:10.3969/j.issn.1000-0852.2011.02.003 (  0) 0)
|
| [59] |
赵晓慎, 吴海波, 陈丹. 集对分析在改进BP神经网络凌汛开河日期预测评估中的应用[J]. 水电能源科学, 2011, 29(12): 101-103. ZHAO Xiaoshen, WU Haibo, CHEN Dan. Study of set pair analysis in improving prediction and evaluation of BP neural network for breaking up date of ice flood[J]. Water resources and power, 2011, 29(12): 101-103. DOI:10.3969/j.issn.1000-7709.2011.12.029 (  0) 0)
|
| [60] |
魏邦友. 载人航天器综合测试数据评估方法的研究[J]. 电子质量, 2017(7): 28-30. WEI Bangyou. Research on evaluation method of comprehensive test data for manned spacecraft[J]. Electronics quality, 2017(7): 28-30. DOI:10.3969/j.issn.1003-0107.2017.07.008 (  0) 0)
|
| [61] |
黄德才, 张丽君, 赵克勤, 等. 基于a+bi型联系数的不确定网格静态调度算法
[J]. 计算机科学, 2007, 34(8): 126-129. HUANG Decai, GONG Weihua, ZHANG Lijun, et al. Grid task dynamic scheduling algorithm based on connective-number[J]. Computer engineering, 2007, 34(8): 126-129. DOI:10.3969/j.issn.1002-137X.2007.08.034 (  0) 0)
|
| [62] |
JIANG Yunliang, YANG Zhangxian, LI Gang, et al. A multi-sensor data fusion method based on the set-pair identity degree and connection number[C]//Proceedings of 2011 Workshop on Digital Media and Digital Content Management. Hangzhou, China, 2011: 298–301.
( 0) 0)
|
| [63] |
王海颖, 刘以安, 薛松, 等. 基于集对分析联系度的多传感器数据融合方法[J]. 智能系统学报, 2017, 12(2): 1-8. WANG Haiying, LIU Yi’an, XUE Song, et al. Sensor data fusion based on connection degree of set pair analysis[J]. CAAI transactions on intelligent systems, 2017, 12(2): 1-8. (  0) 0)
|
| [64] |
李春磊, 莫蓉, 常智勇, 等. 综合考虑零件工艺设计经验和制造稳定性的工艺路线决策[J]. 计算机辅助设计与图形学学报, 2015, 27(12): 2385-2392. LI Chunlei, MO Rong, CHANG Zhiyong, et al. Decision-making of process route considering process planning experience and manufacturing stability[J]. Journal of computer-aided design and computer graphics, 2015, 27(12): 2385-2392. (  0) 0)
|
| [65] |
刘英, 陈志恒, 陈宇. 基于集对理论的砂轮主轴转动系统故障树分析[J]. 机械传动, 2014, 38(5): 77-80. LIU Ying, CHEN Zhiheng, CHEN Yu. Fault tree analysis of grinding wheel spindle rotation system based on set pair analysis theory[J]. Journal of mechanical transmission, 2014, 38(5): 77-80. (  0) 0)
|
| [66] |
卢凯, 荆彬彬, 吴焕, 等. 基于集对分析的干道绿波协调控制方案评价方法[J]. 东南大学学报(自然科学版), 2015, 45(3): 606-611. LU Kai, JING Binbin, WU Huan, et al. Evaluation method of arterial green wave coordinated control scheme based on set pair analysis[J]. Journal of southeast university(natural science edition), 2015, 45(3): 606-611. (  0) 0)
|
| [67] |
赵玉铃, 张廉. 集对分析联系数在黑启动vague集决策中的应用研究[J]. 智能系统学报, 2014, 9(5): 632-640. ZHAO Yuling, ZHANG Lian. Application of the ste-pair analyssi connection number in decision-making of black-start vague set[J]. CAAI transactions on intelligent systems, 2014, 9(5): 632-640. (  0) 0)
|
| [68] |
黄德才, 龚卫华, 张丽君, 等. 基于联系数的网格任务动态调度算法[J]. 计算机工程, 2009, 35(8): 112-115. HUANG Decai, GONG Weihua, ZHANG Lijun, et al. Grid task dynamic scheduling algorithm based on connective-number[J]. Computer engineering, 2009, 35(8): 112-115. DOI:10.3969/j.issn.1000-3428.2009.08.038 (  0) 0)
|
| [69] |
朱红宁, 张斌. 基于SPA的Web服务选取方法[J]. 计算机科学, 2009, 36(11): 32-35. ZHU Hongning, ZHANG Bin. Method of Web service selection based on SPA[J]. Computer science, 2009, 36(11): 32-35. DOI:10.3969/j.issn.1002-137X.2009.11.007 (  0) 0)
|
| [70] |
杨静, 李文平, 张健沛. 一种基于SPA的多数据流同异反分析法[J]. 武汉大学学报(信息科学版), 2011, 36(1): 92-97. YANG Jing, LI Wenping, ZHANG Jianpei. A data mining approach based on identical-different-contrary analysis[J]. Geomatics and information science of Wuhan university, 2011, 36(1): 92-97. (  0) 0)
|
| [71] |
张春英, 郭景峰. 集对社会网络α关系社区及动态挖掘算法
[J]. 计算机学报, 2013, 36(8): 1682-1692. ZHANG Chunying, GUO Jingfeng. The α relationship communities of set pair social networks and its dynamic mining algorithms [J]. Chinese journal of computers, 2013, 36(8): 1682-1692. (  0) 0)
|
| [72] |
陈晓, 郭景峰, 范超智. 基于联系度的主题关注网络社区发现方法研究[J]. 计算机工程与应用, 2017, 53(17): 85-93. CHEN Xiao, GUO Jingfeng, FAN Chaozhi. Community discovering based on connection degree in topic-attention network[J]. Computer engineering and applications, 2017, 53(17): 85-93. DOI:10.3778/j.issn.1002-8331.1608-0324 (  0) 0)
|
| [73] |
晏燕, 郝晓弘, 王万军. 一种隐私保护度量的集对分析方法[J]. 武汉大学学报(工学版), 2015, 48(6): 883-890. YAN Yan, HAO Xiaohong, WANG Wanjun. A set pair analysis method for privacy metric[J]. Journal of tsinghua university(science and technology), 2015, 48(6): 883-890. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


