随着信息技术和互联网的发展，网络正成为人们规划旅游的重要信息来源^[1]。人们逐渐从信息匮乏的时代走入了大数据的时代，在海量数据的背景下，如何快速找到对用户最有价值的信息，显得越来越重要，推荐系统便应运而生^[2]。

以往的推荐系统主要关注于单个用户，在电视节目^[3]、音乐、电影、新闻等方面取得了很好的效果，但是对于旅游领域还没有给出完善的推荐方案^[4]。首先，和电影的数据相比，旅游评分的数据难以获得；其次，用户的评分矩阵比较稀疏；最后，旅游通常是多个用户以群组的形式参与的，因此，结合所有成员偏好的组推荐系统将成为旅游推荐领域的一个研究热点^[5]。基于协同过滤的组推荐系统中，在对单个用户的预测阶段，使用传统的协同过滤算法计算用户(项目)之间的相似度时，没有考虑用户共同评分的项目数和评分关联程度对相似性造成的影响，例如，两个兴趣差别较大的游客，可能同时感兴趣的景点比较少，当用户的共同评分比较少时，传统的协同过滤算法便无法准确地度量用户之间相似性^[6]；在群组成员预测结果的融合阶段，效果比较好的偏好融合策略中有均值策略和最小痛苦策略^[7]，均值策略把成员对项目的平均评分作为群组的得分，然而没有考虑少数成员的不满意度，最小痛苦策略选择成员对项目最小的评分作为群组的得分，却忽略了多数成员的偏好。

本文在组推荐过程中，首先改进了协同过滤算法，它结合相似性影响因子和关联性因子，以解决旅游推荐中面临的数据稀疏性问题；其次在组偏好建模阶段，提出了一种新的融合策略——满意度平衡策略，它同时考虑了组内成员的局部满意度和整体满意度；最后，通过在旅游数据集上的实验分析，验证了所改进的方法能够有效地提高推荐的质量。

1 相关工作 1.1 协同过滤算法

协同过滤算法是电子商务推荐领域中一种最为成功的推荐算法^[8]。它不需要用户主动提供个人需求信息，而是根据他们已有的评分记录，获得用户的潜在偏好。这种推荐算法能否取得良好的效果，很大程度上取决于用户的评分数据。

1.2 组推荐关键技术

组推荐关键技术包括融合方法和融合策略。融合方法分为模型融合和推荐融合。模型融合根据群组成员的用户偏好模型融合成群组偏好模型，然后基于群组偏好模型生成组推荐；推荐融合先根据传统算法获得每个用户的预测评分后，再根据预测评分进行融合，也可以融合推荐项目列表得到群组的推荐列表^[5,7]。两种融合方法各有自己的不足：模型融合易受到评分稀疏性的影响，推荐融合忽略了群组成员之间的交互^[5]。

组推荐系统中常用的融合策略有均值策略、最小痛苦策略、最开心策略^[9]。文献[10]通过一系列实验评估，指出乘法策略、均值策略、最小痛苦策略以及痛苦避免均值策略较好。文献[7]通过对组推荐系统的文献研究分析，发现使用最普遍的策略有均值策略、痛苦避免均值策略及最小痛苦策略，但这些策略对于不同特征的群组适用性也不尽相同。

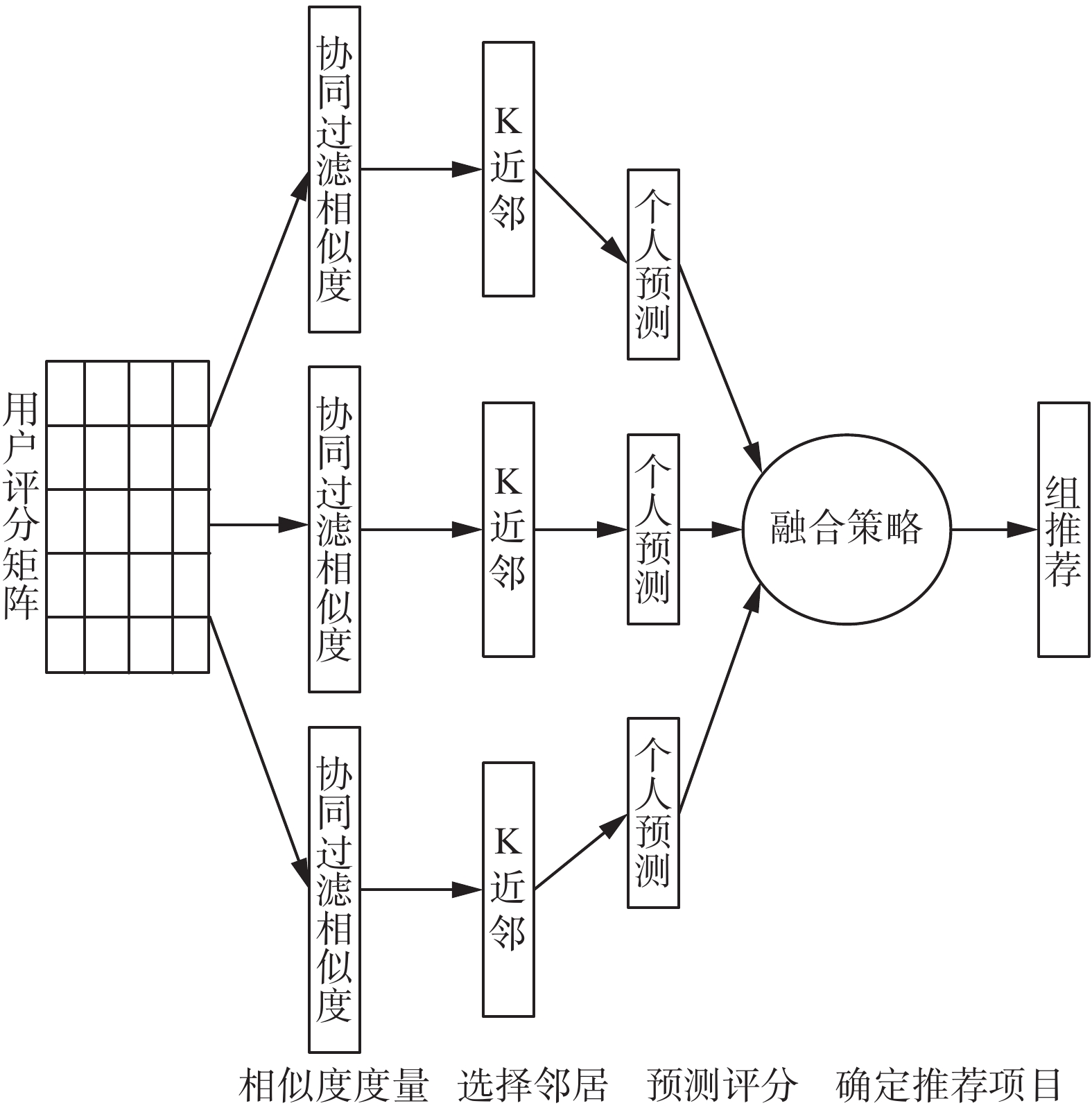
2 基于协同过滤的组推荐

协同过滤算法作为一种基本的方法常常被应用于组推荐系统中。基于协同过滤的组推荐包括4个阶段：相似性度量、选择邻居、预测评分、确定推荐项目^[11]。

首先通过评分矩阵中用户的评分计算两两用户(项目)的相似度，然后根据K近邻的方法预测当前用户对未知项目的评分，最后通过融合策略结合所有组内成员的偏好生成组推荐列表。图1为本文中用到的基于协同过滤的组推荐整体框架。

其中，协同过滤算法可以分为基于用户的最近邻推荐(user-based nearest neighbor recommendation)和基于项目的最近邻推荐(item-based nearest neighbor recommendation)。

2.1 基于用户的最近邻推荐

基于用户的最近邻推荐假设当前用户会喜欢与之有相似偏好的用户喜欢的项目。目前比较常用的相似度计算方法有余弦相似度(cosine similarity)、皮尔森相关相似度(Pearson correlation coefficient)等^[12-13]。本文主要选用相似度定义如式(1)所示。

$ {\rm sim}(m,n) = \frac{{\displaystyle\sum\limits_{i \in {I_{mn}}} {{R_{m,i}} \cdot {R_{n,i}}} }}{{\sqrt {\displaystyle\sum\limits_{i \in {I_m}} {{R_{m,i}}^2} } \sqrt {\displaystyle\sum\limits_{i \in {I_n}} {{R_{n,i}}^2} } }} $

(1)

式中： ${\rm sim}(m,n)$ 表示用户 $m$ 和 $n$ 的余弦的相似度， ${R_{m,i}}$ 表示用户 $m$ 对项目 $i$ 的评分， ${R_{n,i}}$ 表示用户 $n$ 对项目 $i$ 的评分， ${I_m}$ 表示用户 $m$ 评分的项目集合， ${I_n}$ 表示用户 $n$ 评分的项目集合， ${I_{mn}}$ 表示用户 $m$ 和用户 $n$ 共同评分的项目集合。

找出与当前用户 $m$ 有相似偏好的K个用户集合 ${\rm KNN}{_m}$ ，则用户 $m$ 对项目 $i$ 的预测评分为

$ {p_{m,i}} = \overline {{R_m}} + \frac{{\displaystyle\sum\limits_{n \in {\rm{KNN}}_{m}} {{\rm sim}(m,n) \times ({R_{n,i}} - \overline {{R_n}} )} }}{{\displaystyle\sum\limits_{n \in {\rm{KNN}}_{m}} {|{\rm sim}(m,n)|} }} $

(2)

式中 $\overline {{R_m}} $ 、 $\overline {{R_n}} $ 分别表示用户 $m$ 和用户 $n$ 的平均评分。

2.2 基于项目的最近邻推荐

基于项目的最近邻利用用户对项目的评分来计算相似度。本文选用的相似度如式(3)所示。

${\rm sim}(i,j) = \frac{{\displaystyle\sum\limits_{m \in {R_{ij}}} {({R_{m,i}} - \overline {{R_i}} )({R_{m,j}} - \overline {{R_j}} )} }}{{\sqrt {\displaystyle\sum\limits_{m \in {R_{ij}}} {{{({R_{m,i}} - \overline {{R_i}} )}^2}} } \sqrt {\displaystyle\sum\limits_{m \in {R_{ij}}} {{{({R_{m,j}} - \overline {{R_j}} )}^2}} } }}$

(3)

式中： ${\rm sim}(i,j)$ 表示项目 $i$ 和 $j$ 的皮尔森相似度^[14-15]， $\overline {{R_i}} $ 、 $\overline {{R_j}} $ 表示项目 $i$ 和项目 $j$ 的平均得分， ${R_{ij}}$ 表示对项目 $i$ 和 $j$ 都有过评分的用户集合。

找出要预测的项目 $i$ 的K个相似项目集合 ${\rm KNN}{_i}$ ，则用户 $m$ 对项目 $i$ 的预测值为

${p_{m,i}} = \overline {{R_i}} + \displaystyle\frac{{\displaystyle\sum\limits_{j \in {\rm KNN}{_i}} {{\rm sim}(i,j) \times ({R_{m,j}} - \overline {{R_j}} )} }}{{\displaystyle\sum\limits_{j \in {\rm KNN}{_i}} {|{\rm sim}(i,j)|} }} $

(4)

2.3 数据稀疏性问题及算法改进

相似度是协同过滤中的重要指标，决定着预测评分的好坏，同时由于在旅游领域，存在用户自身的综合因素使得旅游推荐不同于以往电子商务领域的推荐。例如，用户可以每月看一场电影，但却很少有人每年旅行很多次。因此在旅游推荐中，不可避免地会存在数据的稀疏性问题。传统的相似度计算方法在评分数据丰富的情况下可以给出很好的效果，但是在旅游推荐中，传统的推荐方法在计算用户(项目)间的相似度时，可能会忽略用户评分数据的稀疏程度对相似度计算结果造成的影响。如表1所示(0表示没有评分)，以基于用户的相似度为例：

1)用户A和用户B共同评分的景点数量多于用户C和D共同评分的景点数量，所以用户A和用户B的相似度应该比用户C和用户D的相似度更高。然而，用户A和B的余弦相似度计算结果为0.838 1，用户C和D的相似度结果为0.910 4(余弦相似度的范围为[0,1])。显然，传统的相似度不能很好地计算他们之间的相似度。为了解决这一问题，本文利用用户对景点共同评分的数目与用户对景点评分总数目的关系来调整用户之间的相似性，本文称之为相似性影响因子 ${h_1}$ ，定义为

$ {h_1} = {2^{\sqrt {^{\displaystyle\frac{{{I_{mn}}}}{{{I_m} \cup {I_n}}}}} }} - 1 $

(5)

式中： ${I_m}$ 为用户 $m$ 评分的景点集合， ${I_n}$ 为用户 $n$ 评分的景点集合。用户 $m$ 和 $n$ 的共同评分景点数 ${I_{mn}}$ 在其全部评分景点 ${I_m} \cup {I_n}$ 中占的比例越大，则相似性影响因子 ${h_1}$ 就越大，相似度的值可能越大；反之 ${h_1}$ 越小，相似度的值可能越小。

2)用户E和用户F根据余弦相似度计算结果为0.854 2，表示他们的偏好很相似；根据皮尔森和修正余弦相似度计算结果为−1，表示他们的偏好完全相反(相似度的范围为[−1,1])。实际上他们的相似度不应该完全相反，也不应该很相似，而是介于两者之间。随着用户和评分矩阵规模的增加，类似这种情况也会影响推荐结果的准确性。为解决此类问题，本文利用用户评分的关联性来调整用户之间的相似性，用户的共同评分向量越接近，相似度的值可能越大，反之相似度的值可能越小。本文称之为关联性因子 ${h_2}$ ，定义为

$ {h_2} = 1 - \sqrt {1 - {{\left( {\frac{{\displaystyle\sum\limits_{i \in {I_{mn}}} {2{R_{m,i}} \cdot {R_{n,i}}} }}{{\displaystyle\sum\limits_{i \in {I_{mn}}} {({R^2}_{m,i} + {R^2}_{n,i})} }}} \right)}^2}} $

(6)

相似度的计算是协同过滤中最重要的一步。旅游领域面临的数据稀疏性问题，使得原有的相似度方法很难准确度量用户之间的相似性。这是因为在用户评分数据稀疏的情况下，传统的方法主要考虑用户共同评分之间的相似性，却忽略了用户在个别项目上的评分是相似的而在其他项目上不一定相似的现象，用户只有在比较多的项目上评分相似时，他们的偏好才能认为是相似的；此外，传统的相似度无法准确区分某些相似度相同但偏好差别很大的用户之间的相似性。

本文提出的相似性影响因子 ${h_1}$ 和关联性因子 ${h_2}$ 全面考虑了用户共同评分项和评分关联性对相似度度量的影响，可以有效缓解由于数据稀疏性问题导致的相似度计算不够准确的问题。改进的相似度 ${\rm sim}{(m,n)_h}$ 如式(7)所示：

${\rm sim}{(m,n)_h} = {h_1} \times (\partial \times {\rm sim}(m,n) + (1 - \partial ) \times {h_2}) $

(7)

式中： $\partial $ 表示参数， $\partial \in [0,1]$ ， ${\rm sim}(m,n)$ 表示传统的相似度，将式(7)代入式(2)即可得到用户对景点的预测评分，如式(8)所示。

${P_{m,i}} = \overline {{R_m}} + \frac{{\displaystyle\sum\limits_{n \in {\rm KNN}{_m}} {\left[ {{h_1} \times \left( {\partial \times \displaystyle\frac{{\displaystyle\sum\limits_{i \in {I_{mn}}} {{R_{m,i}} \cdot {R_{n,i}}} }}{{\sqrt {\displaystyle\sum\limits_{i \in {I_m}} {R_{m,i}^2} } \sqrt {\sum\limits_{i \in {I_n}} {R_{n,i}^2} } }} + (1 - \partial ) \times {h_2}} \right)} \right] \times ({R_{n,i}} - \overline {{R_n}} )} }}{{\displaystyle\sum\limits_{n \in {\rm KNN}{_m}} \left| {\left[ {{h_1} \times \left( {\partial \times \frac{{\sum\limits_{i \in {I_{mn}}} {{R_{m,i}} \cdot {R_{n,i}}} }}{{\sqrt {\sum\limits_{i \in {I_m}} {R_{m,i}^2} } \sqrt {\sum\limits_{i \in {I_n}} {R_{n,i}^2} } }} + (1 - \partial ) \times {h_2}} \right)} \right]} \right| }} $

(8)

同理，基于项目相似度的情况类似。

2.4 修正的偏好融合策略

在个人用户对项目预测评分的基础上，融合策略可以将组内成员的偏好进行融合，从而得到整个组对于项目的得分，根据得分的大小生成最终的推荐列表。由于群组中成员的偏好可能相同，也可能不同，此时单个成员的偏好不能作为整个组的偏好，因此如何获取群组成员的共同偏好，缓解各成员间的偏好冲突，也是组推荐要解决的问题^[7]。目前效果比较好的偏好融合策略有均值策略(average)和最小痛苦策略(least misery)。均值策略选择成员对项目评分的平均值作为群组对于项目的得分，可以表示为

$ {R_{g,i}} = {\rm{avg}}({R_{m,i}}:m \in g) $

(9)

式中： $g$ 表示群组， ${R_{g,i}}$ 表示群组 $g$ 对于项目 $i$ 的得分。

最小痛苦策略选择成员对项目最小的评分作为群组对于项目的得分，可以表示为

$ {R_{g,i}} = \min ({R_{m,i}}:m \in g) $

(10)

均值策略只考虑群组成员的平均偏好程度，但可能忽略了少数成员的不满意度；最小痛苦策略根据组内成员对项目的最小评分做参考，却可能会忽略多数人的感受。如表2所示，根据均值策略，景点1和景点3对于包含用户1、2、3和用户4的群组是等价的，但对于景点1而言，均值策略显然没有考虑用户4的感受，相比较来说，选择景点3可能比景点1更好一些；根据最小痛苦策略，景点3、4和景点5对于群组是等价的，相对于景点3而言，组内成员对景点4或景点5更感兴趣，此时少数人可能服从多数，组成员很可能会优先选择景点5，最小痛苦策略只考虑了成员的最小满意度却忽略了大多数人的偏好。

为此，本文考虑了以上两种策略的不足之处，定义一种修正的方法来平衡组成员局部满意度与整体满意度之间的关系，本文称之为满意度平衡策略(satisfaction balance)，群组 $g$ 对景点 $i$ 的得分用满意度平衡策略表示为 ${\rm balance}{_{g,i}}$ ，定义如式(11)所示。

$\begin{array}{l} {\rm{balanc}}{{\rm{e}}_{g,i}} = {\rm{avg}}({R_{m,i}}:m \in g) + \\ \frac{1}{S}{\rm{avg}}({R_{m,i}}:m \in g)*\min ({R_{m,i}}:m \in g) \end{array}$

(11)

式中： $S$ 表示群组中成员的数目。根据定义，在表2中可以看出，按照满意度平衡策略计算的结果更能反映群组对景点的总体兴趣，根据修正的融合策略得到的组推荐列表为景点5、4、3、2、1。

3 实验方案设计 3.1 数据获取

目前旅游推荐领域还没有公开实验数据集，国内外学术研究使用的数据主要来自旅游网站或问卷的方式。采用调查问卷的方式获取数据可能会存在一些不可避免的缺点：如果设计的问题太多往往会让用户失去耐心，太少反而不会获取足够的信息；可能会涉及到用户隐私问题；用户还可能会存在回忆误差。本文数据集由携程网(http://www.ctrip.com/)爬取桂林市的景点信息整理获得，包括用户ID，景点ID及用户对景点的评分。最初获取的数据集包括18 354个用户对255个景点的48 473条评分，评分范围为1~5分。

3.2 数据预处理

为了方便实验，对获取的数据进行以下处理：

删除用户重复的评分记录；删除没有用户评分的景点；删除评分记录小于3条的用户。最终得到的旅游数据集如表3所示。

3.3 电影数据集

实验中除了旅游数据集之外，还采用了目前在衡量推荐算法中常用的由美国Minnesota大学Grouplens项目提供的Movielens数据集。如表4所示，该数据集由943个用户对1 682部电影的100 000条评分组成，每个用户的评分记录不少于20条，评分范围为1~5分。

3.4 评价标准

平均绝对误差^[16](mean absolute error，MAE)和均方根误差^[8](root-mean-square error，RMSE)是衡量预测评分和真实评分之间相近程度的评价标准，本文使用MAE和RMSE对个人预测结果的准确性进行检验。如式（12）、（13）所示。

${\rm MAE} = \frac{1}{N}\sum\limits_{c = 1}^N {{\rm{|}}{P_c}} - {R_c}|$

(12)

${\rm RMSE} = \sqrt {\frac{{\sum\limits_{c = 1}^N {{{({P_c} - {R_c})}^2}} }}{N}} $

(13)

式中： ${P_c}$ 和 ${R_c}$ 分别表示用户对测试集中项目的预测评分和真实评分，N为评分数目。

归一化折损累计增益(normalized discounted cumulative gain，nDCG)是信息检索中一种衡量推荐列表准确率的评价指标^[5,17]，本文使用nDCG对组推荐的结果进行检验。设 ${q_1}, {q_2}, \cdot \cdot \cdot ,{q_k}$ 为群组推荐项目的排名列表，则用户 $u$ 的DCG和nDCG定义如式(14)、(15)所示：

${\rm DCG}_k^u = {r_{u{q_1}}} + \sum\limits_{c = 2}^k {\frac{{{r_{{\rm uq}{_c}}}}}{{{{\log }_2}(c)}}} $

(14)

$ {\rm n}{\rm DCG}_k^u = \frac{{{\rm DCG}_k^u}}{{{\rm IDCG}_k^u}} $

(15)

式中： ${r_{u{q_c}}}$ 表示用户 $u$ 对群组推荐结果中排在第 $c$ 个位置项目的预测(或真实)评分， ${\rm IDCG}_k^u$ 为用户 $u$ 对于群组的 $k$ 个推荐项目最大的DCG值，计算出群组中各个用户的nDCG值，然后取它们的平均值作为组推荐列表的nDCG。nDCG是介于0~1之间的数，nDCG的数值越大，表明推荐列表中项目的排序越准确，推荐准确度越高。

4 实验结果 4.1 传统的协同过滤和改进的方法比较

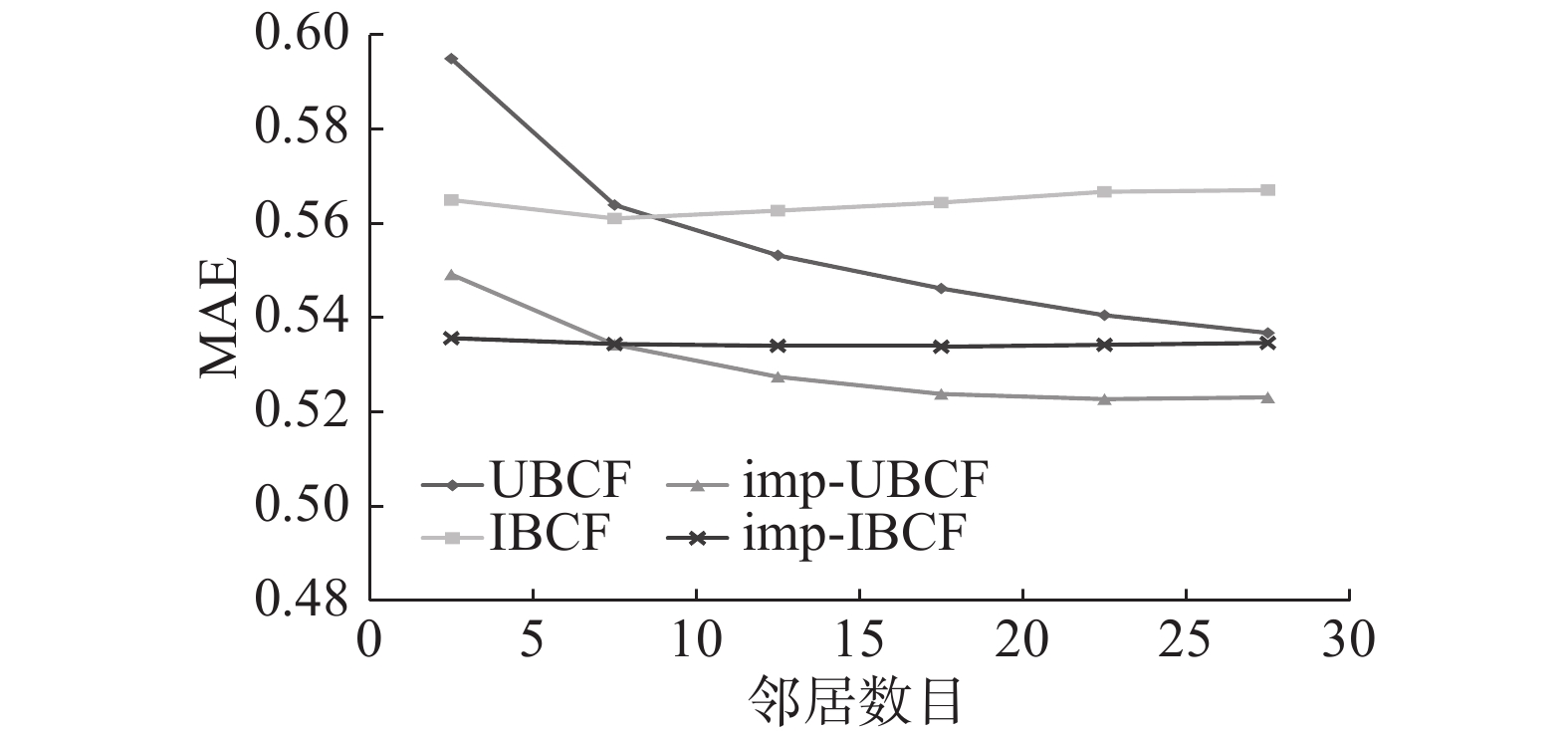
图2和图3分别给出了2.1节中介绍的基于用户的协同过滤(UBCF)和2.2节中介绍的基于项目的协同过滤(IBCF)、通过引入相似性影响因子与关联性因子改进的基于用户的协同过滤(imp-UBCF)和改进的基于项目的协同过滤(imp-IBCF)的折线图。随机选择旅游数据集中80%的评分记录作为训练集，20%的评分记录作为测试集，经多次实验，取 $\partial $ =0，观察邻居数目K从5~30每次增加5时，各个推荐算法的性能。图2、3中可以看出，在相同邻居数目的情况下，无论是使用基于用户的协同过滤还是基于项目的协同过滤预测评分，基于改进方法的MAE和RMSE均低于传统的方法，表明改进的方法在计算用户或项目之间的相似性时可以起到更好的效果，进而提高用户对项目预测评分的准确性。这是因为传统的相似度方法(比如基于用户的相似度)在评分矩阵稀疏的情况下，无法准确度量用户共同评分的景点数量与用户之间相似度的关系，而且在一定程度上也忽略了用户对于不同景点的兴趣差异。

4.2 改进的协同过滤方法检验

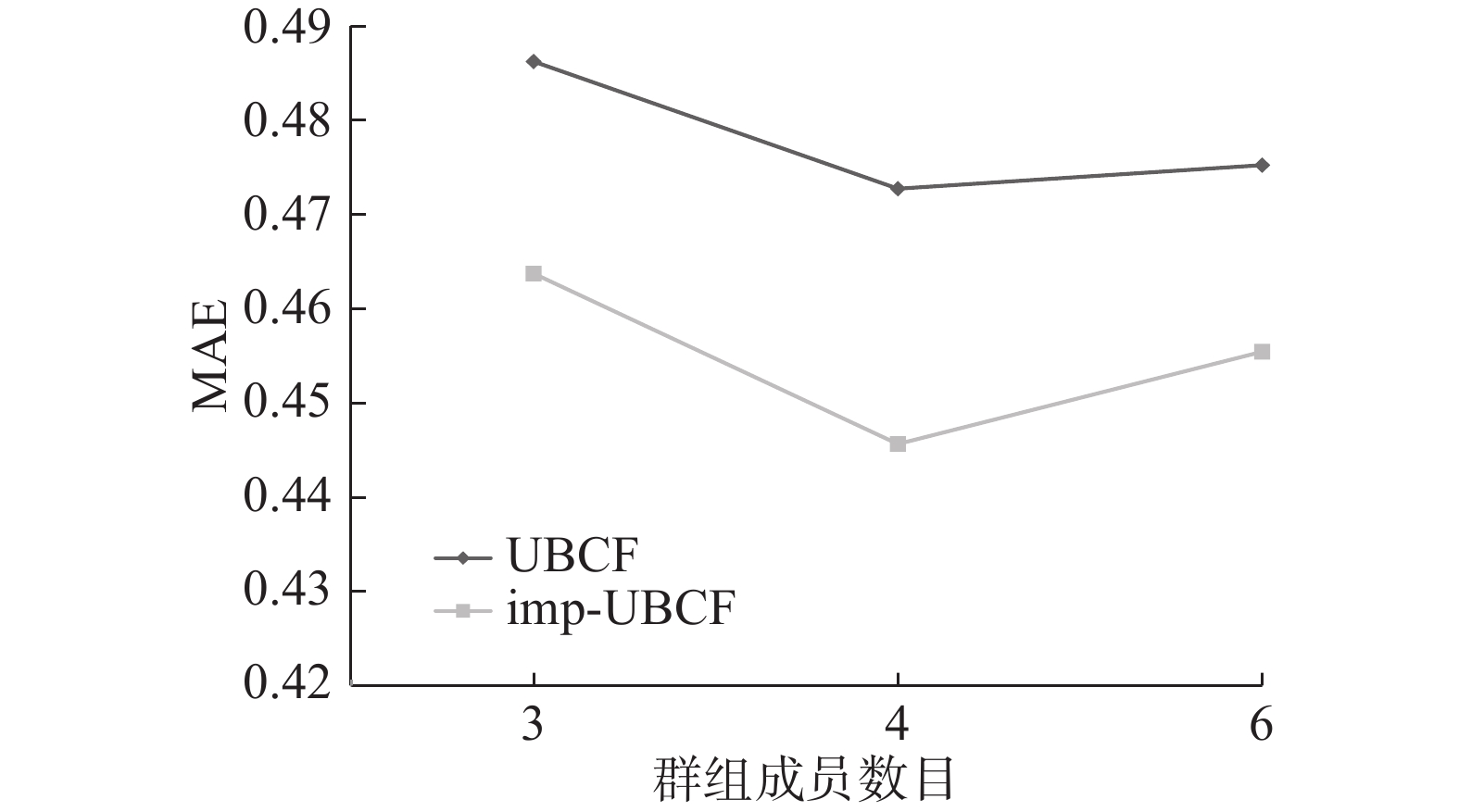
为了验证改进的协同过滤方法在群组中的有效性，随机选择旅游数据集中的3人、4人、6人组成3类群组，重复进行10次实验，取邻居数目K=30。本节使用基于用户的协同过滤和改进的基于用户的协同过滤方法对每一个群组中所有用户的预测评分进行检验，取10次实验的平均值为最后结果，如图4所示，群组中整体的MAE低于传统的方法，表明改进的方法在给群组中所有成员对项目进行预测评分时，计算结果更加准确。

4.3 满意度平衡策略检验 4.3.1 偏好融合策略

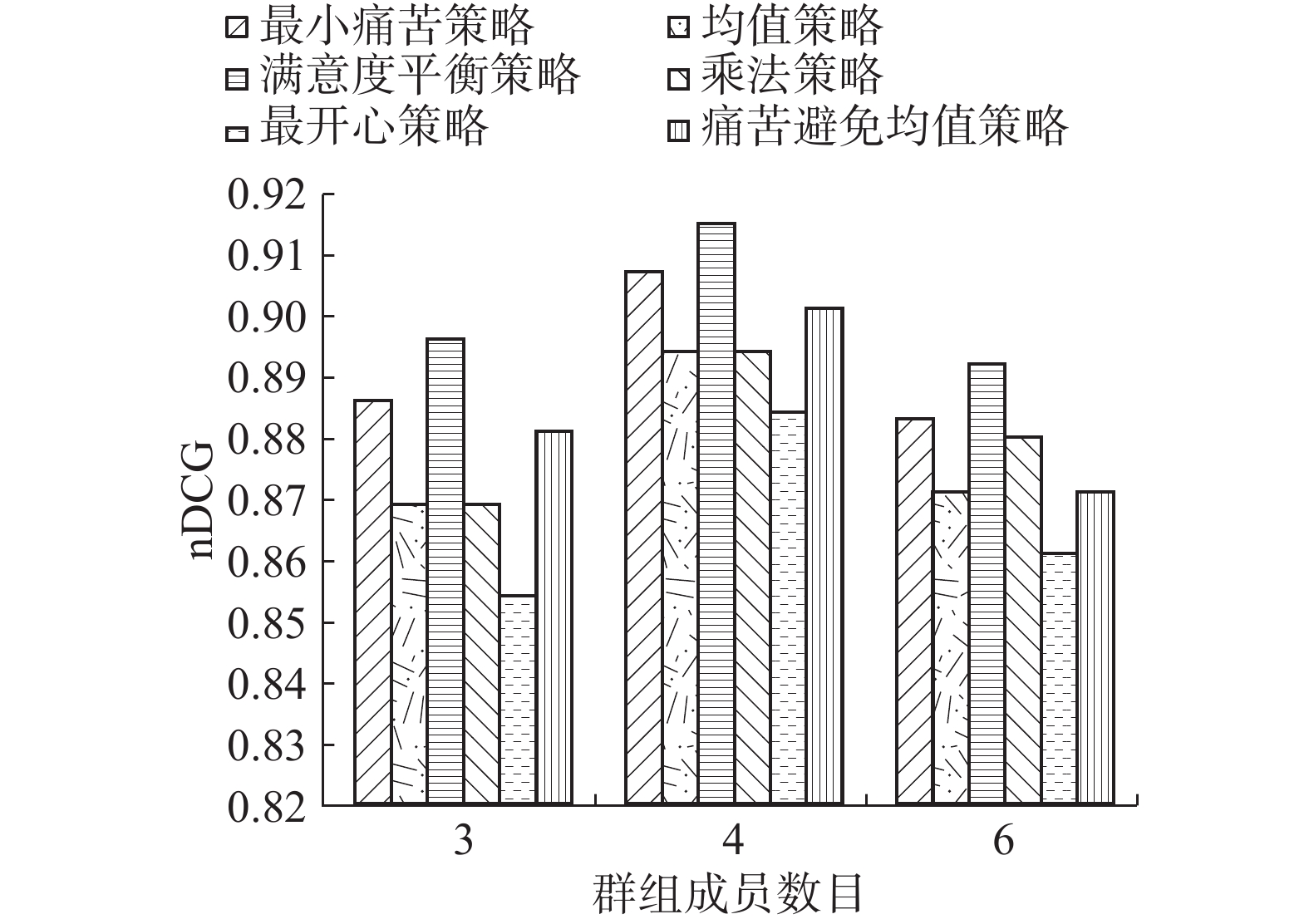
在组偏好融合阶段，常见的融合策略有均值策略(average)、最小痛苦策略(least misery)、乘法策略(multiplicative)^[10]、最开心策略(most pleasure)^[5]、痛苦避免均值策略(average without misery)^[1]。其中，乘法策略通过将成员对项目的评分做乘法得到的结果作为整个组的得分，然后根据得分按照大小排序生成推荐列表；最开心策略选择成员对项目的最高评分作为群组的得分；痛苦避免均值策略在排除单个成员评分低于某个阈值的项目后再根据成员对项目的平均评分作为群组的得分。

4.3.2 偏好融合策略对比与分析

在使用改进的协同过滤方法对群组成员预测评分的基础上，本节实验在旅游数据集上比较了本文提出的满意度平衡策略(satisfaction balance)与常用的融合策略的实验结果。由图5可以看出，在群组的规模不同时，修正的偏好融合策略(satisfaction balance)表现的效果比较好。这是因为least misery是用少数成员的意见决定整个组的选择，推荐的项目可能不是群组中所有用户最喜欢的；average在给群组推荐项目时，只考虑了所有成员的整体满意度，却忽略了组内不同成员的感受；multiplicative是用所有成员的评分乘积作为群组结果，当某些成员之间的偏好差别较大时，群组的得分也可能比较高；most pleasure只考虑了成员的最大满意度；而average without misery虽然排除了成员评分较小的项目，但在其他项目的推荐上仍然存在因少数成员的相对不满意度使得群组得分较高的情况；而本文修正的融合策略考虑了用户的整体满意度和局部满意度之间的关系，使得推荐的项目能够更好地反应出整个群组的偏好，推荐结果更加准确。

4.4 不同数据集下的实验结果

图6为在Movielens数据集上，UBCF、IBCF、imp-UBCF和imp-IBCF的折线图。可以看出，imp-IBCF在Movielens数据集上提高的效果最为明显，和UBCF、IBCF相比，分别提高了5%和6.7%，同样验证了本文所提方法的有效性。

5 结束语

本文针对组推荐系统在旅游推荐领域面临的数据稀疏性问题，提出一种改进的协同过滤方法来提高对单个用户预测评分的准确性；然后针对现有的融合策略——均值策略和最小痛苦策略忽略了局部满意度或整体满意度的问题进行了修正，修正的偏好融合策略同时考虑了两者的不足之处。通过不同的实验证明，本文提出的方法在一定程度上提高了预测的准确性和推荐的准确率。未来的工作是收集旅游领域的文本信息，对用户进行广度的偏好分析，进一步提高推荐的效率。