2. 陆军工程大学 装备模拟训练中心,河北 石家庄 050003;
3. 9804厂军代室,云南 曲靖 655000
2. Equipment Simulation Training Center, Army Engineering University, Shijiazhuang 050003, China;
3. 9804 Military Representative Office, Qujing 655000, China
在当前学科融合的大背景下,网络可控性[1-3]逐渐受到了人们的广泛关注,它是网络科学借鉴了控制科学的思想,将网络看作是一个系统,从整体的角度去研究如何去控制网络,使网络达到预期状态。在目前的研究中,影响可控性的因素是什么、如何提高可控性一直以来都是网络可控性研究中的热点问题。
近年来,网络可控性的研究基本上都是围绕文献[1-2]展开的。文献[1]将Lin的结构可控性定理[4]运用于有向、无权的复杂网络中,基于二部图给出了最小控制输入节点(也称为最小驱动节点)的求解方法,提出了网络可控性的最大匹配理论和最小输入定理。文献[2]则是将研究对象扩充到无向、同权的复杂网络,提出了基于PBH可控性判定的严格可控性理论,具有更广泛的适用性。上述两篇文献奠定了近年来网络可控性研究的基础,为后续诸多研究提供了理论支撑。对于影响可控性因素的探索,从文献[1]就开始了,作者探讨了网络可控性与度分布的关系,并且结合实际网络,发现稀疏异构网络比稠密同构网络更加难以控制。在随后的研究中,文献[5]研究了影响可控性的各种网络特性,发现模块性和聚集系数没有明显的影响,而出度与入度的对称性对网络可控性有一定的影响。文献[6]则主要针对无向网络的可控性,利用模拟退火算法改变网络的度相关性,发现在度分布不变的情况下,网络可控性会随着度相关系数的增大而单调减小。上述文献虽然给出了影响网络可控性的某些因素,但并没有给出具体的可控性优化方法。对于如何提高网络可控性,目前已经开展了诸多研究,如文献[7]通过添边来轻微改动网络结构,从而提高网络的可控性,并且在同构、异构随机网络和不同类型的真实网络中进行了验证。文献[8]针对当前复杂网络中的可控性优化问题,从网络中边的方向性入手,将EOOC问题转换为交换网络的最大独立集问题,最终通过实验表明了网络结构可以决定可控性和优化效果。文献[9]提出了一种提高网络可控性的新算法,通过重新连接网络的边来改变网络结构,从而提高可控性,最后在ER和无标度网络模型中验证了算法的有效性。文献[10]提出了一种提高有向网络可控性的方法,该方法是在保持链路总数不变的情况下,通过改变一小部分链路的方向来实现的,通过数值模拟验证了方法的有效性,并且说明了该方法适用于一些仅知道局部结构信息的网络。从上述文献可以看出,网络可控性的优化研究实质是根据某一特征因素进行的网络结构调整。对于一些具有明显规律的网络结构,目前也已展开了可控性方面的研究,如文献[11]中的分形网络、文献[12]中的确定无标度网络和凯莱树,均通过特征值0来确定最小控制输入的节点个数,进而获取网络的可控性。文献[13]中的星型网络则是通过特征多项式给出了最小控制输入节点个数的计算表达式;文献[14]针对路形拓扑结构,提出了不可控特征值的概念并给出了具体表达式。从上述文献可以看出,某些关键特征值与某些具有特征规律的网络结构之间存在着必然联系,这些特征值对应的特征结构从某种程度上决定了网络的可控性,如果能够找到关键的特征值,调整特征值对应的特征结构,则可以为网络可控性的优化提供新的思路。
综上所述,本文将从具有规律性特征结构的特征值入手,探究0和−1这两个特殊特征值与网络可控性之间的关系。通过消除网络中0/−1对应的规律性特征结构,实现网络可控性的提高,为网络可控性的优化提供新的方法和思路。
1 网络可控性从定性分析的角度来看,网络可控性是指在某种拓扑结构和控制输入下,网络是否可以达到预期状态。这里的控制输入是指对网络中所有节点的控制实施情况,即对网络中的哪些节点进行了控制实施,哪些节点没有进行控制实施。
从定量分析的角度来看,网络可控性是指在某种拓扑结构下,网络运行状态达到预期状态的难易程度,其强弱通常是由量化指标nd[1]表示,即最小控制输入的节点个数Nd与网络节点总数N的比值:
| $ {n_{\rm{d}}} = {N_{\rm{d}}}/N $ | (1) |
这个指标是以网络可控性的定性判定为基础,求解网络可控下对应的最小控制输入,以最小控制输入的节点个数作为可控性量化指标的主要因素,进而对网络可控性进行量化评估。
1.1 定性分析网络可控性的定性分析其实是对网络可控与否的判定,它借鉴了控制科学中可控性[15]的思想,将网络看作是一个系统,以邻接矩阵作为系统矩阵,控制输入矩阵作为输入矩阵,根据可控性的判定条件对网络系统进行可控性判定。具体而言,对于有N个节点、M个控制输入(M≤N)的网络系统,其状态方程可表述为
| ${\dot {{x}}} = {{A}{x}} + {{B}{u}}$ | (2) |
式中:x=[x1 x2
针对式(2)的网络系统,常用的网络可控性判定方法有2种:基本秩判据[1]和PBH秩判据[2]。
基本秩判据是根据式(3)进行可控性判据:
| $ {\rm{rank}}[{{B}}\;{{AB}}\;{{{A}}^2}{{B}} \cdots {{{A}}^{N - 1}}{{B}}] = N $ | (3) |
若网络系统满足式(3),则网络系统是可控的,否则不可控。
PBH秩判据是根据式(4)进行可控性判据:
| ${\rm{rank}}\left[ {{{\textit{λ}} _k}{{I}} - {{A}}} {{B}} \right] = N,\;\;\;\;\;k = 1,2, \cdots ,N $ | (4) |
式中:λk为邻接矩阵A所对应的所有特征值。若网络系统满足式(4),则网络系统是可控的,否则不可控。
从上述2种判定方法不难看出,网络可控性的定性分析取决于邻接矩阵A和控制输入矩阵B,即网络可控与否是由网络的拓扑结构和控制输入共同决定的。
1.2 定量分析从网络可控性的定性分析不难看出,在某种拓扑结构下,对网络所有节点实施控制(即M=N),则网络必定可以达到可控状态。然而,此时所实施的控制不一定是最优的,因为对于任何一种网络拓扑而言,最优的控制输入应该是使得网络达到可控状态时,对网络中最少的节点实施控制。这种针对网络拓扑结构的最优控制即最小控制输入。最小控制输入的节点个数直接反映了在某种拓扑结构下网络达到可控性的难易程度,即可用于可控性的定量分析。因此,对网络可控性进行定量分析的关键是求解出最小控制输入的节点个数。
根据式(3)或式(4)的可控性判据,可以为最小控制输入的求解提供基本思路:针对邻接矩阵A,求出满足式(3)或式(4)的最简矩阵B。最直接的方法是代入法,即针对网络中的所有节点,将可能的控制输入由少至多进行遍历组合,生成所有可能情况下的输入矩阵B,由简至繁逐一代入式(3)或式(4)进行验证,一旦出现判定为可控,则可将此时的矩阵B确定最小控制输入。然而,对于n个节点的网络而言,求出所有矩阵B的计算复杂程度为
式(4)中的PBH判定矩阵[λkI−A B](以下简称PBH矩阵)可以写成以下模式:
| $\left[ {\begin{array}{*{20}{c}} {{{\textit{λ}}_k}}&{ - {a_{12}}}& \cdots &{ - {a_{1n}}} \\ { - {a_{21}}}&{{{\textit{λ}}_k}}&{\cdots}& { - {a_{2n}}} \\ \vdots &{}& {} &{\vdots} \\ { - {a_{n1}}}& { - {a_{n2}}}&{\cdots}&{{{\textit{λ}} _k}} \end{array}\begin{array}{*{20}{c}} {{b_1}}&{}&{}&{} \\ {}&{{b_2}}&{}&{} \\ {}&{}& \ddots &{} \\ {}&{}&{}&{{b_n}} \end{array}} \right]$ |
不难看出,PBH矩阵在满秩的情况下,上式中的矩阵应该满足所有行向量线性不相关,而虚线右边的矩阵B可以消除虚线左边λkI−A中行向量组的相关性,这就为求出矩阵B提供了实现方法:首先计算出λkI−A,再将其进行初等列变换,不改变行相关特性;根据行相关情况,通过设置最少的bi消除λkI−A的行相关性,使得PBH矩阵中的所有行向量均不相关;最后将所有λk对应的bi设置情况进行整合,使得bi可以消除所有λk对应的PBH矩阵中行向量的相关性,即满足式(4)。此时,所对应的bi即组成最小控制输入对应的矩阵B,最小控制输入的节点个数Nd=rank(B)。
求出Nd后,则可根据式(1)得到网络可控性的度量指标nd,完成定量分析。
2 0/−1特征值从最小控制输入的求解可以看出,影响网络可控性的直接因素是PBH矩阵中λk I−A矩阵的行相关性。而行相关性不仅受到邻接矩阵A的影响,还受到特征值λk的影响。虽然对于大部分特征值而言,它们与行相关之间的联系并没有明显的规律性,但0和−1这两个特征值却比较特殊,它们不仅与行相关之间存在着一定联系,更是极大地影响着网络可控性。
2.1 行相关类型对于λkI-A矩阵的行相关性可以分为3类:零向量相关、重复相关和非重复相关。
1)零向量相关即存在全0行的行向量。以Ax表示A的第x行,则零向量相关表现为
| $ {{{A}}_{i}}_{1}={{{A}}_{i}}_{2}=\cdots ={{{A}}_{im}}={{\textit{0}}} $ |
例如A2=A3=0,如下所示:
| $\left[ {\begin{array}{*{20}{c}} 1&0&0& 0 &0 \\ 0&0&0& 0 &0 \\ 0&0&0& 0 &0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}} \right]$ |
2)重复相关即存在完全相同的相关行向量。以Ax表示A的第x行,则重复相关表现为
| $ {{{A}}_i}_1 = {{{A}}_i}_2 = \cdots = {{{A}}_{im}} $ |
例如A1=A2=A3,如下所示:
| $\left[ {\begin{array}{*{20}{c}} 1&0&0& 0 &0 \\ 1&0&0& 0 &0 \\ 1&0&0& 0 &0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}} \right]$ |
3)非重复相关即存在不同的行向量,它们之间存在相关性。以Ax表示A的第x行,则非重复相关表现为
| $ {{{A}}_i}_0 = {k_1}{{{A}}_i}_1 + {k_2}{{{A}}_i}_2 + \cdots + {k_m}{{{A}}_{im}} $ |
例如A3=A1+A2,如下所示:
| $\left[ {\begin{array}{*{20}{c}} 1&0&0& 0 &0 \\ 0&1&0& 0 &0 \\ 1&1&0& 0 &0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}} \right]$ |
在上述3种相关情况中,非重复相关与特征值之间的联系很难找到;而零向量相关与0特征值、重复相关与0/−1特征值之间存在着明显的联系,具体联系可由下述两个定理描述:
定理1 如果矩阵λkI−A中存在着零向量相关,则对应特征值λk一定为0。
证明 设矩阵λkI−A中零向量行为第i行,即
| $ \left[ { - {a_{i1}}{\rm{ }} - {a_{i2}}{\rm{ }} \cdots {\rm{ }} - {a_{i(i - 1)}}{\rm{ }}{{\textit{λ}} _k}{\rm{ }} - {a_{i(i + 1)}}{\rm{ }} \cdots {\rm{ }} - {a_{iN}}} \right] = {{\textit{0}}} $ |
则有
| $\left\{ \begin{array}{l} {a_{ix}} = 0,x{\rm{ = }}1,2, \cdots ,N{\text{且}}x \ne i\\ {{\textit{λ}} _k}{\rm{ = 0}} \end{array} \right.\text{。}\;\;{\text{证毕}}$ |
定理2 如果矩阵λkI−A中存在着行重复相关,则对应特征值λk一定为0或 −1。
证明 设矩阵λkI−A中重复相关的行为第i行和第j行,即
| $ \begin{array}{l} \!\left[ { - {a_{i1}}{\rm{ }} \!-\! {a_{i2}}{\rm{ }}\! \cdots \!{\rm{ }} \!-\! {a_{i(i - 1)}}{\rm{ }}{{\textit{λ}}_k}{\rm{ }} \!-\! {a_{i(i + 1)}}{\rm{ }}\! \cdots \!{\rm{ }} \!- \!{a_{i(j - 1)}}{\rm{ }} \!-\! {a_{ij}}{\rm{ }} \!-\! {a_{i(j + 1)}}{\rm{ }} \cdots {\rm{ }}\,\!-\! {a_{iN}}} \right]\! = \\ \left[ { - {a_{j1}}{\rm{ }} \!-\! {a_{j2}}{\rm{ }} \!\cdots\! {\rm{ }} \!-\! {a_{j(i - 1)}}{\rm{ }} \!- \!{a_{ji}}{\rm{ }}\! - \!{a_{j(i + 1)}}{\rm{ }} \cdots {\rm{ }} \!-\! {a_{j(j - 1)}}{\rm{ }}{{\textit{λ}} _k}{\rm{ }} \!- \!{a_{j(j + 1)}}{\rm{ }} \cdots \!-\! {a_{jN}}} \right] \end{array}$ |
则有
| $\left\{ \begin{array}{l} {a_{ix}} = {a_{jx}},x{\rm{ = }}1,2, \cdots ,N{\text{,}}x \ne i,j\\ {a_{ij}} = {a_{ji}} = - {{\textit{λ}} _k} \end{array} \right.$ |
因为A中的元素仅有0或1,即aij=0或aij=1,所以λk=0或λk=−1。证毕
由定理1和定理2可知,在λkI−A矩阵的所有行相关中,如果存在零向量相关,那么一定是0特征值决定的;如果存在重复相关,那么一定是0/−1特征值决定的。其他非0/−1特征值所对应的λkI−A矩阵不可能出现零向量相关和重复相关。
对于零向量相关、重复相关和非重复相关这3种λkI−A矩阵的行相关性而言,形成零向量相关至少需要有一行为全零行,形成重复相关至少需要有两行完全相同,形成非重复相关至少需要有三行并且通过合适的系数组成相关组。而且由于λkI−A矩阵为对角线均为λk的实对称矩阵,且其中的元素仅有0和 −1两种,因此从形成的难易程度上来看,在 λkI−A矩阵中形成零向量相关、重复相关比非重复相关要容易很多,即所有λkI−A矩阵的行相关中绝大部分都是零向量相关和重复相关。由定理1和定理2可知,零相关均由特征值0决定,重复相关均由特征值0/−1决定,不难得出,相对于其他特征值,特征值0/−1极大地影响着λkI−A矩阵的相关性,即网络中绝大部分的最小控制输入节点是由特征值0/−1所决定的。
3 可控性优化相对于0/−1特征值而言,非0/−1特征值对可控性的影响相对较小,并且难以找到具有明显规律性的特征结构。而0/−1特征值对可控性的影响相对较大,并且具有明显的对应特征结构。因此,可以通过消除0/−1的特征结构,从而减小0/−1对应λkI−A矩阵中的行相关性,最终达到提高网络可控性的目的,实现网络的可控性优化。
3.1 0特征结构在特征值0对应的特征结构中,存在着一种具有明显规律性的特征结构,其具体定义如下:
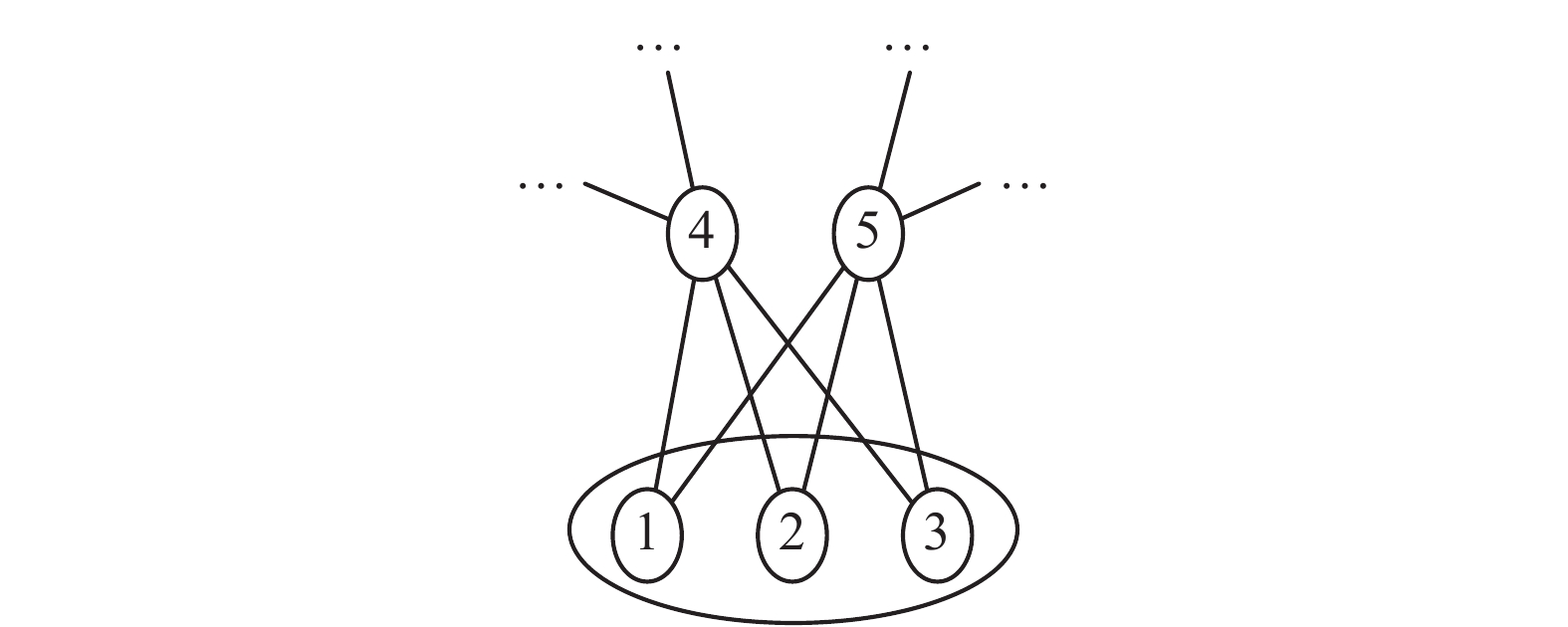
定义1 独立共连结构。独立共连结构是指网络中存在若干节点(称为对象节点),这些节点之间是独立不相连的,且它们与网络中其他节点的连接状况完全相同。如图1中的对象节点1、2、3构成了独立共连结构。
|
Download:
|
| 图 1 独立共连结构 Fig. 1 The isolated link structure | |
对于上述的独立共连结构,存在着一种特殊情况:当对象节点与网络中其他节点的连接情况均为不相连时,对象节点均为孤立节点。
独立共连结构与特征0的关系可由下述定理描述:
定理3 如果一个网络中存在独立共连结构,则该网络的邻接矩阵A具有特征值0。
证明 邻接矩阵A的特征值λk满足:
| $ \varphi ({{\textit{λ}}_k}) = {\rm{det}}({{\textit{λ}}_k}{{I}} - {{A}}) = 0 $ | (5) |
当网络中存在孤立节点时,不妨设节点1为孤立节点,则det(λkI−A)为
| $\left[ {\begin{array}{*{20}{c}} {{{\textit{λ}} _k}}&0&0& \cdots &0 \\ { - {a_{21}}}&{{{\textit{λ}} _k}}&{ - {a_{23}}}& \cdots &{ - {a_{2N}}} \\ \vdots &{}&{}& \ddots & \vdots \\ { - {a_{N1}}}& { - {a_{N2}}} & \cdots & {} &{{{\textit{λ}} _k}} \end{array}} \right]$ |
显然,当λk=0时,det(λkI−A)中存在全0行,使得det(λkI−A)=0,因此φ(0)=0,即0为A的特征值。
当网络中存在不含孤立节点的独立共连结构时,不妨设1到i点为独立共连结构,则det(λk I−A)为
| $\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {{{\textit{λ}}_k}}\!\! & \!\!0\!\! & \!\! \cdots \!\! & \!\!0\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ 0\!\! & \!\!{{{\textit{λ}}_k}}\!\! & \!\! \cdots \!\! & \!\!0\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ \vdots \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \\ 0\!\! & \!\! 0 \!\! & \!\! \cdots \!\! & \!\!{{{\textit{λ}} _k}}\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ { - {a_{i + 1,1}}}\!\! & \!\!{ - {a_{i + 1,2}}}\!\! & \!\! \cdots \!\! & \!\! { - {a_{i + 1,j}}} \!\! & \!\!{{{\textit{λ}}_k}}\!\! & \!\!{ - {a_{i + 1,i + 2}}}\!\! & \!\!{ - {a_{i + 1,N}}} \\ \vdots \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! \vdots \\ { - {a_{N1}}}\!\! & \!\! { - {a_{N2}}} \!\! & \!\! { - {a_{N3}}} \!\! & \!\! { - {a_{N4}}} \!\! & \!\! \cdots \!\! & \!\! { - {a_{N,N-1}}} \!\! & \!\!{{{\textit{λ}} _k}} \end{array}} \!\!\!\!\! \right]$ |
显然,当λk=0时,det(λkI−A)中的1到i行完全相同,使得det(λkI−A)=0,因此φ(0)=0,即0为A的特征值。证毕。
3.2 −1特征结构在特征值 −1对应的特征结构中,存在着一种具有明显规律性的特征结构,其具体定义如下:
定义2 互连共连结构。互连共连结构是指网络中存在若干节点(称为对象节点),这些节点之间是互相连接的,且它们与网络中其他节点的连接状况完全相同。如图2中的对象节点1、2、3构成了互连共连结构。

|
Download:
|
| 图 2 互连共连结构 Fig. 2 The connected link structure | |
互连共连结构与特征 −1的关系可由下述定理描述:
定理4 如果一个网络中存在互连共连结构,则该网络的邻接矩阵A具有特征值 −1。
证明 邻接矩阵A的特征值λk满足式(5),不妨设1到i点为互连共连结构,则det(λkI−A)为
| $\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {{{\textit{λ}} _k}}\!\! & \!\!{ - 1}\!\! & \!\! \cdots \!\! & \!\!{ - 1}\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ { - 1}\!\! & \!\!{{{\textit{λ}} _k}}\!\! & \!\! \cdots \!\! & \!\!{ - 1}\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ \vdots \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! \vdots \!\! & \!\! \vdots \!\! & \!\! \vdots \\ { - 1}\!\! & \!\! { - 1} \!\! & \!\! \cdots \!\! & \!\!{{{\textit{λ}} _k}}\!\! & \!\!{ - {a_{1,i + 1}}}\!\! & \!\! \cdots \!\! & \!\!{ - {a_{1N}}} \\ { - {a_{i + 1,1}}}\!\! & \!\!{ - {a_{i + 1,2}}}\!\! & \!\! \cdots \!\! & \!\! { - {a_{i + 1,j}}} \!\! & \!\!{{{\textit{λ}} _k}}\!\! & \!\!{ - {a_{i + 1,i + 2}}}\!\! & \!\!{ - {a_{i + 1,N}}} \\ \vdots \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! {} \!\! & \!\! \vdots \!\! & \!\! \vdots \\ { - {a_{N1}}}\!\! & \!\! { - {a_{N2}}} \!\! & \!\! { - {a_{N3}}} \!\! & \!\! { - {a_{N4}}} \!\! & \!\! \cdots \!\! & \!\! { - {a_{N,N-1}}} \!\! & \!\!{{{\textit{λ}}_k}} \end{array}}\!\!\!\!\! \right]$ |
显然,当λk=−1时,det(λkI−A)中的1到i行完全相同,使得det(λkI−A)=0,因此φ(−1)=0,即−1为A的特征值。证毕。
3.3 结构优化独立共连结构和互连共连结构是0/−1特征结构中具有明显规律性的结构,为了提高网络的可控性,则可以通过消除网络中的这2种结构,减少0/−1特征值对应λkI−A矩阵的行相关性,即减少最小控制输入的节点个数,从而实现可控性的优化。
本文中的优化方法主要是基于邻接矩阵A来找到两种典型的0/−1特征结构,通过对矩阵A中对应元素的改变来实现节点之间的增边或减边,从而实现结构优化操作。由0·I−A=−A可知,消除独立共连结构的处理对象为矩阵−A(或A),消除全0行则可消除孤立节点,消除相同行则可消除不含孤立节点的独立共连结构;由−1·I−A=−I−A可知,消除互连共连结构的处理对象为矩阵−I−A(或A+I),消除相同行则可消除互连共连结构。在整个结构优化过程中,设置每个步长只允许对一条边进行一次增边或减边操作,则优化的主要步骤如下:
1)逐行判断矩阵A是否存在全0行。如果存在且第i行为全0行,则随机生成一个整数j,有j∈(1,N)且j≠i,令aij=1,aji=1,跳转1)继续运行;如果不存在全0行,则跳转2)。
2)逐行对比矩阵A中的其他行是否存在相同行。如果存在相同行,则获取对象点集CP、共连点集SP,随机生成2个整数i和j,有i∈CP,j∈SP,令aij=0,aji=0,跳转1);如果不存在相同行,则跳转3)。
3)逐行对比矩阵A+I中的其他行是否存在相同行。如果存在相同行,则获取对象点集CP、共连点集SP,随机生成两个整数i和j,有i∈CP,j∈SP,令aij=0,aji=0,跳转1);如果不存在相同行,则完成网络可控性的优化。
上述主要步骤中,为了减小网络的复杂程度,2)和3)均为减边操作,这个过程可能会出现孤立节点,因此2)和3)中进行减边操作后均跳转1),且对特征结构的判断顺序按照上述步骤进行。当经过3)完成优化时,则说明此时的网络中不存在独立共连结构和互连共连结构这两种特征结构,0/−1特征值对应λkI−A矩阵的行相关性极大地减小,最小控制输入也随之减小,整个网络的可控性将得到提高。在优化过程中,由于会消除独立共连结构,优化结果可以保证网络中不存在孤立节点这一特殊的独立共连结构,因此可以使网络结构具有一定的连通性,维持网络的基本通信功能。
4 验证分析为了说明0/−1特征值与网络可控性的关系以及本文可控性优化的有效性,进行3组验证实验。
4.1 0/−1特征值的验证本组实验通过对比0/−1特征值的几何重数和基于PBH求解的最小控制输入个数Nd,来说明0/−1特征值对网络可控性的影响。
特征值0所对应0·I−A矩阵的行相关性可由特征值0的几何重数c(0)量化求得:
| $ c\left( 0 \right)= N - {\rm{rank}}\left( {{A}} \right) $ | (6) |
特征值−1所对应−1·I−A矩阵的行相关性可由特征值−1的几何重数c(−1)量化求得:
| $ c\left( { - 1} \right) = N - {\rm{rank}}\left( {{{A}} + {{I}}} \right) $ | (7) |
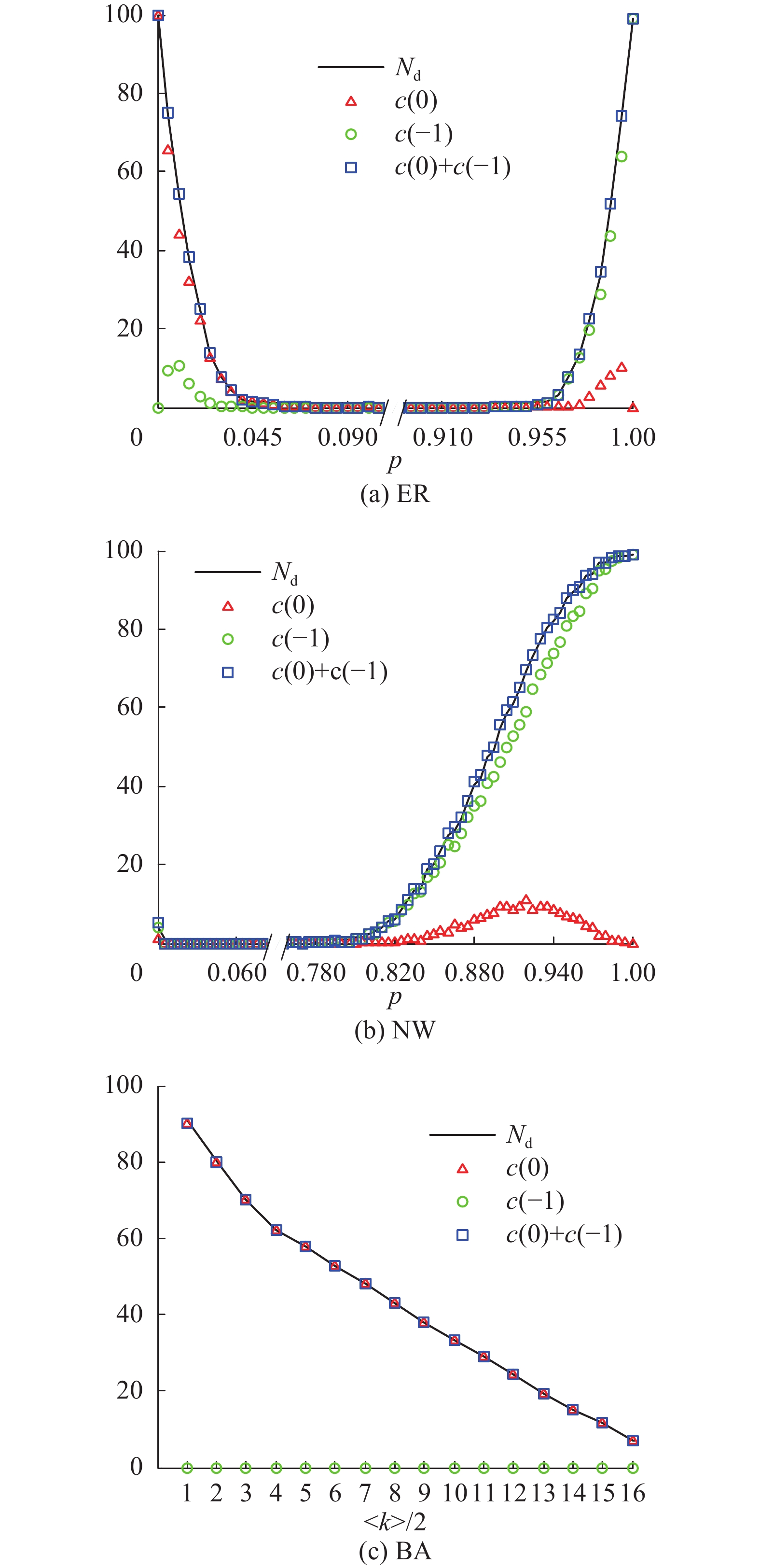
实验中的网络对象为ER、NW、BA 3种典型的复杂网络,且均为无向网络。由于本文旨在研究优化步骤对网络可控性的影响,暂不考虑网络规模,因此为了提高计算速度,所有网络均为100个节点,即N=100。生成不同参数下的ER、NW、BA 3种典型复杂网络,其中,ER网络、NW网络的变化参数为连接概率p,BA网络的变化参数为平均度的半值<k>/2,每个参数均独立生成了20个网络,求出的实验数值均为20个网络的平均值。实验结果如图3所示。
|
Download:
|
| 图 3 3种复杂网络的几何重数和最小控制输入 Fig. 3 Geometric multiplicity and minimum control input of three kinds of complex networks | |
从图3可以看出,0/−1特征值的几何重数之和,基于PBH求得的最小控制输入个数,二者几乎是一致的。这就说明了在所有λkI−A矩阵的行相关情况中,即便有非重复相关也是占极少数,而0/−1特征值对应的相关情况基本决定了网络的最小控制输入,极大地影响着网络可控性。
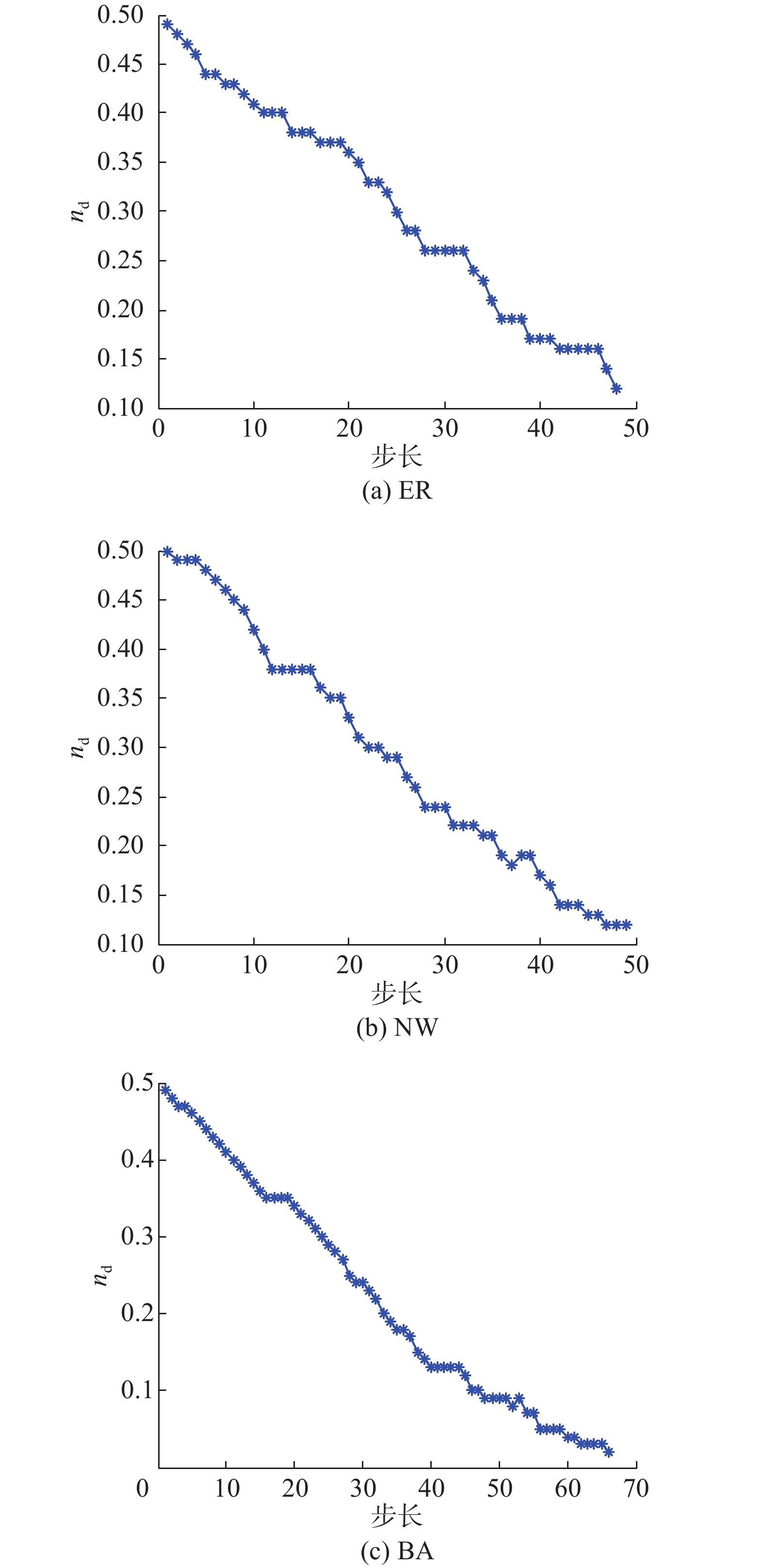
4.2 可控性优化的验证本组实验从4.1节生成的网络中,挑选ER、NW、BA 3个不同类型的网络,挑选网络的最小控制输入个数分别为50、51、50。对3个网络分别实施3.3节的优化步骤,计算每个步长下经过结构控制后网络的可控性。网络可控性的度量指标为根据式(1)计算的nd,实验结果如图4所示。
|
Download:
|
| 图 4 3个网络的网络可控性 Fig. 4 Network controllability of three networks | |
从图4可以看出,虽然在经过某些步长后,nd没有发生变化或者升高,但从整体来看3个网络的可控性指标nd均呈现了降低趋势。nd没有发生变化或者升高是由于在消除两种典型结构的过程中,可能会产生新的结构,出现新的行相关情况,尤其是在消除互连共连结构时,其实很容易就转换成了独立共连结构。但随着2种典型结构的逐渐消除,nd逐渐降低,最小控制输入节点的个数逐渐减小,即网络的可控性逐渐增强。说明经过本文的优化操作后,网络的可控性得到了提高。
4.3 实际网络的验证本组实验主要对2个实际的无线网络进行可控性优化。其中,网络Ⅰ为无线传感器网络,受传感器功耗的限制,其特点是网络连边较少,属于稀疏网络。网络Ⅱ为无线通信网络,为满足通信链路需求,其特点是网络连边较多,属于稠密网络。两个网络的节点数量N和连边数量L、优化过程中增边数量Ladd和减边数量Ldel、优化前可控性度量指标nd和优化后指标
| 表 1 两个无线网络的信息统计 Tab.1 The information of two kinds of wireless networks |
从表1中优化前后的可控性度量指标可以看出,经过可控性优化后,2个网络的可控性度量指标均降低,说明了网络可控性得到了提高。同时,通过2个网络的对比可以看出,对于连边较少的稀疏网络,优化过程中实施增边操作较多,这是由于减边操作极易造成孤立节点,需要通过增边进行弥补消除;而对于连边较多的稠密网络,优化过程中实施减边操作较多,这是由于减边操作不易造成孤立节点,出现增边的情况就相对较少。
5 结束语本文为了确定网络可控性度量指标,阐述了基于PBH的最小控制输入求解方法;通过分析研究0/−1特征值与矩阵λkI-A中行相关性的关系,明确了0/−1特征值对网络可控性的影响,提出了针对0/−1特征结构的可控性优化方法;通过验证分析,证明了0/−1特征值极大地影响着网络可控性,并且经过本文的可控性优化,网络可控性能够得到有效地提高。在下一步的研究中,一方面将对非0/−1特征值,尤其是整数特征值,对应的网络结构进行分析研究,探究减小非重复相关的可控性优化方法;另一方面,将考虑网络结构对通信传输的影响,以通信延迟、传输带宽等网络性能指标为约束条件,对可控性优化方法中的增边或减边操作进一步完善,形成不同的结构调整策略,提高实际中的应用价值。
| [1] |
LIU Yangyu, SLOTINE J J, BARABÁSI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167-173. DOI:10.1038/nature10011 ( 0) 0)
|
| [2] |
YUAN Zhengzhong, ZHAO Chen, DI Zengru, et al. Exact controllability of complex networks[J]. Nature communications, 2013, 4: 2447. DOI:10.1038/ncomms3447 ( 0) 0)
|
| [3] |
侯绿林, 老松杨, 肖延东, 等. 复杂网络可控性研究现状综述[J]. 物理学报, 2015, 64(18): 188901. HOU Lülin, LAO Songyang, XIAO Yandong, et al. Recent progress in controllability of complex network[J]. Acta physica sinica, 2015, 64(18): 188901. DOI:10.7498/aps.64.188901 (  0) 0)
|
| [4] |
LIN C T. Structural controllability[J]. IEEE transactions on automatic control, 1974, 19(3): 201-208. DOI:10.1109/TAC.1974.1100557 ( 0) 0)
|
| [5] |
PÓSFAI M, LIU Yangyu, SLOTINE J J, et al. Effect of correlations on network controllability[J]. Scientific reports, 2013, 3: 1067. DOI:10.1038/srep01067 ( 0) 0)
|
| [6] |
徐明, 徐传云, 曹克非. 度相关性对无向网络可控性的影响[J]. 物理学报, 2017, 66(2): 028901. XU Ming, XU Chuanyun, CAO Kefei. Effect of degree correlations on controllability of undirected networks[J]. Acta physica sinica, 2017, 66(2): 028901. (  0) 0)
|
| [7] |
WANG Wenxu, NI Xuan, LAI Yingcheng, et al. Optimizing controllability of complex networks by minimum structural perturbations[J]. Physical review E, 2012, 85(2): 026115. DOI:10.1103/PhysRevE.85.026115 ( 0) 0)
|
| [8] |
XIAO Yandong, LAO Songyang, HOU Lülin, et al. Edge orientation for optimizing controllability of complex networks[J]. Physical review. E, statistical, nonlinear, and soft matter physics, 2014, 90(4): 042804. DOI:10.1103/PhysRevE.90.042804 ( 0) 0)
|
| [9] |
XU Jiuqiang, WANG Jinfa, ZHAO Hai, et al. Improving controllability of complex networks by rewiring links regularly[C]//Proceedings of the 26th Chinese Control and Decision Conference. Changsha, China, 2014: 642–645.
( 0) 0)
|
| [10] |
HOU Lülin, LAO Songyang, SMALL M, et al. Enhancing complex network controllability by minimum link direction reversal[J]. Physics letters A, 2015, 379(20/21): 1321-1325. ( 0) 0)
|
| [11] |
LI Jingwen, YUAN Zhengzhong, FAN Ying, et al. Controllability of fractal networks: an analytical approach[J]. Europhysics letters, 2014, 105(5): 58001. DOI:10.1209/0295-5075/105/58001 ( 0) 0)
|
| [12] |
XU Ming, XU Chuanyun, WANG Huan, et al. Analytical controllability of deterministic scale-free networks and Cayley trees[J]. European physical journal B, 2015, 88(7): 168. DOI:10.1140/epjb/e2015-60230-3 ( 0) 0)
|
| [13] |
WU Lanping, ZHOU Jikun, YUAN Zhengzhong, et al. Exact controllability of a star-type network[C]//Proceedings of the 27th Chinese Control and Decision Conference. Qingdao, China, 2015: 5187–5191.
( 0) 0)
|
| [14] |
晁永翠, 纪志坚, 王耀威, 等. 复杂网络在路形拓扑结构下可控的充要条件[J]. 智能系统学报, 2015, 10(4): 577-582. CHAO Yongcui, JI Zhijian, WANG Yaowei, et al. Necessary and sufficient conditions for the controllability of complex networks with path topology[J]. CAAI transactions on intelligent systems, 2015, 10(4): 577-582. (  0) 0)
|
| [15] |
胡寿松. 自动控制原理[M]. 6版. 北京: 科学出版社, 2013: 445–456.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


