一场重大的科技革命必以一门新学科作为标志，这门新学科又必须以一支新数学作为支撑。工业革命以牛顿力学为标志学科，以微积分作为数学支撑。信息革命以信息科学作为标志，机制主义人工智能理论^[1-2]是把结构主义、功能主义和行为主义这三大流派有机统一起来的以柔性逻辑^[3]包容的通用人工智能理论，是信息科学的重要发展。那么，什么是信息科学的数学支撑呢？本文对此问题的回答是，因素空间是机制主义人工智能理论的数学基础, 它是为迎接人工智能的深刻革命而作的数学准备。

信息科学与物质科学的根本差别是有没有认识主体的参与。客体是离开认识主体的存在，认识主体按其目标需求从客体信息提取语义信息，再将语义信息转化为知识，提高智能，改造主、客观世界，这就是信息科学的主要内容。因素是信息提取的导向标，是信息向知识转化的分析与融合器。信息生态的机制就是要以因素为导向，首先关注客体的形式与效用这两个方面。用目标需求从后往前倒逼，用储备的知识从前往后疏通，这样前后夹逼，所得到的语义信息就是形式与效用相统一的全信息。客体的状态千变万化，必须用因素来进行分析与综合，例如形状、大小、颜色、质量等，统称为状态因素，状态因素使人形成对事物外形的知觉。事物的内在属性也要用因素来梳理，杯子可以是日常饮具或者是保健食品容器，也可能是供人鉴赏的艺术品，不同的目标需求按效用来观察事物的内在属性，属性因素揭示事物的内在效用。状态因素与属性因素之间的结合衍生出特定的概念；因素之间的相互关联决定事物的因果，提供逻辑推理以进行决策。基于因素空间理论所建立的数据库以培植数据的方式来实现数据生态与知识生态之间的同构，用因素来组织数据，运用知识把传统的搜索技术提到一个新的高度，这些都是机制主义人工智能所需要的数学理论和方法。

1 因素空间的基本框架

什么是因素？按字面来理解，因字既言本事物之所以是，亦言它事物之所以生。前者讲事物构成，后者讲因果关联。因素非因，乃因之素。雨量充沛是丰收的一个原因，但它不是因素。因素是降雨量，由它统领“洪涝”、“雨量充沛”、“雨量欠缺”和“干旱”等性状。因素通过变化来显示其影响。如果降雨量的变化不能改变丰收这一结果的话，那么雨量充沛就不是丰收的原因；降雨量之所以对古代农业那么重要，是因为它的变化既可以使大众喜迎丰收，也可以使遍地颗粒无收，这才使人们知道降雨量对粮食收成来说是多么重要的一个因素，遇到少雨就要考虑防旱。从原因到因素是人在认识上的一种升华。只有掌握因素才能找到原因，看透原因。因素是比属性高一个层次的东西，它是属性的统领，是属性之名。事物都是质与量的统一，属性是质表，因素是质根。属性被动描写事物，因素则具有启发的特质，在信息科学和人工智能的数学描述中，因素是一个特别关键的词。只有强调质根，才能找到事物和认识的成因。哲学家早已对属性下过定义，但至今仍忽视质根。属性像是珍珠，质根是串联珍珠的线头。线头一断，珍珠就洒满遍地，搜索起来格外困难。人脑是信息提取的优化结构，人脑的感觉细胞是按特征(即因素)来组织的；生命科学中所诞生的基因就是生命的质根。基因最早的英文名称是Factor，因素就是广义的基因。信息革命需要将打开生命之门的这把钥匙引向信息之门，哲理指明了因素空间乃是信息科学和人工智能对数学的期望之所在。

1.1 因素与因素空间的数学定义

在数学上，因素被定义成映射，更具体一点地说，因素是一种性状映射，它把事物映射成它们的性状。

定义1^[4] 　设U是所要讨论的一类事物的集合，叫作论域。一个定义在论域U上的映射f: U→X(f)叫作U上的一个因素，其中X(f)是映射f所映照出来的事物性状的集合，叫作f的性状空间。

性状有两种类型，一种是连续的实数值，例如，因素身高可表示为特定的人群U上的一个映射f = $ U \to \left[ {10,250} \right]$ (cm)，它把张三映射成实数185 cm，把李四映射成175 cm $\cdots $ 这样的性状空间叫作定量的性状空间，此时的因素就是我们过去所熟悉的变量，变量是一种特殊的因素，因素就是变量的推广。定量性状空间是欧氏空间 ${R^n}$ 中的一个超矩形( $n = 1$ 或 $n > 1$ )，n叫作性状空间的维数。因素身高还可以有另外一种形式的性状空间：X(身高)={高，中，低}，它把张三映射成高个子，把李四映射成中等个子 $ \cdots $ 这是离散的用自然语言描述的性状，这种性状空间叫作定性的性状空间。性状都是按因素成串地呈现，世界上没有单一的性状，性状的数目m叫作相数， $m$ 必须大于1。单一的特征用来识别时都是二相，例如，脸上长痣是一种特征，但在识别过程中注意的焦点不是去描述痣的特性而是要区别“有痣”和“无痣”，仍是二相映射。为了方便，我们将特征称为二相因素，但在这样称呼时必须声明：特征本来指的是痣，是一个属性，若把它视为因素，则它就不再是一个属性而是一个二相映射了。因素与属性是不同层次的东西，前者统帅后者。当然，同一个词在不同的场合中可以从属性变为因素，也可以从因素变为属性。

只取定量性状空间的因素叫作定量因素，只取定性性状空间的因素叫作定性因素。这样称呼仅仅是为了叙述的方便。严格来说，定性与定量是一对普遍矛盾，它们对立统一地寓于事物之中，相互转化，因素既可以定性，也可以定量，我们对任何因素都同时预备着定性与定量两种性状空间，以备相互转换。在同时出现两种性状空间的时候，我们用 $\underline X \left( f \right)$ 来表示定量性状空间。要将 $X\left( f \right)$ 中的性状转化为 $\underline X \left( f \right)$ 上的模糊或非模糊子集。这些事情要靠模糊集和直觉模糊集等学科来完成。这种工作涉及坐标框架的标定，对于因素空间来说至关重要。

定性映射决定论域的划分。设 $f$ 是定义在论域 $U$ 上的一个因素，按这个因素的性状在论域 $U$ 中定义了一个等价关系~：对任意 $u,v \in U$ ， $u \sim v$ 当且仅当 $f\left( u \right) = f\left( v \right)$ 。一个等价关系决定 $U$ 中对象的一个分类，记对象u所在的类为 ${\left[ u \right]_f} = \left\{ {v \in U\left| {f\left( v \right) = f\left( u \right)} \right.} \right\}$ 。

定义2　记 $H\left( {f,U} \right) = \left\{ {{{\left[ u \right]}}\left| {u \in U} \right.} \right\}$ ，我们将它称为 $f$ 对U的划分。

因素有简单与复杂之分，所谓 $f$ 对 $U$ 比 $g$ 对 $U$ 的划分更细 (记作 $\left. {H\left( {f,U} \right)} \right\}H\left( {g,U} \right)$ )是指：任给一个由 $g$ 所分出的类 ${\left[ u \right]_g}$ ，必有 $f$ 所分出的类 ${\left[ \nu \right]_f}$ 使 ${\left[ v \right]_f} \subseteq {\left[ u \right]_g}$ 。

定义3　设 $f$ ， $g$ 是定义在 $U$ 上的两个因素，如果 $\left. {H\left( {f,U} \right)} \right\}H\left( {g,U} \right)$ ，则称因素 $f$ 比 $g$ 复杂，记作 $f \geqslant g$ 。反之，则称因素 $f$ 比 $g$ 简单，记作 $f \leqslant g$ 。

不难证明，任给 $U$ 上的一个因素集 $F^*,\left( {\left. {F^*,} \right\}} \right)$ 形成一个偏序集。给定U上的一组因素 ${f_j}:U \to X\left( {{f_j}} \right)$ $\left( {j = 1,2, \cdots ,n} \right)$ ，由它们所构成的集合 $F^* = \left\{ {{f_1},{f_2}, \cdots ,{f_n}} \right\}$ 称为元因素集。对F^*的任意子集 $\left\{ {{f_{\left( 1 \right)}},{f_{\left( 2 \right)}}, \cdots ,{f_{\left( k \right)}}} \right\}$ ，可以定义一个U上的合成因素 $F:U \to X\left( F \right)$ ，其状态空间是

$X\left( F \right) = X\left( {{f_{\left( 1 \right)}}} \right) \times X\left( {{f_{\left( 2 \right)}}} \right) \times \cdots \times X\left( {{f_{\left( k \right)}}} \right)$

(1)

记此因素的合成运算为 $F = {f_{\left( 1 \right)}} \cup {f_{\left( 2 \right)}} \cup \cdots \cup {f_{\left( k \right)}}$ 。式(1)的意思是：合成因素的性状空间被定义成其所含元空间的笛卡尔乘积。对于任意两个合成因素，我们可以定义它们的二次合成，其性状空间被定义成两组元的并集中诸元的性状空间的乘积。如此可以在 $F^*$ 的幂集中定义因素之间的任意多次合成运算 $ \cup $ 。类似地，用两组元的交集中诸元性状空间的乘积可以定义因素之间的另外一种运算 $ \cap $ ，叫作分解运算。分解运算可以直观地理解为提取两因素的最大子公因素。分解两个不含公共元的因素，可得零因素0。一组因素称为两两不可约，如果两两之交为0。不难证明 $P\left( {F^*} \right) = (P\left( {F^*} \right); \cup , \cap )$ 形成一个因素格，这个因素格可以由偏序集 $\left( {\left. {F^*,} \right\}} \right)$ 按下述方式形成：

$F \cup G = {\rm{Sup}}\left\{ {F,\;G} \right\},\;F \cap G = {\rm{Inf}}\left\{ {F,\;G} \right\}$

(2)

$F^* = {f_1} \cup {f_2} \cup \cdots \cup {f_n}$ 是在所定义的系统中最大的因素，叫作全因素。由此还可以定义余运算^c。 ${F^c}$ 的性状空间是那些不被F所包含的元性状空间的乘积。不难证明 $P\left( {F^*} \right) = (P(F^*), \cup , \cap {,^c})$ 形成一个因素布尔代数。

定义4　记 ${X_{F^*}} = {\left\{ {X\left( F \right)} \right\}_{ {F \in P\left( {{F^*}} \right)}}}$ ，称 $\phi = \left( {U,\;{X_{F^*}}} \right)$ 为U上的一个因素空间。F*中的因素称为原始因素， $P\left( {F^*} \right)$ 中的其他因素称为合成因素，记 $X = X\left( {{f_1}} \right) \times $ $X\left( {{f_2}} \right) \times \cdots \times X \left( {{f_n}} \right)$ ，叫作总性状空间。对于定性性状空间而言，任意 ${\mathit{\boldsymbol{a}}} = \left( {{a_1}, {a_2}, \cdots ,{a_n}} \right) \in X$ 叫作一个性状颗粒。

这个定义在以前一直引用的文献[5]的基础上做了简化。

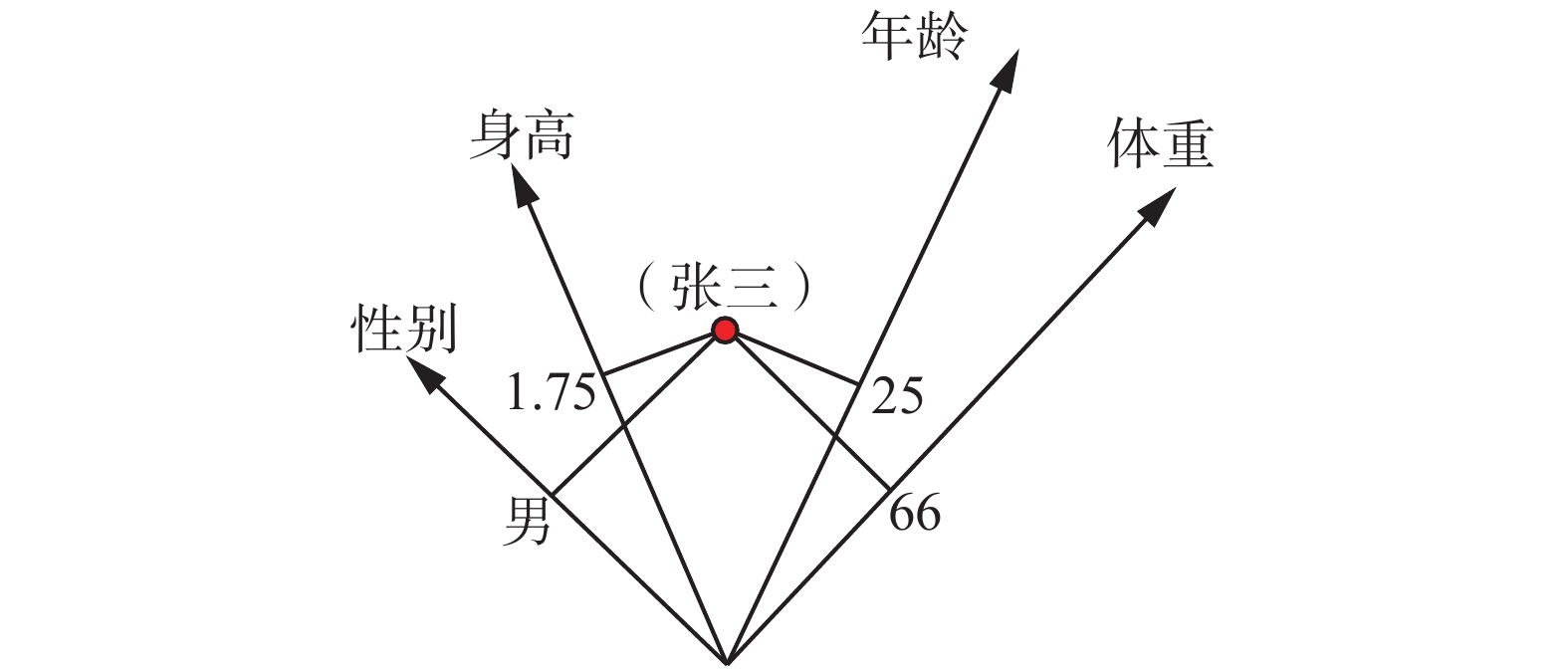
所有笛卡尔空间，例如力学的运动空间、控制论的状态空间、模式识别的特征空间等，都是性状空间。它们都可作为因素空间的特例，因素空间是笛卡尔空间的推广。如图1所示，任何事物都可以像张三这样地被映射成为性状空间中的一个点，因素空间为一般事物的描述提供了普适性的数学框架。一群对象被映射成为性状空间中的样本点集。要对这群对象分类，就必须将它们投射到因素性状空间中来进行分割。

1.2 背景关系与背景分布

定义5^[4] 　给定U上的定性因素空间 $\phi = \left( {U,{X_{F*}}} \right)$ ，对任意 ${\mathit{\boldsymbol{a}}} = \left( {{a_1},{a_2},\cdots,{a_n}} \right) \in X$ ，记其在U上的原相为

$\left[ {\mathit{\boldsymbol{a}}} \right] = {F^{ - 1}}\left( {\mathit{\boldsymbol{a}}} \right) = \left\{ {u \in U\left| {F\left( u \right) = {\mathit{\boldsymbol{a}}}} \right.} \right\}$

(3)

$\left[ {\mathit{\boldsymbol{a}}} \right]$ 可能是空集 $ \phi $ ，若 $\left[ {\mathit{\boldsymbol{a}}} \right] \ne \phi $ ，则称a是一个实性状颗粒，否则称a是一个虚组态。全体实性状的集合记为

$\begin{array}{c}R = F\left( U \right) = \left\{ {{\mathit{\boldsymbol{a}}} = \left( {{a_1},{a_2}, \cdots ,{a_n}} \right) \in X|\exists u \in U;} \right.\\\left. {{f_1}\left( u \right) = {a_1},{a_2}, \cdots ,{f_n}\left( u \right) = {a_n}} \right\}\end{array}$

(4)

式中R叫作因素 ${f_1},{f_2}, \cdots ,{f_n}$ 之间的背景关系，也叫作因素 $F^*$ 的背景集。背景集是实际存在的笛卡尔乘积集。

显然有， $F^*$ 是从 $H\left( {U,F^*} \right)$ 到 $R$ 的同构映射。

定义5多用于定性因素，其中的a是指性状颗粒。但定义5也可用于连续情形，此时a细化为一个实数点。

背景关系是因素空间的核心概念，下面会看到它既可以决定概念的自动生成，又可决定概念之间的一切推理，由它可以建立知识描述的确定性理论框架。但现实中的背景关系多带有不确定性。原因有二：1) 性状粒度往往过大，说一个人的性状容易，说一群人的性状就不确定了，存在着抽样的随机性；2) 定性因素相的划分不明确，例如年龄这个因素，究竟怎样划分青年、中年和老年？存在着模糊性。为此，要引入背景分布和模糊背景关系的概念，为了节省篇幅，本文只介绍背景分布。

设论域 $U = (U,{\mathit{\boldsymbol{A}}},p)$ 是一个概率场， $\phi = \left( {U,{X_{F*}}} \right)$ 是定义在 $U$ 上的一个因素空间。又设 $X = \left( {X,{\mathit{\boldsymbol{B}}}} \right)$ 是总性状空间 $X$ 上的一个可测结构。若所有 ${F^*}$ 中的元 ${f_j}$ 都是从U到X的可测映射，即对任 $B \in {\mathit{\boldsymbol{B}}}$ ，都有 ${f_j}^{ - 1}\left( B \right) = \left\{ {u \in U|{f_j}\left( u \right) \in B} \right\} \in {\mathit{\boldsymbol{A}}}$ ，则不难证明，所有因素 $F \in P\left( {{F^ * }} \right)$ ，包括 ${F^ * }$ ，都是从U到X的可测映射。

定义6　设论域 $U = {\rm{ }}(U,{\mathit{\boldsymbol{A}}},p)$ 是一个概率场， $\phi = \left( {U,{X_{{F^ * }}}} \right)$ 是定义在 $U$ 上的一个因素空间， $X = \left( {X,{\mathit{\boldsymbol{B}}}} \right)$ 是总性状空间上的一个可测结构。若所有 ${F^ * }$ 中的元 ${f_j}$ 都是可测映射，记 $p = {p_{{F^ * }}}$ 为 $p$ 经过 ${F^ * }$ 在 $X$ 上所诱导出来的概率，亦即对任意 $B \in {\mathit{\boldsymbol{B}}}$ ，都有 $p\left( B \right) = p\left( {{F^{ * - 1}}\left( B \right)} \right)$ ，那么 $p$ 叫作因素 ${F^ * }$ 的背景分布。

背景分布是背景关系的随机化。随机化后的因素都可视为广义的随机变量，特别对定性因素而言，因素可以叫作随机词。为了方便，我们常将因素的记号改为随机变量的记号，甚至约定： ${F^ * }$ 中的元因素的替代符号是 ${x_i}(i \!=\! 1,2, \cdots \! ,n)$ ： ${F^ * }\! =\! \left\{ {{x_1}, {x_2}, \cdots \! ,{x_n}} \right\}$ ， $X\left( {{x_i}} \right) = {X_i}$ 。

为了简便，我们以后讲可测因素空间就是指定义6中所说的带有可测结构的因素空间而且所有元都是从 $U$ 到 $X$ 的随机变量。

背景分布 $p$ 是背景关系 $R$ 的随机化。对定性因素而言，不难证明，背景关系 $R$ 就是背景分布的支撑，亦即

$R = \left\{ {a \in X|p\left( a \right) > 0} \right\}$

(5)

由此，可以将背景分布的概念推广到定量因素的情形。

定义7　对定量因素而言，背景分布密度函数 $p\left( x \right)$ 的支撑集 $R$ 叫作因素元之间的背景集。亦即

$R = \cap \left\{ {B \in {\mathit{\boldsymbol{B}}}\left| {{{\smallint}}_B {P\left( x \right)} {\rm{d}}{\mathit{\boldsymbol{x}}} = 1} \right.} \right\}$

(6)

1.3 因素数据库与背景基

数据工作者熟知信息系统和形式背景理论，它们为数据建立了表格，为非数值信息找到了初步的符号表示。因素空间理论正是它们的提升，为信息系统建立坐标框架，把一张形式系统表可视化地变为因素性状空间的一组样本点，背景关系就成为它们的母体。背景关系是因素空间的形骸，塑造这个形骸的工具就是背景基。

将按因素空间思想组织起来的数据叫作因素数据库，主要的库表叫作因素表，具表头 $t = \left( {u;{x_1},{x_2}, \cdots ,{x_k}} \right)$ 。若把对象 $u$ 去掉，以 $s = \left( {{x_1}, {x_2}, \cdots ,{x_k}} \right)$ 为表头，则表中的每一行就是因素空间中的一个点，由于与对象割断了联系，这个点就不再反映个人的隐私。

定义8^[4] 　记 $S = \left\{ {{s_i} = \left( {{x_{1i}},{x_{2i}}, \cdots \! ,{x_{ki}};{y_i}} \right)|i = 1,2, \cdots \! ,} \right.$ m}，叫作相样本或隐私样本。

因素库中首先考虑样本怎样表现背景关系。很明显的事实是，当样本逼近母体时，相样本就变成背景关系。

设 $S$ 是相样本，始终有 $S \subseteq R$ ；所有同表头相样本的并就是背景关系：

$R = \cup \left\{ {S|S{\text{是相样本}}} \right\}$

(7)

只要表头相同，对相样本不断地求并，就可以单调递增地逼近目标。同表头的相样本求并就是行的叠加。这个过程是可以并行处理的。因素库的目标是要将数据培育成背景关系，形成认知包以产生知识。要使这一思想得以实现，关键在于信息压缩。

定义9^[4] 　若每个元性状空间 $X\left( {{f_j}} \right)$ 都是有序集，且背景关系 $R$ 是 $X$ 中的凸集，记 $R$ 的所有顶点所成的集为 $B = B\left( R \right) = \left\{ {P|P{\text{是}}R{\text{的顶点}}} \right\}$ ，叫作背景基。将 $R$ 换作样本 $S$ ，记 $B$ 的所有顶点所成的集为 $B\left( S \right) = $ $ \left\{ {P|P{\text{是}}S{\text{的顶点}}} \right\}$ ，叫作样本背景基。

背景基可以生成背景关系，它是背景关系的无信息损失的压缩，对因素库的实际应用具有重要的意义。无论数据多大，样本背景基的数量始终保持在低维度上。在网上吞吐数据时，每输入一个新的数据，都要判断它是否是样本背景基的内点，若是，则删除此数据，否则将它纳入样本背景基，此时，要逐一检验原有的基点，它若在新基点中变成内点，则淘汰删除之。

给定整值样本 $S$ ，怎样判定谁是它的内点？记 $O$ 是 $S$ 的中心(不一定是整值点)，对于任意一点 $P$ ，从 $P$ 到 $O$ 引一条射线 $PO$ 。

夹角判别法^[4] 　 $P$ 是 $S$ 的一个内点当且仅当在 $S$ 中存在一点 $Q$ ，使射线 $PQ$ 与射线 $PO$ 形成钝角，亦即 $(Q - P,O - P) < 0$ 。

例1　在图2中， $S$ 包含三点： $a \!=\! \left( {2,1} \right){\text{、}}\!\!\!b \!=\! \left( {4,5} \right)$ 、 $c \!=\! \left( {5,3} \right)$ ，试问 $d = \left( {2,4} \right)$ 是内点吗？ $e = \left( {3,2} \right)$ 呢？

解　 $o = \left( {a + b + c} \right)/3 = \left( {3.7,\;3} \right)$

$(o - d,a - d) = (1.7, - 1)(0, - 3) = 3 > 0$

$(o - d,b - d) = (1.7, - 1)\left( {2,1} \right) = 2.4 > 0$

$(o - d,c - d) = (1.7, - 1)(3, - 1) = 6.1 > 0$

都是非负，d不是S的内点。

$(o - e,a - e) = \left( {0.7,{\rm{ }}1} \right)( - 1, - 1) = - 1.7 < 0$

一旦出现负数就是内点，e是S的内点。

这个判别法虽然是近似的，正有改进研究，但此方法却有应用价值。计算量很小，复杂度是 $O\left( {nk} \right)$ ( $n$ 是因素个数， $k$ 是样本点个数)，能适应大数据的需求。

1.4 因素藤、因素神经网络与智联网

因素空间是一个概念划分单元，不同单元联结起来形成因素藤。刘增良^[6]提出了因素神经网络，使因素空间理论和神经网络方法结合起来，把学习机制引入因素空间。因素藤又与因素神经网络相对应，呈现新的活力。黄崇福^[7]提出了智联网，把因素空间作为智联网的数学刻画工具，进一步上升到网络数学，具有比笔者更加广阔的视野和更加宏伟的历史使命。

因素空间是信息系统和形式背景理论的提升，能为客体提供一个可以存放其形式信息和效用信息的坐标系统，把关系数据库中的数据变成可视的样本点，它们的母体所形成的背景分布，乃是因素空间的形骸，塑造它的工具是背景基。

2 形式概念的生成与基本概念半格的提取

1982是不平凡的一年，在这一年中同时出现了3个数学分支，公开宣称以知识和智能作为自己的数学研究对象。在这3个分支中，首先要介绍的是德国数学家R. Wille所提出的形式概念分析(normal concept analysis)^[8]。在他以前，数学家们认为，任何概念的外延都是集合，而任何集合都是概念的外延。Wille明确地对后一句话说不。他提出了内涵和外延的对合性准则，认为只有满足对合性，才能把一个集合视为一个概念的外延。给定对象集 $O$ 和属性集 $A$ ，从它们之中分别取出一组对象 $E$ 和一组属性 $I$ ，记 $f\left( E \right) = \left\{ {a \in A|\forall o \in E;o{\text{具有属性}}a} \right\}$ ,它是 $E$ 中对象共有属性所形成的集。记 $g\left( I \right) = \left\{ {o \in O|} \right.$ $\left. {\forall a \in I;o{\text{具有属性}}a} \right\}$ ，它是 $I$ 中属性共同依附的对象所形成的集。如果 $f\left( E \right) = I$ 且记 $g\left( I \right) = E$ ，则称配对 $a = \left( {I, E} \right)$ 满足对合性，并称 $a$ 是一个以 $I$ 为内涵和以 $E$ 为外延的概念。

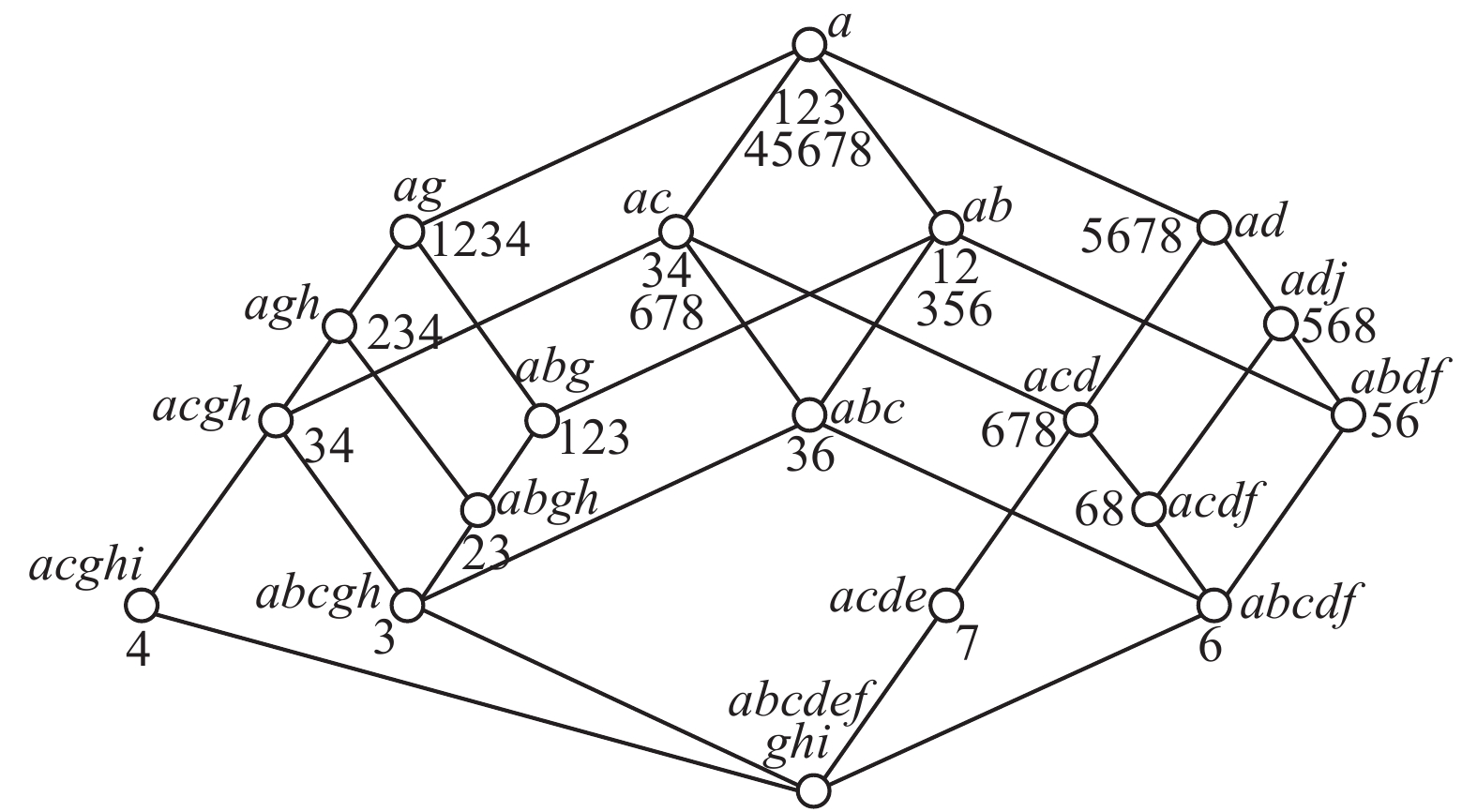
他以科教电影《生物与水》的资料制作了1张形式背景表(见表1)，其中有8类生物和9种属性： $a$ 需要水， $b$ 在水中生活， $c$ 在陆地生活， $d$ 有叶绿素， $e$ 双子叶， $f$ 单子叶， $g$ 能运动， $h$ 有四肢， $i$ 哺乳。表1以对象为行以属性为列，当且仅当第 $i$ 对象具有第 $j$ 属性在第 $i$ 行第 $j$ 列的格子中出现符号“×”。为了检验对合性，他让我们先随意选1个对象，蚂蟥，即取 $E = \left\{ 1 \right\}$ ，它具有属性 $a$ ， $b$ 和 $g$ ，即 $f\left( E \right) = \left\{ {a,b,g} \right\} = I$ 。然后再从这3个属性所在的列，找他们共同依附的对象有蚂蟥、鱼和蛙，即 $g\left( I \right) = \left\{ {1,2,3} \right\} = E'$ ，因 $E' \ne E$ ，故 $E$ 与 $I$ 不满足对合性。继续往前，看这3个对象所共有的属性是 $a$ 、 $b$ 和 $g$ ，即 $f\left( {E'} \right) = \left\{ {a,b,g} \right\} = I$ 。于是， $E'$ 与 $I$ 满足对合性，这样我们便找到了一个对合配对，这就是水生动物的样本概念 $\left( {a \wedge b \wedge g,{\rm{ }}\left\{ {1,2,3} \right\}} \right)$ 。之所以称为样本概念是因为这概念是从表1生成的，表1只是一个样本，所生成的概念是否有效，要看样本是否接近母体。像这样地搜索下去，最后找到了19个概念，按序生成一个概念体系，他称之为概念格(见图3)。

需要强调两点：1)Wille第一次给概念下了一个严格的数学定义，强调了内涵与外延的对合性。内涵是使概念得到统一认识的语义信息，外延是检验信息传递是否符合客观实际的关口。若内涵与外延不对合，信息传递就不可能可靠地反映客观现实，信息科学的根基便会动摇，所有的信息实践活动都将缺乏根据。2)自从他的论文发表以后，计算机就开始自动生成概念，这是人工智能的一大飞跃。机器早就可以证明定理，但机器却从未生成概念。定理只能在已有的概念之间兜圈子，人的智能却能从对比中产生新的概念，为定理制造新的猜想。Wille必定明白：我们不可能也不需要使机器像人脑一样真正地感知世界，但只要机器能机械地按他的算法构建概念体系，又能保证这个体系能随时回归联通到人脑，就能帮助人类大大加速智力建设！因为，信息科学虽与脑学科紧密相连，但却有独立于人脑的特色，其中存在着用数学可以描述的规律。概念体系无需全部浸泡在感知的海洋里，它可以有间歇地脱离实际，脱离大脑，就像我们自己的知识并非每一步都要亲眼见到或经过大脑(理解)一样。关键是，只有坚持内涵与外延的对合性，机器自动生成的概念才能向人脑回归和联通。没有回归联通人脑能力的机器概念体系所具有的功效和价值为零。

Wille的工作缺陷在于：1)他的形式背景表以属性来分列，制造了列表困难，由此导致他的算法复杂。为了寻找对合的概念，从每一行或列开始搜索，再每两行或两列 $ \cdots \cdots $ 这样的搜索方式本身就是指数爆炸的。他一整本书就是为了避免指数爆炸而设立各种算法，但仍然无法摆脱N-hard陷阱。2)Wille所说的概念，都是属性的析取，只含“且”字而不含“或”字，这不是一般概念而是基本概念。对合性只对基本概念成立，带或字的概念是无法对合的。基本概念只能形成半格，所以，他说的概念格应该改为基本概念半格。

在此，我们要介绍1982年由以Pawlak为代表的波兰学派所提出的粗糙集(rough sets)^[9]。粗糙集明确地以数据库为研究对象，他们的学派也是KDD(数据知识发现)的倡导者。粗糙集把重点从属性值转为属性名。用属性名列表，避免了Wille的列表困难。所列的表叫作信息系统，称为关系数据库的库表。他们用数学描述知识，用内外夹逼的思想来刻画概念，提出了决策的一般模型。粗糙集是关系数据库的数学基础。

形式概念分析虽然与粗糙集同年提出，但却隐藏了十余年，后来才引起粗糙集学者们的广泛重视。Wille的严谨性触动了粗糙集作者的粗犷风格，曾在粗糙集文献中说过：划分就是知识。按此说法，任一集合与其余集就是一个划分，就是知识，就有概念，这集合就应当是某个概念的外延，这就直接违反了Wille的对合性原则。在这一点上，粗糙集是有缺点的。然而粗糙集突出了属性名，就是突出了因素，比起形式概念分析，是一个重大的进步，可惜的是，他们并没有把属性名提到因素的高度。粗糙集在人工智能的应用热点是属性约简，靠的是区分矩阵，每一个矩阵方格中放置的是一组属性名。由这个矩阵要造就一个区分函数，中间必须涉及属性名的运算，可是，粗糙集没有定义属性名的运算，把它与属性值的逻辑运算混杂在一起，出现数学描述的漏洞，所提出的算法也过于繁杂，并没有取得应用的实效。尽管存在着这些问题，粗糙集仍取得了重要的发展^[10-11]。

因素空间也在1982年由笔者提出^[12]，早期曾用于模糊智能的研究，直到2012年才与形式概念分析及粗糙集合流。因素空间为概念生成提供了贴切的数学描述。人靠什么分男女？靠的是性别。靠什么分中外？靠的是国籍。靠什么分老少？靠的是年龄。性别、国籍和年龄都是因素。同一个人群按照不同的因素可以做出不同的划分。它们又可以综合起来形成更细的划分。因素是概念的划分器，要讲概念，必须从因素讲起。概念产生于比较，比较发现异同。但是世界上没有绝对的异，也没有绝对的同，所谓异同都是相对于一定因素而言的。因素是比较的角度和依据。风马牛不相及的东西不能进行比较，因为它们之间没有可比较的基础。因素就是比较基。若 $f$ 代表颜色， $a$ 和 $b$ 是有颜色的两个东西，我们便可以用“ $f\left( a \right) = f\left( b \right)?$ ”来比较 $a$ 和 $b$ 在颜色方面的异同。若 $g$ 代表吸引力， $a$ 和 $b$ 是有吸引力可言的两个东西，便可以用“ $g\left( a \right) = g\left( b \right)?$ ”来比较 $a$ 和 $b$ 在吸引力方面的异同。总之，比较离不开因素。一个因素把事物从一个方面进行划分，多个因素把事物从多个方面进行划分。因素越多，对事物的划分就越细，概念产生得就越多。知识发展的生态就是概念的不断分割过程。婴儿出世时只有零概念，其内涵是零描述而外延是混沌一团的宇宙。生存需求的本能因素把母亲从万物中区分出来，在外延上进行分割。人们形象地把外延称为概念的团粒。概念在何时不够用呢？就是目标需求的差异发生在一个概念团粒的内部，用这个概念无法区分差异，在这个时候，认知的需求就要力求打破团粒，使之由粗变细，而相应的内涵便要在原概念(称为上位概念)的内涵上再增添新的划分内容。人类的知识大树这就是这样一步一步形成的。每一步都是上位概念的分割，都要靠因素。知识的图谱必须以因素作为导引。

新因素对上位概念团粒划分的贡献可以用分辨度来刻画，把 $U$ 中任意两个不同的对象序列叫作一个对子。能分辨的对子数目越多，分辨度就越大。

定义10^[4] 　设 $H\left( {U,F} \right) \!\!=\!\! {\left\{ {{C_k} \!\!=\!\! \left( {{u_{k,}}_1, \!\cdots \!,{u_k}_{,n(k)}} \right)} \right\}_{(k =\! 1, 2, \cdots \! ,K)}}$

${d_f} = 1 - [n\left( 1 \right)(n\left( 1 \right) - 1) + \cdots + n\left( K \right)(n\left( K \right) - 1)]/m(m - 1)$

(8)

叫作因素 $f$ 对 $U$ 中对象的分辨度。

现在让我们回到前面所说的背景关系 $R$ 。 $R$ 是性状空间 $X$ 中所有原子内涵所成之集，它当然是描写内涵的。外延是论域中的事情，但是由于 $F$ 是从 $H\left( {U,F} \right)$ 到 $R$ 的同构映射。 $R$ 又是论域的代表，所以背景关系成了内涵与外延的重合体，这就使背景关系 $R$ 是概念生成的双料调色板。

定义11^[4] 　给定定性因素空间 $\left( {U,X\left( F \right)} \right)$ ，设 $R$ 是因素 ${F^*} = \left\{ {{f_1},{f_2}, \cdots ,{f_n}} \right\}$ 的背景关系，则对任意 ${\mathit{\boldsymbol{a}}} \in R$ ，称 $a = \left( {{\mathit{\boldsymbol{a}}},{\rm{ }}\left[ {\mathit{\boldsymbol{a}}} \right]} \right)$ 为原子概念， ${\mathit{\boldsymbol{a}}}$ 和 $\left[ {\mathit{\boldsymbol{a}}} \right]$ 分别叫作概念 $\alpha $ 的原子内涵和原子外延；对任意 $A \subseteq R$ ，记 $\left[ A \right] = \cup \{ \left[ {\mathit{\boldsymbol{a}}} \right]|{\mathit{\boldsymbol{a}}} \in A\} $ ， $\varGamma = \{ \gamma = \left( {A,\left[ A \right]} \right)|A \subseteq R\} $ ,称 $\gamma = \left( {A,\left[ A \right]} \right)$ 分别是以 $A,\left[ A \right]$ 为内涵和外延的概念；称 $\varGamma = (\varGamma , \vee , \wedge ,\neg )$ 是由 $\left( {U,X\left( F \right)} \right)$ 所生成的概念布尔代数。

${\mathit{\boldsymbol{a}}}$ 和 $\left[ {\mathit{\boldsymbol{a}}} \right]$ 都是原子，由于 $F$ 是从 $H\left( {U,F} \right)$ 到 $R$ 的同构映射，它们一定满足Wille的对合性。

这个定义告诉我们，对于定性因素空间而言，原子概念的提取是不需要计算的，只要背景关系知道了，它的每一个性状颗粒就决定一个原子概念。

由原子概念用“且”字连接起来，可以生成其他的所有概念，形成布尔代数，这在计算机上就可实现概念的自动生成，理论上极其简单。自动生成的概念不是怕少而是怕多，设原子概念的个数是 $k$ ，则生成的概念个数就是 ${2^k}$ 。我们需要把概念的范围缩小，非原子概念不一定满足对合性，其中满足对合性的概念是哪些呢？

定义12　内涵能表为合取范式的概念叫作基本概念。

所谓合取范式就是形如 $({a_{11}} \vee {a_{12}} \vee \cdots \vee {a_{1k\left( 1 \right)}}) \wedge \cdots $ $\wedge ({a_n}_1 \vee {a_n}_2 \vee \cdots \vee {a_{nk}}_{\left( n \right)})$ 这样的式子，其中 $ \vee $ 与 $ \wedge $ 分别代表“或”与“且”。每个小括号都是析取式，最后都用且字合起来。它们在因素的相空间中是拟超矩形(联通或不联通的超矩形)。原子概念都是基本概念。所有基本概念的集合对合取运算封闭，形成一个半格，叫作基本概念半格。Wille在图2中所画的就是基本概念半格，只不过在最下面加了一个极限概念，它的外延是空集，内涵无限制。

定义13 　给定因素空间和背景关系。包含所有原子概念的基本概念子半格叫作粒子半格。

通过粒子半格的建立，能在给定因素下将上位概念团粒细化到所有原子概念。在实际运用中，基本概念半格中的概念还嫌多。粒子半格中不一定有最小的半格，要找的是到达原子分割步数尽可能少的粒子半格。下面是所要求的一种基本算法，其复杂度是 $O\left( {{m^2}n} \right)$ 。

基本算法1　最短粒子半格算法^[13]

1) 给定U，计算每个因素对U中对象的分辨度；

2) 选对U分辨度最大的因素f来实现f对U的分类: 置换对象足码即（行足码）使同类对象连接在一起；

3) 用所分出的子类U′取代U, 重复步骤1）和2），直到所有的子类都变成粒子为止，总结出粒子半格。

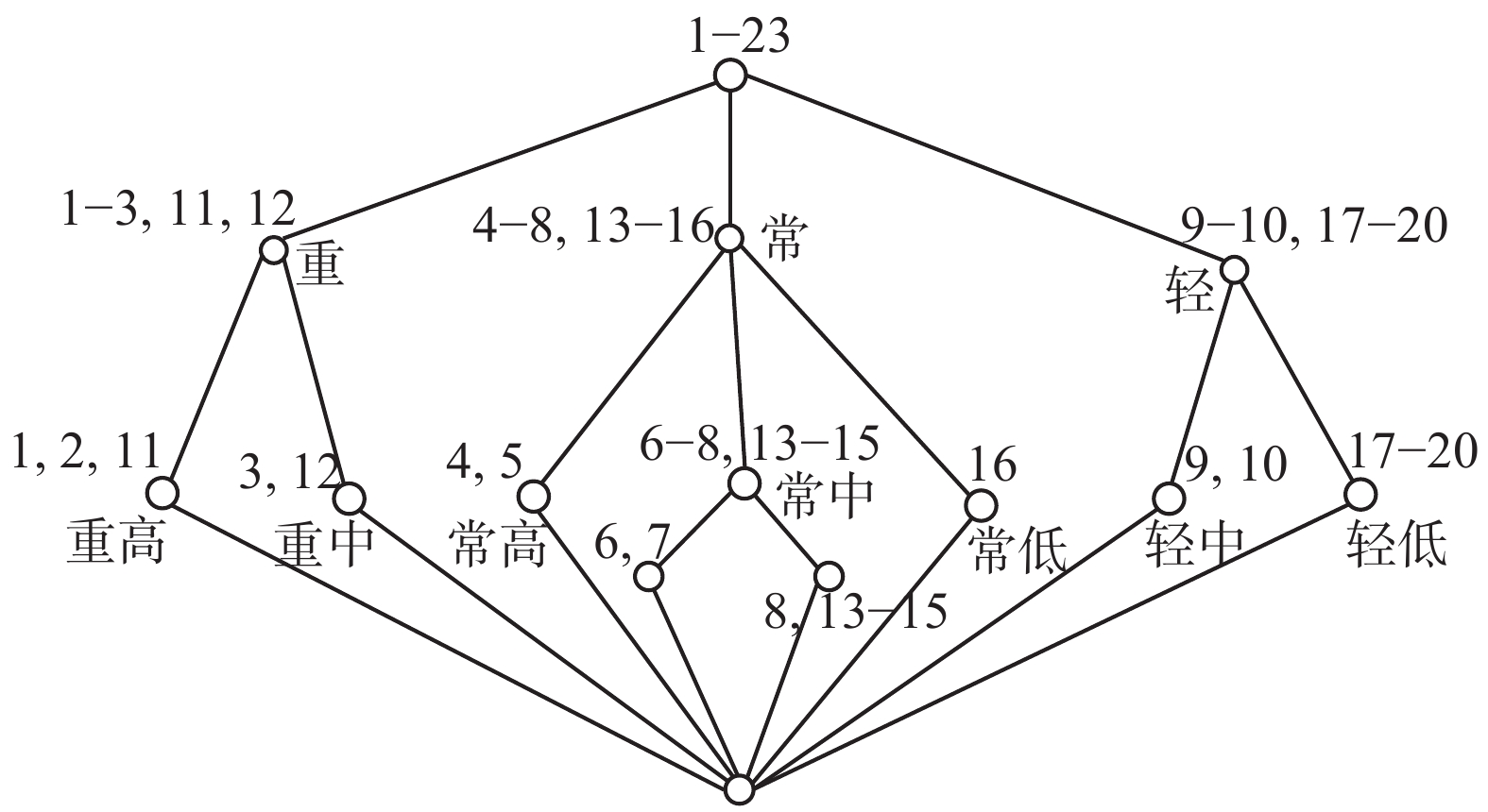
例2　给定表2：

表2中由20个人组成的论域 $U = \left\{ {a,b, \cdots ,t} \right\}$ ，在 $U$ 上有3个因素的定性性状空间：

$X$ (性别)={男，女}， $X$ (身高)={高，中，低}，X(体重)={重，常，轻}，现在的问题是要生成概念布尔代数。

解　将3个因素分别表示为 ${f_1}$ =性别， ${f_2}$ =身高， ${f_3}$ =体重，则它们的性状空间的笛卡尔乘积为

$X = X\left( {{f_1}} \right) \times X\left( {{f_2}} \right) \times X\left( {{f_3}} \right) = $ {男高重，男高常，男高轻，男中重，男中常，男中轻，男低重，男低常，男低轻，女高重，女高常，女高轻，女中重，女中常，女中轻，女低重，女低常，女低轻}

$X$ 被分成18个格子，去掉其中的虚组态，得到 $U$ 上3个因素所形成的背景关系：

$R = $ {男高重，男高常，男中常，男中轻，女中重，女中常，女低常，女低轻}

共有8个原子内涵，这8个原子内涵将U分成8块：

[男高重]={1, 2, 3}, [男高常]={4, 5}, [男中常]={6, 7, 8}, [男中轻]={9, 10}, [女中重]={11, 12}, [女中常]={13, 14, 15}, [女低常]={16}, [女低轻]={17, 18, 19, 20}

于是，对合性地生成8个原子概念：

${\alpha _1}$ =(男高重, {1, 2, 3}), ${a_2}$ =(男高常, {4, 5}), ${\alpha _3}$ =(男中常, {6, 7, 8}), ${\alpha _4}$ =(男中轻, {9, 10}), ${\alpha _5}$ =(女中重, {11, 12}), ${\alpha _6}$ =(女中常, {13, 14, 15}), ${\alpha _7}$ =(女低常, {16}), ${\alpha _8}$ =(女低轻, {17, 18, 19, 20})

由这8个原子概念任意取并，可以生成全部概念。例子说明，从背景关系提取概念代数的方法是直接方法，是自然对合的算法，是无需计算的算法。

布尔代数中的概念并不都是对合的，例如：

${\alpha _1} \vee {\alpha _5}$ =(男高重,{1, 2, 3}) $\vee$ (女中重, {11, 12})=(男高重或女中重, {1, 2, 3, 11, 12})

其内涵与外延不满足对合性，取并以后就不应该再谈对合。

共有2⁸–9=247个非空的新概念，太多，需要寻找基本概念，这时才需要基本算法1。

1) 计算分辨度： $m = 14$

$\begin{array}{c} {f_1} = {\text{性别}},\;n\left( 1 \right) = 10,\;n\left( 2 \right) = 10,\\{c_f}_1 = 1 - (10 \times 9 + 10 \times 9)/\left( {20 \times 19} \right) = \\ 1 - 180/380 = 1 - 9/19 = 10/19 \end{array}$

$\begin{array}{c} {f_2} = {\text{身高}},\;n\left( 1 \right) = 5,\;n\left( 2 \right) = 10,\;n\left( 3 \right) = 5,\\{c_f}_2 = 1 - (5 \times 4 + 10 \times 9 + 5 \times 4)/\left( {20 \times 19} \right) = \\ 1 - 130/380 = 25/38 \end{array}$

$\begin{array}{c} {f_3} = {\text{体重}},\;n\left( 1 \right) = 5,\;n\left( 2 \right) = 9,\;n\left( 3 \right) = 6,\\{c_f}_3 = 1 - (5 \times 4 + 9 \times 8 + 6 \times 5)/\left( {20 \times 19} \right) = \\ 1 - 112/380 = 268/380 \end{array}$

有 ${c_f}_3 > {c_f}_2 > {c_f}_1$ 。

2) 按因 ${f_3}$ (体重)进行足码置换，使对象按重、常、轻分类排列(见表3)。

此时，对象已经按体重排好，得到分类：

$\begin{array}{*{20}{c}}{U = {C_1}\left\{ {1,2,3,11,12} \right\} + {C_2}\left\{ {4,5,6,7,8,13,14,15,16} \right\}} + \\{{C_3}\left\{ {9,10,17,18,19,20} \right\}}\end{array}$

各类分别与内涵重、常、轻对合，得到3个基本概念 ${\beta _1} = ({\text{重}},{C_1}),{\beta _2} = ({\text{常}},{C_2}),{\beta _3} = ({\text{轻}},{C_3})$ 。

3) 再就因素 ${f_2}$ (身高)逐类考察，看看该类对象是否按高、中、低分相排列。在 ${C_1}$ 中，需要对对象 $k$ 和 $c$ 的位置进行置换，得到表4。

此时， ${C_1}$ 中的对象已经按身高排好，于是得到分类： ${C_1} = {C_{11}}\left\{ {1,2,11{\rm{ }}} \right\} + {C_{12}}\left\{ {3,12} \right\}$ 。

两类分别与内涵“重高”和“重中”对合,得到两个基本概念 ${\beta _{11}} = ({\text{重高}},{C_{11}}),{\beta _{12}} = ({\text{重中}},{C_{12}})$ 。

同时， ${C_2}$ 中的对象未经置换就已经按身高排好，于是得到分类：

${C_2} = {C_{21}}\left\{ {4,5} \right\} + {C_{22}}\left\{ {6,7,8,13,14,15} \right\} + {C_{23}}\left\{ {16} \right\}$

3类分别与内涵常高、常中、常低对合，得到3个基本概念 ${\beta _{21}} = ({\text{常高}},{C_{21}})$ ， ${\beta _{22}} = ({\text{常中}},{C_{22}})$ ， ${\beta _{23}} = $ $ ({\text{常低}},{C_{23}})$ 。

同时，C₃中的对象未经置换就已经按性别排好，于是得到分类:

${C_3} = {C_{31}}\{ 9,10\} + {C_{32}}\{ 17,18,19,20\} $

各子类分别与内涵轻中、轻低对合,得到两个基本概念 ${\beta _{31}} = ({\text{轻中}},{C_{31}}),{\beta _{32}} = ({\text{轻低}},{C_{32}})$ 。

4) 再就因素 ${f_3}$ (性别)逐类考察，看看该类对象是否男女分相排列. 发现性别在所有类中的排列都无需置换，类似可将 ${C_{22}} = {C_{221}}\left\{ {6,7} \right\} + {\rm{ }}{C_{221}}\left\{ {8,13,14,15} \right\}$ 得到两个基本概念 ${\beta _{221}} = ({\text{常中男}},{C_{221}}),{\beta _{222}} = $ $({\text{常中女}},$ C₂₂₂)。所有类都无法再划分。

5) 画出基本概念半格图(见图4)

在此半格中共有13个基本概念，即 ${\beta _0} = (\phi ,U)$ ， ${\beta _1} \!=\! ({\text{重}},{C_1})$ ， ${\beta _2} \!=\! ({\text{常}},{C_2})$ ， ${\beta _3} \!=\! ({\text{轻}},{C_3})$ ， ${\beta _{11}} = ({\text{重高}},{C_{11}})$ ， ${\beta _{12}} = ({\text{重中}},{C_{12}})$ ， ${\beta _{21}} = ({\text{常高}},{C_{21}})$ ， ${\beta _{22}} = ({\text{常中}},{C_{22}})$ ， ${\beta _{23}} = ({\text{常低}},{C_{23}})$ ， ${\beta _{31}} = ({\text{轻中}},{C_{31}})$ ， ${\beta _{32}} = ({\text{轻低}},{C_{32}})$ ， ${\beta _{221}} = ({\text{常中男}},{C_{221}})$ ， ${\beta _{32}} = ({\text{常中女}},{C_{222}})$ ，其中，不能再分的有 ${\beta _{11}}$ 、 ${\beta _{12}}$ 、 ${\beta _{21}}$ 、 ${\beta _{23}}$ 、 ${\beta _{31}}$ 、 ${\beta _{32}}$ 、 ${\beta _{221}}$ 、 ${\beta _{222}}$ 等8个，它们就是前述的8个原子概念。其余5个基本概念，除 ${\beta _0} = (\emptyset ,U)$ 外， ${\beta _1}$ =(重, 1, 2, 3, 11, 12), ${\beta _2}$ =(常, 4, 5, 6, 7, 8, 13, 14, 15, 16)， ${\beta _3}$ =(轻, 9, 10, 17, 1819, 20)和 ${\beta _{22}}$ =(常中, 6, 7, 8, 13, 14, 15)。它们都是我们格外关心的非原子的基本概念。

基本概念半格的提取，得到的原子概念是相同的，但中间的基本概念半格不是唯一的，与因素划分的先后次序有关。好的排序会加快实现原子分割，排除冗余的因素最大分辨度原则提供了一种较好的排序。这个算法强调的是对象的足码置换，就是士兵集合按营、连、排、班站队的方法. 具有大数据所要求的快捷性。

回到Wille的例子，怎样用因素空间理论来处理同样的问题呢？

首先，要将以属性值分列的表，改为以因素分列的因素表。它有9个属性，分属于7个因素： ${f_1}$ =需水性，具有性状空间 $X\left( {{f_1}} \right) = \left\{ {Y,N} \right\}$ ， ${f_2}$ =栖性，具有性状空间 $X\left( {{f_2}} \right)$ ={水，陆，两栖}， ${f_3}$ =有无叶绿素，具有性状空间 $X\left( {{f_3}} \right) = \left\{ {Y,N} \right\}$ ， ${f_4}$ =单双子叶，具有性状空间 $X\left( {{f_4}} \right)$ ={单，双}， ${f_5}$ =能动性，具有性状空间 $X\left( {{f_5}} \right) = \left\{ {Y,N} \right\}$ , ${f_6}$ =有无四肢，具有性状空间 $X\left( {{f_6}} \right) = \left\{ {Y,N} \right\}$ ， ${f_7}$ =是否哺乳，具有性状空间 $X\left( {{f_7}} \right) = \left\{ {Y,N} \right\}$ 。于是可将形式背景表1改写为下面的表5，在表中出现了符号*，例如问句是单字叶还是双子叶，这是毫无意义的，不能用No。问蚂蟥有四肢吗？回答虽然是No，但问题却是有意义的。Wille没有区分No和*，都是空白。

蓄水性这个因素对所有对象的呈相都一样，没有变化的因素失去了存在价值，我们把这一列从表中删除。同一因素空间中所有因素必须对所有对象都有意义，因而我们必须分成两个因素空间来处理，对表5的左列进行适当变换，得到了表5的右列，就可以分开了。得到表6，表6的左右两个表，各是一个因素空间。可以有交集，如栖性在两个表中都有。

我们把不起变化的因素删除得到表7。

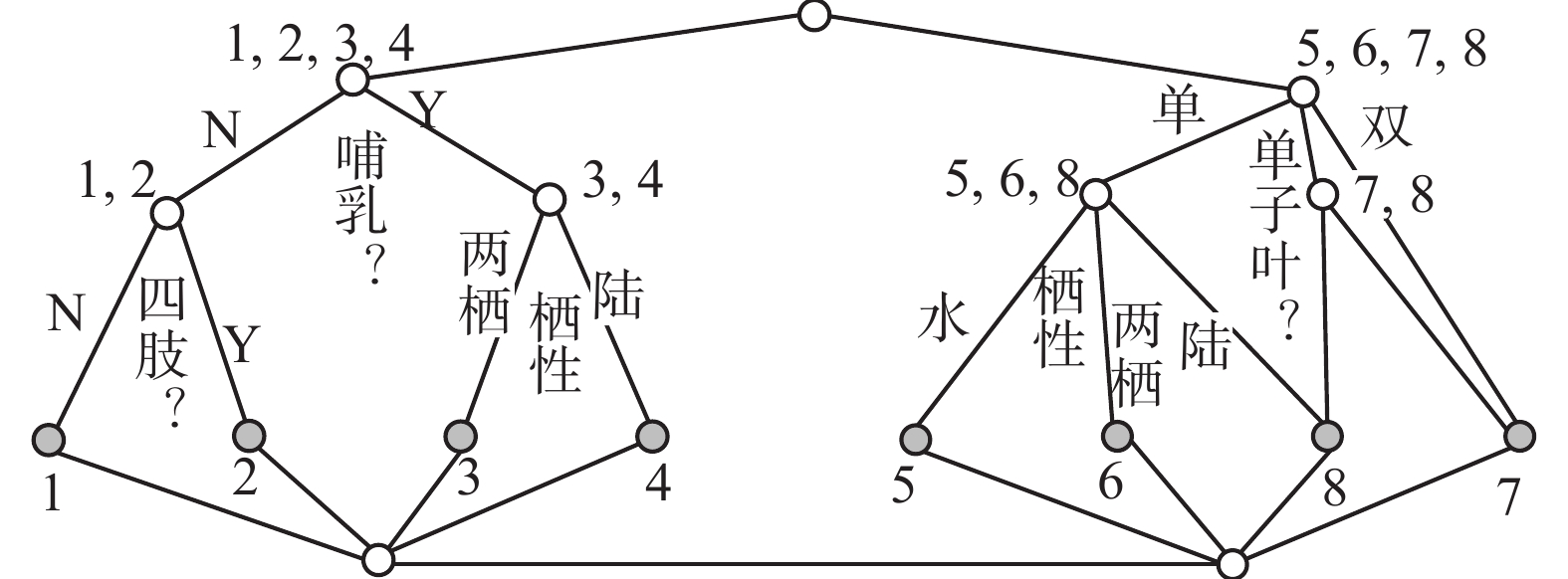
按照因素空间的概念生成理论很容易得到简捷的粒子半格(见图5)。经过适当处理，可以得到清晰的概念体系。动物因素空间生成4个原子概念：1)无肢非哺水动物(NN水，蚂蟥)；2)有肢非哺水动物(YN水，鱼)；3)哺肢两栖动物(YY水，蛙)；4)哺肢陆动物(NN水，蚂蟥)。还生成两个非原子的基本概念：1)非哺水动物(N水，{蚂蟥，鱼})；2)哺肢动物(YY，{蛙，狗})。植物因素空间生成4个原子概念：1)水单植物(水单，水草)；2)两栖单植物(两单，芦苇)；3)陆双子叶植物(陆双，豆)；4. 陆单子叶植物(陆单，豆玉米)。还生成两个非原子的基本概念：1)单子叶植物 (单，{水草，；芦苇，玉米})；2)陆植物 (陆，{豆，玉米})。例毕。

因为Wille关于科教事物的“概念格”不能直接翻译成为一张因素表，所以我们不能用因素空间的结果来和它进行直接的比较。但可以看出，概念格中缺少了几个原子概念，这是不符合实际的。其原因是，对合性与同因素的不同属性值之间的对等性有时会发生冲突。因素空间用性状颗粒来分类的方法可以避免这种冲突。

回顾一下本节的内容，Wille从内涵和外延的对合性出发，给概念下了严格的数学定义，以保障信息传递能可靠地反映现实。他大胆地谱写了计算机自动生成概念的新篇章，使机械制造的概念能随时向人脑回归与联通，这是人工智能的一大飞跃。他的形式背景表以属性来分列，导致算法复杂，无法摆脱N-hard陷阱。他说的概念格也不准确，应该改为基本概念半格。因素空间继承他的理论，把形式背景提升为因素空间的核心理论，用因素统帅属性值，用背景关系来定义原子概念，自然对合，无需计算。对于基本概念也有3次幂以下的简捷算法。

Wille不知道机制主义的人工智能理论，对形式(语法)信息、效用信息和语义全信息不加区分，他所举的例子都是语法信息。所以，本节可以视为形式信息的提取。至于如何用因素空间将形式信息与效用信息向语义信息，提升，是我们在下一节要做的事情。

3 因素之间的关联，语义信息的提升

在介绍语义信息提升之前，先介绍因素之间的关联特性。

定义14　给定可测因素空间，因素 ${f_1},{f_2}, \cdots ,$ f_n可以视为一组随机变量，如果这组随机变量是相互独立的，则称因素 ${f_1},{f_2}, \cdots ,{f_n}$ 相互独立,。如果 ${f_1},{f_2}, \cdots ,{f_n}$ 的背景关系R满足:

$R = X\left( {{f_1}} \right) \times X\left( {{f_2}} \right) \times \cdots \times X\left( {{f_n}} \right)$

(9)

则称因素 ${f_1},{f_2}, \cdots ,{f_n}$ 是相对独立的。

不难证明，相互独立一定相对独立，反之不尽然。不相对独立的一组因素，它们的背景关系不能涵盖整个笛卡尔乘积空间，这说明它们的性状搭配是受到制约的，这种制约反映了它们之间是相互关联的。

定义15　若 $R \ne X\left( {{f_1}} \right) \times X\left( {{f_2}} \right) \times \cdots \times X\left( {{f_n}} \right)$ ，则称因素 ${f_1},{f_2}, \cdots ,{f_n}$ 之间有关联。

取 $n = 2$ ，采用1.2节中约定的简单记号。若 $R \ne X\left( {{x}} \right) \times X\left( {{y}} \right)$ ，则因素 ${{x}}$ 与 ${{y}}$ 之间互有关联。对任意 $x \in X$ ，记 $R\left( x \right) = \{ y \in Y|\left( {x,y} \right) \in R\} $ ，叫作 $R$ 在 $x$ 点的截集，它是 $Y$ 的子集。

对于定性因素而言，记 $\left| {R\left( x \right)} \right| $ 为R(x)中所含性状颗粒的个数。若 $\left| {R\left( x \right)} \right|$ 越小，则 $x$ 对 $y$ 的制约性越强。

记 ${R_X} = \{ x|\exists y \in Y;{\rm{ }}\left( {x,y} \right) \in R\} $ 和 ${R_Y} = \{ y|\exists x \in X; $ ${\rm{ }}\left( {x,y} \right) \in R\}$ 分别叫作 $R$ 在 $X$ 和 $Y$ 中的投影。 ${\left( {{R_X}} \right)^c}$ 叫作 ${{x}}$ 对 ${{y}}$ 的盲区， ${\left( {{R_Y}} \right)^c}$ 叫作 ${{y}}$ 对 ${{x}}$ 的盲区。排除盲区可以提高搜索效率。

$R$ 的领域越小，关联性越强。当小到只有一个性状颗粒 $(a,b)$ 的时候，则输入 $x$ 的任意前提 $A$ ，关联到 ${\mathit{\boldsymbol{y}}}$ 只有两种可能：若 $A$ 包含 $a$ ，则 $y = b$ ，否则 $y \ne b$ 。当 $b$ 是关键性状时， $R$ 可以用作由 ${\mathit{\boldsymbol{x}}}$ 测 ${\mathit{\boldsymbol{y}}}$ 的精准预报器。

对于定性因素而言，若存在一个 $a \in X$ ，使 $\left| {R(a)} \right| = 1$ ，则 ${\mathit{\boldsymbol{x}}}$ 对 ${\mathit{\boldsymbol{y}}}$ 的最大制约强度达到1。此时截集 $R\left( x \right)$ 只能包含一个性状颗粒，设为 $b$ ，这便引出了因果律：若 $x = a$ 则 $y = b$ 。

因素间互为因果，若将因素 ${\mathit{\boldsymbol{x}}}$ 当作条件因素而将 ${\mathit{\boldsymbol{y}}}$ 当作结果因素，对任意 $E \subseteq X,E' \subseteq Y$ ，以E(x)表示 $x \in E$ ，以 $E'\left( y \right)$ 表示 $y \in E$ ，试问在何种条件下，才能保证有 $E\left( x \right) \to E'\left( y \right)$ ？

基本定理^[14] 　 $E\left( x \right) \to E'\left( y \right)$ 恒真当且仅当

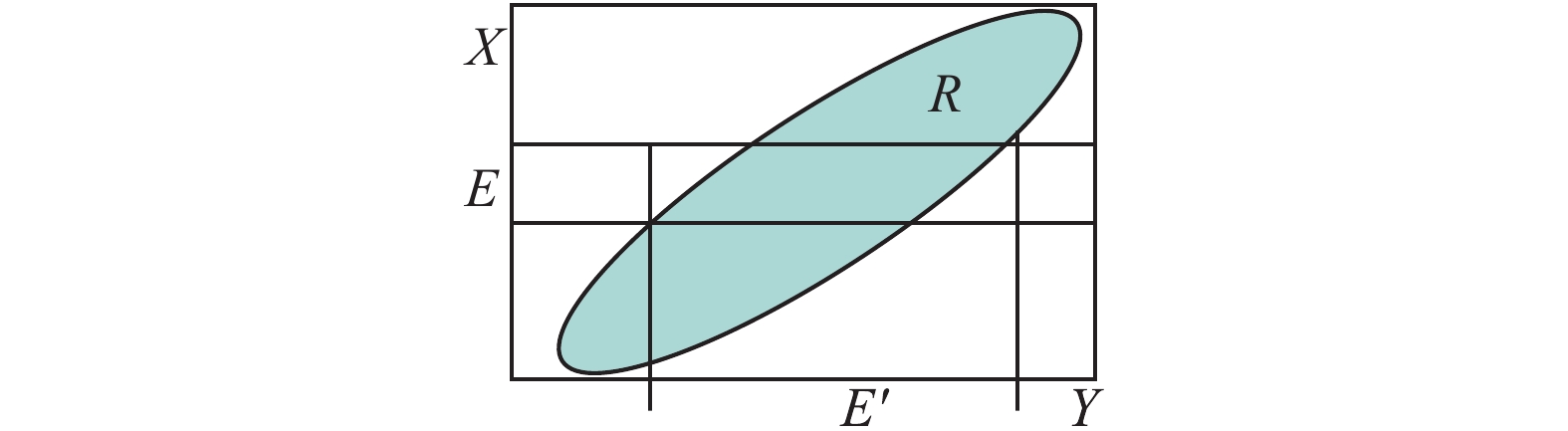
$\left( {E \times Y} \right) \cap R \subseteq \left( {X \times {\rm E}'} \right) \cap R$

(10)

注意， ${{x}}\text{、}{{y}}$ 本身可以是复杂因素， $X,Y$ 可以是任意高维的，这个定理适用于任意维数的空间，它说明背景关系 $R$ 决定了因素 $x$ 到 $y$ 的全部因果律。

这个定理证明的思路很简单，在图6中把 $X$ 的子集 $E$ 拿到 $X \times Y$ 中来就变成它的柱体扩张 $E \times Y$ ；把 $Y$ 的子集 $E'$ 拿到X×Y中来就变成它的柱体扩张 $X \times E'$ 。它们都是 $X \times Y$ 中的子集，就可以检验一下E×Y是否被X×E′所包含，若是，则二者形成前因与后果。但注意， $X \times Y$ 中有很多点是虚空的，背景集 $R$ 才是实际存在的疆域，所以二者都要与 $R$ 取交然后才能比较。式(10)又可写成

$(E \times Y){ \subseteq _R}(X \times E')$

(11)

符号 ${ \subseteq _R}$ 叫作在背景 $R$ 之下的蕴涵关系。因素空间以背景蕴涵为集运算，以背景推理为逻辑。

怎样从表头为 $T = \left( {u;{f_1},{f_2}, \cdots ,{f_{n - }}_1;g = {f_n}} \right)$ 的相样本 $S$ 中来提取因果规则呢？设 $s \in X\left( f \right),t \in X\left( g \right)$ ，记 $\left[ s \right] = \left\{ {u|f\left( u \right) = t} \right\},{\rm{ }}\left[ t \right] = \left\{ {u|g\left( u \right) = t} \right\}$ 。

定义16　如果 $\left[ s \right] \subseteq \left[ t \right]$ ，则称 $\left[ s \right]$ 是因素 $f$ 的一个决定类。因素 $f$ 的所有决定类的并集叫作它对结果的决定域。因素 $f$ 的决定域所占行数 $h$ 与表的行数(即全体对象个数) $m$ 之比称为它对结果的决定度^[14]，记作 $c\left( f \right) = h/m$ 。

条件因素 $f$ 与结果因素 $g$ 都在对 $U$ 进行分类，如果 $f$ 分出的某个类 $\left[ s \right]$ 变成 $g$ 的一个类 $\left[ t \right]$ ，则 $\left[ s \right]$ 中的对象都具有相同的结果 $t$ ，这时就得到一个推理句：“若 $u \in \left[ s \right]$ 则 $g\left( u \right) = t$ ” 。若记 $x = f\left( u \right),x = f\left( u \right)$ ，则推理句变为“若 $x = s$ ，则 $y = t$ ”，简写为s→t。于是，因素表就可以对诸条件因素进行划分，类越分越细，钻入结果类的机会就越来越多，得到的推理句也越来越多，直到不能再分为止。整个表就转化为一组规则，叫作因果规则，这种方法叫作因果分析法。在大数据面前，必须进行因素的约简，这与因素的分类次序相关，下面算法的思想是按决定度的大小次序来排列，使因素能得到较好的约简。

基本算法2　因果关联

给定以表头 $T = $ $\left( {u;{f_1}, \cdots ,{f_k};g} \right)$ 为表头的因素表S，要从表中提取因果关联规则，可采取下列步骤：

1) 计算各个因素 ${f_j}$ 对结果 $g$ 的决定度；

2)选决定度最大的因素对 $U$ 分类，若出现能钻入结果类的类别，就写出相应的因果句；逐次细化分类，直到所分类全部钻入结果类或不能再分为止。所有因果句的全体称为因果规则集。

因果关联规则的提取，是一种有用的归纳方法，具有很高的概括性，是归纳、学习、分类、评价、预测、控制等高级思维活动的统一算法。以它为基础可以向任何领域精细化。该法与决策树的算法很相似，只是用决定度取代了信息增益。在这方面已经发表了很多关于因素空间的文章^[15-19] 。

有了以上的准备，让我们来处理语义信息的提升问题。状态与效用是有紧密关联的两个或两组因素。利用这两组因素的数据可以提取从状态到效用的因果关联，得到一组因果规则作为知识储备起来，当要从形式信息推测效用信息的时候，就要利用状态效用因果关联所提供的一组规则。看看我们所面对的对象，其状态和那条规则的前件相匹配，就推断它有哪种效用。若硬匹配不行，就用相似性测度，选最贴近的一个作为推断，最后将形式信息与效用信息结合起来，得到语义信息，这就是从形式信息向语义信息的提升过程。

例3　服务对象状况到服务效用的因果关联

表8给出了用户（服务对象）的状况和服务效用之间的关联数据，把用户状况看作形式信息，把购买力看作服务效用信息，我们要来分析从形式信息到效用信息的因果关联。具体地说，要提取从用户状况来判断其购买力。表达形式信息有4个因素：f₁=年龄，具有性状空间X(f₁)={老，中，青}；f₂=职业，X(f₂)={师，生，商}；f₃=信贷，X(f₃)={好，可，差}；f₄=收入，X(f₄)={高，平，低}；效用形式的因素是g=购买力，具有性状空间X(g)={购买，不买}。

先看因素f₁与因素g之间的因果关系。按年龄可把9个用户分成老、中、青3类，从表8中可以看到这3类分别是：[老]={1, 5, 6}，[中]={2, 4, 9}, [青]={3, 7, 8}。这3类有哪一类是对购买的决定类呢？在3个老年用户中，用户1和5是不买，用户6是购买，他们的购买情况不一致，就不是对购买的决定类。再看中年用户2、4和9，他们都是购买，于是[中]就可以钻入[购买]，[中]就是g的一个决定类。青年用户不是决定类。所以年龄对g的决定度是3/9。

类似地，对因素职业来说，[师]={1, 2, 9}, [生]={3, 7, 8}，[商]={4, 5, 6}，他们都不是决定类f₂对g的决定度=0；对因素还贷来说，[好]={2, 6, 9}，[可]={3, 4, 5}, [差]={1, 7, 8}，还贷好的用户类[好]钻入[购买]，还贷差的用户类[差]钻入[不买]，都是决定类，f₃对g的决定度是 6/9；对因素收入来说，只有收入高的用户类[高]是决定类，f₄对g的决定度是2/9。

选取决定度最高的因素“信贷”，它有两个决定类，由这两个决定类的钻入情况分别得到两个因果推理句：

因果规则1：信贷好购买。

因果规则2：信贷差不买。

从论域中删除这两个决定类，得到新的论域，取U′=[可]={3,4,5}，得表9。

按表9重新计算各个因素对g的决定度。取决定度最大的因素f₁，它有3个决定类：[老]={5}，[中]={4}，[青]={3}，分别写成下列推理句：

因果规则3：信贷可且年龄不老→购买。

因果规则4：信贷可且年龄老→不买。

因果规则5：信贷可且年龄青→购买。

删除表中的用户3、4和5，表9被删空，因果规则提取完毕。最后共得到五条因果规则。面对一个新用户，只需先查他的信贷状况，再补充考虑其年龄，就可以判断其购买倾向。例毕。

因果规则的可靠性依赖于样本的大小和准确性，还要随时间场合的变化而不断调整。

本节介绍了因素空间如何将形式信息与效用信息关联起来，提升为全面的语义信息。以上两节为机制主义人工智能的信息转化第一定律提供了有用的数学理论。

4 用因素空间下九宫棋

在实现信息向知识的转化中，需要有更好的搜索工具。因素是启发指引搜索的关键词。本节将介绍如何用因素思维实现目标因素与场景因素的对接和搜索，为信息转化的第二定律从数学上作一点探索性的思考。传统人工智能教科书上以九宫棋来讲述搜索策略，为了说明思想，本节特以九宫棋为例来进行阐述。要想使用因素空间理论进行信息的智能化处理，先要在思维上习惯于因素分析。随时随处都要问：“我思考的目标是什么？我面临的对象是什么？要使二者合笼，最为关键的因素是什么？”下面以下九宫棋为例来说明这个问题。

1) 确立目标，选定目标因素

智能是一个目标驱动的活动，下棋也是这样，在任何比赛中，棋手的目标是赢得比赛。获胜是棋手的目标因素。

2) 注意对象，确定对象因素

目标因素的实现离不开对象描述。九宫棋的对象描述依赖于两个对象因素:棋盘和游戏规则。

棋盘。九宫棋的棋盘是由3条横线和3条竖线绘制的9点阵。在人工智能书中，也被描述成3行3列的九宫格。

游戏规则。分别由执黑白两色棋子的棋手交替放子于棋盘未被占用的格子点上，黑子先手。如果一方在1条线(水平、垂直或对角线)上连接放上了3个棋子，该方就赢；如果在棋盘的所有格点都被占用时仍没有赢家，那就成和棋。这两种结局都叫作下完了一盘棋。

一盘棋在下完第t步棋时，黑白子在棋盘上的分布状态可以描述为一个3×3的矩阵 ${\mathit{\boldsymbol{B}}}\left( t \right)$ ，元素 ${b_{ij}}$ 描述第 $i$ 条横线和第 $j$ 条竖线交点所呈现的状况(白、黑或空)， ${\mathit{\boldsymbol{B}}}\left( t \right)$ 叫作一个棋局。下三子棋的论域 $U$ 是所有棋局的集合: $U = \{ \{ B\left( t \right)\} |t = 1,2, \cdots ,{t^ * }\} \} $ ，其中 ${t^ * }$ 是下完一盘棋的步数，总有 ${t^ * } \leqslant 9$ 。

3) 目标因素与对象因素的对接

因素空间在哪里？因素空间在目标因素与对象因素对接的过程中出现。设 $O$ 是目标因素，它有性状空间 $X\left( O \right) = $ {白胜，黑胜，对弈}。对象因素是什么？黑方为了取胜，首先需要从棋盘中选择下子的位置，这就要考虑9个格子点在博弈中各自具有的战略地位。对每一步棋，建立1个因素 ${f_t}$ ， ${f_t}$ 称为第 $t$ 步棋的“点势”，其性状空间是 $X\left( {{f_t}} \right) = $ {中心，顶点，边点}。9个格子点中有1个中心、4个顶点和4个边点。中心是4条线的交汇，顶点是3条线的交汇，边点是2条线的交汇。抢占中心是决定胜负的关键。黑子下了一步棋之后，还要考虑白子如何应对，所涉及的因素记为 ${g_t}$ ，它具有性状空间 $X\left( {{g_t}} \right) = $ {抢占中心，堵于顶点，堵于边点，放任}，于是就出现了一个最简单的因素空间 $\left( {U,{X_F}_o} \right)$ ，其中 ${F_o} = \{ {{f_1},{g_2},{f_3},{g_4},{f_5},{g_6}, \cdots ;}$ ${{h_i}\left( {{t^ * }} \right),O\left( {{t^ * }} \right)} \}$ ， $ h $ 表示 $ f $ 或 $g$ 。

有了因素空间，就可以应用因素空间的理论。将 ${f_1},{g_2},{f_3},{g_4},{f_5},{g_6}, \cdots ,{h_f}\left( {{t^*}} \right)$ 当作条件因素，而将 $O\left( {{t^*}} \right)$ 当作结果因素来设计因素数据库。我们从数据库中选了100个样本点，也就是下了100盘棋来进行学习，得到因素表10(为了节省篇幅，不写被约间的因素)。

应用因素空间的因果分析算法2，可以从表10中提取因果规则：如果 ${f_1}$ =中心，则“ $O\left( {{t^*}} \right)$ =黑胜”的频率是84/90。这一规则说明，只要黑子在第一步占领中心，对方就只有招架之功而无还手之力。黑方很容易取胜。

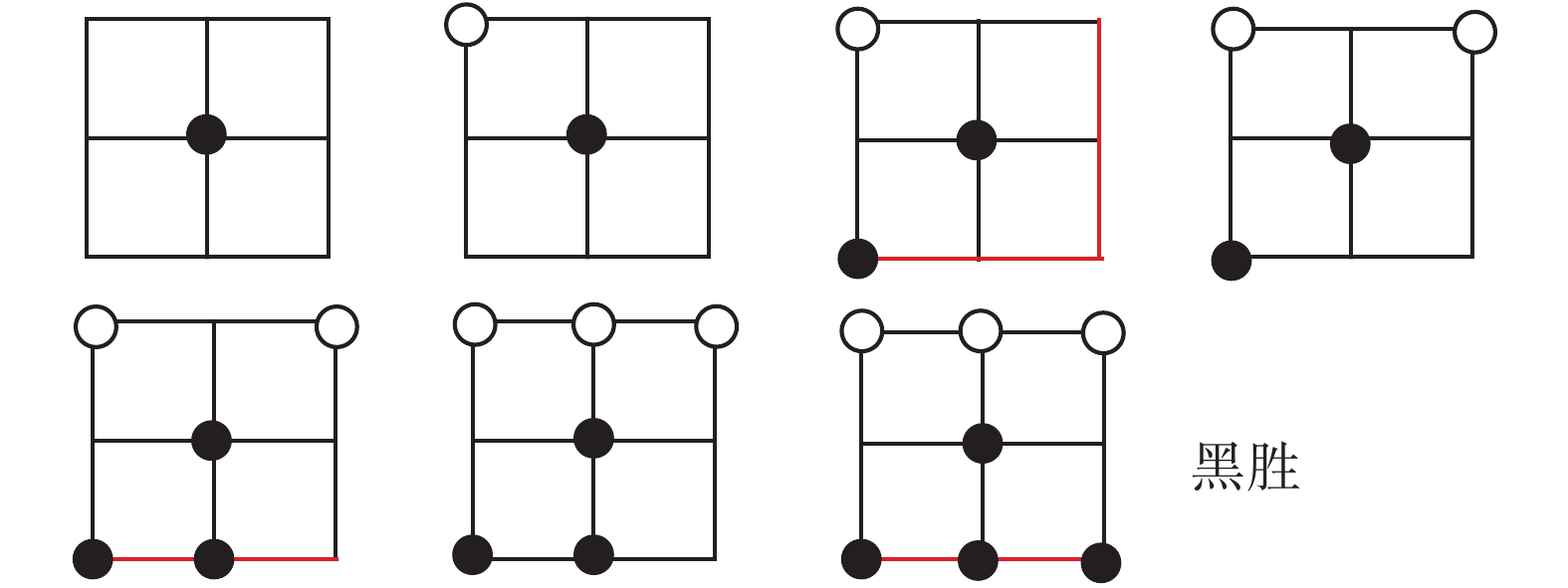
4) 精细化与棋谱

为了使这一规则更加确切，需要分析黑棋不能取胜的原因。要区分情况就要增加因素。当黑子占中心点以后，再下一子，无论下在何处，必与中心相连而构成一字的胜利威胁。此时白子必在对称点上堵截。黑子求胜必须在被围堵的情况下形成一字？在图1的第三局势中，画了两条一字线，只要第二枚黑子下在这两条红线(但不包括右下角)上，黑棋就能取胜，否则下和。这就形成一个棋谱(见图7)。

在这个棋谱中有一个关键词，就是希望线。

定义17　当 ${f_1}$ =中心， ${g_2}$ =堵角，则不与白子相邻的两条边都叫作黑子此时的希望线。

棋谱1　若取 ${f_3}$ 为两条希望线的非公共点，则白棋必在被动堵截中战败。

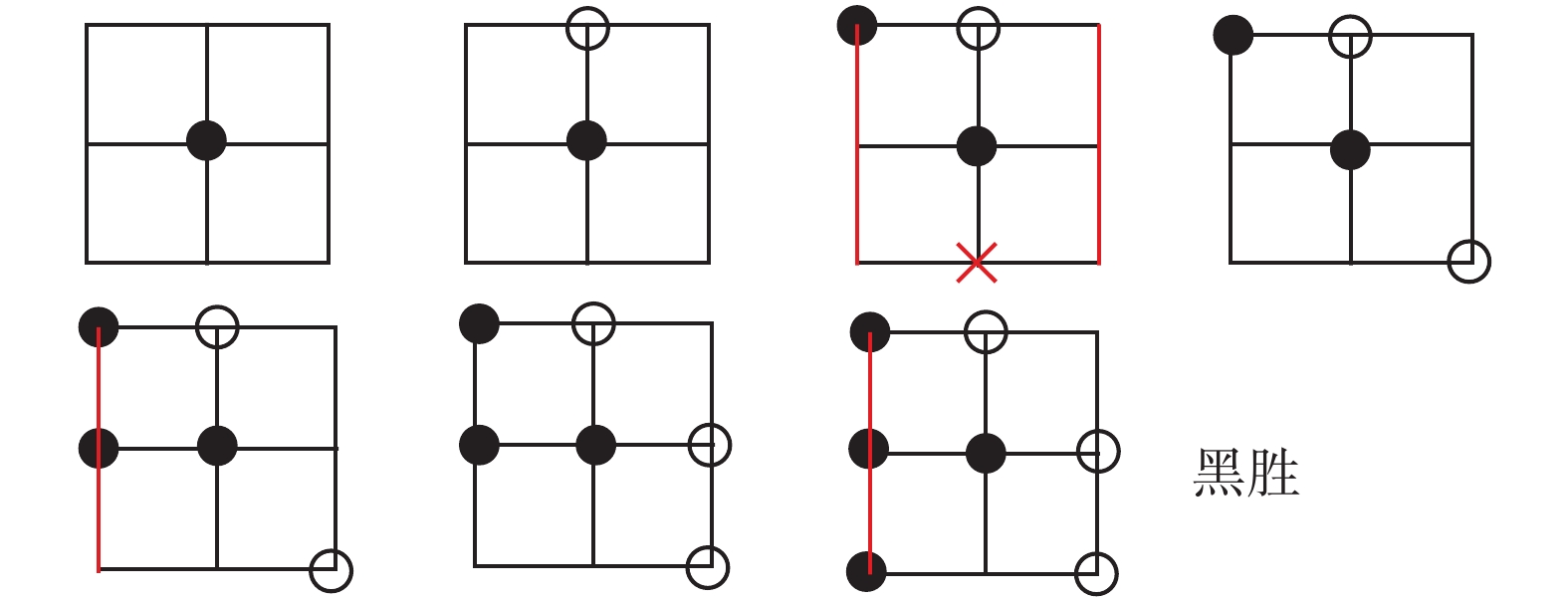
如果白棋堵在边上，在图2的第3局势中，画了两条一字线，第2黑子下在这两条红线的任何一条上，黑棋就能取胜，否则下和。这就形成一个棋谱(见图8)。

定义18　当 ${f_1}$ =中心， ${g_2}$ =堵边，则不包含 ${g_2}$ 及其对称点的两条边都叫作黑子此时的希望线。

棋谱2　若取 ${f_3}$ 在任何一条希望线上，则白棋必在被动堵截中战败。

当黑棋失误被白棋抢占了中心以后，白棋取胜的细节可以进一步引进新的因素 ${g_4}$ 来进行分析，不再详说。如何引进新的因素，在这里还是要靠人的因素思维。

5 因素空间的历史与未来

早在20世纪60年代，笔者参与了在我国高校设立概率论课程的工作。在那时，笔者就用因素空间来处理柯尔莫戈洛夫所提出的概率基本空间^[20]。一枚硬币在一次投掷中可能出现两个基本事件，得到基本空间 $\varOmega $ ={正，反}。要弄清楚这两个基本事件为什么是随机的，就要找出那些影响硬币面向的因素，如硬币性状、手的动作、桌面条件、环境影响等，这些因素都会对结果产生影响。我们可以作这样一个决定论性的假设：当所有因素的状态都固定以后，所得的结果便会唯一确定。如其不然，就必有其他某些具有影响力的因素尚未被考虑到，若把这些被遗漏的因素统统都考虑进去，则这个决定性假设便应告成立。每个因素都有一个状态变化的维度，所有这些因素就张成一个高维空间 $X\left( F \right)$ ，这正是我们后来所说的因素空间。 $F$ 是因素的集合， $F$ 的充分性便确定了从 $\varOmega $ 到 $X\left( F \right)$ 的一个映射，使偶然现象得到必然性的描述。充分的条件可以导致必然的结果；但若存在着难以观测和控制的因素，则人的辨别和控制范围便从点x蜕化成为团粒 $C \subseteq X\left( F \right)$ 。在进行一种试验时，所能识控的范围 $C$ 叫作条件。我们只知 ${\mathit{\boldsymbol{x}}}$ 在 $C$ 中但却不知在其中的何处，当 $C$ 的范围跨越了正反两面的边界时，确定性就转化为随机性，世界是必然的也是随机的，这是辩证的统一，否定任何一方都是错误的。我们不承认随机性可以被消灭，但是却承认二者可以相互转化，只有用因素空间来描述基本空间才能刻画这种转化。柯尔莫戈洛夫心目中所要定义的基本空间其实就是一个因素空间。

不充分的条件也是条件，它虽不能决定结果但却能制约结果的发生频率，体现这种内在必然性联系的就是概率，概率是广义的因果律。概率论是一种广义的因果论，这就注定了概率统计会在人工智能中占有重要的地位，我们现在能对概率论有这样一种较为深刻的认识，是因为有了因素空间。

用因素空间来构造基本空间，可以实现决定性向随机性的逼进。概率论不仅要研究概率的逻辑规律，更应实现随机性向确定性的转化。虽然，大数定律和贝叶斯概率都体现这种转化，但还有很大的发展空间。笔者所提的构架是，将基本空间的因素分为两个部分，可观察、可控的因素算第1部分，这部分因素所导引的变量是非随机变量，余下的因素算第2部分，统归为一个余因素^[12] ，它所引导的变量是随机性的。从中挑选出少数几个特别突出的因素作为精细处理的对象，剩下那些影响微弱且相互独立的众多因素，都归顺于中心极限定理。这样一来，随机变量的一般分解式为

$\xi = f\left( x \right) + {f^ \wedge}\left( x \right) + \delta $

(12)

式中： $f\left( x \right)$ 是一个以向量 ${\mathit{\boldsymbol{x}}}$ 为自变量的普通函数； ${f^ \wedge}\left( x \right)$ 是由样本经过最小二乘或其他方法所拟合出的函数，它是对少数几个调皮的因素所作的精细处理； $\delta $ 是高斯分布，被看作噪音。要减少随机性，就要加深对第二项因素的分析和掌控。

1965年，Zadeh教授提出了模糊集合论^[21]，这是人工智能在数学上取得突破的重要历史进展。他把模糊集定义成从论域 $U$ 到[0, 1]上的一个映射 ${\mu _A}:U \to \left[ {0,1} \right]$ ， ${\mu _A}\left( u \right)$ 表示 $u$ 对 $A$ 的隶属程度；至于论域 $U$ 是什么，则很少有人问津。然而，论域是刻画模糊信息极为重要的一环，笔者提出因素空间的理论来刻画论域，以实现模糊性与清晰性之间的相互转换。例如，年轻是一个模糊概念，要看一个人是否年轻，单就年龄这个因素打分(确定隶属度)相当困难。若加上因素面貌，打起分来就容易一些；若再加上精力、体魄、反应、朝气等因素，打分就更容易了。问题的关键是因素的增加会降低认识的模糊性。

模糊数学与概率论都需要因素空间的理论，借用因素空间可以探讨随机性与模糊性这两种不确定性之间的联系与区别。在随机试验中，事件 $A$ 是因素空间中一个固定的集合，因素的变异点 ${\mathit{\boldsymbol{x}}}$ 在条件域 $C$ 中变，所以随机试验模型的特征是“圈圈固定，点子在变”。模糊试验则相反，要考虑张三是否年轻，张三是论域中的一个固定的点子，年轻这一模糊概念在人的脑海中有着不确定的边界，成了在变的圈圈，模糊试验模型的特征是“点子固定，圈圈在变”。这种对偶性有很深刻的意义，在数学上可用论域 $U$ (地面)和幂集 ${2^U} = P\left( U \right)$ (天上)来作一种转换： $U$ 中的圈圈变成 $P\left( U \right)$ 里的一个点， $U$ 中的点子 $u$ 可以变成 $P\left( U \right)$ 上的一个圈圈 ${u^ \wedge} = \left\{ {A\left| {u \in A} \right.} \right\}$ ，于是地上的模糊试验就可转化成天上的随机试验。天上的随机变量是随机集，相应的统计不是普通的数理统计而是集值统计或区间统计。靠着随机区间对 $u$ 的覆盖频率来确定隶属度 ${\mu _{{\text{年轻}}}}\left( u \right)$ ，隶属曲线就成了随机集的落影，这就形成了模糊落影理论^[22]。文献[22]把序、拓扑和可测结构提升到冪上，建立了8种超拓扑和超可测结构，由之建立了随机集和信度的严密数学理论，证明了4种非可加信度与随机集分布对应关系的存在性和唯一性定理，把测度扩张定理的扩张起点从半环提前到π-系，这是一个有相当难度的数学成果。1988年，北师大张洪敏等研究生在笔者指导下研制出国际第二台模糊推理机^[23]，与日本山川烈在1987年的首台“模糊计算机”相比，推理速度从每秒一千万次提高到一千五百万次，体积不到它的1/10。在钱学森教授的鼓励下，因素空间被作为人工智能的数学支持理论来抓。1994年笔者和李洪兴合著的《知识表示的数学理论》^[5]一书问世，用因素空间描述了概念生成，推理、控制、决策、评价等问题；在1995年又出版了《模糊系统理论和模糊计算机》^[24]，为智能计算机的研制提供了数学基础。

2012年以后，笔者将因素空间的研究重点转向数据智能化的数学理论，与形式概念分析及粗糙集结缘。现有的关系数据库所面临的大数据的挑战是因素空间所要迎头解决的首要问题。因素空间对形式信息的处理对象囊括了非结构化数据。以因素空间为基础的机制主义人工智能是数据智能化的灵魂，它不俯首听命于大数据的摆布，而是要设计、制造、运用和培育数据，用数据来营造信息生态和知识生态，建立信息、知识与神经结构的同构体。它要改变当今世界人工智能自下而上的手工式格局，代之以自上而下与自下而上相结合的发展理念。有许多文章可以参考^[25-50]，尽管作者们在写作的时候还没有形成自己思维的大局。

6 结束语

因素是信息描述的关键词，因素空间是描写事物和信息的普适性框架，它把数据变成可视的样本点，形成背景分布的母体，据以自动概念生成和因果规则，由此可以产生学习、预测、评价和决策控制等一系列的数学操作。因素空间能将形式信息与效用信息关联起来，提升为全面的语义信息，为机制主义人工智能的信息转化第一定律提供了坚实的数学理论。用因素思维实现目标因素与场景因素的对接和搜索，可为信息转化的第二定律提供手段。以因素空间为基础的机制主义人工智能是数据智能化的灵魂，它将要设计、制造、运用和培育数据，用数据来营造信息生态和知识生态，建立信息、知识与神经结构的同构体。总之，因素空间的发展前景巨大，对信息科学和人工智能的发展有重要作用。