尽管人工智能学科已经诞生60多年了，从技术、产品和产业上看都有了巨大的发展，积累了丰富的经验和教训。但是，目前在人工智能学界仍然普遍存在一种思想倾向，只重视模拟单一智能功能的技术和方法研究，轻视关乎智能模拟全局的基础理论（涉及智能的形成机制、智能的逻辑规律和智能的数学基础等）研究。甚至有少数人公开宣扬人工智能是一门实践性科学，它能解决某类智能问题即可，不需要也不存在什么通用理论。面对这些片面认识和主张，人工智能通用理论体系的建立，更加具有重大的理论意义和现实意义。

1 研究背景 1.1 人工智能的理论危机

20世纪中叶人工智能学科的诞生开创了智能信息处理的新纪元。众所周知，各种人工智能学派都是在布尔信息处理和标准逻辑(数理逻辑)基础上建立和发展起来的^[1]，20世纪80年代的人工智能理论危机暴露了布尔信息处理和标准逻辑的应用局限性^[2-3]：

1)由于布尔信息处理和标准逻辑只是根据命题真值而不考虑命题内容进行的推理，尽管它具有可机械执行，无需领域背景知识支撑的优点，但在机械执行过程中也带来了工作效率十分低下、无法克服因信息处理算法的时空复杂度带来的组合爆炸的缺点；

2)由于布尔信息处理和标准逻辑只考虑了确定性推理的需要，必须满足非此即彼的理想化约束。而智能信息处理需要面对的现实问题往往具有各种不确定性，推理的各种逻辑要素常常有信息缺损和不断变化的情况，不允许像传统数学问题那样进行理想化处理，带有亦此亦彼性特征。对于这类问题，布尔信息处理和标准逻辑束手无策，无所适从。

1.2 两种不同的发展倾向

人工智能的理论危机之后，国际上出现了两种完全相反的发展倾向^[3-5]：

1)尽可能回避甚至放弃人工智能的逻辑主义路线，大力发展非逻辑的结构主义(人工神经网络)和行为主义(刺激—反应)路线。在这一发展倾向下，近几十年来基于大数据处理的深度神经网络、各种计算智能、群体智能和机器学习方法有了长足的进步，取得了举世瞩目的应用成果。

2)继续坚持逻辑主义路线，并针对处理各种不确定性的需要，近几十年来涌现出了几十种非标准逻辑和一批不确定性推理理论，它们虽然可满足某些智能信息处理的应用需求，但有时会出现无法容忍的反常结果，这表明这些非标准逻辑和不确定性推理方法在理论上并不成熟，人们还没有精确掌握其立论依据和有效使用范围。

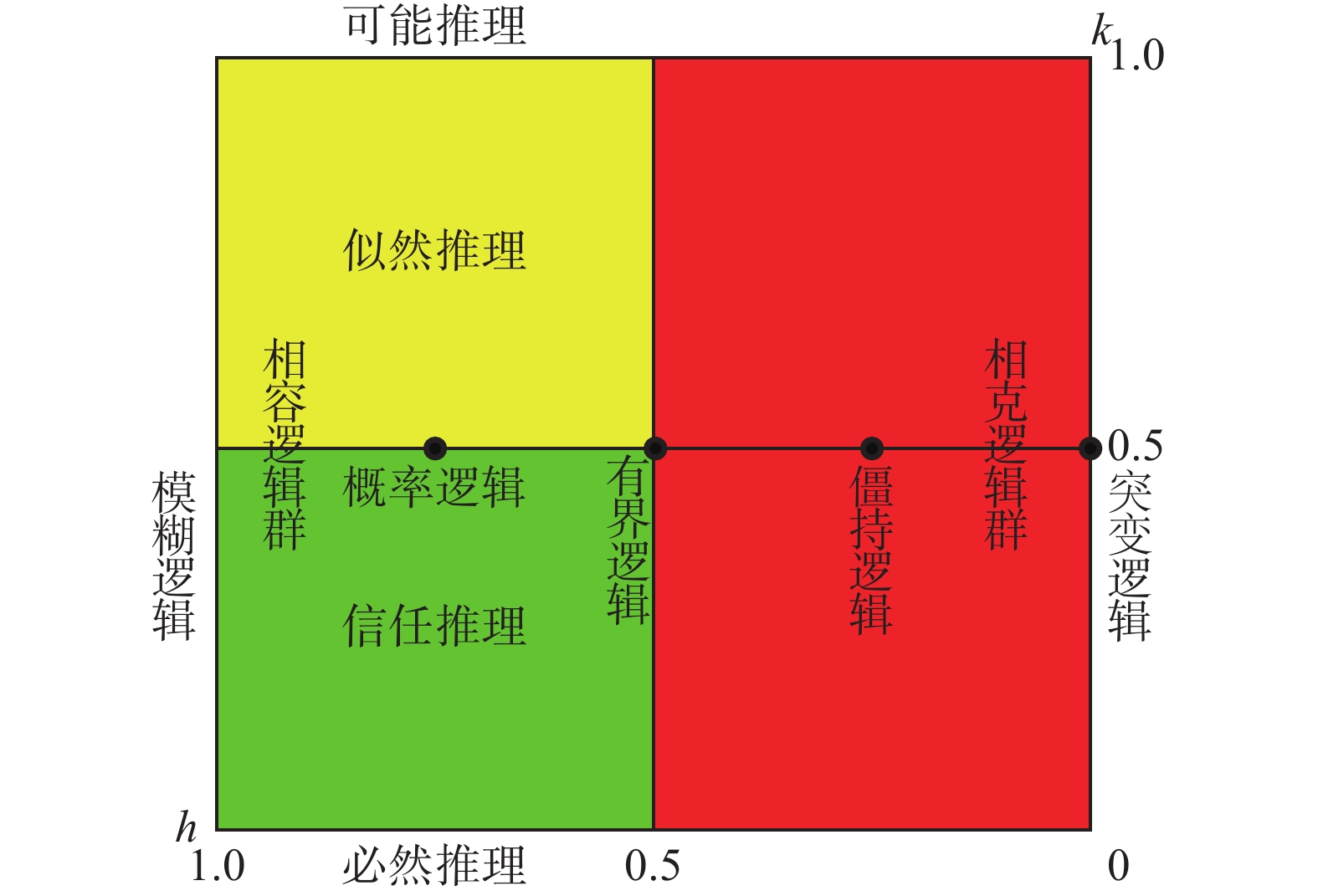
1.3 作者的个人选择

作者相信，对于智能系统来说，结构、功能和行为是三位一体的关系，不能绝然分开孤立存在。而思维和智能本质上都是一种信息处理过程，它们必然受到某种逻辑规律的约束，人工智能理论危机的意义并不是在否定逻辑，而是在告诉人们，智能信息处理中的逻辑规律不仅包含专门针对确定性推理的标准逻辑，还包含处理各种不确定性的非标准逻辑，所以逻辑主义路线不能放弃，一定要继续坚持和发展^[6]。作者根据概率论和已有的不确定性推理理论，系统深入研究了这一路线的发展状况和存在问题，发现已提出的各种非标准逻辑虽然都可以把标准逻辑作为特例包含在自己的体系之内，但它们都不像标准逻辑那样具有普适性，一般都只能适用于某种不确定性中的某个特殊状态下的推理需要，偏离了这个特殊状态使用，推理结果就会出现偏差，偏离大到一定程度后就会出现无法容忍的反常结果。最明显的实例是已获得广泛应用的3个命题级非标准逻辑：模糊逻辑、概率逻辑和有界逻辑。根据概率论的研究结论，它们只能分别适用于相容性相关中的3种不同状态下的不确定性推理：模糊逻辑只适用于两个连续值命题之间具有最大相吸相关的状态，概率逻辑只适用于具有独立相关的状态，有界逻辑只适用于具有最大相斥相关的状态。而相容性相关关系本身是可以从最大相吸状态变化到独立相关状态，再变化到最大相斥状态的(见图1)一个连续的区间，不是3个孤立点。

在这里不难想象，如果偏离了这3个特殊状态点去任意使用这3个非标准逻辑，其推理结果必然会出现偏差。如在独立相关或最大相斥相关状态下不恰当地使用模糊逻辑进行推理，必然会出现无法容忍的反常结果，而现在的实际情况是，许多人都在不分场合地盲目使用模糊逻辑，只要不出现无法容忍的反常结果，一般人都不会选择其他的非标准逻辑使用！历史的经验确实如此，在标准逻辑的应用中，从来都是用一把“万能钥匙”来解决一切问题，没有人会环顾左右而言它。为什么会犯如此低级的错误而不能觉察？因为确定性推理只有一种状态，没有任何不确定性引起的差别存在，用一种标准逻辑来描述就足够了。但是，在专门针对各种不确定性推理而建立的非标准逻辑群中，由于不确定性状态的千差万别，如同密码锁一样，所以必须严格贯彻“一个密码开一把锁”的原则，绝对不允许盲目地乱点鸳鸯谱，是传统的逻辑观把人带入了迷途。

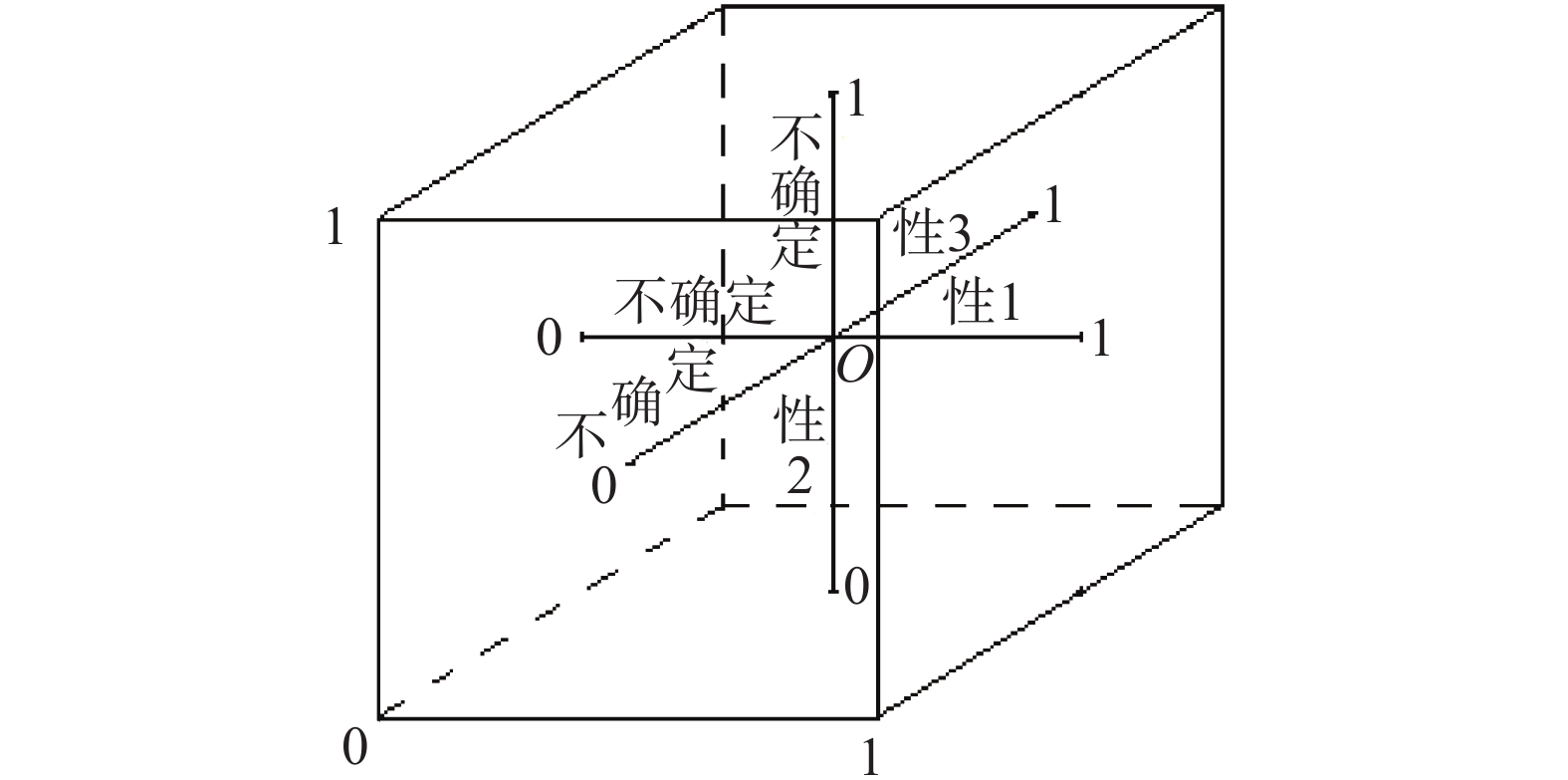
为改变这种根据经验知识建立非标准逻辑系统，而后又不问适用条件盲目使用它来进行各种不确定性推理的混乱状况，作者在20世纪90年代就从人工智能的应用研究转入到人工智能的逻辑基础理论研究，试图根据智能信息处理中需要处理的各种不确定性的特殊需求，精确抽象出一个类似门捷列夫元素周期表的命题泛逻辑理论框架来(见图2)，用它来实现智能信息处理中需要“一串密钥开一把密码锁”的特殊需求。

命题泛逻辑理论框架的结构是一个四维空间[0,1]⁴，空间的中心点O代表有界逻辑，当它的命题真度由连续值(代表命题真值的不确定性)退化为二值时，就退化为适用于确定性推理的标准逻辑(又称为刚性逻辑，在刚性逻辑之外的其他部分称为柔性逻辑)。从O点伸出的4个坐标轴 $k,h,\beta ,e \in \left[ {0,1} \right]$ 代表4种不同类型命题级的不确定性： $k$ 代表命题真度估计误差的不确定性， $h$ 代表两个命题之间广义相关性的不确定性， $\beta $ 代表两个命题之间相对权重的不确定性， $e$ 代表在组合运算中决策阈值的不确定性。各种可能存在的非标准逻辑都是四维空间 ${\left[ {0,1} \right]^4}$ 中连续分布的一些点，每一个点都代表一个柔性命题逻辑(包括已经提出的各种命题级非标准逻辑和可能存在的柔性命题逻辑)，使用者可根据需要处理的各种不确定性类型及其不确定程度值来选择相应的柔性命题逻辑，避免乱点鸳鸯谱的情况发生，精准进行合乎实际需要的不确定性推理。包含更多不确定性的谓词泛逻辑的理论体系可在这个理论框架上进一步研究建立，其主要任务是在命题泛逻辑基础上引入各种柔性量词。

1.4 寻找数学基础理论支撑和广泛的应用检验

作者的这一研究目标已初步实现，1996年在中国科学杂志上提出泛逻辑概念^[7]，2001年在科学出版社出版专著《泛逻辑学原理》，公布了完整的泛逻辑研究纲要，并实现了纲要中的命题泛逻辑部分^[8] 。2005年在瑞士日内瓦的蒙特勒召开了首届世界泛逻辑大会，作者应邀在大会上报告“Research on Universal Logics in China”，引起国际同行的关注和认可，决定第二届世界泛逻辑学术会议在中国进行^[9-10]。2006年作为中国人工智能学会纪念人工智能学科诞生50周年系列丛书之一、英文版Principle of Universal Logics在科学出版社和西北工业大学出版社联合出版，国内外发行^[11]。2007年第二届世界泛逻辑大会在西北工业大学举行，作者是大会两主席之一。2012年作者根据命题泛逻辑的代数结构特征，抽象出泛逻辑的数学基础——连续值逻辑代数^[12]。本文将进一步讨论一个重要的理论话题，上述泛逻辑理论体系的建立有没有严密的数学基础理论支撑。如果没有，说明它还没有脱离经验设计的局限性，在应用中必然缺乏普适性意义。如果它有严密的数学基础理论支撑，那这个数学基础理论是什么？数学界是否认可这个数学理论的存在？这是关系到人工智能学科是否已经从实践经验性学科走向理论性学科的重要标志！

从数学理论支撑角度看，概率论是目前数学界唯一公认的从确定性出发研究随机性和不确定性的数学工具^[13]，作者在建立命题泛逻辑(包含刚性命题逻辑和柔性命题逻辑)的过程中，实际上已将概率论扩展为广义概率论，其明显的标志是将概率论中的相关系数扩张为广义相关系数。具体的贡献有两点：

1)概率论中的相关系数只考虑了两个命题(事件)之间的相容(相生)性相关关系，即从最大相吸相关关系开始，不断向下连续变化到独立相关关系，再不断向下连续变化到最大相斥相关关系。我们引入的广义相关系数已全面考虑了两个命题(事件)之间的相容(相生)性相关和不相容(相克)性相关，即增加了从最大相斥相关关系继续向下连续变化到不同程度的冷战关系，再向下连续变化到不同程度的热战关系，这种相关性扩张更加符合描述客观存在的各种相关关系的需要。

2)在概率论中，原来只给出了最大相吸相关、独立相关和最大相斥相关3个特殊点的逻辑运算公式组，对三点之间连续分布的其他点的逻辑运算公式组没有给出，是用条件概率计算公式来代替的。我们在广义概率论中，把广义相关系数中的每一个点的逻辑运算公式组全都给出了，没有一点遗漏，大大方便了不确定性推理。

所以，广义概率论是对概率论的必要补充和扩张，在数学上具有合理性和严密性。作者提出的连续值逻辑代数，因其离不开广义相关系数的参与，所以也是建立在广义概率论基础上的抽象代数理论。作者的研究表明，将各种智能信息处理原理建立在广义概率论基础上是完全合理和严密的。从本文可以看出，如果进一步把广义概率论与汪培庄教授的因素空间理论^[14-16]密切结合起来，精确刻画信息和知识在因素空间中的组织形态和变换规律，将会形成关于智能科学的更加完善的数学基础理论，共同支撑智能信息处理的逻辑基础——泛逻辑学理论。

从应用检验的角度看，钟义信教授的机制主义人工智能理论^[17-19]是一个通用的人工智能理论体系，它是从模拟人类智能的形成机制入手来建立机器智能系统的，可以应用到各种不同智能信息处理的场合，具有普适性意义，如果在其中进行泛逻辑的应用检验，那是最有效的检验。所以我们三人研究结果的密切结合，将标志着人工智能的通用理论—智能信息处理的逻辑基础—智能信息处理的数学基础三位一体关系的正式形成。

2 关于智能信息处理的哲学思考 2.1 确定论宇宙观是不确定论宇宙观在局部时空中的特例

我们周围存在大中小3个不同的宇宙，它们都处在不断地演化发展之中。大宇宙由各种天体系统运行的时空环境组成；中宇宙由地球上各种生命系统繁衍生息的时空环境组成；小宇宙由人脑思维活动的时空环境(或人体各系统运行的时空环境)组成，它们都是开放的复杂巨系统，具有非线性涌现、自组织、自适应、生态平衡等效应，永远处在不断演化发展的过程中。能源时代形成的确定论宇宙观是演化论宇宙观在局部时空范围中的特例，具有明显的应用局限性。

广义地讲，3个宇宙都具有自然智能，它们能够根据系统的外部环境变化改变自己的内部状态和外部行为方式，以便更好地适应环境，在激烈的生存竞争中求得一席之地立足，所以它们都能成为智能模拟的样板，这是计算智能的立论基础。狭义地讲，智能是专门指人脑思维活动中表现出的一种能力，它能根据自身生存目标和眼前存在的问题，恰如其分地选择或者制定解决问题的策略和方法，并可根据实施效果不断改进提高。即能通过经验记忆和归纳学习，不断优化自己的知识结构和决策方法，提高自己的识别问题和解决问题的水平。

2.2 传统数学问题与智能信息处理的差别

传统数学问题是全面接受非真即假约束的理想问题，可用标准逻辑或刚性集合精确描述，用经典形式演绎解决。智能问题常包含各种不确定性，具有亦此亦彼性，只能用非标准逻辑或柔性集合描述，无法通过经典形式演绎解决。

人在解决智能问题时，常会综合使用本能、直觉、归纳发现、经验知识、启发式搜索、原理性知识和假设前提等进行不确定性推理，选择可信度较高的答案执行，并按执行效果进行修改完善。人工智能在自动证明数学定理时，也不是按形式演绎规则机械执行的，因为组合爆炸会快速消耗掉计算机的时空资源，无法顺利到达证明的终点！只有模拟资深数学家的洞察力，用启发式搜索算法发现可能的最佳证明路径和方法，才能快速接近目标，不能盲目依靠经典形式演绎规则进行机械式推理。

可见，智能方法常是牺牲可靠性和完备性获得求解问题的真实性和即时性。而传统数学方法则是忽视真实性和即时性确保求解问题的可靠性和完备性。未来数学的发展方向应该是给行之有效的智能信息处理原理和方法以严格的数学描述。

2.3 应该关注智能系统的时效性

还有一种具有典型意义的智能问题，即两个独立智能体之间的博弈问题，它可看作高度简化了的生存竞争问题或生态平衡问题，其只考虑了我和非我两方的存在。在二元智能博弈问题中，由于双方同在一个时空环境之中，必须遵守共同的博弈规则，所以这里不仅要比较对弈双方解决眼前问题的智力高低、两者付出的智能多少，更重要的是比较两者智率的大小(解决问题的快慢)。静态看机器的智力和智能都是设计者注入的人类有关能力的一个真子集(永远不可能是全集)，在人机大战中机器之所以能反过来战胜对弈的人，是因为机器思考执行同样一个问题时的智率远高于人脑，达到数百万倍以上。这与压缩式风洞实现超高音速吹风的工作原理(将空气长时间低速压缩进入高压气罐，然后瞬间进行超高音速释放)十分相似。

所以，在比较人机智能的高低时，时效性是一个重要因素。即智能系统(智力、智能、智率)演化的时常数 $\tau $ 与观察时间窗 $\Delta t$ 的比值大小，决定了智能系统外在行为能力的3种典型类型：当 $\displaystyle\frac{{\Delta t}}{\tau } \gg 1$ 时表现为智能系统，当 $\displaystyle\frac{{\Delta t}}{\tau } \cong 1$ 时退化为进化系统，当 $\displaystyle\frac{{\Delta t}}{\tau } \ll 1$ 时退化为图灵系统(逻辑自动机、时序机等)^[20]。

2.4 传统数学问题为何能用刚性推理范式求解

刚性推理范式是基于二值逻辑的推理，其中所有逻辑要素都受非此即彼性约束。传统数学能用刚性推理来求解问题，是它事先已将现实问题中所有不确定性全部忽略，抽象为规律确定不变、状态真假分明、已知条件齐全的理想化问题，可机械式求解。

更深层的哲学信念是：之所以能如此理想化地抽象，是因为人们相信世间万物都受确定不变的客观规律控制，时间是标量，不确定性是人类对客观规律和问题的状态掌握不充分引起的近似性。人类认知的前进方向是不断消除这些认知的不确定性，实现对客观规律和状态参数的全部精准掌握，最后实现绝对的确定性。于是认为，理想化的过程本质上是一个由表及里、去粗取精、去伪存真的必要过程，不会造成认识上的任何损失。

耗散结构理论的创立者伊•普里戈金的专著《确定性的终结》(1996年问世，1998年出中文版)的出版^[21]，宣告了确定性哲学信念的终结，它不符合客观世界的实际情况，犯了认知的方向性误判，必须改正。

2.5 智能信息处理为何必须用柔性推理范式求解

人类之所以有智能，是因为人可根据现实问题的真实状况和变化趋势，在已有经验启发下选择最有效的原理、途径和方法去解决问题。如果这次失败了，可从头再来反复不断地试探下去，并能通过一次次的经验教训的积累进行学习改进，不断完善自身解决问题的能力。

更深层的哲学信念是：相信世间万事万物都处在不断演化发展过程中，时间是矢量，过去、现在和未来扮演着不同的角色，不确定性是客观世界的本质属性，确定性是人在局部时空环境中形成的近似性认知。人类认知的前进方向是不断消除这些近似性认知，精准把握各种不确定性在生态平衡中的演化发展规律，理想化是人类在局部时空中解决问题时不得不采用的权宜之计。

智能信息处理中的柔性推理范式是包含某些不确定性的逻辑推理模式簇，需要处理的不确定性组合不同，推理使用的具体模式必然不同，不可乱点鸳鸯谱。

2.6 在智能信息处理中需要两种推理范式同时并存各司其职

刚性推理范式的特点是：具有逻辑上的严密性和推理路径的完备性，推理过程可机械式一无反顾地进行下去，对有解的理想问题(不管结论是真是假)一定可以获得最后结果。尽管计算机在无启发式知识指导下使用会出现组合爆炸，但人类专家可利用启发性经验知识优化证明过程，快速接近目标。

柔性推理范式的特点是：可精确描述现实问题中包含的各种不确定性，有针对性地进行相应的推理运算，获得准确的结果，不必因为理想化而丢掉许多有用的信息。尽管柔性推理计算过程十分复杂，使用起来很不方便快捷，但是对于计算机信息处理而言，这是轻而易举的事情，而且复杂的演算过程可以放在后台由软硬件执行，用户程序不必关心。在智能信息处理中，许多问题的存在价值就在于它包含的某些不确定性，如果全部都理想化处理了，那么这个问题就根本不存在了，如自动驾驶问题、人脸识别问题、语音识别问题等。

现代数学的发展方向：使用刚性推理范式的传统数学需要向精确描述各种不确定性的方向全面扩张，以便包容智能信息处理中的柔性推理范式，数学不仅不能再将它们继续作为另类来看待，而且要让它们走向数学舞台的中央，这是智能时代对现代数学提出的最大需求！

2.7 有关智能信息处理的若干基本假设

建立智能信息处理的理论体系需要如下基本假设的支撑，在证明中它们可作为公理使用。

假设1　宇宙由两个世界、四大要素组成

宇宙是由物质世界和信息世界组成的对立统一体。物质对象在物理空间中具有占位性(表现为对象的排它性)和惯性(表现为移动对象需要付出的力和能)。物质结构、质量、力和能量是物质世界中的基本科学问题。信息对象在可能性空间中具有占位性(表现为对象的排它性)和惯性(表现为移动对象需要付出的智力和智能)。信息结构、信息量、智力、智能和智率是信息世界中的基本科学问题。

有这样一种科学假设：宇宙由无数的信息子对偶组成，对偶的开合决定了它是物质态还是信息态，两个世界之间可相互联系和转换，时间是把两个世界关联起来的同步信号。

假设2　不确定性是宇宙万物的本质特征

在能源时代人类面对的是封闭的简单机械系统，形成的宇宙观是确定论：人们普遍相信事物的发展变化是由确定不变的客观规律控制的，时间是一个标量，不确定性是由于人们没有精确全面掌握这些客观规律和研究对象的状态参数而引起的，解决问题的科学方法论是还原论，微积分和标准逻辑是其理论基础。

信息时代人类面对的是复杂性开放系统，其中一切事物无不处在演化发展过程中，随着新事物不断涌现，新规律不断显现出来，这说明宇宙在本质上是不确定的，时间是一个矢量，过去、现在和未来分别扮演着不同角色，形成的科学宇宙观是不确定论。因为人们根本不可能在了解整个时空内的全部信息的状态下去认识世界、解决问题，所以不确定性永远无法回避，形成的科学方法论只能是演化论，它必须适应涌现效应和生态平衡的需要，其理论基础必然发生根本性改变。这是智能信息处理中必须面对和解决的新问题。

假设3　必须严格区分两类不同性质的矛盾

与确定性推理排斥一切矛盾不同，在不确定性推理中必须严格区分逻辑矛盾和辩证矛盾，它们是两类不同性质的矛盾。逻辑矛盾是在任何一个逻辑系统中都不允许出现的判定性错误，必须予以排除。如在二值逻辑中判定命题 ${{A}}$ 是真同时又是假，在连续值逻辑中判定命题 ${{B}}$ 的真度是0.7，同时又是0.3，这些都是不允许出现的逻辑矛盾。辩证矛盾是不确定性推理的研究对象，无处不在，必须正面研究。如在二值逻辑中判定钱币同时具有正面和反面，是一个对立统一体，这个辩证矛盾不能排除。如果判定命题 ${{A}}$ (钱币正面向上)是真，同时又判定是假(钱币反面向上)，这就是必须排除的逻辑矛盾。而在连续值逻辑中，判定命题 ${{B}}$ 的真度是0.7，就意味着已经判定 ${{B}}$ 的假度是0.3，这种真假同时存在于命题真度之中的情况，就是一种辩证矛盾(不确定性)，千万不能排斥。

2.8 小结

智能信息处理要面对现实世界中可能存在的各种确定性和不确定性，其右极限是：现实中可能存在的所有不确定性全部包含在待解决的问题中，只有最完整的柔性逻辑才能描述和求解。而传统数学中的形式演绎是智能信息处理的左极限：它通过抽象或忽略，可把现实中所有的不确定性全部理想化为确定性，允许用刚性逻辑描述和求解。一般智能信息处理介于两个极限之间，其中部分因素是确定的，部分因素是不确定的(见图3)。

3 命题泛逻辑的研究目标和研究基础 3.1 命题泛逻辑的研究目标

如前所述，命题泛逻辑的研究目标是建立一个命题泛逻辑理论框架，其结构是一个四维空间 ${\left[ {0,1} \right]^4}$ ，空间的中心点 $O$ 代表有界逻辑(其中包含刚性逻辑 $x,y,z \in \left\{ {\left. {0,1} \right\}} \right.$ )。从 $O$ 点伸出的4个坐标轴 $h,k,\beta ,e \in \left[ {0,1} \right]$ 分别代表4种不同类型的命题级不确定性。各种可能存在的命题级柔性逻辑都是四维空间 ${\left[ {0,1} \right]^4}$ 中连续分布的一个点，使用者可根据需要处理的不确定性及其不确定程度值来选择相应的柔性命题逻辑使用。

下面简单介绍相对于这个研究目标已经具备了哪些研究基础。

3.2 布尔信息处理的有关情况

1)基于逻辑推理法的布尔信息处理

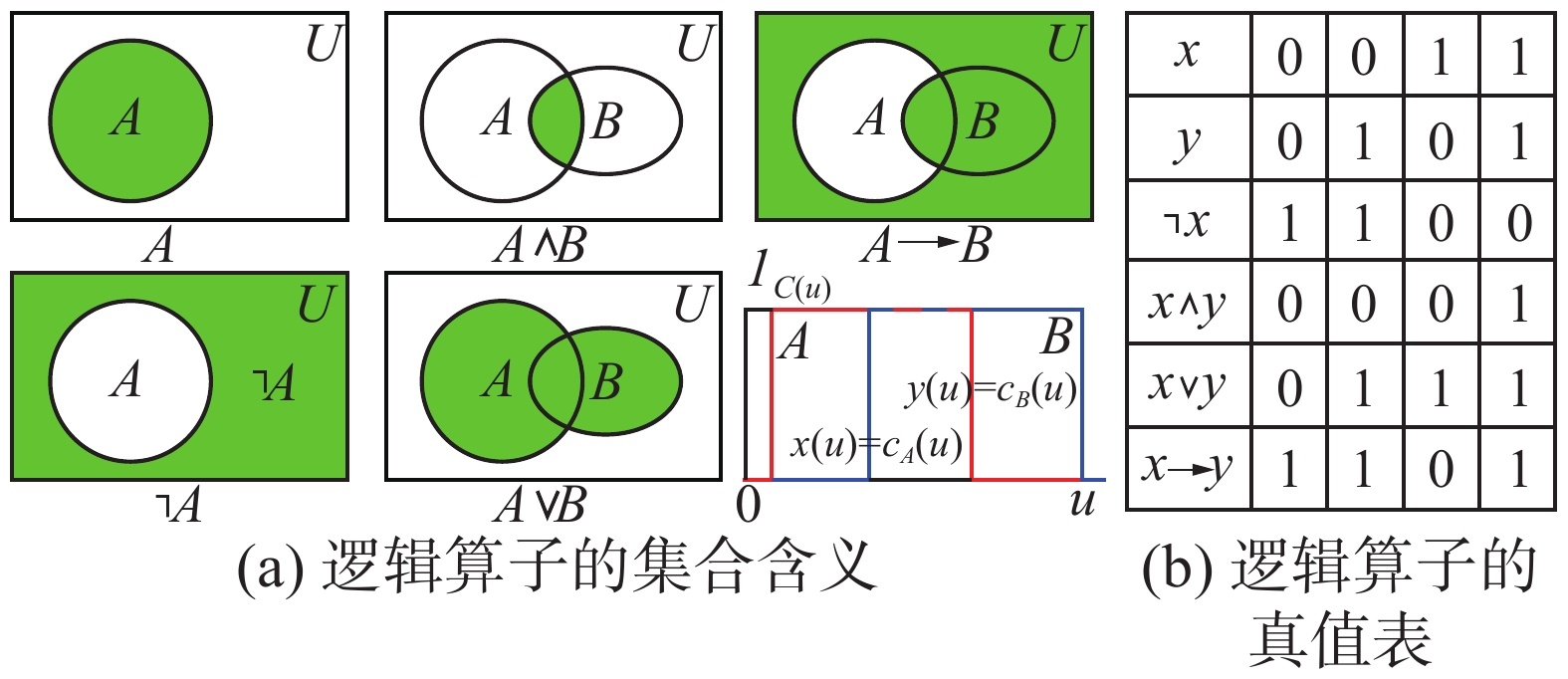
英国数学家G. Boole 1854年在《思维规律》中提出布尔逻辑算子组，它为标准逻辑(刚性逻辑)奠定了理论基础^[22]，可满足布尔信息处理的全部需要。图4给出了布尔逻辑算子组在概率论中的集合意义：设对象域 $U$ 中有两个集合 $A$ 和 $B$ ，当任意事件 $u$ 出现在集合 $A$ 中时，命题 $x\left( {u \in A} \right)$ 的真值是1，否则是0；当任意事件 $u$ 出现在集合 $B$ 中时，命题 $y\left( {u \in B} \right)$ 的真值是1，否则是0。基于这个集合含义，可以证明布尔逻辑算子组是完全正确的。

2)基于神经网络信息变换法的布尔信息处理

1943年心理学家McCulloch和数学家W. Pitts提出二值神经元信息变换模型 ${\rm{M}} - {\rm{P}}$ (又称感知机)^[23]。图5是二值神经元的基本结构，其中 $x,y,z \in \left\{ {\left. {0,1} \right\}} \right.$ , $a{\text{、}}b$ 是输入权系数， $e$ 是反应阈值， $v = ax + $ $ by - e$ 是整合函数，经 $\Gamma \left[ v \right]$ 进行0、1限幅处理后输出 $z$ ，结果只有0或1状态，每一次信息处理都有 $\Delta {\rm{t}}$ 的延迟。

3)布尔信息处理的完备性分析

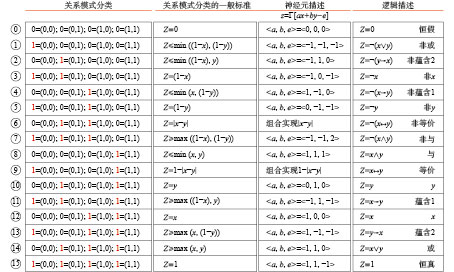
可以以二元信息处理为例来讨论而不失一般性，因为3元信息处理可由两个二元信息处理来完成 $f\left( {x,y,z} \right) = f(f\left( {x,y,z} \right)$ ，四元信息处理也可由两个二元信息处理来完成 $f\left( {x,y,z,w} \right) = f\left( {f\left( {x,y} \right),f\left( {z,w} \right)} \right)$ 等。在二元信息处理中总共只有16种不同的处理模式(0号模式～15号模式)，因为 $x$ 、 $y$ 两个布尔变量只有4个不同的状态组合(00, 01, 10, 11)。每一个状态组合又可以分别与输出 $z = 0$ 或 $z = 1$ 对应，形成 ${4^2} = 16$ 个不同的信息处理模式。这些模式都可以用布尔逻辑算子组来描述，也可以用 ${\rm{M}}{\rm{ - }}{\rm{P}}$ 模型来描述(见图6)。需要说明的是，6号模式是“≠模式”，它需要通过组合运算 $z = \left( {x \wedge \neg y} \right) \vee \left( {\neg x \wedge y} \right)$ 来实现，9号模式是“=模式”，它需要通过组合运算 $z = \left( {\neg x \vee y} \right) \wedge \left( {\neg y \vee x} \right)$ 来实现。同样的，在 ${\rm{M}}{\rm{ - }}{\rm{P}}$ 模型中要利用两层神经元来实现，其中6号模式是 $ z = \neg ((x \to y){\rm{ }} \wedge (y \to x{\rm{ }})) = 1 - $ $ \Gamma \left[ \Gamma \right[ - x + y + 1\left] { + \Gamma } \right[x - y + 1] - 1] = \left| {x - y} \right| $ ，9号模式是 $z = \left( {x \to y} \right) \wedge \left( {y \to x} \right) \!=\! \Gamma [\Gamma \left[ { - x + y + 1} \right] \!+\! \Gamma \left[ {x - y + 1} \right] - 1]{\rm{ }} $ = $ 1 - \left| {x - y} \right|$ 。现在看来它们在神经网络中是不难实现的，遗憾的是1969年M. L. Minsky和S. Papert在Perceptrons^[24]一书中根据这两个特殊模式的存在而轻易地否定了 ${\rm{M - P}}$ 模型的有效性，由于M. L. Minsky在学术界的巨大影响力，致使神经网络的研究一度陷入低潮，延误神经网络发展达几十年之久。

4)布尔信息处理的最基本模式分析

从图6还可以看出，布尔逻辑算子组 $\left\{ {\left. {\neg , \wedge , \vee , \to } \right\}} \right.$ 并不是由最基本信息处理模式组成的，其中包含的是常用的模式，它们可进一步由最基本的模式来表示。例如，用11号模式“→”就可以表示 $\neg x = x \to 0$ ， $x \wedge y = \left( {x \to \left( {y \to 0} \right)} \right) \to 0,x \vee y = \left( {x \to 0} \right) \to y,$ 这种表示方法在理论证明中经常使用。而在集成电路设计中，为了基础门电路单一化，常用1号模式(与非)或7号模式(或非)来表示其他各种模式。

可见在布尔信息处理中有两类方法：一类是标准逻辑推理法，另一类是布尔神经元信息变换法。两者相互等价，是一一对应的关系。由模式参数 $\left\langle {a,b,e} \right\rangle $ 组成的状态编码反映了16种信息处理模式的内在属性 $\Gamma \left[ {ax + by - e} \right]$ ，在两类方法中都可以作为区分不同信息处理模式的标志码。所以本文将集中讨论逻辑推理法，其结论可以一一对应地推广到神经元变换法中。可见，在传统观念中把神经网络法与逻辑推理法对立起来看是没有道理的。

上面就是基于标准逻辑推理法和二值神经元信息变换法的刚性信息处理范式的概貌，它们是完备的。基于柔性逻辑推理法和基于柔性神经元信息变换法的柔性信息处理范式将在它们的基础上通过放开某些约束条件，引入相应的不确定性来实现。

3.3 连续值信息处理的有关情况

连续值逻辑推理法。1920年波兰学者J. Luckasiewicz提出三值逻辑，1921年美国学者E.L. Post提出多值逻辑^[25]，其中包括具有连续值的有界逻辑： $x,y,z \in \left[ {0,1} \right],\neg x = 1 - x;x \wedge y = \Gamma \left[ {x + y - 1} \right]$ ； $x \vee y = $ $ \Gamma \left[ {x + y} \right];x \to y = \Gamma \left[ {1 - x + y} \right]$ 。

其实，在二值逻辑中布尔算子组已有4种形式不同但是结果等价的计算公式：

$\begin{array}{c}x \wedge y = \min \left( {x,y} \right) = xy = \Gamma \left[ {x + y - 1} \right] = \\{\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. {\min \left( {x,y} \right)} \right|\max \left( {x,y} \right) = 1;0} \right\}} \right.\\x \vee y = \max \left( {x,y} \right) = x + y - xy = \Gamma \left[ {x + y} \right] = \\{\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. {\max \left( {x,y} \right)} \right|\min \left( {x,y} \right) = 0;1} \right\}} \right.\\x \to y = {\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. 1 \right|x \leqslant y;y} \right\}} \right. = \min \left( {1,x/y} \right) = \\\Gamma \left[ {1 - x + y} \right] = {\mathop{\rm ite}\nolimits} \left( {\left. y \right|x = 1;1} \right)\end{array}$

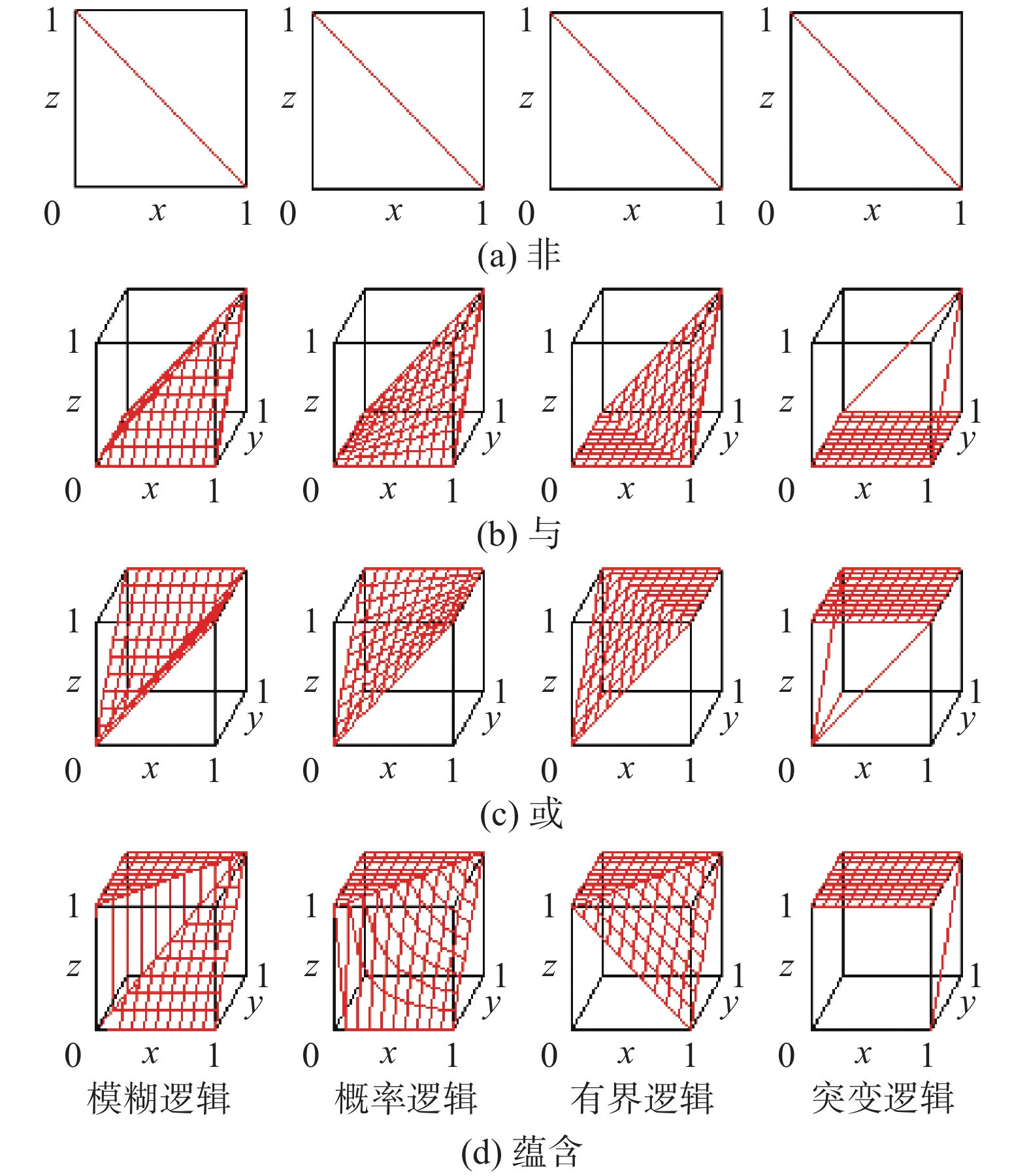
当命题的真值从二值 $x,y,z \in \left[ {0,1} \right]$ 扩张为连续值 $x,y,z \in \left\{ {0,1} \right\}$ 后，由于中间过渡值的参与，这4种原来等价的不同公式计算出来的结果不再等价了，它们被分裂为4种不同的连续值逻辑(见图7)。

模糊逻辑：

$\begin{array}{c}\neg x = 1 - x;x \wedge y = \min \left( {x,y} \right);x \vee y = \max \left( {x,y} \right);\\x \to y = {\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. 1 \right|x \leqslant y;y} \right\}} \right.\end{array}$

概率逻辑：

$\begin{array}{c}\neg x = 1 - x;x \wedge y = xy;x \vee y = x + y - xy;\\x \to y = \min \left( {1,x/y} \right)\end{array}$

有界逻辑：

$\begin{array}{c}\neg x = 1 - x;x \wedge y = \Gamma \left[ {x + y - 1} \right];\\x \vee y = \Gamma \left[ {x + y} \right];x \to y = \Gamma \left[ {1 - x + y} \right]\end{array}$

突变逻辑：

$\begin{array}{c}\neg x = 1 - x;x \wedge y = {\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. {\min \left( {x,y} \right)} \right|\max \left( {x,y} \right) = 1;0} \right\}} \right.;\\x \vee y = {\mathop{\rm ite}\nolimits} \left\{ {\left. {\left. {\max \left( {x,y} \right)} \right|\min \left( {x,y} \right) = 0;1} \right\}} \right.;\\x \to y = {\mathop{\rm ite}\nolimits} \left( {\left. y \right|x = 1;1} \right)\end{array}$

进一步研究发现，这4个非标准逻辑之间有严格的大小顺序关系，是连续变化区间中的4个特殊点，尽管前3个连续值逻辑算子组已由概率论证明：模糊逻辑算子组在最大相吸相关时成立；概率逻辑算子组在独立相关时成立；有界逻辑算子组在最大相斥相关时成立，可以说是有可靠的数学理论支撑。唯独突变逻辑算子组没有数学理论依据。但是，我们可以证明，模糊逻辑算子组是柔性信息处理算子组的上极限，突变逻辑算子组是柔性信息处理算子组的下极限，所以我们不能轻易否定突变逻辑算子组的存在价值。而且人们有理由进一步思考，在这4种逻辑算子的间隙中是否还存在其他的柔性信息处理算子组？这些柔性信息处理算子组都代表什么逻辑？能在什么情况下使用？

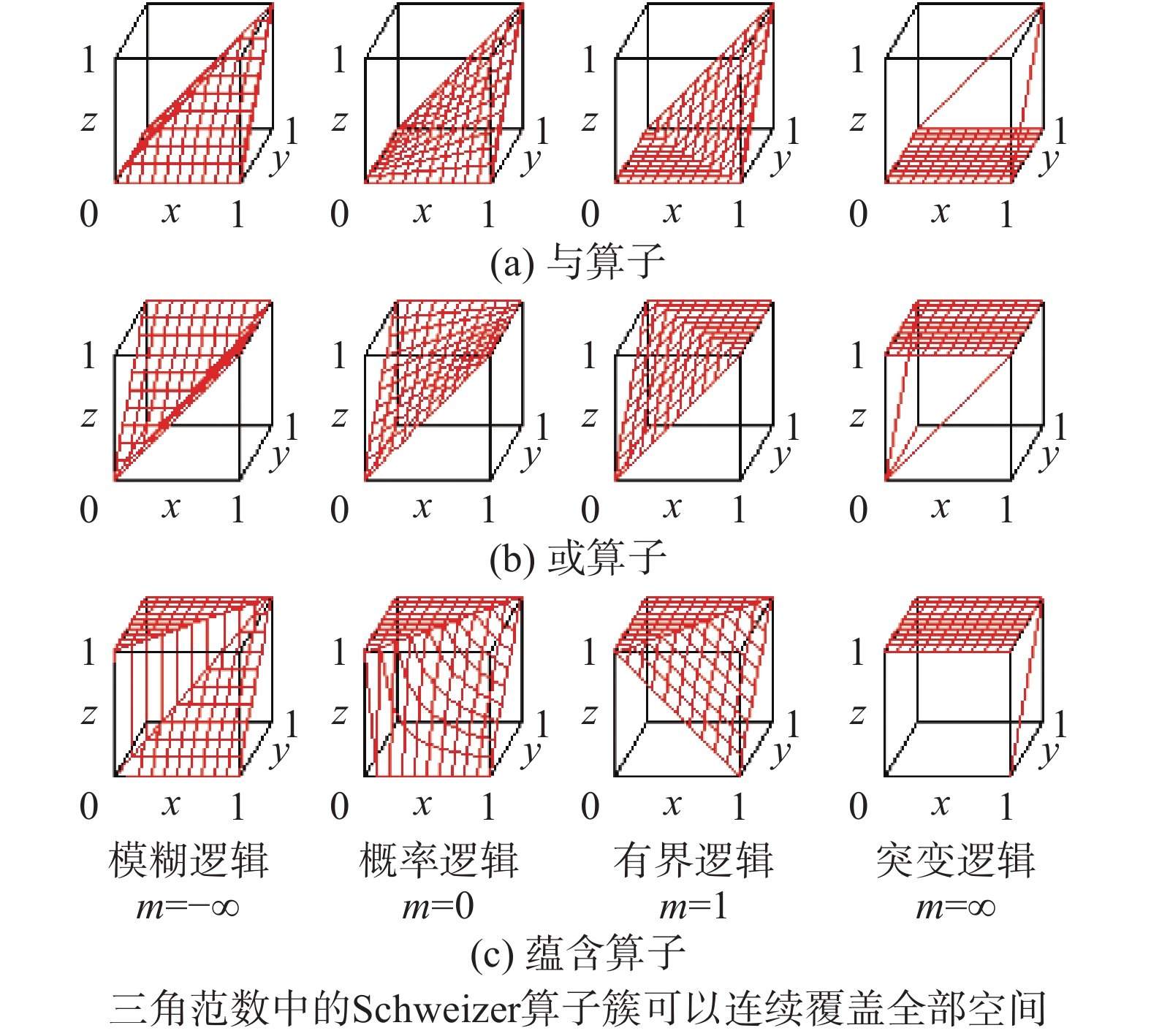
3.4 三角范数理论的启发

1942年K. Menge提出三角范数(triangular norm)概念，主要研究各种算子中不同运算模型应共同满足的抽象定义、一般性质和生成方法，常用的连续值域为 $\left[ {0,1} \right]$ 。根据三角范数理论的研究，上述4个连续值逻辑全部包含于Schweizer算子簇 ${x^m},m \in \left( { - \infty ,\infty } \right)$ 中。概率论只孤立发现了前3个逻辑点 $\left( {m = - \infty ,0,1} \right)$ ，而Schweizer 算子簇则包含了连续区间 $m \in \left( { - \infty ,\infty } \right)$ 中的所有逻辑点，其中包括突变逻辑点 $m = \infty $ ，以及在这4个特殊逻辑点空隙中间存在的所有逻辑点^[26](见图8)。由此可以看出，智能信息处理可以利用Schweizer算子簇将概率论进一步扩张完善，而且这个扩张完善的空间很大！这一发现给了我们深入探索下去的勇气，并有了得心应手的数学工具。

4 智能信息处理的理论依据是广义概率论 4.1 柔性命题的真度是它在因素空间中对应集合的概率测度

柔性命题的真度与刚性命题的真值有很大差别，因为标准逻辑是在矛盾对立(分明集合)中确定命题的真值，满足非真即假的理想化约束。而柔性逻辑是在矛盾对立统一(柔性集合)中确定柔性命题的真度，满足亦真亦假性，它真假有度，矛盾双方共处一体。所以在柔性命题的真度中，可通过真度数值的不同变化，来包容辩证矛盾并实现矛盾双方的相互转化。

1)柔性命题真度的确定方法

参照刚性命题真值的定义方法，定义柔性命题的真度是论域 $U$ 中事件 $u$ 属于不分明集合 $A$ 的隶属度(见图9)。请读者注意：本文所说的不分明集合概念不等同于模糊数学中使用的“不分明集合”概念。学术界已习惯于把“不分明集合”等同于“模糊集合”，意思是其中的逻辑规律一定服从“模糊逻辑”。而本文的研究结果表明，在不分明集合中存在无穷多个柔性逻辑，模糊逻辑只能在两个命题之间具有最大相吸相关关系时使用，在偏离最大相吸相关关系的场合需要使用其他的柔性逻辑，否则会出现计算偏差。所以，在容易引起概念混淆的上下文场合，我们会用一个新词“柔性集合”来表示边界不清晰的不分明集合，避免把它与“模糊集合”联系起来^{[8, 27]}。

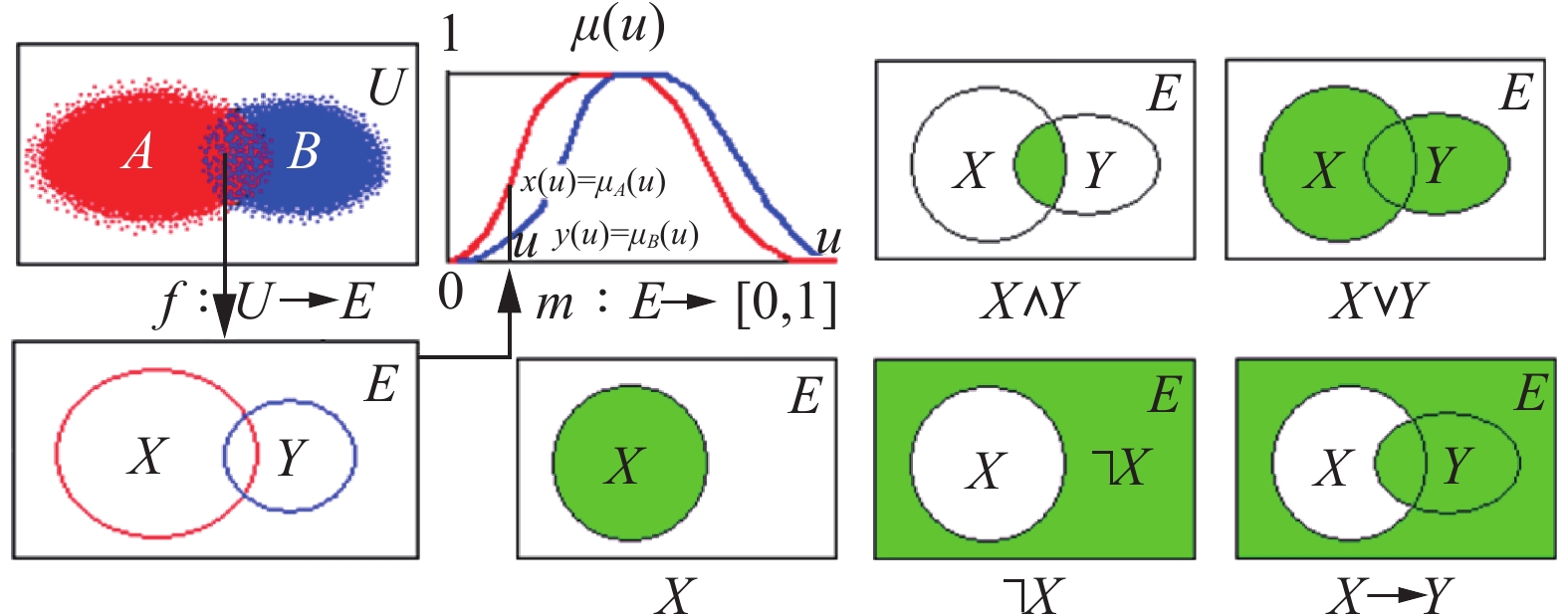
用什么可靠方法来精确确定论域 $U$ 中事件 $u$ 属于不分明集合 $A$ 的隶属度呢？我们选择的是通过在与不分明集合 $A$ 对应因素空间E中，与事件 $u$ 对应的分明集合 $X$ 的概率测度来精确确定，具体过程为(见图10)：设事件 $u$ 的论域是 $U$ ， $U$ 中有两个不分明集合 $A$ 、 $B$ ，柔性命题 $x\left( {u \in A} \right)$ 和 $y\left( {u \in B} \right)$ 的隶属度需要在它对应的因素空间E中确定， $x$ 等于 $E$ 中分明集合 $X$ 的概率测度， $y$ 等于 $E$ 中分明集合 $Y$ 的概率测度。这是通过决定柔性命题真度的因素空间 $E$ 中对应的分明集合 $X$ , $Y$ 上的刚性判断，来完成论域 ${{U}}$ 中柔性命题真度的柔性判断。由于概率论是成熟的数学理论，通过它来精确定义柔性命题的真度是可靠和严谨的。

2) 两级间接定义的方法在智能信息处理中具有普适性意义

在智能信息处理中常常需要把原始数据库中的数据(常是布尔信息)归纳抽象为知识，然后再把知识库中较低层的知识归纳抽象为更高层的知识，如此一层一层地不断归纳抽象下去，知识的粒度越来越大，关系网络越来越简化，直到知识的粒度和关系网络的复杂度满足智能决策的需要为止。概率论已是一个公认的数学基础理论，它在理论上架起了从确定性推理(分明关系)出发通向随机性(不确定性知识、不分明集合)推理的桥梁，可操作性好，可靠性高。上面这种通过在因素空间 $E$ 中分明集合 $X$ 上的刚性判断获得集合的概率测度，然后用来间接定义更上一层论域 $U$ 上 $u \in A$ (不分明集合)的柔性命题真度，在数学上是严格和可靠的。这种定义柔性命题真度的方式等价于在概率计量逻辑^[28]中，通过计算一阶谓词 $\forall xP\left( x \right)$ , $x \in X$ (分明集合)的公式概率真度，来定义更高一层柔性命题 $u \in A$ (不分明集合)的真度。这是在归纳抽象过程中实现知识粒度增长和关系网络简化的可靠数学方法，开始是实现从确定性知识到不确定性知识的可靠提升，然后是进一步实现从不确定性知识到更高一层不确定性知识的可靠提升(即其中的集合 $X$ 也可以提升为不分明集合)，这个提升过程可不断地递归下去，没有最大层限制。关于因素空间的更多性质，请读者参阅汪培庄教授的文章。

4.2 命题真度变化对各种逻辑运算的影响表现在它的基模型上

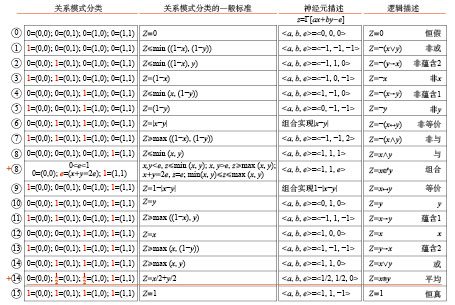
1) 18种不同的柔性信息处理模式

把没有引入其他不确定性的连续值逻辑运算模型组称为命题泛逻辑的基模型组，作者已研究证明常用的基模型组就是有界逻辑算子组，它仅包容了命题真度的不确定性 $x,y,z \in \left[ {0,{\rm{ }}1} \right]$ ，在基模型组中不仅给定了两个端点0, 1的变换关系(与标准逻辑一致)，而且给定了标准逻辑没有的中间过渡值的变换关系，是引入其他不确定性的基准平台。图11给出了基模型状态下的全部18种柔性信息处理模式，它比布尔信息处理模式多了2种，第1种是由14号模式(或)扩张出来的平均运算模式 ${14^ + }(x/2 + y/2)$ ，即出现了参数 $a = 1/2,\;b = 1/2$ 的模式，第2种是由或8号模式(与)扩张出来的组合运算模式 ${8^ + }\left( {\Gamma \left[ {x + y - e} \right]} \right.$ ，其中 $0 < e < 1$ ，当 $e = 1$ 时退化为8号模式，当 $e = 0$ 时退化为14号模式。由不同模式参数 $ < a,{\rm{ }}b,{\rm{ }}e > $ 组成的状态编码反映了18种柔性信息处理模式的内在属性 $\Gamma \left[ {ax + by - e} \right]$ ，可作为区分不同信息处理模式的标志码，在逻辑推理法和神经元变换法中都可使用。

2) 常用的7种基模型

从图11可以看出，常用的基模型有7个，它们是：

①非运算的基模型　 $\neg x = N\left( x \right) = 1 - x$

②与运算的基模型　 $x \wedge y = T\left( {x,y} \right) = \Gamma \left[ {x + y - 1} \right]$

③或运算的基模型　 $x \vee y = S\left( {x,y} \right) = \Gamma \left[ {x + y - 1} \right]$

④蕴含运算的基模型　 $x \to y \!=\! I\left( {x,y} \right) \!=\! \Gamma \left[ {1 \!-\! x \!+\! y} \right]$

⑤等价运算的基模型　 $x \leftrightarrow y \!=\! Q\left( {x,y} \right) \!=\! 1 \!-\! \left| {x \!-\! y} \right|$

⑥平均运算的基模型　 x®y = $ M(x,y) \!=\! {\rm{1 \! -\! [\{ (1 \! - \! x)/ }}$ $ 2 + {\rm{(1 - y)/2\} ]}} $

⑦组合运算的基模型　 x©y $ \!= \!{C^e}(x,y) \!=\! \Gamma [x \!+\! y \!- \!0.5]$

其中 $e \in \left[ {0,{\rm{ }}1} \right]$ 是表示弃权的幺元， ${\rm{ite}}\left\{ {y|x;z} \right\}$ 是条件表达式，意思是“如果 $x$ ，则 $y$ ；否则 $z$ ”。

4.3 破译不确定性推理的密码

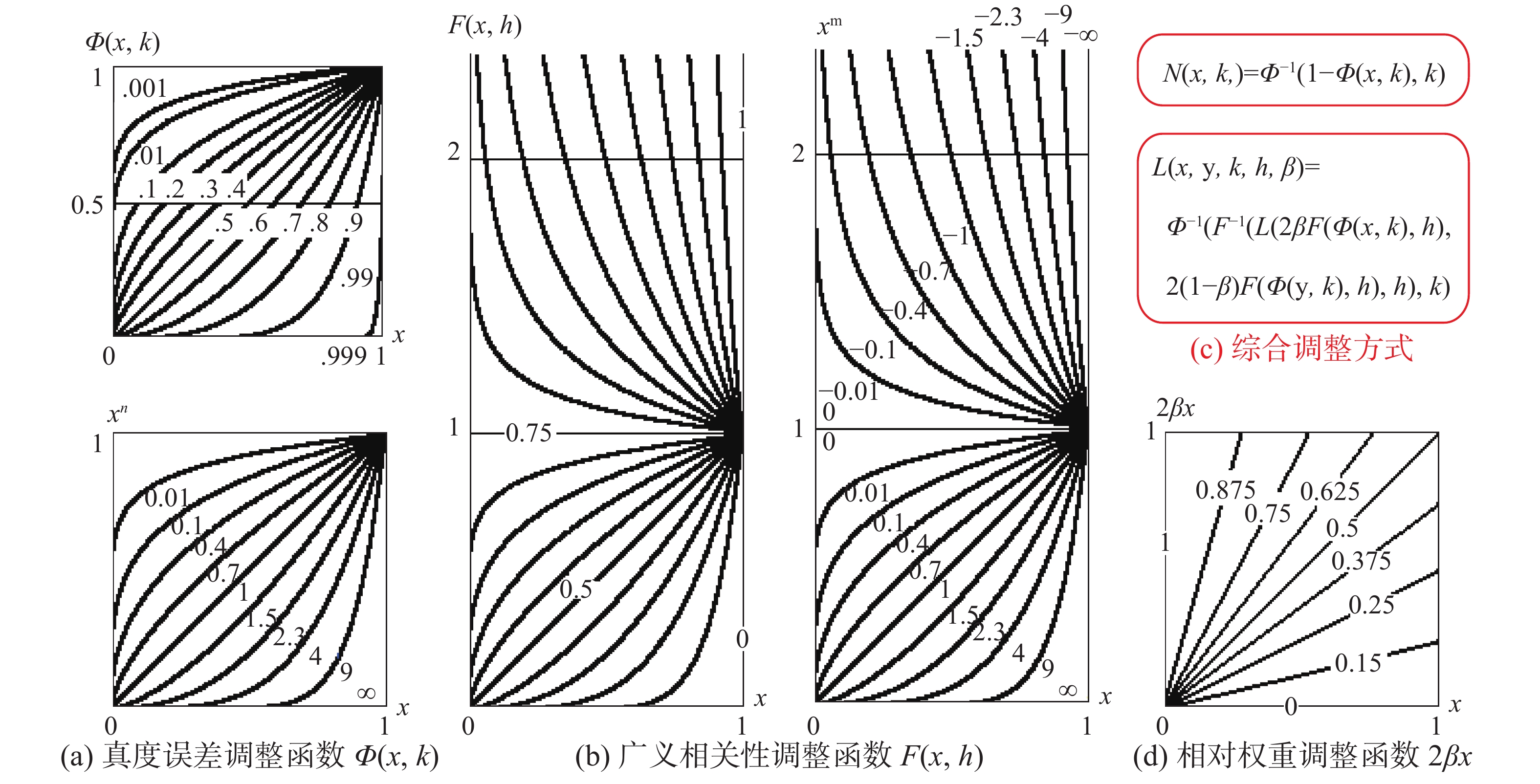
图12列举了我们研究发现的命题泛逻辑中能够包容的5种不确定性，它们对各型逻辑运算基模型的影响方式和程度如图13所示。命题真度不确定性的引入已经告诉我们，当把标准逻辑命题真值的二值属性 $x,y,x \in \{ 0,1\} $ 扩张为命题真度 $x,y,x \in [0,1]$ 之后，就发现了不确定性推理状态的千差万别，每一种推理状态就像一把密码锁，只能用一串对应的密码 $ < k,h,\beta ,e > $ 才能打开这把特殊的锁，在这里根本不存在可以随意开锁的万能钥匙，这是在标准逻辑中万万想不到的逻辑规律。

1)命题真度误差的不确定性

在概率测度中允许出现估计误差，无估计误差的是可加概率测度(additive measure)，满足 $P(X) +$ $ P(\neg X) = 1$ 的性质，有估计误差的是不可加概率测度(inadditive measure)，满足 $P(X) + P(\neg X) \ne 1$ 的性质。误差的正负和大小用误差系数 $k \in [0,1]$ 刻画，其中 $k = 1$ 表示最大正误差， $k = 0.5$ 表示无误差， $k = 0$ 表示最大负误差。

利用三角范数理论可以证明，误差系数的连续变化对柔性命题逻辑运算基模型的调整可由N性生成元完整簇 $\varPhi (x,k){\rm{ }} = {x^n}$ , $n \in \left( {0,\infty } \right)$ , $n = \displaystyle\frac{{ - 1}}{{{\rm{lo}}{{\rm{g}}_2}k}}$ 来完成。 $\varPhi (x,k)$ 对一元运算基模型 $N\left( x \right)$ 的作用方式：

$N\left( {x,k} \right) = {\varPhi ^{ - 1}}\left( {N\left( {\varPhi \left( {x,k} \right)} \right),k} \right)$

它对6种二元运算基模型L(x, y)的作用方式是：

$L\left( {x,y,k} \right) = {\varPhi ^{ - 1}}\left( {L\left( {\varPhi \left( {x,k} \right),\varPhi \left( {y,k} \right)} \right),k} \right)$

误差系数是不确定性推理密码串 $ \left\langle {k,h,\beta ,e} \right\rangle $ 中的第1位密码，确定 $k$ 数值的公式为 $k = N(k,k)$ 。

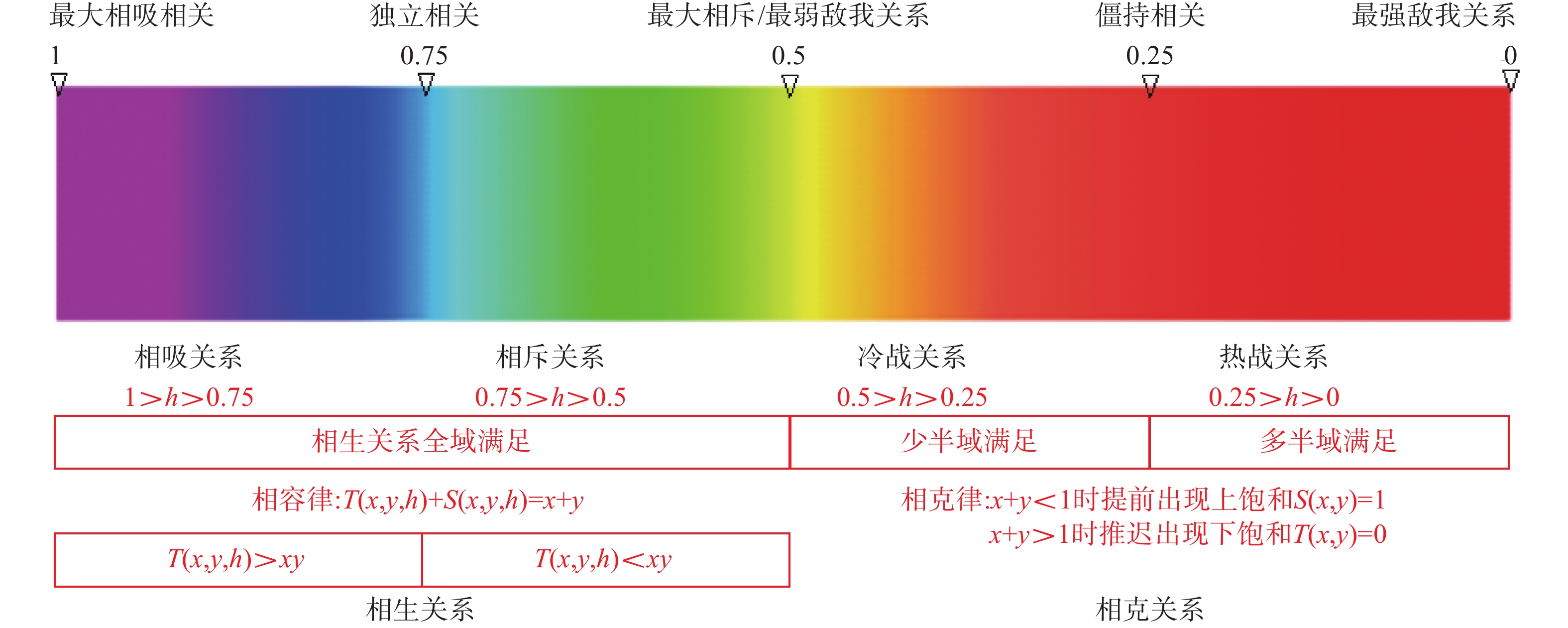
2) 两个命题之间广义相关关系的不确定性

图14描述了广义相关关系的不确定性，通过广义相关系数 $h \in [0,1]$ 的变化可描述从相容相关到相克相关的连续变化过程对各逻辑运算基模型的调整过程，形成一个连续分布的逻辑谱。

其中 $ h \in [0.5,1] $ 是朋友关系的逻辑抽象，它只有亲、疏程度的差别，不会相互损伤消耗，其数学特征是 $ T\left( {x,y,h} \right) + S\left( {x,y,h} \right) = x + y $ , 其中 $ T(x,y,{\rm{ }}1){\rm{ }} = {\rm{min}}(x,y) $ , $ S(x,y,{\rm{ }}1){\rm{ }} = {\rm{max}}(x,y) $ 是最大相吸相关， $ T(x,y,{\rm{ }}0.75){\rm{ }} = xy $ , $ S(x,y,0.75) = x + y - xy $ 是独立相关， $ T(x,y,{\rm{ }}0.5){\rm{ }} = {\rm{max}}(0, $ $ x + y - 1) $ ,  $ S(x,y,{\rm{ }}0.5){\rm{ }} = {\rm{min}}(1,x + y) $ 是最大相斥相关。 $ h \in \left( {0.75,1} \right] $ 是相吸相关阶段， $ h \in \left[ {0.5,0.75} \right) $ 是相斥相关阶段。

$h \in \left[ {0,0.5} \right)$ 是敌我关系的逻辑抽象，必然发生相互损伤和过分消耗资源的行为，其数学特征满足相克律：当x+y<1时，会提前出现上饱和效应，S(x, y, h)=1; 当x+y>1时，会推迟出现下饱和效应，T(x, y, h)=0。其中T(x, y, 0.25)=0和S(x, y, 0.25)=1的机会正好是一半一半，所以h=0.25点代表的是僵持关系；当h>0.25时，T(x, y, h)=0和S(x, y, h)=1的机会小于一半甚至趋近于0，代表的是冷战关系，主要是因为扩军备战和储备战略资源；当h<0.25时，T(x, y, 0)=0和S(x, y, 0)=1的机会大于一半甚至趋近于1，代表的是热战关系，主要是因为人员的大量伤亡和物资的大量消耗。到了h=0时，突然变成T(x, y, 0)=ite{min(x, y)|max(x, y)=1; 0}和S(x, y, 0)= ite{max(x, y)|min(x, y)=0; 1}，代表敌人已经完全消灭，胜利一方已经控制了一切。这些都是特别重要的逻辑特征点。

利用三角范数理论可以证明，广义相关系数h对逻辑运算基模型的影响全部反映在T性生成元完整簇 $F(x,h) = {x^m}$ , $m \in ( - \infty ,\infty )$ 上， $F(x,h)$ 对6种二元运算基模型 $L(x,y)$ 的作用方式是：

$L(x,y,h) = {F^{ - 1}}(L(F(x,h),F(y,h)),h)$

广义相关系数是不确定性推理密码串 $ \left\langle {k,h,\beta ,e} \right\rangle $ 中的第2位密码，确定 $h$ 数值的公式为 $h = 3{\smallint _I}{\smallint _I}T(x,y,h)\cdot$ ${\rm{d}}x{\rm{d}}y$ 。

3) 两命题之间相对权重的不确定性

两命题之间相对权重的不确定性用偏袒系数 $\beta \in \left[ {0,{\rm{ }}1} \right]$ 表示，其中 $\beta = 1$ 表示最大偏 $x$ 状态， $y$ 失去作用； $\beta = 0.5$ 表示无偏袒状态， $x$ , $y$ 等权； $\beta = 0$ 表示最小偏 $x$ 状态， $x$ 失去作用。

利用三角范数理论可以证明，偏袒系数 $\beta $ 对6种二元运算基模型 $L(x,y)$ 的作用方式为

$L(x,y,\beta ) = L(2\beta x,{\rm{ }}2(1 - \beta )y)$

偏袒系数是不确定性推理密码串 $ < k,h,\beta ,e > $ 中的第3位密码，确定 $\beta $ 数值的公式为 $\beta = T(1,0,0.5,0.5,\beta )$ 。

4) 组合运算中决策阈值的不确定性

在有界逻辑中组合运算模型为

$\begin{array}{c}{C^e}\left( {x,y} \right) = {\rm{ite}}\{ {\rm{min}}\left( {e,\max \left( {0,x + y - e} \right)} \right)|x + y < 2e;\\N\left( {{\rm{min}}\left( {N\left( e \right),{\rm{max}}\left( {0,N\left( x \right) + N\left( y \right) - N\left( e \right)} \right)} \right)} \right)|\\x + y{\rm{ > }}2e;e\} = {\rm{min}}\left( {1,{\rm{max}}\left( {0,x + y - e} \right)} \right)\end{array}$

它是一个完整的组合算子簇，其中引入了决策阈值 $e \in \left[ {0,{\rm{ }}1} \right]$ 的不确定性，其基模型算子是x©^0.5y = $ \varGamma [x + y - 0.5]$ 。

决策阈值 $e$ 是不确定性推理密码串 $ \left\langle {k,h,\beta ,e} \right\rangle $ 中的第4位密码，确定 $e$ 数值的公式为 $e = {C^e}(x,{\rm{ }}2e - x)$ 。在这里可以看出，在柔性信息处理中，本来是模式标志码位的 $e$ ，现在又多了一重身份，它在组合运算( ${8^ + }$ 模式)中同时扮演了决策阈值不确定性程度密码位的角色，由于它可在 $\left[ {0,{\rm{ }}1} \right]$ 中连续变化，用斜体字母 $e$ 表示。

目前我们尚未发现第5种影响柔性命题逻辑运算模型的不确定性因素存在。

4.4 7种逻辑运算的公理及模型

1)非运算公理及模型

非运算公理　非运算模型 $N(x)$ 是 $\left[ {0,{\rm{ }}1} \right] \to \left[ {0,{\rm{ }}1} \right]$ 的一元运算，满足以下非运算公理： $x \in \left[ {0,{\rm{ }}1} \right]$ ；边界条件N1， $N\left( 0 \right) = 1,\;\;N\left( 1 \right) = 0$ ；单调性N2， $N(x)$ 单调减, ${\rm{if}}\forall x,y \in \left[ {0,{\rm{ }}1} \right]$ ,若 $x < y$ , 则 $N(x) \geqslant N(y)$ ；逆等性N3， $N(x)$ 有逆等性, ${\rm{if}}\,\,\forall x \in \left[ {0,{\rm{ }}1} \right]$ , $N(x){\rm{ }} = {N^{ - 1}}(x)$ 是逆函数。

非运算模型　非运算模型只受误差系数k的影响，是 $N$ 范数完整簇 $N(x,k)$ , 它由生成基 $N(x) = 1 - x$ 和 $N$ 性生成元完整簇 $\varPhi (x,k) = {x^n}$ , $k = {2^{ - 1/n{\rm{ }}}}$ ， $n = \displaystyle\frac{{ - 1}}{{{\rm{lo}}{{\rm{g}}_2}k}}$ 相互作用而生成。

$N(x,k){\rm{ }} = {\varPhi ^{ - 1}}(1 - \varPhi (x,k),k){\rm{ }} = {\rm{ }}{(1 - {x^n})^{1/}}^n$

其中， $N(x,{\rm{ }}1) = {\rm{ite}}\{ 0|x = 1;{\rm{ }}1\} $ 是最大非算子， $N(x,{\rm{ }}0.5){\rm{ }} = $ 1 – x是中心非算子， $N(x,{\rm{ }}0) = {\rm{ite}}\{ 1|x = 0;{\rm{ }}0\} $ 是最小非算子。

一般两次非运算的误差系数可不相等 $\left( {{k_1} \ne {k_2}} \right)$ ，满足非合成律(又称为否定之否定律，螺旋式上升律) $N(N(x,{k_1}){\rm{ }},{k_2}){\rm{ }} = 1 - N(x,{k_3})$ ， ${k_3} = {k_1}\left( {1 - {k_2}} \right)/({k_1} + {k_2} -$ $2{k_1}{k_2})$ 。当 $\left( {{k_1} \ne {k_2}} \right)$ 时，满足对合律 $N(N(x,k){\rm{ }},k){\rm{ }} = x$ 。

2)与运算公理及模型

与运算公理　与运算模型 $T(x,y)$ 是 ${\left[ {0,{\rm{ }}1} \right]^2} \to \left[ {0,{\rm{ }}1} \right]$ 的二元运算, 它必须满足以下的与运算公理： $x,y,z \in $ [0, 1]；边界条件T1， $T(0,y) = 0$ , $T(1,y) = y$ ；单调性T2， $T(x,y)$ 关于 $x,y$ 单调增；结合律T3， $T(T(x,y),z) = $ $ T(x,T(y,z))$ ；上界性T4， $T(x,y) \leqslant {\rm{min}}(x,y)$ 。

与运算模型　与运算模型可受 $k,h,\beta $ 的联合影响，是一个运算模型完整簇，即

$T(x,y,k,h,\beta ) = {({\rm{max}}(0,{\rm{ }}2\beta {x^{nm}} + 2(1 - \beta ){y^{nm}} - 1))^{1/}}^{mn}$

当 $\beta = 0.5$ 时，偏袒性的影响消失， $T(x,y,k,h) = ({\rm{max}}(0, $ ${{x^{nm}} +y^{nm}} - 1){)^{1/}}^{mn}$ ；当 $k = 0.5$ 时，误差的影响消失， $T(x,y,h) = {\rm{ }}{({\rm{max}}(0,{x^m} + {y^m} - 1))^{1/}}^m$ 。

与运算模型有4个特殊算子：模糊与算子 $T\left( {x,y,{\rm{ }}1} \right) = {\rm{min}}\left( {x,y} \right)$ ，概率与算子 $T\left( {x,y,\;0.75} \right) = xy$ ，有界与算子 $T\left( {x,y,{\rm{ }}0.5} \right) = {\rm{max}}\left( {0,x + y - 1} \right)$ ，突变与算子

$T\left( {x,y,{\rm{ }}0} \right) = \operatorname{ite} \left\{ {{\rm{min}}\left( {x,y} \right)|{\rm{max}}\left( {x,y} \right) = 1;{\rm{ }}0} \right\}$

一般情况下，因两个命题x, y可能是真度相等，而不一定是 $h = 1,\;\beta = 0.5$ ，所以 $T(x,x,k,h,\beta ) \leqslant x$ 幂等律不一定成立。只有在 $x,y$ , 是同一个命题的特殊条件下，必然有 $h = 1$ ， $\beta = 0.5$ ， $T\left( {x,x,k,1} \right) = $ x幂等律才能成立。矛盾律成立的条件是 $T\left( {x,N\left( {x,k} \right),k,0.5,0.5} \right)= $ 0，因为一个命题和它自己的非命题必然是最大相斥相关，等权， $h = 0.5, \, \beta = 0.5$ 。如果是其他的 $h, \, \beta$ 值，矛盾律不一定成立。

3) 或运算公理及模型

或运算公理　或运算模型 $S\left( {x,y} \right)$ 是 ${\left[ {0,1} \right]^2} \to $ [0, 1]的二元运算, 它必须满足以下的或运算公理: $x$ , $y$ , $z \in \left[ {0,1} \right]$ ；边界条件S1， $S\left( {1,y} \right) = 1$ , $S\left( {0,y} \right) = y$ ；单调性S2， $S\left( {x,y} \right)$ 关于 $x$ , $y$ 单调增；结合律S3， $S\left( {S\left( {x,y} \right),z} \right) = $ $ S\left( {x,S\left( {y,z} \right)} \right)$ ；下界性S4， $S\left( {x,y} \right) \geqslant {\rm{max}}\left( {x,y} \right)$ 。

或运算模型　或运算模型可受 $k$ , $h$ , $\beta $ 的联合影响，是一个运算模型完整簇，即

$\begin{array}{c}S\left( {x,y,k,h,\beta } \right) = \\{\left( {1 - {{\left( {{\rm{max}}\left( {0,2\beta {{\left( {1 - {x^n}} \right)}^m} + 2\left( {1 - \beta } \right){{\left( {1 - {y^n}} \right)}^m} - 1} \right)} \right)}^{1/m}}} \right)^{1/n}}\end{array}$

当 $\, \beta = 0.5$ 时，偏袒性的影响消失， $S\left( {x,y,k,h} \right) = $ ${\left( {1 - {{\left( {{\rm{max}}\left( {0,{{\left( {1 - {x^n}} \right)}^m} + {{\left( {1 - {y^n}} \right)}^m} - 1} \right)} \right)}^{1/m}}} \right)^{1/n}}$ ；当 $k = 0.5$ 时，误差的影响消失， $S\left( {x,y,h} \right) = \left( {1 - \left( {{\rm{max}}\left( {0,{{\left( {1 - x} \right)}^m} + } \right.} \right.} \right.$ $ {\left( {1 - y} \right)^m} - 1)){)^{^{1/m}}}$ 。 $S\left( {x,y,h} \right)$ 有4个特殊算子:模糊或算子 $S\left( {x,y,{\rm{ }}1} \right) = {\rm{max}}\left( {x,y} \right)$ ，概率或算子 $S\left( {x,y,{\rm{ }}0.75} \right) = x + $ y – xy，有界或算子 $S\left( {x,y,{\rm{ }}0.5} \right) = {\rm{min}}\left( {1,x + y} \right)$ ，突变或算子 $S\left( {x,y,{\rm{ }}0} \right) = {\rm{ite}}\left\{ {{\rm{max}}\left( {x,y} \right)|{\rm{min}}\left( {x,y} \right) = 0;1} \right\}$ 。

一般情况下，因两个命题 $x$ , $y$ 可能是真度相等，而不一定是 $h = 1$ ， $\beta = 0.5$ ，所以 $S\left( {x,x,k,h,\beta } \right) \geqslant x$ 幂等律不一定成立。只有在 $x$ , $y$ 是同一个命题的特殊条件，必然是 $h = 1$ ， $\beta = 0.5$ ， $S\left( {x,x,k,{\rm{ }}1,{\rm{ }}0.5} \right) = x$ 幂等律才能成立。排中律成立的条件是 $S\left( {x,N\left( {x,k} \right),k,0.5,0.5 } \right) =$ 1，因为一个命题和它自己的非命题必然是最大相斥相关，等权， $h = 0.5, \, \beta=0.5$ 。如果是其他的 $h, \, \beta$ 值，排中律不一定成立。

在 $S\left( {x,y,k,h} \right)$ 和 $T\left( {x,y,k,h} \right)$ 之间存在对偶律： $N\left( {S\left( {x,y,k,h} \right),k} \right) \!=\! T\left( {N\left( {x,k} \right),N\left( {y,k} \right),k,h} \right)$ ， $N( {T\left( {x,y,k,h} \right),} $ $S k) =\left( {N\left( {x,k} \right),N\left( {y,k} \right),k,h} \right)$ ，当 $h \in \left[ {0.5,{\rm{ }}1} \right]$ 时, $S\left( {x,y,h} \right)$ 和 $T\left( {x,y,h} \right)$ 满足相容律 $S\left( {x,y,h} \right) + T\left( {x,y,h} \right) = x + y$ 。

4) 蕴涵运算公理及模型

蕴涵运算公理　蕴涵运算模型 $I\left( {x,y} \right)$ 是 ${\left[ {0,1} \right]^2} \to $ [0, 1]的二元运算, 它必须满足以下的蕴涵运算公理: $x$ , $y$ , $z \in \left[ {0,1} \right]$ ；边界条件I1， $I\left( {0,y} \right) = 1$ , $I\left( {1,y} \right) \!=\! y$ , $I\left( {x,1} \right) \!=\! 1$ ；单调性I2， $I\left( {x,y} \right)$ 关于 $y$ 单调增, 关于 $x$ 单调减；连续性I3， $I\left( {x,y} \right)$ 关于 $x$ , $y$ 连续；保序性I4， $I\left( {x,y,k,h} \right) = 1$ , if $x \leqslant y$ (除 $h = 0$ 和 $k = 1$ 外)；推演性I5， $T\left( {x,I\left( {x,y} \right)} \right) \leqslant y$ (假言推论，MP规则)。

蕴涵运算模型　蕴涵运算模型可受 $k$ , $h$ , $\beta $ 联合影响，是一个运算模型完整簇，即

$I\left( {x,y,k,h,\beta } \right) = {\left( {{\rm min}\left( {1,1 - 2\beta {x^{nm}} + 2\left( {1 - \beta } \right){y^{nm}}} \right)} \right)^{1/mn}}$

当 $\beta = 0.5$ 时，偏袒性的影响消失， $I\left( {x,y,k,h} \right) = $ ${({\rm{min}}(1,1 - x^{nm}} + {y^{nm}}){)^{^{1/mn}}}$ ；当 $k = 0.5$ 时，误差的影响消失， $I\left( {x,y,h} \right) = {\left( {{\rm{min}}\left( {1,1 - {x^m} + {y^m}} \right)} \right)^{1/m}}$ 。

$I\left( {x,y,h} \right)$ 有4个特殊算子: 模糊蕴涵 $I\left( {x,y,1} \right) = $ $ {\rm{ite}}\left\{ {1|x \leqslant y;y} \right\}$ ，概率蕴涵 $I\left( {x,y,0.75} \right) = \min \left( {1,y/x} \right)$ ，有界蕴涵 $I\left( {x,y,0.5} \right) = {\rm{min}}\left( {1,1 - x + y} \right)$ ，突变蕴涵 $I\left( {x,y,0} \right) = $ $ \operatorname{ite} \left\{ {y|x = 1;1} \right\}$ 。

一般情况下MP规则 $T\left( {x,I\left( {x,y,k,h,\beta } \right)k,h,\beta } \right) \leqslant y$ 是成立的，但是在两组 $k$ , $h$ , $\beta $ 不一致的特殊情况下，随便使用MP规则是存在风险的。

5)等价运算公理及模型

等价运算公理　等价运算模型 $Q\left( {x,y} \right)$ 是 ${\left[ {0,{\rm{ }}1} \right]^2} \to $ [0, 1]的二元运算，必须满足以下的等价运算公理: $x$ , $y$ , $z \in \left[ {0,1} \right]$ ；边界条件Q1， $Q\left( {1,y} \right) = y$ , $Q\left( {x,1} \right) = x$ ；单调性Q2， $Q\left( {x,y} \right)$ 关于 $\left| {x - y} \right|$ 单调减；连续性Q3， $Q\left( {x,y} \right)$ 关于 $x$ , $y$ 连续；保值性Q4， $Q\left( {x,y} \right) = 1$ , if $x = y$ (除 $h = 0$ 和 $k = 1$ 外)。

等价运算模型　等价运算模型可受k, h, β的联合影响，是一个运算模型完整簇，即

$\begin{array}{c}{Q(x,y,k,h,\beta ) = }\\{{\rm{ite}}\left\{ {\left. {{{\left( {1 + \left| {2\beta {x^{nm}} - 2\left( {1 - \beta } \right){y^{nm}}} \right|} \right)}^{1/mn}}} \right|} \right\}}\\\left. {m \leqslant 0;{{\left( {1 - \left| {2\beta {x^{nm}} - 2\left( {1 - \beta } \right){y^{nm}}} \right|} \right)}^{1/mn}}} \right\}\end{array}$

当 $\beta = 0.5$ 时，偏袒性的影响消失， $Q\left( {x,y,k,h} \right) = $ ${\rm{ite}}\left\{ {{{\left( {1 + \left| {{x^{nm}} - {y^{nm}}} \right|} \right)}^{\frac{1}{{mn}}}}\left| {m \leqslant 0} \right.;{\rm{ }}{{\left( {1 - \left| {{x^{nm}} - {y^{nm}}} \right|} \right)}^{\frac{1}{{mn}}}}} \right\}$ ；当 $k = $ 0.5时，误差的影响消失， $Q\left( {x,y,h} \right) \!\!=\!\! {\rm{ite}}\left\{ {\left. {{{\left( {1 \!\!+\!\! \left| {{x^m} \!-\! {y^m}} \right|} \right)}^{1/m}}} \right|m0;} \right.$ $\left. {{{\left( {1 - \left| {{x^m} - {y^m}} \right|} \right)}^{1/m}}} \right\}$ 。

$Q\left( {x,y,h} \right)$ 有4个特殊算子:模糊等价 $Q\left( {x,y,1} \right) = $ $ {\rm{ite}}\left\{ {1|x = y;{\rm{min}}\left( {x,y} \right)} \right\}$ ，概率等价 $Q\left( {x,y,0.75} \right) = $ ( ${\rm{I}}$ 等价)，有界等价 $Q\left( {x,y,0.5} \right) = 1 - \left| {x - y} \right|$ ( ${\rm{S}}$ 等价)，突变等价 $Q\left( {x,y,0} \right) = {\rm{ite}}\left\{ {x|y = 1;\;y|x = 1;1} \right\}$ 。

6)平均运算公理及模型

平均运算公理　平均运算模型 $M\left( {x,y} \right)$ 是 ${\left[ {0,{\rm{ }}1} \right]^2} \to $ [0, 1]的二元运算，必须满足以下的平均运算公理: $x$ , $y$ , $z \! \in \! \left[ {0,{\rm{ }}1} \right]$ ；边界条件M1， ${\rm{min}}\left( {x,y} \right) \! \leqslant \! M\left( {x,y} \right) \! \leqslant \! {\rm{max}}\left( {x,y} \right)$ ；单调性M2， $M\left( {x,y} \right)$ 关于 $x$ , $y$ 单调增；连续性M3， $M\left( {x,y} \right)$ 关于 $x$ , $y$ 连续；幂等性M4， $M\left( {x,x} \right) = x$ 。

平均运算模型　平均运算模型可受 $k$ , $h$ , $\beta $ 的联合影响，是一个运算模型完整簇，即

$M\left( {x,y,k,h,\beta } \right) = {\left( {1 - {{\left( {\beta {{\left( {1 - {x^n}} \right)}^m} + \left( {1 - \beta } \right){{\left( {1 - {y^n}} \right)}^m}} \right)}^{1/m}}} \right)^{1/n}}$

当 $\beta = 0.5$ 时，偏袒性的影响消失， $M\left( {x,y,k,h} \right) = $ $ {\left( {1 - {{\left( 0.5{{{\left( {1 - {x^n}} \right)}^m} + 0.5 {{\left( {1 - {y^n}} \right)}^m}} \right)}^{1/m}}} \right)^{1/n}}$ ；当 $k = 0.5$ 时，误差的影响消失， $M\left( {x,y,h} \right) \!=\! 1 - {\left( 0.5 {{{\left( {1 \!-\! x} \right)}^m} + 0.5 {{\left( {1 - y} \right)}^m}} \right)^{1/m}}$ 。

$M\left( {x,y,h} \right)$ 有4个特殊算子:模糊平均 $M\left( {x,y,1} \right) = $ ${\rm{max}}\left( {x,y} \right)$ ，概率平均 $M\left( {x,y,{\rm{ }}0.75} \right) = 1 - {\left( {\left( {1 - x} \right)\left( {1 - y} \right)} \right)^{1/2}}$ ，有界平均 $M\left( {x,y,0.5} \right) = \left( {x + y} \right)/2$ (算术平均)，突变平均 $M\left( {x,y,0} \right) = {\rm{min}}\left( {x,y} \right)$ 。

常见的平均算子：几何平均 $1 \!-\! M\left( {1 \!-\! x,1 \!-\! y,0.75} \right) = $ $ {\left( {xy} \right)^{1/2}}$ ，调和平均 $1 - M\left( {1 - x,1 - y,0.866} \right) = 2xy/(x + y)$ 。

7)组合运算公理及模型

组合运算公理　组合运算模型 ${C^e}\left( {x,y} \right)$ 是 ${\left[ {0,{\rm{ }}1} \right]^2} \to $ [0, 1]的二元运算，必须满足的组合运算公理: $x,y,z \in $ $ \left[ {0,{\rm{ }}1} \right]$ ；边界条件 ${\rm{C_1}}$ ，当 $x,y < e$ 时, ${C^e}\left( {x,y} \right) \leqslant {\rm{min}}\left( {x,y} \right)$ ;当 $x,\;y > e$ 时, ${C^e}\left( {x,y} \right) \geqslant {\rm{max}}\left( {x,y} \right)$ ；当 $x + y = 2e$ 时, ${C^e}\left( {x,y} \right) = $ e; 否则, ${\rm{min}}\left( {x,y} \right) \leqslant {C^e}\left( {x,y} \right) \leqslant {\rm{max}}\left( {x,y} \right)$ ；单调性 ${\rm{C_2}}$ ， ${C^e}\left( {x,y} \right)$ 关于 $x,y$ 单调增；连续性 ${\rm{C_3}}$ ， ${C^e}\left( {x,y} \right)$ 关于 $x,y$ 连续；幺元律 ${\rm{C_4}}$ ， ${C^e}\left( {x,e} \right) = x$ 。

组合运算模型　组合运算模型可受 $k,h,\beta ,{\rm{ }}e$ 的联合影响，是一个运算模型完整簇，即

$\begin{array}{c}{C^e}(x,y,k,h,\beta ) = {\rm{ite\{ min}}(e,{\rm{ }}({\rm{max}}(0,{\rm{ }}2\beta {x^{nm}} + \\2(1 - \beta ){y^{nm}} - {e^{nm}}){)^{1/mn}}|2\beta x + 2(1 - \beta )y < 2e;\\(1 - ({\rm{min}}(1 - {e^n},{\rm{ }}({\rm{max}}(0,{\rm{ }}2\beta {\left( {1 - {x^n}} \right)^m} + 2(1 - \beta ){\rm{ }}{\left( {1 - {y^n}} \right)^m} - \\{\left( {1 - {e^n}} \right)^m}){)^{1/m}}){)^{1/n}})|2\beta x + 2(1 - \beta )y > 2e;e\} \end{array}$

当 $\beta = 0.5$ 时，偏袒性的影响消失， $ {C^e}\left( {x,y,k,h} \right) = $ $ {\rm{ite}}\{ {\rm{min}}(e,{\left( {{\rm{max}}\left( {0,{x^{nm}} + {y^{nm}} - {e^{nm}}} \right)} \right)^{1/mn}}| x + y < 2e;$ (1–(min $(1 - {e^n},{(\max (0,{(1 - {x^n})^m} + {(1 - {y^n})^m} - {(1 - {e^n})^m}))^{^{1/m}}}){)^{^{1/n}}})$ |x + $ y > 2e;e\} $ 当 $k = 0.5$ 时，误差的影响消失，即

$\begin{array}{c}{C^e}\left( {x,y,h} \right) = {\rm{ite}}\{ {\rm{min}}(e,{\rm{ }}{\left( {{\rm{max}}\left( {0,{x^m} + {y^m} - {e^m}} \right)} \right)^{1/m}}\\|x + y < 2e;\\(1 - (\min \left( {1 - e,{\rm{ }}{{\left( {{\rm{max}}\left( {0,{\rm{ }}{{\left( {1 - x} \right)}^m} + {{\left( {1 - y} \right)}^m} - {{\left( {1 - e} \right)}^m}} \right)} \right)}^{1/m}}} \right)\\|x + y > 2e;e\} \end{array}$

${C^e}\left( {x,y,h} \right)$ 有4个特殊算子:模糊组合 ${C^e}\left( {x,y,1} \right) = $ ite $ \left\{ {{\rm{min}}\left( {x,y} \right)\left| {x + y < 2e;{\rm{max}}\left( {x,y} \right)} \right|x + y > 2e;e} \right\}$

概率组合 有界组合 ${C^e}\left( {x,y,0.5} \right) =\Gamma $ [x + y – e]，突变组合 ${C^e}\left( {x,y,0} \right) = {\rm{ ite}}\left\{ {0\left| {x,y < e;1} \right|x,y > e;e} \right\}$ 。

4.5 柔性命题逻辑的健全使用

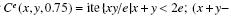
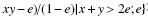
通过上面的讨论，我们已全面掌握了柔性命题逻辑中18种信息处理模式的类型编码 $ \left\langle a,{\rm{ }}b,{\rm{ }}e \right\rangle $ 和在每一个类型中，各种不确定性的程度编码 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ ，知道了应该根据实际处理的不确定性推理的需要，按照这两组编码 $ \left\langle a,{\rm{ }}b,{\rm{ }}e \right\rangle $ 和 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ 来正确选择相应的逻辑算子簇和其中的具体算子。现在结合现有的模糊逻辑、概率逻辑和有界逻辑来进一步深入分析它们在使用中为什么会出现计算偏差，甚至是无法容忍的错误，建立安全使用柔性命题逻辑的有关准则。

在刚性逻辑中有了可靠性和完备性的保证，就可以在各种应用场合安全地使用，没有任何例外。刚性逻辑具有可靠性和完备性的充分条件是满足以下规律：L1幂等律， $P \wedge P = P$ ；L2幂等律， $P \vee P = P$ ；L3矛盾律， $\neg P \vee P = 0$ ； $\neg P \vee P = 0$ ；L4排中律， $\neg P \vee $ P = 1；L5对合律， $\neg \neg P = P$ ； ${\rm{L}}6 \,{\rm{ MP}}$ 规则， $P,P \to Q| = Q$ 。其中有一些条件是冗余的，可以用不同方式进一步简化。

前面已经知道，将各种不确定性引入逻辑系统之后，推理的结果因为不确定参数 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ 的影响已经演变成一组不确定解，原来单个存在的逻辑算子被展开成一个连续分布的逻辑算子谱，由无限多个不同的算子组成。而这里所谓的使用安全性只能保证 $x,y,z \in \{ 0,{\rm{ }}1\} $ 时两个端点的使用安全性，对于中间过渡值 $x,y,z \in (0,{\rm{ }}1)$ 的使用安全性，并没有提供保证。如现行的模糊逻辑 $(\neg x = 1 - x;x \wedge y ={\rm{min}}\left( {x,y} \right);$ $ x \vee y = {\rm{max}}\left( {x,y} \right);$ $x \to y = {\rm{ ite}}\{ 1|x \leqslant y;y\} )$ 。

虽然具有可靠性和完备性，但其中的规律L3和L₄不成立。现行的概率逻辑 $\left( {\neg x = 1 - x;x \wedge y = xy} \right.;$ $\left. {x \vee y = x + y - xy;x \to y = {\rm{min}}\left( {1,x/y} \right)} \right)$ 虽然具有可靠性和完备性，但其中的规律L1、L2、L3和L4不成立。现行的有界逻辑 $\left( {\neg x = 1 - x;x \vee y = \Gamma \left[ {x + y - 1} \right];} \right.$ $x \vee y = {\Gamma} \left[ {x + y} \right];$ $\left. {x \to y = {\Gamma} \left[ {1 - x + y} \right]} \right)$ 虽然具有可靠性和完备性，但其中的规律L1和L2不成立。而且，这些重要逻辑规律的缺失，会在推理过程中产生严重的信息畸变，如在概率逻辑中，由于幂等律L1不成立，一个真度是0.9的命题，自己和自己与运算2次变成了0.81，与运算4次变成了0.656 1，8次变成了0.430 5，16次变成了0.185 3，这时一个绝对偏真的命题却发挥着绝对偏假命题的作用。又如在模糊逻辑中，由于矛盾律L3不成立，一个真度是0,7的命题，其非命题是0.3，两者与出来的绝对假命题0变成了偏假命题0.3。这些实例都说明在柔性命题逻辑的应用中，光靠确保逻辑的可靠性和完备性(即 $x,y,z \in \{ 0,{\rm{ }}1\} $ 时两个端点的使用安全性)是不够的，还需要确保中间过渡值 $x,y,z \in (0,{\rm{ }}1)$ 的使用安全性。所以我们把这两种不同的使用安全性结合起来，统称为柔性命题逻辑的健全性(integrity)，用它来确保柔性命题逻辑的使用安全。由前面的研究成果不难知道，确保柔性命题逻辑健全性的必要条件是满足如下逻辑规律^[29]。

L1 幂等律 $T\left( {x,x,k,{\rm{ }}1,{\rm{ }}0.5} \right) = x$ 。因为同一个命题必然是最大相吸相关的、等权的，所以必须是h = 1， $\, \beta = 0.5$ 的特殊状态，在一般状态下幂等律不成立。

L2 幂等律 $S\left( {x,x,k,{\rm{ }}1,{\rm{ }}0.5} \right) = x$ 。因为同一个命题必然是最大相吸相关的、等权的。所以必须是h = 1， $\, \beta = 0.5$ 的特殊状态，在一般状态下幂等律不成立。

L3 矛盾律 $T(x,N\left( {x,k} \right){\rm{ }},k,{\rm{ }}0.5,0.5 ) = 0$ 。因为一个命题和它自己的非命题必然是最大相斥相关的，所以必须是 $h =\beta= 0.5$ 的特殊状态，在一般状态下矛盾律不成立。

L4 排中律 $S(x,N\left( {x,k} \right),k,\;0.5,\;0.5 ) = 1$ 。因为一个命题和它自己的非命题必然是最大相斥相关的，所以必须是 $h =\beta= 0.5$ 的特殊状态，在一般状态下排中律不成立。

L5 对合律 $N\left( {N\left( {x,k} \right),k} \right) = x$ 。因为满足对合律的条件是两次非运算的误差系数相等 ${k_1} = {k_2} = k$ ，在 ${k_1} \ne {k_2}$ 的一般状态下，对合律扩张为否定之否定定律(螺旋式上升律) $N\left( {N\left( {x,{k_1}} \right),{k_2}} \right){\rm{ }} = 1 - N\left( {x,{k_3}} \right),{k_3} =$ $ {k_1}\left( {1 - {k_2}} \right)/\left( {{k_1} + {k_2} - 2{k_1}{k_2}} \right)$ 。

L6 MP规则 $T(x,I(x,y,k,h,\beta ),k,h,\beta ) \leqslant y$ 。它在两次 $k,h,\beta $ 相同的特殊状态下成立，如果两组参数 $k,h,\beta $ 不一致，使用MP规则 $T(x,I(x,y,{k_1},{h_1},{\beta _1}){k_2},{h_2},{\beta _2}) \leqslant y$ 是存在风险的。

这些安全使用柔性命题逻辑的必要性条件说明，我们一定要打破在标准逻辑中养成的思维定式，以为选择了一组满足 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ 参数条件的逻辑算子组就可以建立一个逻辑 $\rlap{--} L(k,h,\beta ,{\rm{ }}e)$ ，只要证明了 $\rlap{--} L(k,h,\beta ,\;e)$ 逻辑的可靠性和完备性，就可以放心大胆地使用了。情况没有这么简单，在柔性命题逻辑中这一使用逻辑进行推理的习惯是很不安全的，在构造一个逻辑系统 $\rlap{--} L(k,h,\beta ,\;e)$ 时，还必须明确知道由于每一个逻辑算子都有它对应的不确定性类型属性 $ \left\langle a,{\rm{ }}b,{\rm{ }}e \right\rangle $ 和程度属性 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ ，不能随便使用，所以必须严格准确地把握健全性标准：命题自己和自己一定是最大相吸相关的 $\left( {h = 1} \right)$ 、等权的 $\left( {\beta = 0.5} \right)$ ；命题和自己的非命题一定是最大相斥相关的 $\left( {h = 0.5} \right)$ 、权重互补的(一个是 $\beta $ ，另一个是 $1 - \beta $ )；对合律只能在两次非运算的误差系数相等的情况下使用；MP规则只能在两次 $k,h,\beta $ 相同的特殊情况下使用等。另外，除了特殊需要外，在蕴含运算和等价运算中不能使用加权运算（必须是 $\beta $ =0.5），否则会导出错误结果。这些都是柔性命题逻辑中需要“一把钥匙开一把锁”的重要属性的体现，是泛逻辑研究中的最重大的发现。

4.6 柔性神经元的信息变换过程

由于神经元信息变换模式与逻辑推理模式有一一对应的关系，上述关于柔性命题逻辑的研究成果可用来把M-P神经元模型扩张为连续值神经元(相当于基模型状态)，然后再引入其他各种不确定性，继续扩张为柔性神经元模型(详细见图15)，这里不一一叙述了。

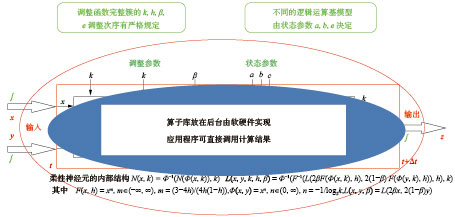
4.7 柔性信息处理完整算子库及其正反向利用方式

1)我们可进一步想象，柔性命题逻辑或者柔性神经元模型本身就是一个关于各种不确定性信息处理的完整的命题级算子库，其中包括了各种可能存在的命题级算子，没有一个遗漏。使用者通过算子的类型属性编码 $ \left\langle a,{\rm{ }}b,{\rm{ }}e \right\rangle $ 可以选择合适的算子簇，再通过算子的不确定性程度属性编码 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ 可在算子簇中选择合适的算子使用(见图16)，保证不会出现乱点鸳鸯谱的现象。尽管这个算子簇的计算过程十分复杂，但是它是确定不变的，可以事先计算好用软硬件形式存放在后台，供应用程序调用直接获得推理结果(如同查对数表或者三角函数表一样)，不必关心具体的计算过程。

2)应用程序使用算子库的两者方式。正向使用算子库的方式是：已知处理对象的因素空间关系网络 $W = \left\{ {{w_i}|i = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \cdots ,{\rm{ }}n} \right\}$ ，其中每一个 ${w_i}$ 都是一个柔性逻辑推理结点或者柔性信息变换的神经元，全部具有算子簇类型属性编码 $ \left\langle {a_i},\;{b_i},\;{e_i} \right\rangle $ 和不确定性程度属性编码 $ \left\langle {k_i},{h_i},{\beta _i},{\rm{ }}{e_i} \right\rangle $ ，根据这些编码参数可从算子库中准确选择相应的算子进行计算，形成精确的结果数据集合 $S = \left\{ {{s_i}|{\rm{ }}i = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \cdots ,{\rm{ }}n} \right\}$ ，反馈给应用程序使用。

反向使用算子库的方式是：已知待识别对象的实测数据集合 $S' = \left\{ {s{'_i}|{\rm{ }}i = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \cdots ,{\rm{ }}n} \right\}$ ，对这些数据进行统计分析和知识挖掘，可获得对象可能具有的因素空间关系网络 $W' = \left\{ {{{w'}_i}|i = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \cdots ,{\rm{ }}n} \right\}$ ，其中每一个 ${{w'}_i}$ 都是一个柔性逻辑推理结点或者柔性信息变换的神经元，具有相应的类型参数 $ \left\langle a'{\rm{ }}b',{\rm{ }}e' \right\rangle $ 和不确定性程度参数 $ \left\langle k',h',b',{\rm{ }}e' \right\rangle $ ，利用这些可能具有的特性参数可从算子库中获得精确的计算结果S = $ \left\{ {{s_i}|{\rm{ }}i = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \cdots ,{\rm{ }}n} \right\}$ 。一般情况下， $S$ 和 $S'$ 之间一定存在偏差，利用某种算法不断消除两者之间的偏差，让 $S$ 不断逼近 $S'$ ，也就是让两个 $ \left\langle a, b, e \right\rangle $ 和 $ \left\langle a',{\rm{ }}b',{\rm{ }}e' \right\rangle $ 不断逼近，两个 $ \left\langle k,h,\beta ,{\rm{ }}e \right\rangle $ 和 $ \left\langle k',h',\beta ',{\rm{ }}e' \right\rangle $ 不断逼近，最后达到准确识别对象客观属性的目的。

这两种使用方式还可在信息处理程序中混合使用。

5 下一步的研究工作 1) 柔性命题逻辑在生成其他逻辑中的作用

上面介绍的是一维空间[0,1]中的柔性命题逻辑，用 $L(x,y,k,h,\beta )$ 表示，它利用升维规则可向上扩张为多维空间 ${\left[ {0,\;1} \right]^n},n = 2,\;3,\;4$ ，代表有n个一维的柔性命题逻辑(见图17)。

例如二维柔性命题逻辑由两个一维柔性命题逻辑定义：

${\mathit{\boldsymbol{L}}^2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},\mathit{\boldsymbol{k}},\mathit{\boldsymbol{h}},\mathit{\boldsymbol{\beta }}} \right) = \left\langle L({x_1},{y_1},k,h,\beta ),L({x_2},{y_2},k,h,\beta ) \right\rangle$

它可以描述不分明概念的前后变迁过程，命题真度在变迁前后都有精确值描述，可上下自由变化。

如果严格满足 ${x_1} \leqslant {x_2},{y_1} \leqslant {y_2}$ 约束，则 ${\mathit{\boldsymbol{L}}^2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},\mathit{\boldsymbol{k}},\mathit{\boldsymbol{h}},\mathit{\boldsymbol{\beta }}} \right)$ 退化为粗糙柔性命题逻辑，命题真度没有精确值，只有上下近似值区间的约束^[30]。

三维柔性命题逻辑由3个一维柔性命题逻辑定义：

$\begin{array}{c}{\mathit{\boldsymbol{L}}^3}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},\mathit{\boldsymbol{k}},\mathit{\boldsymbol{h}},\mathit{\boldsymbol{\beta }}} \right) = \langle L\left( {{x_1},{y_1},k,h,\beta } \right),\\L\left. {\left( {{x_2},{y_2},k,h,\beta } \right)} \right),L\left( {{x_3},{y_3},k,h,\beta } \right) \rangle \end{array}$

它可以描述不分明概念的历史变迁过程，命题真度在变迁前、现在、未来都有精确值描述，可上下自由变化。

如果严格满足 ${x_1} \leqslant {x_2} \leqslant {x_3},{y_1} \leqslant {y_2} \leqslant {y_3}$ 的约束，则 ${\mathit{\boldsymbol{L}}^3}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},\mathit{\boldsymbol{k}},\mathit{\boldsymbol{h}},\mathit{\boldsymbol{\beta }}} \right)$ 退化为容差柔性命题逻辑，它有一个精确的数学期望值 ${x_2}$ 和 ${y_2}$ ，还允许有下偏差 ${x_1}$ 和 ${y_1}$ ，上偏差 ${x_3}$ 和 ${y_3}$ ，如此等等。

利用降值规则可通过一维柔性命题逻辑生成离散值命题逻辑，如三值逻辑 $\left\{ {0,{u} ,{\rm{1}}} \right\}$ 、五值逻辑等等。

2) 柔性命题逻辑 ${\mathit{\boldsymbol{L}}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{ y}}},{\mathit{\boldsymbol{k}}},{\mathit{\boldsymbol{h}}}} \right)$ 中可能包含更多的非标准逻辑

对柔性命题逻辑 ${\mathit{\boldsymbol{L}}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{ y}}},{\mathit{\boldsymbol{h}}}} \right)$ 的相容部分我们研究比较透彻，相克部分比较初步，对于 ${\mathit{\boldsymbol{L}}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{ y}}},{\mathit{\boldsymbol{k}}},{\mathit{\boldsymbol{h}}}} \right)$ 逻辑，整个研究都比较初步，只知道其中包含了可能推理、似然推理、信任推理和必然推理^[31]，相克逻辑群也有广阔的空间可以发展(见图18)，这些都需要进一步研究。

3) 在柔性命题逻辑基础上建立柔性谓词逻辑，实现辩证逻辑的数学化

关键是定义各种柔性量词，用数学方法描述各种辩证逻辑规律，这需要进一步深入长期的研究^[32]。

6 结束语

从这些研究成果可以看出，数理形式逻辑（即标准逻辑，简称刚性逻辑）在理论上没有错误，不应该像某些人鼓吹的那样“推翻重建”。但是也应该看到，尽管数理形式逻辑可描述和解决所有满足“非此即彼性”约束的理想化问题，是一个通用性的逻辑工具（万能钥匙）。可是在面对智能信息处理中大量且普遍存在的、具有“亦此亦彼性”特征的现实问题时，它是无能为力的，必须有针对性地建立各种数理辩证逻辑（即泛逻辑，简称柔性逻辑）。建立数理辩证逻辑的基本途径和方法是在数理形式逻辑基础上，逐步放开某些方面的“非此即彼性”约束，引入相应的“亦此亦彼性”。本文的研究结果表明，这条研究途径是可行的，也证明了正确使用数理辩证逻辑的基本要求是：必须严格地贯彻辨证施治的原则，精确地利用“一把钥匙开一把锁”的方法解决问题。