2. 南京邮电大学 自动化学院,江苏 南京 210003
2. College of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
符号网络是指边具有正或负符号属性的网络,符号为正表示网络中两节点间具有相互信任的、积极的朋友关系,负边则表示不信任的、消极的敌对关系。具有符号属性的网络普遍存在[1],研究链路的符号属性有利于理解网络的基本结构特征,理解信任和不信任的传播方式。另外,社会符号网络的边符号属性能够直接反映节点间的态度,因此在推荐系统[2]、舆情分析与观点形成[3]、网络欺凌与社会排斥[4]等问题中均能通过符号分析获得应用。符号网络的研究始于Heider[5]基于社会心理学对人类关系的研究,而随着复杂网络研究兴起,符号网络的结构特征与演化规律受到更多研究者的关注[6-7],如何通过部分观测到的网络符号预测未知的边符号成为符号网络中非常重要的研究方向。
符号预测方法大致可以分为两类:1)考虑网络局部特征的方法;2)考虑网络全局特征的方法。考虑网络局部特征的方法主要利用节点的邻域特征,如:节点出边、入边的符号以及相邻三元组各边标注符号特征进行符号预测。这类方法主要基于网络局部特征以及社会学相关理论实现边符号的预测,所有基于弱结构平衡[8]和地位理论[9]的预测方法均要求两节点间具有共同邻居时算法才有效,但统计结果发现,现实的符号网络中有很大比例的节点不能构成三元组。Guha等[10]最早基于网络模型研究符号预测问题,他们将信任网络表示为矩阵并运用不同的矩阵运算代表信任关系在网络上的不同传播方式,实现了信任关系的预测。Leskovec等[11]采用机器学习的方法对符号预测问题进行了研究,他们利用节点的出度、入度、节点的嵌入性以及基于地位理论的所有16种待预测边所处的三角形的关系模式作为特征采用逻辑回归模型训练分类器,得到了较高的预测精度。文献[12]则通过网络局部特征和地位理论为特征采用SVM算法进行二值分类实现符号预测。相对于Leskovec考虑长度为3的有序环构建的网络特征,Chiang等[13]利用Katz指标提出一个不平衡测度指标并通过长度为
受以上研究的启发,从真实网络数据的统计分析出发,结合节点局部标注特征和网络全局结构特征设计了一种新的基于低秩矩阵分解的符号预测模型,解决了符号网由于数据稀疏和网络局部特征利用不足带来的预测精度不高的问题。
1 相关理论 1.1 基本定义定义符号网络
| ${A_{ij}} = \left\{ \begin{array}{l}1,\quad i{\text{与}}j{\text{之间有正边}}\\0,\quad {\text{边符号未知或不存在边}}\\ - 1,\quad i{\text{与}}j{\text{之间有负边}}\end{array} \right.$ |
符号网络G可能为有向图也可能为无向图,当G为有向图时A为非对称矩阵,若G为无向图则A为对称矩阵。
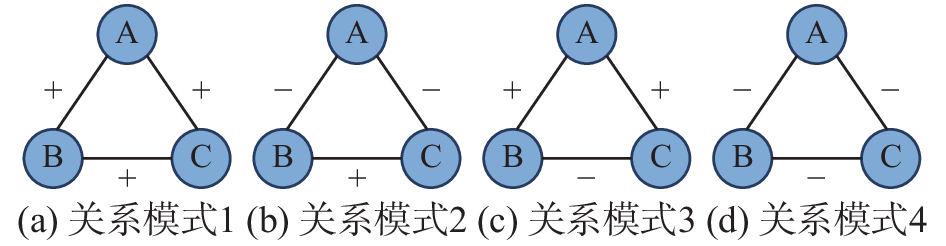
1.2 结构平衡与弱结构平衡理论结构平衡理论把人与人之间的关系分为积极和消极两种,被形式化地描述为符号网络,边的正、负符号分别表示积极关系和消极关系。此时符号网络中3个节点间的关系共形成4种三角形模体,如图1所示。从社会心理学角度看,以下结论成立:朋友的朋友是朋友;朋友的敌人是敌人。据此判定图1(a)、(b)是平衡的,而图1(c)、(d)是不平衡的。不平衡的结构具有向平衡结构转换的趋势。在三角形模体中判断局部平衡性时可以通过三条边符号之积来实现:三符号积为正则平衡,否则不平衡。Cartwright和Harary[20]将Heider[2]的社会学结论形式化地描述为图结构并证明符号网络平衡的充分必要条件是:网络中的节点能够被划分为两个子集,每个子集内的所有边均为正,子集间的边均为负。
|
Download:
|
| 图 1 符号网中4种三角形关系模式 Fig. 1 Four relationship patterns of triads in signed network | |
平衡网络的判别条件比较严苛,现实中很难找到平衡网络的情形,因此Davis[8]放宽结构平衡的约束提出了弱结构平衡理论,弱结构平衡理论规定:只要三角形模体中不存在两正一负的关系就构成弱平衡,在该条件下,图1(a)、(b)、(d)代表的情形均可看作平衡的结构。当网络满足弱平衡结构时,节点可以被分成
根据弱结构平衡的定义,当符号网络满足
图2(a)给出了一个满足弱平衡网的示例,图中8个节点被分成3个子集,图2(b)为图2(a)对应的邻接矩阵A,若补齐图2(a)中缺失的边,使其成为完全图,该图对应的邻接矩阵为块对角矩阵X,块内很明显矩阵的秩

|
Download:
|
| 图 2 弱平衡结构与矩阵的低秩特性 Fig. 2 Weakly balanced network and low-rank structure | |
因此可以把符号预测问题看作矩阵填充问题:已知被部分观测到的矩阵
| $\begin{array}{l}\begin{array}{*{20}{c}}{\min } & {{\rm{Rank}}({{X}})}\end{array}\\\begin{array}{*{20}{c}}{{\rm{s}}{\rm{.t}}{\rm{.}}} & \begin{array}{l}{X_{ij}} = {A_{ij}},\forall e(i,j) \in O,\\{X_{ij}} \in \{ \pm 1\} ,\forall e(i,j) \notin O\end{array}\end{array}\end{array}$ | (1) |
式(1)的目标函数是
当符号预测被近似为低秩矩阵分解问题时,邻接矩阵
| $\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\! {\mathop {\min }\limits_{{{{P}}^{\rm{T}}},{{Q}} \in {\mathbb{R}^{k \times n}}} }{C = \displaystyle\sum\limits_{e(i,j) \in {\rm O}} {l({A_{ij}},\sum\limits_{k = 1}^\kappa {{P_{ik}}{Q_{kj}}} )} + \lambda {{\left\| {{P}} \right\|}^2} + \lambda {{\left\| {{Q}} \right\|}^2}} \end{array}$ | (2) |
式(2)中l为损失函数用于评价预测值与原矩阵间的误差,后两项为正则化项,用来防止过拟合损失函数,可根据具体问题进行选择。虽然上式是非凸的,但是实践证明该方法在很多矩阵填充问题中均取得了很好的预测效果。
基本矩阵分解模型充分利用了邻接矩阵的全局低秩特性,但是,在被符号网络所代表的社会关系网中,不同节点的标注行为常常具有偏置现象:网络“喷子”也被称为“Troll”的节点,该类节点为引起别人的注意会故意攻击其他人,“Troll”节点会发出比其余节点更多的负边;与此相对应的,有些节点会收到低于平均水平的评价,它们可能受到“网络欺凌”,这一现象的社会心理学根源是“认知失调”,人们通常为保持与他人态度的一致而调整自己的行为因此而攻击收到过负面评价的人。从真实符号网络的统计特征发现,这两类节点在符号网中确实存在,虽然数量不多但其作用巨大。在符号预测问题中仅考虑平均后的全局特征并不能完全反映网络结构特征,节点的局部标注特征需要在预测模型中得以体现。现定义待预测边的局部标注特征为
| ${b_{ij}} = \mu + U{i_{\rm{out}}} + U{j_{\rm{in}}}$ | (3) |
式中:

|
Download:
|
| 图 3 标注行为的偏置现象 Fig. 3 Bias behavior of signed edges | |
| $\begin{array}{c}\mathop {\min }\limits_{{{{P}}^{\rm{T}}},{{Q}} \in {{\mathbb{R}}^{k \times n}}} C = \displaystyle\sum\limits_{e(i,j) \in {\rm O}} {l({A_{ij}} - ({b_{ij}} + \sum\limits_{k = 1}^\kappa {{P_{ik}}{Q_{kj}})} } ) + \\\;\;\;\;\;\;\;\;\lambda (\left\| {{P}} \right\|_1^2 + \left\| {{Q}} \right\|_1^2 + U{i_{\rm{out}}}^2 + U{j_{\rm{in}}}^2)\end{array}$ | (4) |
根据式(4)可知:节点i对节点j的符号可被预测为
损失函数l可以有多种选择,本文选择Square_loss为损失函数,于是优化目标函数可写成:
| $\begin{array}{c}\mathop {\min }\limits_{{{{P}}^{\rm{T}}},{{Q}} \in {{\mathbb{R}}^{k \times n}}}C = {\displaystyle\sum\limits_{e(i,j) \in {\rm O}} {\left\| {{A_{ij}} - ({b_{ij}} + \sum\limits_{k = 1}^\kappa {{P_{ik}}{Q_{kj}})} } \right\|} ^2} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda (\left\| {{P}} \right\|_1^2 + \left\| {{Q}} \right\|_1^2 + U{i_{\rm{out}}}^2 + U{j_{\rm{in}}}^2)\end{array}$ | (5) |
对式(5)给出的优化问题可以采用随机梯度下降法进行求解,令
| ${P_i} \leftarrow {P_i} + \alpha ({e_{ij}}{Q_j} - \lambda {P_i})$ | (6) |
| ${Q_j} \leftarrow {Q_j} + \alpha ({e_{ij}}{P_i} - \lambda {Q_j})$ | (7) |
| $U{i_{\rm{out}}} \leftarrow U{i_{\rm{out}}} + \alpha ({e_{ij}} - \lambda U{i_{\rm{out}}})$ | (8) |
| $U{j_{\rm{in}}} \leftarrow U{j_{\rm{in}}} + \alpha ({e_{ij}} - \lambda U{j_{\rm{in}}})$ | (9) |
通过反复迭代并不断优化参数,使观测矩阵A与分解后矩阵
实验中的3个真实大型社会网络数据来自于斯坦福大学的SNAP2项目,Epinions给出了用户间“who-trust-whom”的关系,Slashdot是一个技术相关的新闻网站,允许用户根据自身观点标记其他用户为friend/foe,Wikipedia是维基百科申请管理员身份的投票关系网,若一个用户被大多数其他用户同意则当选为某一学科的管理员负责百科词条的维护,若该用户未受到大多数其他用户的赞成票则选举失败。表1给出了3个网络的统计特征。
| 表 1 数据集统计特征 Tab.1 Statistics of datasets |
表1的统计结果显示:3个符号网络中正边占比均在75%以上,而负边占比较少,互惠边(reciprocal edges)是指两用户间持有相同态度,这样的互惠边在网络中占有一定比例,且互惠边中正边居多,这与人们社会心理有关,当一个人讨厌另一个人反应的是不予理睬,“爱的反义词不是恨而是冷漠”。而一个人对另一个人的示好通常显示出“镜子效应”。统计结果还发现:发出50%以上负边的节点只占网络节点极少部分,且大部分的负边都是由一些特定节点发出的,这些节点充满反社会特征,并通过攻击别人博取别人的关注,这些节点发出的新边为负的可能性极大,而收到50%以上负边的节点也的确存在,即“网络欺凌”是事实,存在“人云亦云”的现象。统计结果还显示,符号网络中有一定比例的节点无法构成三元组,此时基于结构平衡理论的预测算法将失效。
3.2 预测效果与分析为证明所提带有偏置的矩阵分解模型MF-Bias (matrix factorization with bias)对符号预测问题的有效性,将它与以下基准预测算法进行比较。
1) OutDegree(简写为OD):若
2) InDegree(简写为ID):若
3) LR (logistic regression)[11]:将符号预测问题看作二值分类问题,采用逻辑回归模型训练分类器,得到了较高的预测精度。
4) MF(matrix factorization)[17]:由Hsieh等提出的基本矩阵分解模型。
3.2.1 评价指标1)均方根误差(RMSE)
它是衡量模型误差率的常用方法,反映了观测值与真值偏差的平方和观测次数n比值的平方根,计算公式为
| ${\rm{RMSE}} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^n {{{({p_i} - {a_i})}^2}} }}{n}} $ | (10) |
式中:
2)精确性(Accuracy)
用于评价预测算法对符号预测的准确程度,精确性计算公式为
| ${\rm{Accuracy}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{P + N}}$ | (11) |
式中:
|
Download:
|
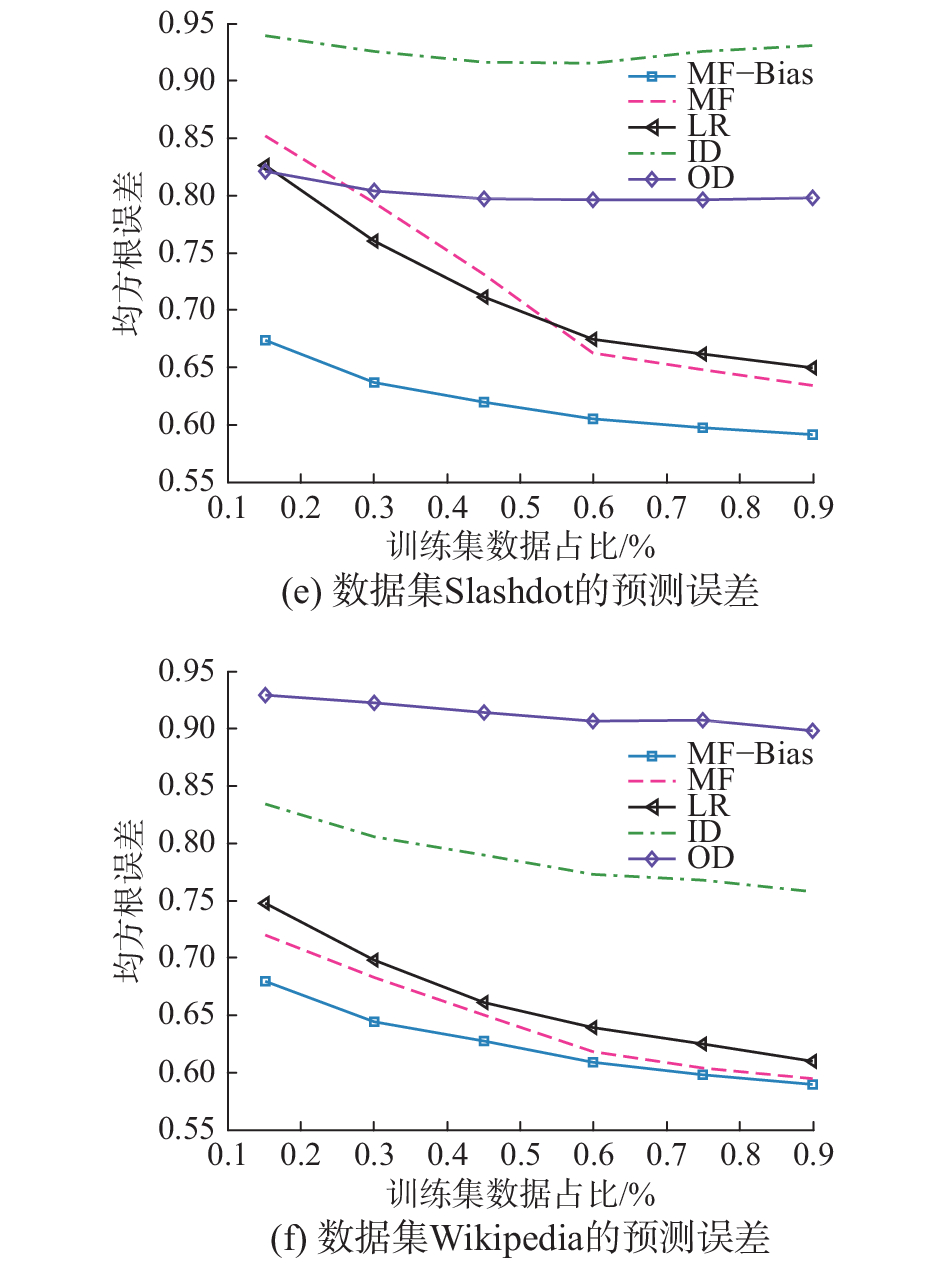
| 图 4 3个符号网络的预测结果 Fig. 4 Three signed networks predicted results | |
给定部分观察的符号网络,符号推断的目标就是通过符号网中已知边符号推断出未知边的符号。本文构建的符号网络模型为有向网络,需要说明的是,所提算法也适用于无向符号网络。实验采用随机抽样的方法将数据集分为训练集(training data set)和测试集(testing data set)。训练集被看作部分观测的符号网络,利用测试集训练模型,然后对测试集中边符号进行预测;测试集分别为整个符号网络的15%,30%,
图4的实验结果显示:随着抽样数据的增加,预测误差(RMSE)减小,预测精确度增加。基于低秩矩阵分解的方法(包括MF、MF-Bias)获得了比其他算法更好的预测效果,这说明在符号网络中节点标注的偏置现象确实存在,同时,由于MF-Bias充分考虑了节点的局部偏置特性,得到了相较于基本矩阵分解算法好的预测精度,例如:在数据集Epinions上当训练集为90%时,预测精确度为95.04%,相较于基本矩阵分解方法提高了0.6%,LR方法提高了2.3%,在其他两个数据集上也得到了与图4(a)相似的结果(见图4(b)~(c)),RMSE误差分析结果(见图4(d)~(f))与预测精确度得到相似的结论:本文所提MF-Bias模型获得了最小预测误差。实验表明:带有偏置的矩阵分解方法能够很好地对抗数据稀疏带来的问题并提高预测效果。尽管两种启发式算法(ID和OD)的预测精度都低于矩阵分解模型和逻辑回归模型,但是它们的特点是计算复杂度低,因为它们仅仅使用待预测边两端节点的局部信息且能在一定程度上反映数据的结构特性。不同数据集ID和OD的效果截然不同,在Slashdot上OD好于ID,在Wiki上ID好于OD,可见仅考虑出度或入度作为预测依据不够合理,用户在不同数据集上的行为特征值得进一步思考。
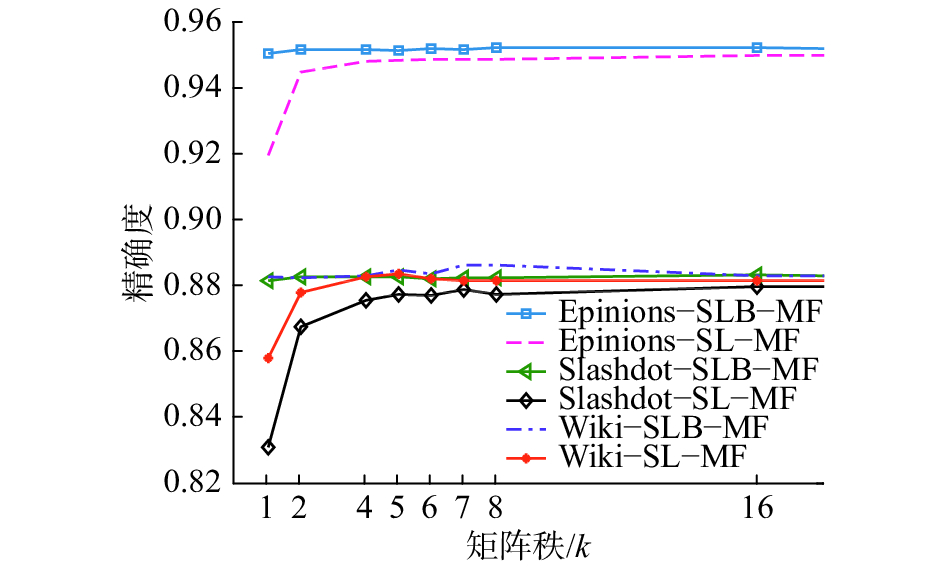
3.3 秩与预测精度根据1.3节可知,符号网络邻接矩阵的秩与弱平衡结构间存在必然联系:当符号网络满足
|
Download:
|
|
图 5 预测精度与矩阵的秩
|
|
真实的复杂系统中对立关系普遍存在,利用符号网络对这些复杂系统建模能够很好地表达节点间的对立关系,符号属性对分析、理解复杂网络的拓扑结构、功能、动力学行为具有十分重要的理论意义。要利用符号属性,首要的问题就是对未知边符号的正确预测。本文对已有的符号网络预测方法进行了分类和总结。为了同时利用节点的局部特征和全局特征进行符号预测,在基于利用网络全局特征的低秩矩阵分解方法的基础上改写优化目标函数使之能够描述待预测边两端节点的出度和入度局部特征,给出了带有偏置的低秩矩阵分解方法。实验结果证实:添加节点局部特征后的低秩矩阵分解方法能够得到较其他基准算法好的预测效果,且互惠信息能够进一步提高预测精度。
未来符号预测的研究方向会向两个不同方向发展:1)进一步利用丰富的元数据信息,因为元数据蕴含了用户间的熟识度、声誉、语义与态度等重要信息,元数据可以在缺少结构信息时保证预测精度,当然付出的代价是模型复杂度升高,运算速度降低;2)降低模型复杂度以适应于数量巨大的在线符号网络挖掘,此时基于网络局部信息的符号预测方法具有优势,因为这类算法易于被并行化,从而提高运算速度,当然负面影响会带来一定预测效果的下降。如何充分利用局部信息的研究还显得不足,如节点间除了出度和入度还有哪些连接特点能用结构平衡理论或地位理论来解释。当节点间的嵌入性很低时结构平衡等社会学理论将失效,怎样保证预测的精确度?
另外,还需进一步丰富符号网络结构的理论研究,目前用于符号预测的理论只有结构平衡理论和地位理论,近年并未有较大突破。也就是说,对符号网络结构演化、动力学行为的分析仍然不能解释符号网络结构的形成,从而制约了符号预测方法的进一步发展,根据3.3节的研究发现本文所提算法对矩阵的秩鲁棒,及在秩取5和7时预测效果最好,这一结果的深层社会学理论含义及其与符号网络形成机制间的联系将另文讨论。这也是下一步将要研究的内容。
符号网络作为近年来从基本复杂网络衍生出的新网络模型和符号预测问题作为新模型上的新问题,人们对它们的理解还远远不够,符号网络的拓扑结构、动力学行为以及在个性化推荐、态度预测、用户特征分析与聚类等方面的应用将会受到更多的研究和关注。
| [1] |
程苏琦, 沈华伟, 张国清,等. 符号网络研究综述[J]. 软件学报, 2014, 25(1): 1-15. CHENG Suqi, SHEN Huawei, ZHANG Guoqing et al. Survey of signed network research[J]. Journal of software, 2014, 25(1): 1-15. (  0) 0)
|
| [2] |
TANG Jiliang, AGGARWAL C, LIU Huan. Recommendations in signed social networks[C]//Proceedings of the 25th International Conference on World Wide Web. Montréal, Canada, 2016: 31–40.
( 0) 0)
|
| [3] |
LI Dong, XU Zhiming, CHAKRABORTY N, et al. Polarity related influence maximization in signed social networks[J]. PLoS one, 2014, 9(7): e102199. DOI:10.1371/journal.pone.0102199 ( 0) 0)
|
| [4] |
EVERETT M G, BORGATTI S P. Networks containing negative ties[J]. Social networks, 2014, 38: 111-120. DOI:10.1016/j.socnet.2014.03.005 ( 0) 0)
|
| [5] |
HEIDER F. Attitudes and cognitive organization[J]. The Journal of psychology: interdisciplinary and applied, 1946, 21(1): 107-112. DOI:10.1080/00223980.1946.9917275 ( 0) 0)
|
| [6] |
SZELL M, LAMBIOTTE R, THURNER S. Multirelational organization of large-scale social networks in an online world[J]. Proceedings of the national academy of sciences of the United States of America, 2010, 107(31): 13636-13641. DOI:10.1073/pnas.1004008107 ( 0) 0)
|
| [7] |
CHU Lingyang, WANG Zhefeng, PEI Jian, et al. Finding gangs in war from signed networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, USA, 2016: 1505–1514.
( 0) 0)
|
| [8] |
DAVIS J A. Clustering and structural balance in graphs[J]. Human relations, 1967, 20(2): 181-187. DOI:10.1177/001872676702000206 ( 0) 0)
|
| [9] |
LESKOVEC J, HUTTENLOCHER D, KLEINBERG J. Signed networks in social media[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. Atlanta, USA, 2010: 1361–1370.
( 0) 0)
|
| [10] |
GUHA R, KUMAR R, RAGHAVAN P, et al. Propagation of trust and distrust[C]//Proceedings of the 13th International Conference on World Wide Web. New York, USA, 2004: 403–412.
( 0) 0)
|
| [11] |
LESKOVEC J, HUTTENLOCHER D, KLEINBERG J. Predicting positive and negative links in online social networks[C]//Proceedings of the 19th International Conference on World Wide Web. Raleigh, USA, 2010: 641–650.
( 0) 0)
|
| [12] |
WANG Guannan, GAO Hui, CHEN Lian, et al. Predicting positive and negative relationships in large social networks[J]. PLoS one, 2015, 10(6): e0129530. DOI:10.1371/journal.pone.0129530 ( 0) 0)
|
| [13] |
CHIANG K Y, NATARAJAN N, TEWARI A, et al. Exploiting longer cycles for link prediction in signed networks[C]//Proceedings of the 20th ACM international Conference on Information and Knowledge Management. Glasgow, Scotland, UK, 2011: 1157–1162.
( 0) 0)
|
| [14] |
蓝梦微, 李翠平, 王绍卿, 等. 符号社会网络中正负关系预测算法研究综述[J]. 计算机研究与发展, 2015, 52(2): 410-422. LAN Mengwei, LI Cuiping, Wang Shaoqing, et al. Survey of sign prediction algorithms in signed social networks[J]. Journal of computer research and development, 2015, 52(2): 410-422. DOI:10.7544/issn1000-1239.2015.20140210 (  0) 0)
|
| [15] |
SONG Dongjin, MEYER D A. Link sign prediction and ranking in signed directed social networks[J]. Social network analysis and mining, 2015, 5: 52. DOI:10.1007/s13278-015-0288-7 ( 0) 0)
|
| [16] |
KUNEGIS J, SCHMIDT S, LOMMATZSCH A, et al. Spectral analysis of signed graphs for clustering, prediction and visualization[C]//Proceedings of the 2010 SIAM International Conference on Data Mining. Columbus, USA, 2010: 559–570.
( 0) 0)
|
| [17] |
HSIEH C J, CHIANG K Y, DHILLON I S. Low rank modeling of signed networks[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China, 2012: 507–515.
( 0) 0)
|
| [18] |
MENON A K, ELKAN C. Link prediction via matrix factorization[C]//Proceedings of the 2011 European Conference on Machine Learning and Knowledge Discovery in Databases. Athens, Greece, 2011: 437–452.
( 0) 0)
|
| [19] |
AGRAWAL P, GARG V K, NARAYANAM R. Link label prediction in signed social networks[C]//Proceedings of the 23rd International Joint Conference on Artificial Intelligence. Beijing, China, 2013: 2591–2597.
( 0) 0)
|
| [20] |
CARTWRIGHT D, HARARY F. Structural balance: a generalization of Heider’s theory[J]. Psychological review, 1956, 63(5): 277-293. DOI:10.1037/h0046049 ( 0) 0)
|
| [21] |
CANDÈS E J, TAO T. The power of convex relaxation: near-optimal matrix completion[J]. IEEE transactions on information theory, 2010, 56(5): 2053-2080. DOI:10.1109/TIT.2010.2044061 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


