专家系统[1]作为一种人工智能系统,已经被广泛应用于图像处理、医疗检测、地质勘探、石油化工等领域。利用专家系统进行决策时,需要先将有用的信息表示成知识,知识的表示形式有很多种,其中应用最广泛的是产生式规则,即IF-THEN规则。置信规则(belief rule)是在传统IF-THEN规则的结果部分加入置信分布转化而来的,由一组置信规则组成的集合称为置信规则库(belief rule base, BRB)。置信规则对应的是系统的输入信息,而实际工程中包含的信息既可能是定性知识也可能是定量数据,同时,信息中往往存在着含糊或模糊不确定性、不精确性以及不完整性。为了能够有效利用带有这些不确定性的信息,Yang等[2]于2006年在D-S证据理论[3-4]、决策理论[5]、模糊理论[6]和传统的IF-THEN规则库基础上提出了基于证据理论的置信规则库推理方法(belief rule-base inference methodology using the evidential reasoning approach, RIMER)。RIMER方法作为BRB系统的核心,能够对具有线性或非线性关系的输入和输出进行建模,具有处理各种不确定性的能力。目前,BRB系统已被广泛应用到输油管道泄漏[7-8]、石墨成分检测[9]、消费者偏好预测[10]、军事能力评估[11]和出租车乘车概率预测[12]等领域。
利用BRB系统对实际问题进行建模时,要先确定其内部参数的取值,各个参数的不同取值会对BRB系统的推理能力造成一定的影响,传统的参数取值确定方法是专家根据经验给定其值,但当参数个数较多或系统较复杂时,专家很难确定参数取值。鉴于此,Yang等[10]最先提出一种通用的BRB参数学习模型,该模型以满足各个参数约束条件为基础,通过最小化由置信规则库推理得出的模拟输出值和真实数据的输出值二者的差值来训练BRB参数。在Yang的基础上,Chen等[13]提出了包括前提属性参考值在内的全局参数学习方法。不过以上两种参数学习方法均是建立在MATLAB工具自带的FMINCON函数的基础上,参数学习效率不高。鉴于此,常瑞等[14]、吴伟昆等[15]提出结合梯度下降法的BRB参数学习方法,这种方法虽然优于FMINCON函数,但其涉及的公式推导过于复杂,只能训练少量的参数,不适合用来学习大量的参数,且参数学习的收敛速度过慢。为了提高BRB系统参数学习的收敛速度和精度,苏群等[16]、王韩杰等[17]相继提出基于群智能算法的参数学习方法。以上参数学习方法均能够优化BRB参数取值,从而提高BRB的推理能力,但是,这些参数学习方法都是建立在Yang等[10]提出的参数学习模型基础上的,无法避免重复的搜索过程,需要不断地进行迭代。此外,因为BRB系统构建时需要覆盖所有的前提属性的参考值,当前提属性和前提属性参考值过多时,会出现“组合爆炸”问题。为了解决该问题,专家学者们提出了各自的降维方法:Zhou等[18]提出“统计效用”的概念,根据每条规则的统计效用值来确定是否删减该规则,如果某条规则的统计效用值越小,说明该规则对整体系统的贡献越小,就可以将其删除;Chang等[19]提出利用灰靶理论、多维尺度变换、主成分分析来选择关键前提属性,从而减少前提属性的数量;王应明等[20]引入粗糙集理论,提出客观的规则约简方法,该方法不需要借助BRB以外的任何先验知识。这些BRB结构优化方法虽然可以在一定程度上避免组合爆炸问题,但是会降低BRB的推理能力。为了从根本上解决BRB参数取值以及组合爆炸问题,Liu等[21]对原有的置信规则进行扩展,在规则的前件部分也加入置信分布,提高其对含糊、不完整和不确定信息的表示能力,改进后的规则库被称为扩展置信规则库(extended belief rule base, EBRB)。同时,Liu等[21]还提出了一种简单且有效直接利用训练数据生成初始扩展置信规则的规则生成机制,数据驱动型的规则生成机制可以详细表示出数据中包含的各种信息,不需要进行反复迭代的参数学习过程也不会造成组合爆炸问题。但正因为扩展置信规则是根据训练数据集得到的,数据集的质量对EBRB系统的推理能力影响要更大,相互矛盾、不一致的数据容易降低EBRB的推理准确性。在EBRB中,数据的不一致是指两条或多条规则的前提属性取值大致相同,但评价结果却完全不同或与专家知识相冲突。
针对EBRB系统中的数据不一致性的问题,Alberto等[22]提出动态规则激活方法,该方法通过调整改进后的相似性度量公式中的参数来选择不一致性最小的激活规则集合,不过,该方法中用于衡量激活规则集合不一致性的公式只考虑了规则数量对其的影响,没有考虑规则激活权重对其的影响。要减小激活规则集合之间的不一致性,最简单的方法就是舍弃部分不一致性较高的激活规则,这部分激活规则不参与最终的合成推理过程,但这部分激活规则可能带有重要的信息,而且很难确定这部分激活规则的具体数量。为了减小激活规则集合的不一致性同时保留激活规则集合中的大部分重要信息,本文提出了基于NSGA-II的扩展置信规则库激活规则多目标优化方法,将激活规则的不一致性与激活权重和分别作为目标函数,通过求解多目标优化问题获得相对较优的激活规则集合并用于最终的合成推理。本文首先介绍扩展置信规则库和多目标优化问题的基础知识,然后介绍如何利用NSGA-II求解Pareto的最优解,最后通过非线性函数问题和输油管道检漏实例对所提方法进行实验验证,并分析说明所提方法的有效性和可行性。
1 扩展置信规则库系统与问题提出 1.1 扩展置信规则生成扩展置信规则库由一系列扩展置信规则(extended belief rule)组成,其中第
| $\begin{array}{l}\!\!\!\!\!\! {R_k}:{\rm{if}}\left\{ {{{A,}}{{{\alpha }}^{{k}}}} \right\}{\rm{then}}\left\{ {\left( {{D_1},{\beta _1}^k} \right),\left( {{D_2},{\beta _2}^k} \right),\cdots,\left( {{D_N},{\beta _N}^k} \right)} \right\}\\\!\!\!\!\!\! {\rm{with}}{\rm{ \;a \;rule\; weight \;}}{\theta _{\rm{k}}}{\rm{\;and \;attribute\; weight \;}}{\delta _i}\end{array}$ | (1) |
式中:
与BRB系统复杂烦琐的规则生成机制不同,Liu等[21]提出的规则生成机制简单且有效,可直接将训练数据转化为扩展置信规则。假设
| ${\gamma _{i,j}}{\text{ means }}{{{A}}_{i,j}}$ | (2) |
然后,将输入
| $S({x_i}) = \{ ({\gamma _{i,j}},{\alpha _{i,j}}),i = 1,2,\cdots,{T_k},j = 1,2,\cdots,{J_i}\} $ | (3) |
式中
| ${\alpha _{i,j}} = \frac{{{\gamma _{i,j + 1}} - {x_i}}}{{{\gamma _{i,j + 1}} - {\gamma _{i,j}}}},{\gamma _{i,j}} \leqslant {x_i} \leqslant {\gamma _{i,j + 1}},j = 1,2,\cdots,{J_i} - 1$ | (4) |
| ${\alpha _{i,j + 1}} = 1 - {\alpha _{i,j}},{\gamma _{i,j}} \leqslant {x_i} \leqslant {\gamma _{i,j + 1}},j = 1,2,\cdots,{J_i} - 1$ | (5) |
| ${\alpha _{i,{\text{s}}}} = 0,s \ne j,j + 1,s = 1,2,\cdots,{J_i}$ | (6) |
通过式(4)~(6)可得到
假设第
| $d_i^k = \sqrt {\sum\limits_{j = 1}^{{J_i}} {{{(\alpha _{i,j} - \alpha _{i,j}^k)}^2}} } $ | (7) |
则
| $S_i^k = 1 - d_i^k$ | (8) |
第
| $\omega _k = \frac{{{\theta _k}\displaystyle\prod\limits_{i = 1}^{{T_k}} {{{(S_i^k)}^{\overline \delta_i}}} }}{{\sum\limits_{l = 1}^L {\left[ {{\theta _l}\displaystyle\prod\limits_{i = 1}^{{T_k}} {{{(S_i^l)}^{\overline \delta_i}}} } \right]} }},\overline \delta_i = \frac{{{\delta _i}}}{{\mathop {\max \{ {\delta _i}\} }\limits_{i = 1,2,\cdots,{T_k}} }}$ | (9) |
式中:
用证据推理方法(evidential reasoning, ER)[23]得到推理结果前,要先按式(10)~(13)计算评价结果置信度的基本可信值:
| $m_{n,i}{\text{ = }}\omega _i\beta _{n,i}$ | (10) |
| $m_{H,i} = 1 -\omega _i\sum\limits_{n = 1}^N {\beta _{n,i}} = \overline m _{H,i} + \tilde m _{H,i}$ | (11) |
| $\tilde m _{H,i} = \omega _i(1 - \sum\limits_{n = 1}^N {\beta _{n,i}} )$ | (12) |
| $\overline m _{H,i} = 1 - \omega _i$ | (13) |
式中:
| $C_n{\text{ = }}k\left[ {\prod\limits_{j = 1}^L {(m _{n,j} + \overline m _{H,j} + \tilde m _{H,j}) - \prod\limits_{j = 1}^L {(\overline m _{H,j} + \tilde m _{H,j})} } } \right]$ | (14) |
| $ {\tilde C_H} {\text{ = }}k\left[ {\prod\limits_{j = 1}^L {(\overline m _{H,j} + \tilde m _{H,j}) - \prod\limits_{j = 1}^L {\overline m _{H,j}} } } \right]$ | (15) |
| $ {\overline C_H} {\text{ = }}k\prod\limits_{j = 1}^L {\overline m _{H,j}} $ | (16) |
| ${k^{ - 1}}{\text{ = }}\sum\limits_{n = 1}^N {\prod\limits_{j = 1}^L {(m _{n,j} + \overline m _{H,j} + \tilde m _{H,j}) - (N - 1)\prod\limits_{j = 1}^L {(\overline m _{H,j} + \tilde m _{H,j})} } } $ | (17) |
| $\beta _n = \frac{{{C_n}}}{{1 - {C_H}}},\,n = 1,2,\cdots,N$ | (18) |
| $\beta _H = \frac{{{{\tilde C}_H}}}{{1 - {C_H}}}$ | (19) |
根据式(14)~(19)可得到式(20)所示的具有置信分布形式的BRB推理输出:
| $f(x) = \{ ({D_n},\beta _n),n = 1,2,\cdots,N\} $ | (20) |
基于上述ER解析算法,Wang等[25]进一步推导出了组合所有的置信规则的计算公式,即
| $\beta _j = \frac{{\mu \times \left[ {\displaystyle\prod\limits_{k = 1}^L {({\omega _k}\beta _{j,k} + 1 - {\omega _k}\sum\limits_{i = 1}^N {\beta _{i,k}} ) - \prod\limits_{k = 1}^L {(1 - {\omega _k}\sum\limits_{i = 1}^N {\beta _{i,k}} )} } } \right]}}{{1 - \mu \times \left[ {\displaystyle\prod\limits_{k = 1}^L {(1 - {\omega _k})} } \right]}}$ | (21) |
| $\begin{array}{c}\mu = \left[ {\sum\limits_{j = 1}^N {\prod\limits_{k = 1}^L {({\omega _k}{\beta _{j,k}} + 1 - {\omega _k}\sum\limits_{i = 1}^N {{\beta _{i,k}}} ) - } } } \right.\\{\left. {(N - 1)\prod\limits_{k = 1}^L {(1 - {\omega _k}\sum\limits_{i = 1}^N {{\beta _{i,k}}} )} } \right]^{ - 1}}\end{array}$ | (22) |
Liu等[21]提出的EBRB规则生成机制虽然简单且有效,但也使得EBRB系统的推理性能容易受训练数据的质量影响,由于训练数据生成的扩展置信规则库可能存在不一致的规则即规则相互矛盾的问题,这些不一致的规则会降低EBRB系统的推理准确性,尤其当这些不一致规则同时成为激活规则。在EBRB中,这些激活权重大于零的规则被称为激活规则,激活规则是用来进行ER合成推理的,即EBRB系统的推理结果就是依靠这些激活规则得到的。由此可见,激活规则对于最终推理结果的重要性,而相互矛盾的、不一致的激活规则会对最终的BRB系统推理结果造成一定的干扰,进而影响BRB系统的推理能力。为此,Alberto等[22]对式(8)进行改进,提出动态规则激活方法,通过不断重复的搜索过程以找到不一致性最小的激活规则集合,该方法能够有效减小激活规则之间的不一致性,但其参数取值需要不断迭代,而且参数增加和减小幅度也较难确定。此外,实际工程应用中,训练数据总数都比较多,当采用Liu等[21]提出的规则激活方法时,多数规则的激活权重都会大于零,激活规则数量的增多,意味着规则间的不一致性增大。要减小激活规则之间的不一致性,最简单的方法就是尽可能多地减少激活规则的数量,不一致性较高的这部分激活规则不参与最终的合成推理过程,但这种方法不一定有效,因为激活规则数量一旦减少,原有激活规则集合中包含的信息就会减少,如果这些不参与最终合成推理过程的激活规则包含了原有激活规则中绝大部分重要信息,则EBRB的推理准确性也会受到一定程度的影响。在EBRB中,激活规则的激活权重代表激活规则的重要性,激活权重越大,说明该激活规则越重要,其中包含的重要信息越多。鉴于此,为了减小激活规则之间的不一致性,同时保留住原有激活规则集合的绝大部分重要信息,本文提出激活规则多目标优化方法,把激活规则之间的不一致性以及激活规则的激活权重总和作为优化目标,通过NSGA-II来求解较优的激活规则集合用于最终的合成推理。
2 基于NSGA-II的EBRB激活规则多目标优化方法 2.1 多目标优化问题在实际应用问题中,所求解的优化目标通常包含多个,且它们之间经常是相互矛盾、冲突的。也就是说,对于这一类问题,几乎找不到一个可以同时满足所有优化目标的最优解。一个由m个决策参数和n个目标变量组成的多目标优化问题的数学表达式[26]为
| $\begin{gathered} {\text{Min/Max }}y = F(x) = ({f_1}(x),{f_2}(x),\cdots,{f_n}(x)) \hfill \\ {\text{sub to: }}{g_i}(X) \leqslant 0,i = 1,2,\cdots,{k_g} \hfill \\ {\text{ }}{h_i}(X) = 0,i = 1,2,\cdots,{k_h} \hfill \\ {\text{where: }}x = ({x_1},{x_2},\cdots,{x_m}) \in X \subseteq R \hfill \\ {\text{ y}} = ({y_1},{y_2},\cdots,{y_m}) \in Y \subseteq R{\text{ }} \hfill \\ \end{gathered} $ | (23) |
式中:
定义 1 (可行解)如果存在一个决策参数
定义 2 (可行解集合)可行解集合是指所有可行解组成的集合,记作
定义 3 (Pareto占优)假设
1)
2)
定义 4 (Pareto最优解)若多目标优化问题的一个可行解
2000年Kalyanmoy Deb等[27]首次提出了带精英策略的快速非支配排序遗传算法(简称NSGA-II),该方法是众多求解多目标优化问题方法中应用最为广泛的一种。NSGA-II算法是非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA)的改进,运行速度更快,复杂度更低,且其求解的Pareto最优解集收敛性更好。算法首先随机产生一定规模数量的初始种群,然后利用非支配排序方法对种群中所有个体进行分层,接着执行遗传算法的选择、交叉和变异3个操作产生第一代子群。从第二代子群开始,先将父代种群和子代种群中所有个体合并在一起,然后利用快速非支配排序方法对其进行分层,并计算每个非支配分层中所有个体的拥挤距离,在此基础上从中选出较优的个体组成新的父代种群,接着执行遗传算法的选择、交叉和变异3个操作产生下一代子群,直至达到程序结束条件时终止,算法的具体流程如图1所示。
NSGA-II算法中个体的优劣之分主要由个体的两个属性取值来决定,一个是其所在的非支配分层级别,另一个是个体的拥挤距离。前者是通过快速非支配排序方法确定,NSGA-II的快速非支配方法与NSGA的非支配排序方法相比,计算复杂度从原先的
确定完每个个体所在的非支配分层级别以及拥挤距离之后,就可以确定种群所有个体的优劣,假设其中两个个体
1)
2)
则称个体

|
Download:
|
| 图 1 NSGA-II算法流程 Fig. 1 The process of NSGA-II | |
数据驱动型的EBRB规则数量等于训练数据集数量,每条置信规则对应一个训练数据,当训练数据过多时,由式(9)计算得到的激活规则数量也会比较多,但很多激活规则之间存在相互矛盾、不一致的情况,这些激活规则会对推理造成一定的干扰。为了减少不一致激活规则对EBRB推理准确性的影响,本文提出基于NSGA-II的激活规则多目标优化方法,因此,多目标优化的两个目标函数分别为激活规则集合的不一致性以及激活权重和,其中,激活规则集合的不一致性用Liu等[21]提出的方法来衡量,假设
| ${\rm{SRA}}({R_P},{R_{{q}}}) = \mathop {\min }\limits_{i = 1}^T (1 - \sqrt {\sum\limits_{j = 1}^{{J_i}} {{{(\alpha _{i,j}^p - \alpha _{i,j}^q)}^2}} } )$ | (25) |
| ${\rm{SRC}}({R_P},{R_{{q}}}) = 1 - \sqrt {\sum\limits_{i = 1}^N {{{(\beta _i^p - \beta _i^q)}^2}} } )$ | (26) |
根据文献[21],规则
| ${\text{Cons}}({R_p},{R_q}) = \exp ( - \frac{{{{({\text{SRA(}}{R_p},{R_q})/{\text{SRC}}({R_p},R{}_q) - 1.0)}^2}}}{{1/{\text{SRA}}{{({R_p},{R_q})}^2}}})$ | (27) |
那么,第
| ${\text{Incons(}}i{\text{) = }}\sum\limits_{k = 1,k \ne i}^l {[1.0 - {\text{Cons}}({R_i},{R_k})]} $ | (28) |
由此可得NSGA-II的优化目标为
| $\begin{gathered} {\text{Min}}F(R) = ({f_1}(R),{f_2}(R)) \hfill \\ {f_1}(R) = \sum\limits_{k = 1}^l {{\text{Incons}}(k)} \hfill \\ {f_2}(R) = 1.0 - \sum\limits_{k = 1}^l {{\omega _k}} \hfill \\ \end{gathered} $ | (29) |
式中:
基于NSGA-II的激活规则多目标优化方法具体流程如图2所示,该方法根据激活规则集合的不一致性以及激活权重和来求解最终参与ER合成推理的激活规则集合R。本文方法首先计算每条扩展置信规则的激活权重,激活权重大于零的规则组成激活规则集合,然后对激活规则集合进行二进制编码,1表示该激活规则参与最终ER合成推理过程,0表示该激活规则不参与ER合成推理,不同的激活规则集合,其中被标识为1和0的规则不同,根据式(27)计算得到的规则不一致性以及激活权重和也不同,故接下来需要利用NSGA-II算法求解最优化目标(式(28))的Pareto最优解集,这些Pareto最优解集中编码为1对应的激活规则之间的不一致性既要最小同时激活权重和也要最大,然后从最优解集中选择一个合适的Pareto最优解,该最优解中编码为1对应的激活规则组成最终的激活规则集合并用于ER合成推理得出结果。本文方法的整体时间复杂度包括:1)EBRB系统查询激活规则复杂度
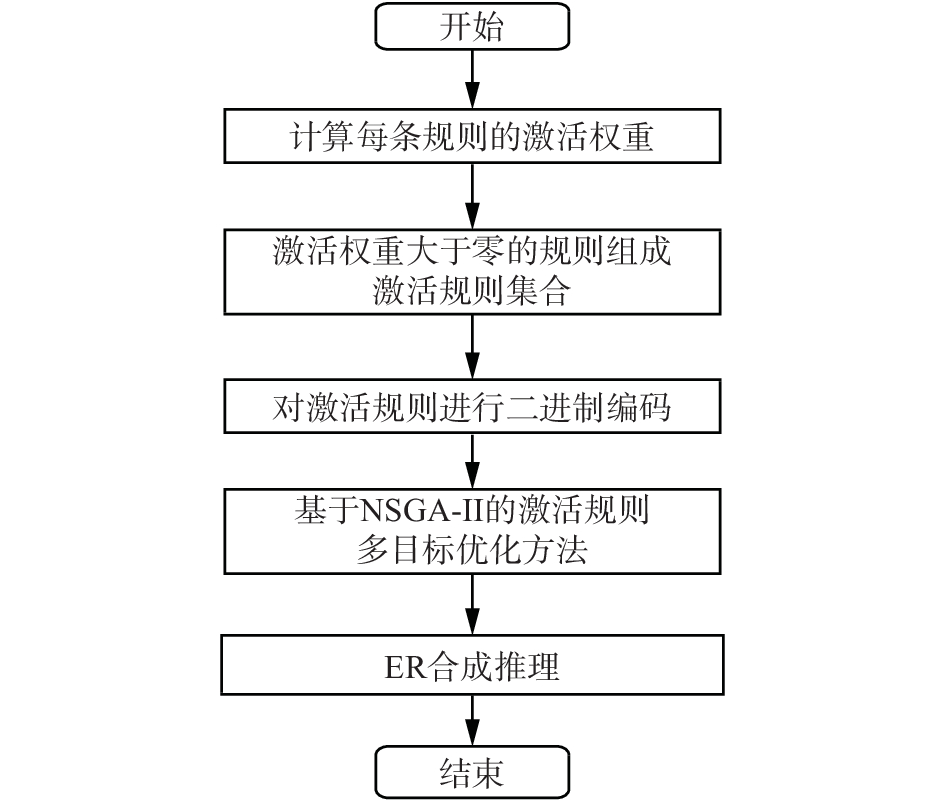
|
Download:
|
| 图 2 激活规则多目标优化方法 Fig. 2 The activated rules multi-objective optimization approach | |
本文引入非线性函数和输油管道检漏实例为研究对象以验证本文方法的有效性。实验中用到的NSGA-II算法的各个参数值分别为:个体交叉概率为0.9,个体变异概率为0.03,种群规模为100,进化代数为1 000。实验环境为:Inter(R) Core(TM) i5-4570 CPU @ 3.20 GHz;8 GB内存;Windows 10操作系统;算法实现平台Visual Studio 2010。
3.1 非线性函数问题为了验证本文方法的有效性,引入一个非线性函数作为基准测试函数进行测试以说明本文方法的性能。非线性函数的数学表达式为
| $f(x) = x\sin ({x^2}),0 \leqslant x \leqslant 3$ | (30) |
在EBRB系统构建中,选取函数的自变量
| 表 1 非线性函数问题实验结果 Tab.1 The results on nonlinear function |
从表1可以发现,NSGA-II_EBRB系统的推理准确性要比Liu_EBRB系统的推理准确性高,这主要是因为Liu_EBRB系统中用来参与ER合成推理的规则是所有激活权重大于零的激活规则,这部分规则的不一致性较高且会降低EBRB系统的推理能力,而NSGA-II_EBRB通过减少激活规则的不一致性,选择不一致性更小同时拥有原来激活规则中绝大部分信息的激活规则进行ER合成推理,最终合成推理的激活规则数只占原来激活规则总数的49.89%,这些激活规则不一致性较低,从而提高EBRB系统的推理能力。
3.2 输油管道检漏实例为了验证本文所提方法的有效性,引入一个具体的实际问题——输油管道泄漏问题[7]作为实例。该实例的研究对象为安装在英国的一条1 000多米长的输油管道,当输油管道发生泄漏时,管道的泄漏大小(leak size,LS)会随输油管道输入输出的流量差(flow difference,FD)和输油管道内的平均压力差(pressure difference,PD)变化而变化,因此,该实例的EBRB系统的前提属性为FD和PD,结果属性为LS。其中FD、PD的参考值由专家根据经验给出,分别为
该实验的测试数据是发生泄漏的2 008组数据,训练数据按照一定比例分别从3个时间段随机选取500组数据,因此构建的EBRB系统总共有1 500条规则,然后利用本文提出的方法构建NSGA-II_EBRB系统,并将实验结果和Liu_EBRB系统相比较,衡量的指标为平均绝对误差(mean absolute difference,MAE)。
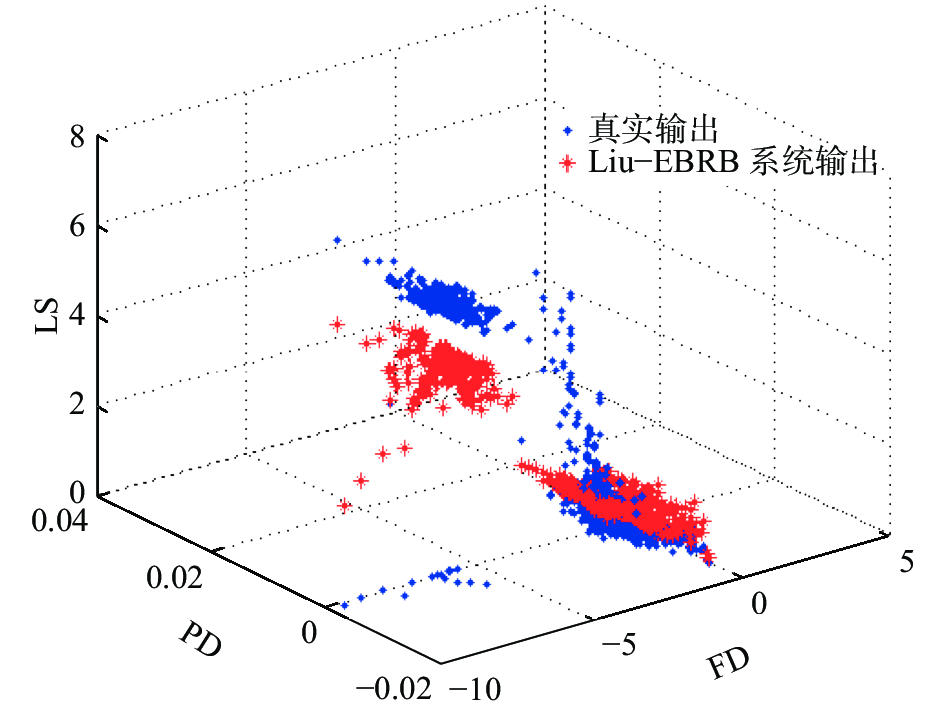
Liu_EBRB系统、NSGA-II_EBRB系统产生的推理输出和测试数据的真实输出对比如图3、4所示。分析图3、4可以发现,Liu_EBRB系统在
|
Download:
|
| 图 3 Liu_EBRB输出和真实输出 Fig. 3 Liu_EBRB output and real output | |

|
Download:
|
| 图 4 NSGA-II_EBRB输出和真实输出 Fig. 4 NSGA-II_EBRB output and real output | |
为了进一步验证本文方法的有效性和可行性,表2列出了Liu_EBRB系统、BK_EBRB系统和NSGA-II_EBRB系统产生的推理输出和测试数据的真实输出的MAE值,其中BK_EBRB系统是指根据文献[28]中的方法构建的EBRB系统。如表2所示,和Liu_EBRB系统的MAE相比,NSGA-II_EBRB系统比Liu_EBRB系统的MAE值减小了61.61%;和BK_EBRB系统相比,NSGA-II_EBRB系统要比BK_EBRB(theta=0.7)的MAE值减小56.92%;和BK_EBRB(theta=0.4)的MAE值相差无几。
| 表 2 输油管道泄漏实例实验结果 Tab.2 The results on pipeline leak detection |
数据驱动型的扩展置信规则库系统易受数据质量的影响,其推理能力常因不一致的数据而降低。因此,本文提出基于NSGA-II的扩展置信规则库激活规则多目标优化方法,通过NSGA-II来求解不一致性更小的激活规则集合,该方法既筛选出了不一致性更小的激活规则,同时又保留了原来激活规则集合中绝大部分信息,这些最终参与ER合成推理的激活规则一致性更高,更具代表性,能有效提高EBRB系统的推理能力。然而,本文方法还有许多需要改进的地方,如何从Pareto最优解集中选择一个最合适的解,如何减少算法的复杂度等,这些都是将来的研究工作重点。
| [1] |
周志杰, 杨剑波, 胡昌华, 等. 置信规则库专家系统与复杂系统建模[M]. 北京: 科学出版社, 2011.
( 0) 0)
|
| [2] |
YANG Jianbo, LIU Jun, WANG Jin, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE transactions on systems, man, and cybernetics-part A: systems and humans, 2006, 36(2): 266-285. DOI:10.1109/TSMCA.2005.851270 ( 0) 0)
|
| [3] |
DEMPSTER A P. A generalization of Bayesian inference[J]. Journal of the royal statistical society. Series B (methodological), 1968, 30(2): 205-247. ( 0) 0)
|
| [4] |
SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.
( 0) 0)
|
| [5] |
HWANG C L, YOON K. Multiple attribute decision making: methods and applications a state of the art survey[M]. New York: Springer, 1981: 22–34.
( 0) 0)
|
| [6] |
ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [7] |
ZHOU Zhijie, HU Changhua, YANG Jianbo, et al. Online updating belief rule based system for pipeline leak detection under expert intervention[J]. Expert systems with applications, 2009, 36(4): 7700-7709. DOI:10.1016/j.eswa.2008.09.032 ( 0) 0)
|
| [8] |
XU Dongling, LIU Jun, YANG Jianbo, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J]. Expert systems with applications, 2007, 32(1): 103-113. DOI:10.1016/j.eswa.2005.11.015 ( 0) 0)
|
| [9] |
YANG Jianbo, LIU Jun, XU Dongling, et al. Optimization models for training belief-rule-based systems[J]. IEEE transactions on systems, man, and cybernetics-part A: systems and humans, 2007, 37(4): 569-585. DOI:10.1109/TSMCA.2007.897606 ( 0) 0)
|
| [10] |
YANG Ying, FU Chao, CHEN Yuwang, et al. A belief rule based expert system for predicting consumer preference in new product development[J]. Knowledge-based systems, 2016, 94: 105-113. DOI:10.1016/j.knosys.2015.11.012 ( 0) 0)
|
| [11] |
JIANG Jiang, LI Xuan, ZHOU Zhijie, et al. Weapon system capability assessment under uncertainty based on the evidential reasoning approach[J]. Expert systems with applications, 2011, 38(11): 13773-13784. ( 0) 0)
|
| [12] |
杨隆浩, 蔡芷铃, 黄志鑫, 等. 出租车乘车概率预测的置信规则库推理方法[J]. 计算机科学与探索, 2015, 9(8): 985-994. YANG Longhao, CAI Zhiling, HUANG Zhixin, et al. Belief rule-base inference methodology for predicting probability of taking taxi[J]. Journal of frontiers of computer science and technology, 2015, 9(8): 985-994. (  0) 0)
|
| [13] |
CHEN Yuwang, YANG Jianbo, XU Dongling, et al. Inference analysis and adaptive training for belief rule based systems[J]. Expert systems with applications, 2011, 38(10): 12845-12860. DOI:10.1016/j.eswa.2011.04.077 ( 0) 0)
|
| [14] |
常瑞, 张速. 基于优化步长和梯度法的置信规则库参数学习方法[J]. 华北水利水电学院学报, 2011, 32(1): 154-157. Chang Rui, Zhang Su. An algorithm for training parameters in belief rule-bases based on the gradient methods with optimization step size[J]. Journal of north China institute of water conservancy and hydroelectric power, 2011, 32(1): 154-157. (  0) 0)
|
| [15] |
吴伟昆, 杨隆浩, 傅仰耿, 等. 基于加速梯度求法的置信规则库参数训练方法[J]. 计算机科学与探索, 2014, 8(8): 989-1001. WU Weikun, YANG Longhao, FU Yanggeng, et al. Parameter training approach for belief rule base using the accelerating of gradient algorithm[J]. Journal of frontiers of computer science and technology, 2014, 8(8): 989-1001. (  0) 0)
|
| [16] |
苏群, 杨隆浩, 傅仰耿, 等. 基于变速粒子群优化的置信规则库参数训练方法[J]. 计算机应用, 2014, 34(8): 2161-2165. SU Qun, YANG Longhao, FU Yanggeng, et al. Parameter training approach based on variable particle swarm optimization for belief rule base[J]. Journal of computer application, 2014, 34(8): 2161-2165. DOI:10.11772/j.issn.1001-9081.2014.08.2161 (  0) 0)
|
| [17] |
王韩杰, 杨隆浩, 傅仰耿, 等. 专家干预下置信规则库参数训练的差分进化算法[J]. 计算机科学, 2015, 42(5): 88-93. WANG Hanjie, YANG Longhao, FU Yanggeng, et al. Differential evolutionary algorithm for parameter training of belief rule base under expert intervention[J]. Computer science, 2015, 42(5): 88-93. DOI:10.11896/j.issn.1002-137X.2015.05.018 (  0) 0)
|
| [18] |
ZHOU Zhijie, HU Changhua, YANG Jianbo, et al. A sequential learning algorithm for online constructing belief-rule-based systems[J]. Expert systems with applications, 2010, 37(2): 1790-1799. DOI:10.1016/j.eswa.2009.07.067 ( 0) 0)
|
| [19] |
CHANG Leilei, ZHOU Yu, JIANG Jiang, et al. Structure learning for belief rule base expert system: a comparative study[J]. Knowledge-based systems, 2013, 39: 159-172. DOI:10.1016/j.knosys.2012.10.016 ( 0) 0)
|
| [20] |
王应明, 杨隆浩, 常雷雷, 等. 置信规则库规则约简的粗糙集方法[J]. 控制与决策, 2014, 29(11): 1943-1950. WANG Yingming, YANG Longhao, CHANG Leilei, et al. Rough set method for rule reduction in belief rule base[J]. Control and decision, 2014, 29(11): 1943-1950. (  0) 0)
|
| [21] |
LIU Jun, MARTINEZ L, CALZADA A, et al. A novel belief rule base representation, generation and its inference methodology[J]. Knowledge-based systems, 2013, 53: 129-141. DOI:10.1016/j.knosys.2013.08.019 ( 0) 0)
|
| [22] |
CALZADA A, LIU Jun, WANG Hui, et al. A new dynamic rule activation method for extended belief rule-based systems[J]. IEEE Transactions on knowledge and data engineering, 2015, 7(4): 880-894. ( 0) 0)
|
| [23] |
YANG Jianbo. Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J]. European journal of operational research, 2001, 131(1): 31-61. DOI:10.1016/S0377-2217(99)00441-5 ( 0) 0)
|
| [24] |
WANG Yingming, YANG Jianbo, XU Dongling. Environmental impact assessment using the evidential reasoning approach[J]. European journal of operational research, 2006, 174(3): 1885-1913. DOI:10.1016/j.ejor.2004.09.059 ( 0) 0)
|
| [25] |
WANG Yingming, YANG Jianbo, XU Dongling, et al. Consumer preference prediction by using a hybrid evidential reasoning and belief rule-based methodology[J]. Expert systems with applications, 2009, 36(4): 8421-8430. DOI:10.1016/j.eswa.2008.10.052 ( 0) 0)
|
| [26] |
ZITZLER E. Evolutionary algorithm for multi-objective optimization: methods and applications[D]. Zurich: Swiss Federal Institute of Technology, 1999.
( 0) 0)
|
| [27] |
DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[C]//Proceedings of the 6th International Conference Paris Parallel Problem Solving from Nature PPSN VI. Kanpur, India, 2000.
( 0) 0)
|
| [28] |
苏群, 杨隆浩, 傅仰耿, 等. 基于BK树的扩展置信规则库结构优化框架[J]. 计算机科学与探索, 2016, 10(2): 257-267. SU Qun, YANG Longhao, FU Yanggeng, et al. Structure optimization framework of extended belief rule base based on BK-tree[J]. Journal of frontiers of computer science and technology, 2016, 10(2): 257-267. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


