2. 烟台大学 计算机与控制工程学院,山东 烟台 264005
2. School of Computer and Control Engineering, Yantai University, Yantai 264005, China
属性约简[1-7]是粗糙集理论[1-3]的核心研究内容之一,在数据挖掘、机器学习、决策分析、智能信息处理等领域取得了诸多研究成果。属性约简的目的是删除冗余属性,只保留使决策表某种分类特征不变的最小属性子集。差别矩阵方法是一种用于求取所有属性约简的有效方法,该方法由Skowron[8]于1982年提出,并将差别矩阵应用于正域约简中。诸多学者在此基础上做了大量的研究工作。Kryszkiewicz[9]于1999年在不完备信息系统下引入广义决策保持约简的概念,并提出基于差别矩阵的广义决策保持约简方法;2007年,邓大勇等[10]首先分析了不相容信息系统下几种约简目标之间的关系;2009年,Miao等[11]进一步分析了3种约简目标之间的关系,提出不可分辨关系保持约简以及相应的差别矩阵构造方法;Zhou等[12]在2011年对现有的13种属性约简目标进行总结,并将所有约简目标分为4类,完善了现有约简目标之间的关系。
分布约简保持了信息系统约简前后每条规则置信度不变。2003年,张文修等[13]提出了分配约简、分布约简以及最大分布约简的概念,并分别给出了基于差别矩阵的分配约简、分布约简以及最大分布约简方法;2007年,徐伟华等[14]在优势关系下提出了两种约简概念,即分布约简和最大分布约简,同时建立了基于差别矩阵的分布和最大分布约简的具体方法。如某一段时间内的温度、湿度等区间值数据在现实环境中大量存在,它较好地表示了许多不确定类型数据,区间值决策系统是经典Pawlak决策系统的推广,充分地考虑了数据的不确定性,在近几年得到了广泛关注。2009年,张楠等[15]定义了
基于上述研究,文献[13]和[14]分别对等价关系和优势关系下的最大分布约简进行了研究,但未有区间值决策系统的最大分布约简讨论。置信度表示了信息系统中规则的可信程度,置信度越大,规则的可信程度越高;置信度越小,规则的可信程度越低,在实际应用中,人们往往关注置信度最大的规则。为此,本文提出了区间值决策系统的最大分布约简概念,为区间值决策系统提供了一种求取所有属性约简的新方法。
1 基本知识 1.1 区间值决策系统的粗糙近似基于相容关系的区间值粗糙集模型是经典Pawlak粗糙集模型的推广,首先给出相关概念和性质。
给定区间值信息系统[15-18]
如果属性集
定义1 设
1)区间值交运算为
| ${\eta _1} \cap {\eta _2} = \left\{ {\begin{array}{*{20}{l}}{0, \quad (u_i^k < l_j^k) \vee (u_j^k < l_i^k)\;\;}\\{[{\rm{max}}(l_i^k,l_j^k),{\rm{min}}(u_i^k,u_j^k)], \quad \text{其他}}\end{array}} \right.$ |
2)区间值并运算为
| ${\eta _1} \cup {\eta _2} = [{\rm{min}}(l_i^k,l_j^k),{\rm{max}}(u_i^k,u_j^k)]\;$ |
目前,度量区间值相似度比较合理的主要方法有Jaccard相似率、悲观相似率和乐观相似率,本文统一采用Jaccard相似率来度量两个区间值的相似度。
定义2
| $\alpha _{ij}^k{\rm{ = }}\frac{{{\rm{|}}[l_i^k,u_i^k] \cap [l_j^k,u_j^k]{\rm{|}}}}{{{\rm{|}}[l_i^k,u_i^k] \cup [l_j^k,u_j^k]{\rm{|}}}}$ |
Jaccard相似率为两个区间数的交集与并集长度的比值,它适合度量长度相似的两个区间数。
例1 区间值决策系统
| 表 1 不协调区间值决策系统 Tab.1 Inconsistent interval-valued decision systems |
令
| ${\eta _1} \cap {\eta _2} = [0.86,3.13] \cap [{\rm{ - }}0.12,2.13] = {\rm{[0}}{\rm{.86,2}}{\rm{.13]}}$ |
| ${\eta _1} \cup {\eta _2} = [0.86,3.13] \cup [{\rm{ - }}0.12,2.13] = [{\rm{ - }}0.12,3.13{\rm{]}}$ |
计算
| $\alpha _{12}^1 = \frac{{|[l_1^1,u_1^1] \cap [l_2^1,u_2^1]|}}{{|[l_1^1,u_1^1] \cup [l_2^1,u_2^1]|}} = 0.391$ |
定义3[15] 对于区间值决策系统
| ${T}_{\{ {a_k}\} }^\alpha = \{ ({x_i},{x_j})|({x_i},{x_j}) \in U \times U,\alpha _{ij}^k > \alpha \} $ |
其中
关于条件属性子集
| ${T}_A^\alpha = \{ ({x_i},{x_j})|({x_i},{x_j}) \in U \times U,\alpha _{ij}^k > \alpha ,{a_k} \in A\} $ |
性质1[15] 对于区间值决策系统
| ${T}_A^\alpha = \mathop \cap \limits_{{a_k} \in A} {T}_{\{ {a_{k\} }}}^\alpha $ |
性质2[18] 设区间值决策系统
1)自反性:任意xi∈U,则
2)对称性:任意xi,xj∈U,若
3)非传递性:任意
定义4[18] 设区间值决策系统
| $S_A^\alpha ({x_i}) = \{ {x_j}|{x_j} \in U,({x_i},\,{x_j}) \in {T}_A^\alpha \} $ |
对任意
| $S_A^\alpha (U) = \{ S_A^\alpha ({x_1}),S_A^\alpha ({x_2}), \cdots ,S_A^\alpha ({x_n})\} $ |
其中
经典粗糙集中对象间的二元关系为等价关系,具有自反性、传递性、对称性,导出的等价类集合是对论域的划分,而定义4中的相容类是对论域的覆盖。
定义5 给定区间值决策系统
| $\overline {{\rm{apr}}_A^\alpha } (X) = \{ {x_i}|{x_i} \in U,S_A^\alpha ({x_i}) \cap X \ne \text{Ø} \} $ |
| $\underline {{\rm{apr}}_A^\alpha } (X) = \{ {x_i}|{x_i} \in U,S_A^\alpha ({x_i}) \subseteq X\} $ |
集合
| ${\rm{POS}}_A^\alpha (X) = \underline {{\rm{apr}}_A^\alpha } (X)$ |
下近似是由肯定属于
定义6[16] 给定区间值决策系统
| $\mu _A^\alpha (X) = \frac{{|\underline {{\rm{apr}}_A^\alpha } (X)|}}{{|\overline {{\rm{apr}}_A^\alpha } (X)|}}$ |
近似分类精度表示确定性规则占可能性规则的比例,近似分类精度越大,区间值信息系统中确定性规则越多;反之,确定性规则越少。
定义7[16] 对于区间值决策系统
| $\overline {{\rm{apr}}_A^\alpha } (D) = \{ {x_i}|{x_i} \in U,{D_j} \in U/D,S_A^\alpha ({x_i}) \cap {D_j} \ne \text{Ø} \} $ |
| $\underline {{\rm{apr}}_A^\alpha } (D) = \{ {x_i}|{x_i} \in U,{D_j} \in U/D,S_A^\alpha ({x_i}) \subseteq {D_j}\} $ |
决策属性D关于
| ${\rm{POS}}_A^\alpha (D) = \overline {{\rm{apr}}_A^\alpha } (D)$ |
定义8[16] 设区间值决策系统
| $\mu _A^\alpha (D) = \frac{{|\underline {{\rm{apr}}_A^\alpha } (D)|}}{{|\overline {{\rm{apr}}_A^\alpha } (D)|}}$ |
定义5和定义6是关于集合
定义9[13] 对于区间值决策系统
若存在一个对象
例2 如表1所示的区间值决策系统,令
| ${{T}}_C^{0.6}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&0&0&0 \\ 0&0&1&0&1&1 \\ 0&0&0&1&0&0 \\ 0&0&1&0&1&1 \\ 0&0&1&0&1&1 \end{array}} \right]$ |
根据相似率布尔矩阵,计算阈值
| $S_C^{0.6}(U) = \{ S_C^{0.6}({x_1}),S_C^{0.6}({x_2}), \cdots ,S_C^{0.6}({x_6})\} $ |
式中:
计算条件属性集C的近似分类精度:
| $\mu _C^{0.6}(D) = \frac{{|\underline {{\rm{apr}}_C^\alpha } (D)|}}{{|\overline {{\rm{apr}}_C^\alpha } (D)|}} = \frac{3}{6} = 0.5$ |
文献[16]提出不协调区间决策系统的分布约简。
定义10 设区间值决策系统
| $\begin{array}{c}\mu _A^\alpha ({x_i}) = (D({D_1}/S_A^\alpha ({x_i})),D({D_2}/S_A^\alpha ({x_i})), \cdots ,\\D({D_j}/S_A^\alpha ({x_i}), \cdots ,D({D_{|U|}}/S_A^\alpha ({x_i})))\end{array}$ |
式中
定义11 设区间值决策系统
| ${\rm{DM}}_D^\alpha (i,j) = \left\{ {\begin{array}{*{20}{l}} {\{ {a_k}|{a_k} \in C \wedge \alpha _{ij}^k < \alpha \} ,\quad \mu _A^\alpha ({x_i}) \ne \mu _A^\alpha ({x_j})} \\ { \text{Ø} ,\quad \mu _A^\alpha ({x_i}) = \mu _A^\alpha ({x_j})} \end{array}} \right.$ |
式中:
定义12 设区间值决策系统
| $f_D^\alpha (C)({\bar a_1},{\bar a_2}, \cdots ,{\bar a_{|C|}}) = \wedge \{ \vee {\rm{DM}}_D^\alpha (i,j):{\rm{DM}}_D^\alpha (i,j) \ne \text{Ø} \} $ |
此函数简称分布可辨识函数。这里的
利用分配率和吸收率将
定理1 设区间值决策系统
基于可辨识矩阵的分布约简算法(distribution reduction algorithm based on discernibility matrix,DRADM)描述如下。
算法1 DRADM
输入 区间值决策系统
输出 区间值决策系统的所有分布保持约简结果。
1)计算区间值决策系统
2)根据每个对象对应的相容类,计算每个对象相对于每一个决策类的概率分布
3)根据每个对象的可信度不同构造分布约简可辨识矩阵
4)由可辨识矩阵
5)利用分配率和吸收率将
例3 如表1所示的区间值决策系统,令
计算每个对象对应的概率分布:
计算分布保持约简可辨识矩阵:
| ${{\bf{DM}}}_D^{0.6}(6,6) = \left[ {\begin{array}{*{20}{c}} \text{Ø} &{}&{}&{}&{}&{} \\ {{a_1},{a_2},{a_3},{a_4}}&\text{Ø} &{}&{}&{}&{} \\ {{a_1},{a_2}}&{{a_3},{a_4}}&\text{Ø} &{}&{}&{} \\ {{a_1},{a_2},{a_3}}&\text{Ø} &{{a_3}}&\text{Ø} &{}&{} \\ {{a_1},{a_2}}&{{a_3},{a_4}}&\text{Ø} &{{a_3}}&\text{Ø} &{} \\ {{a_1},{a_2}}&{{a_3},{a_4}}&\text{Ø} &{{a_3}}&\text{Ø} &\text{Ø} \end{array}} \right]$ |
计算分布约简可辨识函数:
| $f_D^{0.6}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_3} \wedge ({a_2} \vee {a_1})$ |
转化后的分布约简可辨识函数为
| $h_D^{0.6}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = ({a_1} \wedge {a_3}) \vee ({a_2} \wedge {a_3})$ |
因此分布保持约简为
本节在区间值决策系统中引入最大规则置信度的概念,提出了不协调区间值决策系统的最大分布约简算法。
定义13 设区间值决策系统
| $m_A^\alpha ({x_i}) = D({D_{{j_0}}}/S_A^\alpha ({x_i}))= \mathop {{\rm{max}}}\limits_{j \leqslant q} D({D_j}/S_A^\alpha ({x_i})) $ |
| $\gamma _A^\alpha ({x_i}) = \{ {D_j}|D({D_j}/S_A^\alpha ({x_i})) = D({D_{{j_0}}}/S_A^\alpha ({x_i})\} $ |
若对任意的xi∈U,有
定义14 设区间值决策系统
1)
2)任意
那么称属性子集A为区间值决策系统基于相容关系的最大分布约简。DS的所有约简集合记为
定理2 设区间值决策系统
证明 记
“
| $\begin{gathered} D({D_k}/S_A^\alpha ({x_i})){\rm{ = }} \hfill \\ \frac{{\sum {\{ |{D_k} \cap S_C^\alpha ({x_j})|:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))\} } }}{{|S_A^\alpha ({x_i})|}}{\rm{ = }} \hfill \\ \sum {\left\{ {\frac{{|{D_k} \cap S_C^\alpha ({x_j})|}}{{|S_C^\alpha ({x_j})|}}} \right.} \times \left. {\frac{{|S_C^\alpha ({x_j})|}}{{|S_A^\alpha ({x_i})|}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))} \right\} \leqslant \hfill \\ \sum {\left\{ {\frac{{|{D_{{j_0}}} \cap S_C^\alpha ({x_j})|}}{{|S_C^\alpha ({x_i})|}}} \right.} \times \left. {\frac{{|S_C^\alpha ({x_j})|}}{{|S_A^\alpha ({x_i})|}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))} \right\}{\rm{ = }} \hfill \\ \frac{{|{D_{{j_0}}} \cap S_A^\alpha ({x_i})|}}{{|S_A^\alpha ({x_i})|}}{\rm{ = }}D({D_{{j_0}}}/S_A^\alpha ({x_i})) \hfill \\ \end{gathered} $ |
故
另一方面,任意的
| $\begin{gathered} D({D_{{k_0}}}/S_A^\alpha ({x_i})){\rm{ = }} \\ \sum {\left\{ {\frac{{|{D_{{k_0}}} \cap S_C^\alpha ({x_j})|}}{{|S_C^\alpha ({x_j})|}}} \right.} \times \left. {\frac{{|S_C^\alpha ({x_j})|}}{{S_A^\alpha ({x_i})}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))} \right\}{\rm{ = }} \\ \sum {\left\{ {m_C^\alpha ({x_j}) \times \frac{{|S_C^\alpha ({x_j})|}}{{|S_A^\alpha ({x_i})|}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))} \right\} > } \\ \sum {\left\{ {D({D_{{j_0}}}/S_C^\alpha ({x_j})) \times \frac{{|S_{\rm{AT}}^\alpha ({x_j})|}}{{|S_A^\alpha ({x_i})|}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i})) } \right\}} = \\ \sum {\left\{ {\frac{{|{D_{{j_0}}} \cap S_C^\alpha ({x_j})|}}{{|S_C^\alpha ({x_j})|}}} \right.} \times \left. {\frac{{|S_C^\alpha ({x_j})|}}{{|S_A^\alpha ({x_i})|}}:S_C^\alpha ({x_j}) \in J(S_A^\alpha ({x_i}))} \right\} = \\ \frac{{|{D_{{j_0}}} \cap S_A^\alpha ({x_i})|}}{{|S_A^\alpha ({x_i})|}} = D({D_{{j_0}}}/S_A^\alpha ({x_i})) \end{gathered} $ |
与
因此,证明了对任意
定义15 设区间值决策系统
| ${\rm{DM}}_{D{\rm{Max}}}^\alpha(i,j) = \left\{ {\begin{array}{*{20}{l}}{\{ {a_k}|{a_k} \in C \wedge \alpha _{ij}^k < \alpha \} ,\quad\gamma _A^\alpha ({x_i}) \ne \gamma _A^\alpha ({x_j})}\\{\text{Ø} ,\quad \gamma _A^\alpha ({x_i}) = \gamma _A^\alpha ({x_j})}\end{array}} \right.$ |
基于α-相容类的最大分布可辨识矩阵是一个相对于主对角线对称的矩阵,在进行运算时只需考虑其上三角或下三角部分即可。
定理3 设区间值决策系统
证明 “
“
定义16 设区间值决策系统
利用分配率和吸收率将
定理4 设区间值决策系统
证明 “
“
基于差别矩阵的分布约简算法(maximum distribution reduction algorithm based on discernibility matrix,MDRADM)描述如算法2。
算法2 MDRADM
输入 区间值决策系统DS,阈值
输出 区间值决策系统的所有最大分布保持约简结果。
1)计算区间值决策系统DS在阈值
2)根据每个对象对应的相容类,计算每个对象相对于每一个决策类的概率分布
3)根据每个对象的概率分布,计算所对应的最大分布
4)根据每个对象的可信度不同构造最大分布约简可辨识矩阵
5)由可辨识矩阵
6)利用分配率和吸收率将
算法2是通过可辨识矩阵求得区间值决策表的所有最大分布保持约简,因此算法在最坏情况下的时间复杂度为
例4 如表1所示的区间值决策系统,令
计算决策属性
计算每个对象对应的概率分布:
计算每个对象对应的最大分布:
计算最大分布约简可辨识矩阵:
| ${\bf{DM}}_{D{\rm{Max}}}^{0.6}(6,6) = \left[ {\begin{array}{*{20}{c}} \text{Ø} &{}&{}&{}&{}&{}\\{{a_1},{a_2},{a_3},{a_4}}& \text{Ø} &{}&{}&{}&{}\\ \text{Ø} &{{a_3},{a_4}}& \text{Ø} &{}&{}&{}\\{{a_1},{a_2},{a_3}}& \text{Ø} &{{a_3}}& \text{Ø} &{}&{}\\ \text{Ø} &{{a_3},{a_4}}& \text{Ø} &{{a_3}}& \text{Ø} &{}\\ \text{Ø} &{{a_3},{a_4}}& \text{Ø} &{{a_3}}& \text{Ø} & \text{Ø} \end{array}} \right]$ |
计算最大分布约简可辨识函数:
| $f_D^{0.6}{(C)_{{\rm{Max}}}}({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_3}$ |
因此,最大分布保持约简结果为{a3}。
例5 如表1所示的区间值决策系统,令
| $h_D^{0.4}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_1} \vee {a_4}$ |
| $h_D^{0.5}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = ({a_1} \wedge {a_3}) \vee ({a_2} \wedge {a_3})$ |
| $h_D^{0.6}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = ({a_1} \wedge {a_3}) \vee ({a_2} \wedge {a_3})$ |
| $h_D^{0.7}(C)({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = ({a_1} \wedge {a_3}) \vee ({a_2} \wedge {a_3})$ |
最大分布保持约简结果为
| $h_D^{0.4}{(C)_{{\rm{Max}}}}({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_1} \vee {a_4}$ |
| $h_D^{0.5}{(C)_{{\rm{Max}}}}({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_3}$ |
| $h_D^{0.6}{(C)_{{\rm{Max}}}}({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_3}$ |
| $h_D^{0.7}{(C)_{{\rm{Max}}}}({\bar a_1},{\bar a_2},{\bar a_3},{\bar a_4}) = {a_3}$ |
性质3 设区间值决策系统
本节对提出的最大分布约简算法进行实验验证,实验包括两部分:1)比较最大分布约简方法和其他约简方法的约简结果,验证了性质3的正确性;2)比较了最大分布保持、分布保持和正域保持3种约简算法的约简效率。采用UCI标准测试集进行实验。实验环境为PC机,操作系统为Windows 7旗舰版64 位;内存为6.0 GB DDR3,CPU为Intel i5-3470。
实验选取8组标准UCI数据集,对缺失数据通过将对应属性下占多数属性值进行替换,对名词性数据采用{0,1}替换,对连续型数据采用等频分割[19]的方法,所有数据预处理均在WEKA3.6进行,数据集信息如表2所示,
| 表 2 UCI数据集信息 Tab.2 UCI data sets information |
由于表格有限,表3~10中数据集名称均为相应数据集名称的缩写。
| 表 3 约简结果对比(
|
| 表 4 约简结果对比(
|
| 表 5 约简结果对比(
|
| 表 6 约简结果对比(
|
| 表 7 约简结果对比(
|
| 表 8 约简结果对比(
|
| 表 9 约简结果对比(
|
| 表 10 约简结果对比(
|
由于采用的UCI数据集都是单值数据,因此需将单值数据转换为区间值数据,单值数据转换为区间值数据的方法在文献[19]中已经描述,先将该方法改进,引进阈值
设区间值决策系统
| $\sigma _t^k = \sqrt {\frac{1}{{|{D_k}| - 1}}\sum\limits_{{x_i} \in {D_k}} {{{({a_t}({x_j}) - \bar a_t^k)}^2}} } $ |
式中
区间值的左右区间分别为
| $l_i^t = {a_t}({x_i}) - \lambda \bar a_t^k$ |
| $u_i^t = {a_t}({x_i}) + \lambda \bar a_t^k$ |
式中
在本节中,讨论了最大分布约简与其他约简方法之间的关系[20],选取正域保持约简算法(PRADM)[17]和分布保持约简算法(DRADM)。
表3~6为
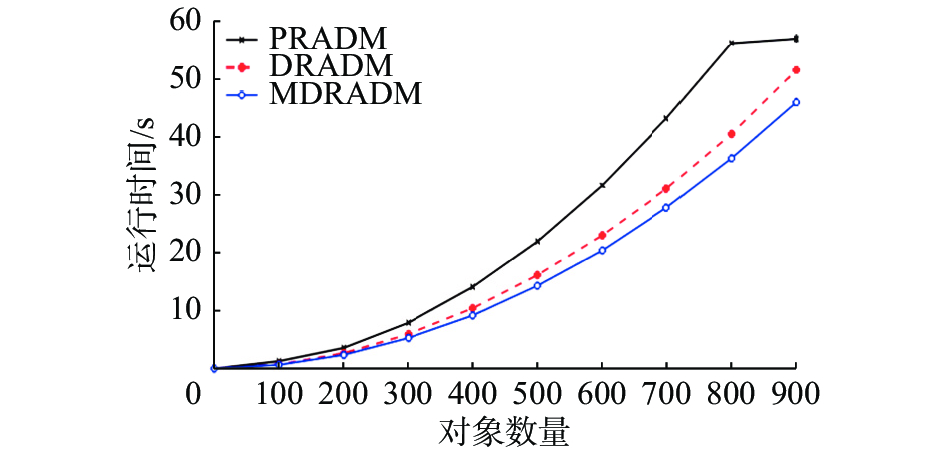
本节选取Mammographic Mass数据集,对比两个算法随对象数量的增加耗时变化情况。图1~5为
|
Download:
|
|
图 1 约简效率对比 (
|
|
|
Download:
|
|
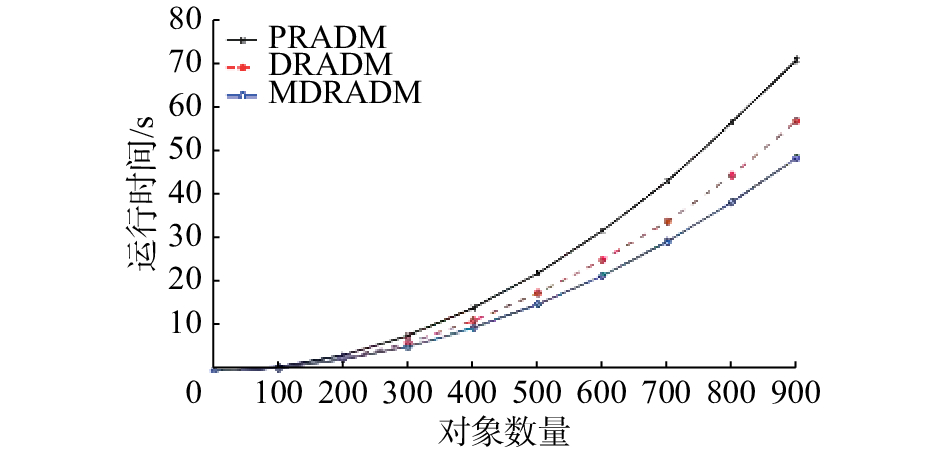
图 2 约简效率对比 (
|
|

|
Download:
|
|
图 3 约简效率对比 (
|
|
|
Download:
|
|
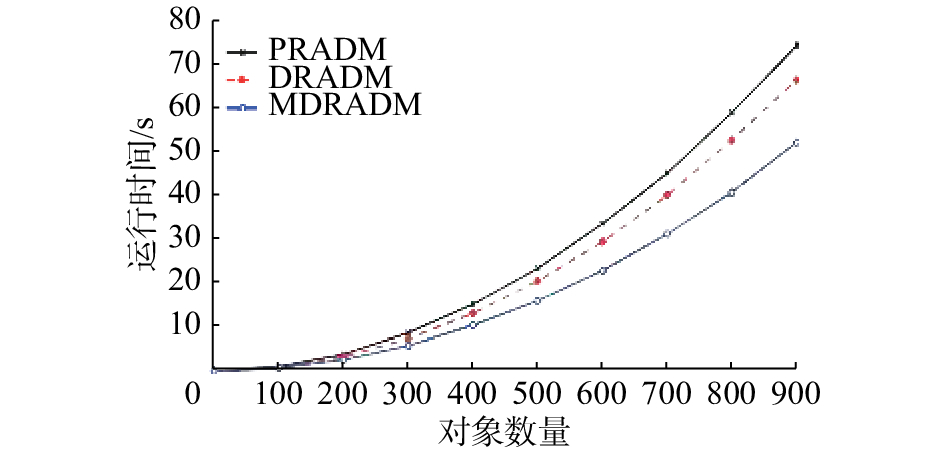
图 4 约简效率对比 (
|
|
|
Download:
|
|
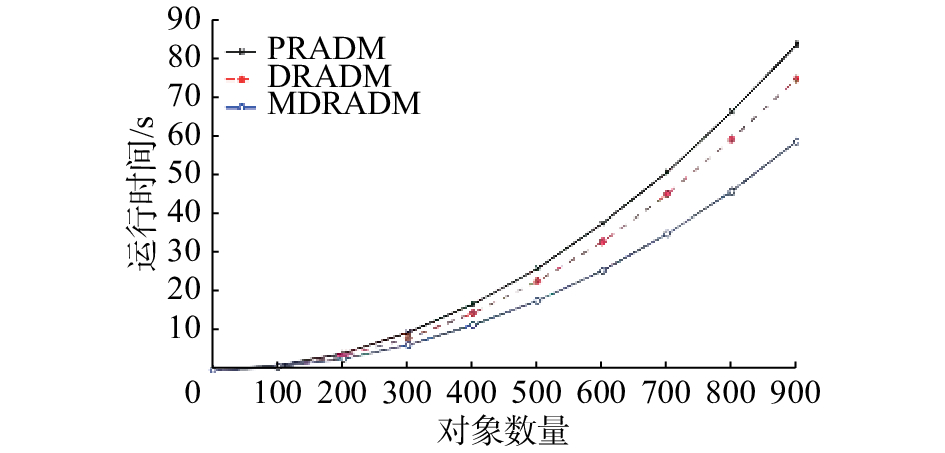
图 5 约简效率对比 (
|
|
图1~5中虚线表示PRADM随着对象数量增加运行时间变化曲线,空心圆点实线表示MDRADM随着对象数量增加运行时间变化曲线,交叉点实线表示DRADM随着对象数量增加运行时间变化曲线。实验结果表明,在对象数较少情况下,由于差别矩阵较简单,PRADM、DRADM和MDRADM运行时间几乎没有差别,但随着对象数量的增加,3种算法的运行时间差异越来越明显;由于MDRADM差别元素是DRADM差别元素的一个子集,PRADM的差别矩阵为非对称矩阵,故MDRADM的运行时间小于PRADM和DRADM运行时间。当
属性约简是粗糙集理论研究的热点问题之一,在实际应用中具有重要意义,主要作用有:1)提取更加泛化的规则;2)针对应用中的海量数据,能够压缩数据集规模。分布保持约简能够保持信息系统在约简前后置信度不变,而人们往往只关注置信度最大的规则,具有广泛的应用价值。
本文在相关研究成果的基础上,在不协调区间值决策系统中提出最大分布约简的概念,构造了基于可辨识矩阵的最大分布约简算法,该算法保持了在知识约简前后各个规则的最大置信度不变。实验选取8组UCI数据集将本文算法与已有的两种约简算法的约简结果和效率进行对比。实验结果表明,分布约简包含最大分布约简,并且最大分布约简算法比其他两种算法具有更高的效率。由于本文提出的算法是在可辨识矩阵基础上的,其时间和空间复杂度较高,不利于在实际应用中推广,故提出高效率的约简算法是未来研究方向之一。
| [1] |
PAWLAK Z. Rough sets[J]. International journal of computer & information sciences, 1982, 11(5): 341-356. ( 0) 0)
|
| [2] |
PAWLAK Z. Rough sets: theoretical aspects of reasoning about data[M]. Boston: Kluwer Academic Publishers, 1992.
( 0) 0)
|
| [3] |
王国胤, 姚一豫, 于洪. 粗糙集理论与应用研究综述[J]. 计算机学报, 2009, 32(7): 1229-1246. WANG Guoyin, YAO Yiyu, YU Hong. A survey on rough set theory and applications[J]. Chinese journal of computers, 2009, 32(7): 1229-1246. (  0) 0)
|
| [4] |
QIAN Yuhua, LIANG Jiye, PEDRYCZ W, et al. Positive approximation: an accelerator for attribute reduction in rough set theory[J]. Artificial intelligence, 2010, 174(9/10): 597-618. ( 0) 0)
|
| [5] |
WANG Feng, LIANG Jiye, QIAN Yuhua. Attribute reduction: A dimension incremental strategy[J]. Knowledge-based systems, 2013, 39: 95-108. DOI:10.1016/j.knosys.2012.10.010 ( 0) 0)
|
| [6] |
CHEN Hongmei, LI Tianrui, RUAN Da, et al. A rough-set based incremental approach for updating approximations under dynamic maintenance environments[J]. IEEE transactions on knowledge and data engineering, 2013, 25(2): 274-284. DOI:10.1109/TKDE.2011.220 ( 0) 0)
|
| [7] |
HU Qinghua, YU Daren, XIE Zongxia. Information-preserving hybrid data reduction based on fuzzy-rough techniques[J]. Pattern recognition letters, 2006, 27(5): 414-423. DOI:10.1016/j.patrec.2005.09.004 ( 0) 0)
|
| [8] |
SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[M]//SŁOWIŃSKI R. Intelligent Decision Support. Dordrecht: Springer, 1992, 11: 331–362.
( 0) 0)
|
| [9] |
KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information sciences, 1998, 112(1/2/3/4): 39-49. ( 0) 0)
|
| [10] |
邓大勇, 黄厚宽, 李向军. 不一致决策系统中约简之间的比较[J]. 电子学报, 2007, 35(2): 252-255. DENG Dayong, HUANG Houkuan, LI Xiangjun. Comparison of various types of reductions in inconsistent systems[J]. Acta electronica sinica, 2007, 35(2): 252-255. (  0) 0)
|
| [11] |
MIAO Duoqian, ZHAO Yan, YAO Yiyu, et al. Relative reducts in consistent and inconsistent decision tables of the Pawlak rough set model[J]. Information sciences, 2009, 179(24): 4140-4150. DOI:10.1016/j.ins.2009.08.020 ( 0) 0)
|
| [12] |
ZHOU Jie, MIAO Duoqian, PEDRYCZ W, et al. Analysis of alternative objective functions for attribute reduction in complete decision tables[J]. Soft computing, 2011, 15(8): 1601-1616. DOI:10.1007/s00500-011-0690-7 ( 0) 0)
|
| [13] |
张文修, 米据生, 吴伟志. 不协调目标信息系统的知识约简[J]. 计算机学报, 2003, 26(1): 12-18. ZHANG Wenxiu, MI Jusheng, WU Weizhi. Knowledge reductions in inconsistent information systems[J]. Chinese journal of computers, 2003, 26(1): 12-18. (  0) 0)
|
| [14] |
徐伟华, 张文修. 基于优势关系下不协调目标信息系统的分布约简[J]. 模糊系统与数学, 2007, 21(4): 124-131. XU Weihua, ZHANG Wenxiu. Distribution reduction in inconsistent information systems based on dominance relations[J]. Fuzzy systems and mathematics, 2007, 21(4): 124-131. (  0) 0)
|
| [15] |
张楠, 苗夺谦, 岳晓冬. 区间值信息系统的知识约简[J]. 计算机研究与发展, 2010, 47(8): 1362-1371. ZHANG Nan, MIAO Duoqian, YUE Xiaodong. Approaches to knowledge reduction in interval-valued information systems[J]. Journal of computer research and development, 2010, 47(8): 1362-1371. (  0) 0)
|
| [16] |
张楠, 许鑫, 童向荣, 等. 不协调区间值决策系统的知识约简[J]. 小型微型计算机系统, 2017, 38(7): 1585-1589. ZHANG Nan, XU Xin, TONG Xiangrong, et al. Knowledge reduction in inconsistent interval-valued decision systems[J]. Journal of Chinese computer systems, 2017, 38(7): 1585-1589. (  0) 0)
|
| [17] |
张楠, 许鑫, 童向荣, 等. 不协调区间值决策系统的分布约简[J]. 计算机科学, 2017, 44(9): 78-82, 104. ZHANG Nan, XU Xin, TONG Xiangrong, et al. Distribution reduction in inconsistent interval-valued decision systems[J]. Computer science, 2017, 44(9): 78-82, 104. DOI:10.11896/j.issn.1002-137X.2017.09.016 (  0) 0)
|
| [18] |
刘鹏惠, 陈子春, 秦克云. 区间值信息系统的决策属性约简[J]. 计算机工程与应用, 2009, 45(28): 148-150, 229. LIU Penghui, CHEN Zichun, QIN Keyun. Decision attribute reduction of interval-valued information system[J]. Computer engineering and applications, 2009, 45(28): 148-150, 229. DOI:10.3778/j.issn.1002-8331.2009.28.044 (  0) 0)
|
| [19] |
ZHANG Xiao, MEI Changlin, CHEN Degang, et al. Multi-confidence rule acquisition and confidence-preserved attribute reduction in interval-valued decision systems[J]. International journal of approximate reasoning, 2014, 55(8): 1787-1804. DOI:10.1016/j.ijar.2014.05.007 ( 0) 0)
|
| [20] |
史德容, 徐伟华. 区间值模糊决策序信息系统的分布约简[J]. 计算机科学与探索, 2017, 11(4): 652-658. SHI Derong, XU Weihua. Distribution reduction in interval-valued fuzzy decision ordered information systems[J]. Journal of frontiers of computer science and technology, 2017, 11(4): 652-658. DOI:10.3778/j.issn.1673-9418.1602002 (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


