人脸识别因其友好性、无侵害、易获取等特点,成为图像处理和计算机视觉中受关注的领域之一。提取区分性好、鲁棒性好的人脸特征,构建高效可靠的分类器,来提升人脸识别的正确率,一直是人脸识别研究的难点与重点[1]。
经典的人脸识别算法有Eigenface[2]、Fisherface[3]、拉普拉斯脸[4]等。2009年,John Wright等[5]提出一种基于稀疏表示分类(sparse representation based classification,SRC)人脸识别算法。SRC算法首先在训练图像上对未知图像做编码处理,然后通过计算最小编码误差来估计未知图像属于哪一类,从而达到分类目的。SRC的快捷与高效性,使得它广泛用于人脸识别领域。SRC过度强调l1范数的作用,忽略了用所有类别信息表示测试样本的协同作用。因此,Zhang等[6]提出协同表征(collaborative representation,CR)是稀疏分类的关键和本质,而非强稀疏性,CR便在模式识别中被广泛采用。如Zhao[7]、Liu[8]提出核协同用于人脸识别和图像分类等。SRC与CR采用固定字典分类可能缺乏足够的区分信息,因此研究者们对带稀疏约束的字典学习算法展开了研究,并取得较好的效果。如Yang等[9]提出Fisher区分字典学习算法(fisher discrimination dictionary learning,FDDL),Chen等[10]提出稀疏嵌入字典学习算法(sparse embedded dictionary learning,SEDL)等。最近,基于深度学习的卷积神经网络在人脸识别也取得理想的效果。如Sun等[11]提出DeepID算法、Yi 等[12]提出的WebFace算法等。上述算法在人脸识别虽然取得明显效果,但它们都采用多样本做训练,与实际应用情况不符合,因此用于单样本人脸识别效果将下降。
与字典学习、深度学习相比,SRC与CR算法使用训练样本少,计算复杂度更低。虽然SRC和CR算法对受污染的待测样本有较好的识别能力,但训练样本不受污染是前提。可变光照会改变人脸图像的灰度分布,而传统的主成分分析[13](principal component analysis,PCA)等算法不能很好地提取光照不变量,因此Gabor小波被广泛用于人脸光照不变特征提取。如文献[14]提出基于Gabor滤波的二值模式方法(histogram sequence of local Gabor binary patterns,HSLGBP);文献[15]提出基于Gabor小波低秩恢复稀疏表示分类法。由于Gabor变换存在直流分量和带宽受限,从而Log-Gabor[16]变换被提出,刘元等[17]将其用于人脸识别。Log-Gabor仍然存在维数高、耗时长的缺点。为降低特征维数,文献[18]提出正交梯度相位脸(orthogonal gradient phase face,OGPF),文献[19]提出正交梯度二值模式(orthogonal gradient binary pattern,OGBP)。文献[20]在文献[18-19]的基础上改进,提出中心对称梯度幅值相位模式(center-symmetric gradient magnitude and phase patterns,CSGMP),并取得较好的效果。
受文献[6,19]的启发,本文提出一种基于正交Log-Gabor滤波二值模式(orthogonal Log-Gabor binary pattern,OLGBP)的人脸识别算法。采用正交Log-Gabor滤波器组提取人脸特征并做特征融合得到OLGBP特征,将这些特征组合成字典,最后采用协同表征分类。
1 相关工作 1.1 协同表征假定有k类训练样本,每个人脸样本可表示为列向量v。则第i类训练样本可以表示为
Di=[vi,1 vi,2 ··· vi, n]
其中vi, j表示第i类中的第j个人脸列向量,ni表示第i类训练样本的总个数,m表示训练样本的维数,n表示样本总数,n=n1+n2+…+nm。用这些训练样本的线性组合构成字典D∈R,则测试样本y的协同表征系数
| $\hat a = \mathop {\arg \min }\limits_a \{ \left\| {{ y} - { {Da}}} \right\|_2^2 - \lambda \left\| { a} \right\|_2^2\} $ | (1) |
则系数
| $\widehat a = {({{ D}^{\rm T}}{ D} + \lambda \cdot { I})^{ - 1}}{{ D}^{\rm T}}y$ | (2) |
然后进行最小误差重构,误差最小项为测试样本所对应的项。重构公式为
| ${\rm identity}\left( { y} \right) = \mathop {\arg \min }\limits_i \left\{ {\frac{{{{\left\| {{ y} - {{ D}_i}\widehat {{{ a}_i}}} \right\|}_2}}}{{{{\left\| {\widehat { a}} \right\|}_2}}}} \right\}$ | (3) |
Gabor滤波器良好的空间局部性和方向选择性,被用于提取人脸多个方向的结构特征和空间频率,同时对光照和光照变化具有良好的鲁棒性。但Gabor滤波器存在两点不足:1)有直流分量,2)带宽受限。因此,Field提出Log-Gabor滤波器[12]。Log-Gabor滤波器带宽与人类视觉通道的带宽更接近,更适合对图像编码。二维Log-Gabor在频域上定义为
| ${\rm LG}\left( {u,v} \right) = \exp \left( { - \frac{{{{\left( {\log \left( {\displaystyle\frac{{{u_1}}}{{{u_2}}}} \right)} \right)}^2}}}{{2{{\left( {\log \left( {\displaystyle\frac{k}{{{u_0}}}} \right)} \right)}^2}}}} \right) \cdot \exp \left( { - \frac{{v_1^2}}{{{{\left( {2{\sigma _v}} \right)}^2}}}} \right)$ | (4) |
其中:
| $\left\{ \begin{aligned} &{u_1} = u\cos \;\theta + v\sin \;\theta \\ &{v_1} = - u\sin \;\theta + v\cos \;\theta \end{aligned} \right.$ |
式中:u0代表滤波器的中心频率;k控制滤波器在u1方向的带宽;σv控制滤波器在v1方向的带宽;θ代表滤波器的方向角度。
一幅图像的Log-Gabor特征就是该幅图像与Log-Gabor函数做卷积的结果。假定图像为
| ${\varphi _{u,v}}\left( {x,y} \right) = I\left( {x,y} \right) \otimes {{\rm {LG}}_{u,v}}\left( {x,y} \right)$ | (5) |
式中:
Log-Gabor滤波器组所提取的特征维数过高,从而导致计算机内存占有率高,算法识别耗时长,效率低下。受文献[19]的启发,提出正交Log-Gabor滤波器组。
正交Log-Gabor滤波器组是从Log- Gabor滤波器组中抽取正交方向的Log-Gabor特征。为了防止丢失有用的特征,因此在不同尺度上采取交叉选取正交方向。假定滤波器组选取5个尺度,8个方向。则全局Log-Gabor滤波器组的幅值特征如图1所示,正交Log-Gabor滤波器组的幅值特征如图2所示。

|
Download:
|
| 图 1 全局特征 Fig. 1 Global feature | |

|
Download:
|
| 图 2 正交特征 Fig. 2 Orthogonal feature | |
由图2可以看出,正交Log-Gabor滤波器组所提取的特征将是全局Log-Gabor滤波器组所提特征的一半。因此,所提特征维数是全局特征维数的一半,从而可实现特征降维。又由于正交特征的方向是正交的,因此所提特征在一定程度上减少了冗余。由上述分析可知,算法的计算开销将减少,相比同类算法识别速度有一定的提升。
2 OLGBP 2.1 人脸的OLGBP特征OLGBP特征提取过程:
1) 将样本分别与正交Log-Gabor滤波器组卷积,得到LG特征。
2) 首先对LG做虚、实分解,得到LGR和LGI。然后将LGR和LGI二值化,并进行同尺度不同方向的特征融合。最后,将融合特征转十进制。二值化模式定义为
| $P_{u,v}^{\operatorname{Re} }\left( {\textit{z}} \right) = \left\{ {\begin{array}{*{20}{c}} 1,&{\operatorname{Re} \left( {{{\rm {LG}}_{u,v}}\left( {\textit{z}} \right)} \right) > 0} \\ 0,&{\operatorname{Re} \left( {{{\rm {LG}}_{u,v}}\left( {\textit{z}} \right)} \right) \leqslant 0} \end{array}} \right.$ | (6) |
| $P_{u,v}^{\operatorname{Im} }\left( {\textit{z}} \right) = \left\{ {\begin{array}{*{20}{c}} 1,&{\operatorname{Im} \left( {{{\rm {LG}}_{u,v}}\left( {\textit{z}} \right)} \right) > 0} \\ 0,&{\operatorname{Im} \left( {{{\rm {LG}}_{u,v}}\left( {\textit{z}} \right)} \right) \leqslant 0} \end{array}} \right.$ | (7) |
式中:Re(LGu,v(z))代表Log-Gabor特征的实部,Im(LGu,v(z))代表Log-Gabor特征的虚部。
十进制编码模式定义为
| $T_u^{\operatorname{Re} }\left( {\textit{z}} \right) = \sum\limits_{v = 0}^{n - 1} {P_{u,v}^{\operatorname{Re} }\left( {\textit{z}} \right)} \times {2^v}$ | (8) |
| $T_u^{\operatorname{Im} }\left({\textit{z}} \right) = \sum\limits_{v = 0}^{n - 1} {P_{u,v}^{\operatorname{Im} }\left( {\textit{z}}\right) \times {2^v}} $ | (9) |
其中,n为方向的个数,
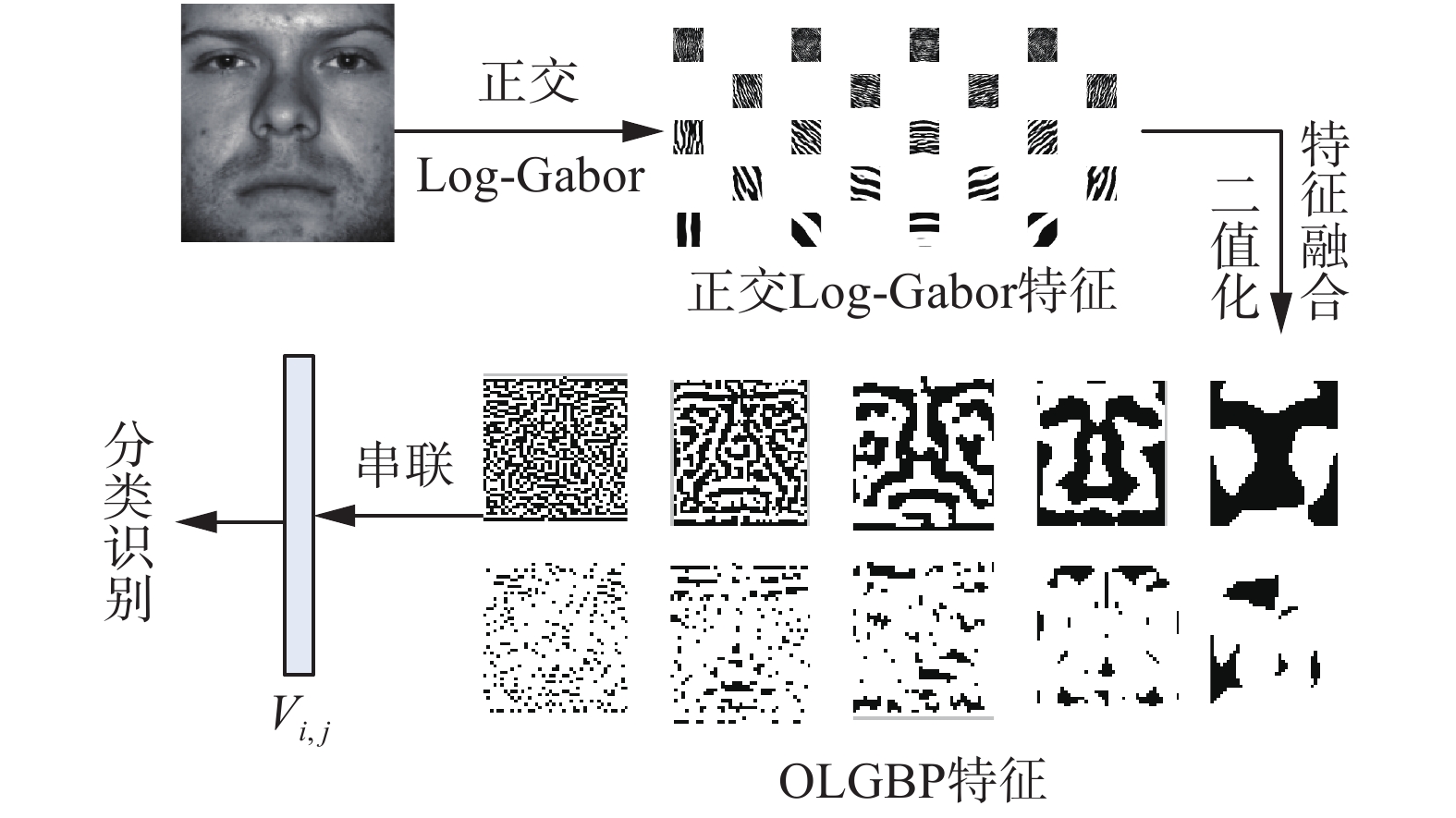
该算法通过协作表征分类,因此将提取的OLGBP特征组合成稀疏字典D进行稀疏编码,选取式(3)的最小值所在类作为测试样本的类别。人脸识别流程如图3所示。
|
Download:
|
| 图 3 人脸识别流程图 Fig. 3 Face recognition flow chart | |
为验证OLGBP算法的有效性,算法在AR人脸库、Extend Yale B人脸库和CAS- PEAL-R1人脸库分别进行仿真实验。实验环境为MATLAB R2013a,计算机硬件配置为 Windows7 32位系统,Intel(R) Pentium(R) B940 2.0 GHz,2 GB运行内存。
AR人脸库包含了126人的4 000多幅人脸图像,涵盖表情、光照和遮挡3种变化,原图像的尺寸为120×165。随机从库中选取50名男性和50名女性,每人4幅光照变化的图像进行实验。实验中,选择AR人脸库每个人的第1幅图像作为训练样本,剩余3幅做测试样本,图像尺寸为83×60,部分图像如图4所示。

|
Download:
|
| 图 4 AR 人脸库部分图像 Fig. 4 Example images in AR database | |
Extend Yale B人脸库包含了38人正面姿态下的2 432幅图像,涵盖64种不同光照,原图像的尺寸为168×192。根据光照入射角度分为5个子集:子集1的入射角度为0°~12°(每人7幅);子集2的入射角度为13°~25°(每人12幅);子集3的入射角度为26°~50°(每人12幅);子集4的入射角度为51°~77°(每人14幅);子集5的入射角度大于77°(每人19幅)。实验中,选择子集1每个人的第1幅图像作为训练样本,其他子集做测试样本,图像尺寸为96×84,部分图像如图5所示。

|
Download:
|
| 图 5 Extend Yale B 人脸库部分图像 Fig. 5 Example images in Extend Yale B database | |
CAS-PEAL-R1人脸库包含正面图像库和姿态图像库,由1 040名中国人的99 450幅人脸图像组成,原图像的尺寸为100×100。实验中,采用正面图像库的光照变化图像做实验,随机选取其中199人(每人9幅),每人的第i(i=1,2,3,4,5)幅作为训练样本,其余为测试样本,图像尺寸为83×60,部分图像如图6所示。

|
Download:
|
| 图 6 CAS-PEAL-R1人脸库部分图像 Fig. 6 Example images in CAS-PEAL-R1 database | |
1)滤波器尺度u与方向v对识别率的影响
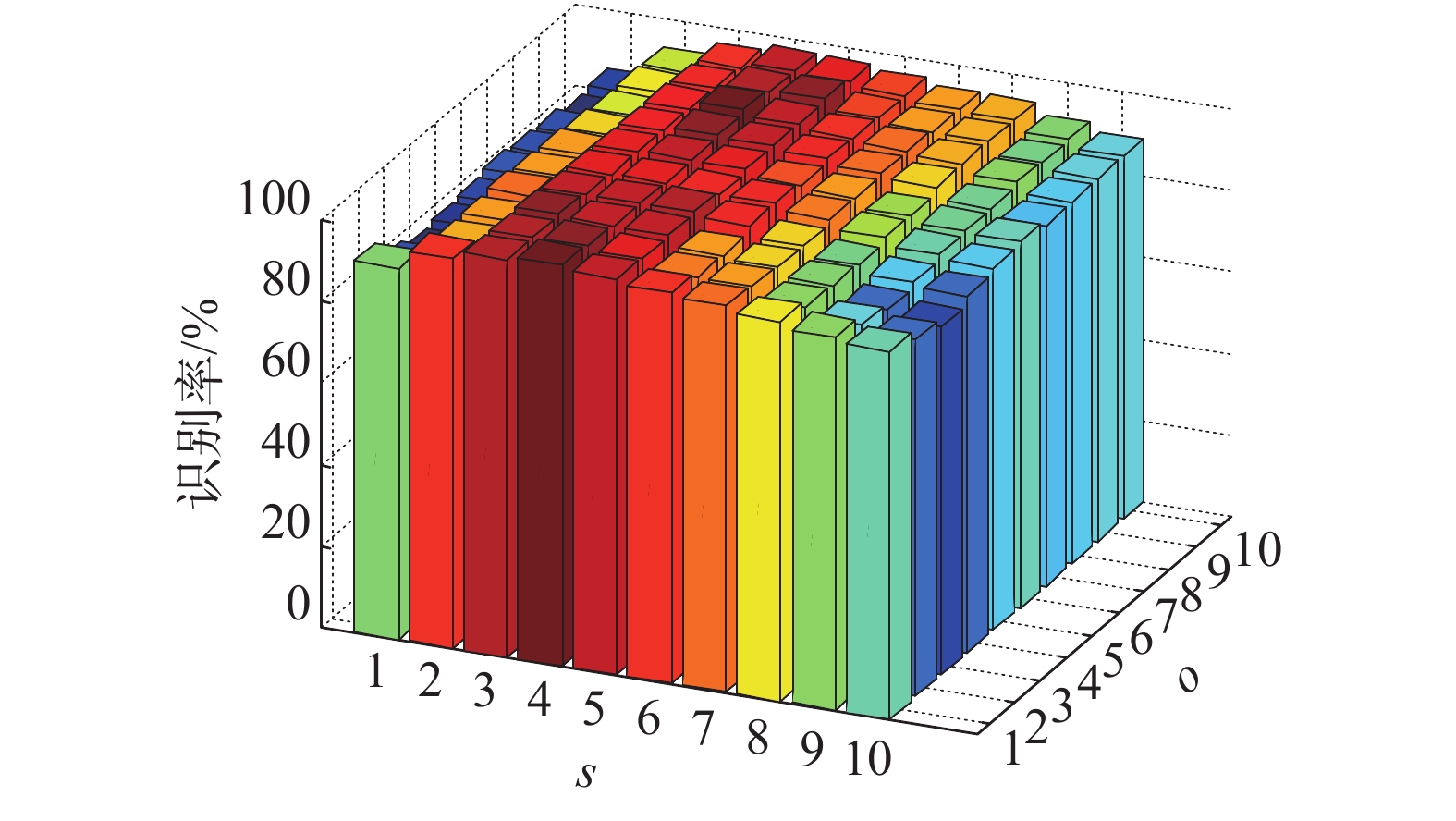
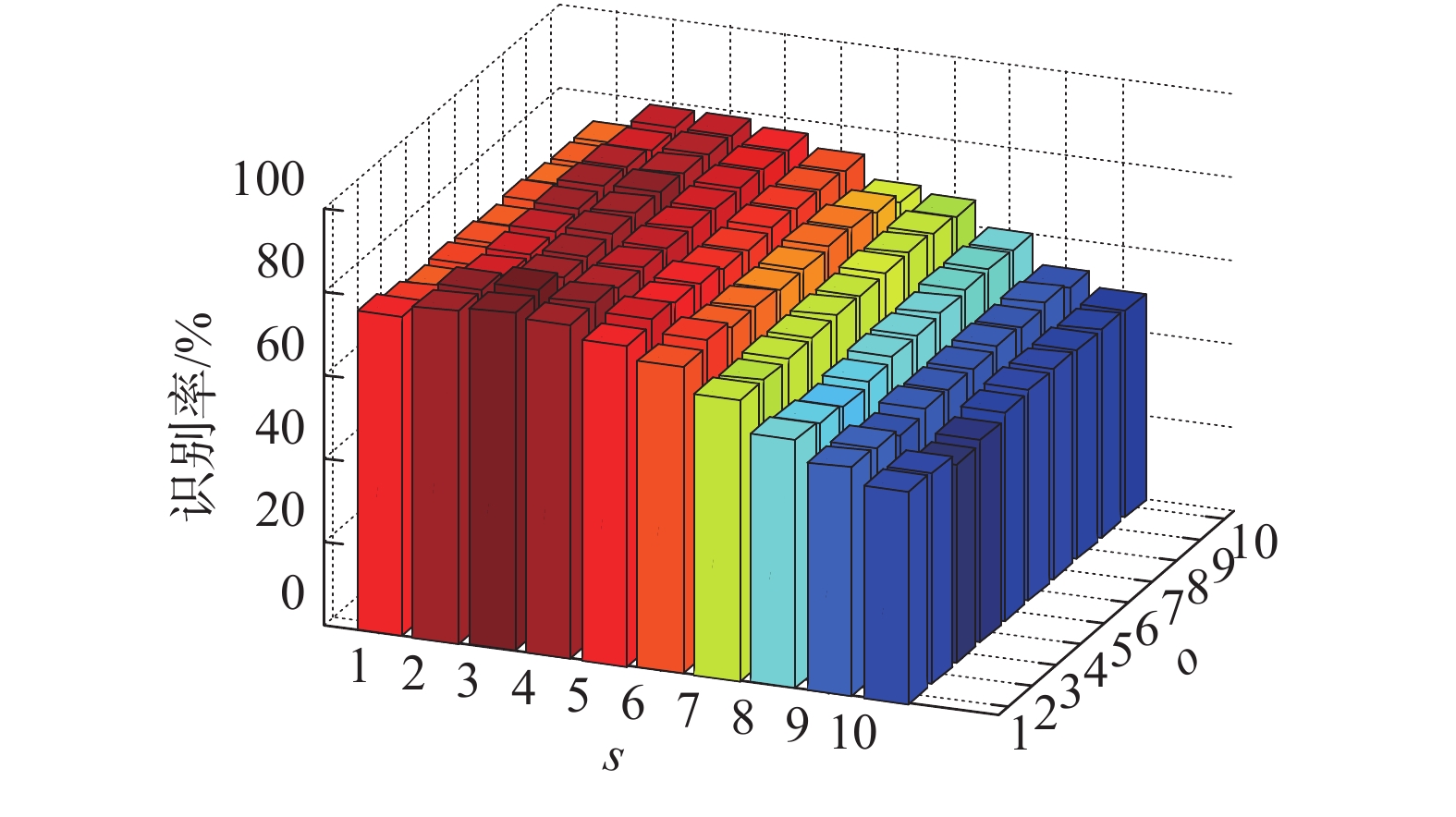
多数情况下,在使用Gabor滤波器时均采用5个尺度、8个方向,为验证滤波器尺度s与方向o分别对算法识别率的影响,OLGBP算法将在AR人脸库和CAS-PEAL-R1人脸库上进行实验。特征维数设定为90,实验结果如图7、8所示。
|
Download:
|
| 图 7 s、o在AR的实验结果 Fig. 7 s and o’s result in AR | |
|
Download:
|
| 图 8 s、o在CAS-PEAL-R1的实验结果 Fig. 8 s and o’s result in CAS-PEAL-R1 | |
图7和图8中横坐标分别代表滤波器的尺度个数s、方向个数o。纵轴代表滤波器的识别率。从图7和图8可以看出,当取小尺度数和较少的方向数时,所提取到的人脸信息少,导致识别率较低。当取大尺度数和较大的方向数时,所提取的人脸信息过多造成冗余,导致有用信息丢失,识别率下降。因此,在保证识别率的前提下,算法的计算开销尽可能小,则Log-Gabor滤波器组的尺度数选3、方向数选2都有较好的识别率。
2)正交特征和全局特征对识别率的影响
为验证正交特征和全局特征对识别率的影响,OLGBP算法和LGBP算法将在AR人脸库、CAS-PEAL-R1人脸库和Extend Yale B人脸库的S4上进行实验。Log-Gabor滤波器和正交Log-Gabor滤波器均设定为3个尺度2个方向,特征维数设定为90维,实验结果如表1所示。
| 表 1 算法识别结果 Tab.1 Algorithm’s results |
从表1可以看出,在维数降至90的前提下,AR库上LGBP的识别率比OLGBP高0.33%,CAS-PEAL-R1库上LGBP的识别率比OLGBP高0.69%,Extend Yale B的S4上LGBP的识别率比OLGBP低1.43%。由此可知,除S4外OLGBP算法的识别率比LGBP算法的识别率稍低,但总体上相差不大。但LGBP算法产生了12幅LG特征图像,OLGBP算法只产生了6幅LG特征图像,因此OLGBP特征维数是LGBP特征维数的1/2。说明取正交方向的LG特征,在一定程度上可减少特征冗余,实现特征降维,提高算法的效率。
3)编码系数比较
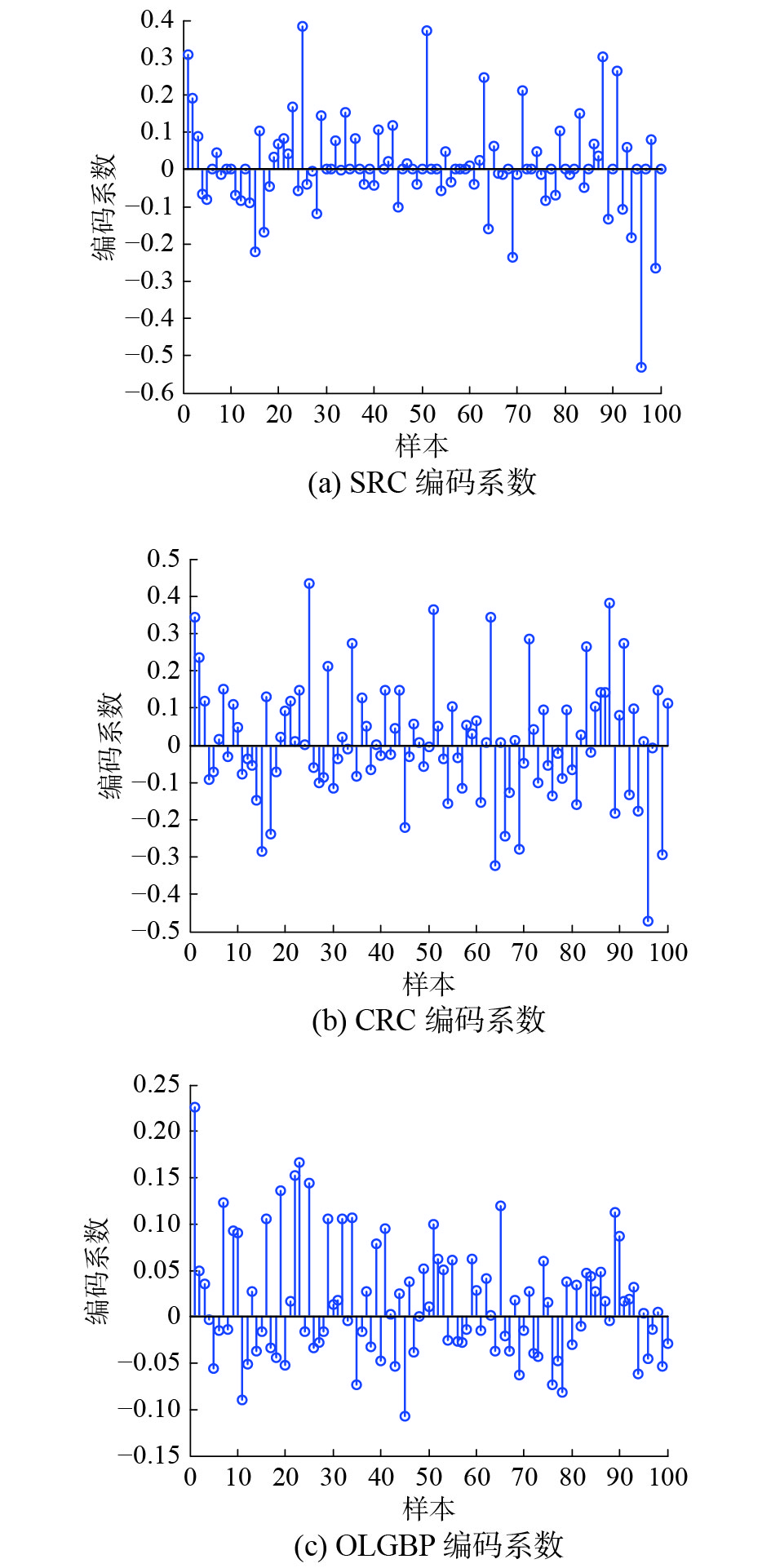
为验证OLGBP编码系数的有效性,OLGBP算法将与SRC、CRC算法作对比。对比实验将在AR人脸库进行,以AR库第一幅人脸图像为例。
从图9可以看出,相同样本各算法的编码系数各不相同。SRC与CRC编码系数相似,它们将第一类样本归于其他类,而OLGBP算法实现准确分类。由此可以说明,OLGBP算法相对SRC和CRC算法提取的特征更具有区分性。
|
Download:
|
| 图 9 各算法编码系数对比 Fig. 9 The coding coefficients of algorithms | |
为验证OLGBP算法的有效性,分别与SRC算法[5]、CRC_RLS算法[6]、OGPF算法[12]、OGBP算法[13]、CSGMP算法[14]进行对比。SRC算法参数λ=0.01。CRC_RLS算法中参数λ=0.001。在OGPF算法中,方向数为5,高斯标准差σ=0.9。在OGBP算法中,方向数为8,高斯标准差σ=1。在CSGMP算法中,CSLDP尺寸为3×3,高斯标准差σ=0.6。OLGBP算法中,CRC_RLS的参数λ=0.001,Log-Gabor的尺度s=3、方向o=2,最小波长为3,缩放因子为2。实验中OLGBP、SRC和CRC_RLS算法的AR库和CAS-PEAL-R1库人脸尺寸为83×60,Extend Yale B 库的人脸尺寸为96×84。其余算法的人脸尺寸为都为100×100。所有实验进行20次,并对结果取平均值。
从表2可以看出,OGPF、OGBP、CSG- MP和OLGBP各算法都取得了良好的识别率。SRC和CRC_RLS算法只考虑了稀疏表示,并没有对图像提取更加显著的特征;OGPF算法提取人脸5个方向的梯度相位特征,使用于分类的信息更加丰富;OGBP算法是OGPF算法的改进,它将梯度相位进行8个方向的量化并赋予不同的权值;CSGMP算法利用了梯度幅值和梯度相位的互补性,提取了人脸不变特征。OLGBP算法采用正交Log-Gabor滤波器组提取多尺度下的特征图,并通过对虚部和实部二值编码充分挖掘了人脸信息,取得了良好的识别率。
| 表 2 AR人脸库上识别结果 Tab.2 Face recognition results in AR |
从表3可以看出:CRC_RLS算法虽然在第1、2、4幅图有很好的效果,但第4、5幅图的识别率低,导致算法识别率不稳定,可靠性降低。OLGBP算法通过提取多尺度、多方向特征对单样本进行了细节的扩充,再通过虚实分解和编码使得人脸结果信息更丰富,相比其他算法识别率得到提升且稳定性较好。
| 表 3 CAS-PEA-R1人脸库上识别结果 Tab.3 Face recognition results in CAS-PEA-R1 |
表4的复杂光照的实验结果可以看出子集2中人脸光照条件良好,算法识别率都很高;子集3~5中人脸光照条件越来越差,没有进行特征提取的SRC、CRC_RLS算法和只进行局部特征提取的CSGMP算法识别率下降最快;OGPF和OGBP利用梯度信息,识别率下降慢;OLGBP通过提取多尺度正交方向信息,对虚部和实部分别编码提高了抗干扰的能力,在剧烈的光照下也有较高的识别率。
| 表 4 Extend Yale B人脸库上识别结果 Tab.4 Face recognition results in Extend Yale B |
为对比算法的复杂程度,在AR库的光照集进行试验。以AR库每人的第一张人脸作为训练样本,光照变换人脸作为测试样本,测试算法识别一张人脸所花的时间为
| $ t = {T_1} + {T_2} $ |
式中:T1表示提取一幅人脸特征消耗的平均时间,T2表示一张测试样本与多张训练样本匹配消耗的平均时间。各算法在AR光照集的特征维数与耗时结果如表5所示。
| 表 5 不同算法在光照集的特征维数与耗时 Tab.5 Different algorithm’s dimension and time in different illumination set ms |
从表5可以看出:OLGBP算法比OGPF、OGBP和CSGMP的特征维数都要小,且OLGBP的每一项平均耗时都低于上述3种算法,其原因在于OGPF采样了5个方向的特征,OGBP采样了8个方向的特征,CSGMP采用CSLDP算子维数相对较小但特征提取时间太长,而OLGBP只采样2个方向的特征。SRC算法和CRC_RLS算法没有提取特征,因此特征提取耗时项为0。由于SRC采取l1来求解稀疏系数,因此特征匹配耗时远远高于其他算法。OLGBP是CRC_RLS的改进,因此增加了特征提取、特征匹配的耗时。结合表2~5来看,OLGBP算法不仅识别率高,而且算法的时间开销少,可以满足时性的要求。
4 结束语正交Log-Gabor滤波二值模式算法首先采用Log-Gabor滤波组提取多尺度正交方向的LG特征,然后对LG特征进行虚实分解并编码、融合,最后将OLGBP特征组合成稀疏字典采用协作表示进行分类。实验结果表明:正交方向的LG特征可以减少特征的冗余,降低特征维数。对LG的虚实分解,可以充分提取人脸所隐藏的信息。对多尺度多方向LG特征的融合即可以增强特征的判断能力,也可以进一步实现降维。
采用正交Log-Gabor滤波器组所提特征数是全局Log-Gabor滤波器组所提特征数的一半。因此,所提特征维数是原来特征维数的一半,从而可实现特征降维。又由于OLGBP特征的方向是正交的,因此所提特征在一定程度上减少了冗余,识别率基本保持不变。由上述分析可知算法的计算开销可减少,相比同类算法识别速度得到提升。在AR、Extend Yale B和CAS-PEAL-R1人脸库的实验结果表明:OLGBP算法不仅对光照变化的人脸有较高的识别率,而且还降低了识别时间,因此说明了该算法对光照的有效性。未来的工作将进一步对特征提取做研究分析,通过改进特征提取算法,使得特征维数和识别时间降低并提高算法的识别率。
| [1] |
ADINI Y, MOSES Y, ULLMAN S. Face recognition: the problem of compensating for changes in illumination direction[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(7): 721-732. DOI:10.1109/34.598229 ( 0) 0)
|
| [2] |
TURK M, PENTLAND A. Eigenface for recognition[J]. Journal of cognitive neuroscience, 1991, 3(1): 71-86. DOI:10.1162/jocn.1991.3.1.71 ( 0) 0)
|
| [3] |
BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 ( 0) 0)
|
| [4] |
HE Xiaofei, YAN Shuicheng, HU Yuxiao, et al. Face recognition using laplacianfaces[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(3): 328-340. DOI:10.1109/TPAMI.2005.55 ( 0) 0)
|
| [5] |
WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 ( 0) 0)
|
| [6] |
ZHANG Lei, YANG Meng, FENG Xiangchu. Sparse representation or collaborative representation: Which helps face recognition?[C]//Proceedings of 2011 IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 471–478.
( 0) 0)
|
| [7] |
ZHAO Jia, WANG Yanjiang, LIU Baodi. Kernel collaborative representation for face recognition[C]//Proceedings of the 12th International Conference on Signal Processing. Hangzhou, China, 2014: 1423–1427.
( 0) 0)
|
| [8] |
LIU Weiyang, LU Lijia, LI Hui, et al. A novel kernel collaborative representation approach for image classification[C]//Proceedings of 2014 IEEE International Conference on Image Processing. Paris, France, 2014: 4241–4245.
( 0) 0)
|
| [9] |
YANG Meng, ZHANG Lei, FENG Xiangchu, et al. Fisher discrimination dictionary learning for sparse representation[C]//Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain, 2011: 543–550.
( 0) 0)
|
| [10] |
CHEN Yefei, SU Jianbo. Sparse embedded dictionary learning on face recognition[J]. Pattern recognition, 2017, 64: 51-59. DOI:10.1016/j.patcog.2016.11.001 ( 0) 0)
|
| [11] |
SUN Yi, WANG Xiaogang, TANG Xiaoou. Deep learning face representation from predicting 10,000 classes[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA, 2014: 1891–1898.
( 0) 0)
|
| [12] |
YI Dong, LEI Zhen, LIAO Shengcai, et al. Learning face representation from scratch[J]. Computer science, arXiv: 1411.7923, 2014.
( 0) 0)
|
| [13] |
CANDÈS E J, LI Xiaodong, MA Yi, et al. Robust principal component analysis?[J]. Journal of the ACM, 2011, 58(3): 11. ( 0) 0)
|
| [14] |
ZHANG Wenchao, SHAN Shiguang, GAO Wen, et al. Local Gabor binary pattern histogram sequence (LGBPHS): a novel non-statistical model for face representation and recognition[C]//Proceedings of the 10th IEEE International Conference on Computer Vision. Beijing, China, 2005, 1: 786–791.
( 0) 0)
|
| [15] |
杜海顺, 张旭东, 金勇, 等. 基于Gabor低秩恢复稀疏表示分类的人脸图像识别方法[J]. 电子学报, 2014, 42(12): 2386-2393. DU Haishun, ZHANG Xudong, JIN Yong, et al. Face image recognition method via Gabor low-rank recovery sparse representation-based classification[J]. Acta electronica sinica, 2014, 42(12): 2386-2393. DOI:10.3969/j.issn.0372-2112.2014.12.008 (  0) 0)
|
| [16] |
FIELD D J. Relations between the statistics of natural images and the response properties of cortical cells[J]. Journal of the optical society of America A, 1987, 4(12): 2379-2394. DOI:10.1364/JOSAA.4.002379 ( 0) 0)
|
| [17] |
刘元, 吴小俊. 基于Log-Gabor滤波与黎曼流形学习的图像识别算法[J]. 模式识别与人工智能, 2015, 28(10): 946-952. LIU Yuan, WU Xiaojun. Image recognition algorithm based on Log-Gabor wavelet and Riemannian manifold Learning[J]. Pattern recognition and artificial intelligence, 2015, 28(10): 946-952. (  0) 0)
|
| [18] |
CHEN XI, ZHANG Jiashu. Illumination robust single sample face recognition using multi-directional orthogonal gradient phase faces[J]. Neurocomputing, 2011, 74(14/15): 2291-2298. ( 0) 0)
|
| [19] |
杨恢先, 蔡勇勇, 翟云龙, 等. 基于正交梯度二值模式的单样本人脸识别[J]. 计算机应用, 2014, 34(2): 546-549. YANG Huixian, CAI Yongyong, ZHAI Yunlong, et al. Single sample face recognition based on orthogonal gradient binary pattern[J]. Journal of computer applications, 2014, 34(2): 546-549. (  0) 0)
|
| [20] |
杨恢先, 翟云龙, 蔡勇勇, 等. 基于中心对称梯度幅值相位模式的单样本人脸识别[J]. 光电子·激光, 2015, 26(5): 969-977. YANG Huixian, ZHAI Yunlong, CAI Yongyong, et al.. Face recognition based on center-symmetric gradient magnitude and phase patterns[J]. Journal of optoelectronics·laser, 2015, 26(5): 969-977. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


