传统的转子永磁型电机需要对其转子加装专门的装置，才能克服转子在运作时所产生的离心力，因此导致此电机结构复杂，制造成本高昂。磁通切换型永磁电机(flux-switching permanent magnet, FSPM)将永磁体放在定子侧，是一种较新的定子永磁型电机，其克服了以上所述的转子永磁电机存在的问题，被认为具有广泛的应用价值^[1-3]。定子永磁型电机具有直流偏置磁场、定子外漏磁和端部漏磁等独特的电磁现象^[4]，这使得此类电机的分析和计算难度进一步加大。对于FSPM电机的高性能控制，结合矢量控制和电流滞环控制的电机控制方法^[5]，目前被国内外学者采用较多。针对不同的控制要求，FSPM电机还可以采用SVPWM控制和弱磁控制等策略^[6-7]。近年来，对于FSPM电机的调速系统，一些先进控制算法^[8-10]也越来越多地被应用于其中。文献[11]提出了一种基于电压空间矢量的脉宽调制技术(SVPWM)的控制策略，其目的在于使电机获得幅值恒定的圆形磁场，提高了系统的精确度，因此在交流电机的调速系统中得到了较为广泛的应用。文献[12]提出了一种带积分条件的自整定模糊PI控制方法，该方法对电机非线性电磁方面的特性具有良好的适应能力。

自抗扰控制(ADRC)是韩京清教授创立的一种不依赖于被控过程模型的原创性控制思想和方法^[13]，其核心是将系统的外部扰动以及内部未建模动态结合在一起作为“总扰动”，通过扩张状态观测器(ESO)对系统各个状态和总扰动进行在线估计，并及时地将总扰动补偿到反馈控制中。高志强等学者提出了线性自抗扰控制(LADRC)^[14]，将ADRC的主要环节进行了线性化处理，使得获得的LADRC具有结构简单、易于性能分析和参数整定等特点^[15]，因此极大地促进了自抗扰控制理论的深入发展及在工程中的推广与应用^[16-19]。

以定子12槽、转子10极的三相FSPM电机作为本文的研究对象，定子绕组采用集中式分布，其转子结构和开关磁阻电机相似。本文在掌握了其工作原理的基础上，建立了FSPM电机的稳态和动态仿真模型，并尝试将LADRC引入到电机的调速系统中，数值仿真结果表明本文所提出的LADRC控制方案能够有效地提高系统的鲁棒性和抗干扰能力。

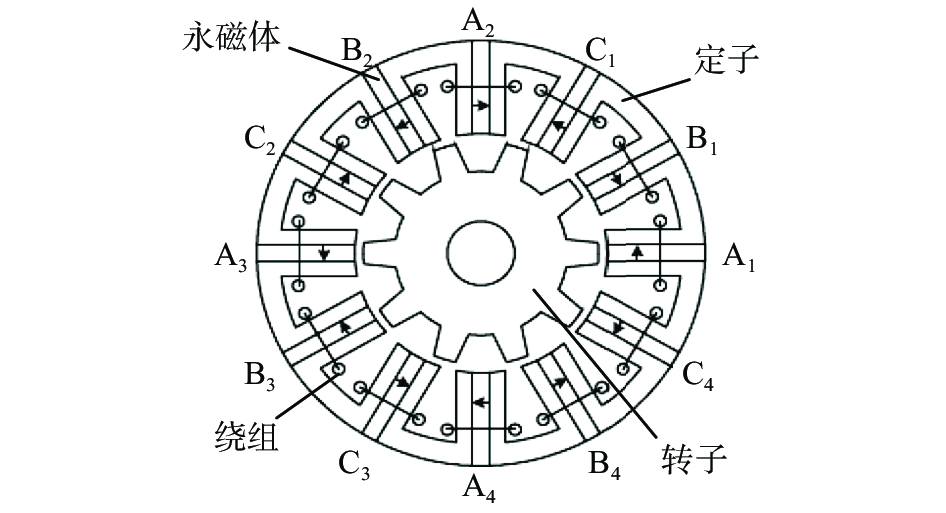
1 数学模型

三相12/10极FSPM电机的结构剖面如图1所示，定子部分由U型磁芯顺次组装而成，每两个磁芯之间嵌入一块永磁体，转子上无绕组和永磁体。将12个电枢线圈共分为3组，每4个串联成一相电枢绕组。

当转子齿与同一相线圈下分别属于两个U型单元的定子齿对齐时，FSPM电机的电枢绕组里匝链的永磁磁链的极性会发生变化，通过FSPM电机定转子齿之间这种独特的设计，来产生感应电势，可以实现磁通之间的切换。

假设FSPM电机的三相绕组结构与参数相同，忽略铁芯损耗，由此可得其在定子坐标系下的电压方程：

$\left[ \begin{array}{l}{u_a}\\{u_b}\\{u_c}\end{array} \right] = {R_{ph}}\left[ \begin{array}{l}{i_a}\\{i_b}\\{i_c}\end{array} \right] + {L_1}\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ \begin{array}{l}{i_a}\\{i_b}\\{i_c}\end{array} \right] + \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ \begin{array}{l}{\psi _a}\\{\psi _b}\\{\psi _c}\end{array} \right] + \left[ \begin{array}{l}{e_{ma}}\\{e_{mb}}\\{e_{mc}}\end{array} \right]$

(1)

式中：u_a、u_b、u_c为三相电压；i_a、i_b、i_c为三相电流； ${R_{ph}}$ 为绕组电阻； ${L_1} = {L_0} - {M_0}$ ，其中L₀、M₀分别为自感和互感的基波分量；ψ_a、ψ_b、ψ_c为三相绕组匝链的总磁链；e_ma、e_mb、e_mc为三相反电动势。

在电机运行过程中，如果转矩脉动过大则会对电机的正常运行产生负面影响。由于FSPM电机自身的永磁气隙磁密度比较高，该电机的齿槽转矩要比传统的转子永磁型电机在数值上大得多。因此考虑齿槽转矩影响后的瞬时电磁转矩为

${T_{em}} = \frac{{{P_{em}}}}{{{\omega _r}}} = {T_{pm}} + {T_r} + {T_{cog}}$

(2)

式中： ${P_{em}}$ 为电磁功率； ${T_{pm}}$ 、 ${T_r}$ 和 ${T_{cog}}$ 分别为电机的永磁、磁阻和齿槽转矩。

FSPM电机的机械运动方程可以表示为

${T_{em}} = J\frac{{{\rm{d}}{\omega _r}}}{{{\rm{d}}t}} + {T_L} + {B_v}{\omega _r}$

(3)

${\omega _r} = \frac{{{\rm{d}}{\theta _r}}}{{{\rm{d}}t}}$

(4)

式中： ${\omega _r}$ 为电机机械角速度； ${T_L}$ 为负载转矩； $J$ 为系统的转动惯量； ${B_v}$ 为系统的摩擦系数。

FSPM电机的反电动势和电流均为正弦波波形，因此其在转子旋转坐标系下(d-q 轴)的模型和正弦波永磁同步电机类似。忽略铁芯饱和，经过Park变换后的 FSPM模型为

$\left[ \begin{array}{l}\!\!\!\! {u_d} \!\!\!\! \\\!\!\!\! {u_q} \!\!\!\! \\\!\!\!\! {u_0} \!\!\!\! \end{array} \right] = \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ \begin{array}{l}\!\!\!\! {\psi _d} \!\!\!\! \\\!\!\!\! {\psi _q} \!\!\!\! \\\!\!\!\! {\psi _0} \!\!\!\! \end{array} \right] + \left[ {\begin{array}{*{20}{c}}\!\!\!\! {{R_{ph}}} & 0 & 0 \!\!\!\! \\\!\!\!\! 0 & {{R_{ph}}} & 0 \!\!\!\! \\\!\!\!\! 0 & 0 & {{R_{ph}}} \!\!\!\! \end{array}} \right]\left[ \begin{array}{l}\!\!\!\! {i_d} \!\!\!\! \\\!\!\!\! {i_q} \!\!\!\! \\\!\!\!\! {i_0} \!\!\!\! \end{array} \right] + \left[ {\begin{array}{*{20}{c}}\!\!\!\! { - {\omega _e}{\psi _q}} \!\!\!\! \\\!\!\!\! {{\omega _e}{\psi _d}} \!\!\!\! \\\!\!\!\! 0 \!\!\!\! \end{array}} \right]$

(5)

${T_{em}} = \frac{3}{2}\frac{{{P_{em}}}}{{{\omega _r}}}{\rm{ = }}\frac{3}{2}{P_r}\left[ {{\psi _m}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}} \right] + {T_{cog}}$

(6)

式中：u_d、u_q、i_d、i_q、ψ_d、ψ_q分别为定子电压和定子磁链在直轴和交轴上的分量； ${\omega _e}$ 为电角速度， ${\omega _e} = {P_r}{\omega _r}$ ； ${P_r}$ 为转子极数。

永磁磁链从定子abc坐标系变换到转子d-q坐标系后，仅仅只在d轴绕组中匝链一个恒定的永磁磁链，FSPM的直轴永磁磁链 ${\psi _{md}}$ 和交轴永磁磁链 ${\psi _{mq}}$ 满足以下关系式：

$\left\{ \begin{array}{l}{\psi _{md}} = {\psi _m}\\{\psi _{mq}} = 0\end{array} \right.$

(7)

2 基于LADRC的FSPM矢量控制 2.1 矢量控制

近年来矢量控制已在无刷交流调速系统中得到了较为广泛的应用。对调速系统而言，其运行区域一般可分为恒转矩区和恒功率区，其中恒转矩区是指电机转速处于低于额定转速的运行区域，恒功率区则相反。

目前在恒转矩区常采用的电流控制方法有4种，分别为 ${i_d} = 0$ 、恒磁链、 $\cos \phi = 1$ 和最大转矩电流比控制；这4种电流控制算法是根据给定的电磁转矩 $T_{{em}}^*$ 对直轴电流 $i_d^*$ 和交轴电流 $i_{q}^*$ 的大小进行合理的分配。

在恒功率区通常采取弱磁控制，弱磁控制的目的在于通过在d轴施加与永磁磁链极性相反的电流分量以产生一个电枢反应磁链来减小或抵消永磁磁链，因此能够减小合成电动势，保持电枢绕组电压的平衡，扩宽了系统的调速范围。

${i_d} = 0$ 是上述4种电流控制算法中最简单的一种，这种控制方法使得用来调节磁场的直轴电流为0，并根据给定的电磁转矩 ${T^*_{em}}$ 通过计算得到交轴电流 ${i^*_q}$ ，本文采用 ${i_d} = 0$ 控制，则其电磁转矩公式可简化为

${T_{em}} = {T_{pm}} + {T_{cog}} = \frac{3}{2}{P_r}{\psi _m}{i_q} + {T_{cog}}$

(8)

2.2 线性自抗扰控制

自抗扰控制技术是基于控制理论基础上发展起来的一种新型实用技术，它不仅吸收了现代控制理论的丰硕成果，更是对PID控制的延续和升华。通过实时地估计系统的总扰动并加以补偿，实现动态系统的反馈线性化，将非线性系统转化为线性系统的串联积分器的形式，然后针对该串联积分器标准型设计反馈控制。

下面以一阶LADRC为例来说明控制器的设计原理。设一类不确定对象为

$\dot y = - ay + w + bu$

(9)

式中： $u$ 为控制量； $y$ 为输出量； $w$ 为未知外部扰动； $b$ 为系统的放大倍数。为了将系统转化为标准的串联积分器的形式，设 $f = - ay + w + \left( {b - {b_0}} \right)u$ 为总扰动； ${b_0}$ 为 $b$ 的估计值。

将式(9)写成状态方程的形式：

$\left\{ \begin{array}{l}{{\dot x}_1} = {x_2} + {b_0}u\\{{\dot x}_2} = \dot f = h\\y = {x_1}\end{array} \right.$

(10)

式中： ${x_2} = f$ 是未知的被扩张的状态变量，且 $\dot f = h$ ，可由式(11)表示的线性扩张状态观测器 $\left( {{\rm{LESO}}} \right)$ 估计出来：

$\left\{ \begin{array}{l}{{\dot z}_1} = {z_2} - {\beta _1}\left( {{z_1} - y} \right) + {b_0}u\\{{\dot z}_2} = - {\beta _2}\left( {{z_1} - y} \right) \end{array} \right.$

(11)

通过选择合适的观测器增益 $\,{\beta _1}\text{、}{\beta _2}$ ， ${\rm{LESO}}$ 各状态量 ${z_i}(t)$ 可分别对系统式(10)中的各个状态量 ${x_i}(t)$ 进行跟踪和估计，即

${z_1}\left( t \right) \to y\left( t \right),{z_2}\left( t \right) \to f$

选取控制律为

$u = \frac{{\left( { - {z_2} + {u_0}} \right)}}{{{b_0}}}$

(12)

将式(9)简化为一个积分串联结构，即

$\dot y = \left( {f - {z_2}} \right) + {u_0} \approx {u_0}$

(13)

设计P控制器对给定值与反馈值的误差进行校正:

${u_0} = {k_p}\left( {v - {z_1}} \right)$

(14)

转速调节器采用一阶线性自抗扰控制器。FSPM电机的转速方程表示为

$\begin{array}{c}{{\dot \omega }_r} = \displaystyle\frac{1}{J}\left( {{T_{{\rm{em}}}} - {T_L} - {B_v}{\omega _r}} \right) = \\a\left( x \right) + bu\end{array}$

(15)

式中： $u$ 为输入， $u = {T_{{\rm{em}}}}$ ； $b = \displaystyle\frac{1}{J}$ ； ${B_v}$ 为摩擦系数，一般取为0。

设 $f = a\left( x \right) + \left( {b - {b_0}} \right)u$ ， $f$ 为转速环的总扰动。将式(15)转化为如式(16)标准形式：

$\left\{ \begin{array}{l}{{\dot \omega }_r} = f + {b_0}u\\y = {\omega _r} \end{array} \right.$

(16)

转速环采用二阶线性扩张状态观测器：

$\left\{ \begin{array}{l}e = {z_1} - y\\{{\dot z}_1} = {z_2} - {\beta _1}\left( {{z_1} - {\omega _r}} \right) + {b_0}u\\{{\dot z}_2} = - {\beta _2}\left( {{z_1} - {\omega _r}} \right) \end{array} \right.$

(17)

P控制器：

${u_0} = {k_{\rm{p}}}\left( {v - {z_1}} \right)$

(18)

则系统式(15)等同于以下线性系统：

${\dot \omega _r} = {u_0} $

(19)

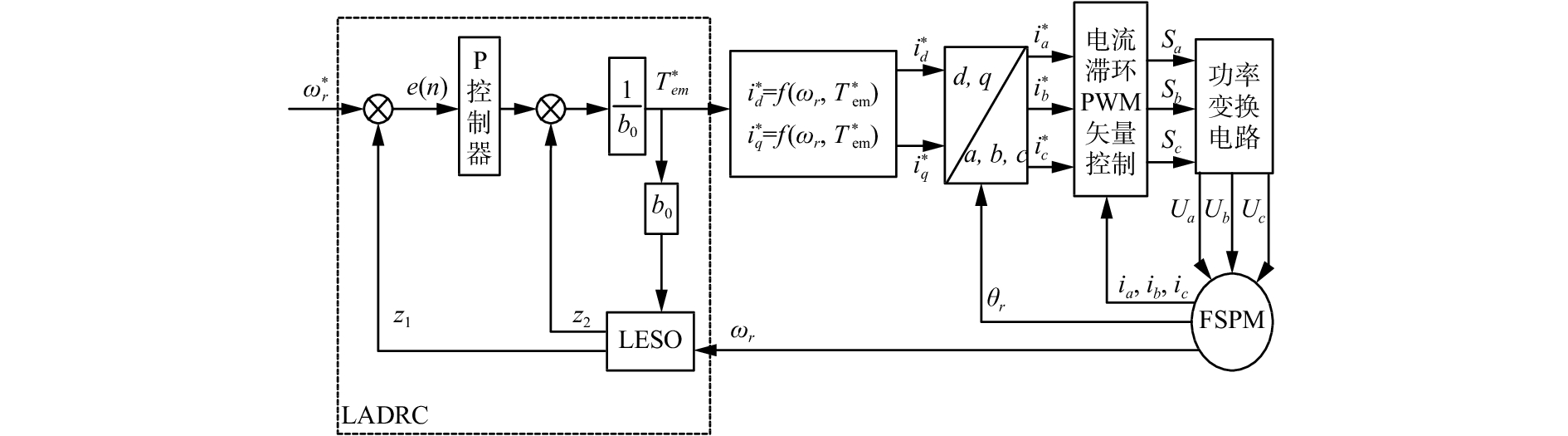
本文采用电流滞环比较的PWM矢量控制策略，并将线性自抗扰控制器引入到FSPM电机的调速系统中，整个闭环系统的控制结构如图2所示。

3 基于MATLAB/Simulink的仿真

为了验证所建立FSPM电机数学模型的正确性，分别建立其稳态和动态仿真模型。

3.1 稳态仿真结果

FSPM电机的稳态模型是在给定转速和转矩的前提下建立的，对电机的机械特性进行研究。根据表1设置三相FSPM电机的电磁和电气参数。

图3(a)为电机实际三相电流波形，图3(b)为给定电流 $i_a^ * $ 和反馈电流 ${i_a}$ 的对比曲线。可以看出电流的跟踪效果较好。图3(c)为转矩分量曲线，可以看出 ${T_{em}}$ 的平均值在理论值上下波动；而磁阻转矩 ${T_r}$ 近乎为零，因为选取了 ${i_d} = 0$ 控制；明显看出齿槽转矩是造成电磁转矩脉动的主要原因，与理论分析一致。图3(d)为直轴电流 ${i_d}$ 和交轴电流 ${i_q}$ 的实时波形，可以看出， ${i_d}$ 在0值附近波动， ${i_q}$ 在4.37 A附近波动，与理论值一致。

3.2 动态仿真结果

本节重点研究了将一阶LADRC引入到FSPM电机的调速系统之后系统的动态响应，并与采用传统PI控制的转速响应进行对比分析。LADRC参数选取为： ${b_0} = 12.5,{\omega _{o1}} = 120,{k_{p1}} = 200$ 。动态仿真主要从以下3个方面进行研究。

1) 空载启动

图4为FSPM电机在空载时的启动特性，电机转速的设定值为600 r/min。从图4(a)、(b)中可以看出，经过参数整定后的LADRC能使电机在很短的时间内(0.004 2 s)运行到设定的转速值，并且几乎没有超调。PI控制器参数整定为： ${k_p} = 1.805,{k_i} = 0.01$ ，此时得到系统的超调量为2.5%，调节时间为0.055 s。因此可以得出结论，LADRC较PI控制具有更优的转速跟踪效果。由图4(c)、(d)可见，因为电机空载启动，因此电磁转矩稳定在0值附近，稳态时交轴电流也近乎为0值。

2) 负载转矩恒定，转速突变

图5是在保持额定负载为4 N·m不变的情况下，仿真时间在0.015 s时，将给定转速由600 r/min突变为1 000 r/min时系统的动态响应曲线。

由图5(a)、(b)可知，在转速突变时，LADRC控制器的参数无需再次调节就可以达到良好的控制效果。而PI控制器的参数需要重新调节，整定后的参数为： ${k_p} = 2.25,{k_i} = 0.06$ 。仿真结果说明，采用LADRC控制的FSPM电机的转速响应曲线脉动更小，并且能以较快的速度恢复到稳态值；同时也说明经过参数整定后的LADRC控制器在转速突变时参数无需重新调整，因此比PI控制器具有更强的鲁棒性。

从图5(c)、(d)中可以看出，系统的电磁转矩和交轴电流都有一个小的抖动，电磁转矩最终达到4 N·m，交轴电流稳定在理论计算值1.6 A。

3) 转速恒定，负载转矩突变

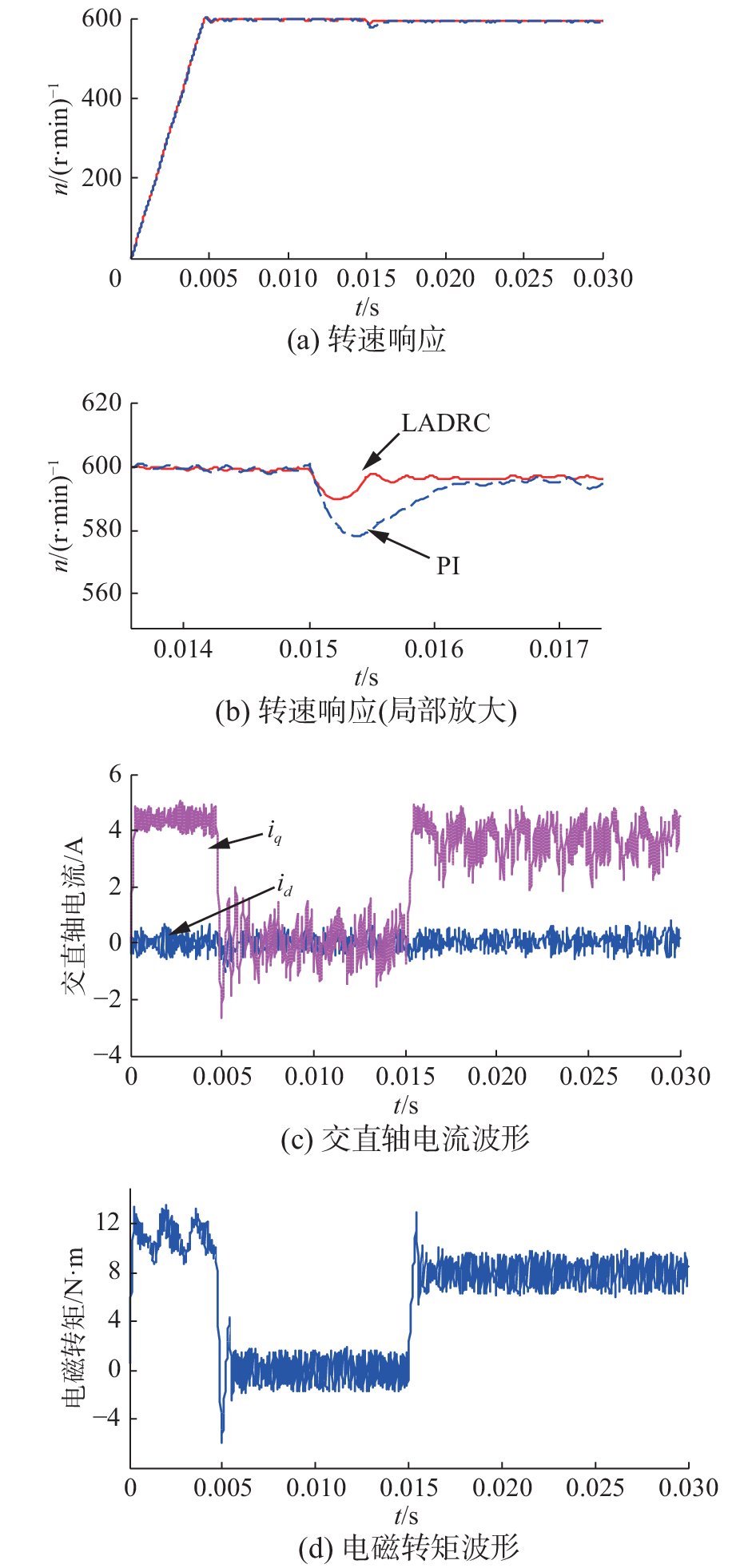
图6显示的是在保持转速为600 r/min不变的情况下，负载转矩在0.001 5 s时由0 N·m突变为8 N·m时电机的动态响应特性。

从图6(a)、(b)中可见，LADRC控制在突加负载扰动时较PI控制的电机转速具有更优的动态响应特性，此时PI控制器参数为: ${k_{\rm{P}}} = 2.05,{k_{\rm{I}}} = 0.02$ 。在0.015 s的时候负载突增到8 N·m，为了达到稳定的平衡状态，系统电磁转矩需要增大，而电磁转矩的增大依赖于交轴电流的增大。因此，由图6(c)、(d)可见，交轴电流在0.015 s时有突变，经过一个短暂的过渡阶段后，电磁转矩在8 N·m附近波动，电机进入稳定运行状态。

4 结束语

为实现FSPM电机的高性能控制，本文提出了基于线性自抗扰的新型矢量控制方案。建立的FSPM电机的稳态和动态仿真模型为系统分析该调速系统的实际控制效果提供了理论分析的工具。通过与传统的PI控制进行对比分析，验证了经过参数整定后的LADRC具有更好的转速跟踪效果，并且在转速突变或负载摄动时无需再进行参数整定，因此LADRC较PI具有更强的抗干扰能力和鲁棒性，有助于今后进一步研究线性自抗扰控制器在FSPM电机运行控制中的应用。