2. 香港科技大学 计算机科学及工程学系, 香港 999077
2. Department of Computer Science & Engineering, Hong Kong University of Science and Technology, Hong Kong 999077, China
1931年,Zipf[1]发现在自然语言中,词的频率与它在词汇表中的排名成反比,服从幂律分布,他把这种现象称为上下文语言模型中词的突发性。后来发现,在金融、基因表达、计算机视觉等方面的数据也存在这种突发现象。网络搜索已成为人们日常生活中必不可少的一部分,用户提交的搜索查询词是人类智慧的结晶,并在搜索查询和微博等网络信息中显现出与传统的自然语言不同的特点,网络搜索中每一个用户的搜索条目都包括查询词和URL两项。已经提出的Dirichlet Compound Multinomial (DCM)模型[2]和Dirichlet Compound Multinomial Latent Dirichlet Allocation (DCMLDA)模型[3]可以对文章中词的突发性现象建模,但如果直接应用于网络搜索建模却不是很理想。虽然大多数的点击图模型[4]及其变体[5-6]可以对网络搜索建模,但都是针对用户群体进行研究而忽略了用户个人特点。
本文通过分析用户查询日志来获取网络搜索突发现象,并提出了两个模型:SBM(search burstiness model)和CS-SBM(coupling-sensitive search burstiness model)。SBM是一个单极模型,假设查询词和URL之间主题独立,突发性的相关信息存储在偏Dirichlet先验里。CS-SBM充分考虑查询词和URL之间的关联。本文还用Beta分布刻画了用户搜索的时间特性,使前面提出的模型能够用来捕获时间上的突发性。
1 相关工作Madsen指出,多项分布经常用于文本建模。然而,多项分布能获取到文档中词汇的突发性现象,即一个词如果出现过一次,那么它很有可能再次出现[7]。因此Madsen提出了Dirichlet多项分布(DCM)来代替传统的多项分布。DCM拥有一级自由度,能获取到词的突发性,但是没有涉及文档中词汇的主题。文献[2]将DCM模型扩展成为了混合DCM分布,该模型能够训练表示一组文档,其中每一个文档都来自不同的高级主题。但是,该模型还是不能建模一个文档包含多个主题单词的情景。
上述工作中,之所以不能很好地刻画文档主题,其主要原因是DCM更关注突发性现象而非获取文档主题。2003年Blei[8]提出的Latent Dirichlet Allocation (LDA)是非监督的贝叶斯生成模型,它可以将文档集中每篇文档的主题按照概率分布的形式给出。LDA包括词汇、主题和文档3层。LDA引入了Dirichlet先验分布,成为了一个完备的贝叶斯模型。LDA文档生成过程为,从Dirichlet分布中采样文档与主题、主题与词汇分布,再重复从文档-主题多项式分布中采样主题以及由主题-词汇多项式分布生成词汇的过程,逐步生成整个文档。LDA已经在学术和工业界得到广泛应用。但是,LDA模型并不能预测词汇突发性出现的趋势。
为了能够在获取主题的同时预测词汇突发性现象,G.Doyle[3]提出了DCMLDA主题模型,该模型结合了DCM和LDA的优势,直接将DCM扩展合并到主题模型里面形成了一个比LDA更加复杂的模型。在DCMLDA中对于每个主题k和每个文档d服从新的多项式分布θkd,每个主题k都有不同的、非均匀的βk向量。对于每一个文档d, φkd根据Dirichlet(βk)的变化而变化,因此每个主题实例在文档之间是相互联系的。文档中的主题实例允许在同一主题不同文档中每一个词汇的概率不同,这也就是突发现象。
随着带有时间标记的文本集合(例如,数字化的报纸、杂志、博客等)数量和体积的增加,如何有效地搜索这些数据变得更加重要。上述模型都难以发现主题的演化趋势。在这个背景下,文献[9]等提出了Topic Over Time(TOT)模型。TOT将文档的时间信息作为服从Beta分布的变量,将每个主题通过Beta分布与时间信息相关联。TOT假设每个生成的词汇对应的时间信息也是通过它所属主题相关的Beta分布采样生成,这样主题与时间信息也有关系。TOT不依赖马尔可夫假说,这样能够避免在离散化过程中遇到时间粒度选取的问题。
另外,文献[10]系统地总结了自然语言处理中主题模型的发展,对LDA模型进行了详细的分析,并对主题模型的发展趋势进行了预测。根据微博的特殊形式,在LDA的基础上进行了改进,分别提出了(MicroBlogs-LDA)MB-LDA模型[11]和(MicroBlogs-HDP)MB-HDP模型[12],同时证明了提出模型能够很好地对微博进行主题挖掘。
以前的工作都是集中在对自然语言文本中的同质项目进行分析,即对一个文档中的同质词汇进行建模。然而在网络搜索分析中,文档是由查询词和URL两个异构项目组成,并且带有时间信息。因此,本文结合网络搜索查询的文本特点,提出并研究了将主题模型运用到网络搜索分析中,对查询词和URL这两个异构项目和它们之间的关系进行建模。
2 以用户为中心的概率主题模型本节主要介绍了SBM和CS-SBM主题模型,以及获取主题时间突发性的策略。
提出的模型应具备以下条件:
1) 查询词和URL的突发性现象研究要分开建模[13]。
2) 建模时,网络搜索特点,包括查询词、URL和session 3个维度都要考虑在内[14-15]。
session是指在短时间内提交的满足相同信息需求的一系列查询。为了避免同一会话中包含不相干的查询而导致的性能降低,本文优先考虑同一会话中查询词之间的语义一致性。通过对比分析,本文采用文献[16]提出的一系列规则来划分搜索session。这些规则用于评估查询之间的词汇相似性,并在检测相关搜索查询时表现出很高精度。
2.1 查询词和URL独立的主题模型(SBM)SBM的生成过程是基于查询词和URL相互独立的假设。与LDA和DCMLDA等传统主题模型不同,SBM中的文档有查询词、被点击URL和查询时间三项。图 1是SBM的搜索主题模型概率图。首先,从超参数为α的Dirichlet分布中抽样生成文档与主题之间的关系矩阵θ,θ是一个D×K的矩阵,其中D代表文档数量,K代表主题数。对于每一个主题k,从超参为βk和δk的Dirichlet分布中分别取样生成查询词与主题之间的关系矩阵θ和URL与主题之间的关系矩阵Ω。θ和Ω是D×K×V的三维矩阵,V代表训练语料库中出现的所有词的词表。对于文档中的每一个session,从参数为θd的多项分布中选择一个主题z,从参数为φzd的查询词的多项分布中,采样生成查询词w。然后,生成点击事件的二项分布,如果URL被点击了,从参数为Ωzd的URL的多项分布中,采样生成URL u。变量θ和δ是基于单个特定文档的,因此SBM可以为每一个用户查询词和URL的突发性建模。

|
图 1 SBM网络搜索分析主题模型 Fig.1 SBM web search analysis topic model |
SBM中的Gibbs采样方法借鉴了LDA和DCMLDA中Gibbs采样的方法,并进行了推导。模型的完全似然函数为
| $ P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta } \right.} \right) = P\left( {\mathit{\boldsymbol{u}}\left| {\mathit{\boldsymbol{z}},\delta } \right.} \right)P\left( {\mathit{\boldsymbol{w}}\left| {\mathit{\boldsymbol{z}},\beta } \right.} \right)P\left( {\mathit{\boldsymbol{z}}\left| \alpha \right.} \right) $ |
展开上式中的多项分布和Dirichlet分布,利用多项分布和Dirichlet分布的共轭性质,分别积分掉参数θ和φ以后,通过借鉴LDA和DCMLDA中Gibbs采样的方法,在SBM中概率P(z|α)为
| $ P\left( {\mathit{\boldsymbol{z}}\left| \alpha \right.} \right) = {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{z = 1}^K {{\alpha _z}} } \right)}}{{\prod\limits_{z = 1}^K {\mathit{\Gamma }\left( {{\alpha _z}} \right)} }}} \right)^D}\prod\limits_{d = 1}^D {\frac{{\prod\limits_{z = 1}^T {\mathit{\Gamma }\left( {{n_{dz}} + {\alpha _z}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{z = 1}^Z {\left( {{n_{dz}} + {\alpha _z}} \right)} } \right)}}} $ |
式中ndz为第d个文档中主题z的数量。
概率P(w|z, β)为
| $ \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{w}}\left| {\mathit{\boldsymbol{z}},\beta } \right.} \right) = \prod\limits_{d = 1}^D {\prod\limits_{k = 1}^K {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {{\beta _{kw}}} } \right)}}{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{\beta _{kw}}} \right)} }}\frac{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{n_{dkw}} + {\beta _{kw}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {{n_{dkw}} + {\beta _{kw}}} \right)} } \right)}}} \right)} } $ |
式中ndkw为第d个文档中第k个主题下查询词w的个数。
当该session中没有URL被点击时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 0,{z_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta } \right.} \right) \propto \frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)} } \right)}}\sum\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _w}} \right)}}} } \end{array} $ |
式中:CdkDK表示文档d中分配主题为k的session的数量,CkwdKWD表示文档d中查询词w被分配主题k的次数,Niw表示第i个session中查询词w的个数。
当一个session中有URL被点击时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 1,{z_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta } \right.} \right) \propto \frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _w} + {N_{iw}}} \right)} } \right)}}\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)}}} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{kud}^{KUD} + {\beta _{uk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{kud}^{KUD} + {\beta _{uk}} + {N_{iu}}} \right)} } \right)}}\prod\limits_{u = 1}^U {\frac{{\mathit{\Gamma }\left( {C_{kud}^{KUD} + {\beta _{uk}} + {N_{iu}}} \right)}}{{\mathit{\Gamma }\left( {C_{kud}^{KUD} + {\beta _{uk}}} \right)}}} } \end{array} $ |
式中,CkudKUD表示文档d中URL u被分配主题k的次数,Niu表示第i个session中URL u的数量。
2.2 查询词和URL相关联的主题模型(CS-SBM)查询词和URL通过搜索引擎紧密地结合在一起,这使得本文研究的问题变得更加复杂。被点击的URL是由对应的查询词经过搜索得出的。在网络搜索的情境中,URL是提交查询词给搜索引擎后返回的结果。因此,URL和查询词是相关的。为了获取它们两者之间的关系,这里引入变量Δqku来代表“查询词-URL”的多项分布,其先验由δ表示。“查询词-URL”多项式通过目前已经被广泛采用的点击图来获得,点击图由搜索查询和被点击的URL两部分组成。用于表示全局部分的CS-SBM定义为CS-SBM-G。因为本文重点研究以单个用户为核心的信息能否增强主题模型的表现,所以基于单个用户“查询词-URL”多项分布的CS-SBM定义为CS-SBM-U。
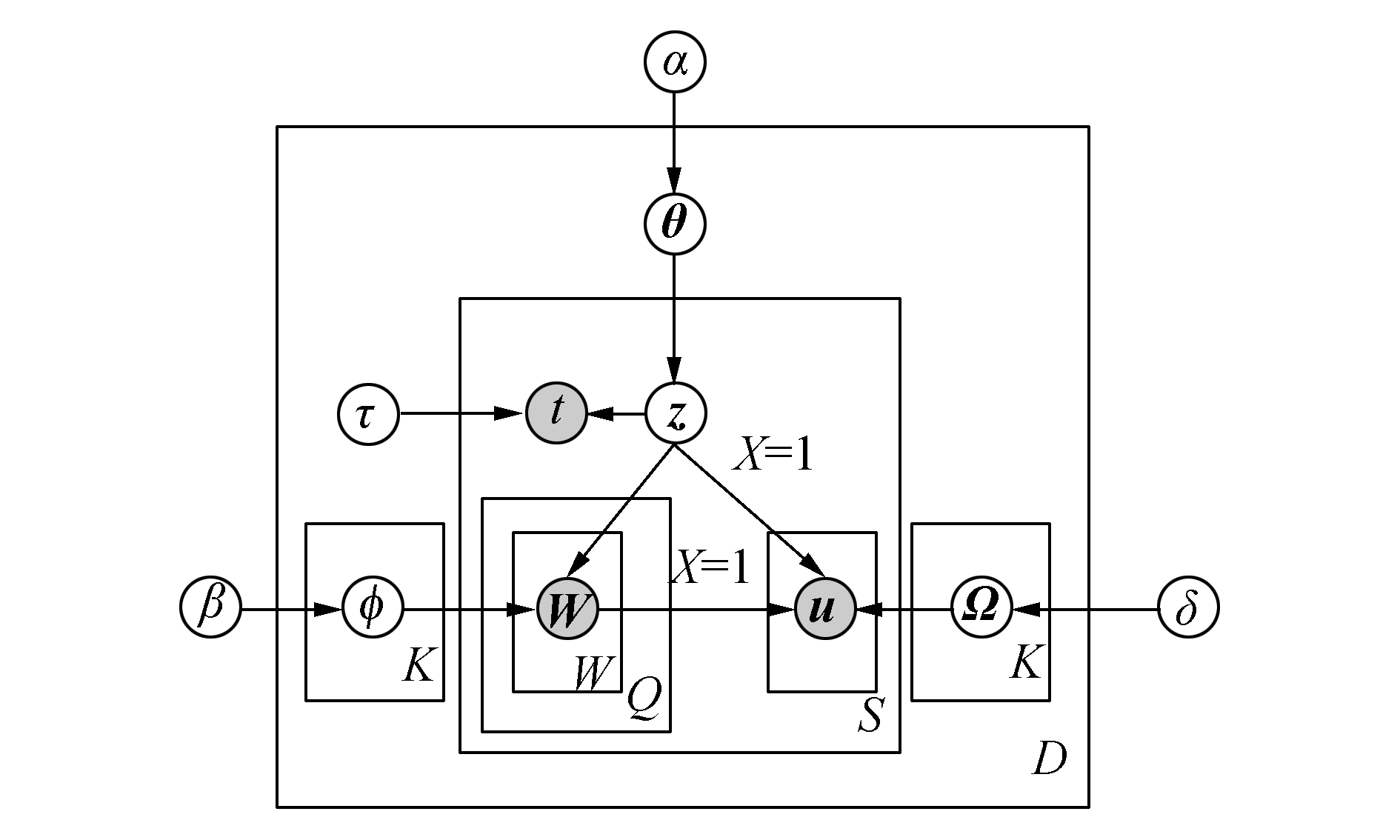
图 2给出了CS-SBM的生成过程。与SBM相比,查询词的生成过程不变,两者最主要的区别在于,CS-SBM在URL生成的时候要考虑查询词的影响,对于session中每一个查询项q,首先生成点击事件的二项分布,如果URL被点击了,则从参数为Ωqz的URL多项分布中采样生成URL u。
|
图 2 CS-SBM网络搜索分析主题模型 Fig.2 CS-SBM web search analysis topic model |
模型的完全似然函数为
| $ P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta } \right.} \right) = P\left( {\mathit{\boldsymbol{u}}\left| {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{w}},\delta } \right.} \right)P\left( {\mathit{\boldsymbol{w}}\left| {\mathit{\boldsymbol{z}},\beta } \right.} \right)P\left( {\mathit{\boldsymbol{z}}\left| \alpha \right.} \right) $ |
在CS-SBM中,同样采用了与LDA类似的Gibbs采样方法。P(z|α)和P(w|z, β)都与SBM中的相同。两者主要的区别就是给定的主题中的w和u不再相互独立。u的生成过程可能受到主题z和相关搜索查询q的影响。
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{u}}\left| {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{w}},\delta } \right.} \right) = }\\ {\int {\prod\limits_{d = 1}^D {\prod\limits_{i = 1}^{{N_d}} {P\left( {{\mathit{\boldsymbol{u}}_{di}}\left| {{\Delta _{qd{i^z}di}}} \right.} \right)} } \prod\limits_{q = 1}^Q {\prod\limits_{z = 1}^K {p\left( {{\Delta _{qz}}\left| \delta \right.} \right){\rm{d}}\Delta } } } = }\\ {\int {\prod\limits_{z = 1}^K {\prod\limits_{q = 1}^Q {\prod\limits_{u = 1}^U {\Delta _{qzu}^{{n_{qzu}}}\prod\limits_{q = 1}^Q {\prod\limits_{z = 1}^K {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {{\delta _{qu}}} } \right)}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{qu}}} \right)} }}\prod\limits_{u = 1}^U {\Delta _{qzu}^{{n_{qu}} - 1}} } \right){\rm{d}}\Delta } } } } } } = }\\ {\prod\limits_{q = 1}^Q {\left( {\frac{{\mathit{\Gamma }{{\left( {\sum\limits_{u = 1}^U {{\delta _{qu}}} } \right)}^K}}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{qu}}} \right)} }} \times \prod\limits_{z = 1}^K {\prod\limits_{q = 1}^Q {\frac{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{n_{qzu}} + {\delta _{qu}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {{n_{qzu}} + {\delta _{qu}}} \right)} } \right)}}} } } \right)} } \end{array} $ |
式中,nqzu是第z个主题的第q个查询中的URL u的数量。
当session中没有URL被点击时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 0,{z_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta ,\mathit{\Psi }} \right.} \right) \propto }\\ {\frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot \frac{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)} } \right)}} \cdot }\\ {\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _w}} \right)}}} } \end{array} $ |
当session中有URL被点击时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 1,{z_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{t}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta ,\mathit{\Psi }} \right.} \right) \propto }\\ {\frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot \frac{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)} } \right)}} \cdot }\\ {\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _w}} \right)}}} \prod\limits_{q \in {s_i}} {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{qzu}^{QZU} + {\delta _{qu}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{qzu}^{QZU} + {\delta _{qu}} + {N_{iu}}} \right)} } \right)}}} \cdot }\\ {\prod\limits_{u \leftarrow q} {\frac{{\mathit{\Gamma }\left( {C_{qzu}^{QZU} + {\delta _{qu}} + {N_{iu}}} \right)}}{{\mathit{\Gamma }\left( {C_{qzu}^{QZU} + {\delta _u}} \right)}}} } \end{array} $ |
式中:CqzuQZU表示在一个session里查询项q中的URL u被分配主题为z的次数;Niw表示session i中URL的数量。
2.3 主题在时间上的突发性网络搜索中另一个常见现象就是时间上的突发性。一个用户更倾向于在一个很短的时间内集中查询一些内容。因此,本文假设每一个用户的查询轨迹都有一个时间上的突发性,这种突发性由与查询相关的时间戳来体现。因为时间粒度是很难设定的,所以本文采用TOT中提出的方法,使用连续的Beta分布来捕获主题时间上的突发性。通过引入Beta分布,使一个主题能够更容易在一个短的时间周期内出现。在这种情况下,本文从整个语料库级别(定义为X-TG)和基于单一用户级别(定义为X-TU)出发,刻画一个主题在时间上的变化趋势。
因为主题-周期的多项分布是固定的(对每一个用户而言),所以主题中存在的时间周期将会证明突发性。每天或者每小时都可以观察到突发性现象,这表明去离散化是更合适的。
下面是SBM和CS-SBM在添加了时间信息以后的模型算法。
the same as the original model
for each session s in d do
choose a topic z:Multinomial(θd);
generate timestamps t~Beta(τz)(X-TG) or
t:Beta(τzd) (X-TU);
the same as the original model
end for
它主要的变化在于,对文档中的每一个session,从参数为θd的多项分布中采样一个主题z,然后根据数据集的不同,从Beta分布Beta(τz)和Beta(τzd)分别生成基于全局的时间戳和基于特定用户的时间戳。
TS-SBM的Gibbs采样与LDA方法类似。本文给出了一些简单的推导。首先,模型的完全似然函数为
| $ \begin{array}{l} P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{t}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta ,\tau } \right.} \right) = P\left( {\mathit{\boldsymbol{t}}\left| {\mathit{\boldsymbol{z}},\tau } \right.} \right)P\left( {\mathit{\boldsymbol{u}}\left| {\mathit{\boldsymbol{z}},\delta } \right.} \right) \cdot \\ P\left( {\mathit{\boldsymbol{w}}\left| {\mathit{\boldsymbol{z}},\beta } \right.} \right)P\left( {\mathit{\boldsymbol{z}}\left| \alpha \right.} \right) \end{array} $ |
如果session中没有URL被点击,那么此时的条件概率是:
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 0,{\mathit{\boldsymbol{z}}_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta ,\tau } \right.} \right) \propto }\\ {\prod\limits_{j = 1}^T {\frac{{{{\left( {1 - {t_j}} \right)}^{{\tau _{dk1}} - 1}}t_j^{{\tau _{^{_{dk2} - 1}}}}}}{{B\left( {{\tau _{dk1}},{\tau _{dk2}}} \right)}}} \frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)} } \right)}}\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _w}} \right)}}} } \end{array} $ |
式中:τdk1和τdk2是Beta分布的超参数。
对于SBM模型,如果session中有URL被点击,此时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 1,{\mathit{\boldsymbol{z}}_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta } \right.} \right) \propto }\\ {\prod\limits_{j = 1}^T {\frac{{{{\left( {1 - {t_j}} \right)}^{{\tau _{dk1}} - 1}}t_j^{{\tau _{^{_{dk2} - 1}}}}}}{{B\left( {{\tau _{dk1}},{\tau _{dk2}}} \right)}}} \frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _w} + {N_{iw}}} \right)} } \right)}}\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)}}} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{kud}^{KUD} + {\delta _{uk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{kud}^{KUD} + {\delta _{uk}} + {N_{iu}}} \right)} } \right)}}\prod\limits_{u = 1}^U {\frac{{\mathit{\Gamma }\left( {C_{kud}^{KUD} + {\delta _{uk}} + {N_{iu}}} \right)}}{{\mathit{\Gamma }\left( {C_{kud}^{KUD} + {\delta _{uk}}} \right)}}} } \end{array} $ |
对于CS-SBM模型,当session中有URL被点击时的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{z_i} = k\left| {{X_i} = 1,{z_{ - i}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{t}},\mathit{\boldsymbol{u}},\alpha ,\beta ,\delta ,\mathit{\Psi }} \right.} \right) \propto }\\ {\prod\limits_{j = 1}^T {\frac{{{{\left( {1 - {t_j}} \right)}^{{\tau _{dk1}} - 1}}t_j^{{\tau _{^{_{dk2} - 1}}}}}}{{B\left( {{\tau _{dk1}},{\tau _{dk2}}} \right)}}} \frac{{C_{dk}^{DK} + {\alpha _k}}}{{\sum\limits_{k' = 1}^K {\left( {C_{dk'}^{DK} + {{\alpha '}_k}} \right)} }} \cdot }\\ {\frac{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _{wk}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{t = 1}^W {\left( {C_{kwd}^{KWD} + {\beta _w} + {N_{iw}}} \right)} } \right)}}\prod\limits_{w = 1}^W {\frac{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _{wk}} + {N_{iw}}} \right)}}{{\mathit{\Gamma }\left( {C_{kwd}^{KWD} + {\beta _w}} \right)}}} \cdot }\\ {\prod\limits_{q \in {s_i}} {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{qzu}^{QZU} + {\delta _{qu}}} \right)} } \right)}}{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {\left( {C_{qzu}^{QZU} + {\delta _{qu}} + {N_{iu}}} \right)} } \right)}}} \prod\limits_{u \leftarrow q} {\frac{{\mathit{\Gamma }\left( {C_{qzu}^{QZU} + {\delta _{qu}} + {N_{iu}}} \right)}}{{\mathit{\Gamma }\left( {C_{qzu}^{QZU} + {\delta _u}} \right)}}} } \end{array} $ |
时间的参数按照如下方法更新:
| $ {\tau _{kd1}} = {{\bar t}_{kd}}\left[ {\frac{{{{\bar t}_{kd}}\left( {1 - {{\bar t}_{kd}}} \right)}}{{s_{kd}^2}} - 1} \right] $ |
| $ {\tau _{kd2}} = \left( {1 - {{\bar t}_{kd}}} \right)\left[ {\frac{{{{\bar t}_{kd}}\left( {1 - {{\bar t}_{kd}}} \right)}}{{s_{kd}^2}} - 1} \right] $ |
式中,tkd和skd2表示每一个文档中主题z时间上的样本均值和样本偏方差。
3 参数估计关于超参数α和β设置问题,一些LDA应用采用默认相同值的方法获得了成功,例如由Griffiths和Steyers[17]提出的α=50/k,β=0.01,K是主题的数量。因此,在LDA中没有必要去研究超参数。然而,在本文提出的模型中,超参数的设置是至关重要的。因为LDA中的φ和Ω值,也被包括在SBM和CS-SBM的β和δ中。
SBM完全似然P(w, u, z|α, β, δ)的计算如下所示:
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta } \right.} \right) = }\\ {\prod\limits_d {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{k = 1}^K {{\alpha _k}} } \right)}}{{\sum\limits_{k = 1}^K {\mathit{\Gamma }\left( {{\alpha _k}} \right)} }}} \right)} \frac{{\prod\limits_{k = 1}^T {\mathit{\Gamma }\left( {{m_{dk}} + {\alpha _k}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{k = 1}^T {\left( {{m_{dk}} + {\alpha _k}} \right)} } \right)}} \cdot }\\ {\prod\limits_{d,k} {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {{\beta _{wk}}} } \right)}}{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{\beta _{wk}}} \right)} }}} \right)\frac{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{n_{kwd}} + {\beta _{wk}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {{n_{kwd}} + {\beta _{wk}}} \right)} } \right)}}} \right)} \cdot }\\ {\left. {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {{\delta _{uk}}} } \right)}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{uk}}} \right)} }}} \right)\frac{{\prod\limits_{u = 1}^U {\mathit{\Gamma }\left( {{n_{kud}} + {\delta _{uk}}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{u = 1}^U {\left( {{n_{kud}} + {\delta _{uk}}} \right)} } \right)}}} \right)} \end{array} $ |
CS-SBM完全似然P(w, u, z|α, β, δ)的计算如下所示:
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta } \right.} \right) = }\\ {\prod\limits_d {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{k = 1}^K {{\alpha _k}} } \right)}}{{\sum\limits_{k = 1}^K {\mathit{\Gamma }\left( {{\alpha _k}} \right)} }}} \right)} \frac{{\prod\limits_{k = 1}^T {\mathit{\Gamma }\left( {{m_{dk}} + {\alpha _k}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{k = 1}^T {\left( {{m_{dk}} + {\alpha _k}} \right)} } \right)}} \cdot }\\ {\prod\limits_{d,k} {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {{\beta _{wk}}} } \right)}}{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{\beta _{wk}}} \right)} }}} \right)\frac{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{n_{kwd}} + {\beta _{wk}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {{n_{kwd}} + {\beta _{wk}}} \right)} } \right)}}} \right)} \cdot }\\ {\prod\limits_{k = 1}^K {\prod\limits_{q = 1h}^Q {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {{\delta _{qu}}} } \right)}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{qu}}} \right)} }}} \right)\frac{{\prod\limits_{u = 1}^U {\mathit{\Gamma }\left( {{n_{qku}} + {\delta _{qu}}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{u = 1}^U {\left( {{n_{qku}} + {\delta _{qu}}} \right)} } \right)}}} \right)} } } \end{array} $ |
SBM-T完全似然P(w, u, z|α, β, δ)的计算如下所示:
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta } \right.} \right) = }\\ {\prod\limits_d {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{k = 1}^K {{\alpha _k}} } \right)}}{{\sum\limits_{k = 1}^K {\mathit{\Gamma }\left( {{\alpha _k}} \right)} }}} \right)} \frac{{\prod\limits_{k = 1}^T {\mathit{\Gamma }\left( {{m_{dk}} + {\alpha _k}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{k = 1}^T {\left( {{m_{dk}} + {\alpha _k}} \right)} } \right)}} \cdot }\\ {\prod\limits_{d,k} {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {{\beta _{wk}}} } \right)}}{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{\beta _{wk}}} \right)} }}} \right)\frac{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{n_{kwd}} + {\beta _{wk}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {{n_{kwd}} + {\beta _{wk}}} \right)} } \right)}} \cdot } \right.} }\\ {\left. {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {{\delta _{uk}}} } \right)}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{uk}}} \right)} }}} \right)\frac{{\prod\limits_{u = 1}^U {\mathit{\Gamma }\left( {{n_{kud}} + {\delta _{uk}}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{u = 1}^U {\left( {{n_{kud}} + {\delta _{uk}}} \right)} } \right)}}} \right)\prod\limits_{d,s,i} {p\left( {{r_{dsi}}\left| {{\tau _{d{k_s}}}} \right.} \right)} } \end{array} $ |
CS-SBM-T完全似然P(w, u, z|α, β, δ, τ)的计算如下所示:
| $ \begin{array}{*{20}{c}} {P\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{z}}\left| {\alpha ,\beta ,\delta ,\tau } \right.} \right) = }\\ {\prod\limits_d {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{k = 1}^K {{\alpha _k}} } \right)}}{{\sum\limits_{k = 1}^K {\mathit{\Gamma }\left( {{\alpha _k}} \right)} }}} \right)} \frac{{\prod\limits_{k = 1}^T {\mathit{\Gamma }\left( {{m_{dk}} + {\alpha _k}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{k = 1}^T {\left( {{m_{dk}} + {\alpha _k}} \right)} } \right)}} \cdot }\\ {\prod\limits_{d,k} {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {{\beta _{wk}}} } \right)}}{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{\beta _{wk}}} \right)} }}} \right)\frac{{\prod\limits_{w = 1}^W {\mathit{\Gamma }\left( {{n_{kwd}} + {\beta _{wk}}} \right)} }}{{\mathit{\Gamma }\left( {\sum\limits_{w = 1}^W {\left( {{n_{kwd}} + {\beta _{wk}}} \right)} } \right)}}} \right)} \cdot }\\ {\prod\limits_{k = 1}^K {\prod\limits_{q = 1}^Q {\left( {\left( {\frac{{\mathit{\Gamma }\left( {\sum\limits_{u = 1}^U {{\delta _{qu}}} } \right)}}{{\sum\limits_{u = 1}^U {\mathit{\Gamma }\left( {{\delta _{qu}}} \right)} }}} \right)\frac{{\prod\limits_{u = 1}^U {\mathit{\Gamma }\left( {{n_{qku}} + {\delta _{qu}}} \right)} }}{{\mathit{\Gamma }\left( {\prod\limits_{u = 1}^U {\left( {{n_{qku}} + {\delta _{qu}}} \right)} } \right)}}} \right) \cdot } } }\\ {\prod\limits_{d,s,i} {p\left( {{r_{dsi}}\left| {{\tau _{d{k_s}}}} \right.} \right)} } \end{array} $ |
进行对数似然转换:
| $ \begin{array}{*{20}{c}} {\alpha .' = \sum\limits_{d,k} {\left( {\ln \mathit{\Gamma }\left( {n{._{kd}} + {\alpha _k}} \right) - \ln \mathit{\Gamma }\left( {{\alpha _k}} \right)} \right)} + }\\ {\sum\limits_d {\left( {\ln \mathit{\Gamma }\left( {\sum\limits_k {{\alpha _k}} } \right) - \ln \mathit{\Gamma }\left( {\sum\limits_k {n{._{kd}} + {\alpha _k}} } \right)} \right)} } \end{array} $ |
| $ \begin{array}{*{20}{c}} {\beta {{.'}_k} = \sum\limits_{d,k,w} {\left( {\ln \mathit{\Gamma }\left( {{n_{wkd}} + {\beta _{wk}}} \right) - \ln \mathit{\Gamma }\left( {{\beta _{wk}}} \right)} \right)} + }\\ {\sum\limits_{d,k} {\left( {\ln \mathit{\Gamma }\left( {\sum\limits_w {{\beta _{wk}}} } \right) - \ln \mathit{\Gamma }\left( {\sum\limits_w {{n_{wkd}} + {\beta _{wk}}} } \right)} \right)} } \end{array} $ |
对于SBM:
| $ \begin{array}{*{20}{c}} {\delta {{.'}_k} = \sum\limits_{d,k,u} {\left( {\ln \mathit{\Gamma }\left( {{n_{ukd}} + {\delta _{uk}}} \right) - \ln \mathit{\Gamma }\left( {{\delta _{uk}}} \right)} \right)} + }\\ {\sum\limits_{d,k} {\left( {\ln \mathit{\Gamma }\left( {\sum\limits_u {{\delta _{uk}}} } \right) - \ln \mathit{\Gamma }\left( {\sum\limits_u {{n_{ukd}} + {\delta _{uk}}} } \right)} \right)} } \end{array} $ |
对于CS-SBM:
| $ \begin{array}{*{20}{c}} {\delta {{.'}_q} = \sum\limits_{q,k,u} {\left( {\ln \mathit{\Gamma }\left( {{n_{qku}} + {\delta _{qu}}} \right) - \ln \mathit{\Gamma }\left( {{\delta _{qu}}} \right)} \right)} + }\\ {\sum\limits_{q,k} {\left( {\ln \mathit{\Gamma }\left( {\sum\limits_u {{\delta _{qu}}} } \right) - \ln \mathit{\Gamma }\left( {\sum\limits_u {{n_{qku}} + {\delta _{qu}}} } \right)} \right)} } \end{array} $ |
上面的每一个公式无论α.′、β.k′还是δ.k′、δ.q′都定义了一个向量。本文采用文献[18]中提出的有限空间的BFGS方法使它最大化。运行Gibbs采样,然后选择α、β和δ使P(w, u, z|α, β, δ, τ)完全似然最大化,直到达到稳定状态。重复上述过程,直到α、β和δ收敛。
4 实验结果分析 4.1 数据集本文选择的实验数据是搜狗搜索发布的匿名查询日志。它是搜狗在网上公开发布的用户查询日志。该日志包括了用户2008年6月整月的网络查询记录。日志主要包括5部分,即用户匿名ID、查询词、查询时间、点击的URL的排名、点击的URL。这些数据是按照匿名用户的ID顺序依次排列的。本文选取了在一个月内查询日志条目大于500条的用户进行建模。首先,将同一用户的搜索查询日志放到一个文档中。然后,用文献[16]提出的方法将搜索查询日志切分成了647 164个session,用于下一步搜索主题的发现。接下来,根据文献[16]提出的停用词列表过滤掉那些没有意义的查询词。同时,例如www.sougou.com、www.baidu.com等主要的搜索引擎和门户网站也要过滤掉[19],因为它们没有提供有用信息。每一个文档的时间戳是由搜索日志上提供的查询时间决定的,并且根据文献[20]提出的SSTM模型中用到的方法,将时间按照先后顺序归一化到(0, 1)。实验数据中,每一个文档都包括了一些session,每一个session都包括一些查询词、URL(如果有点击事件)和时间戳。
本文选用了两个衡量标准。第1个衡量标准是用部分Held-Out数据评估模型预测未知数据的能力。第2个衡量标准,本文参照了文献[21]提出的方法,即在观察部分用户搜索记录以后,预测剩余查询项的能力。两个衡量标准都选择了困惑度作为评估模型泛化能力的衡量指标。一般而言,模型的困惑度越低,表明泛化能力越强,对模型的拟合程度越高。由于很少有概率模型做有关获取网络搜索查询突发性和时间上的主题突发性研究,很难找到提出模型的直接竞争对手。所以本文选取了3个常用的主题模型作为比较基线,即LDA、DCMLDA和TOT。
4.2 模型困惑度分析对于第一个衡量标准,困惑度义如下:
| $ {\rm{Perplexit}}{{\rm{y}}_{{\rm{held - out}}}}\left( M \right) = {\left( {\prod\limits_{d = 1}^D {\prod\limits_{i = 1}^{{N_d}} {p\left( {{w_i}\left| M \right.} \right)} } } \right)^{\frac{{ - 1}}{{\sum\limits_{d = 1}^D {\left( {{N_d}} \right)} }}}} $ |
式中,M是模型通过训练过程学习到的,Nd是指第d个文档中词汇数量。图 3展示了困惑度的比较结果,从中可以发现这两个提出的模型与3个基线模型相比表现出了更好的预测未知数据的能力。因此,把搜索主题数设置为1 000时,SBM、CS-SBM、LDA、DCMLDA、TOT的困惑度分别为430.347、400.16、1 080.41、995.76、830.23。SBM和CS-SBM自身的困惑度低,并且随着主题数增加困惑度还会进一步降低。实验结果表明,SBM和CS-SBM更适合于从给予的用户搜索历史中预测用户未来网络搜索查询。

|
图 3 Held-out数据的困惑度 Fig.3 Perplexity of held-out data |
第2种衡量标准的困惑度为
| $ \begin{array}{*{20}{c}} {{\rm{Perplexit}}{{\rm{y}}_{{\rm{portion}}}}\left( M \right) = }\\ {{{\left( {\prod\limits_{d = 1}^D {\prod\limits_{i = P + 1}^{{N_d}} {p\left( {{w_i}\left| {M,{W_{a:P}}} \right.} \right)} } } \right)}^{\frac{{ - 1}}{{\sum\limits_{d = 1}^D {\left( {{N_d}} \right)} }}}}} \end{array} $ |
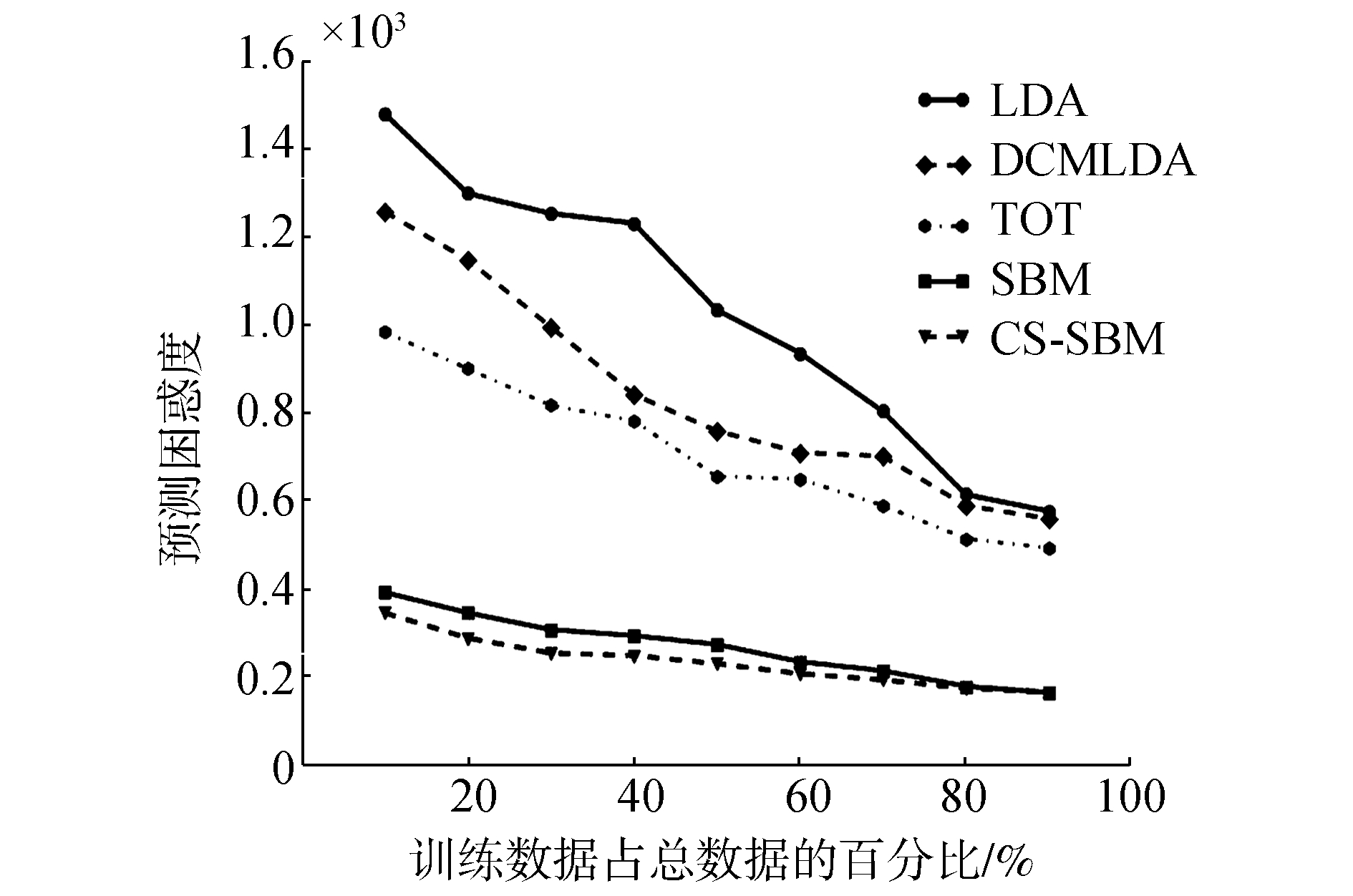
第2种衡量标准可以评估提出的模型在观察一部分用户搜索历史记录以后,预测剩余查询项的能力。例如,从用户的查询日志中得到已经观察的查询词w1:P,那么剩余查询项的预测分布为P(w|W1:P)。测试数据的困惑度是根据上面的困惑度公式进行计算。举例来说,选择数据集中前80%的搜索查询词作为观察训练数据,剩余的20%作为测试数据。图 4呈现了部分观察数据的预测困惑度,LDA、DCMLDA、TOT的困惑度分别是684.83、671.09、561.26。本文中提出的模型再次取得了显著的优势,其中SBM的困惑度是206.76,而CS-SBM达到了204.87。实验结果表明,SBM和CS-SBM有着更好的预测剩余查询项的能力。
|
图 4 Observed数据的困惑度 Fig.4 Perplexity of observed data |
发现搜索主题的合理性是判断模型是否成功的一个重要指标。本文中的实验结果证明了提出的模型在发现搜索主题方面表现突出,同时还准确地预测了查询主题在时间上的演化趋势。
实验中设置主题的数目为K=50。搜索主题是从Gibbs采样的1000次迭代中单次采样提取的。在表 1~4中,展示了4个由SBM和CS-SBM分别在语料库级上和单个用户级上发现的搜索主题,并列出了各主题概率值最大的前5个词汇及其概率。主题名称是根据该主题下词汇具体的语义信息定义的。图 5~8中,直方图显示了主题在时间轴上的概率分布,光滑曲线为拟合Beta分布的概率密度函数曲线。下面将选取图中的两个搜索主题进行具体分析。

|
图 5 CS-SBM网络搜索分析主题模型 Fig.5 Latent evolutions of SBM-TG discovered search topics |
| 表 1 SBM-TG发现的搜索主题分布情况 Tab.1 SBM-TG discovered search topics distribution |
| 表 2 SBM-TU发现的搜索主题分布情况 Tab.2 SBM-TU discovered search topics distribution |
| 表 3 CS-SBM-TG发现的搜索主题分布情况 Tab.3 CS-SBM-TG discovered search topics distribution |
| 表 4 CS-SBM-TG发现的搜索主题分布情况 Tab.4 CS-SBM-TG discovered search topics distribution |
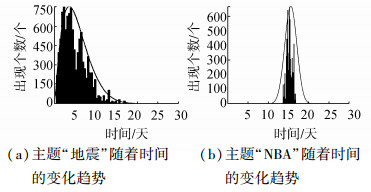
表 1~2中的第一个主题是“地震”,通过图 5~6可以发现,本文提出的SBM模型在语料库级上和单个用户级上都成功获取了主题时间上的突发性。根据其时间分布来看,由于刚刚发生过汶川地震,因此在6月份的前半个月,人们对地震的搜索比较频繁,但随着时间的推移,搜索数量逐渐减少。从语料库级的分析结果看,“汶川、地震、救灾”等高频词汇都与地震相关。对于单个用户,本文从实验结果中选择了一位有大量查询日志并且有地震主题的用户做具体分析描述。结果发现,在这个主题下的词,例如地震、汶川、唐山、四川等词汇出现的概率较高。总体来看,汶川地震引起了人们广泛的关注,对于全局来说,用户更关注地震救援工作;对于表 2中的个人用户来说,他们只是关注地震本身,而没有救援相关的查询。
|
图 6 SBM-TU发现的搜索主题在时间上的演化趋势 Fig.6 Latent evolutions of SBM-TU discovered search topics |
表 3~4中,最后一个主题是“欧洲杯”,图 7~8中,CS-SBM的实验结果显示关于“欧洲杯”这个话题的查询从第十天到第三十天越来越多,这也符合随着欧洲杯的进行人们关注的热情越来越高的现象。从整个语料库得到的结果来看,搜索主题“欧洲杯”主要包括欧洲杯、瑞士、奥地利等词。其中“瑞士”和“奥地利”是本届欧洲杯的举办地,这些词汇都与欧洲杯的主题紧密相关。而对于表 4中的个人用户,我们仍然从实验结果中选取了与“欧洲杯”主题相关的用户进行分析说明。它包括欧洲杯、西班牙、冠军等关键词,这证明了该用户更关注于欧洲杯的冠军归属问题。

|
图 7 CS-SBM-TG发现的搜索主题在时间上的演化趋势 Fig.7 Latent evolutions of CS-SBM-TG discovered search topics |

|
图 8 CS-SBM-TU发现的搜索主题在时间上的演化趋势 Fig.8 Latent evolutions of CS-SBM-TU discovered search topics |
总体而言,发现的搜索主题与实际的情况大体相吻合,而且能较好地反应主题变化的趋势。
5 结束语本文提出了两个主题模型SBM和CS-SBM,从全局和基于特定用户来建模网络搜索分析。SBM主要是用于获取网络查询的突发现象。CS-SBM主要添加了查询词和URL之间的关系,获取了主题突发性。为了使SBM和CS-SBM可以获取时间上的突发性,本文采用Beta分布拟合主题在时间上的变化的策略。本文还设计了一系列的实验验证了提出模型拥有较好的泛化能力、主题发现能力和反应主题时间上突发性的能力。本文的贡献主要有三个方面:第一,研究了搜索引擎用户行为分析中突发性现象;第二,提出了两种新型的模型用来捕获网络搜索中各个方面的突发性;第三,通过大量的实验验证了模型的有效性。下一步工作中,将把这些模型运用到团购广告投放。通过发现用户的搜索主题,然后将同一主题下的用户按照社团发现的规则进行分类,并进行广告投放。
| [1] |
SUNEHAG P. Using two-stage conditional word frequency models to model word burstiness and motivating TF-IDF[J]. Journal of machine learning reasearch, 2017, 2: 8. ( 0) 0)
|
| [2] |
ELKAN C. Clustering documents with an exponential-family approximation of the Dirichlet compound multinomial distribution[C]//Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh. Pennsylvania, USA, 2006:289-296.
( 0) 0)
|
| [3] |
DOYLE G, ELKAN C. Accounting for burstiness in topic models[C]//Proceedings of the 26th Annual International Conference on Machine Learning Montreal. QC, Canada, 2009:281-288.
( 0) 0)
|
| [4] |
XUE G R, ZENG H J, CHEN Z, et al. Optimizing web search using web click-through data[C]//Proceedings of the thirteenth ACM international conference on Information and Knowledge Management. Washington, USA, 2004:118-126.
( 0) 0)
|
| [5] |
GUO F, LIU C, WANG Y M. Efficient multiple-click models in web search[C]//Proceedings of the Second ACM International Conference on Web Search and Data Mining. Barcelona, Spain, 2009:124-131.
( 0) 0)
|
| [6] |
张宇, 宋巍, 刘挺, 等. 基于URL主题的查询分类方法[J]. 计算机研究与发展, 2012, 49(6): 1298-1305. ZHANG Yu, SONG Wei, LIU Ting, et al. Query classification based on url topic[J]. Journal of computer research and development, 2012, 49(6): 1298-1305. (  0) 0)
|
| [7] |
MADSEN R E, KAUCHAK D, ELKAN C. Modeling word burstiness using the dirichlet distribution[C]//Proceedings of the 22nd international conference on Machine iearning. Bonn, Germany, 2005:545-552.
( 0) 0)
|
| [8] |
BLEI D M, NG A Y, JORDAN M I. Latent dirichlet allocation[J]. Journal of machine learning research, 2003, 3(1): 993-1022. ( 0) 0)
|
| [9] |
WANG X, MCCALLUM A. Topics over time:a non-Markov continuous-time model of topical trends[C]//Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. Philadelphia, USA, 2006:424-433.
( 0) 0)
|
| [10] |
徐戈, 王厚峰. 自然语言处理中主题模型的发展[J]. 计算机学报, 2011, 34(8): 1423-1436. XU Ge, WANG Houfeng. The development of topic model in natural language processing[J]. Chinese journal of computers, 2011, 34(8): 1423-1436. (  0) 0)
|
| [11] |
张晨逸, 孙建伶, 丁轶群. 基于MB-LDA模型的微博主题挖掘[J]. 计算机研究与发展, 2011, 48(10): 1795-1802. ZHANG Chenyi, SUN Jianling, DING Yiqun. Topic mining for microblog based on mb-lda model[J]. Journal of computer research and development, 2011, 48(10): 1795-1802. (  0) 0)
|
| [12] |
刘少鹏, 印鉴, 欧阳佳, 等. 基于MB-HDP模型的微博主题挖掘[J]. 计算机学报, 2015, 38(7): 1408-1419. LIU Shaopeng, YIN Jian, OUYANG Jia, et al. Topic mining from microblogs based on MB-HDP model[J]. Chinese Journal of Computers, 2015, 38(7): 1408-1419. DOI:10.11897/SP.J.1016.2015.01408 (  0) 0)
|
| [13] |
JIANG D, TONG Y, SONG Y. Cross-lingual topic discovery from multilingual search engine query log[J]. ACM transactions on information systems (TOIS), 2016, 35(2): 9. ( 0) 0)
|
| [14] |
JIANG D, LEUNG K W T, NG W. Query intent mining with multiple dimensions of web search data[J]. World wide web, 2016, 19(3): 475. DOI:10.1007/s11280-015-0336-2 ( 0) 0)
|
| [15] |
JIANG D, YANG L. Query intent inference via search engine log[J]. Knowledge and information systems, 2016, 49(2): 661-685. DOI:10.1007/s10115-015-0915-7 ( 0) 0)
|
| [16] |
HUANG J, EFTHIMIADIS E N. Analyzing and evaluating query reformulation strategies in web search logs[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management. Hong Kong, China, 2009:77-86.
( 0) 0)
|
| [17] |
GRIFFITHS T L, STEYVERS M. Finding scientific topics[J]. Proceedings of the national academy of sciences, 2004, 101(1): 5228-5235. ( 0) 0)
|
| [18] |
ZHU C, BYRD R H, LU P, et al. Algorithm 778:L-BFGS-B:Fortran subroutines for large-scale bound-constrained optimization[J]. ACM transactions on mathematical software (TOMS), 1997, 23(4): 550-560. DOI:10.1145/279232.279236 ( 0) 0)
|
| [19] |
MANNING C D, RAGHAVAN P, SCHVTZE H. Introduction to information retrieval[M]. Cambridge: Cambridge University Press, 2008: 1-16.
( 0) 0)
|
| [20] |
JIANG D, NG W. Mining web search topics with diverse spatiotemporal patterns[C]//Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval. Dublin, Ireland, 2013:881-884.
( 0) 0)
|
| [21] |
LI W, MCCALLUM A. Pachinko allocation:DAG-structured mixture models of topic correlations[C]//Proceedings of the 23rd International Conference on Machine Learning. Pittsburgh, USA, 2006:577-584.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


