近几十年来，越来越多的群体智能算法被提出，并以其操作简单、不受求解对象约束等特点在工程领域得到广泛应用。蚁狮优化算法(ant lion optimizer，ALO)是澳大利亚学者Seyedali Mirjalili^[1]通过研究蚁狮捕食蚂蚁的仿生学机制，提出的一种智能优化算法。ALO算法以其调节参数少、求解精度高的优点，备受科研工作者的青睐，目前已被成功应用于天线布局优化、分布式系统的选址和控制器增益值优化等工程领域^[2-4]。

文献[5]为改善种群多样性，通过对基本算法的精英化过程引入了权值操作，提出了MALO算法，但是随着种群不断向精英靠拢，多样性仍会不可避免地降低，因而该方法没有从根本上提高算法的全局搜索能力；文献[6]为减小适应值较差个体对种群的误导，提出一种具有混沌侦查机制的CIALO算法，提高了种群对求解域的映射能力，但并未改善算法的收敛速度。

针对以上不足，本文提出一种具有Levy变异和精英自适应竞争机制的蚁狮优化算法(ALO with Levy variation and adaptive Elite competition, LEALO)。服从Levy分布的随机数具有短距离游走结合偶尔长距离跳跃的特征，利用其对种群较差的个体进行变异，可以改善种群多样性，实现对求解域的充分探索，从而提高算法的全局搜索能力；多个精英之间的自适应并行竞争，有助于种群更快地锁定更优的区域，保证算法收敛速度的同时避免了较大的计算量。本文选择标准函数对LEALO算法进行测试，并与基本ALO算法^[1]、MALO算法^[5]和CIALO^[6]算法进行比较，结果表明LEALO算法具有更高的寻优精度和收敛速度。最后将其用于硅单晶热场温度模型的参数辨识中，仿真结果说明了该算法良好的优化能力。

1 蚁狮优化算法及其缺点 1.1 ALO算法原理

蚁狮是一种靠捕食蚂蚁生存的蚁蛉科昆虫，以其独特的狩猎方式得名。蚁狮“狩猎”时先在沙地上挖出“陷阱”，然后躲入穴底等待“猎物”，一旦蚂蚁进入“陷阱”，为防止其逃走蚁狮会立刻向外刨出沙土使其滑入穴底进而捕食。Mirjalili将二者间的仿生学机制公式化再现，提出了蚁狮优化算法。该算法的主要步骤如下。

1.1.1 蚁狮修筑陷阱

根据适应值，通过轮盘赌操作从上一代的蚂蚁种群中选择个体。被选中的个体将和精英一起作为蚁狮修筑“陷阱”。

1.1.2 蚂蚁随机游走

按照式(1)产生随机游走的蚂蚁种群：

$\begin{array}{c}X\left( t \right) = \left[ {0,{{cumsum}}\left( {2r\left( {{t_1}} \right) - 1} \right),} \right. \\{{cumsum}}\left( {2r\left( {{t_2}} \right) - 1} \right), \cdots ,{{cumsum}}\left. {\left( {2r\left( {{t_n}} \right) - 1} \right)} \right]\end{array}$

(1)

式中： ${ cumsum}$ 为蚂蚁游走位置的累积， $n$ 是设置的最大迭代次数， $t$ 为游走的步数， $r\left( t \right)$ 为随机数0或1。为了保证蚂蚁在求解空间内游走，需对其爬行位置进行标准化：

$X_i^t = \frac{{\left( {X_i^t - {a_i}} \right) \times \left( {d_i^t - c_i^t} \right)}}{{\left( {{b_i} - {a_i}} \right)}} + c_i^t$

(2)

式中： ${a_i}$ 和 ${b_i}$ 为游走过程中第 $i$ 个变量的最小值和最大值， $c_i^t$ 和 $d_i^t$ 为第 $t$ 代第 $i$ 个变量的最小值和最大值。

1.1.3 蚂蚁进入陷阱

蚂蚁爬入陷阱的过程，可以看作蚂蚁围绕修筑“陷阱”的蚁狮游走，即蚂蚁游走的区域边界受蚁狮位置的影响：

$\left\{ {\begin{array}{*{20}{c}} {c_i^t = { Antlion}_j^t + {c^t}} \\ {d_i^t = { Antlion}_j^t + {d^t}} \end{array}} \right.$

(3)

式中： ${c^t}$ 和 ${d^t}$ 分别为第 $t$ 代所有变量中的最小值和最大值， $c_i^t$ 和 $d_i^t$ 分别是第 $i$ 只蚂蚁的所有位置里的最小值和最大值， ${ Antlion}_j^t$ 是第 $t$ 代选中的第 $j$ 个蚁狮。

1.1.4 蚂蚁滑落穴底

一旦蚂蚁进入陷阱，为阻止其逃走，蚁狮会立即向穴外刨出沙土使其滑入穴底。该过程可以看作蚂蚁绕蚁狮游走的半径在不断缩小：

$\left\{ {\begin{array}{*{20}{c}} {{c^t} = \displaystyle\frac{{{c^t}}}{I}} \\ {{d^t} = \displaystyle\frac{{{d^t}}}{I}} \end{array}} \right.$

(4)

式中： $I =+ {10^w} \cdot t/T$ ， $T$ 为最大迭代次数(w=2, t>0.1T; w=3, t>0.5T; w=4, t>0.75T; w=5, t>0.9T; w=6, t>0.95T)。

1.1.5 蚁狮重筑陷阱

若游走的蚂蚁种群中出现了适应值高于蚁狮的个体，则该个体为新的精英。即该个体将作为蚁狮在下一代修筑“陷阱”：

${ Antlion}_j^t = { Ant}_i^t,\;f\left( {{ Ant}_i^t} \right) < f\left( {{ Antlion}_j^t} \right)$

(5)

式中： $t$ 为当前代数， ${{ Ant}^t}_i$ 是第 $t$ 代适应值最佳的第 $i$ 个蚂蚁， $f$ 为适应值函数。

1.1.6 蚂蚁种群精英化

绕精英游走的蚂蚁种群，影响着绕轮盘赌选择的个体游走的蚂蚁种群。

${ Ant}_i^t = \frac{{R_A^t + R_E^t}}{2}$

(6)

式中： $R_A^t$ 表示绕轮盘赌选中的蚁狮游走的蚂蚁种群， $R_E^t$ 表示绕精英蚁狮游走的蚂蚁种群。

1.2 ALO算法缺点

在ALO算法中，蚂蚁种群绕精英蚁狮的随机游走保证了寻优过程的收敛性，轮盘赌操作在一定程度上有助于提高蚂蚁种群的全局搜索能力。但是，算法仍存在以下问题：蚁狮的捕食半径的随着迭代次数的增加阶段性收缩，会导致种群多样性的逐渐降低，算法一旦陷入局部最优就难以跳出；若当代精英和轮盘赌选择的个体并不处于全局最优区域时，整个种群在单个精英带领下会降低算法的收敛速度。

2 改进算法(LEALO)

针对ALO算法存在的缺点，本文引入Levy变异和并行的自适应精英竞争机制。将服从Levy分布的随机数用于种群较差个体的变异，可以有效改善种群的多样性，提高算法的全局搜索能力；多个精英同时带领种群探索加快了算法的收敛速度。另外，引入精英的个数随迭代次数的增加而减少的自适应机制可以避免较大的计算量。

2.1 Levy变异机制

Levy游走一词是由法国数学家保罗·列维提出的，而后有学者发现很多生物群体的活动方式均可以用Levy游走模式进行描述^[7]。研究人员们通过对生物群体基于Levy游走模式的活动方式进行研究，形成了一种Levy飞行觅食假说，即Levy游走可以提高觅食效率，基于Levy游走的觅食方式自然适应性更强。Levy飞行表现为长期短距离游走和偶尔长距离跳跃的结合，这种长距离跳跃具有方向多变性的特点^[8]。

利用Levy飞行特点形成Levy变异机制来提高种群的多样性，保证了种群对附近区域详细搜索的同时又具有一定的突变性。两种方式交替从而实现对求解域的充分遍历，有助于提高算法的全局搜索能力^[9]。Levy飞行服从Levy分布，其概率密度函数如下：

${P_{\alpha ,\gamma }}\left( z \right) = \frac{1}{\text{π} }\int_0^\infty {\exp \left( { - \gamma {q^\alpha }} \right)} \cos \left( {qz} \right){ d}q$

(7)

式中： $0 < \alpha \leqslant 2$ 控制Levy分布图形的锐度， $\gamma > 0$ 控制分布的尺度。当 $\alpha = 2$ 时，Levy分布等同于高斯分布， $\alpha = 1$ 时，Levy分布等同于柯西分布。对于一般的 $\alpha $ 取值，通过Levy分布的概率密度函数分析较为困难，所以通常采用模拟方法产生Levy分布的随机数^[10-12]。为了使Levy飞行轨迹充分遍历设定的求解域，对文献[13]的模拟公式做修改如式 (8)：

${\left\{ {\begin{array}{*{20}{l}} {{\delta _\mu } = \left\{ {\displaystyle\frac{{\varGamma \left( {1 + \beta } \right)\sin \left( {\text{π} \beta /2} \right)}}{{\varGamma \left[ {\left( {1 + \beta } \right)/2} \right]{2^{\left( {\beta - 1} \right)/2}}\beta }}} \right\}}^{1/\beta } \\ [5pt] {{\delta _v} = 1} \end{array}} \right.}$

(8)

$\left\{ {\begin{array}{*{20}{c}} {\mu \sim N\left( {0,\delta _\mu ^2} \right)} \\ {v \sim N\left( {0,\delta _v^2} \right)} \end{array}} \right.$

(9)

$\left\{ {\begin{array}{*{20}{l}} {S = \displaystyle\frac{\mu }{{{{\left| v \right|}^{1/\beta }}}}} \\ {{\lambda _i} = { cumsum}\left( {{S_i}} \right)} \end{array}} \right.$

(10)

式中： $i = 1,\;2, \cdots ,n$ 为寻优的维度， ${ cumsum}\left( {{S_i}} \right)$ 为前 $i$ 次Levy飞行位置的累积。

$L\left( {{\lambda _i}} \right) = \left\{ {\begin{array}{*{20}{l}} {l_b}, & {{\lambda _i} < l_b} \\ {a \cdot {\lambda _i}}, & {l_b < {\lambda _i} < u_b} \\ {u_b}, & {{\lambda _i} > u_b} \end{array}} \right.$

(11)

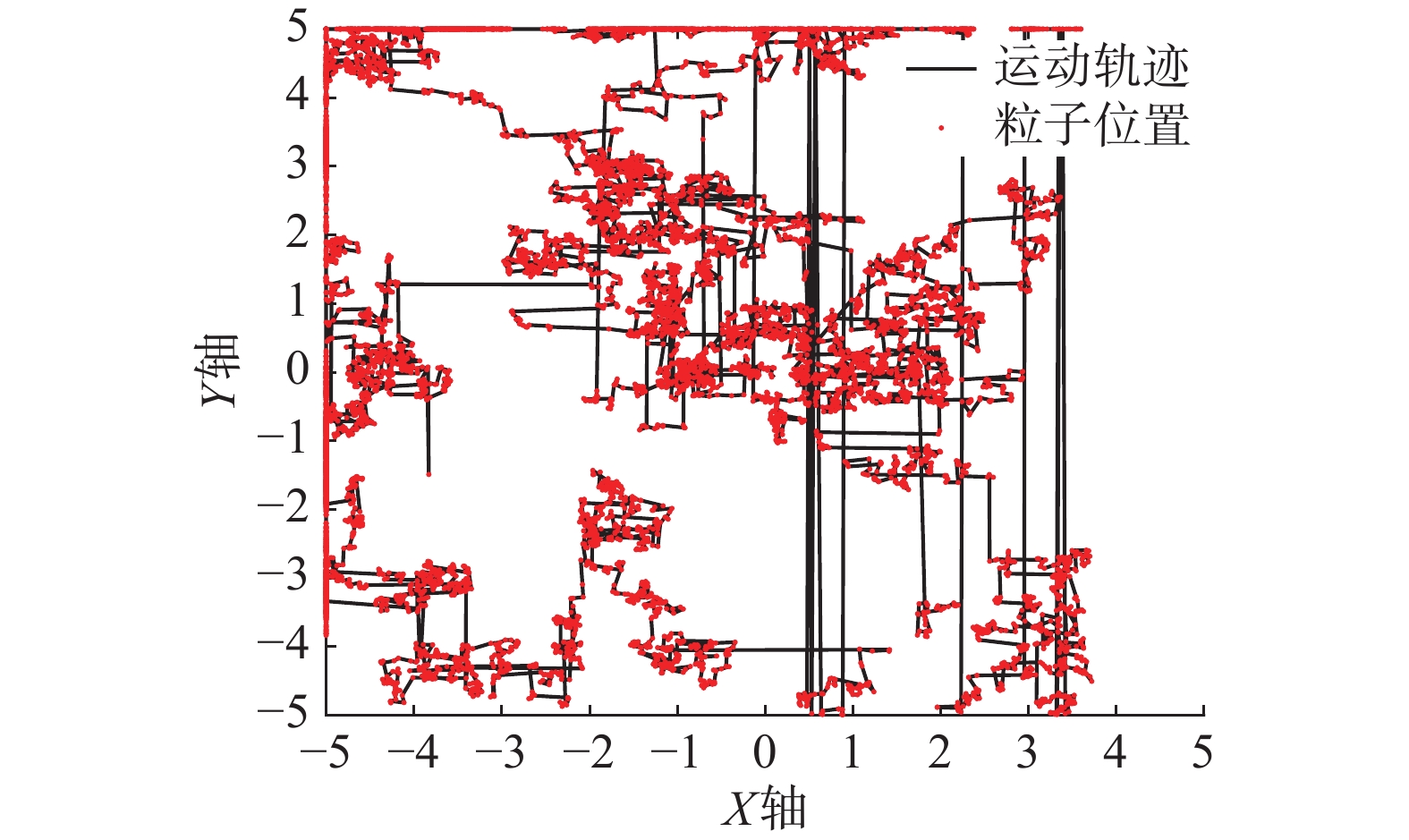
根据式(8)~(10)计算得到Levy飞行轨迹，式(11)通过尺度因子 $a$ 和限幅操作将Levy飞行位置映射在求解域 $\left[ {l_b,u_b} \right]$ 内。取 $a = 0.5,l_b = - 5,u_b = 5$ 模拟出二维的Levy飞行轨迹如图1所示，充分验证了Levy飞行短距离结合偶尔长距离跳跃的特征，对求解域实现了充分的探索。因此选择适当数量的蚁狮种群进行Levy变异可以显著改善整个种群的多样性，从而提高算法的全局搜索能力。

计算出Levy飞行路径后 $L\left( \lambda \right)$ ，选择适应值较差的若干个体 ${x_i}$ 按照式(12)进行变异操作：

$x_i' = L\left( {{\lambda _i}} \right)$

(12)

2.2 精英自适应竞争机制

单个精英所拥有的极值信息极其有限，因此有必要建立精英库存储历代较佳的个体(变异后适应值较佳的个体也会被存入精英库)。对ALO算法引入精英竞争机制，在每一代的寻优中，多个精英之间并行竞争，而不是通过轮盘赌的方式选择。在多个精英的同时带领下，种群能够快速锁定相对较优解的所在区域，有助于加快算法收敛速度^[14-15]。

为保证寻优前期的收敛速度，应选取较多个精英参与竞争；而后期，应减少精英个数避免较大的计算量。因此并行竞争的精英个数应随着迭代次数的增加而衰减。这种自适应选取方式在保证算法寻优速度的同时避免了不必要的计算量。设置精英个数范围为 $\left[ {{n_{ min}},{n_{ max}}} \right]$ ，则对于当代精英个数 $n\left( t \right)$ 和迭代次数 $t$ ，构造如下关系式：

$\left\{ {\begin{array}{*{20}{l}} {n\left( t \right) = { round}\left( {\displaystyle\frac{{{n_{\min }}}}{{1 + \left( {\displaystyle\frac{{{n_{\min }}}}{{{n_{\max }}}} - 1} \right)h\left( t \right)}}} \right)} \\ {h\left( t \right) = 1 - {{\left( {\displaystyle\frac{t}{T}} \right)}^2}} \end{array}} \right.$

(13)

式中： ${ round}()$ 为取整函数， $T$ 为设置的最大迭代次数。设置精英个数的范围为 $\left[ {1,5} \right]$ 时，随迭代次数的增加，精英个数变化曲线如图2所示。

建立容量为 $n$ 的精英库，每代寻优完成后对其更新，使得库内始终存放的是截止当前代为止最优的 $n$ 个个体。根据式(13)确定精英个数，蚂蚁种群按照式(1)、(2)绕多个精英游走，式(3)变为

$\begin{array}{c} c_i^t = { Elite}_j^t + {c^t},d_i^t = { Elite}_j^t + {d^t} \hfill \\ i = 1, 2,\cdots ,n \times N;j = 1,2, \cdots ,n \hfill \\ \end{array}$

(14)

式中： ${{ Elite}^t}_j$ 为来自精英库的精英， $N$ 为设定的种群数目。式(4)不作变化，式(6)中的 ${{ Ant}^t}_i$ 代表被 $n$ 个精英精英化后的蚂蚁种群，即 $i = 1, 2,\cdots ,n \times N$ 。式(5)变为

$\sum\limits_{i = 1}^{n \times N} {{f_{ sort}}\left( {{ Ant}_i^t} \right)} \Rightarrow \sum\limits_{i = 1}^n {{ Antlion}_i^{t + 1}}$

(15)

式中： ${f_{ sort}}$ 为排序函数， $ \Rightarrow $ 表示提取排序后的前 $n$ 个较优个体作为下一代蚁狮种群。

2.3 LEALO算法执行伪代码

Algorithm: LEALO algorithm

$N$ —The number of searching individuals

$T$ —The max iters

$n$ —The number of selected elites in elites library

Initialize Antlions position

Building Elites library

while the max iters $T$ is not met

　　Get $n$ using Eqs.(13)

　　for every elite $ii = 1,\;2, \cdots ,n$

　　　for every ant $i = 1,\;2, \cdots N$

　　　　Select a antlion from the Antlions;

　　　　Ants walk around iith elite using Eq.(1)

　　　　Normalize ants using Eq.(2);

　　　　Update ants using Eqs.(14)(4);

　　　　Elitism the ants using Eqs.(6);

　　　　Calculate the objective values of ants;

　　　　Update the Elites library using Eq.(15);

　　　end for

　　end for

　　Make Levy-mutation using Eq.(8)(9)(10)(11)(12)

end while

3 测试对比分析与应用 3.1 仿真实验

下面通过6个标准函数测试LEALO算法的寻优精度和收敛速度，测试函数设置见表1。其中f₁、f₂为单峰函数， ${f_3} \sim {f_6}$ 为多峰函数。

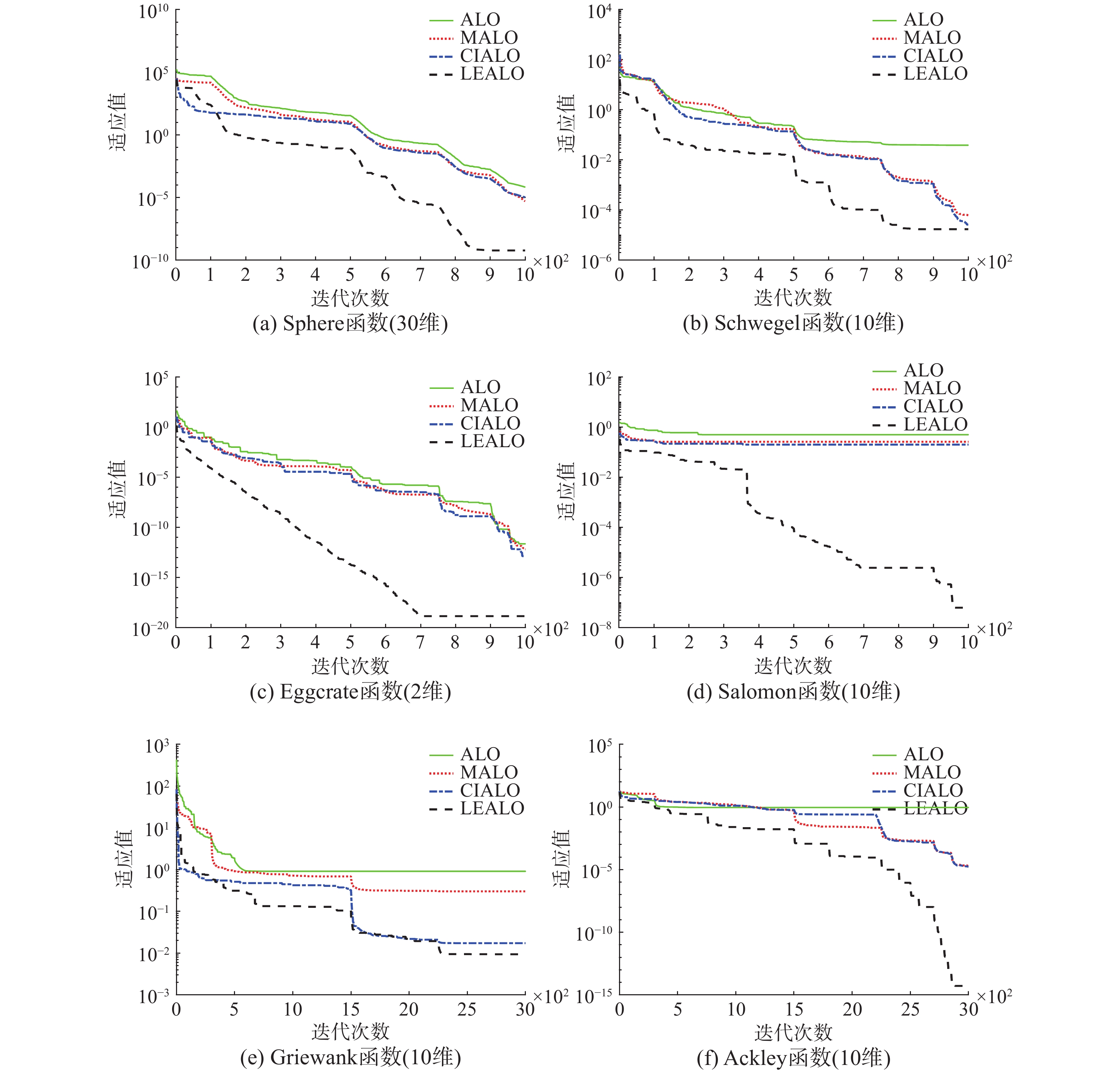
仿真平台，操作系统：win7旗舰版(64 b)；CPU：Intel(R)Core(TM)i5-4590；主频：3.30 GHz；RAM：4.00 GB；编程工具：MATLAB2016b。选择3种算法(ALO、MALO、CIALO)和LEALO算法进行对比，测试100次，分别统计历代最优解、平均解和寻优成功率(当寻优值达到设置精度时，视作寻优成功)。因3种改进算法效果均优于基本ALO算法(结果见图3)，考虑到表格篇幅，只给出3种改进算法的测试结果，如表2所示。

精度方面：对于函数f₁，MALO算法高于CIALO算法；对于函数f₂、f₃、f₄、f₅、f₆，MALO算法低于CIALO算法。寻优成功率方面：对于函数f₃、f₅，CIALO算法高于MALO算法。整体而言，这两种算法的寻优精度和成功率均不高，而LEALO算法在寻优精度和寻优成功率上均远优于MALO算法和CIALO算法。

为了使寻优精度和收敛速度对比更为直观，分别取经过100次测试的4种算法收敛曲线平均值，绘制在对数坐标系中，如图3所示。对于函数f₁、f₃、f₄、f₆，LEALO算法的寻优精度远高于MALO和CIALO算法；对于函数f₂、f₅，LEALO算法寻优精度略高于和MALO和CIALO算法，但是收敛速度明显快于这两种算法；对于函数f₄、f₅，MALO和CIALO算法均早早陷入局部最优不再收敛，而LEALO算法能够不断跳出局部最优对求解域进行充分探索，在得到更高精度解的同时保证了较快的收敛速度。综合表2和图3得出，LEALO算法有效克服了基本ALO算法及MALO和CIALO两种改进算法易陷入局部最优、收敛速度慢的缺点，对于高维度变量的多峰函数可以实现高精度快速寻优。

3.2 硅单晶热场温度模型参数的辨识

硅单晶是一种重要的半导体材料，基于直拉法的单晶炉是制备硅单晶的关键设备^[16]。为了得到高品质硅单晶，通常通过调节加热器功率来有效控制炉内的热场温度，因此有必要建立精确的热场温度模型。本文针对拉晶过程中的引晶阶段，采用式(16)作为该阶段的热场温度模型，基于现场采集的大量数据，对模型参数进行离线辨识，进而得到热场温度模型。

$\frac{{T\left( s \right)}}{{P\left( s \right)}} = \frac{{{K_1}}}{{{L_1}{s^2} + {L_2}s + 1}}{{ e}^{ - \tau s}}$

(16)

式中： $T\left( s \right)$ 和 $P\left( s \right)$ 分别为热场温度和加热器功率，K₁、L₁、L₂、τ为模型未知参数。

上面已证实了LEALO算法对包含多维参数的多峰函数的寻优能力，现将LEALO算法应用于热场温度模型的离线辨识^[17]。设置种群个数为30，最大迭代次数1 000，辨识20次，所得参数如表3所示。模型离散化的采样周期为0.1，真实数据采样间隔 $\Delta t = 6\;{ s}$ 。在加热器功率作用下，辨识所得最佳参数模型输出与硅单晶热场温度系统真实输出对比如图4所示。

图4表明，离线辨识所得最佳参数模型的输出较好地拟合了热场温度的真实数据，从而说明了LEALO算法具有较好的离线参数辨识能力。

4 结束语

作为一种新的寻优算法，蚁狮算法具有调节参数少、寻优精度高的特点。本文针对其缺点提出一种具有Levy变异和精英自适应竞争机制的LEALO算法。选择部分较差的个体进行Levy变异，保证了种群丰富度从而实现对求解区域进行充分探索，可以有效提高种群全局搜索能力；多个精英之间的并行竞争，削弱了单个精英对种群的误导，加快了寻优的收敛速度，精英竞争的自适应操作在保证寻优效率的同时，避免了较大的计算量。并与基本ALO算法及改进的MALO和CIALO算法进行对比，测试结果表明本文所提出的LEALO算法具有更好的寻优精度和收敛速度。最后将LEALO算法应用于硅单晶热场温度模型的参数辨识，仿真结果说明了该算法具有较好的优化能力。