2. 南京理工大学 经济管理学院, 江苏 南京 210094;
3. 江苏科技大学 数理学院, 江苏 镇江 212003
2. School of Economics and Management, Nanjing University of Science and Technology, Nanjing 210094, China;
3. School of Mathematics and Physics, Jiangsu University of Science and Technology, Zhenjiang 212003, China
作为粗糙集理论[1-2]研究的核心内容,属性约简[3-4]问题一直是众多学者关心的焦点。所谓属性约简,是在给定某一度量标准的前提下,期望利用较少的属性,能够超越利用原始数据中所有的属性所得到的性能或达到与其基本相当的性能。近年来,根据不同的需求目标以及不同类型的拓展粗糙集模型[5-8],众多研究者提出了诸如信息熵[9]、决策代价[10-11]、分类刻画[12]等类型的度量标准作为属性约简的定义。这些不同类型的属性约简大体上可以被划分为两大类[13-14]:1)面向粗糙集不确定性度量的属性约简;2)面向粗糙集学习性能的属性约简。
为了从数据中获取约简,在粗糙集领域的研究中有两大类方法:穷举法与启发式方法。分辨矩阵与回溯策略是穷举法的典型算法,虽然穷举法可以帮助我们得到所有的约简,但由于其计算复杂度过高,并不适用于现实世界中的大规模数据处理。启发式算法是借助贪心的搜索策略求得数据中的一个约简,虽然启发式算法有可能陷入局部最优,仅能得到超约简,但因其速度优势依然得到了广大研究学者的认可。
在启发式约简求解过程中,属性重要度扮演着重要的角色,在向约简集合不断增加属性的过程中,每次都加入重要度最大的属性,直至满足所定义的约简标准。但不难发现属性重要度的计算都是基于计算所有样本的基础上,这会带来两个问题:1)每次计算都需要扫描所有样本,时间消耗过大;2)未考虑数据扰动带来的属性重要度变化问题。虽然王熙照等[15]已经提出了利用边界样本求解属性重要度的方法,这一思想可以进一步降低启发式约简求解的时间消耗[16],但他们没有考虑数据扰动问题。微小的数据扰动有可能会使约简的结果大相径庭,这不仅表明约简本身不具备稳定性,而且也会致使根据约简所得到的分类及预测等结果也呈现不稳定性。针对上述问题,笔者期望利用启发式算法,求得具有较高稳定性的约简。借助集成学习[17-18]的基本思想,可以设计一种集成属性重要度的计算方法,对由不同边界样本所得到的属性重要度进行集成,其目的是使属性重要度的输出更为鲁棒。
1 邻域粗糙集在粗糙集理论中,一个决策系统可以表示为二元组
给定论域
| ${\rm{Int}}({x_i}) = \mathop {\min }\limits_{1 \leqslant j \leqslant n,j \ne i} {r_{ij}} + \delta \times (\mathop {\max }\limits_{1 \leqslant j \leqslant n,j \ne i} {r_{ij}} - \mathop {\min }\limits_{1 \leqslant j \leqslant n,j \ne i} {r_{ij}})$ | (1) |
式中:
| $\delta ({x_i}) = \{ {x_i} \in U|{x_j} \ne {x_i},{r_{ij}} \leqslant {\rm{Int}}({x_i})\}$ | (2) |
定义1[19-20] 给定一个决策系统DS,根据D可以得到所有决策类的合集形如
| $\underline {{N_B}} D = \bigcup\limits_{i{\rm{ = }}1}^N {\underline {{N_B}} {X_i}} $ | (3) |
| $\overline {{N_B}} D = \bigcup\limits_{i{\rm{ = }}1}^N {\overline {{N_B}} {X_i}} $ | (4) |
对于任一决策类Xi有
| $\underline {{N_B}} {X_i} = \{ {x_i} \in U|{\delta _B}({x_i}) \subseteq {X_i}\} $ | (5) |
| $\overline {{N_B}} {X_i} = \{ {x_i} \in U|{\delta _B}({x_i}) \cap {X_i} \ne \text{Ø} \} $ | (6) |
定义2 给定一个决策系统DS,
| $\gamma (B,D) = \frac{{{\rm{|}}\underline {{N_B}} D{\rm{|}}}}{{|U|}}$ | (7) |
式中|NBD |与|U|分别表示集合NBD 与U的基数。
显然0≤γ(B, D)≤1成立。γ(B, D)表示属于条件属性B的基础上,某种决策类的样本占总体样本的比例。若
定义3 给定一决策系统DS,
定义3所示的约简是一个能够保持决策系统中依赖度不发生变化的最小属性子集。根据定义2所示的依赖度,可以进一步考察属性的重要度。
给定一个决策系统DS,
| ${\rm{Sig}}(a,B,D) = \gamma (B \cup \{ a\} ,D) - \gamma (B,D)$ | (8) |
根据上述属性重要度,算法1构建了一个启发式求解过程,其目标是获得以式(8)所示重要度为依据的属性排序序列。
算法1 启发式算法
输入 邻域决策系统
输出 属性排序seq。
1) seq←Ø,γ(seq, D)=0;
2) 若AT–seq = Ø,则转至5),否则转至3);
3)
4) 选择aj,满足Sig(aj, seq, D)=max{Sig(ai, seq, D):
5) 输出seq。
2.2 集成属性重要度算法1在迭代过程中,求解属性重要度是利用全体样本所得到的依赖度差异,如式(8)。但这种重要度计算方法忽视了数据扰动对重要度计算产生的影响,当样本集发生变化时,属性重要度势必也会发生相应的变化,从而导致约简变化。如何降低样本集变化所引起的约简变化程度,其本质是期望所求约简应尽可能稳定、鲁棒,因此需要重新考察属性重要度的计算方法。
从分类学习的角度来看,不同样本对学习性能的贡献程度是不相同的。一般来说,那些对于学习性能影响比较重要的样本大都分布在边界区域上[15-16]。从这一考虑出发,可以将边界区域的样本挑选出来,作为计算属性重要度的依据。一个可行且直观的办法是采用聚类算法对原始样本集进行聚类,在各类簇中挑选出距离类簇中心较远的样本,将这些样本组合成一个新的决策系统,这实际上是一个采样的过程(具体描述如算法2所示)。又因为传统的聚类算法,如k-means聚类的结果并不稳定,其初始类簇中心是随机选取的,故可以在原始样本集上通过多次聚类后得到多个决策系统,分别在这多个决策系统上求得各个属性的重要度并进行融合,最后选择融合重要度较高的属性,其具体描述如算法3所示。
算法2 基于k-means聚类的采样
输入 邻域决策系统
输出 采样后的决策系统
1)
2) 利用k-means聚类获得U上的类簇C =
3) for j = 1 to N
①计算类簇Cj中每个样本到类簇中心的平均距离
②将Cj中到类簇中心的距离大于平均距离
end for
4) 输出
算法3 重要度集成的启发式算法
输入 邻域决策系统
输出 属性排序seq。
1) seq←Ø,γ(seq, D)=0;
2) for r = 1 to k
利用算法2进行采样得到决策系统DSr;
end for
3) 若AT–seq = Ø,则转至7),否则转至4);
4) for r = 1 to k
end for
5)
| ${\rm{Sig}}({a_i},{\rm{AT}},D) = \frac{{\displaystyle\sum\limits_{r = 1}^K {{\rm{Si}}{{\rm{g}}_r}({a_i},{\rm{AT}},D)} }}{k};$ |
6) 选择aj,满足Sig(aj, seq, D)=max{Sig(ai, seq, D):
7) 输出seq。
在邻域粗糙集上求解属性重要度的时间复杂度为O(
为了验证所提算法的有效性,本文从UCI数据集中选择了9组数据,数据的基本描述如表1所示。实验中取k=5,即进行5次聚类采样,由算法3得到的属性序列不仅和传统的启发式算法比较,而且和王熙照等 [15]提出的基于样例选取的求解属性重要度算法对比分析。
| 表 1 实验数据的基本信息 Tab.1 Data sets description |
为了比较3种约简算法在样本扰动情况下属性的排序结果,采用了5折交叉验证来实现。具体过程为:在每个数据集上,将数据集随机地平均分成5份,即
度量属性序列的稳定性,就是在样本扰动时度量不同属性序列之间的相似性,相似性越高,说明所得到的属性序列越稳定,可使用式(9)[21]计算属性序列的相似性:
| ${\rm{Sta}} = \frac{{2\displaystyle\sum\limits_{i = 1}^{d - 1} {\displaystyle\sum\limits_{j = i + 1}^d {{\rm{Sim}}({\rm{se}}{{\rm{q}}_i},{\rm{se}}{{\rm{q}}_j})} } }}{{d \times (d - 1)}}$ | (9) |
式中:
| ${\rm{Sim}}({\rm{se}}{{\rm{q}}_i},{\rm{se}}{{\rm{q}}_j}) = 1 - 6 \times \sum\limits_{l = 1}^n {\frac{{{{({\rm{seq}}_i^l - {\rm{seq}}_j^l)}^2}}}{{n \times ({n^2} - 1)}}}$ | (10) |
式中:n表示属性个数,
表2列出了4个不同的邻域半径下3种约简算法所求得的属性序列的稳定性结果。
| 表 2 属性序列的稳定性对比 Tab.2 Comparisons of stabilities of attribute sequences |
观察表2可以发现,在大多数的半径参数δ下,利用算法3所求得的属性序列相似度都比利用算法1及文献[15]算法所求得的属性序列相似度高,这说明算法3在增加属性的过程中所得到的属性序列是比较稳定的。
此外,为了检验新算法约简结果稳定性在统计学上是否具有显著性差异,对各算法的属性序列稳定性的值,采用Friedman检验[22]分别计算它们的秩及APV(adjusted p-value),判断其是否拒绝原假设。其中,显著性水平α设为0.05。统计分析结果如表3所示。
| 表 3 各个算法的统计结果 Tab.3 Statistical results of various algorithms |
从表3可以看出,算法3在各个算法里的秩最小,这表明算法3性能最好。此外,算法1与文献[15]的算法的APV值均小于显著性水平α=0.05,这意味着算法3与其余两种算法有着显著性的差异。
3.2 分类结果的一致性比较在求解属性排序序列的过程中,将重要度较大的属性逐个添加到约简结果中。在属性序列逐步增长的过程中,不同序列在同一分类器上也会产生不同的分类结果。借助交叉验证,由属性序列
| 表 4 联合分布矩阵 Tab.4 Joint distribution matrix |
在表4中,当前
| $Q = \frac{{{a_{uv}}{d_{uv}} - {b_{uv}}{c_{uv}}}}{{{a_{uv}}{d_{uv}} + {b_{uv}}{c_{uv}}}}$ | (11) |
式中Q的取值范围为[−1, 1]。Q值为0时,表示两个排序序列在同一分类器上的预测结果毫不相关;Q值越大,表示当前两个排序结果在同一分类器上的预测结果的一致性越高。整体的一致性可取平均值
|
Download:
|
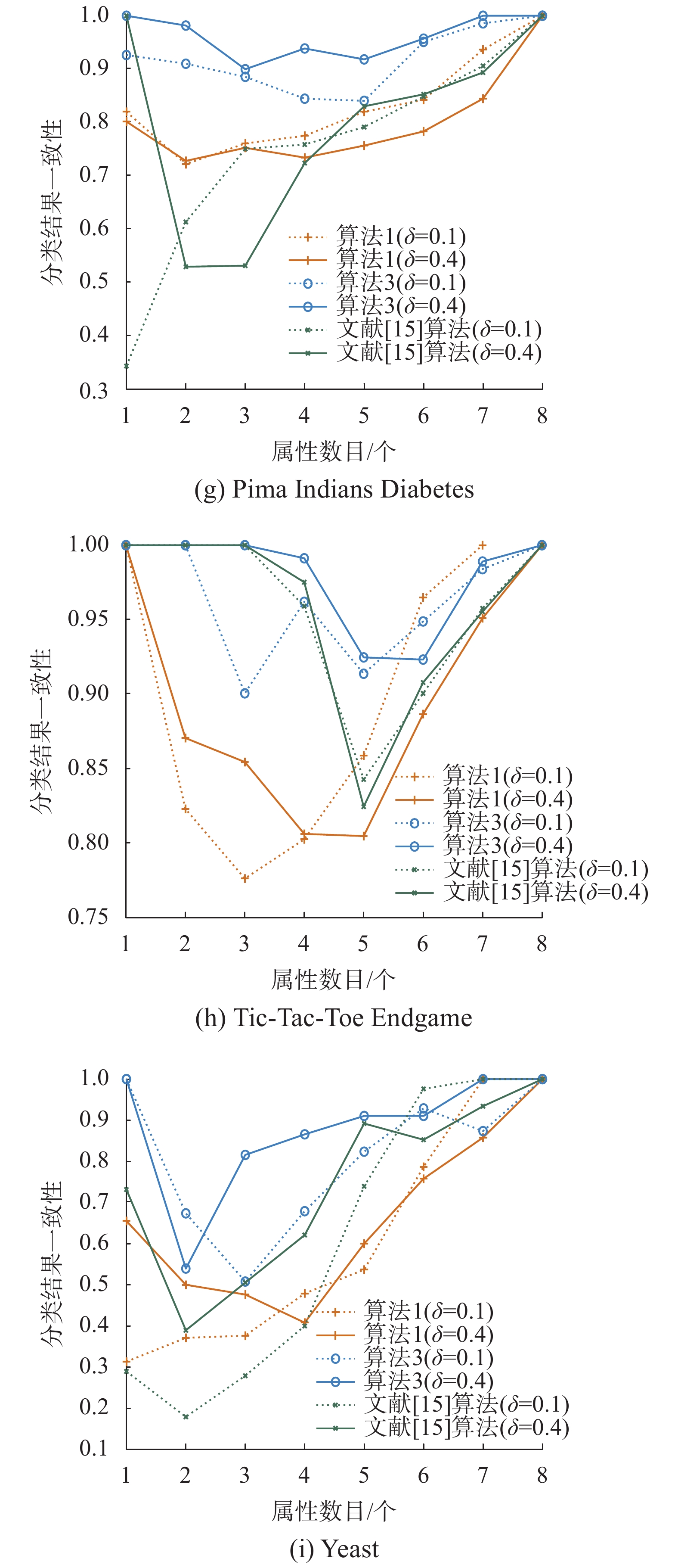
| 图 1 分类结果一致性的对比 Fig. 1 Comparisons of classification agreements | |
由图1可知,随着属性逐个加入排序序列中在相同的邻域半径参数下,算法3在依次增加属性时做出分类结果的一致性总体比算法1以及文献[15]算法要高,验证了由算法3求得属性序列做出分类结果的稳定性要高于算法1以及文献[15]算法。
3.3 分类精度比较随着当前重要度最大的属性逐渐加入到属性序列中去,进一步考虑当前属性序列的分类精度,对此,分别在邻域参数δ=0.1与δ=0.4时比较了3种约简算法的分类精度,实验结果如图2所示。

|
Download:
|
| 图 2 分类精度的对比 Fig. 2 Comparisons of classification accuracies | |
通过图2可知,在相同的邻域半径参数下,随着属性逐个加入到排序序列中,其分类精度也在不断提高,当属性达到一定个数时,分类精度也趋于平稳。总体来说,由算法1、算法3和文献[15]的算法得到的属性序列的分类精度是差不多的。尽管算法3得到的属性序列在样本扰动下的稳定性以及分类结果的一致性较算法1和文献[15]的算法能够得到提升,但是未能有效提升属性序列的分类精度。
4 结束语利用邻域粗糙集求解约简时,提出了一种可以得到稳定约简的启发式算法框架。这种新的算法在多次采样基础上利用集成的思想求解属性重要度,从而可以用来提高约简的稳定性。实验结果表明,新算法在有效地提升约简稳定性的同时,亦能提高由约简所做出分类结果的稳定性。在本文工作的基础上,下一步工作主要有:1)针对稳定的属性约简与分类度量指标之间的关系进行深入讨论,以期能够在获得稳定约简的基础上,提升分类精度等相应的学习性能;2)文中聚类采样方法未能考虑到原始样本分布情况,对于某些非凸型分布的样本,或许不能有效地抽取到边界样本。进一步考虑数据的分布情况,寻求更有效的方法抽取到边界样本也是笔者的下一步工作。
| [1] |
PAWLAK Z. Rough sets: theoretical aspects of reasoning about data[M]. Boston, Mass, USA: Kluwer Academic Publishers, 1991.
( 0) 0)
|
| [2] |
PAWLAK Z. Rough sets[J]. International journal of computer & information sciences, 1982, 11(5): 341-356. ( 0) 0)
|
| [3] |
JU Hengrong, LI Huaxiong, YANG Xibei, et al. Cost-sensitive rough set: a multi-granulation approach[J]. Knowledge-based systems, 2017, 123: 137-153. DOI:10.1016/j.knosys.2017.02.019 ( 0) 0)
|
| [4] |
XU Suping, YANG Xibei, YU Hualong, et al. Multi-label learning with label-specific feature reduction[J]. Knowledge-based systems, 2016, 104: 52-61. DOI:10.1016/j.knosys.2016.04.012 ( 0) 0)
|
| [5] |
DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International journal of general systems, 1990, 17(2/3): 191-209. ( 0) 0)
|
| [6] |
胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报, 2008, 19(3): 640-649. HU Qinghua, YU Daren, XIE Zongxia. Numerical attribute reduction based on neighborhood granulation and rough approximation[J]. Journal of software, 2008, 19(3): 640-649. (  0) 0)
|
| [7] |
YANG Xibei, CHEN Zehua, DOU Huili, et al. Neighborhood system based rough set: models and attribute reductions[J]. International journal of uncertainty, fuzziness and knowledge-based systems, 2012, 20(3): 399-419. DOI:10.1142/S0218488512500201 ( 0) 0)
|
| [8] |
LIANG Jiye, WANG Feng, DANG Chuangyin, et al. An efficient rough feature selection algorithm with a multi-granulation view[J]. International journal of approximate reasoning, 2012, 53(6): 912-926. DOI:10.1016/j.ijar.2012.02.004 ( 0) 0)
|
| [9] |
ZHANG Xiao, MEI Changlin, CHEN Degang, et al. Feature selection in mixed data: a method using a novel fuzzy rough set-based information entropy[J]. Pattern recognition, 2016, 56: 1-15. DOI:10.1016/j.patcog.2016.02.013 ( 0) 0)
|
| [10] |
JU Hengrong, YANG Xibei, YU Hualong, et al. Cost-sensitive rough set approach[J]. Information sciences, 2016, 355-356: 282-298. DOI:10.1016/j.ins.2016.01.103 ( 0) 0)
|
| [11] |
JIA Xiuyi, LIAO Wenhe, TANG Zhenmin, et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information sciences, 2013, 219: 151-167. ( 0) 0)
|
| [12] |
YANG Xibei, QI Yunsong, SONG Xiaoning, et al. Test cost sensitive multigranulation rough set: model and minimal cost selection[J]. Information sciences, 2013, 250: 184-199. DOI:10.1016/j.ins.2013.06.057 ( 0) 0)
|
| [13] |
MIN Fan, HE Huaping, QIAN Yuhua, et al. Test-cost-sensitive attribute reduction[J]. Information sciences, 2011, 181(22): 4928-4942. DOI:10.1016/j.ins.2011.07.010 ( 0) 0)
|
| [14] |
SONG Jingjing, TSANG E C C, CHEN Degang, et al. Minimal decision cost reduct in fuzzy decision-theoretic rough set model[J]. Knowledge-based systems, 2017, 126: 104-112. DOI:10.1016/j.knosys.2017.03.013 ( 0) 0)
|
| [15] |
王熙照, 王婷婷, 翟俊海. 基于样例选取的属性约简算法[J]. 计算机研究与发展, 2012, 49(11): 2305-2310. WANG Xizhao, WANG Tingting, ZHAI Junhai. An attribute reduction algorithm based on instance selection[J]. Journal of computer research and development, 2012, 49(11): 2305-2310. (  0) 0)
|
| [16] |
杨习贝, 颜旭, 徐苏平, 等. 基于样本选择的启发式属性约简方法研究[J]. 计算机科学, 2016, 43(1): 40-43. YANG Xibei, YAN Xu, XU Suping, et al. New heuristic attribute reduction algorithm based on sample selection[J]. Computer science, 2016, 43(1): 40-43. DOI:10.11896/j.issn.1002-137X.2016.01.009 (  0) 0)
|
| [17] |
LI Yun, SI J, ZHOU Guojing, et al. FREL: a stable feature selection algorithm[J]. IEEE transactions on neural networks and learning systems, 2014, 26(7): 1388-1402. ( 0) 0)
|
| [18] |
周林, 平西建, 徐森, 等. 基于谱聚类的聚类集成算法[J]. 自动化学报, 2012, 38(8): 1335-1342. ZHOU Lin, PING Xijian, XU Sen, et al. Cluster ensemble based on spectral clustering[J]. Acta automatica sinica, 2012, 38(8): 1335-1342. (  0) 0)
|
| [19] |
YANG Xibei, ZHANG Ming, DOU Huili, et al. Neighborhood systems-based rough sets in incomplete information system[J]. Knowledge-based systems, 2011, 24(6): 858-867. DOI:10.1016/j.knosys.2011.03.007 ( 0) 0)
|
| [20] |
QIAN Yuhua, WANG Qi, CHENG Honghong, et al. Fuzzy-rough feature selection accelerator[J]. Fuzzy sets and systems, 2014, 258: 61-78. ( 0) 0)
|
| [21] |
LI Jingzheng, YANG Xibei, SONG Xiaoning, et al. Neighborhood attribute reduction: a multi-criterion approach[J]. International journal of machine learning and cybernetics, 2017. DOI:10.1007/s13042-017-0758-5 ( 0) 0)
|
| [22] |
DEMŠAR J. Statistical comparisons of classifiers over multiple data sets[J]. Journal of machine learning research, 2006, 7: 1-30. ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


