2. 江苏科技大学 电子信息学院, 江苏 镇江 212003;
3. 同济大学 电子与信息工程学院,上海 200092
2. Department of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. College of Electronics and Information Engineering, Tongji University, Shanghai 200092, China
隶属度函数M(x)取值位于[0, 1],用以表征x属于M的程度高低。隶属度函数常用于模糊评价函数,其特点是评价结果不是觉得的肯定或否定,而是用模糊集来表示。确定隶属度函数是模糊理论在实际应用中的重要环节。目前构造隶属函数的方法主要有:模糊统计法[1-2]、指派方法[3]、二元对比排序法等[1]。然而,传统方法存在各种各样的问题[4-5],文献[6]对隶属度函数的不同确定方法原理进行了详细阐述。其中,模糊统计方法较直观地反映了模糊概念中的隶属程度,但其计算量较大,隶属度函数精度直接受离散化的区间大小的影响;指派法受限于指派者的经验知识;二元比较法中如何实现个体整体隶属度排序是难点,且二元比较法获得的隶属度函数是离散表示的。为获得更符合客观实际的连续隶属函数,文献[7]尝试通过最小二乘法来构建隶属度函数,通过最小化误差的平方和找到一组数据的最佳函数匹配,需通过试凑确定多项式的最佳阶数;文献[8]提出采用抛物线作为隶属度函数的上升或下降沿,但该方法可能出现局部隶属度大于1的情况;文献[9]采用贝塞尔曲线逼近方式,当曲线的幂次较低时,该方法修改曲线的功能较弱,灵活性受到限制;文献[10]设计了基于贝塞尔曲线理论的备件需求模糊隶属度函数构建方法,此方法无需事先假设隶属度函数的形态,简单易用、使用灵活,但该方法中拟合误差最小的控制点选择方法是难点。综上所述,使用贝塞尔曲线确定隶属度函数形态,可以使曲线经过模糊统计结果规定的任意点,且可以避免抛物线隶属度函数中隶属度大于1的情况[11]。但是贝塞尔曲线的控制点选择是难点[12-13]:1)对于经过给定点的贝塞尔曲线,控制点的选择并不是唯一的;2)如果以贝塞尔曲线作为隶属度函数上升沿或下降沿,则要求贝塞尔曲线必须为凸的,这将对控制点的选择附加更多的约束,而文献[9-10]均没有就这个问题进行讨论。对于高阶贝塞尔曲线,最佳拟合问题本质上是多变量优化问题。差分进化算法因其简单的结构和稳定的性能,在多变量优化领域有着广泛的应用[14-15]。然而,在应用差分进化算法求解最佳贝塞尔曲线控制点前,必须确定控制点选择的标准,并解决控制点约束问题[16]。本文采用拟合误差和控制点与目标点距离联合的策略评价控制点,使给定目标点后最佳控制点唯一。使用新的增量极坐标方案对控制点进行编码,保证了所得贝塞尔曲线均为凸的,避免了硬约束方案对计算资源的浪费。仿真结果证实了本方法的有效性。
1 基于统计分析确定隶属度函数在确定隶属度函数形态前,首先需要确定各隶属度函数的区间。隶属度函数区间的划分有很多种方法。以评价学生成绩为例,隶属度函数确定的原则为使最终的分类满足规定的要求或者默认的满足正态分布,即中间档次人数占主要。设论域,并以优、良和差表示上的模糊集,为了确定每个模糊集的隶属度函数,需要确定5个区间的边界a、b、c和d(图1)。

|
图 1 典型隶属度函数 Fig.1 Typical membership functions |
常见的划分方法有:
1) 基于距离的方法。将论域等距地划分,每个区间长度为
| $\frac{{\mathop {\max }\limits_{i \in [1,n]} {x_i} - \mathop {\min }\limits_{i \in [1,n]} {x_i}}}{5}$ | (1) |
式中n为样本数量。
2) 基于分位数的方法。使用该方法,可以将每个区间内的数据点数量划分为相同或不同的,具体选择可根据所需分类结果的统计分布决定。若区间内数据数量相同,则五区间分位数取为
3) 基于均值的方法。该方法以
在隶属度函数区间确定后,应根据区间内数据的分布,进一步确定隶属度函数的形态。以区间
| $\left\{ {\begin{array}{*{20}{c}}{\left( {\displaystyle\frac{{a + b}}{2},\displaystyle\frac{s}{{s + t}}} \right),}&\text{上升沿}\\{\left( {\displaystyle\frac{{a + b}}{2},\displaystyle\frac{t}{{s + t}}} \right),}&\text{下降沿}\end{array}} \right.$ | (2) |
式中:s为
1) 直线型。直线型隶属度构成梯形隶属度函数。显然梯形隶属度函数无法经过任意给定点。
2) z函数或s函数。常见的z形下降沿函数:
| $f\left( {x;a,b} \right) = \left\{ {\begin{array}{*{20}{l}}{1,} \quad {x \leqslant a}\\[3pt]{1 - 2{{\left( {\displaystyle\frac{{x - a}}{{b - a}}} \right)}^2}}, \quad {a \leqslant x \leqslant \displaystyle\frac{{a + b}}{2}}\\[7pt]{2{{\left( {\displaystyle\frac{{x - b}}{{b - a}}} \right)}^2}}, \quad {\displaystyle\frac{{a + b}}{2} \leqslant x \leqslant b}\\[7pt]0,\quad{x \geqslant b}\end{array}} \right.$ | (3) |
由定义可知,该函数中心对称,意味着无法做出凸形的下降沿函数,也无法做出过任意给定点的曲线。
3) 抛物线。文献[8]提出采用抛物线作为隶属度函数的上升或下降沿。同时指出,经过给定三点的抛物线是唯一的。但是,过三点的抛物线可能出现局部函数值大于1的情况,使得下降或上升沿非单调,这对于隶属度函数是不允许的。
4) 贝塞尔曲线。贝塞尔曲线是光滑的连续曲线,在工程与设计等领域有广泛应用[17]。贝塞尔曲线可以在端点固定的情况下,通过调整控制点对曲线形态进行细致的调整,且调整后的曲线仍然是连续光滑的。有关贝塞尔曲线的详细介绍,可参考文献[18]。
2 问题描述贝塞尔曲线的一般参数公式为
| ${\mathit{\boldsymbol{B}}}(t) = \sum\limits_{i = 0}^n {\left( {\begin{array}{*{20}{c}}n\\i\end{array}} \right)} {{\mathit{\boldsymbol{P}}}_i}{(1 - t)^{n - i}}{t^i}$ | (4) |
式中:
为不失一般性,以求取过3个点的贝塞尔曲线为例,对于二阶贝塞尔曲线有
| ${\mathit{\boldsymbol{B}}}(t){ = }{{\mathit{\boldsymbol{P}}}_0}{\left( {1 - t} \right)^2}{ + }2{{\mathit{\boldsymbol{P}}}_1}t(1 - t){ + }{{\mathit{\boldsymbol{P}}}_2}{t^2}$ | (5) |
由于首末端点
| $\min \left\| {{\mathit{\boldsymbol{B}}}(t) - {\mathit{\boldsymbol{OP}}}} \right\|$ | (6) |
式中
| $\min \left\| {{\mathit{\boldsymbol{B}}}(t) - {\mathit{\boldsymbol{OP}}}} \right\| + w \cdot \min \left\| {{{\mathit{\boldsymbol{P}}}_1} - {\mathit{\boldsymbol{OP}}}} \right\|$ | (7) |
意思为最小化拟合点与目标点距离的同时最小化控制点与目标点的距离。其中w为第二部分的加权值。
一般地,过m点的n阶贝塞尔曲线可通过最小化式(8)确定:
| $\begin{array}{c}\min \sum\limits_{j = 1}^{m - 2} {\left\| {{\mathit{\boldsymbol{B}}}({t_j}) - {\mathit{\boldsymbol{{OP}}}_j}} \right\|} = \\\min = \sum\limits_{j = 1}^{m - 2} {\left\| {\sum\limits_{i = 0}^n {\left( {\begin{array}{*{20}{c}}n\\i\end{array}} \right){{\mathit{\boldsymbol{P}}}_i}{{\left( {1 - {t_j}} \right)}^{n - i}}t_j^i - {{\mathit{\boldsymbol{OP}}}_j}} } \right\|} \end{array}$ | (8) |
由于贝塞尔曲线必经过首末端点,对剩余的m–2个目标点,确定曲线需要m–2个不同的参数t,同时需要确定n–1个控制点,即2n–2个参数。共计2n+m–4个参数需要优化。
3 基于差分进化算法的贝塞尔曲线控制点优化方法典型的差分进化变异操作为[19]
| ${\mathit{\boldsymbol{x}}}_i^{'d} = \left\{ {\begin{array}{*{20}{l}}{x_{r1}^d + F(x_{r2}^d + x_{r3}^d)},\quad{r < CR \vee d = {r_D}}\\ [5pt]{x_r^d},\quad \text{其他}\end{array}} \right.$ | (9) |
式中:
求解过m点的n阶贝塞尔曲线,所需优化的向量为
|
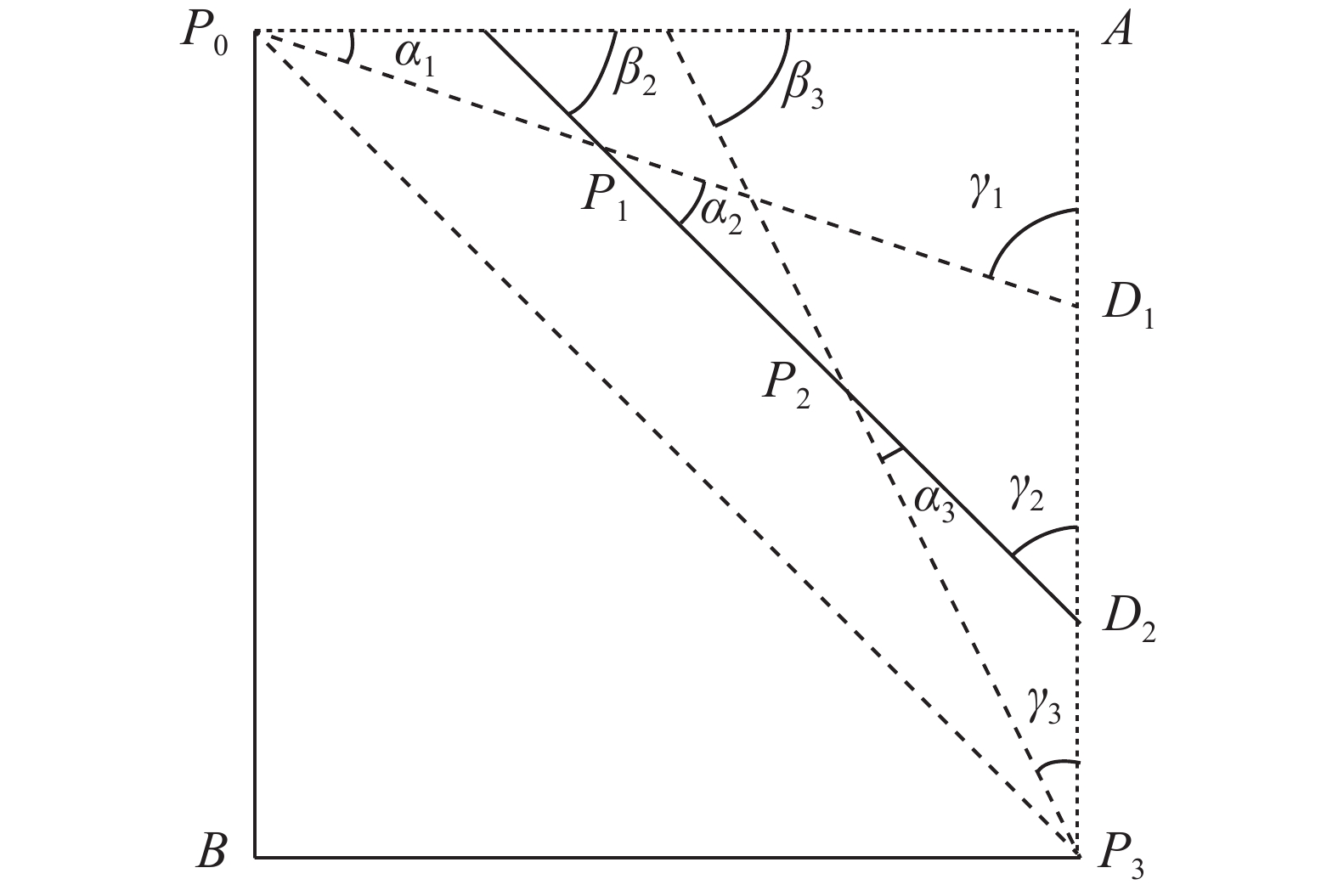
图 2 两控制点贝塞尔曲线示意图 Fig.2 Beizer curve with two control points |
为了使得到的控制点与首末端点组成凸多边形,有如下两种方法:
1)将所有控制点合并为一点,这样首末端点与控制点共同组成三角形,可保证所得曲线总是凸的。进一步,如果该控制点位于矩形的上半部分,则得到的贝塞尔曲线向上凸起,反之向下。
2)设计新的编码与解码方法保证搜索空间由凸多边形构成。仍然以图2为例,使用类似极坐标的方法对控制点进行编码。每个控制点需要角度和长度两位进行表达,对于过3点的3阶贝塞尔曲线,共需5位编码。所有编码的取值范围均为[0, 1]。对任意的编码
| ${\alpha _1} \in [0,{\arctan}\frac{{{P_{0y}} - {P_{3y}}}}{{{P_{3x}} - {P_{0x}}}}]$ | (10) |
于是,有
| ${\alpha _1}{\rm{ = }}{x_1}{\arctan}\frac{{{P_{0y}} - {P_{3y}}}}{{{P_{3x}} - {P_{0x}}}}$ | (11) |
为了使任意[0, 1]之间的任意编码均满足约束,令x2表示
| $d({{{P}}_0},{{{D}}_1}) = \frac{{{P_{3x}} - {P_{0x}}}}{{\cos {\alpha _1}}}$ | (12) |
由此,有
| $\begin{array}{l}{P_{1x}} = {P_{0x}} + \cos {\alpha _1} \cdot d({{{P}}_0},{{{P}}_1})\\{P_{1y}} = {P_{0y}} - \sin {\alpha _1} \cdot d({{{P}}_0},{{{P}}_1})\end{array}$ | (13) |
至于控制点P2,可知
| ${\alpha _i}{\rm{ = }}{x_{2i - 1}}\left( {{\arctan}\frac{{{P_{i - 1y}} - {P_{n,y}}}}{{{P_{n,x}} - {P_{i - 1,x}}}} - \sum\limits_{j = 0}^{i - 1} {{\alpha _j}} } \right),i \in [1,n - 1]$ | (14) |
式中
| $d({{{P}}_{i - 1}},{{{P}}_i}) = {x_{2i}}\frac{{{P_{n,x}} - {P_{i - 1,x}}}}{{\cos \sum\nolimits_{j = 0}^{i - 1} {{\alpha _j}} }}$ | (15) |
| ${P_{i,x}} = {P_{i - 1,x}} + d({{{P}}_{i - 1}}{{{P}}_i})\cos \sum\limits_{j = 0}^{i - 1} {{a_j}} $ | (16) |
| ${P_{i,y}} = {P_{i - 1,x}} - d({{{P}}_{i - 1}},{{{P}}_i})\sin \sum\limits_{j = 0}^{i - 1} {{\alpha _j}} $ | (17) |
对于过m点的n阶贝塞尔曲线,使用贝塞尔曲线的n-1个控制点和m-1个参数的编码组成向量
1)初始化种群内各向量
2)对每个变量进行解码,并按照式(7)或式(8)计算每个向量的代价函数;
3)按照式(9)对种群进行交叉,生成同等规模的实验向量,对实验向量解码,并按照(7)或式(8)计算每个向量的代价函数;
4)种群中相应的实验向量与旧向量进行比较,如果代价函数更小,则用实验向量代替旧向量;
5)如果达到停止条件,则退出优化并显示结果;否则返回 3)。
4 贝塞尔曲线上的隶属度确定方法贝塞尔曲线为参数曲线,在根据起始端点和中间点得到最佳控制点后,曲线形态唯一确定,但曲线上的隶属度(即纵坐标)无法直接通过横坐标值计算得出,必须通过
| $\mathop {\min }\limits_{t \in [0,1]} {\left( {x - {B_x}(t)} \right)^2}$ | (18) |
当贝塞尔曲线为凸时,该最小化问题是凸优化问题,可通过基于梯度的优化算法求解。为了获得较快的收敛速度,本文使用BFGS算法求解式(18)给出的最小化问题。BFGS算法是由4位提出者姓氏首字母(Broyden-Fletcher-Goldfarb-Shanno)命名的无约束数值最优化算法。BFGS是一类准牛顿算法,即通过近似而不是精确计算Hessian矩阵来确定算法搜索方向及步长。由于快速的收敛性,BFGS算法广泛的应用于连续无约束优化问题中[20]。BFGS算法流程在各类数值优化教科书中均有述及,不再赘述。通过优化式(18)得到给定横坐标x对应参数t后,可由式(4)求得对应的纵坐标,也就是隶属度值。
5 算例以某班级学生两门成绩为例,进行区间划分比较,隶属度函数形态比较和各阶贝塞尔曲线之间的对比。第一门课程成绩数据为{14, 90, 70, 80, 60, 66, 60, 36, 39, 76, 60, 33, 60, 81, 46, 65, 60, 40, 86, 84, 74, 80, 35, 47, 22, 65, 83, 26, 89, 37, 15, 81, 69, 41, 62, 1, 89, 33, 60, 91, 19, 0, 92, 65, 60, 68, 35, 89, 35, 64, 24, 71, 40, 35, 31, 40, 71, 46, 40, 40}。第二门课程成绩为{61, 94, 87, 74, 76, 87, 72, 66, 27, 79, 74, 74, 84, 84, 63, 69, 68, 60, 69, 98, 94, 72, 67, 72, 85, 84, 91, 79, 94, 87, 67, 73, 91, 41, 84, 21, 96, 89, 83, 97, 81, 71, 94, 66, 92, 94, 62, 76, 65, 84, 84, 92, 88, 72, 75, 65, 91, 83, 92, 79}。
5.1 实验1以距离、分位数、均值–距离、均值–分位数4种不同方式划分区间。其中分位数法采用等分位数,均值–分位数法使用中位数。划分区间如表 1。
| 表 1 4种方法分隔点对比 Tab.1 Separation points of four methods |
表格中a表示对于“差”的隶属度为1的上限,d表示对于“优”的隶属度为1的下限。相应地,每个区间内数据所占比例如表 2。
| 表 2 4种方法各区间比例对比 Tab.2 Proportion of intervals by four methods |
可以发现,在不同的课程中,基于距离的两类方法均出现了某区间比例不均衡的情况。其中课程一单纯的距离法大于d的区间,即对于“优”的隶属度为1的比例占25%,课程二此项比例更是达到了46%。而在经过模糊评价后,占优的比例将更高,这样的评价标准显然不符合需求。此外,课程–均值–距离法中的[a, b]区间也存在比例过大的情况。相对而言,单纯的分位数方法得到各区间比例基本相等,这是由分位数的特性决定的。最后两个区间比例不等是因为有相同的多个数据点。
5.2 实验2以均值–分位数得到的区间划分为基础,分别确定梯形、抛物线和贝塞尔曲线的隶属度函数。贝塞尔曲线使用2阶曲线,并采用差分进化算法求解最佳控制点。所得隶属度函数如图3所示。其中左侧为课程一的隶属度,右侧为课程二的隶属度函数。

|
图 3 3种隶属度函数形态对比 Fig.3 Comparison of three kind of membership functions |
图中圆圈代表隶属度函数需要穿过的点,该点横坐标分别为
对比两门课程的隶属度函数可以发现,由于课程二的平均成绩更高,故3种隶属度函数的上升沿和下降沿均向右移动,且由于课程二的数据方差较小,上升沿的与下降沿的区间都较窄。但不论采用什么样的数据,本文所采用的方法均可以对数据集作出合理的评价,使得最终的优良率保持一定的稳定。最终的优良差比例如下:
| 表 3 3种隶属度函数划分对比 Tab.3 Proportion of three kind of membership functions % |
为了验证本方案在高阶贝塞尔曲线下的有效性,以课程一数据为例,求解2~5阶贝塞尔曲线隶属度函数。依据3.2节的描述,本例为过3点的贝塞尔曲线求解问题,可以对2~5阶贝塞尔曲线分别取长度为3、5、7和9的编码串代表曲线参数。由于编码串无约束,可使用任意全局优化算法求解。本实验采用差分进化算法求解贝塞尔曲线。选择[a, b]区间的局部隶属度函数分别绘制2~5阶的贝塞尔曲线如图4。其中折线为连接起的控制点。

|
图 4 2~5阶贝塞尔曲线隶属度 Fig.4 Beizer membership function of order 2~5 |
可以看出,各阶贝塞尔曲线均穿过了指定点,并且保持凸形态,满足模糊评价所需的隶属度函数要求。随着曲线阶数增加,曲线与控制点连接的折线越发靠近。需要指出的是,对于作为隶属度函数的贝塞尔曲线,二阶曲线已可以满足所有要求,而高阶贝塞尔曲线的求解方法在其他领域可以得到更好的应用。
6 结束语本文在统计分析确定隶属度函数区间的基础上,确定了使隶属度划分均衡化的区间内关键点,使用贝塞尔曲线拟合区间起点、终点和关键点。提出了以极坐标和线段比例为基础的增量式编码方案表达贝塞尔曲线的控制点。编码统一为[0, 1]之间的小数,方便任意全局优化算法的应用,具有普适性。且任意[0, 1]编码都可以解码为满足约束的控制点,解决了控制点选择的约束问题。本编码方案可以简单的扩展至过任意点的任意阶贝塞尔曲线上,具备良好的适应性。经过算例验证,所得隶属度函数可以对不良分布的数据集进行正确的模糊分类,同时避免了抛物线型函数隶属度大于1的情况。
| [1] |
侯世旺, 朱慧明. 基于模糊统计的不确定质量特性控制图研究[J]. 统计与决策, 2016(16): 25-28. HOU Shiwang, ZHU Huiming. Research on uncertain quality control chart based on fuzzy statistics[J]. Statistics and decision, 2016(16): 25-28. (  0) 0)
|
| [2] |
张明, 陈楠, 吴陈. 一种改进的模糊统计方法[J]. 华东船舶工业学院学报: 自然科学版, 2004, 18(4): 58-61. ZHANG Ming, CHEN Nan, WU Chen. An improved fuzzy statistical method[J]. Journal of East China shipbuilding institute: natural science edition, 2004, 18(4): 58-61. (  0) 0)
|
| [3] |
袁力, 姜琴. 隶属函数确定方法探讨[J]. 郧阳师范高等专科学校学报, 2009, 29(6): 44-46. YUAN Li, JIANG Qin. Discussion on the method of determining membership function[J]. Journal of Yunyang normal college, 2009, 29(6): 44-46. (  0) 0)
|
| [4] |
HASUIKE T, KATAGIRI H, TSUBAKI H. A constructing algorithm for appropriate piecewise linear membership function based on statistics and information theory[J]. Procedia computer science, 2015, 60: 994-1003. ( 0) 0)
|
| [5] |
董炜, 陈卫征, 徐晓滨, 等. 基于可分性测度的模糊隶属函数确定方法[J]. 控制与决策, 2014, 29(11): 2089-2093. DONG Wei, CHEN Weizheng, XU Xiaobin, et al. Determining method of fuzzy membership function based on separability measure[J]. Control and decision, 2014, 29(11): 2089-2093. (  0) 0)
|
| [6] |
马万元, 耿秀丽. 基于概率统计的模糊隶属函数计算研究[J]. 数学理论与应用, 2016(3): 93-100. MA Wanyuan, GENG Xiuli. Research on the fuzzy membership function determination based on probability statistics[J]. Mathematical theory and applications, 2016(3): 93-100. (  0) 0)
|
| [7] |
袁杰, 史海波, 刘昶. 基于最小二乘拟合的模糊隶属函数构建方法[J]. 控制与决策, 2008, 23(11): 1263-1266, 1271. YUAN Jie, SHI Haibo, LIU Chang. Construction of fuzzy membership functions based on least squares fitting[J]. Mathematical theory and applications, 2008, 23(11): 1263-1266, 1271. (  0) 0)
|
| [8] |
王石青, 邱林, 王志良, 等. 确定隶属函数的统计分析法[J]. 华北水利水电学院学报, 2002(1): 68-71. WANG Shiqing, QIU Lin, WANG Zhiliang, et al. Determine the membership function based on statistical analysis[J]. Journal of North China institute of water conservancy and hydroelectric power, 2002(1): 68-71. (  0) 0)
|
| [9] |
MEDAGLIA A S L, FANG S C, NUTTLE H L W, et al. An efficient and flexible mechanism for constructing membership functions[J]. European journal of operational research, 2002, 139(1): 84-95. ( 0) 0)
|
| [10] |
王林, 富庆亮. 基于贝塞尔曲线理论的备件需求模糊隶属度函数构建模型[J]. 运筹与管理, 2011, 20(1): 87-92. WANG Lin, FU Qingliang. A model for the construction of spare parts dem and fuzzy membership function based on bezier curves theory[J]. Operations research and managent science, 2011, 20(1): 87-92. (  0) 0)
|
| [11] |
ZAKARIA R, WAHAB A F. Fuzzy set theory in modeling uncertainty data via interpolation rational bezier surface function[J]. Applied mathematical sciences, 2013, 45(7): 2229-2238. ( 0) 0)
|
| [12] |
AZAR M M. Maneuver planning with higher order rational Bezier curves[OL/EB]. [2017-04-02]. http://www.freepatentsonline.com/9785146.html
( 0) 0)
|
| [13] |
DERKSEN R W, ROGALSKY T. Bezier-PARSEC: an optimized aerofoil parameterization for design[J]. Advances in engineering software, 2010, 41(7): 923-930. ( 0) 0)
|
| [14] |
丁青锋, 尹晓宇. 差分进化算法综述[J]. 智能系统学报, 2017, 12(4): 431-442. DING Qingfeng, YIN Xiaoyu. Research survey of differential evolution algorithms[J]. CAAI transactions on intelligent systems, 2017, 12(4): 431-442. (  0) 0)
|
| [15] |
DAS S, SUGANTHAN P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 4-31. ( 0) 0)
|
| [16] |
ZHANG M, JU Z. A novel fuzzy support vector machine based on differential evolution[J]. Icic express letters, 2017, 11(7): 1159-1165. ( 0) 0)
|
| [17] |
陈成, 何玉庆, 卜春光, 等. 基于四阶贝塞尔曲线的无人车可行轨迹规划[J]. 自动化学报, 2015, 41(3): 486-496. CHEN Cheng, HE Yuqing, BU Chunguang, et al. Feasible trajectory generation for autonomous vehicles based on quartic bezier curve[J]. Acta automatica sinica, 2015, 41(3): 486-496. (  0) 0)
|
| [18] |
MARSH D. Applied geometry for computer graphics and cad[M]. 2006.
( 0) 0)
|
| [19] |
R STORN, K PRICE. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. ( 0) 0)
|
| [20] |
Y X YUAN. A modified bfgs algorithm for unconstrained optimization[J]. IMA journal of numerical analysis, 1991, 11(3): 325-332. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


