城市道路通行时间的准确估计和预测对于改善城市交通状况是至关重要的,其目标在于计算准确的道路网通行时间信息, 以便选择道路网中更好的路线使通行时间最小。若欲准确评估路段通行时间,最核心的就是从道路传感器中获取良好的车辆实时信息。然而,在大多数情况下,只能获得离散的车辆速度和位置信息, 具体的时空轨迹信息难以实时获取。因此,必须开发适当的方法来估计道路网路段通行时间。
目前,针对城市道路通行时间估计和预测的研究主要包括两类方法,即基于传感器数据的预测以及基于城市全球定位系统(global positioning system,GPS)数据的预测方法。
第一类方法的研究主要依赖于各种类型传感器采集的数据进行预测,主要包括:环形线圈检测器[1-3]、自动车辆识别[4-5]、摄像机、远程通信微波传感器[6]和自动化牌照识别[7]等。通常,这些数据需要相应精度级别的传感器来获取。然而由于传感器的安装和维护费用高昂,导致基于传感器获取数据的道路通行时间预测方法的应用难以普及。
第二类方法是基于GPS数据估计城市地区交通动态需求和道路网动态变化,因其具有极大的应用价值而引起国内外学者的广泛关注。通过车辆或移动手机中的GPS设备获取的数据可以成为监测城市交通量的可行来源[8]。随着从车辆和手机中获得的GPS数据越来越多,基于这些大规模分散数据估计路段通行时间已变为现实。因为手机数据涉及个人隐私等问题,大量研究主要以车辆GPS数据为主。Zhan等[9]基于轨迹数据估计城市交通流量;Zheng等[10]基于稀疏车辆数据提出了估计城市路段通行时间的ANN模型;Hunter等[11]利用GPS车辆数据统计路段通行时间;Herring等[12]认为出租车相比普通车辆在城市中具有更高渗透率,利用出租车GPS数据可以更好表现道路网情况,因此他们基于500辆出租车的GPS数据,估计和预测了旧金山城市范围内离散的交通状况。然而,所有上述方法仅适用于GPS轨迹数据。但是,现实世界中大量出租车GPS数据仅含起点终点(origin-destination,OD)信息,如纽约公布的出租车行驶数据集[13]等。由于全球定位系统起点终点(GPS-OD)数据中,仅包含出租车一次运营过程的起点和终点,而不包含本次运营的路线信息,于是基于GPS-OD数据进行路网通行时间估计,不仅需要拟合路段时间,还需要分析出租车运行路线,给城市道路网路段通行时间估计问题带来了新的挑战。Zhan[14-15]等利用纽约出租车GPS-OD数据,估计道路网路段通行时间。但是,他只考虑了道路单车道对车辆行驶的影响,当路段较宽时,车道数可能更多,单车道不能很好地刻画道路网精细化程度。
为了克服上述的问题,本文基于出租车数据提出了一种城市道路网路段通行时间估计方法,主要贡献在于:
1)建立了基于出租车GPS-OD数据集的双车道道路网通行时间估计模型。假设道路网每条路段为双车道,能够更准确地描述道路网通行情况,为了避免训练数据量不足而导致的过拟合问题,建立了双车道间通行时间多项式关联关系模型。
2)采用优化非线性最小二乘方法估计路段每小时平均通行时间,从而实现路网通行时间拟合。
3)设计多组实验,分析双车道通行时间之间不同多项式关系对道路网路段通行时间估计结果的影响,确定效果最优的多项式关系。通过多组估计不同时段路段通行时间的实验,验证了本文所提双车道预测方法相比于单车道方法能够更准确地估计道路网路段的通行时间。
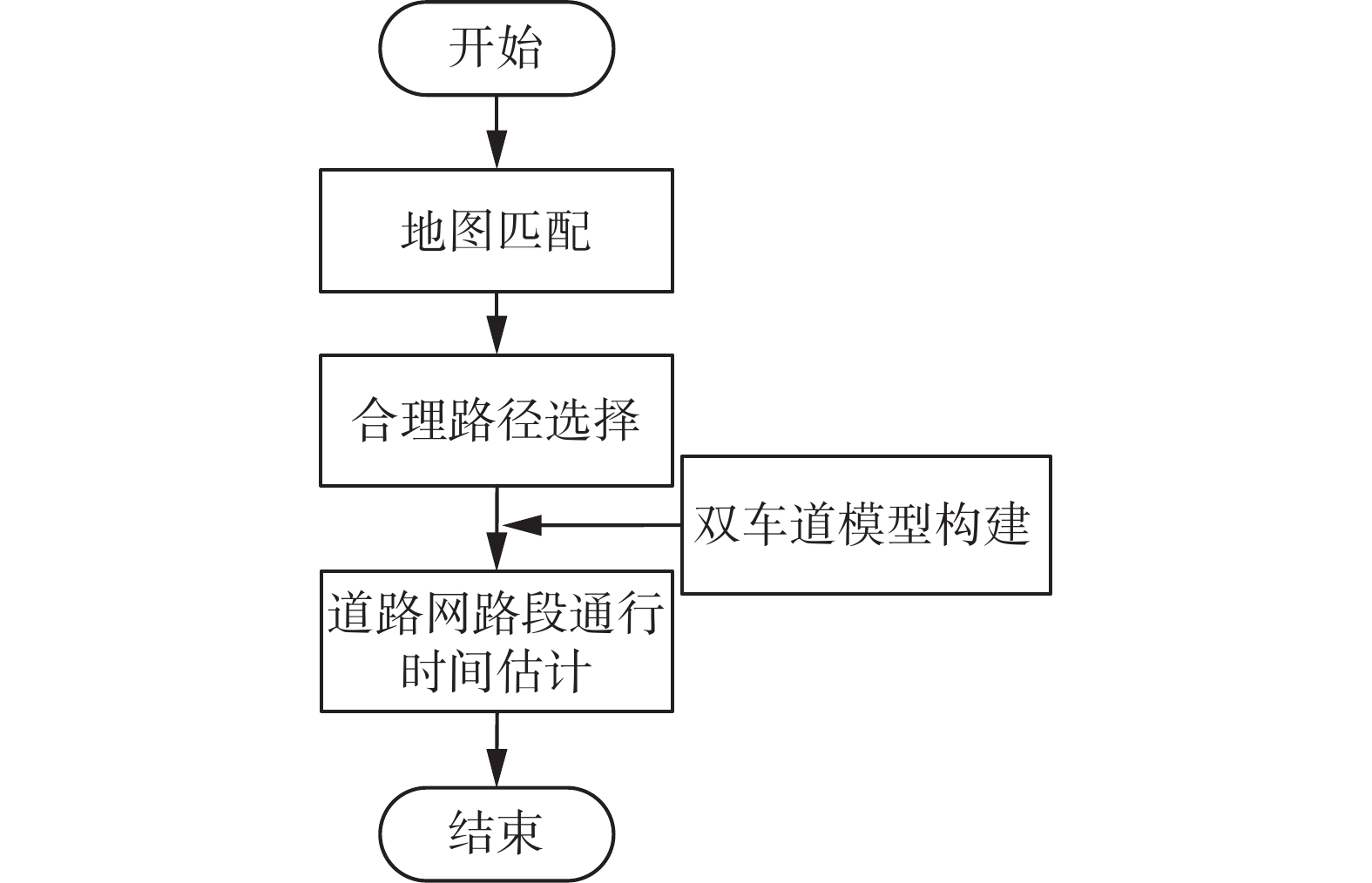
1 道路网路段通行时间估计模型本节将介绍估计道路网路段通行时间模型,该模型的总体框架如图1所示,主要包括以下4个步骤:1)地图匹配。GPS数据中的起点和终点映射到道路网中,以减小GPS误差带来的影响,将原始数据转化为可用数据。2)路径选择。采用k-最短路径算法[16],构建每段行程的路径集合,并根据MNL(multinominal logit model)[17]模型计算司机选择不同路径的可能性,最后筛选合理的路径集合作为估计路段时间过程的基础。3)双车道通行时间模型构建。为精细刻画道路网通行时间程度,提出双车道通行时间多项式关联关系模型。4)路段通行时间估计。将步骤2)中筛选出的多条路径作为出租车某次行程的可能发生事件以计算每次行程的期望时间,最后将路段通行时间估计问题转换为行程观测时间与期望时间均方误差最小问题。
|
图 1 模型总体框架 Fig.1 General framework for model |
下面将详细介绍地图匹配、路径选择模型、路段双车道通行时间间多项式关联关系模型,道路网路段通行时间估计方法。
1.1 地图匹配GPS数据因接收设备老化,信号传播延迟等原因存在一定定位误差,需要预先对原始GPS数据进行地图匹配,其具体作用将起点和终点映射到道路网中,将原始数据转换为可用数据,便于道路网分析。
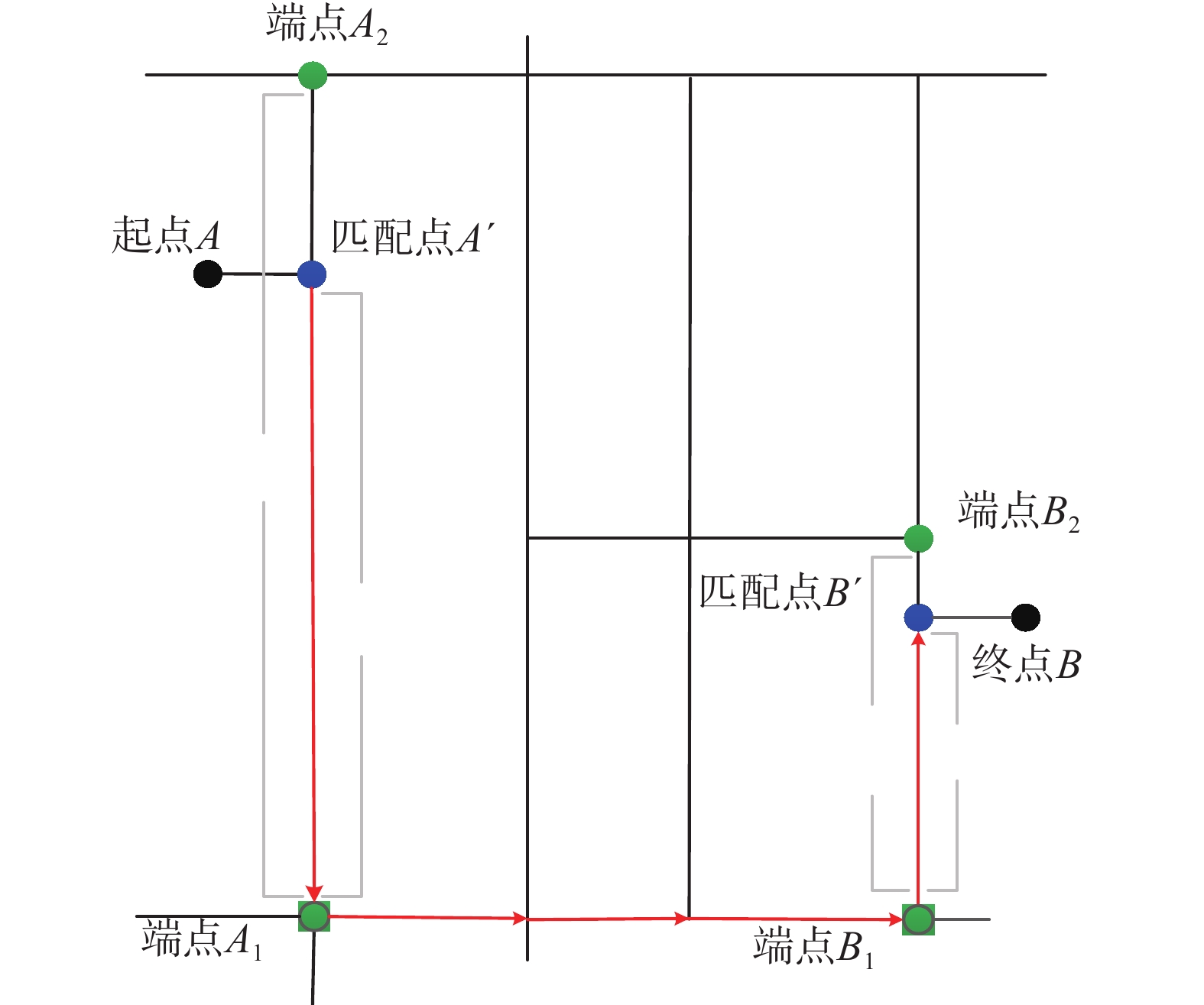
图2说明了数据地图匹配过程,其中端点(A1,A2,B1,B2)为路径相交节点,首先将原始起点和终点(A,B)匹配到最近路段的垂足上(A′,B′),匹配后的点的位置用路段两个端点(A1和A2,B1和B2)和
|
图 2 地图匹配示例 Fig.2 Illustration of data mapping |
将GPS-OD数据进行地图匹配后,得到了道路网中每次行程的起点终点数据。由于路径选择信息的缺失,在估计城市道路网时间时需要推断实际的路径。但在城市的道路网中,对于某一确定的出租车行程,所有路径的集合是非常大的。考虑到交通网中观测数目过于庞大,对整个空间进行路径搜索非常耗时,减少路径数目是很有必要的。这里,采用k-最短路径搜索算法生成最初的路径集合,然后利用数据中记录的行程距离来排除不合理的路径。
计算每段行程的可选路径集合后,由于缺少司机社会和行为特征,不能用传统的计量经济学模型来估计司机所选择的路径。因为司机做出决策之前不可能知道实际的路径时间。但是,他们可以通过经验推测道路网通行时间,因此本文基于MNL模型利用可选路径集合中的路径时间和距离表示路径成本Cm求不同路径的选择概率。为降低复杂性,定义路径选择模型为
| ${P_m}({\mathit{\boldsymbol{t}}},d,\theta ) = \frac{{\exp [ - \theta {C_m}({\mathit{\boldsymbol{t}}},{d_m})]}}{{\displaystyle\sum\nolimits_{j \in {R_i}} {\exp [ - \theta {C_j}({\mathit{\boldsymbol{t}}},{d_j})]} }}$ | (1) |
式中:Pm表示某一行程中可选路径m的选择概率与道路网路段通行时间t、行程中各个可选路径的距离d、参数θ有关。Cm表示路径m的成本与道路网路段通行时间t和路径距离dm有关,参数θ用于表示司机感知不同时间段道路网通行时间不同时的路径成本变化,θ大表示感知错误小,司机倾向于选择成本小的路径,而θ小意味着感知错误较大,成本越大的路径越有可能被选择。在此模型中,θ和道路网通行时间都是待估参数。
假设每个司机在同一起点终点的行程下,更偏好选择行程时间和距离更短的路径,那他们就能够行驶更多行程数量,获得更多收益。在建立合理的路径集合时,设置阈值用于排除违反上述选择行为假设的路径。路径距离在行程观测距离一定比例内的才会被使用。因为数据中记录的行程距离不精确(只到160 m),设置工作日行程距离阈值为15%~25%,周末为20%~25%,消除那些偏离记录中行程距离太多的不合理路径。阈值设定取决于一个小时内可用的行程数据量。
根据城市出租车计价规则:开始行程收取基本费用,超过基本乘车距离和时间,按相应比例收取叠加费用。考虑到实际情况下票价计算的复杂,采用行程时间和距离的线性模型表示行程成本,如式(2)所示。
| ${\rm{fare}} = {\beta _0} + {\beta _1} \cdot {\rm{time}} + {\beta _2} \cdot {\mathop{\rm distance}\nolimits} $ | (2) |
式中:fare表示行程成本,β0为常数,β1、β2是行程时间和距离的成本系数。根据文献[14],β1、β2的估计值为0.275/min和2.516/km。
| ${C_m}({\mathit{\boldsymbol{t}}}{\rm{, }}{d_m}) = {\beta _1} \cdot {g_m}({\mathit{\boldsymbol{t}})} + {\beta _2} \cdot {d_m}$ | (3) |
式中:dm是路径m的距离,路径m的通行时间
| ${g_m}({\mathit{\boldsymbol{t}}}) = {a_1}{t_O} + {a_2}{t_D} + \sum\nolimits_{l \in L} {{t_l}} $ | (4) |
式中:t0是起点所在路段的通行时间,tD是终点所在路段的通行时间,L是道路网的路段集合,tl是路段l的通行时间,
在城市道路网中许多道路分为左侧车道、直行车道和右侧车道。左侧和直行车道在行驶过程中会出现等待红绿灯的情况,右侧车道则可以直接通行。若只考虑单车道情况,将会忽略左侧和直行车道上等待红绿灯的时间。若加入多车道,但不考虑车道间关系,可能导致待估变量数目太多,拟合效果较差,或样本数不足的情况。假定同一路段上左侧车道和直行车道上的车辆通行时间服从相似的分布,并根据路段车道间车流量会相互影响的实际情况,我们认为路段上为双车道,且存在一定的多项式关系,如式(5)所示。
| $y = {\displaystyle\sum} _{i = 2}^k{\gamma _i}{x^i} + {\gamma _1}x + {\gamma _0},\, k = 2,3, \cdots $ | (5) |
式中:x是路段上一条车道的通行时间,y表示与x相关的另一条车道的通行时间,多项式γ为待估参数。
1.4 道路网路段通行时间估计道路网路段通行时间估计是最小化行程观测时间与期望时间之间的均方差,将出租车实际路径选择作为隐含变量,路段通行时间t、双车道之间的多项式关系参数γ和比例参数θ作为待估参数,观测i的期望时间
| $E({Y_i}|{R_i}) = \sum\nolimits_{m \in {R_i}} {{g_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}}){P_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},d,\theta )} $ | (6) |
式中:Yi是观测i的时间变量,Ri是根据观测i的OD行程记录建立的可能路径集, t是道路网路段通行时间向量,γ是双车道间多项式关系参数,d是Ri的所有路径距离,
对于一条路径,其距离是确定的,道路网路段通行时间向量t,双车道间多项式关系参数γ和比例参数θ是待估参数,那么
| $E({Y_i}|{R_i}) = f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )$ | (7) |
进一步,行程观测时间yi与行程期望时间
| ${r_i} = {y_i} - f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )$ | (8) |
则误差平方定义为
| $S({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta ) = \sum\nolimits_{i \in D} {r_i^2 = \sum\nolimits_{i \in D} {{{({y_i} - f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta ))}^2}} } $ | (9) |
由此,所估计的道路网路段通行时间为
| ${\mathit{\boldsymbol{t}}} = \arg \;\mathop {\min }\limits_{\mathit{\boldsymbol{t}}} S({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )$ | (10) |
利用Levenberg-Marquardt(LM)[18]方法解决非线性最小二乘问题。该方法是一种广泛用于求解最小二乘拟合和非线性规划问题的优化算法。在各种问题上,它优于一般的梯度下降方法和著名的高斯–牛顿(GN)方法[18]。传统的高斯–牛顿法是计算代价高的线性搜索法。更新的高斯–牛顿法类似于牛顿法,当近似的Hessian矩阵近似奇异时变成了数学问题。如果利用不恰当的初始值,则容易不能收敛到最优。另一方面,Levenberg-Marquardt方法利用信任域策略而不是线性搜索方法,在更新步骤前确定步长。在LM中利用不同的Hessian近似方法也有助于确保每次迭代时矩阵的正定性,具有更好的鲁棒性,这意味着在许多情况下,即使初始值远离最终优值,Levenberg-Marquardt法也能找到一个近似解。在Bonnans和Gilbert[19]中表明Levenberg-Marquardt具有快速局部收敛性能。
本文中,利用LM算法求解的目标函数为行程期望时间:
| $E({Y_i}|{R_i}) = f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta ) = \sum\nolimits_{m \in {R_i}} {{g_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}})\frac{{{P_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )}}{{{S_{{R_i}}}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )}}} $ | (11) |
简单起见,定义
| ${P_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta ) = \exp \theta ( - {\beta _1} \cdot {g_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}}) - {\beta _2} \cdot {d_m})$ | (12) |
式(1)的分母写成
| ${S_{{R_i}}}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta ) = \sum\nolimits_{j \in {R_i}} {\exp \theta ({\beta _1} \cdot {g_m}({\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}}) - {\beta _2} \cdot {d_m})} $ | (13) |
求解Jacobian矩阵为
| ${{\mathit{\boldsymbol{J}}}_{il}} = \frac{{\partial f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )}}{{\partial {t_l}}},l = 1,2,\cdots,N$ | (14) |
| ${{\mathit{\boldsymbol{J}}}_{ip}} = \frac{{\partial f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )}}{{\partial \gamma }},p = N + 1,\cdots,N + k + 1$ | (15) |
| ${{\mathit{\boldsymbol{J}}} _{iq}} = \frac{{\partial f({R_i},{\mathit{\boldsymbol{t}}},{\mathit{\boldsymbol{\gamma }}},\theta )}}{{\partial \theta }},q = N + k + 2$ | (16) |
Jacobian矩阵是一个
路段通行时间t,车道间多项式关系参数γ,比例参数θ在第v次迭代更新为
| $\begin{array}{l}{\mathit{\boldsymbol{t}}} \approx {{\mathit{\boldsymbol{t}}}^{v + 1}} = {{\mathit{\boldsymbol{t}}}^v} + {{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{t}}}}^{(v)}\\{\mathit{\boldsymbol{\gamma }}} \approx {{\mathit{\boldsymbol{\gamma }}}^{v + 1}} = {{\mathit{\boldsymbol{\gamma }}}^v} + {{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{\gamma }}}}^{(v)}\\\theta \approx {\theta ^{v + 1}} = {\theta ^v} + {{\mathit{\boldsymbol{u}}}_\theta }^{(v)}\end{array}$ | (17) |
得到待估参数在第v次迭代求解增量正规方程时的更新方向为
| $({{\mathit{\boldsymbol{J}}}^{(v){\rm{T}}}}{{\mathit{\boldsymbol{J}}}^{(v)}} + \lambda {\mathit{\boldsymbol{I}}}){{\mathit{\boldsymbol{u}}}^{(v)}} = {{\mathit{\boldsymbol{J}}}^{(v){\rm{T}}}}{r_i}$ | (18) |
当迭代结束后,式(17)所得t值即为所估计的道路网路段通行时间,γ为双车道间多项式关系参数,θ为表示司机对道路网感知程度的比例参数。
通过分析可以发现,上述函数非凸,可能有多个局部最优点。在具体求解时,考虑将初始值默认为整个道路网当前时段下的平均速度,能较快较好地收敛到合适的最优的值。
3 实验结果与分析我们采用纽约出租车行程数据集,数据由城市出租车豪华轿车委员会(New York City Taxi and Li- mousine Commission,NYTLC)收集。其特点是每个出租车都安装了GPS设备采集数据。纽约有北美最大的出租车市场,12 779(2006年)辆黄色纪念章出租车每年大约服务2.4亿人次。在曼哈顿,乘坐出租车人数是所有出行人数的25%[20]。数据集包含2010—2015年出租车行程数据,其中包括行程开始和结束(OD数据)的地理位置、行程距离、时间和票价等信息,而缺少出租车的确切轨迹。但是,大量的数据(一天450 000~550 000的记录数量)可以推断出租车可能路线,并进一步估计道路网的路段通行时间。
基于Python语言编程实现前面部分讨论的模型。硬件配置为i5处理器,3.2 GHz CPU,4 GB内存。在实验中利用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)来评估估计结果:
| ${\rm{RMSE = }}\sqrt {\frac{1}{n}\displaystyle\sum _{i = 1}^n{{(T_i^{{{{\rm{Pr}}}}} - T_i^{{{{\rm{Ob}}}}})}^2}} $ | (19) |
| ${\rm{MAPE = }}\frac{1}{n}\displaystyle\sum_{i = 1}^n\left| {\frac{{T_i^{{\rm{Pr}}} - T_i^{{\rm{Ob}}}}}{{T_i^{{\rm{Ob}}}}}} \right| \times 100\% $ | (20) |
式中:
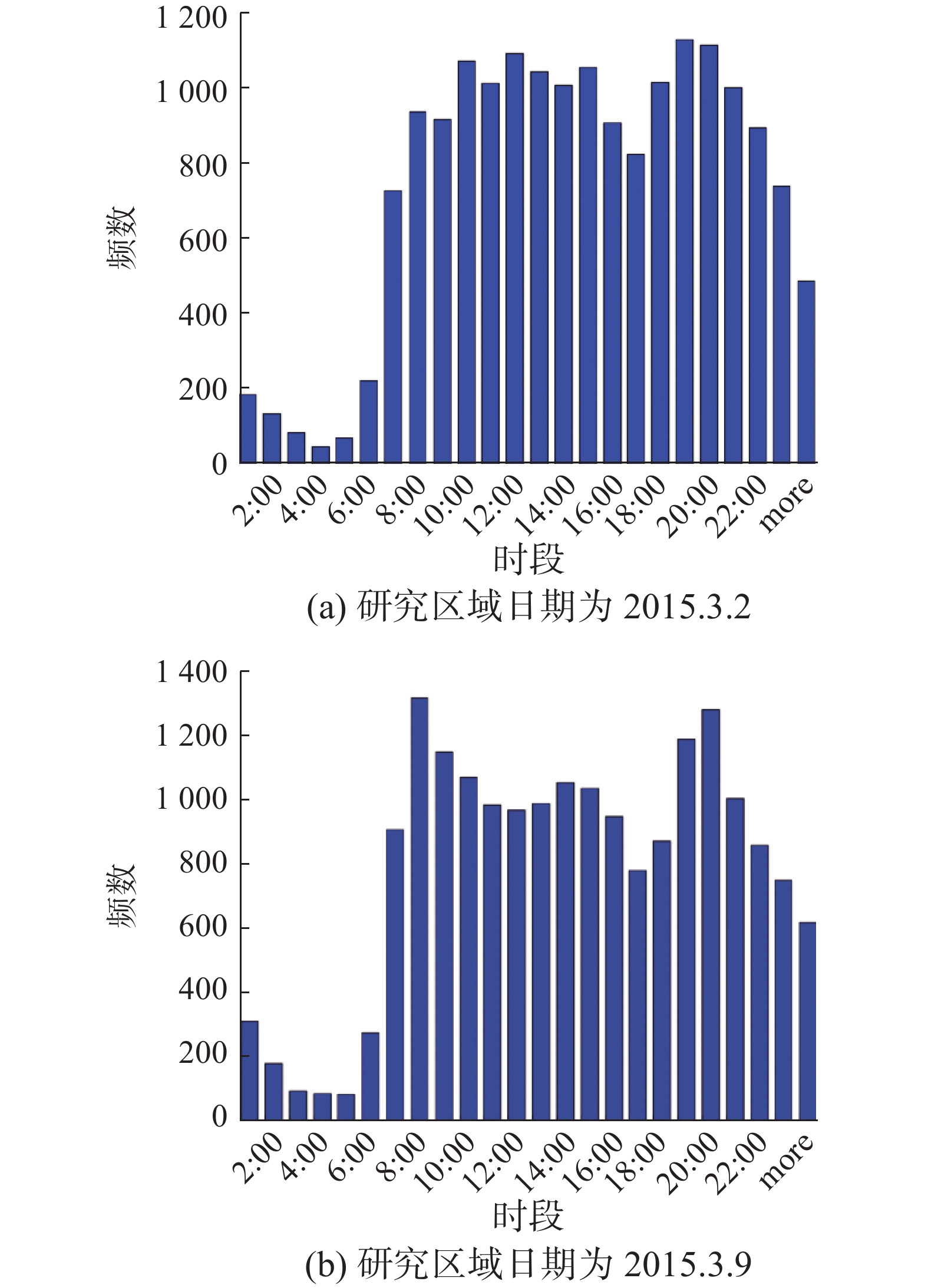
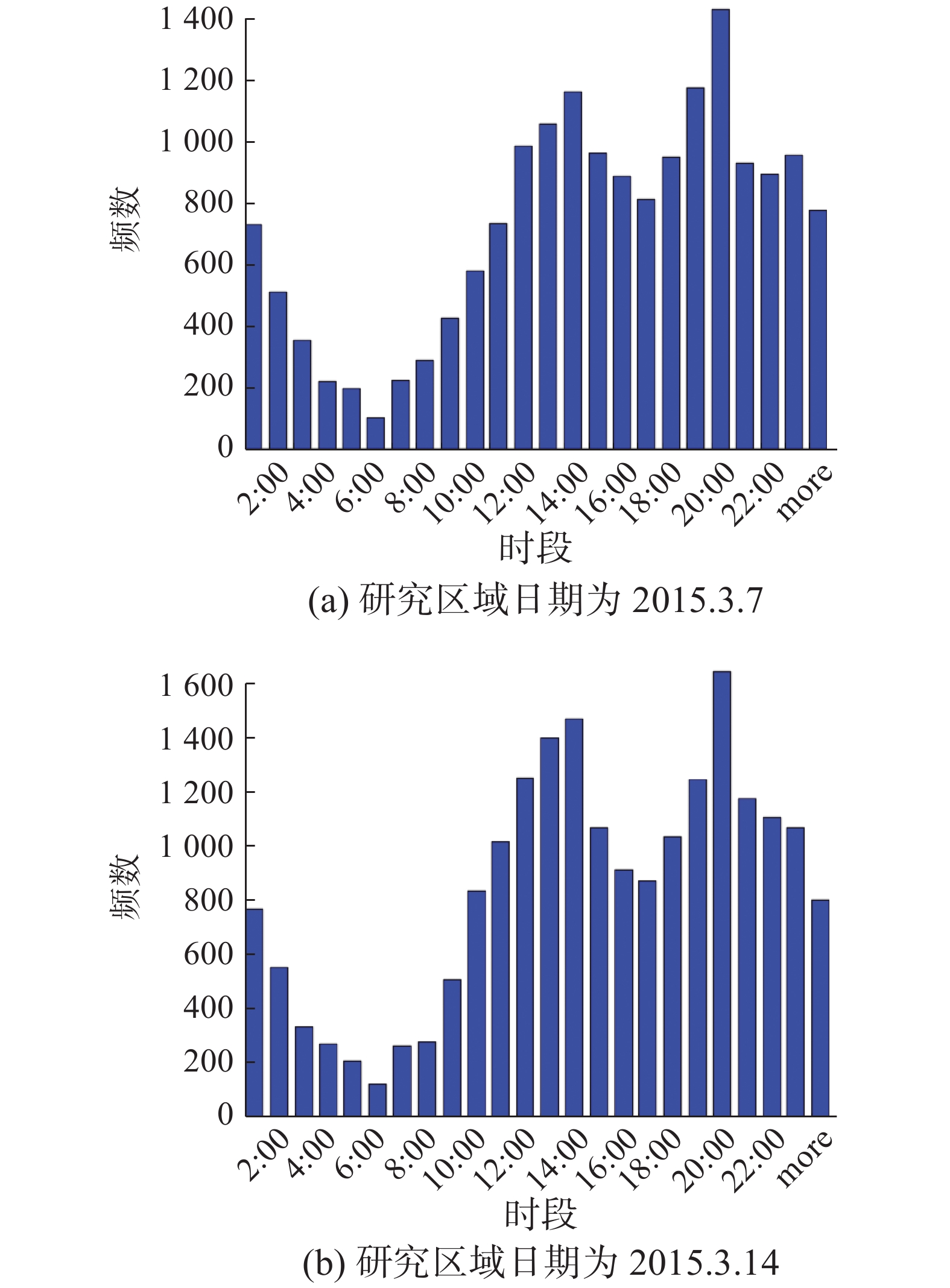
实验中利用纽约出租车两周(3/2/2015—3/15/2015)的OD行程数据测试所提出的方法。实验区域位于曼哈顿中央公园东南部一块1 508 m2的范围,相关道路网如图3所示,包含208个节点和386条边。道路网中有348条道路是单向街道,38条是双向街道。图4、5分别展示了在该范围内工作日(3/2/2015和3/9/2015,周一)和周末(3/7/2015和3/14/2015,周六)的行程频数。通过统计和观察图4、5可以发现,该区域内工作日(周一)一小时内将近1 200条行程数,周六大约1 000条的行程数。且每周同一天行程观测数近似服从同一分布。

|
图 3 研究区域测试道路网:曼哈顿市中心 Fig.3 Test network of study region: midtown Manhattan |
若实验数据以分钟为单位采样,行程数和信息量太少不能保证良好的统计意义。若以天为单位采样,不具有良好的代表性和研究意义。因此实验以小时为单位采样,从相应的数据中估计道路网通行时间。
|
图 4 研究区域内周一每小时观测数目直方图 Fig.4 Histogram for number of hourly observations in the study region on Monday |
|
图 5 研究区域内周六每小时观测数目直方图 Fig.5 Histogram for number of hourly observations in the study region on Saturday |
为了验证提出的算法性能,在实验中引入了Zhan[14]提出的单车道道路通行时间估计模型进行比较。设计了两组实验,第一组实验分析单车道与双车道间不同多项式关系对估计道路网路段通行时间结果的影响,并确定效果最优的多项式关系,第二组为不同时段估计路段通行时间的实验。
3.2.1 双车道间通行时间多项式关联关系模型下的估计误差实验为了验证2.3节所提双车道模型的有效性,以3/2/2015—3/15/2015中9:00–10:00为研究时段分别计算不同车道关系下的模型估计误差,实验结果如表1所示。通过观察可以发现,双车道模型整体上RMSE和MAPE相比Zhan等[14]提出的单车道方法要低:当转换模型为二阶、三阶、四阶多项式时,一周中有半数以上的时间段双车道模型误差低于单车道模型;当转换模型为五阶、六阶多项式时,一周中的RMSE和MAPE全都低于单车道模型结果。当双车道通行时间之间多现实转换模型取为六阶多项式时,周一到周六实验所得的RMSE和MAPE分别比单车道低3.45,5.33,0.21,0.13,0.06,0.41和39.8%,11.7%,1.75%,2.6%,1.5%,5.4%。上述分析证明,高阶多项式的双车道模型能够更好地刻画道路网的精细化程度,相比单车道模型能够更准确地估计道路网通行时间。
| 表 1 不同车道关系下的模型估计误差 Tab.1 Model estimation error in different lane conditions |
该实验分为训练和测试两个阶段,首先基于第3节训练求出道路网路段通行时间t,双车道间六阶多项式参数γ、θ 3个值,然后在测试阶段输入新的OD行程记录,并根据式(6)求出该行程记录的期望时间和误差。
基于两周的GPS数据(3/2/2010-3/15/2010),其中每周同一天数据的80%作为训练样本,剩下20%第2周的数据作为测试样本,估计一天中4个时间段(9:00—10:00,13:00—14:00,19:00—20:00,21:00—22:00)的道路网路段通行时间。分别采用Zhan[14]单车道模型和本文双车道为六阶多项式关系的模型对道路路段通行时间进行估计,通过观察表2可见,双车道模型在更多数据情况下结果都优于单车道模型。
| 表 2 模型估计误差 Tab.2 Model estimation error |
除了时间段(3月9日周三21:00—22:00),双车道模型路段通行时间估计结果的MAPE低于40%,可以观察到单车道模型和双车道模型在周三21:00—22:00误差值最大。可发现周三(3/11/2015)有纽约洋基对战巴尔的摩金莺的橄榄球比赛,比赛结束后可能导致大量拥堵以及密集人群流动,该事件可能与误差结果有较大关系。且双车道模型遇到异常情况时,效果更加稳健,其结果比单车道模型低94%。
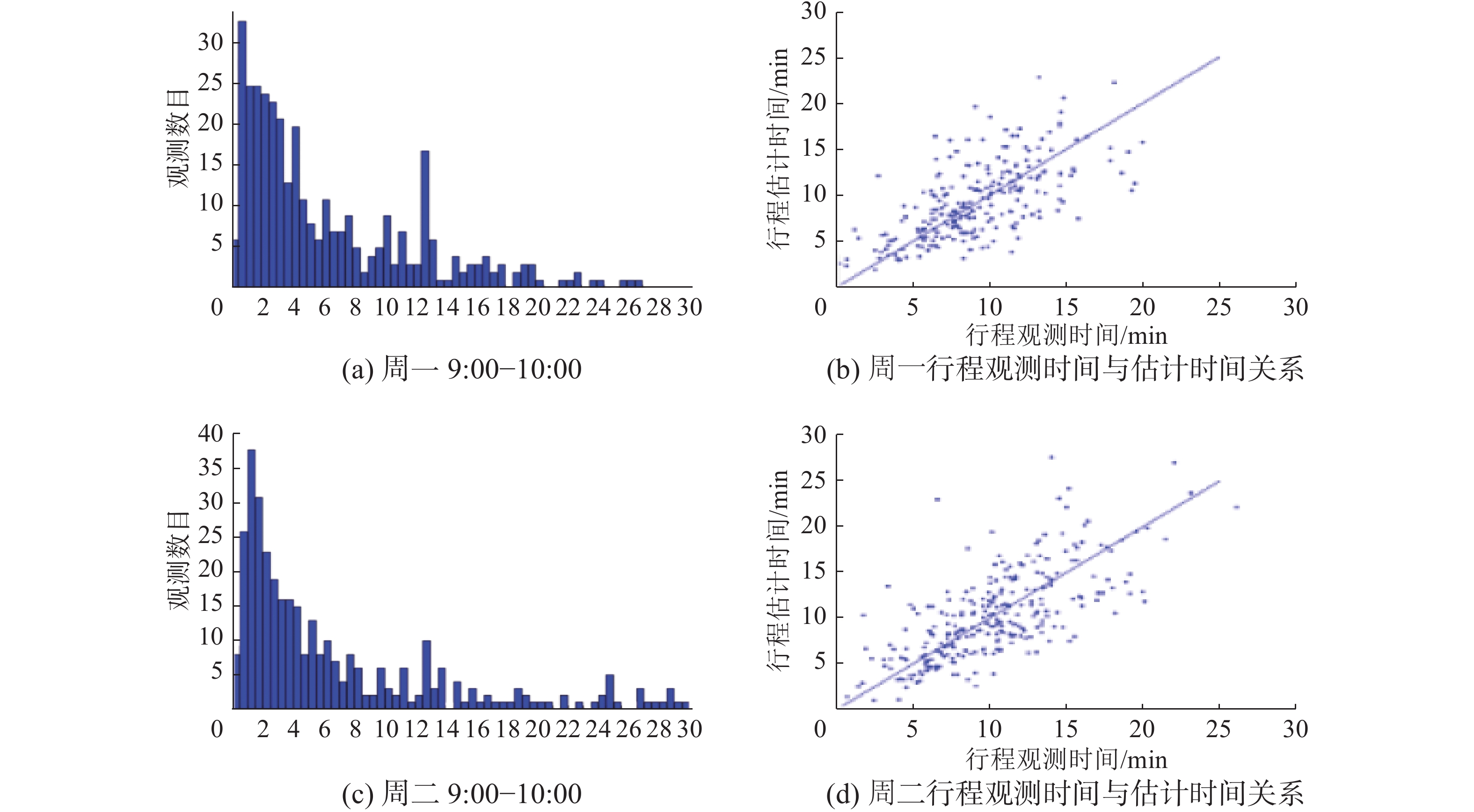
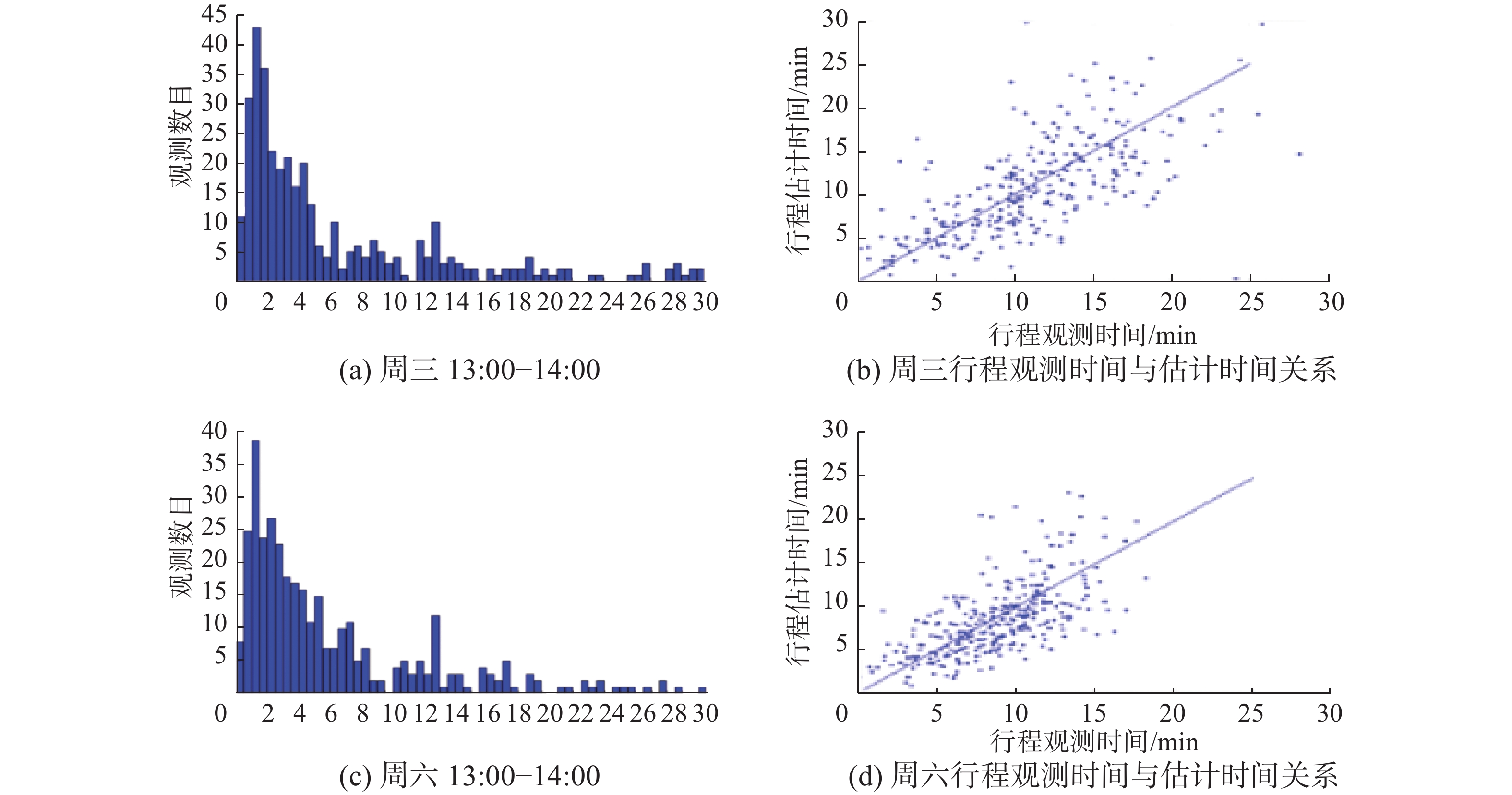
我们用道路网路段通行速度而不是道路网路段通行时间直观表示估计结果,图6表示周一、周二9:00—10:00, 路段估计时间直方图和行程观测时间与估计时间之间的关系图,其中X轴表示路段通行速度,Y轴表示该速度的路段数目。子图中X轴为行程观测时间,Y轴为模型估计时间。图7表示周三,周六13:00—14:00的关系。其他时间段的关系与其相似,不多作赘述。
|
图 6 周一、周二路段估计时间直方图和行程观测时间与估计时间之间的关系 Fig.6 Histogram of estimated link speed and correlation plot of observed and estimated path travel time for Monday, Tuesday |
|
图 7 周三,周六路段估计时间直方图和通行观测时间与估计时间之间的关系 Fig.7 Histogram of estimated link speed and correlation plot of observed and estimated path travel time for Wednesday, Saturday |
|
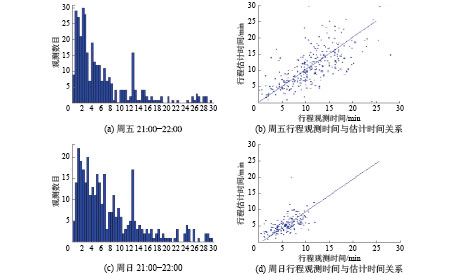
图 8 周五、周日路段估计时间直方图和通行观测时间与估计时间之间的关系 Fig.8 Histogram of estimated link speed and correlation plot of observed and estimated path travel time for Friday, Sunday |
由于路段通行时间是以小时为单位估计的,所以一小时内道路的变化也会导致模型的误差(Fosgerau和Fukuda[21])。司机之间的选择偏好(例如,一些司机驾驶速度快,偏好选择短路径,一些司机驾驶速度慢,偏好采取相对较长的路径等)也可能导致误差。观察到某些行程在测试的道路网中长达20 min,这使得在路径选择中有很多不确定性,从而导致了一些误差。
4 结束语本文提出了一种基于出租车GPS-OD数据来估计城市道路网通行时间的新模型。为了更精细地刻画道路网,该模型基于双车道估计行程期望时间,为了避免训练数据量不足而导致的过拟合问题,建立了双车道间通行时间多项式关联关系模型,并通过最小化行程期望时间和行程观测时间之间的误差来估计道路网通行时间。实验结果表明本文提出的方法能够有效地估计道路网每小时通行时间。为充分利用城市出租车数据估计道路网时间提供新的可能性。在下一步工作中,我们将利用GPS数据进一步研究城市交通流量的估计问题。
| [1] |
COIFMAN B, CASSIDY M. Vehicle reidentification and travel time measurement on congested freeways[J]. Transportation research part a: policy and practice, 2002, 36(10): 899-917. ( 0) 0)
|
| [2] |
ZHANG X, ZHANG B, LIU L, et al. Estimating foliar nitrogen concentration with hyperspectral remote sensing image[C]//Third International Asia-Pacific Environmental Remote Sensing Remote Sensing of the Atmosphere, Ocean, Environment, and Space. Beijing, 2003: 187–193.
( 0) 0)
|
| [3] |
WU C C, LEE W M G. Control of vaporous naphthalene by scrubbing with surfactants[J]. Journal of environmental engineering, 2004, 130(3): 276-281. ( 0) 0)
|
| [4] |
PARK D, RILETT L. Forecasting multiple-period freeway link travel times using modular neural networks[J]. Transportation research record: journal of the transportation research board, 1998(1617): 163-170. ( 0) 0)
|
| [5] |
LI R, ROSE G. Incorporating uncertainty into short-term travel time predictions[J]. Transportation research part c: emerging technologies, 2011, 19(6): 1006-1018. ( 0) 0)
|
| [6] |
YEON J, ELEFTERIADOU L, LAWPHONGPANICH S. Travel time estimation on a freeway using discrete time Markov chains[J]. Transportation research part B: methodological, 2008, 42(4): 325-338. ( 0) 0)
|
| [7] |
HASAN S, CHOUDHURY C, BEN-AKIVA M, et al. Modeling of travel time variations on urban links in London[J]. Transportation research record: journal of the transportation research board, 2011(2260): 1-7. ( 0) 0)
|
| [8] |
HERRERA J C, WORK D B, HERRING R, et al. Evaluation of traffic data obtained via GPS-enabled mobile phones: the mobile century field experiment[J]. Transportation research part c: emerging technologies, 2010, 18(4): 568-583. ( 0) 0)
|
| [9] |
ZHAN X, ZHENG Y, Yi X, et al. Citywide traffic volume estimation using trajectory data[J]. IEEE transactions on knowledge and data engineering, 2017, 29(2): 272-285. ( 0) 0)
|
| [10] |
ZHENG F, VAN ZUYLEN H. Urban link travel time estimation based on sparse probe vehicle data[J]. Transportation research part c: emerging technologies, 2013, 31(0): 145-157. ( 0) 0)
|
| [11] |
HUNTER T, HERRING R, ABBEEL P, et al. Path and travel time inference from GPS probe vehicle data[J]. NIPS analyzing networks and learning with graphs, 2009, 12(1). ( 0) 0)
|
| [12] |
HERRING R, HOFLEITNER A, ABBEEL P, et al. Estimating arterial traffic conditions using sparse probe data[C]//13th International IEEE Conference on Intelligent Transportation Systems. Madeira Island, Portugal, 2010: 929–936.
( 0) 0)
|
| [13] |
Taxi data from new york taxi and limousine commission. [2016-05-14] http://www.nyc.gov/html/tlc/html/home/home.shtml.
( 0) 0)
|
| [14] |
ZHAN X, HASAN S, UKKUSURI S V, et al. Urban link travel time estimation using large-scale taxi data with partial information[J]. Transportation research part c: emerging technologies, 2013, 33(0): 37-49. ( 0) 0)
|
| [15] |
ZHAN X, UKKUSURI S V, YANG C. A Bayesian mixture model for short-term average link travel time estimation using large-scale limited information trip-based data[J]. Automation in construction, 2016, 72: 237-246. ( 0) 0)
|
| [16] |
YEN J Y. Finding the k shortest loopless paths in a network[J]. Management science, 1971, 17(11): 712-716. ( 0) 0)
|
| [17] |
DAGANZO C. Multinomial probit: the theory and its application to demand forecasting[M]. Elsevier, 2014.
( 0) 0)
|
| [18] |
CHEN Y, OLIVER D S. Levenberg–Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification[J]. Computational geosciences, 2013, 17(4): 689-703. ( 0) 0)
|
| [19] |
BONNANS J F, GILBERT J C, LEMARÉCHAL C, et al. Numerical optimization: theoretical and practical aspects [M]. Springer Science and Business Media, 2013.
( 0) 0)
|
| [20] |
KING D A, PETERS J R, DAUS M W. Taxicabs for improved urban mobility: are we missing an opportunity [C]//Transportation Research Board 91st Annual Meeting. Washington DC, USA, 2012 (12-2097).
( 0) 0)
|
| [21] |
FOSGERAU M, FUKUDA D. Valuing travel time variability: Characteristics of the travel time distribution on an urban road[J]. Transportation research part c: emerging technologies, 2012, 24(0): 83-101. ( 0) 0)
|
| [22] |
孙锋, 黄玲, 叶盈. 混行条件下直线式公交站点停靠车辆数优化[J]. 哈尔滨工程大学学报, 2015, 36(2): 152-155. SUN Feng, HUANG Ling, YE Ying, et al. Optimizing the number of buses stopping at on-line stops under mixed traffic conditions[J]. Journal of Harbin Engineering University, 2015, 36(2): 152-155. (  0) 0)
|
| [23] |
徐程, 曲昭伟, 陶鹏飞. 动态交通数据异常值的实时筛选与恢复方法[J]. 哈尔滨工程大学学报, 2016, 37(2): 211-217. XU Cheng, QU Zhaowei, TAO Pengfei, et al. Methods of real-time screening and reconstruction for dynamic traffic abnormal data[J]. Journal of Harbin Engineering University, 2016, 37(2): 211-217. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


