近年来，社会存在诸多潜在的安全问题，一旦发生必会引起严重的社会后果。而在安全问题发生之前，运动目标在行为上会表现出不同程度的异常，因此，及时识别异常行为对防止潜在危险的发生具有重要的现实意义^[1-2]。随着公众对社会安全要求的日益增加，异常行为检测技术成为了计算机视觉的新兴研究方向，广泛应用于智能监控^[3-4]、医学诊断、运动分析等领域，并受到国内外研究学者的广泛关注。Jiang等^[5]采用上下文感知方法来检测异常，通过跟踪获取行人运动轨迹，并与正常行为轨迹进行比较，将偏离较大的轨迹视为异常，该方法依赖于获取目标轨迹的跟踪算法，因此无法长时间适应视觉上下文的变化；Bouttefroy等^[6]对运动轨迹的相关特征进行提取，并通过估计概率分布模型来识别异常行为，该方法需要准确获取行人运动轨迹，若发生遮挡便容易丢失目标，应用具有较大的局限性；Zhao等^[7]提出一种完全无监督的动态稀疏编码方法来检测异常事件，由于正异常行为样本分布的不平衡，导致对行人异常行为的识别效果较差；Lu等^[8]提出稀疏组合学习框架，提取视频底层特征，通过学习正常行为的表示方式来区分异常，该方法需大量正常行为作为正样本进行训练，无法达到实时性检测；Li等^[9]通过采用轨迹稀疏重构分析方法对行人异常行为进行检测，该方法对不同尺寸样本均能达到良好的检测性能，但受控制点参数的影响，也无法满足实时性要求。

本文提出一种联合加权稀疏重构轨迹与直方图熵的异常行为检测算法。该算法对运动轨迹进行训练，构造正常行为字典，同时对测试行人轨迹进行稀疏重构作为轨迹特征，并计算幅值方向直方图熵作为熵特征。通过对异常行为多特征进行联合加权，实现对异常行为的检测。虽然本文算法在时间上也无法达到实时性要求，但在复杂场景中可以实现更加精确的异常行为检测率。

1 行人检测 1.1 运动目标检测

本文采用背景相减法对运动目标进行检测，其关键在于对背景的建模，考虑到存在天气、光照及树叶摆动等引起的前景像素变化，需要对背景进行实时动态更新，图1为运动前景提取流程图。

1.1.1 背景建模

常用背景建模方法^[10]包括混合高斯建模^[11]、码本建模^[12]、双背景建模^[13]及均值建模^[14-15]等。均值建模法是将当前遍历到的所有帧像素值取平均作为背景的估计，由式(1)表示：

${\rm bg}(x,y) = \frac{1}{N}\sum\limits_{i = 1}^N {{f_i}(x,y)}$

(1)

该建模方法在监控设备固定的情况下，能较完整地从视频中获取背景模型。因此，本文通过融合均值背景结合双边滤波法对背景进行建模。

1.1.2 背景更新

为了降低光照、天气等对运动像素变化的影响，需对背景进行动态更新，本文采用分块分类^[16]的背景更新算法，具体的更新过程如式(2)所示：

${\rm bg}{_n}(i,j) = \left\{ \begin{array}{l}{f_n}(i,j),\;\;\;\;\;\left| {{f_n}(i,j) - {\rm bg}{_{n - 1}}(i,j)} \right| < T_d\\\\\alpha {\text{×}}{\rm bg}{_{n - 1}}(i,j) + \beta {f_{n - 1}}(i,j) + \\\quad\quad\;\;(1 - \alpha - \beta ){f_n}(i,j), \quad\quad\quad \text{其他}\end{array} \right.$

(2)

式中：阈值 $T_d$ 设置为30， $\alpha $ 与 $\beta $ 为权重， $\alpha + \beta < 1$ 。

算法通过计算当前帧与前一帧背景对应点像素值的绝对差，若小于给定的阈值，认为是由光照、天气等因素带来的细微变化，便将当前像素点设置成当前背景像素点，提供给下一帧考虑；若绝对差超出给定阈值，则认为当前帧中存在运动的物体，便结合前一帧背景，前一帧图像和当前帧图像来对当前帧背景进行更新。

1.1.3 运动前景提取

获得更新的背景模型之后，对当前帧与当前背景模型进行差分操作，提取当前存在运动的像素点形成二值图像，通过选取适当的阈值去除由非运动目标带来的像素值的细微变化，并进行相应的形态学处理，从而提取感兴趣的运动前景，提取过程可表示为式(3)：

${\rm fg}{_n}(i,j) = \left\{ \begin{array}{l}0,\;\;\;\;\left| {{f_n}(i,j) - {\rm bg}{_n}(i,j)} \right| < T\\1,\;\;\; \text{其他}\end{array} \right.$

(3)

式中：阈值 $T$ 设置为30， ${f_n}(i,j)$ ， ${\rm bg}{_n}(i,j)$ 分别表示当前帧像素值和背景像素值，此处选取视频第93帧作为当前帧， ${\rm fg}{_n}(i,j)$ 表示提取到的运动前景，图2显示了3种方法对运动前景的提取效果图。

1.2 行人识别

由于本文研究的异常行为检测是基于室外环境的，为保证运动前景只含行人，需要从复杂运动前景中区分行人与其他运动目标，并对行人进行跟踪获取运动轨迹，实现进一步的异常行为识别。

在监控设备固定的情况下，若只考虑直立行走的行人，而刚性车辆不易发生形变，因此选择外接矩形高宽比作为主要特征以区分行人与车辆，图3中(a)、(b)分别表示车辆和行人的外接矩形框。

选取视频序列任意10帧，分别计算行人与车辆高宽比 $\eta _1$ 、 $\eta _2$ ，表1为 $\eta_ 1$ 和 $\eta_ 2$ 的数值分布，此处列出6组实验得出的数据。

由表1可知，行人高宽比 $\eta_ 1$ 范围为1.92~3.24，车辆高宽比 $\eta_2$ 范围为0.49~0.86，因此可选择适当高宽比阈值 $\delta $ ，用于区分运动前景中的行人与车辆，实现对行人的识别。本文设置阈值 $\delta $ 为1.5，分别对3个视频进行验证，行人识别结果如图4所示。

2 行人跟踪

时空上下文(STC)算法通过对行人目标及相应场景中局部上下文区域的时空关系进行建模，并统计相应的低阶特征，通过结合时空上下文信息，实现对行人目标的跟踪，行人跟踪可视为对目标置信度图的求解过程。

对于第 $k$ 帧，采用式(4)计算置信图 $c(k)$ ，并将置信图响应最大的位置作为该帧的质心位置 ${k^*}$ 。

$c(k) = \sum\limits_{v(z) \in {K^c}} {P(k,v(z)|o)} = \sum\limits_{v(z) \in {K^c}} {P(k|v(z),o)P(v(z)|o)} $

(4)

式中： $P(k|v(z),o)$ 为行人当前位置与局部上下文之间的时空关系， $P(v(z)|o)$ 为上下文先验概率。

STC算法采用式(5)对置信图 $c(k)$ 进行建模，并采用式(6)对上下文先验概率 $P(v(z)|o)$ 进行建模。

$c(k) = b \times \exp ( - {\left| {\frac{{k - {k^*}}}{\sigma }} \right|^\beta })$

(5)

$P(v(z)\left| o \right.) = I(z) \times b \times \exp ( - {\frac{{\left| {z - {k^*}} \right|}}{{{\sigma ^2}}}^2})$

(6)

式中： $\sigma $ 为尺度函数， $b$ 为正则化常数， $\beta $ 为形状参数，设置为1， $I(z)$ 表示图像在 $z$ 处的像素值。

空间上下文 $P(k|v(z),o)$ ，表示行人目标与局部上下文之间的相似度，定义方式如式(7)所示：

$P(k|v(z),o) = {h^{{\rm sc}}}(k - z)$

(7)

将式(6)和式(7)代入式(4)中计算置信图 $c(k)$ 的具体表达形式，如式(8)所示：

$\begin{array}{c}c(k) = \displaystyle\sum\limits_{z \in {\Omega _c}({k^*})} {{h^{{\rm sc}}}(k - z)} \times I(z) \times b \times \exp ( - \displaystyle\frac{{{{\left| {z - {k^*}} \right|}^2}}}{{{\sigma ^2}}}) = \\{h^{{\rm sc}}}(k) \otimes (I(z) \times b \times \exp ( - \displaystyle\frac{{{{\left| {z - {k^*}} \right|}^2}}}{{{\sigma ^2}}}))\end{array}$

(8)

式中： $ \otimes $ 为卷积操作符，通过将傅里叶变换操作应用于卷积操作中，可大大加快运行速度。

对式(8)进行快速傅里叶变换，再进行傅里叶反变换，便可得到目标与局部上下文之间的时空关系，即空间上下文模型，如式(9)所示：

$\begin{array}{c}{h^{{\rm sc}}}(k) = {F^{ - 1}}\left( {\displaystyle\frac{{F(c(k))}}{{F(I(z) \times \alpha \times \exp ( - \displaystyle\frac{{{{\left| {z - {k^*}} \right|}^2}}}{{{\sigma ^2}}}))}}} \right){\rm{ = }}\\{F^{ - 1}}\left( {\displaystyle\frac{{F(b \times \exp ( - \displaystyle\frac{{{{\left| {k - {k^*}} \right|}^\beta }}}{\alpha }))}}{{F(I(z) \times \alpha \times \exp ( - \displaystyle\frac{{{{\left| {z - {k^*}} \right|}^2}}}{{{\sigma ^2}}}))}}} \right)\end{array}$

(9)

式中 $F$ 表示快速傅里叶变换。

获取到第 $k$ 帧视频序列的时空上下文模型 $H_k^{{\rm sc}}(K)$ 之后，可通过式(10)求第 $k + 1$ 帧的置信图 $c(k + 1)$ 来确定该帧目标质心位置 ${(k + 1)^*}$ 。

$\begin{array}{c}c(k + 1) = {F^{ - 1}}(F(H_{k + 1}^{{\rm sc}}(k)) \text{•} \\F(I(k + 1) \times \alpha \times \exp ( - \displaystyle\frac{{{{\left| {z - k_k^*} \right|}^2}}}{{{\sigma ^2}}}))\end{array}$

(10)

将置信图最大的位置作为行人目标在第 $k + 1$ 帧的质心位置，计算过程如式(11)所示：

${(k + 1)^*} = \arg \mathop {\max }\limits_{k \in {\Omega _c}(k_k^*)} c(k + 1)$

(11)

并通过该模型更新第 $k + 1$ 帧的上下文模型，更新过程如式(12)所示：

$H_{k + 1}^{{\rm sc}}(k) = (1 - \lambda )H_k^{{\rm sc}}(k) + \lambda h_k^{{\rm sc}}(k)$

(12)

式中 $\lambda $ 为学习率。

基于STC算法在处理目标部分遮挡时的优越性，为了进一步解决跟踪过程中目标被短时完全遮挡及目标旋转的问题，本文在STC算法基础上融入卡尔曼滤波器及HOG特征。

图5为当行人存在完全遮挡时，采用4种算法进行行人跟踪的结果对比图。从图中可以看出，当目标未发生完全遮挡时，本文算法与文献[17]算法，文献[18]算法和文献[19]算法在跟踪效果方面相差不多；一旦被跟踪的行人目标被完全遮挡，即从(a)中的#154和(b)中的#183开始，本文算法的跟踪效果比其他3种算法更加准确，而且更加鲁棒。

这是因为在通过STC算法预测下一帧目标质心位置之前，本文算法将当前帧的质心位置作为卡尔曼滤波算法起始位置，并结合目标HOG特征，对目标下一帧的质心位置进行最佳预测，有效地提高行人跟踪精度，具体跟踪精度对比如图6所示。

3 行人异常行为检测

在实际监控场景中，对行人异常行为的检测主要是通过对行人运动轨迹进行分析，或采用运动幅值方向直方图熵进行判别。文献[20]通过引入轨迹稀疏重构分析，提出最小二乘三次样条曲线逼近方法检测异常行为，该方法检测性能受控制点参数的影响；文献[21]提出基于幅值的加权方向直方图描述行为，计算运动区域内直方图熵来判断行为的异常，该方法可较好地反映异常行为的发生，但单一特征无法满足高精度的异常行为表达。

为了解决最小二乘三次样条曲线逼近方法受控制点参数的影响，本文提出一种控制点参数自适应的方法对行人运动轨迹进行表示。并通过加权考虑行人运动轨迹的稀疏重构残差和幅值方向直方图熵等多种特征，对人体行为进行多种表达，从而有效提升行人异常行为的检测率。

3.1 控制点参数自适应的运动轨迹表示

根据本文跟踪算法获取一组行人运动轨迹，由于视频中行人出现的帧数不同，因此运动轨迹可视为由不同长度的坐标序列组成。对于时空轨迹序列 $(x,y,t)$ ，本文采用自适应曲线控制点以参数化 $P = \left\{ {\left. {K_1^X,K_2^X, \cdots ,K_p^X,K_1^Y,K_2^Y, \cdots ,K_p^Y} \right\}} \right.$ 的方式来表示轨迹 $T = \left\{ {\left. {({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_t},{y_t})} \right\}} \right.$ 的形状和时空特征，以提取定长参数向量对轨迹进行表示。其中 $p$ 为控制点个数， $K_p^X$ 与 $K_p^Y$ 分别为第 $p$ 个控制点的归一化横纵坐标， $t$ 为轨迹长度。

轨迹 $T$ 上的点 $({x_i},{y_i})$ 所经过的总距离 ${d_i}$ 可表示为 $\displaystyle\sum\limits_{i = 1}^{n - 1} {\sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2}} } (n = 2, 3, \cdots ,t)$ ，定义参数向量 ${ v} = \left\{ {\left. {{v_1},{v_2}, \cdots ,{v_t}} \right\}} \right.$ ，其中 ${v_n}$ 可表示为式(13)：

${v_n}{\rm{ = }}\left\{ \begin{array}{l}\displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^{n - 1} {\sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2}} } }}{{\displaystyle\sum\limits_{i = 1}^{t - 1} {\sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2}} } }},\quad\quad i \ne 0\\0,\;i = 0\end{array} \right.$

(13)

及节点向量 ${ \kappa} $ ，表示为式(14)：

${ \kappa} {\rm{ = }}\left( {0,0,0,0,\frac{1}{{p{\rm{ - 3}}}},\frac{2}{{p{\rm{ - 3}}}}, \cdots ,\frac{{p{\rm{ - }}4}}{{p{\rm{ - 3}}}},1,1,1,1} \right)$

(14)

根据^[22]，采用式(15)计算三次B样条基函数，

$\begin{array}{c}{\psi _{p,q}}({v_n}) = \displaystyle\frac{{{v_n} - {\kappa _p}}}{{{\kappa _{p + q - 1}} - {\kappa _p}}}{\psi _{p,q - 1}}({v_n}) + \\\displaystyle\frac{{{\kappa _{p + q}} - {v_n}}}{{{\kappa _{p + q}} - {\kappa _{p + 1}}}}{\psi _{p + 1,q - 1}}({v_n})\end{array}$

(15)

式中： ${\psi _{p,1}}\left( {{v_n}} \right){\rm{ = }}\left\{ \begin{array}{l}1,\;\;\;\;\;\;\;\;\;{\kappa _p} \leqslant {v_n} < {\kappa _{p + 1}}\\0,\;\;\;\;\;\;\; \text{其他}\end{array} \right. $

并通过式计算自适应的控制点参数，使原始轨迹与其近似轨迹之间的误差平方和达到最小，从而对行人运动轨迹进行有效表示

${\rm P}^{\rm XY}={\left( { \varOmega ^{\rm T} \varOmega } \right)^{ - 1}} \varOmega^{\rm T} {\rm T}^{\rm XY}$

(16)

式中 ${ \varOmega} {\rm{ = }}\left[ {\begin{array}{*{20}{l}}{{\psi _{1,4}}\left( {{v_1}} \right)\;\; \cdots \;\;{\psi _{p,4}}\left( {{v_1}} \right)}\\{\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots }\\{{\psi _{1,4}}\left( {{v_t}} \right)\;\; \cdots \;\;{\psi _{p,4}}\left( {{v_t}} \right)}\end{array}} \right]$ 。

图7显示了正/异常行为运动轨迹样本及特征表示，其中左侧为运动轨迹样本图，右侧为相应的特征表示图。

3.2 基于幅值方向直方图的异常行为表示

本文将行人异常行为定义为运动幅度变化大、运动方向不一致的一些不规则行为，如打斗、抢劫等，这些行为都具有运动速度快、方向紊乱等特征。由于行人运动幅值方向直方图^[23]具有旋转平移不变性，能够很好地反映出行人动作的幅度大小，直方图熵能够反映运动方向的混乱程度，因此可采用幅值方向直方图熵对异常行为进行表示。

首先将运动轨迹分成8个子区域，以每45°作为一个区域边界，对于行人运动轨迹上的每一个点 $({x_0},{y_0}),({x_1},{y_1}), \cdots ,({x_n},{y_n})$ ，分别根据式(17)计算每个轨迹点的切线方向属于哪个子区域中，若某个运动轨迹的所有点的切线方向均稳定处于少量几个子区域，则该运动轨迹为正常行为的概率更大，而如果某运动轨迹的所有切线方向占了绝大部分的子区域，说明该运动轨迹更加紊乱，更有可能为异常行为所产生的运动轨迹。

$\theta = \arcsin (\frac{{{y_i}}}{{\sqrt {x_i^2 + y_i^2} }})\;\;i = 0,1, \cdots ,n$

(17)

对于打架、抢劫等剧烈运动，通过计算基于幅值的加权方向直方图可有效抑制由噪声造成的小范围方向混乱，实现更好的异常行为识别，假设第 ${ R}$ 帧的直方图模型如式(18)所示，

$H(R) = {\left\{ {\left. {{h_j}(R)} \right\}} \right._{j = 1,2, \cdots ,m}} = {\left\{ {\left. {C\sum\limits_{i = 1}^j {w{F_i}\Phi (a({F_i}) - j)} } \right\}} \right._{j = 1,2, \cdots ,m}}$

(18)

式中： $m$ 为直方图区间的个数，此处取12。 ${h_j}(R)$ 为第 $R$ 个区域直方图模型， $C$ 为归一化参数， $\omega {F_i}$ 为第 $i$ 个加权幅值方向直方图， $\alpha ({F_i})$ 为第 $i$ 个幅值方向直方图的强度， $j$ 为方向区间， $\varPhi $ 为Kronecker delta函数。

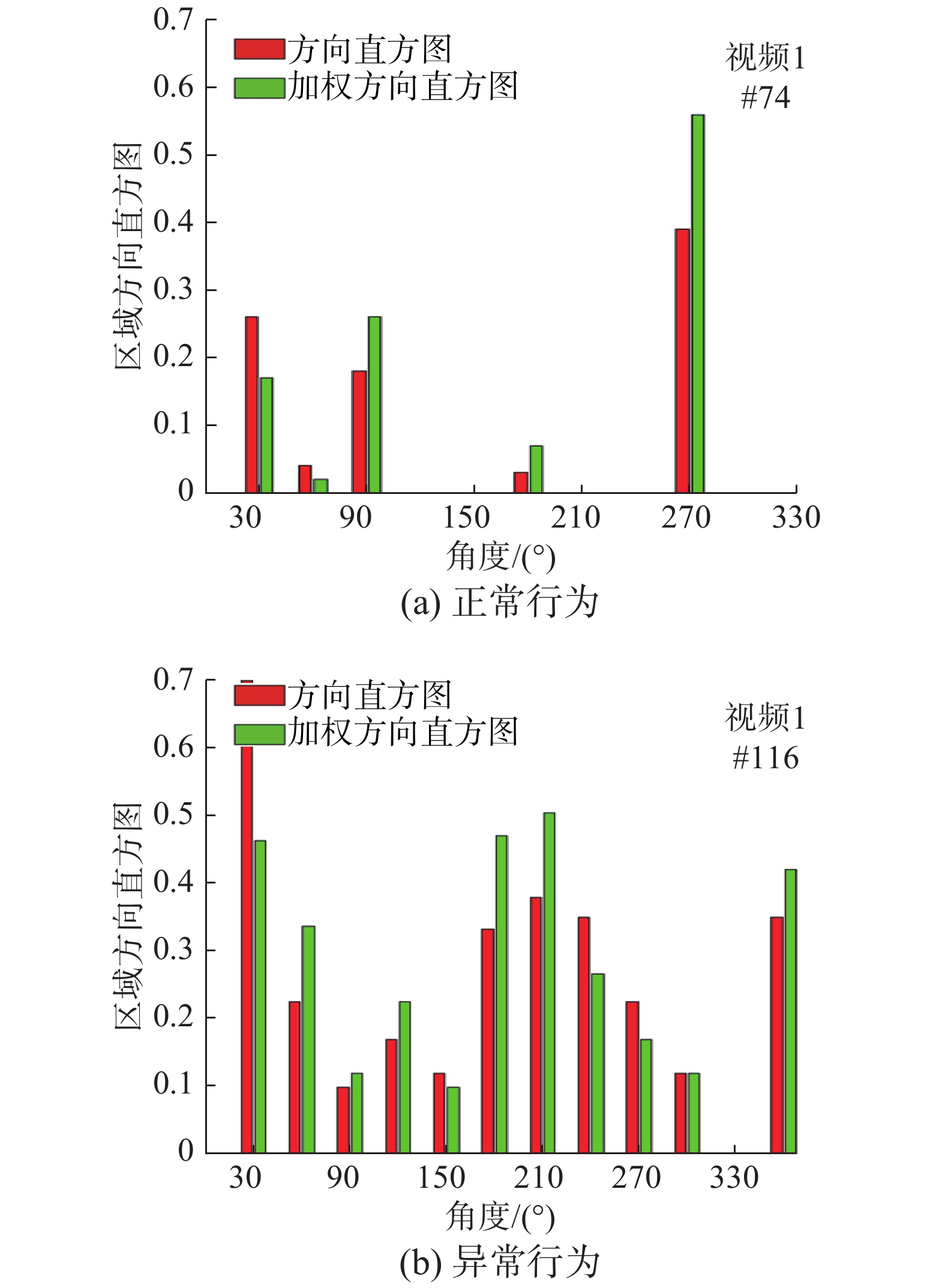
针对实验选取了部分视频序列进行幅值方向直方图的计算，与正常行为相比，异常行为往往具有运动幅度较大的特点，因此当某区域存在异常行为时，该区域的运动幅值偏大，而且方向比较混乱，而正常行为则运动幅度小，方向比较一致。其中正常行为与异常行为的加权幅值方向直方图的实验结果如图8所示。

3.3 加权重构轨迹与直方图熵的异常行为检测

基于室外监控场景，对于行人异常行为的检测，本文通过计算待检测运动轨迹与正常行为轨迹字典的稀疏重构残差，同时考虑加权幅值方向直方图熵值，结合行人运动的多种特征，实现对行人异常行为的高精度识别。

3.3.1 正常行为字典建立

在真实监视场景中，正常运动轨迹的训练样本集合非常大，因为绝大多数人的行为都是正常的，而异常运动轨迹的训练样本却很小，因此学习正常行为字典具有高计算复杂度。以文献[24]为基础，采用式(19)定义一种分层框架学习字典的数学模型。

${N_\ell } \approx \arg \mathop {\min }\limits_{{{\rm{D}}_\ell },{\Upsilon _\ell }} \left\| {{{ \varTheta} _\ell } - {N_\ell }{{ \varUpsilon} _\ell }} \right\|_F^2 + {\partial _\ell }\Psi \left( {{{ \varUpsilon} _\ell }} \right)$

(19)

式中： ${N_\ell }$ 为正常行为第 $\ell $ 层的子字典， ${ { \varUpsilon} _\ell }$ 为数据 ${{ \varTheta} _\ell }$ 的系数矩阵， ${\partial _\ell }$ 为 $\ell $ 层的平衡参数， $\varPsi $ 为规则项，通常为混合范数。

对于某层任一数据点，通过与上层字典原子的关系预先规划下层可预选编码路径及激活原子，随着分层学习字典层数的增加，由于相似数据点选择的原子具有多样性，因此在定义下层字典时，原子数目选择为上一层的2倍。

具体正常行为字典训练过程如算法1所示。

算法1　行为字典树结构学习算法

输入　跟踪获取的行人时空运动轨迹序列T；

输出　正常行为字典集 ${N_{{d}}}$ 。

1) 初始化训练参数。规则化平衡参数 ${\partial _1}, {\partial _2} \cdots ,{\partial _\ell }$ ，随机初始化各层子字典 ${N_{\rm{i}}}$ 原子个数 ${n_i}$ 及数据点稀疏矩阵 ${\bf sm}{_i}$ ，邻层原子数目的倍数 $\varGamma = 2$ ；

2) 学习第1层字典。基于文献^[25]，学习 ${{ N}_1}$ 作为第1层训练字典，构建数据点与原子之间的稀疏矩阵并更新 ${\bf sm}{_1}$ ，满足条件时停止迭代优化；

3) 预先规划下层稀疏矩阵。将第1层的重构残差作为第2层的输入，以此类推，由 ${\bf sm}{_i}$ 根据式 ${n_\ell } \in \left\{ {\left. {{n_{\ell ,i}}\left| {i = \left( {\zeta - 1} \right) \times n + j,\;\;\zeta = 1,2, \cdots ,N} \right.} \right\}} \right.$ ， $j$ 为稀疏索引号，预先规划下层稀疏矩阵 ${\bf sm}{_{ i + 1}}$ 作为初始稀疏矩阵；

4) 稀疏矩阵约束编码路径。采用初始化字典集 ${{{N}}_i}$ 编码轨迹，根据编码系数更新 ${{{N}}_i}$ ，满足条件时停止迭代优化；

5) 迭代条件判断。若行为字典训练的树结构层数未达到，则重复步骤3)与4)。

通过充分考虑相邻层之间原子的父子节点关系，为每层建立一个子字典，将下层原子与上层相互关联。随着层数的增加，正常行为轨迹的特征可实现由模糊特征到细节特征的变化，该训练算法能有效解决传统字典学习中原子关联缺失的问题。

3.3.2 稀疏重构运动轨迹

通过激活与给定输入轨迹相似度高的少量样本，使整个系数向量保持稀疏。稀疏重构^[26]是将待检测的行人轨迹通过正常行为字典中的行人轨迹以一个稀疏向量进行表示，具体表示如式(20)所示：

${T_{{ {\rm{wd}}}}} \approx \lambda {N_{{d}}}$

(20)

式中： ${T_{{ {\rm{wd}}}}}$ 表示待检测的行人运动轨迹, ${N_{{{{d}}}}}$ 表示正常行为字典中的行为轨迹， $\lambda $ 表示某个待检测运动轨迹与正常行为字典之间的稀疏重构系数，其值绝大部分为0。

由于正常行为字典中的行人运动轨迹帧数与待检测运动轨迹帧数可能不一致，因此在对运动轨迹进行稀疏重构之前，需要对帧数较多的运动轨迹进行截取，保证正常行为字典中选择的运动轨迹与待检测的行人运动轨迹具有相同的帧数。若待检测的运动轨迹能够在正常行为字典中找到少量相似度高的轨迹进行表示，此时稀疏向量中存在少量接近数值1的向量值，而当待检测的运动轨迹在正常行为字典中找不到相似度高的轨迹进行表示，此时稀疏向量中存在大量接近数值0的向量值。所以无论待检测的行人轨迹为正常行为或是异常行为，都满足稀疏重构时的稀疏性。

L₁范数不仅可以尽可能地近似表示待检测轨迹，而且能够在正常字典中样本较少的情况下对稀疏系数进行高效求解。当然，对于稀疏系数而言，与数值0的差值越大，表明待检测运动轨迹与正常行为字典中的轨迹越不相似，因此，为了充分表现出相似值大小对最优 $\lambda $ 的影响，采用迭代加权L₁范数计算稀疏系数，计算公式如式(21)所示：

${\rm{argmin}}{\left\| {{\omega ^{\left( \tau \right)}}\lambda } \right\|_1}\;\;\;\;\;\;\;\;{\rm s.t.}\;{\left\| {\lambda {{N}} - {{{T}}_{{\rm{wd}}}}} \right\|_2} \leqslant \varepsilon $

(21)

式中： $\tau $ 表示迭代加权次数， $\omega _i^{(\tau )}$ 表示在第 $i$ 次迭代过程中的权值， $\varepsilon $ 表示残差阈值，通常取10^-2。

3.3.3 直方图熵

运动信息熵^[27]可用来描述行为方向的紊乱程度，因此通过计算区域内直方图熵可以更准确地对异常行为进行描述，首先计算每个区域直方图模型 ${\left\{ {\left. {{h_j}(R)} \right\}} \right._{j = 1,2, \cdots ,m}}$ 的熵值，计算过程如式(22)所示。

${E_H} = - \sum\limits_{j = 1}^m {{h_j}(R)} {\log _2}({h_j}(R))$

(22)

${E_H}$ 值越大，说明运动幅值强度越大，方向越紊乱，那么将最大的 ${E_H}$ 值用于表示运动强度，即 ${E_{\max }} = \max (E_H^1,E_H^2, \cdots ,E_H^n)$ ， $n$ 为区域个数，为了提高 ${E_H}$ 值在[0, 1]变化，对其进行归一化操作。同时考虑到行人异常行为通常发生在一个时间段内，在对异常行为进行判断时，需要综合某个时间段内的熵值变化从而避免由噪声产生的偶尔几帧熵值的突然变化而形成的误差。对于每一帧图像，计算该图像前10帧的直方图熵值的平均值 ${A_{{\rm{ent}}}}$ ，与当前帧直方图熵值进行比较，作出当前帧是否为异常帧的最终判断。

当 ${E_H} \geqslant T$ 时，认为当前帧中出现幅度较大的异常行为，具体的根据阈值判断异常行为的过程如式(23)，其中熵阈值T通过平均熵值 ${A_{{\rm ent}}}$ 进行更新，对异常行为判断的结果进行优化。经过实验，当熵阈值T设置为0.5时，对异常行为的识别精度更高。

$\left\{ \begin{array}{l}{E_{\max }} \geqslant T,\;\;\;\;{\text{异常行为}}\\{E_{\max }} < T,\;\;\;\;{\text{正常行为}}\end{array} \right.$

(23)

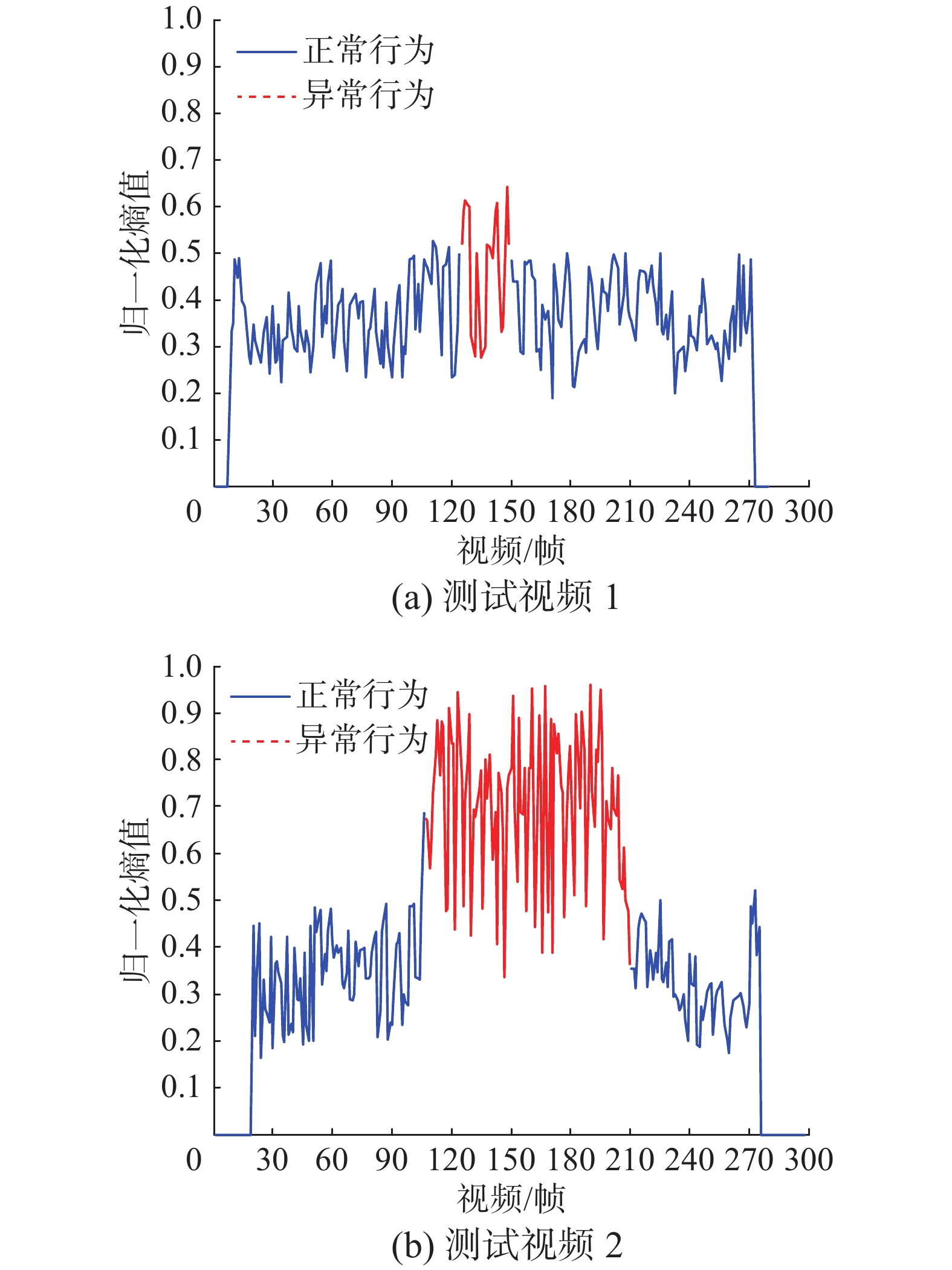
图9为不同视频段直方图熵的变化曲线，其中细实线表示检测结果为正常行为，粗实线表示检测结果为异常行为。从图中可与看出，视频1共272帧，第122~150帧之间发生异常；视频2共275帧，第107~209帧之间发生异常。

3.3.4 联合加权重构轨迹与直方图熵

在获取待检测运动轨迹 ${T_{{\rm{wd}}}}$ 及相应的稀疏重构系数 $\lambda $ 之后，通过计算每个测试样本之间的稀疏重构残差 $\gamma $ 来建立分类器。定义特征函数 $\delta $ 来保留正常行为稀疏系数，若运动轨迹正常，系数设置为1，否则设置为0，基于运动轨迹的稀疏重构残差 $\gamma $ 的计算过程如式(24)所示：

${\gamma _t}\left( {{T_{{\rm{wd}}}}} \right) = {\left\| {{T_{{\rm{wd}}}} - {\lambda _t}\delta } \right\|_2}\;\;\;\;\;\;t = 0,1$

(24)

式中 $t$ 为行为类别(正常/异常)。

本文实验在测试时，采用轨迹重构残差 $\gamma $ 与阈值 $\eta $ 之间的关系作为判断行为是否异常的条件之一，判断过程如式(25)所示：

${\Re _t} = \mathop {\min }\limits_{t = 0,1} \frac{{{1 / {{\gamma _t}\left( {{T_{{\rm{wd}}}}} \right)}}}}{{\displaystyle\sum\limits_{i = 0}^t {{1 / {{\gamma _t}\left( {{T_{{\rm{wd}}}}} \right)}}} }} \leqslant \eta $

(25)

此处阈值 $\eta $ 设置为0.03，测试运动轨迹 ${\Re _t}$ 若满足式(25)，则认为该行人运动可能存在异常，需进一步考虑运动幅值方向直方图熵值 ${E_H}$ ，结合行人运动的多种特征，通过联合加权的方式对行人异常行为进行检测，检测过程如式(26)所示：

$\bar \lambda \propto \varsigma \min {\gamma _t}\left( {{T_{{\rm{wd}}}}} \right) + \upsilon {E_{Hj}}\left( R \right)$

(26)

式中： $\varsigma $ 、 $\upsilon $ 表示权值系数。权重 $\varsigma $ 与 $\upsilon $ 的选取好坏将直接影响到实验中异常行为的检测准确率，为了选择合适的权重，设置初始权重 $\varsigma $ 为0.05，根据 $\varsigma $ 值确定 $\upsilon $ 的取值，并设置权重 $\varsigma $ 的增长步长为0.05，共选取19组数据进行试验，采用式(26)计算在不同权重下的异常行为检测准确率。表2为权重 $\varsigma $ 与 $\upsilon $ 的选取值及对应的异常行为检测精度，图10为权重 $\varsigma $ 选取不同值时的异常行为检测精度。

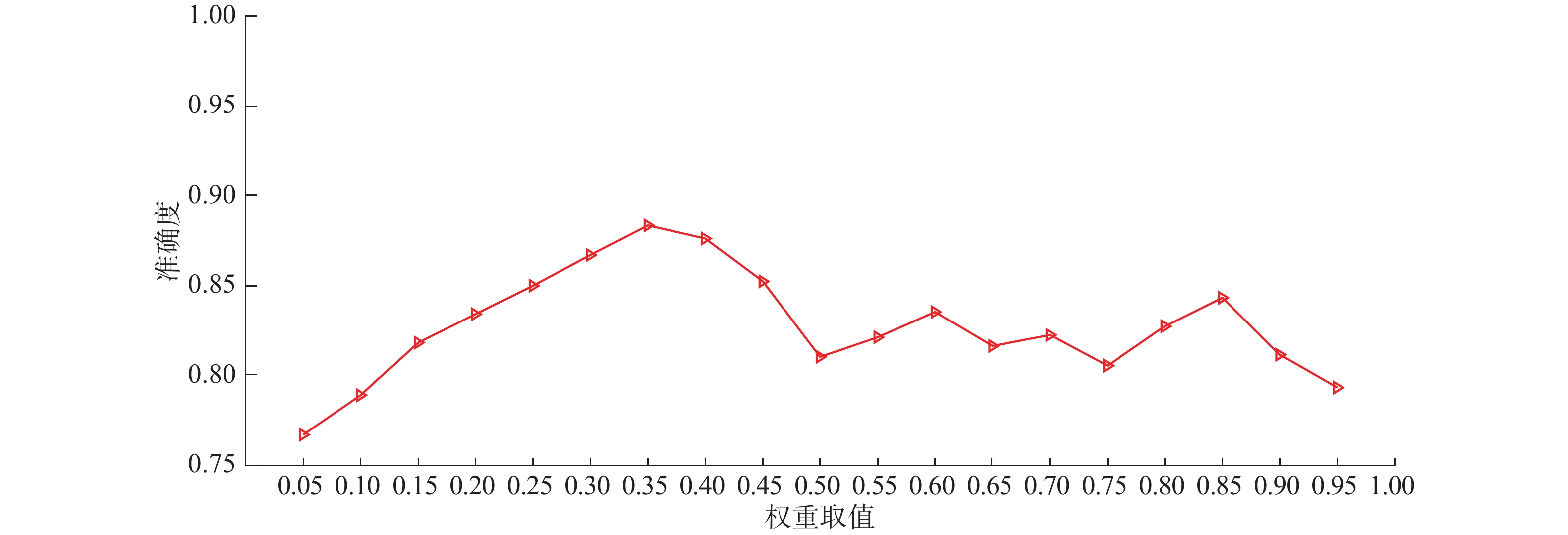
从图10中可以看出，当 $\varsigma $ 选取为0.35时异常行为检测准确度最高，因此本文将 $\varsigma $ 、 $\upsilon $ 分别设置为0.35与0.65， $\bar \lambda $ 表示最终的行为检测类别。通过对多种运动特征进行联合加权考虑，该方法不仅可消除运动轨迹特征表示时受控制点参数的影响，同时可以提升仅采用直方图熵值进行异常行为检测的异常行为检测准确率。

4 实验与结果分析

实验所用机器为Microsoft Windows 10 Professional操作系统；3.30 GHz, Intel Core i5-6600处理器；4 GB内存；Intel HD Graphics 530显卡；使用Matlab R2014a和Microsoft Visual Studio 2013开发平台对算法进行实现。

4.1 实验数据集

采用中国科学院自动化研究所模式识别实验室(http://www.cbsr.ia.ac.cn/china/Action%20Database 20CH.asp)提供的CASIA行为分析数据集进行实验，该视频集由室外环境下3个不同视角的摄像机拍摄而成，CASIA共有1 446段视频数据，每段视频含有200~300帧不等，帧大小为320×240，其中多人交互行为包括抢劫、打斗、尾随等。

假设一般情况下，拍摄到的行人行为是正常的，异常行为设定为出现打斗、抢劫画面的情况，如图11所示。

4.2 评价标准

考虑到正异常行为分布的不平衡性，若仅采用单一评价标准无法较好的分析模型检测性能。实验通过检测精度 $P$ 、错误率 ${\rm MR}$ 和 ${\rm ROC}$ 曲线3个评价指标对结果进行衡量。假设某时刻发生异常，若被检测为异常称为 ${\rm TP}$ ，未被检测为异常称为 ${\rm FN}$ ；假设某时刻未发生异常，若被检测为异常称为 ${\rm FP}$ ，未被检测为异常称为 ${\rm TN}$ 。

检测精度 $P$ 表示正确检测出异常行为的概率，错误率 ${\rm MR}$ 表示将正常行为检测为异常行为的概率，计算过程如式(27)所示：

$P = \frac{{{\rm TP}}}{{{\rm TP} + {\rm FP}}},\;\;\;{\rm MR} = \frac{{{\rm FP}}}{{{\rm FP} + {\rm TN}}}$

(27)

${\rm{ROC}}$ 曲线用于描述检测精度与错误率之间的平衡关系。

4.3 实验结果分析

对监控视频中的行人打斗、抢劫两种异常行为进行检测，本实验分别在打斗视频和抢劫视频中进行测试，以打斗异常为例，检测结果如图12所示。

此处采用混淆矩阵对本文算法在打斗视频及抢劫视频中的结果进行统计，统计结果如表3~4。

表3为本文算法在打斗视频中的行为统计结果，当出现行为发起者双方位置顺序发生调换且运动熵很大时，打斗行为被误认为是抢劫行为，共错检9帧；在打斗过程中，出现两者无交互行为的瞬间，被误认为是正常行为，该情况共出现17帧。当两者均在跑动时，此时运动熵很大，且轨迹也是交错的，该种正常行为被误检为打斗异常，共8帧。

表4为本文算法在抢劫视频中的行为统计结果，当抢劫者加速夺过物品，但未超过被夺者的位置，被误检为打斗行为，共4帧；在抢劫者加速跑向被夺者，但尚未抓住行李时的正常行为，被误认为抢劫行为，共4帧。

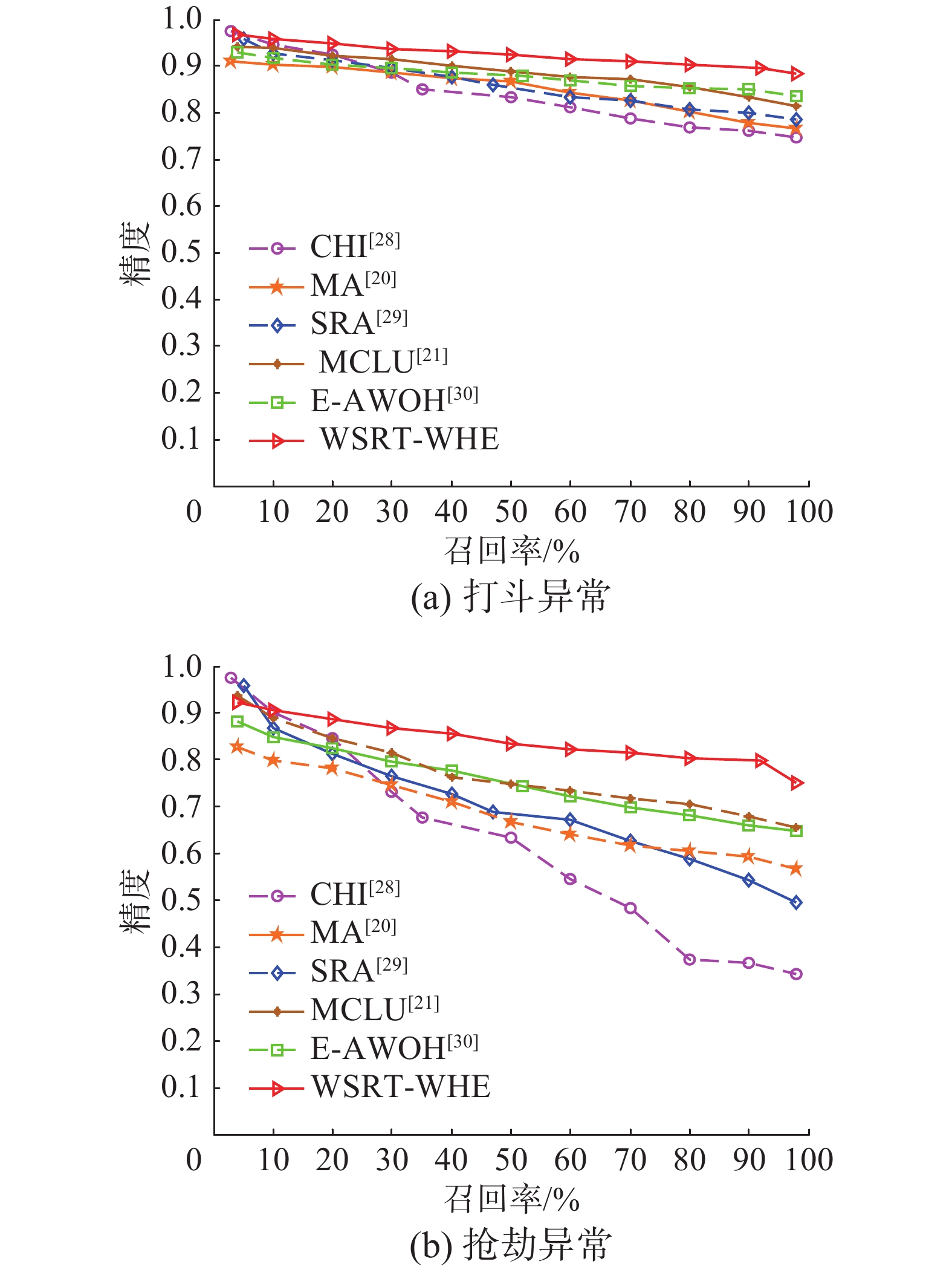
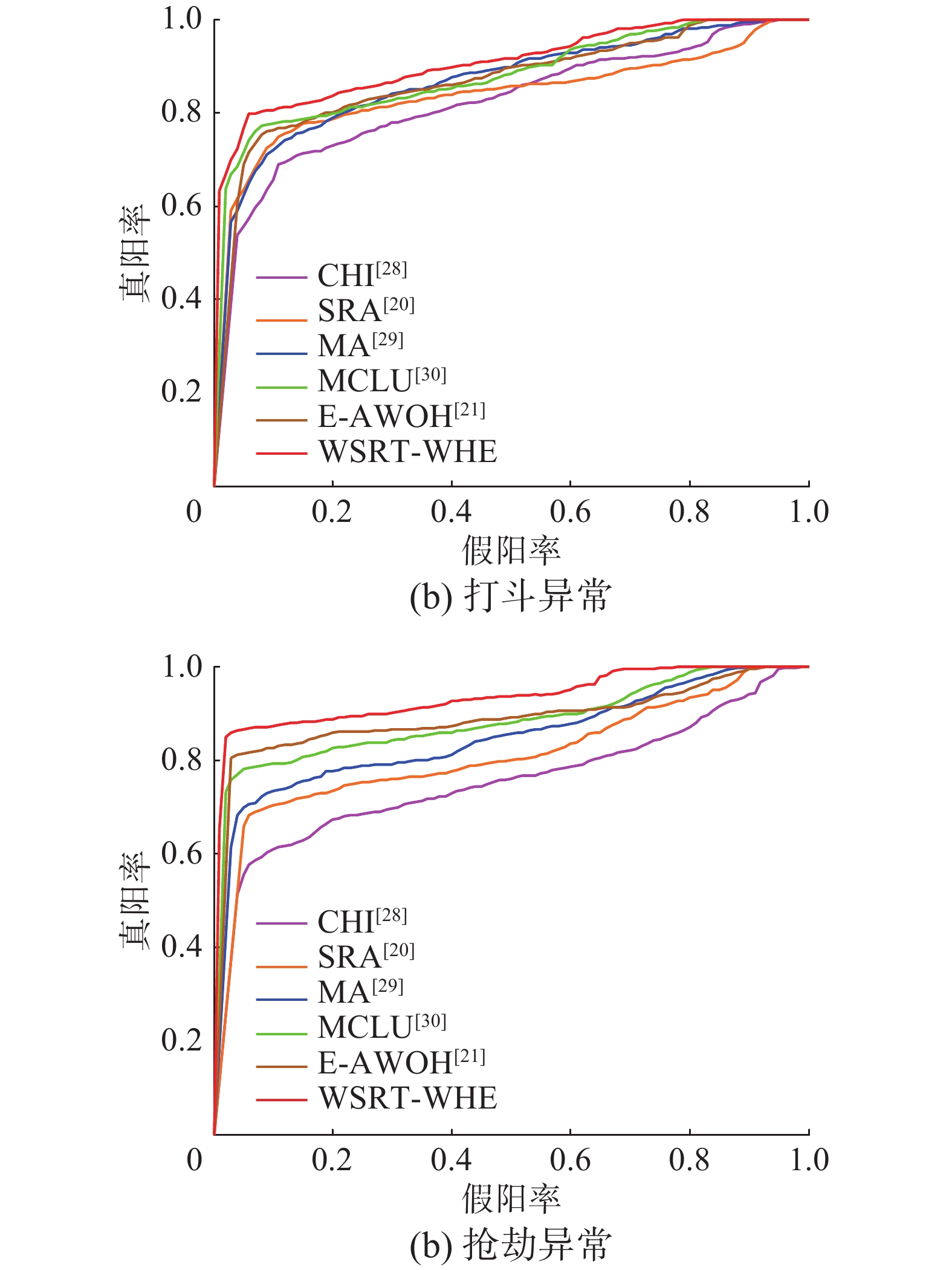
为验证本文算法对行人异常行为检测的优越性，通过与基于轨迹稀疏重构分析^[20]，基于幅值加权方向直方图熵^[21]，基于角点历史信息^[28]、基于矩阵近似^[29]及基于加权样本选择与主动学习^[30]的异常行为检测算法进行对比，此处将算法^{[20-21, 28-30]}分别表示成SRA算法、E-AWOH算法、CHI算法、MA算法和MCLU算法，将本文算法记为WSRT-WHE算法，实验对打斗和抢劫视频中的异常行为进行检测，检测精度对比图如13(a)、13(b)所示，具体检测精度和错误率数据见表5和表6。

通过分析检测精度图可得，CHI算法充分利用了图像的时空信息，并且克服了场景光照影响，但对于存在遮挡时，跟踪获得的运动轨迹不清晰,对异常行为的判断影响较大，因此检测精度较低，对于抢劫异常更为明显，仅达51.72%；SRA算法通过对跟踪轨迹进行线性重构，并根据其与正常行为字典集的稀疏重构系数及重构残差来判断行为是否异常，该方法可用于较小行为字典集，但检测性能受控制点参数的影响，固定个数控制点导致检测性能无法达到最佳，在抢劫异常中，仅76.71%；MCLU算法在选取不确定样本时考虑到样本的多样性，并通过一个权重值解决数据不平衡问题，该方法在视频监控异常行为检测中取得较好的效果，达79.17%，但权值的选择问题仍然有待解决；MA算法使用低秩矩阵近似对行为模式进行建模，根据与模型子空间的运动偏差来识别异常的行人行为，但该方法的检测效果依赖于运动偏差阈值的定义；E-AWOH算法通过计算区域内运动幅值直方图熵来描述行为混乱程度，无需精确轨迹便可较准确的检测出行人异常，对于抢劫异常，可达到81.26%。

本文算法对于跟踪过程中存在遮挡时，跟踪丢失导致轨迹紊乱的情况，通过结合卡尔曼滤波器和HOG特征，可精确获取受短时遮挡目标的运动轨迹，有效解决CHI算法跟踪轨迹不清晰的问题；在对轨迹进行表示时，提出自适应的控制点参数选择，有效解决SRA算法中受控制点个数的影响。本文算法的联合加权思想来自于MCLU算法，通过考虑目标运动的多种特征对人体行为进行描述。相比MA算法、E-AWOH算法，本文方法可有效提升行人异常行为的检测精度，在打斗异常及抢劫异常中分别实现了92.79%和84.62% 的检测精度。

分析表5和表6可知，对于异常打斗和异常抢劫行为的检测，本文算法在检测精度方面达到最佳，尤其对于打斗行为的检测，高达92.79%；在检测错误率方面，本文算法略低于其他方法2%~5%，说明本文算法在检测行人交互中出现的行人打斗和抢劫等异常行为时具有较好的鲁棒性。

针对打斗与抢劫视频中的异常行为检测，ROC曲线图如图14所示，分析ROC曲线图可得出，本文算法相比于5种对比算法，在两组异常行为的检测过程中，检测精度与错误率之间可以达到更好的平衡。

基于学习的方法对特征要求很高，针对视频中行人发生异常时存在遮挡的问题，该类方法检测效果不佳。本文通过时空上下文算法结合卡尔曼滤波器和HOG特征，有效解决了异常发生时目标被遮挡的问题。在目标存在遮挡的监控场景中，实现有效的检测和跟踪，可获取更加清晰的运动轨迹，采用自适应控制点参数对运动轨迹进行表示，同时结合运动幅值直方图熵，实现对目标运动的详细描述，从而满足于进一步对异常行为的研究。

5 结束语

本文针对存在完全遮挡时，运动目标跟踪易产生漂移的问题，在时空上下文的基础上，融入卡尔曼滤波器及HOG特征，对于短时间内完全遮挡的行人具有较好的跟踪效果。通过自适应选择控制点参数对运动轨迹进行表示，同时考虑到目标运动直方图熵，本文提出一种联合加权稀疏重构轨迹与幅值方向直方图熵的行人异常行为检测方法，在识别行人交互中存在的打斗和抢劫异常时，检测率可达92%以上。但本文方法仍存在一些不足，比如在获得幅值方向直方图时，需计算轨迹上每个点所在子区域范围，计算过程复杂，且无法达到实时性要求，对于时间性能的提升将是下一步研究的重点。