非平衡数据的分类问题广泛存在于电信诈骗检测、医疗诊断、网络入侵监控[1]、生物信息学、文本分类[2]、语言识别[3] 、监测石油泄漏卫星图像[4]等领域中,在这些实际应用中,很多数据的结构并不是理想化、均匀、平衡地分布。在非平衡数据分类过程中,由于正类样本数量相对稀少,其所要表达的信息受到了限制,从而在分类时很难正确分析出数据的分布以及内部规律,导致少数类的分类精度降低,所以在分类过程中非平衡数据中少数类的数据稀少是导致分类性能下降的直接原因之一[5]。如何能够在分类之前对数据进行预处理,弥补少数类样本在分布信息方面不足的问题,以达到将数据平衡化的目的,从而提高分类器的性能,是非平衡数据学习过程中的重点所在。
在目前的研究中,用于解决非平衡数据分类问题的常用策略大致分为两种,即数据层面的方法和算法层面的方法。算法层面的方法主要包括集成学习方法和代价敏感学习方法[6];数据层面的方法主要思想是基于重采样技术也就是对少数类样本的过采样和对多数类样本的欠采样。
作为数据层面的处理方法,重采样方法简单、直观,倍受研究人员青睐[7-9],在过采样研究中,2002年Chawla提出的SMOTE [10](synthetic minority over-sampling technique)算法是其中的一个经典算法,现有很多算法都是在此原型的基础上提出的。SMOTE算法在少数类样本与其K个近邻之间的连线上产生随机的合成样本,完成对少数类样本的过采样,提高了少数类样本数量,使分类器更好地对未知少数类样本进行预测,有效地提高了分类精度。但是,由于SMOTE算法无区分地对所有少数类样本进行过采样,在少数类极度稀缺时很容易造成过拟合。为了解决这一问题,文献[11]提出了基于SMOTE的改进方法(adaptive SMOTE,ASMOTE)方法[11],该方法根据样本集内部实际分布特性,自适应地调整合成样本产生过程中的近邻选择策略,避免了原始方法中样本生成的盲目性,进而一定程度上提高了分类算法的准确率。在文献[12]提出的Borderline-SMOTE方法中,改变了传统的思路,认为边界样本具有更多的信息,通过查找出的“危险样本”作为种子来产生新的合成样本。在此基础上,Haibo He等[13]对以上算法进行了改进,根据样本的“危险”程度,也就是少数类样本在学习中的难易程度,使用加权的方法,构造合成样本的分布函数,来确定这些样本合成新样本的数目。
上述文献中所涉及的采样思想大多为基于线性距离,有一定的局限性,易受数据集中样本分布结构的影响。本文提出了一种新的非平衡数据集处理方法——基于密度的重采样算法DS-SMOTE,旨在识别任意形状的簇,并且扩大“危险样本”的范围,对簇中的“稀疏样本”进行重采样,达到数据集的平衡。在本文实验中,选择了C4.5算法作为基准分类算法,C4.5算法是具有代表性的决策树基准算法,在分类数据不平衡的情况下与同类分类器相比具有良好的分类性能,故选择C4.5算法作为基准分类算法。
1 基于密度的过采样方法基于密度的方法能够用于识别任意形状的簇,如“S”形以及椭圆形簇 [14]。为了更好地对非平衡数据集的分布进行刻画,结合SMOTE的思想,本节提出一种基于密度的过采样方法。
1.1 SMOTE算法SMOTE[7]是过采样方法中的经典算法。其主要思想基于k近邻算法,对每个少数类样本o,从它的k个最近邻中随机选择一个样本a,在o~a之间的连线上随机产生合成样本,一般地,取k=5 [15]。
SMOTE过采样方法通过对数据集中每一个少数类样本随机地选取k个最近邻,并在该少数类样本与其选取的最近邻之间的连线上随机产生合成样本。在步骤1)中,通过获取的过采样比例以及少数类样本的数量,产生新样本数量;在步骤2)~5)中,循环遍历每一个少数类样本,获取其k近邻,并将其k近邻的索引保存于数组nnarry中,作为合成新样本的参数获取新样本,这里选取最近邻个数k=5,例如:已知过采样比例为300%,那么需要从每个少数类样本的5个最近邻中随机选取3个样本,作为合成新样本的素材;其中Populate方法详细介绍了合成样本的产生过程。在步骤3)中,根据少数类样本的属性数以及新样本的数量进行遍历,步骤5)用于求得样本间的欧式距离;在步骤8)中,根据公式,得到少数类样本与其近邻之间的合成样本。新生成的样本使得分类器能够从学习过程中产生更大更抽象的决策边界,有效地使少数类的决策边界变得更加明显,从而获得更好的分类效果。
SMOTE算法
SMOTE(T, N, K)
输入 少数类样本数量T;过采样百分比N%;样本近邻个数k;
输出 (N/100)*T个少数类合成样本。
1) N=(int)(N/100);
2) for i=1:T
3) 计算第i个样本的k个最近邻, 其k近邻的索引保存于nnarry中;
4) Populate(N, i, nnarry);
5) endfor
Populate(N, i, nnarry)方法
1) While N~=0
2) 选择1~k之间的随机整数, 记为nn。随机选择第i个样本的k近邻中的一个近邻。
3) for attr=1:numattrs
4) (numattrs为样本的属性个数)
5) dif = sample[nnarry[nn][attr]] – sample [i][attr];
6) (sample[][]为原始少数类样本集合)
7) gap=rand();
8) synthetic[newinder][attr] = sample[i][attr] + gap*dif;
9) (newinder为合成样本总量, 初始值为0)
10) endfor
11) newindex++;
12) N=N+1;
13) endwhile
1.2 Borderline-SMOTE算法Borderline-SMOTE算法在SMOTE算法的基础上进行了改进[12]。不同于SMOTE算法,Borderline-SMOTE算法避免了在过采样过程中样本选择的随机性,选择类边界样本,作为种子样本合成新样本。在样本空间中,如某一样本周围的邻居样本较多,则这个样本较为稠密,就决策树分类算法而言,产生的叶子节点——规则较多,容易产生过拟合问题,所以不宜在这个样本与其近邻之间添加新的样本。Borderline-SMOTE算法尝试着在训练过程中尽量地去学习边界特征,认为边界样本在分类中比远离边界的样本更容易被错分,一个类的边界样本携带了更多的信息,对分类器分类性能的好坏起到了决定性的作用。因此,在Borderline-SMOTE算法中,加入了识别边界样本的过程:若一个少数类样本的m近邻中,半数以上为多数类样本,则认为这个样本为容易被错分的危险样本;否则为安全样本。在危险样本与其k近邻之间合成新样本,完成对边界少数类样本的过采样,以此加强少数类的决策边界,以获得好的分类结果。
1.3 基于密度的过采样算法设某类的样本集合为S={si, i=1, 2,
定义1 参数ε(ε>0)为对象o的邻域区域的半径,即o的邻域半径。则一个对象o的ε-邻域是指以o为圆心、以ε为半径的空间,定义为
| $\psi {\rm{ = \{ }}\varepsilon ,\theta |2 \cdot D\left( {{{\mathit{\boldsymbol{s}}}_i}\left. {,o} \right)} \right. \cdot {\rm{cos}} \; \theta \leqslant \varepsilon {\rm{\} }}$ | (1) |
式中:D(si, o)为对象o以外的样本si到对象o的距离,采用欧式距离方法计算[16];θ为点o与si连线与水平轴之间的夹角。
定义2 对象o的ε-邻域的密度是指对象o在ε-邻域内的对象数量。
定义3 一个样本数量为m的类在邻域半径为ε时,类中样本的密度阈值Min Pts为类中样本i的ε-邻域密度Mi的均值。
| ${\rm{Min}} \, {\rm{Pts}} = \frac{1}{m}\sum\limits_{i = 1}^m {{M_i}} $ | (2) |
为了确定对象o是否为稀疏点,即对象o的ε-邻域是否稀疏,本文中使用参数Min Pts,作为稠密区域的密度阈值。如果一个对象o的ε-邻域密度M≥Min Pts,则o为一个稠密对象,如果一个对象o的ε-邻域密度M<Min Pts,则o为一个稀疏对象。一个类中的稀疏对象构成此类的种子样本集合(seeds)。
根据SMOTE算法思想,DS-SMOTE算法根据式(3)在种子样本与其近邻之间合成新样本:
| ${\rm{new}} \Rightarrow o + D\left( {{\rm{seed}}_i \left. {,o} \right)} \right. \times r$ | (3) |
式中:o为目标对象,D(seedi, o)为种子样本seedi与其近邻样本o之间的欧氏距离,r为随机数,且r∈(0, 1)。
DS-SMOTE算法的核心思想为:在SMOTE算法的基础上,在少数类中抽取种子样本集合后对其进行过采样。在算法中,我们对少数类中稀疏对象进行样本采集得到一个种子样本集合,产生种子集合的过程主要包括:计算少数类中样本的邻域半径、计算该类的密度阈值、产生稀疏对象集合作为种子样本集。DS-SMOTE算法产生的合成样本分布于稀疏对象及其近邻之间,最终得到与多数类样本数量相等的少数类样本集合。
DS-SMOTE算法
输入 训练集T, 原始样本集合中多数类S1 = {x1, x2,
1) 对于少数类集合S2, 在整个训练集T中对S2中的每一个样本yi计算其近邻。若其近邻类别都为多数类, 则认为yi为噪声, 且不会出现在下一步计算中;
2) 选择少数类集合S3, 执行ε= getE(S3)得到少数类邻域半径ε;
3) 求得邻域半径为ε时, 每个少数类样本的密度;
4) for j = 1, |min|
5) 令yi的ε-邻域密度=1;
6) for j = 1, |min|
7) 计算其他少数类样本与样本yi的欧式距离D;
8) if D<=ε
9) yi的ε-邻域密度+1;
10) endfor
11) endfor
12) endfor
13) 根据式(2), 求得密度阈值Min Pts;
14) for j = 1, |min|
15) if yi的ε-邻域密度≤密度阈值
16) yi为稀疏对象, 将yi加入种子样本集合;
17) endfor
18) endfor
19) 产生种子集合seed;
20) 产生随机数r;
21) 根据式(3)合成新样本, 得到样本集合new;
22) train = train∪new;
DS-SMOTE算法中,需要输入非平衡数据集合T,以及参数邻域半径ε、密度阈值Min Pts。首先在步骤1)中,排除少数类中的噪声产生新的少数类集合,S3;在步骤2)中,算法选取了少数类样本集合S3进行操作,根据密度的概念:对象o的ε-邻域密度是指对象o在ε-邻域内的对象数量,遍历每个少数类样本求得其ε-邻域的密度,并在步骤3)~12)中取少数类样本密度的均值作为判断少数类集合中样本是否稠密的密度阈值。
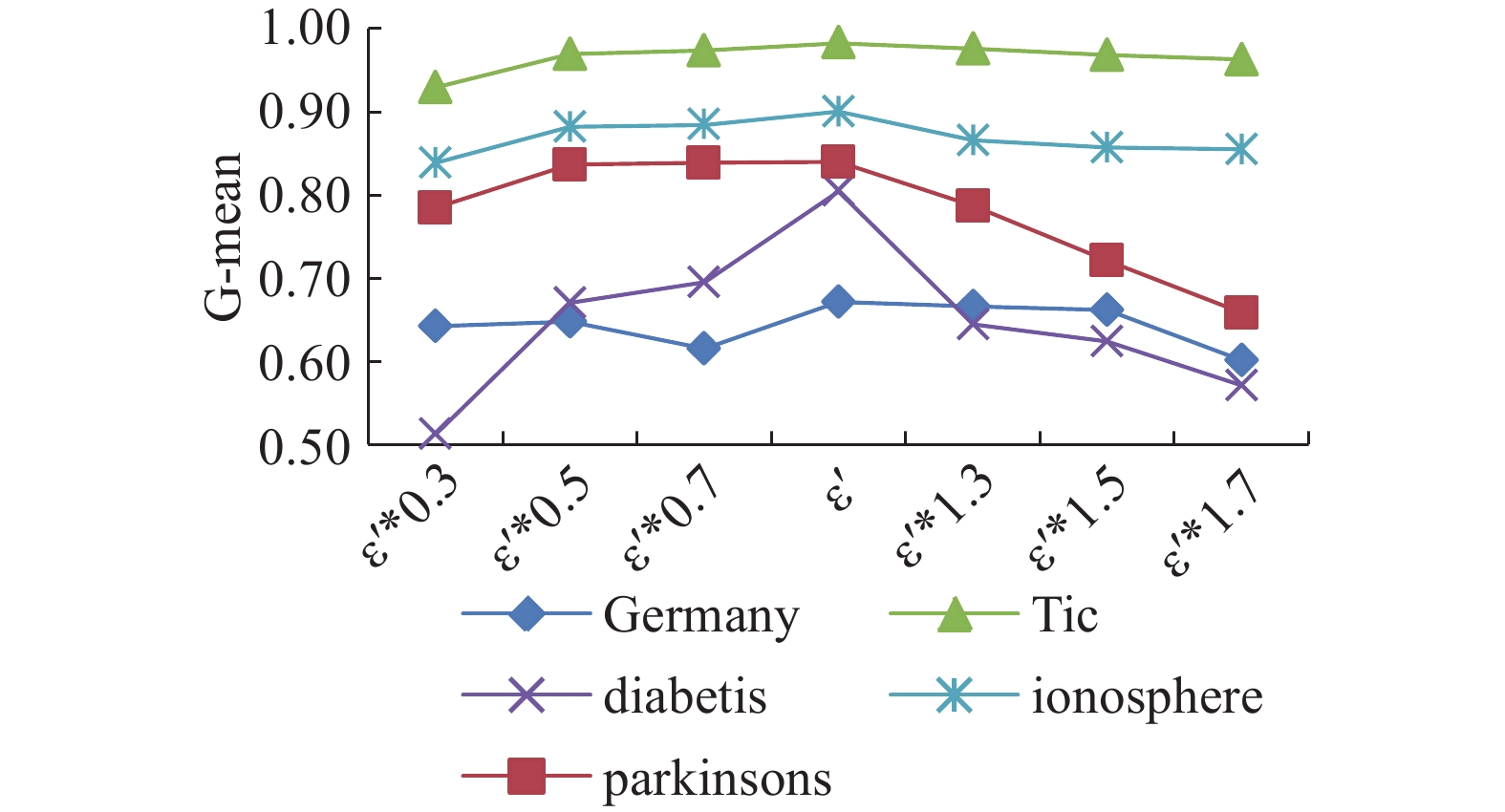
如何排除人工的方法,为少数类设置恰当的邻域半径是基于密度的分类算法中的一个亟待解决的问题。本文选择非平衡类分类中一般性的评估标准:F-value以及G-mean值进行评估,经实验分析,选择类内样本间平均距离作为邻域半径。表1与表2分别随机选取5个数据集进行实验分析,选取了邻近样本间平均距离ε′值的一系列大于零的点,如ε′*0.3、ε′*0.5、ε′*0.7以及ε′*1.3、ε′*1.5、ε′*1.7进行测试。经过测试,在图1与图2中可看出,结果呈现出一定的规律性:ε值的变化对不同的数据集的影响不尽相同,在ε值等于ε′或邻近取值时F-value以及G-mean值水平较高,随着取值向ε′的两侧远离,F-value以及G-mean值或保持平稳,或有所下降。说明选取类内样本间平均距离作为邻域半径具有一定的普适性,并且对分类器的分类性能有一定的保证。由于其脱离了人工选择的邻域半径设置方法,所以这种邻域半径的设置方法也提高了DS-SMOTE方法的可操作性。
在步骤14)~18)中,使用循环遍历的方式判断少数类样本的稀疏性,并将稀疏样本加入种子集合,作为在步骤21)中合成新样本的素材。在步骤21)中引用了直观、易操作的SMOTE算法的思想产生合成样本,一定程度上避免了随机过采样方法容易造成的分类器过拟合问题,最终在稀疏对象及其近邻之间合成新样本,达到少数类与多数类样本在数量上的一致。
| 表 1 不同邻域半径取值下的G-mean值 Tab.1 The G-mean under different neighborhood radius |
| 表 2 不同邻域半径取值下的F-value值 Tab.2 The F-value under different neighborhood radius |
|
图 1 不同邻域半径取值下的G-mean值 Fig.1 The G-mean under different neighborhood radius |

|
图 2 不同邻域半径取值下的F-value值 Fig.2 The F-value under different neighborhood radius |
一个分类器算法在二分类问题中的性能往往使用混淆矩阵来评估,分别将两类分为正类(positive)、负类(negative),如表3所示[17]。混淆矩阵的列用来表示类的预测结果,混淆矩阵的行用来表示类的实际类别[18]。其中,TN (true negative)表示负类样本中被划分正确的样本数,即真负类;TP(true positive)表示正类样本中被划分正确的样本数,即真正类;FN(false negative)表示负类样本中被划分错误的样本数,也就是负类中的样本被划分为正类的样本数,即假负类;FP(flase positive)表示正类样本中被划分错误的样本数,也就是正类中的样本被划分为负类的样本数,即假正类[19]。
| 表 3 二分类问题中的含混矩阵 Tab.3 The confusion matrix of 2-class problem |
准确率(Precision)和召回率(Recall)是分类性能的两个最基本的指标[20]。准确率(Precision)也称为查准率,召回率(Recall)也称为查全率,即正类(少数类)的分类准确率。定义为
| ${\rm{Precision = }}\frac{{{\rm{TP}}}}{{{\rm{TP + FP}}}}$ | (4) |
| ${\rm{TPR = Recall = }}\frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}$ | (5) |
F-value是准确率和召回率的调和平均,实验中令β值为1,即F1度量。定义如下:(式中β为调整准确率(Precision)和召回率(Recall)所占比重的参数,一般地令β=1)。
| ${\rm{F \text{-} value = }}\frac{{\left( {{\rm{1 + }}{\beta ^{\rm{2}}}} \right) \times {\rm{Recall}} \times {\rm{Precision}}}}{{{\beta ^{\rm{2}}}{\rm{ \times Recall + Precision}}}}$ | (6) |
在非平衡类分类问题中,G-mean值用来衡量分类器对于两类样本分类的平均性能[21],是对算法性能的总体评价。
| ${\rm{G \text{-} mean = }}\sqrt {{\rm{Recall}} \times {\rm{TNR}}} $ | (7) |
本文选用Recall(TPR)、TNR、Precision、F-value、G-mean等值作为实验过程中算法性能指标的度量。
2.2 实验数据为了测试文中实现的采样方法与同类方法对非平衡数据的分类效果,文中采用了11个UCI数据集进行实验和分析,如表4所示。非平衡数据中的非平衡度为正类与负类样本数量之比,实验中所选取的数据集分别具有不同的非平衡程度,正类的比例从0.097~0.629不等。这些数据集中的数据大多为数值型的两类样本数据,其中,statimage数据集中的样本有7个类别,为了构造极其不平衡的样本集合,人为将第4类样本作为少数类样本,其余样本合为一类作为多数类样本,从而得到一组非平衡度为0.097的两类数据样本;thyroid数据集中具备3类样本,通过将类别为2和3的样本合为一类,从而获得了一组非平衡度为0.194的两类数据样本。表4同时给出了各数据集的属性个数、总样本数量、正类样本数量、负类样本数量以及正负类样本数量的比值——非平衡度。
| 表 4 实验所用UCI数据集 Tab.4 The UCI datasets for experiments |
为了验证DS-SMOTE算法处理非平衡数据集的有效性,C4.5算法是具有代表性的决策树基准算法,在分类数据不平衡的情况下与同类分类器相比具有良好的分类性能,实验中采用了C4.5算法作为分类算法,并与SMOTE算法、Borderline-SMOTE算法进行了对比。本文采用了十折交叉验证方法进行实验测试,测试结果均为10次实验均值,并针对Recall(TPR)、TNR、Precision、F-value、G-mean等指标进行分析。
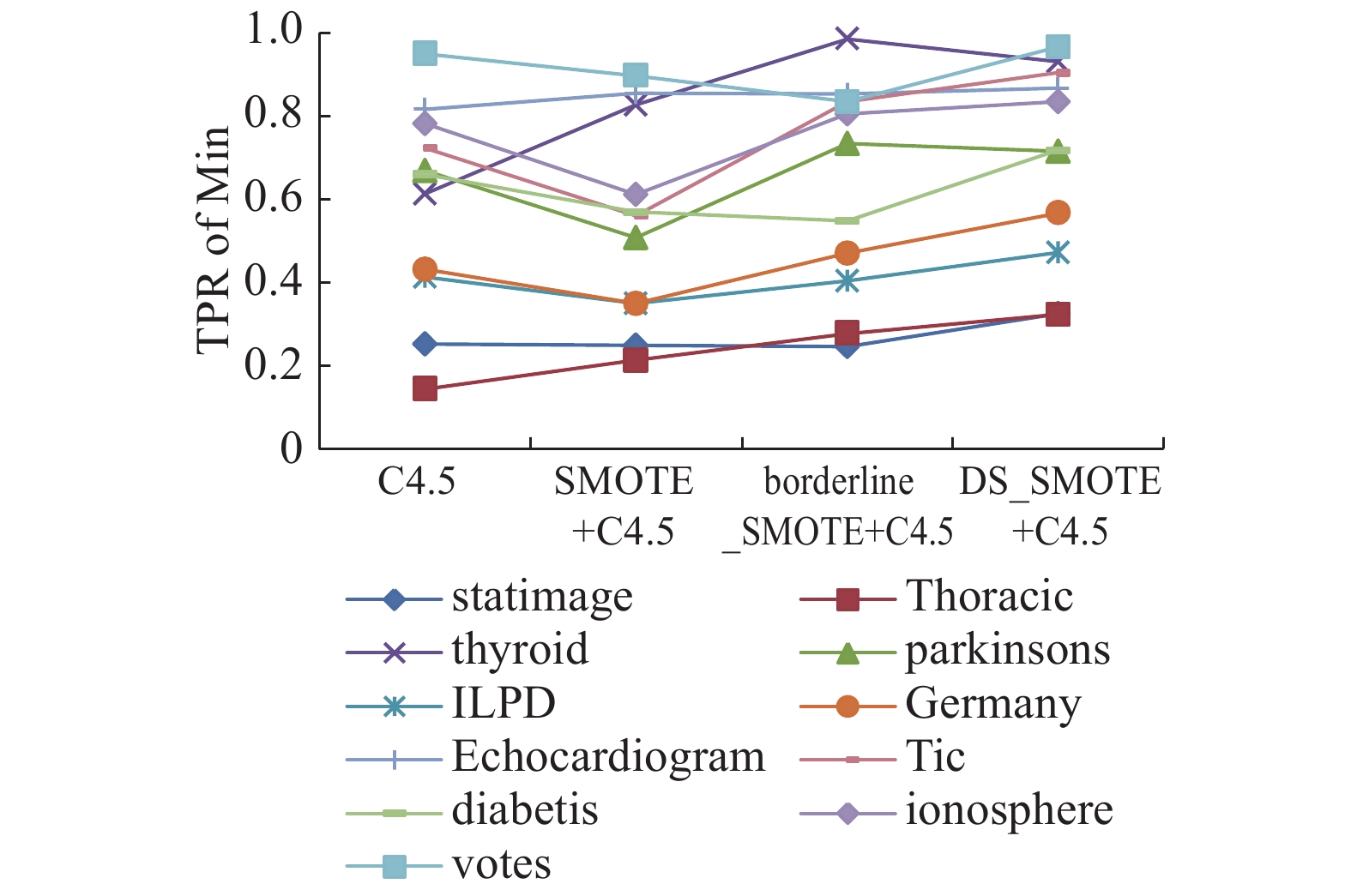
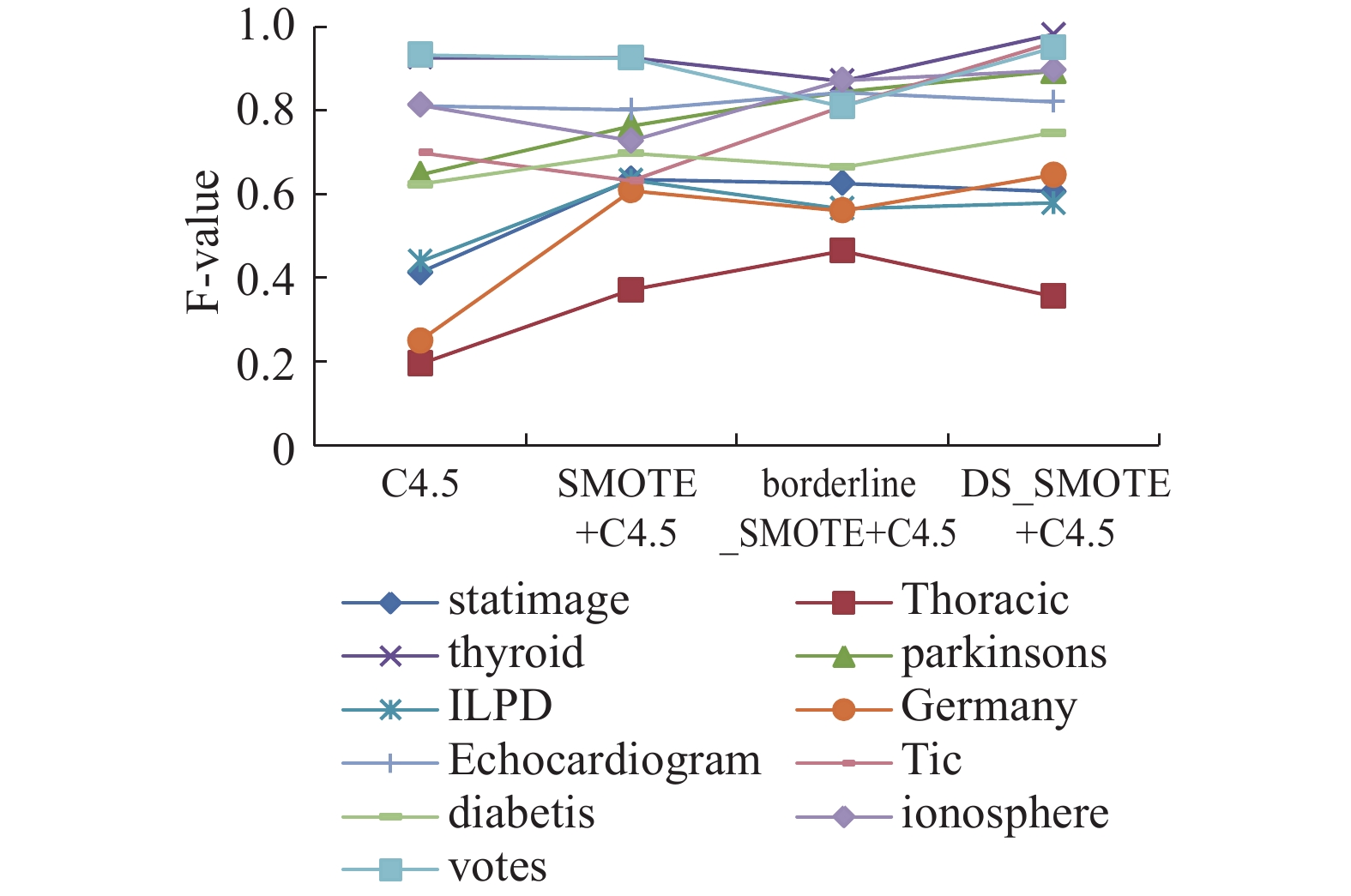
为了对比算法的优势,图3~7分别绘制了4种算法策略在11个数据集上的测试结果趋势曲线。其中,横坐标为4种算法策略,纵坐标取值在0~1之间,表中加粗的数据为一系列数据中的最大值。通过以下图表可以看出,使用DS-SMOTE方法进行过采样,少数类的分类性能有所上升。
|
图 3 少数类准确率变化曲线图 Fig.3 The variation curve for TPR of min |
|
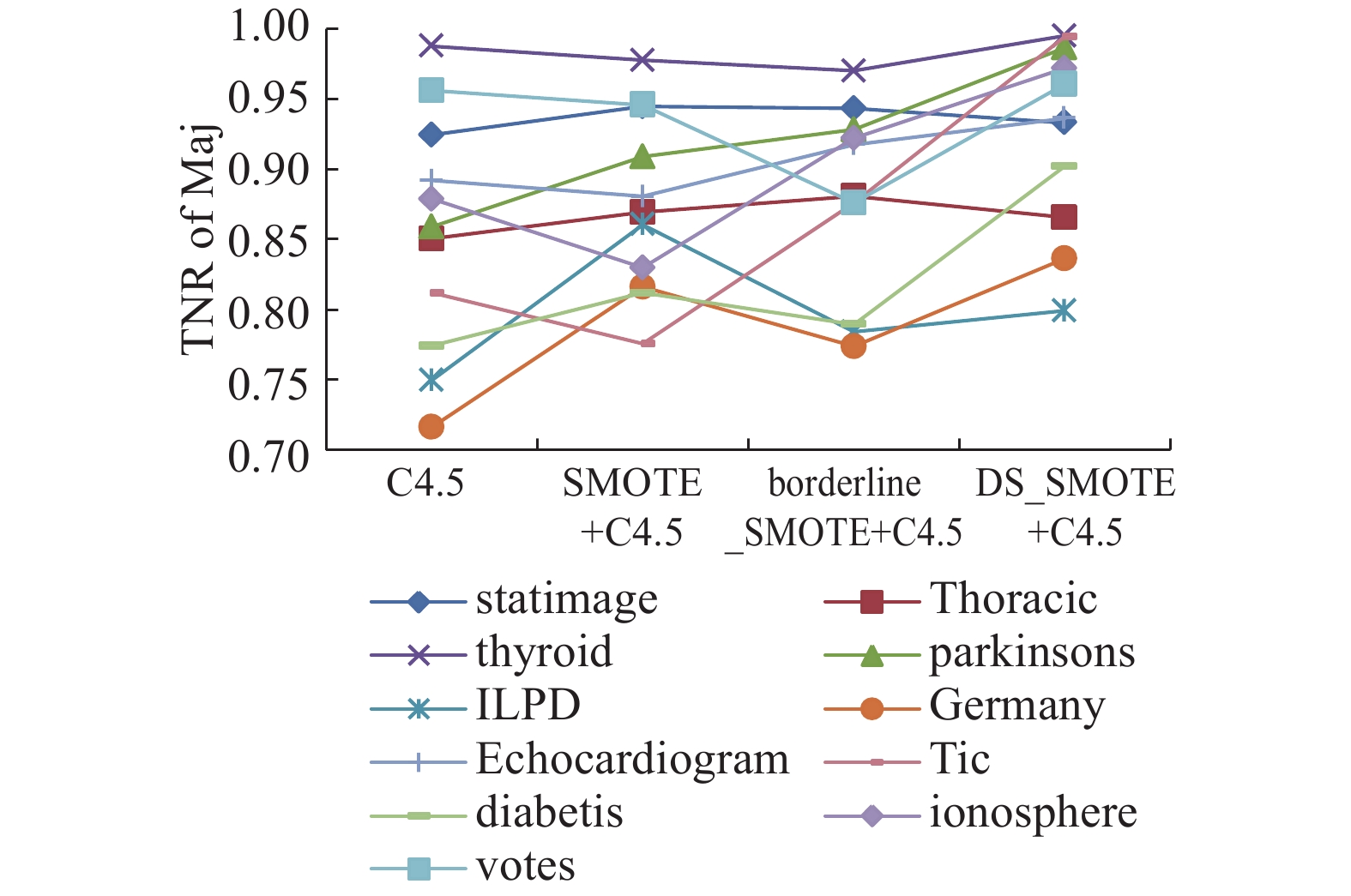
图 4 多数类准确率变化曲线图 Fig.4 The variation curve for TNR of major |
|
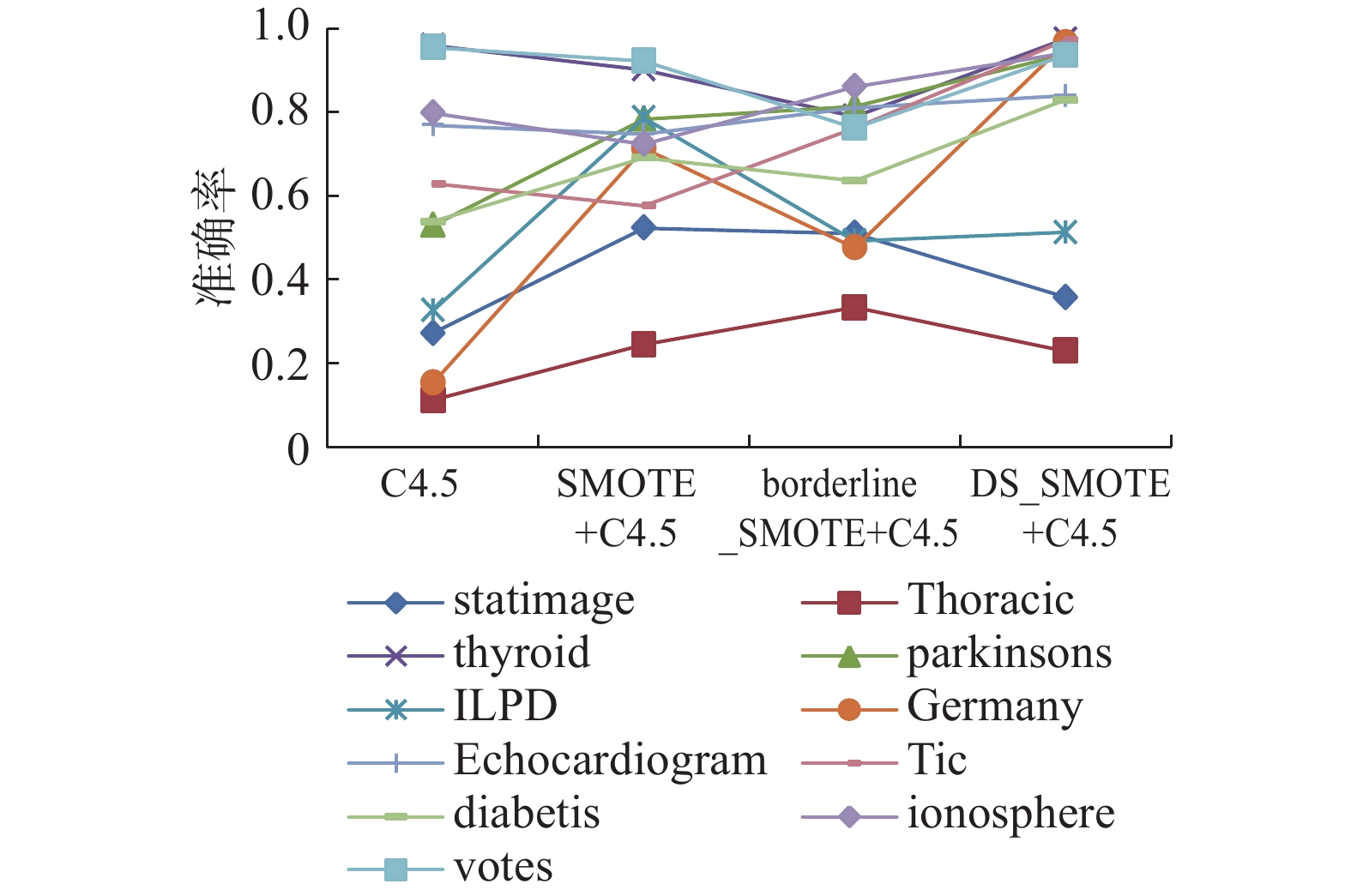
图 5 准确率变化曲线图 Fig.5 The variation curve of precision |
在表5中,大部分数据集在DS-SMOTE算法处理后分类的TNR值大于使用SMOTE算法与Borderline-SMOTE算法,对于少数类样本绝对稀少、非平衡程度较大的数据集statimage 、thyroid和parkinsons分类效果较差,表明在处理少数类绝对稀少的非平衡类分类问题中,DS-SMOTE算法仍有待改进;表6中多数类样本的分类精度保持较高,可见DS-SMOTE算法在保证多数类分类准确率的前提下对少数类的分类准确率有一定程度的改善;在表7和8中可以观察到,DS-SMOTE没有消除在两类的极端不平衡时对Precision、F-value值的影响;G-mean值作为非平衡数据整体分类性能的评价指标,往往能够指示一个方法在非平衡数据集的分类性能好坏,表9显示出DS-SMOTE算法在大部分的数据集上的G-mean值有显著的优势,说明本文提出的算法在这些数据集上有较好的总体分类性能。
|
图 6 F-value变化曲线图 Fig.6 The variation curve of F-value |

|
图 7 G-mean变化曲线图 Fig.7 The variation curve of G-mean |
实验结果表明本文提出的算法在少数类信息不足的情况下,分类效果有一定程度的改进,能够在不降低多数类分类精度的同时,保证分类器对少数类的识别,并具有良好的适应性。
| 表 5 少数类准确率 Tab.5 The TPR of min |
| 表 6 多数类准确率 Tab.6 The TNR of Major |
| 表 7 准确率 Tab.7 Precision |
| 表 8 F-value Tab.8 F-value |
| 表 9 G-mean Tab.9 G-mean |
基于数据采样的方法是解决非平衡数据分类问题的一个重要途径,本文在SMOTE算法的基础上,结合密度的概念,提出了基于密度的过采样方法,以提高非平衡数据分类的准确率。实验结果表明,本文的方法在处理非平衡数据分类问题上具有良好的效果。另外,在本文中使用类内样本间平均距离作为邻域半径,通过实验证明,这种取值方法避免了人工取值的难题,具有普适性和可操作性,也使得分类器的分类性能得到了一定的保证。但是,如何通过自适应方法产生类的邻域半径,是本文进一步的研究方向。
| [1] |
CHARTE F, RIVERA A J, JESUS M J D, et al. Addressing imbalance in multilabel classification: Measures and random resampling algorithms[J]. Neurocomputing, 2015, 163: 3-16. ( 0) 0)
|
| [2] |
RADIVOJAC P, CHAWLA N V, DUNKER A K, et al. Classification and knowledge discovery in protein databases[J]. Journal of biomedical informatics, 2004, 37(4): 224-239. ( 0) 0)
|
| [3] |
LIU Y, CHAWLA N V, HARPER M P, et al. A study in machine learning from imbalanced data for sentence boundary detection in speech[J]. Computer speech and language, 2006, 20(4): 468-494. ( 0) 0)
|
| [4] |
KUBAT M, HOLTE R C, MATWIN S. Machine learning for the detection of oil spills in satellite radar images[J]. Machine learning, 1998, 30(2): 195-215. ( 0) 0)
|
| [5] |
QIAN H, HE G. A survey of class-imbalanced data classification[J]. Computer engineering and science, 2010, 5: 025. ( 0) 0)
|
| [6] |
翟云, 王树鹏, 马楠. 基于单边选择链和样本分布密度融合机制的非平衡数据挖掘方法[J]. 电子学报, 2014, 42(7): 1311-1319. ZHAI Yun, WANG Shupeng, MA Nan, et al. A data mining method for imbalanced datasets based on one-side link and distribution density of instances[J]. Chinise journal of electronics, 2014, 42(7): 1311-1319. (  0) 0)
|
| [7] |
CHARTE F, RIVERA A J, JESUS M J D, et al. Addressing imbalance in multilabel classification: Measures and random resampling algorithms[J]. Neurocomputing, 2015, 163: 3-16. ( 0) 0)
|
| [8] |
GONG C, GU L. A novel smote-based classification approach to online data imbalance problem[J]. Mathematical problems in engineering, 2016, 35: 1-14. ( 0) 0)
|
| [9] |
BIAN J, PENG X G, WANG Y, et al. An efficient cost-sensitive feature selection using chaos genetic algorithm for class imbalance problem[J]. Mathematical problems in engineering, 2016, 6: 1-9. ( 0) 0)
|
| [10] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16(1): 321-357. ( 0) 0)
|
| [11] |
杨智明, 乔立岩, 彭喜元. 基于改进SMOTE的不平衡数据挖掘方法研究[J]. 电子学报, 2007, 35(B12): 22-26. YANG Zhimin, QIAO Liyan, PENG Xiyuan. Research on datamining method for imbalanced dataset based on improved SMOTE[J]. Chinese journal of electronics, 2007, 35(B12): 22-26. (  0) 0)
|
| [12] |
HAN H, WANG W Y, MAO B H. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[C]//International Conference on Intelligent Computing. Springer Berlin Heidelberg, 2005, 3644(5): 878-887.
( 0) 0)
|
| [13] |
HE H, BAI Y, GARCIA E A, et al. ADASYN: Adaptive synthetic sampling approach for imbalanced learning[C]//IEEE International Joint Conference on Neural Networks. IEEE Xplore, 2008: 1322-1328.
( 0) 0)
|
| [14] |
GRZYMALA-BUSSE J W, STEFANOWSKI J, WILK S. A comparison of two approaches to data mining from imbalanced data[J]. Journal of intelligent manufacturing, 2005, 16(6): 565-573. ( 0) 0)
|
| [15] |
EZ J, KRAWCZYK B, NIAK M. Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets[J]. Pattern recognition, 2016, 57(C): 164-178. ( 0) 0)
|
| [16] |
NANNI L, FANTOZZI C, LAZZARINI N. Coupling different methods for overcoming the class imbalance problem[J]. Neurocomputing, 2015, 158(C): 48-61. ( 0) 0)
|
| [17] |
NAGANJANEYULU S, KUPPA M R. A novel framework for class imbalance learning using intelligent under-sampling[J]. Progress in artificial intelligence, 2013, 2(1): 73-84. ( 0) 0)
|
| [18] |
ZHANG X, SONG Q, WANG G, et al. A dissimilarity-based imbalance data classification algorithm[J]. Applied intelligence, 2015, 42(3): 544-565. ( 0) 0)
|
| [19] |
JIANG K, LU J, XIA K. A novel algorithm for imbalance data classification based on genetic algorithm improved SMOTE[J]. Arabian journal for science and engineering, 2016, 41(8): 3255-3266. ( 0) 0)
|
| [20] |
XU Y, YANG Z, ZHANG Y, et al. A maximum margin and minimum volume hyper-spheres machine with pinball loss for imbalanced data classification[J]. Knowledge-based systems, 2016, 95: 75-85. ( 0) 0)
|
| [21] |
ANWAR N, JONES G, GANESH S. Measurement of data complexity for classification problems with unbalanced data[J]. Statistical analysis and data mining the asa data science journal, 2014, 7(3): 194-211. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


