2. 中国中医科学院 中医临床基础医学研究所,北京 100700;
3. 中国中医科学院 中医药数据中心,北京 100700;
4. 上海金灯台信息科技有限公司,上海 201800
2. Institute of Basic Research in Clinical Medicine of Traditional Chinese Medicine, China Academy of Chinese Medical Science, Beijing 100700, China;
3. National Data Center of Traditional Chinese Medicine, China Academy of Chinese Medical Science, Beijing 100700, China;
4. Shanghai Menorah Information Technology Co. Ltd, Shanghai 201800, China
数据挖掘在中医辅助诊断中受到日益重视,而计算机辅助诊断本质上是一个数据挖掘分类任务[1],分类性能的好坏直接影响到了辅助诊断的能力。在现实生活中,经常出现不均衡数据。例如在医学中的医疗诊断问题,患有某种病的个体往往是少数的;机械方面的故障检测[2]中有研究表明,在旋转机械中齿轮故障占其故障的10%左右。类似的问题也存在于图像检测、通信领域客户流失预测[3]等领域中。对于不均衡数据分类,传统的数据挖掘分类方法上往往倾向于多数类(较多的一类数据),而对于少数类(较少的一类数据)的分类效果较差。但在实际生活中,人们更加关注少数类的分类情况。例如对中医临床数据进行的疾病分类过程中,人们更加关注有病个体的分类情况。少数类的分类性能直接影响到了计算机的辅助诊断能力,同时也关系到医生的诊断效率。在不均衡数据的分类中,少数类错分为多数类的代价远远高于多数类错分为少数类的代价,一些“偏爱”多数类的传统分类方法就不再适用。
不均衡数据引起了人们的重视。近年来,针对不均衡数据分类提出了很多算法,已有的算法主要是从数据集的层面、分类器层面以及分类器和数据相结合的这3种方式[4]来处理使不均衡数据分类。数据集的层面主要有欠采样和过采样,但是这两种方法并没有针对数据的实际特点,因此分类效果有待进一步提高。在中医临床的不均衡数据中,如果仅仅使用欠采样,可能会丢失很多有重要信息的数据;使用过采样简单复制又会出现过于拟合的现象。中医临床数据很多特征来自于人体相关参数的测量,但是对于某类疾病,某些特征是不相关的或者是冗余的,甚至某些特征会影响分类器的性能[5]。实际上对于某类疾病而言,有些特征没有包含或者包含极少的疾病状态信息,它们对分类结果几乎没有影响,因此需要使用特征选择移除冗余特征[6]。
本文结合中医临床不均衡数据的实际情况,在已有研究的基础上结合欠采样和特征选择提出了不均衡的装袋算法(asymmetric bagging, AB)[12]的改进算法,基于预测风险的最远病例不均衡装袋算法(prediction risk based feature selection for FPUSAB, PRFS-FPUSAB)来处理不均衡分类问题和特征选择问题。
1 不均衡数据分类性能评价传统分类的性能评价是从分类器的整体分类情况来考虑,即考虑所有样本的分类精度。缺乏类别的针对性,特别是比较受关注的少数类。在不均衡数据中,少数类样本更容易错分并且所占比例不大,所以对少数类的误分在总体分类性能上指标变化也不大。如果以准确度作为衡量指标,往往可能具有欺骗性,并且对数据的变化很敏感。例如,一个数据集中只有10%的少数类样本,有90%的多数类样本。一个最简单的分类方法就是将所有少数类均分类为多数类,那么可以得到90%的准确度。虽然表面来看,准确度值很高,但是实际上此分类方法是失败的,因为少数类未得到正确分类。因此准确度作为性能评价指标不能全面体现分类算法的分类能力。
针对传统的性能指标存在的缺陷,很多学者在研究不均衡数据分类时使用以下几个性能指标。表1为二类分类混淆矩阵,TP、FP、FN、TN分别代表真正、真负、假正、假负。
| 表 1 二类分类混淆矩阵 Tab.1 Confusion matrix |
表1中将少数类称为正性或者阳性,多数类称为负性或者阴性,第1行与第2行分别表示实际的少数类和多数类数量。TN与TP分别表示分类后被正确分类的多数类和少数类。FP表示实际是少数类而被误分为多数类的数量,FN表示实际为多数类而被误分为少数类的数量。根据表1中内容,相关定义如下。
灵敏度(Sensitivity):亦称真阳性率(TPR)、召回率(Recall),表示所有正类样本中被正确分类的样本比例,可用来衡量对正类样本的分类能力,计算如式(1),即
| ${\rm{Sensitivity}} = \frac{\rm{TP}}{{\rm{TP}} + {\rm{FN}}}$ | (1) |
特异度(Specificity):亦称真阴性率,与真阳性率相对,它表示所有负类样本中被正确分类的样本比例,可用来衡量对负类样本的分类能力,计算如式(2),即
| $\rm{Specificity} = \frac{\rm{TN}}{\rm{TN + FP}}$ | (2) |
平均准确度(balanced accuracy):
| ${\rm{Bacc}} = \frac{1}{2}\left( {\frac{\rm{TP}}{\rm{TP + TN}} + \frac{\rm{TN}}{\rm{TN + FP}}} \right)$ | (3) |
阳性预测值PPV(positive predictive value):
| $\rm{PPV} = \frac{\rm{TP}}{\rm{TP + FP}}$ | (4) |
阴性预测值NPV(negative predictive value):
| $\rm{NPV} = \frac{\rm{TN}}{\rm{TN + FP}}$ | (5) |
整个数据集被正确分类的正确率Correction:
| $\rm{Correction} = \frac{\rm{TP + TN}}{\rm{TP + TN + FP + FN}}$ | (6) |
以上几个分类指标虽然在一定程度上能够比较准确地衡量模型的性能,但是在更一般的分类问题中它们仍然是有局限性。为了解决这个问题,人们从医疗分析领域引入了一种新的模型性能评判方法:受试者工作特征曲线分析(receiver operating characteristic,ROC)[7],ROC分析的主要内容是二维平面上的ROC曲线,平面以false positive rate(FPR)为横坐标,以true positive rate(TPR)为纵坐标。对于某个分类器,可以基于其在测试样本上的TPR和FPR性能来获得二维点。以这种方式,分类器可以映射到ROC平面上的点。调整此分类器使用的阈值以获取多个不同的点,连接这些点最终可以得到一个经过(0,0),(1,1)的曲线,这就是此分类器的ROC曲线。引入ROC后,衡量不同分类算法的性能可以用曲线下面积(area under the curve, AUC)作为评价指标,AUC就是处于ROC曲线下方的那部分面积的大小。面积越大,模型分类性能越强,模型性能越好,ROC曲线越接近左上角。
2 数据层面解决不均衡数据分类方法从数据出发,在对数据集进行重构的过程中使用某种机制来获得更均衡的数据分布,这种方式称为重采样,其实质相当于一种预处理数据均衡化方法。研究者先后提出多种采样技术,归纳起来可分为3种:欠采样、过采样、基于前二者的混合采样[8]。
欠采样是从原数据集中移除一些多数类样本,以实现类别样本数目相同。最基本的随机欠采样是随机地从原始数据集中移除多数类样本,缩小多数类的规模,以实现具有和少数类样本数量相同。但该方法在将多数类样本删除的同时有可能会丢失具有代表性意义的样本信息,造成信息丢失影响分类效果。而过采样是使用某种机制来往原始数据集添加样本,使得多数类和少数类均衡分布。最基本的随机过采样通过随机复制少数类样本使数据均衡分布,由于只是简单地将少数类复制后添加到原始数据集中,会出现很多“重复”样本,进而出现过于拟合现象[9]。
赵自翔等[10]指出了欠采样和过采样的优缺点并基于欠采样提出了一种新的采样方式并取得了较好的效果,但是这种采样方式主要是尽量往均衡靠近,没有从根本上解决不均衡。同时针对已有采样方式的问题,已有的研究尝试将欠采样与过采样相结合。例如朱明等[11]提出了RU-SMOTE-SVM算法,该算法结合了随机欠采样方法和人工合成少数类样本的SMOTE算法;李等[12]结合混合抽样策略和Bagging提出了不均衡装袋算法,在生物信息学上的不均衡数据分类上取得了较好的效果。
中医临床数据采集的是来自病人身体体征相关的实际数据,由于对合成样本的真实性的质疑,所以中医临床数据较少使用SMOTE人工合成少数类样本的方法进行疾病分类。在欠采样和过采样在对不均衡数据分类的效果上,DRUMMOND等[13]为欠采样在性能上优于过采样。
3 PRFS-FPUSAB算法在中医临床数据中,每一个样本都是个体的生命体征数据,当把它们放到样本空间时,每一个样本就是样本空间的一个样本点。在随机欠采样过程中,如果保留某一个有限区域中的样本点时,可能有大量的有价值样本点被丢弃;如果随机选取的样本都集中在某一个区域,那么会造成过于拟合的现象。对应实际情景:如果在选取病人病例时选取了很多具有同样特征且未患病的人,那么根据他们的情况来判断其他不具有这些特征的人的患病情况时,往往不会得到想要的结果,或者判断趋于随机。如果能在样本的每一区域均保留一定量的样本,则能够预防最坏的“失真”情况发生。对于某一区域样本来讲,它们到一个定点的距离应该是相差不大的。对应的临床实际:在一个具有相似特征的病人群体中选取具有一个来代表这个群体,每一个群体选取一个,那么遇到新病患的时候,我们判断的依据就多了,就能够更有效地对疾病进行分类。
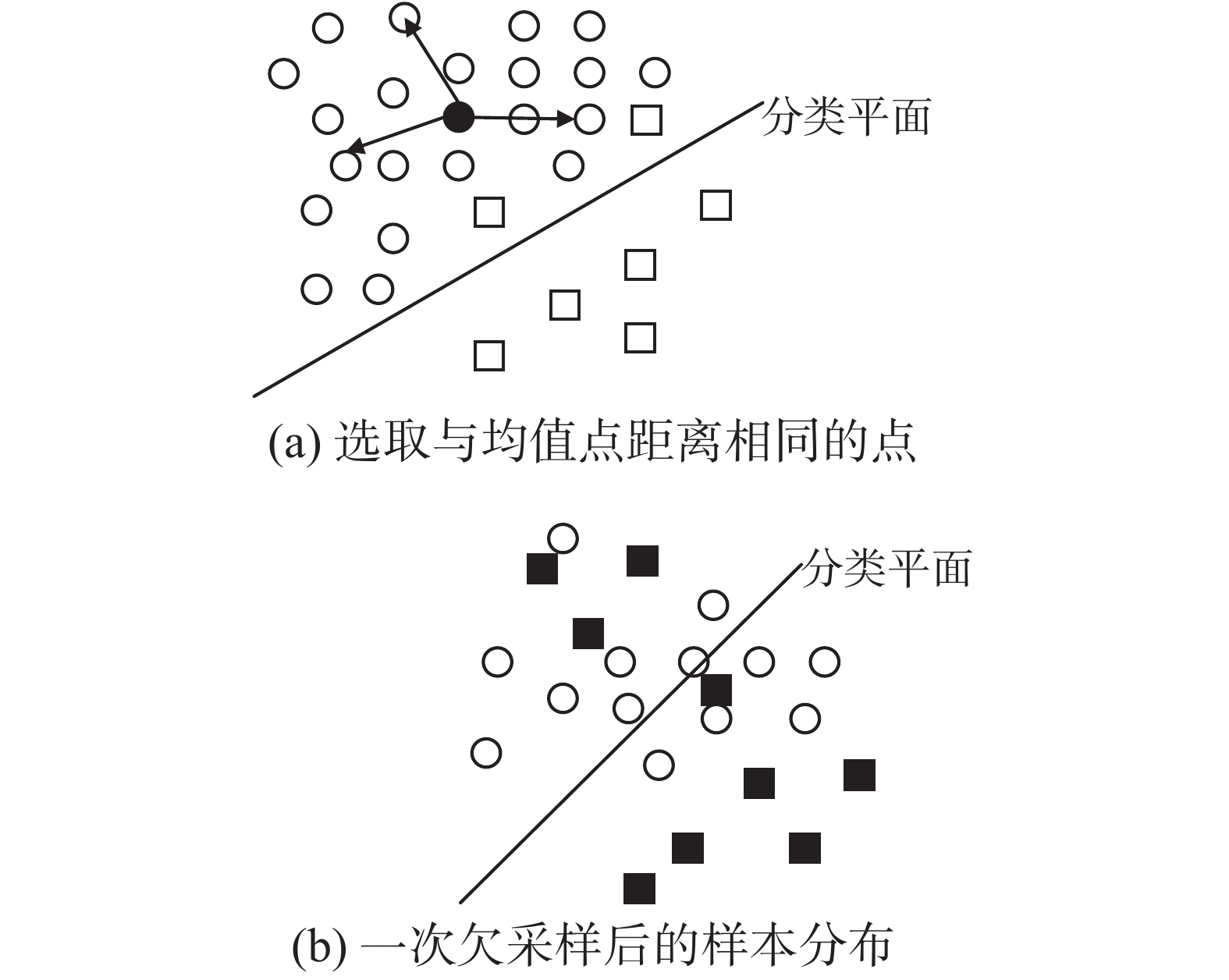
因此,为了在一次欠采样过程中尽可能保持多数类样本本来的类别特点,采用如下的方法:如图1(a)中黑色圆点为多数类样本的均值点,计算所有多数类样本与该均值点的距离,在距离相近的每个小区域中,保留一个点而去掉余下的点,并将保留下的所有多数类样本作为新的多数类样本集和原有的正类样本一起组成新训练集,如图1(b)所示。
|
图 1 最远病例抽样方式 Fig.1 Furthest patient sampling method |
传统的分类算法在均衡的数据集上具有很好的效果。不均衡的装袋算法(asymmetric bagging, AB)算法基于均衡的思想运用随机欠采样,每次从多数类中随机选取与少数类等量的样本,再将这部分样本和少数类合并在一起构成新的数据集,然后反复多次构成多个训练子集。基于在均衡数据的分类中SVM取得了比较好的分类效果[14],AB算法将构成的新的若干个均衡数据集交由SVM进行训练,最后由训练成的若干个模型集成决策获得测试样本的分类结果。但是AB使用的是随机欠采样,就不能避免出现“失真”情况。
3.1 Asymmetric Bagging算法输入 测试数据集(Training data set Sr), 子集的特征数F;
输出 集成的模型。
1) 数据的预处理。删除缺失比较严重的数据,并对缺失较少的数据进行填充。
2) 将Training data set分为有病的数据子集
3) 根据循环抽样的次数,产生训练小模型:
FOR i = 1 to M
① 从
② 用SVM的方法训练Sk并计算这个子集的fauc。
FOR j = 1 to F
③ 使用SVM分类器训练较小的子集Sk得到模型NK。
End for
4)集成获得的模型NK,通过最大投票法来决定分类问题。
中医临床数据症状的模糊性的一个重要表现是中医临床数据的特征繁多,可能会出现多个特征用于记录同一症状,或者某些特征数据与疾病是不相关的,甚至某些特征会影响分类器的性能[5]。这些情况会带来干扰,降低分类性能。由于中医临床数据中存在着这些问题结合数据挖掘,在针对某类疾病进行分类研究时,需要特征选择去除不相关特征和冗余特征,力求以最少的特征来表达原始信息,并达到最优的预测或分类精度。特征选择对应现实意义相当于中医辨证论治过程中讲究的抓主症。在中医临床诊断过程中,抓主症需要医生具有丰富的经验,而这些经验需要经过很长的时间才能培养起来。如果能通过使用特征选择来辅助医师进行抓主症,那么对于推动中医的发展具有非常重要的意义。
在已有研究[15]的基础上,使用预测风险标准来处理中医临床不均衡数据疾病分类特征选择的问题。PRFS(prediction risk based feature selection)是一种以prediction risk为特征重要性评价准则的特征选择算法。评价准则prediction risk由Moody和Utans[16]首先提出,通过计算数据中某个特征在所有样本上的取值都替换成均值后评价指标的变化,来评价该特征的价值。由于所分类的数据是不均衡数据,结合不均衡分类数据评价指标,基于不均衡数据的预测风险标准相应的公式为
| ${x_i} = {f_{{\rm{auc}}}} - {f_{{\rm{auc}}}}\left( i \right)$ | (7) |
式中:fauc是应用整个训练集分类计算出来的曲线下面积,fauc(i)是当训练集第i个特征用它的平均值替换后计算出来的曲线下面积。如果第i个特征引起的面积变化是最小的,那么第i个特征将会被删除。
结合上面叙述基于欠采样的数据采样方法,Bagging算法、SVM提出了AB的改进算法基于预测风险的最远病例不均衡装袋算法(全称PRFS-FPUSAB)。在PRFS-FPUSAB算法中,首先通过计算多数类样本的中心点(多数类样本均值点),然后计算多数类中所有样本和中心点的距离,根据距离从大到小排列多数类样本。再根据设定的Bagging中的袋数bagnumber、少数类样本数量,从已按照距离从大到小排列的数据集中移出多数类样本,构成bagnumber个小的数据子集。在每次生成数据子集后,首先使用预测风险标准进行特征选择,然后将经过特征选择后的数据交由SVM进行训练,待所有数据子集训练完成后构成若干个小的模型,最后对测试集分类的结果由这些小模型投票决定。在对数据子集进行特征选择的过程中,仍然使用SVM分类器计算fauc(i),然后使用式对特征i进行判断是否保留,如果不满足条件,移除特征i。同时记录对于每次选择的特征,这部分在算法中没有说明。
3.2 PRFS-FPUSAB算法输入 测试数据集(Training data set Sr), 循环抽样次数(number of circles M), 子集的特征数F。
输出 集成的模型。
1) 数据的预处理。删除缺失比较严重的数据,并对缺失较少的数据进行填充。
2) 将Training data set分为有病的数据子集
3) 计算无病的病例
4) 根据距离按照从大到小对病例的顺序并
5) 根据循环抽样的次数,产生训练小模型:
6) 判断M是否大于Countne%Countne,如果大于则终止程序。
FOR i = 1 to M
FOR j = 1 to Countpo
① 置count为0;
② 如果count% M=0,则从
③ 从
End for
④ 将
FOR i = 1 to F
⑤ 用SVM方法训练St并计算这个子集的fauc。将训练子集中第i个特征值置为平均值,计算fauc(i),根据式(7)计算预测风险Pj,如果Pj大于0,就选中第j个特征。
End for
⑥ 根据训练St选中的特征子集构成较小的子集Srt,同时记录所选择的特征。
⑦ 使用SVM分类器训练较小的子集Srt得到模型Nk。
End for
7) 集成获得的模型Nk,通过最大投票法来决定分类问题。
在PRFS-FPUSAB算法中,由于在一个群体中选取一个并且选取的样本只出现一次,因此对集成模型的规模也有限制,集成规模bagnumber最多不能超过不均衡程度Ratio(多数类数量和少数类数量之比)。
4 数据集来源与预处理实验采用临床采集的经络电阻值数据,共3 053例样本。本文中选取其中的原穴经络电阻数据,数据包含左右各十二原穴、性别、身高、体重、年龄等28个特征。
在采集的3 053例样本中,不同类别疾病数据缺失情况不同,如表2。在删除严重缺失的数据并对不严重的数据并填充后,我们发现对于健康与亚健康类疾病较为完整样本534例,其中健康类数据439例,亚健康类数据95例;对于睡眠情绪类疾病剩余2 214例样本,睡眠情绪类疾病具体有睡眠障碍、焦虑症、抑郁症3种亚型。在使用数据进行实验时,我们对数据集的样本类别作了一些归并,全部归并为为二类问题。其中患有睡眠情绪类疾病206例,未患睡眠情绪类疾病数2 008例。需要注意的是,传统中医并没有亚健康这个概念,也没有归纳出睡眠情绪类疾病这个病种。亚健康、睡眠情绪类疾病都是西医的诊断。我们的研究工作基础是结合中医的临床数据对于西医的疾病进行分类。
| 表 2 实验所用数据集信息 Tab.2 The dataset for the experiment |
针对收集的中医临床数据可以发现健康与亚健康数据中健康个体超过了亚健康个体,在睡眠情绪类疾病未患病人数远超过患病人数,而在临床过程中往往更加关注少数类个体。在针对收集的中医临床数据可以发现健康与亚健康数据中健康个体超过了亚健康个体,在睡眠情绪类疾病未患病人数远超过患病人数,而在临床过程中往往更加关注少数类个体。在需要注意的是,传统中医并没有亚健康这个概念,也没有归纳出睡眠情绪类疾病这个病种。亚健康、睡眠情绪类疾病都是西医的诊断。我们的研究工作基础是结合中医的临床数据对于西医的疾病进行分类。
5 实验结果与分析为了分析算法性能,采用多种方法进行实验分析。在传统的分类算法上,选择具有代表性的decision tree(J48)、Naive Bayes、SVM、Bagging;在已有的不均衡数据分类算法中,选择不均衡的支持向量机(unbalanced SVM,unSVM)、基于不均衡的支持向量Bagging(Bagging based on unbalanced SVM,unBagging)、Asymmetric Bagging算法,使用上述7种方法同PRFS-FPUSAB算法进行比较。所有的实验使用10-fold交叉验证去评估AUC以及相关的性能,为了排除随机性,每次实验重复10次。其中decision tree(J48)、Naive Bayes、Bagging使用JAVA语言调用Weka[17]相关的分类器;SVM、unSVM、unBagging、Asymmetric Bagging使用JAVA语言调用LibSVM[18],相关程序都基于JAVA语言实现。在试验中为了便于比较使用算法的性能Bagging、Asymmetric Bagging、PRFS-FPUSAB、SVM使用相同的参数设置。在实验中其他方法的参数使用默认的参数设置。实验主要是测试PRFS-FPUSAB算法能否提高AUC、Bacc以及通过特征选择的特征是否符合中医学相关理论。由于PRFS-FPUSAB算法对装袋的数量有所限制,为了比较在Bagging、unBagging、AB、PRFS-FPUSAB算法袋数的设置上为1。分类结果如表3、表4所示,表中health表示亚健康类疾病、sleep表示睡眠情绪类疾病。
| 表 3 中医临床亚健康类疾病不均衡数据分类结果 Tab.3 Sub -health disease imbalance data classification results |
| 表 4 中医临床睡眠情绪类疾病不均衡数据疾病分类结果 Tab.4 Sleep disorders disease disequilibrium data disease classification results |
从表3、表4中可以看出传统的分类算法J48、Naive Bayes、SVM对于不均衡数据的分类效果较差;相比较而言,AB、PRFS-FPUSAB对于不均衡数据分类较好;unSVM并没有有效的改善的SVM的性能,unBagging相较于Bagging只是很小的改善了性能;Bagging算法的效果也比较差。
就主要分类指标AUC、Bacc而言,PRFS-FPUSAB算法优于其他算法。在decision tree(J48)、Naive Bayes、SVM、Bagging这几个方法中,Naive Bayes对于不均衡数据分类有一个比较好的效果。虽然Naive Bayes在AUC方面和AB算法相差不大,但是在Bacc方面明显Asymmetric Bagging算法优于Naive Bayes。为什么Naive Bayes在AUC方面和AB算法相差不大呢,主要原因是在比较实验中,我们只装了一袋,也就是说实际上只是从多数类中随机选择了和少数类相同数量的样本放在一起和少数类构成新的训练集,然后交给SVM进行训练。由于这里只训练出了一个模型,所以分类效果会差一些。同时可以看出即使只建立了一个模型,FPUSAB算法也是优于AB算法的。那么装的袋数会对分类的效果造成一个什么样的影响呢?如果装的袋数多了,AB算法是否会优于PRFS-FPUSAB算法呢?继续用实验探讨。
从图2中可以看出,随着集成模型的增加,AUC、Bacc出现增长趋势,由于Bagging、unBagging采用的是随机欠采样,所以随着集成规模的增加出现振荡性的变化;而AB的效果要比PRFS-FPUSAB的效果要差。当N大于3,AB下降幅度要比PRFS-FPUSAB大,说明PRFS-FPUSAB稳定性要优于AB。当N为3时,PRFS-FPUSAB、AB效果最好。PRFS-FPUSAB算法AUC约为0.80,Bacc约为0.73;AB算法AUC约为0.67,Bacc约为0.64。

|
图 2 亚健康类疾病分类结果 Fig.2 Sub-health classification results |

|
图 3 睡眠情绪类疾病分类结果 Fig.3 Sub-health classification results |
从图3中可以看出,对于睡眠情绪类疾病不均衡数据分类AUC、Bacc结果随着集成模型数量出现不同变化趋势。由于采样的随机性Bagging、unBagging出现振荡性的变化;而对于AB、PRFS-FPUSAB当N小于5时,AB存在着一个振荡的变化,PRFS-FPUSAB存在着一个较为稳定的增长;当N大于5时,AB、PRFS-FPUSAB都存在着一个下滑的趋势,从下滑的幅度以及整体的效果来看,PRFS-FPUSAB要优于AB。当N为5时,PRFS-FPUSAB、AB效果最好。在最优值方面,PRFS-FPUSAB算法AUC最优约为0.85,Bacc最优约为0.80;AB AUC最优约为0.75,Bacc最优约为0.72。
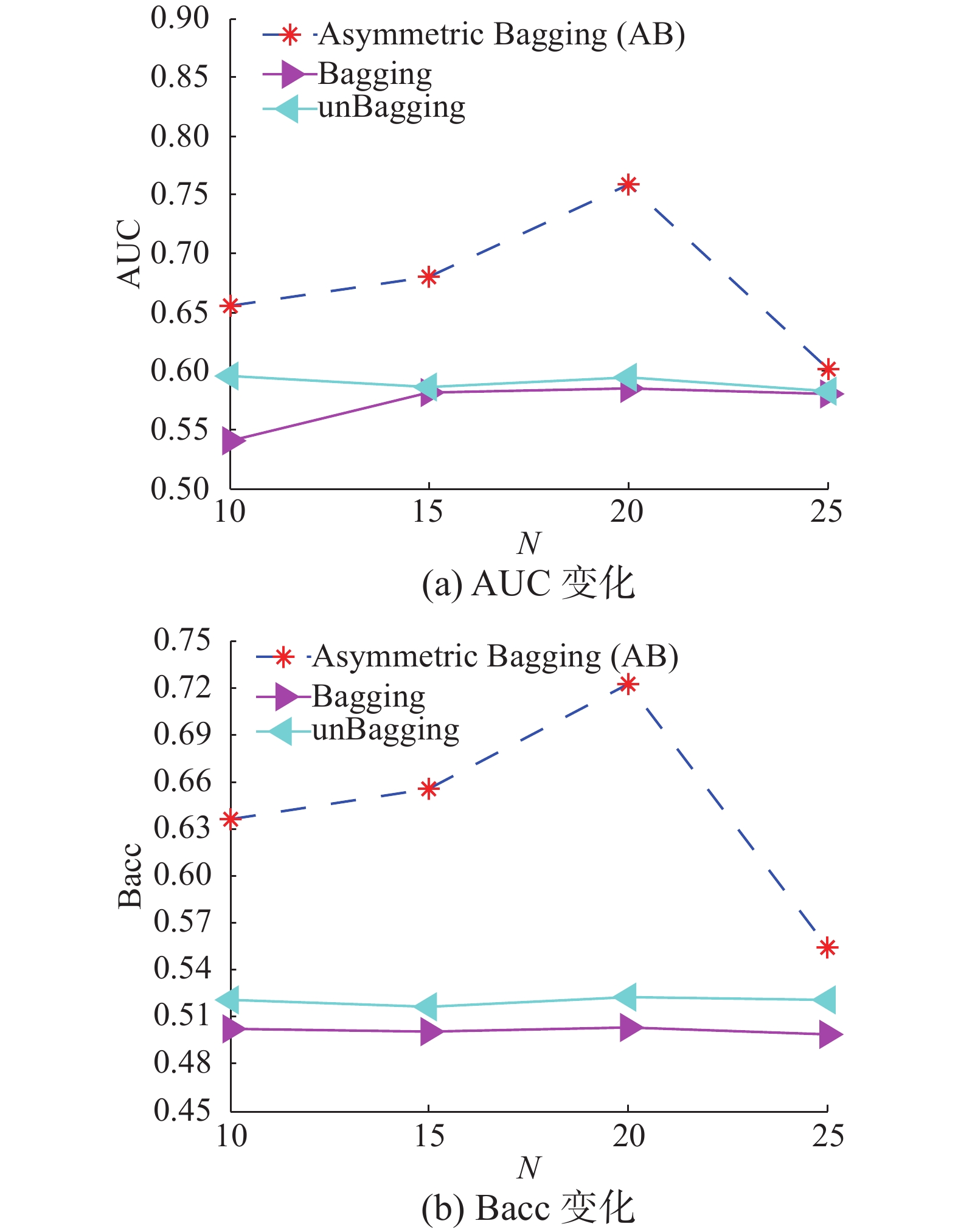
在PRFS-FPUSAB算法中由于改进采样方式对集成的数量进行了限制。但是Bagging、unBagging、AB对于集成规模并没有限制。是否这几个算法随着集成规模的增加会有不同的效果,或者说当这几个算法在集成规模较大时是否由于PRFS-FPUSAB算法呢,继续用实验进行探讨。由于health类疾病和sleep类疾病的不均衡规模不同,在health类疾病我们选取的规模为{10, 15, 20, 25},在sleep类疾病我们选取的规模为{15, 20, 25, 30, 35, 40, 45, 50}。
|
图 4 亚健康类疾病分类结果随着集成规模变化曲线图 Fig.4 The change of sub-health classification results |
从图4中可以看出,随着集成规模的增加,health类不均衡疾病数据的分类结果AUC、Bacc呈现出了一定幅度的增长,但是很快地又回落了。由于这种采样的方式是随机的,造成结果出现了振荡性的变化。AB算法最优 AUC约为0.75,Bacc约为0.71。与PRFS-FPUSAB算法最优结果相比,AB算法要相对差一些。

|
图 5 睡眠情绪类疾病分类结果随着集成规模变化 Fig.5 The change of sleep classification results |
从图5中可以看出,随着集成规模的增加,sleep类不均衡疾病数据的分类结果AUC、Bacc呈现出了振荡性的变化,大致趋势为先增加后下降,并且下降趋势为结果越来越差。由于采样的方式的随机造成了结果出现了振荡性的变化。AB算法最优AUC约为0.75,Bacc约为0.72。与PRFS-FPUSAB算法最优结果相比,AB算法要相对差一些。
从以上的探讨性实验可以看出,PRFS-FPUSAB算法是几种算法中最优的。经过统计分析发现,相较于改进前的AB算法,PRFS-FPUSAB算法在AUC上平均提升16%,在Bacc上平均提升13%。改进后的算法较好地提升了分类性能。
对于健康、亚健康类疾病PRFS-FPUSAB算法选择出的特征有age、height、weight,对应的穴位有阳池左、合谷右、神门右、太溪右。根据选择出的特征,我们对健康与亚健康人群穴位电阻值进行了对比,如表5所示。
| 表 5 健康、亚健康特征选择后穴位平均值 Tab.5 The mean value of acupoints after feature selection |
从表5可以看出,亚健康人群右侧的合谷、神门、太溪的穴位平均值要高于健康个体,而在左侧的阳池穴亚健康个体的穴位平均值要低于健康个体平均值。从中医理论上讲,亚健康与健康人群的判别标准中出现的4个原穴分别属于大经、心经、肾经和三焦经,而亚健康人群之所以在这四经上表现出特异性,多由于亚健康的表现与四经络的生理功能异常密切相关。亚健康状态的表现多种多样,《亚健康中医诊疗指南》将其归纳为躯体、心理、社会交往3个方面。临床诊疗中亚健康的这些表现恰好与以上4条经络及其脏腑功能异常有关,这也解释了为何亚健康人群在这4条经的原穴上与健康人群有着显著差异。
针对睡眠情绪类疾病选中的特征有神门左、神门右、太冲左、腕骨左、腕骨右、身高、体重。由于睡眠情绪类疾病和健康、亚健康可用样本数量不一致,将身高、体重转换为BMI指数重新统计分析。
| 表 6 睡眠情绪类疾病特征选择分析结果 Tab.6 Sleep emotional disease feature selection analysis results |
与睡眠情绪类疾病密切相关的特征神门、太冲、腕骨分别是心经、肝经和小肠经的原穴。从中医理论角度进行分析,睡眠情绪类疾病与这3条经脉关系密切:心臧神;肝主疏泄,调畅情志;小肠经与心经相表里,心经实火可以下移小肠。睡眠情绪类疾病患者BMI指数偏低,说明该类疾病患者体型偏瘦,这与中医理论中瘦人多火,火热易扰心神的观点是一致的,如表6所示。
综合上面探讨可知,通过特征选择的特征符合中医学有关疾病理论,并且找到的诊断子集能够有效提升分类性能。在临床诊断中,可以通过特征选择辅助医生抓主症。
6 结束语本文中结合中医临床数据实际提出了Asymmetric Bagging的改进算法PRFS-FPUSAB处理中医临床不均衡数据的疾病分类问题和特征选择问题。实验表明,与改进前的算法相比,PRFS-FPUSAB算法在AUC上平均提升16%,在Bacc上平均提升13%。改进后的算法较好地提升了分类性能,通过特征选择后的特征也符合中医学相关理论。虽然使用PRFS-FPUSAB算法在AUC以及Bacc上分类性能有较好的提高,但是从分类器的角度研究不均衡数据分类,更好地提高AUC以及Bacc还需进一步研究。
| [1] |
邹永杰. 基于特征提取的分类集成在脾虚证诊断中的应用[J]. 计算机应用与软件, 2010, 27(3): 22-25. ZOU Yongjie. Applying feature selection-based classification ensemble in spleen asthenia diagnosis[J]. Computer applications and software, 2010, 27(3): 22-25. (  0) 0)
|
| [2] |
刘天羽, 李国正. 齿轮故障不均衡分类问题的研究[J]. 计算机工程与应用, 2010, 46(20): 146-148. LIU Tianyu, LI Guozheng. Research on imbalanced problems in gear fault diagnosis[J]. Computer engineering and applications, 2010, 46(20): 146-148. (  0) 0)
|
| [3] |
谢娜娜, 房斌, 吴磊. 不均衡数据集上文本分类方法研究[J]. 计算机工程与应用, 2013, 49(20): 118-121. XIE Nana, FANG Bin, WU Lei. Study of text categorization on imbalanced data[J]. Computer engineering and applications, 2013, 49(20): 118-121. (  0) 0)
|
| [4] |
陶新民, 郝思媛, 张冬雪, 等. 不均衡数据分类算法的综述[J]. 重庆邮电大学学报: 自然科学版, 2013, 25(1): 101-43. TAO Xinmin, HAO Siyuan, ZHANG Dongxue, et al. Overview of classification algorithms for unbalanced data[J]. Journal of chongqing university of posts and telecommunications, 2013, 25(1): 101-43. (  0) 0)
|
| [5] |
LIUT Y, LI G Z. The imbalanced data problem in the fault diagnosis of rolling bearing[J]. Computer engineering and science, 2010, 32(5): 150-153. ( 0) 0)
|
| [6] |
YU K S. A Network intrusion detection model based on data ming and feature selection schemes[J]. Microelectronics and computer, 2011, 28(8): 74-76. ( 0) 0)
|
| [7] |
ZWEIG M H, CAMPBELLmpbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine[J]. Clinical chemistry, 1993, 39(4): 561-77. ( 0) 0)
|
| [8] |
浮盼盼. 大规模不均衡数据分类方法研究[D]. 大连: 辽宁师范大学, 2014. FU Panpan. Research on classification methods for large-scale imbalanced data [D]. Liaoning normal university, 2014. (  0) 0)
|
| [9] |
MIERSWA I. Controlling overfitting with multi-objective support vector machines[C]//Genetic and Evolutionary Computation Conference. London, UK, 2007: 1830–1837.
( 0) 0)
|
| [10] |
赵自翔, 王广亮, 李晓东. 基于支持向量机的不均衡数据分类的改进欠采样方法[J]. 中山大学学报: 自然科学版, 2012, 51(6): 10-16. ZHAO Zixiang, WANG Guangliang, LI Xiaodong. An improved SVM based under-sampling method for classifying imbalanced data[J]. Acta scientiarum naturalium universitatis sunyatseni, 2012, 51(6): 10-16. (  0) 0)
|
| [11] |
朱明, 陶新民. 基于随机下采样和SMOTE的不均衡SVM分类算法[J]. 信息技术, 2012(1): 39-43. ZHU MING, TAO Xingmin. The SVM classifier for unbalanced data based on combination of RU-Undersample and SMOTE[J]. Information technology, 2012(1): 39-43. (  0) 0)
|
| [12] |
LI G Z, MENG H H, LU W C, et al. Asymmetric bagging and feature selection for activitiesprediction of drug molecules[C]//International Multi-Symposiums on Computer and Computational Sciences. [S.l.], 2007: 1–11.
( 0) 0)
|
| [13] |
DRUMMOND C, HOLTE R C. C4.5, Class imbalance, and cost sensitivity: why under-sampling beats over-sampling[C]//Proc of the Icml Workshop on Learning from Imbalanced Datasets II, 2003: 1–8.
( 0) 0)
|
| [14] |
BHAVANI S, NAGARGADDE A, THAWANI A, et al. Substructure-based support vector machine classifiers for prediction of adverse effects in diverse classes of drugs[J]. Journal of chemical information and modeling, 2007, 46(7): 2478-2486. ( 0) 0)
|
| [15] |
潘主强, 张林, 颜仕星, 等. 中医睡眠情绪类疾病不均衡数据的分类研究[J]. 济南大学学报: 自然科学版, 2017, 31(1): 55-60. PAN Zhuqiang, ZHANG Lin, YAN Shixing, et al. Classification research on imbalanced TCM clinical data of sleep and emotion disorder disease[J]. Journal of university of Jinan: science and technology, 2017, 31(1): 55-60. (  0) 0)
|
| [16] |
UTANS J, MOODY J. Selecting neural network architectures via the prediction risk: application to corporate bond rating prediction[C]//International Conference on Artificial Intelligence on Wall Street. [S.l.], 1991: 35–41.
( 0) 0)
|
| [17] |
WITTEN I H, FRANK E. Data mining: practical machine learning tools and techniques with Java implementations [M]. Morgan Kaufmann Publishers Inc, 2011: 206–207.
( 0) 0)
|
| [18] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. Acm transactions on intelligent systems and technology, 2007, 2(3): 389-396. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


