2. 武汉纺织大学 数学与计算机学院, 湖北 武汉 430200;
3. 福建师范大学 体育科学学院, 福建 福州 350117
2. School of Mathematics and Computer, Wuhan Textile University, Wuhan 430200, China;
3. Physical Science School, Fujian Normal University, Fuzhou 350117, China
由于健身跑不受时间、场地和季节的影响,方法简便、费时少、见效快,已成为全民健身的主要锻炼项目[1]。为了提高健身跑的趣味性和娱乐性,市面上已涌现出一批基于智能手机的健身跑系统[2]。这些系统使用智能手机内置的GPS、加速度、方向、磁力、陀螺仪和旋转矢量等传感器输出与运动状态相关的信号,经处理后可获取健身跑的步长步频[3-5]、加速度[6-9]和速度[10-12]等运动数据,在此基础上提供运动数据的保存、统计、显示和分享等功能。
为了能在提高锻炼效益的同时,避免过度运动对人们身心造成的伤害[13-14],近年来已提出一些健身跑的运动建模技术。这些技术除需要借助智能手机内置传感器采集运动数据外,往往还要利用外置传感器和手机的蓝牙通信功能收集脉搏、心率、血压、血氧浓度等生理数据,在此基础再应用算法对获取的运动数据和生理数据进行分析以构建健身跑运动模型。Sornanatha等[15]利用脉搏血氧仪采集心率、血压、血氧浓度等数据,提出了一种健身者运动强度控制模型。B. W. Fudge等[16]利用加速度、心率和耗氧量等数据,构建了健身跑运动监控过程模型。孙泊等[17]基于加速度、耗氧量等数据,提出了一种健身跑的能耗过程模型。Garcia等[18]运用无监督聚类和隐马尔可夫模型,基于加速度、心率和血氧浓度等数据建立了一种运动强度分析模型。Cheng[19]和Scalzi[20]通过心率、速度和疲劳程度3个要素刻画健身跑的运动模型,并运用带参数的微分方程组定义了模型空间。Cheng和Scalzi的参数模型通过疲劳程度的变量来模拟健身跑中的复杂生理过程,在缺乏血压、血氧浓度、耗氧量等数据的情况下也能构建较为精确的健身跑运动模型。
基于Cheng和Scalzi的参数化模型,Brzostowski等[21]提出了一种基于智能手机的健身跑运动建模方法。Brzostowski方法依照文献[22]的研究成果要求运动者将智能手机绑缚于腰部进行健身跑。在健身跑过程中滤除掉手机坐标系下的三轴加速度信号中的重力分量后,进一步进行变换,可生成速度信号。此外,Brzostowski方法还利用智能手机的蓝牙通信模块从心率带接收心率信号。并在采集的速度数据和心率数据的基础上,运用麦夸特Levenberg-Marquardt,LM算法在Cheng和Scalzi的模型空间中搜索最佳健身跑模型。Brzostowski方法虽然已得到一定的应用,但仍存在一些不足。Brzostowski方法未考虑健身跑中绑缚于腰部的手机经常发生的间歇性姿态变化产生的脉冲噪声会对获取加速度数据的精度产生影响。因为这些脉冲噪声不仅对三轴加速度信号产生干扰,而且还会导致手机坐标系发生偏移甚至旋转,从而影响到三轴加速度信号中重力分量的滤除。另外,受制于搜索空间,LM算法容易陷入局部最优,因而难以获取全局最优的健身跑运动模型。
针对上述问题,本文提出了一种基于智能手机的健身跑演化建模方法。本文的主要贡献有:
1) 提出了基于智能手机多传感器和中值滤波的速度数据采集方法(multi-sensor of smartphone and median filter for speed data acquisition in fitness running,MM4SA)。MM4SA方法运用中值滤波器滤除手机间歇性的姿态变化对三轴加速度信号产生的脉冲噪声,并结合方向传感器输出的方向信号对手机三轴加速度中包含的重力分量进行过滤。
2) 设计了一种健身跑演化建模算法GA。GA算法可在Cheng和Scalzi等定义的庞大的模型空间中,搜索出较优的健身跑运动模型。
3) 招募10名大学生进行健身跑并收集他们运动过程中的速度数据和心率数据,开展了本文方法与Brzostowski方法的实验对比。实验结果表明,本文方法可以较Brzostowski方法获取更为精确的速度和健身跑运动模型。
1 Brzostowski提出的健身跑运动建模方法下面给出Brzostowski提出的健身跑运动建模方法中的速度数据采集和建模算法。
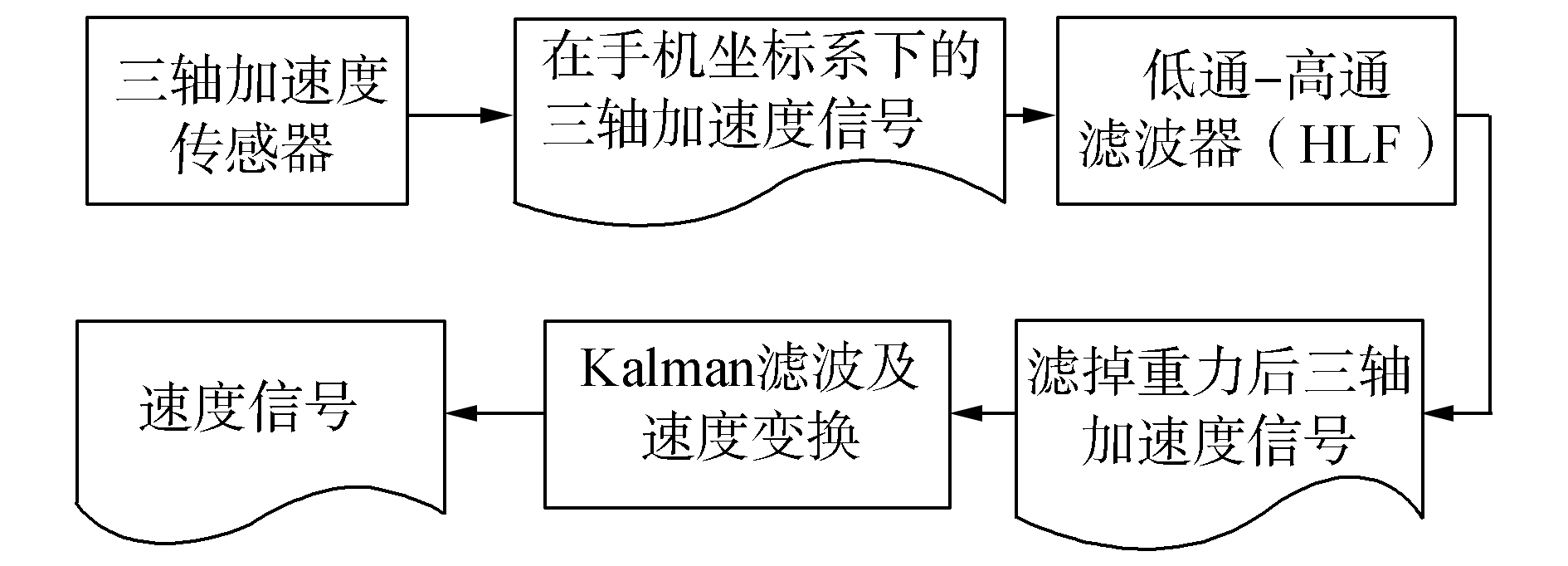
1.1 健身跑速度数据采集Brzostowski的健身跑速度采集方法的流程如图 1所示,其包括获取加速度信号、低通-高通滤波和速度信号输出3个步骤。
|
图 1 Brzostowski健身跑运动速度采集方法 Fig.1 Brzostowski's approach to speed acquisition in fitness running |
首先,智能手机内置的三轴加速度传感器输出手机三轴坐标系[23]下,并且包含有重力分量的加速度信号。手机坐标系是以手机屏幕为基准定义的一种相对坐标系。手机屏幕中心为坐标系原点,平行于屏幕短边的方向为x轴正方向,平行于屏幕长边的方向为y轴正方向,垂直于手机屏幕向上的方向为z轴正方向。
其次,将含有重力分量的三轴加速度信号送入低通-高通滤波器(low-pass and high-pass filter,HLF)滤除重力分量后,经Kalman[21]滤波由加速度到速度的变换,最后输出健身跑的速度信号。
图 1中HLF对于获取精确的速度数据起着关键作用,因而下文将Brzostowski健身跑速度数据采集方法简记为HLF方法。
1.2 健身跑建模算法Brzostowski在Cheng和Scalzi等提出的参数化模型[19]基础上,运用麦夸特(Levenberg-Marquardt,LM)算法搜索最优健身跑运动模型。
Cheng的模型由(1)式的微分方程组定义。(1)式刻画了心率、疲劳程度和速度之间的非线性关系。(1)式中的x1(t)、x2(t)和u(t)分别表示t时刻较0时刻(平静状态下)的心率增量、疲劳程度增量,以及t时刻的速度;a1、a2、a3、a4和a5为5个待定的正实数参数。
| $ \left\{ \begin{array}{l} {x_1}\prime \left( t \right) =-{a_1}{x_1}\left( t \right) + {a_2}\left( {{x_2}\left( t \right) + {u^2}\left( t \right)} \right)\\ {x_2}\prime \left( t \right) =-{a_3}{x_2}\left( t \right) + \frac{{{a_4}{x_1}\left( t \right)}}{{1 + {\rm{exp}}\left( {{a_5}-{x_1}\left( t \right)} \right)}} \end{array} \right. $ | (1) |
Brzostowski方法根据运动者一段时间健身跑所采集的数据速度和心率数据,使用LM算法按照心率增量x1(t)最小平方误差准则,确定(1)式中5个待估参数的值。
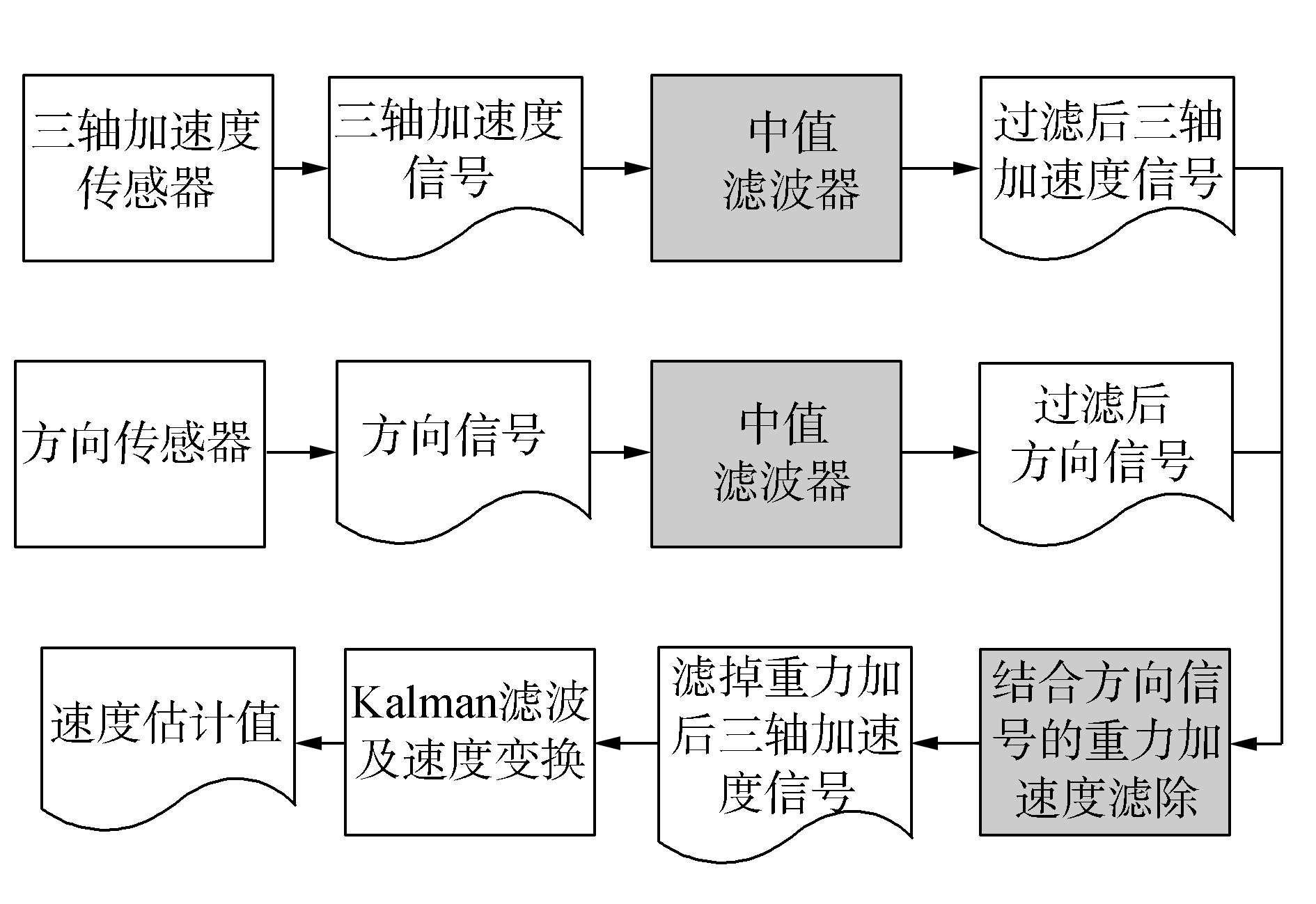
2 智能手机多传感器和中值滤波的健身跑速度数据采集方法 2.1 MM4SA方法的总体流程MM4SA方法利用方向传感器[24-25]捕获健身跑中手机姿态变化的方向信号,并运用该信号帮助过滤手机三轴加速度传感器输出信号中的重力分量;进一步借助中值滤波器[26]对三轴加速度信号和方向信号进行降噪和平滑处理。图 2给出了MM4SA方法的流程。图 2中灰色背景标识的中值滤波器、结合方向信号的重力加速度滤除两个步骤是MM4SA方法不同于HLF方法的步骤,下面将重点予以阐述。
|
图 2 基于智能手机多传感器和中值滤波的速度数据采集方法MM4SA的流程 Fig.2 Speed acquisition process in MM4SA approach using multi-sensors in smartphone and median filter |
图 2中的两个中值滤波器分别用于去除健身跑中因固定于腰部的手机发生间歇性姿态变化,而产生的三轴加速度信号和方向信号的脉冲噪声。下面以手机坐标系下x轴的加速度信号ax(t)为例,说明中值滤波器的工作原理。y和z轴上的加速度信号,以及方向信号的中值滤波也是类似的。
式(2)定义了ax(t)信号在t时刻的加速度经中值滤波后的值。在式(2)中,l和Θwnd分别为滤波窗口的大小、滤波窗口中加速度信号样本的集合。Med是对Θwnd样本集合取中值操作,即先对Θwnd中的加速度信号样本,按照从小到大的顺序进行排列后,再取第m+1个样本的值。
| $ \left\{ \begin{array}{l} {a_x}\left( t \right) = {\rm{Med}}({\mathit{\Theta }_{{\rm{wnd}}}})\\ {\mathit{\Theta }_{{\rm{wnd}}}} = \{ {a_x}\left( {t\prime } \right)\left| {\left( {t-m} \right) \le t\prime \le t + m} \right.\\ \;\;\;\;\;\;\;\;\;{\rm{且}}l = 2 \times m + 1, m \in N\} \end{array} \right. $ | (2) |
智能手机三轴加速度传感器输出的加速度信号值是基于手机三轴坐标系的,并且其中还包含重力分量值。健身跑中手机的姿态变化可导致手机坐标系发生小幅偏移甚至旋转,进而使得重力对三轴加速度传感器输出信号的影响也随之改变。
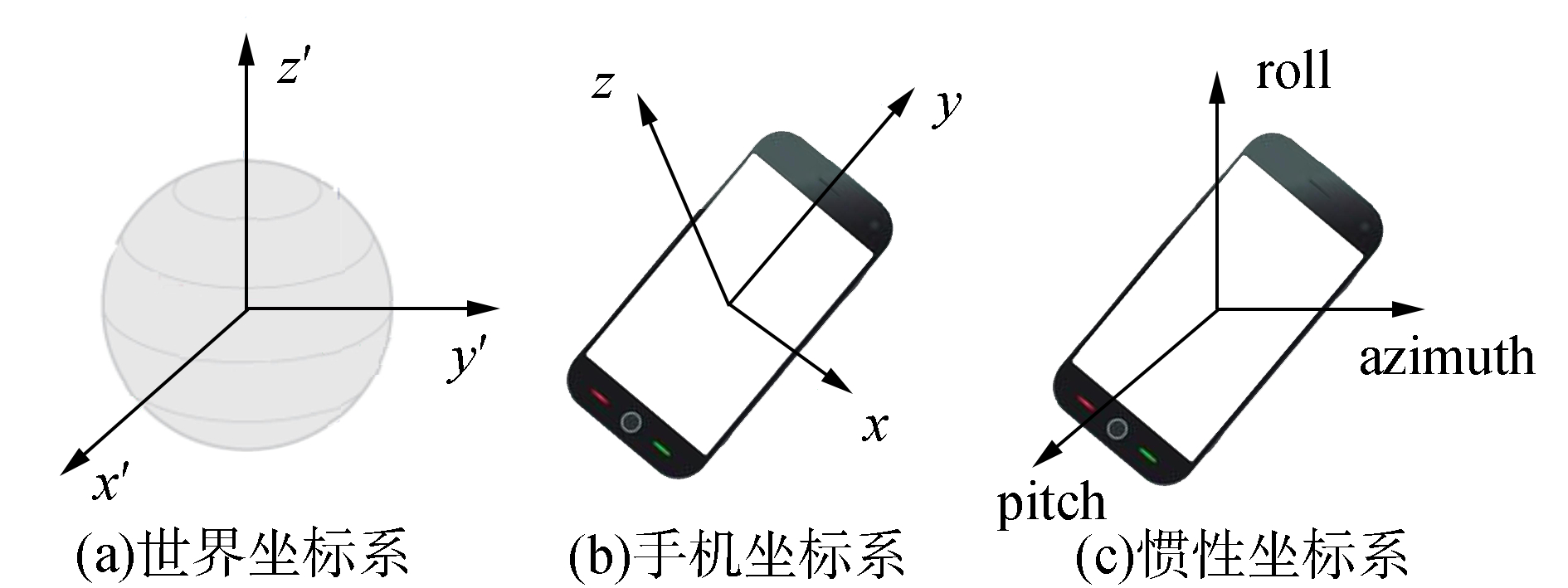
智能手机内置的方向传感器通过捕获手机坐标系与惯性坐标系的相对位置,能够输出手机坐标系变化的信号。图 3(c)示意了用于描述手机运动状态的惯性坐标系。它的中心点与手机坐标系的中心点重合,3个坐标轴pitch(与地面相切,指向正西)、azimuth(垂直于地面指向正西)和roll(与地面相切,指向正北)分别与图 3(a)所示的世界坐标系中3个坐标轴x′、y′和z′平行。世界坐标系是一种绝对坐标系,它通过经纬度和高程描述地球上每个点的方位信息。为了反映重力加速度g对手机坐标系下加速度信号的影响,可将其看作惯性坐标系azimuth轴上的常量。
|
图 3 3种不同的坐标系 Fig.3 Three different coordinate systems |
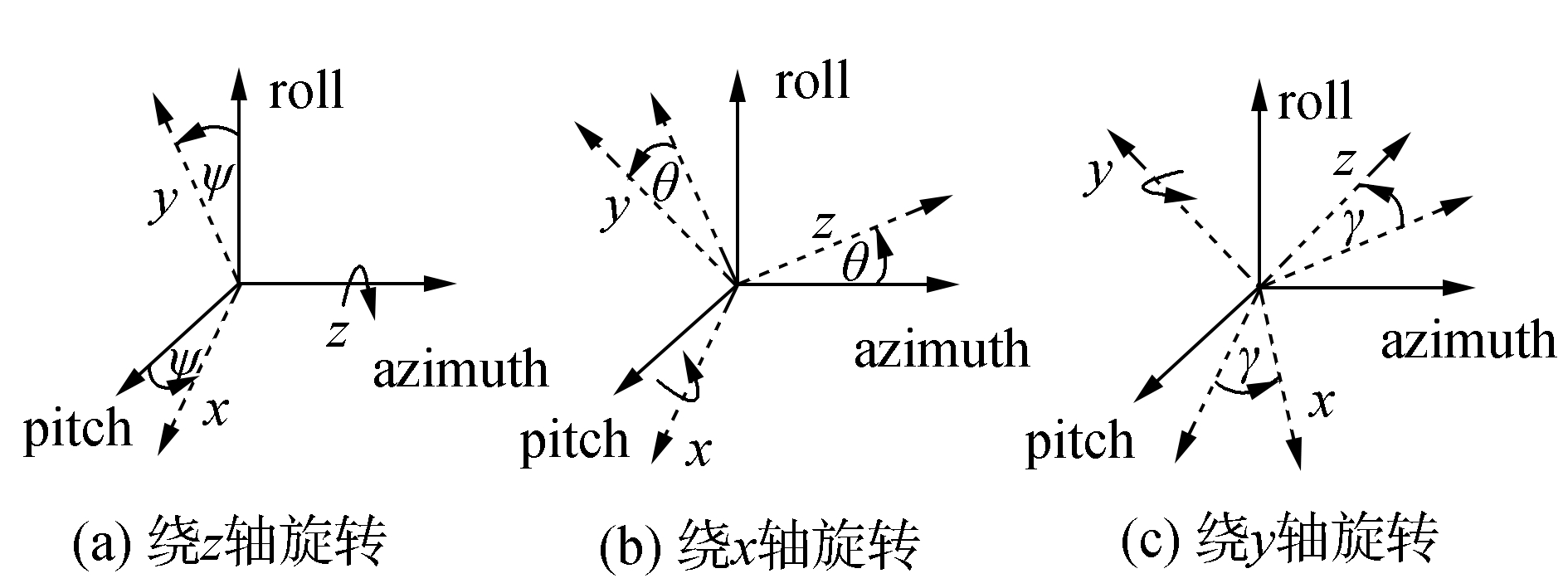
根据空间几何原理,手机姿态变化而引起的手机坐标系变化,可通过惯性坐标系分别对绕手机坐标系z、x、y轴旋转一定的航向角φ、俯仰角θ和滚转角γ进行描述。图 4给出了惯性坐标系到手机坐标系的3个转换步骤,它们分别对应式(3)、(4)和(5)的变换矩阵。
|
图 4 惯性坐标系到手机坐标系的转换步骤 Fig.4 Transformations from inertia coordinate system to smartphone coordinate system |
| $ \boldsymbol{M}(\varphi (t)) = \left[{\begin{array}{*{20}{c}} {\cos (\varphi (t))}&{\sin (\varphi (t))}&0\\ {-\sin (\varphi (t))}&{\cos (\varphi (t))}&0\\ 0&0&1 \end{array}} \right] $ | (3) |
| $ \boldsymbol{M}(\theta (t)) = \left[{\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos (\theta (t))}&{\sin (\theta (t))}\\ 0&{-\sin (\theta (t))}&{\cos (\theta (t))} \end{array}} \right] $ | (4) |
| $ \boldsymbol{M}(\gamma (t)) = \left[{\begin{array}{*{20}{c}} {\cos (\gamma (t))}&0&{-\sin (\gamma (t))}\\ 0&1&0\\ {\sin (\gamma (t))}&0&{\cos (\gamma (t))} \end{array}} \right] $ | (5) |
| $ \left[{\begin{array}{*{20}{c}} {{g_x}(t)}\\ {{g_y}(t)}\\ {{g_z}(t)} \end{array}} \right] = \boldsymbol{M}(\varphi (t)) \cdot \boldsymbol{M}(\theta (t)) \cdot \boldsymbol{M}(\gamma (t)) $ | (6) |
智能手机内置的方向传感器通过融合手机内置的加速度传感器、地磁传感器可以输出方向信号φ(t)、θ(t)和γ(t)。结合方向角信号可将惯性坐标系下的重力加速度g旋转变换至手机坐标系下,进而获取g在x、y和z轴上各个分量信号gx(t)、gy(t)、gz(t)。坐标变换如(6)式。最后,将三轴加速度传感器输出的信号滤除变换后的重力分量,便可获得人体加速度信号。
3 基于智能手机的健身跑演化建模算法根据健身跑运动过程中采集的数据速度和心率数据,本文设计了一种遗传算法(genetic algorithm,GA)对式(1)中的5个参数进行演化优化,进而构建出健身跑运动模型。
GA算法中个体编码采用实数编码,其长度为5。按照式(1)和采集的速度数据,可采用四阶龙格-库塔法[27]求解出心率增量x1(t)的估计值。并定义心率增量估计值与实测值的残方差,适应度函数是GA算法里的专业术语,一般定义适应度值越小,个体越优。交叉算子采用整体算术杂交法。变异算子采用常规的单点变异算子。选择策略采用带精英保留的轮盘赌方法。具体的算法流程定义如下所示。
算法 健身跑演化建模算法GA
输入 种群大小n,交叉概率pc(0 < pc < 1),变异概率pm(0 < pm < 1),心率实测值,速度u(t);
输出 式(1)中的参数a1、a2、a3、a4和a5。
1) 演化代数t←0;
2) 产生初始种群P(t);
3) 根据估计的速度值u(t)和式(1),采用四阶龙格-库塔法求解心率增量的估计值,定义心率增量估计值与实测值的残差平方和作为适应度函数,计算P(t)中每个个体的适应度值;
4) 从种群P(t)中选择最优个体并赋给X变量;
5) 若不满足停机条件,执行下列6)~11)循环;
6) 基于P(t)和交叉概率pc,通过整体算术交叉算子生成中间种群PC(t);
7) 基于PC(t)和变异pm,通过变异算子生成中间种群PM (t);
8) 计算PM (t)中每个个体的适应度值;
9) 按基于精英保留的轮盘赌选择策略从种群PM(t)和P(t)中选出n个个体生成下一代种群P(t+1);
10)从种群P(t+1)中找出最优个体并赋给X变量;
11)t←t+1;
12)满足停机条件,循环结束;
13)将得到的最优个体X作为最优参数输出。
4 实验为了验证本文健身跑速度数据采集和演化建模算法的有效性,下面首先介绍实验数据集,然后定义验证的问题和度量指标,再阐述所使用的统计方法,最后展示实验结果。
4.1 实验数据集我们基于Android智能手机和外置的心率带已开发了一套健身跑指导系统(简称i酷跑)。i酷跑的数据采集模块可在运动者健身跑中,每隔1 min将从智能手机采集到的三轴加速度数据、方向传感器数据,以及从心率带收集的心率数据实时存储到云服务器中。并在云端运行本文GA算法,为了便于实验对比,LM算法也被部署在云端进行运行。
为了开展本文的验证工作,我们招募了10名大学生志愿者进行健身跑,以构建实验数据集。这些学生的具体情况如表 1所示。在表 1中,为了保护隐私,用P1~P10代指各受试者的真实姓名。给每位受试者提供1条SUUNTO SS020566000心率带、配备android 4.4的小米3智能手机1部并安装i酷跑系统。选用h/p/cosmos 5.0专业跑步机获取各受试者健身跑过程中的精确速度数据,并将其视为实际速度。在对受试者进行必要的使用培训后,进行时长为30 min的实验。整个实验过程在福建师范大学旗山校区体育科学学院的体育运动实验中心进行。图 5给出了一名受试者在h/p/cosmos 5.0跑台上进行健身跑的情况。实验结束后,将云端存储的受试者的三轴加速度数据、方向数据、心率数据与跑步机上存储的实际速度数据进行整合,形成10名受试者对应的10个数据集。每个数据集共有30行数据,每行数据对应于每分钟采集的三轴加速度数据、方向数据、心率数据和实际速度数据。

|
图 5 受试者在h/p/cosmos 5.0跑台上进行健身跑 Fig.5 A subject running on the treadmill produced by h/p/cosmos 5.0 company |
| 表 1 受试者情况表 Tab.1 Basic subject information |
问题1 RQ1。与HLF方法相比,本文MM4SA方法是否可以获取更为精确的速度数据?
每个受试者在健身跑过程中速度的平均绝对误差IΔv被作为度量指标定量地回答RQ1。IΔv的定义如(7)式所示,方法对应的IΔv越小说明越优。
| $ {I_{\Delta v}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\hat V}_i}-{V_i}} \right|} $ | (7) |
式中:N为观测周期数,对应于数据集中行数;Vi表示跑步机输出的受试者第i分钟的实际速度; 而
问题2 RQ2。与LM算法相比,本文GA算法构建的健身跑运动模型是否更加精确?
为了公平起见,每个数据集中的实际速度数据(跑步机输出)和心率数据被用于构建受试者的健身跑运动模型。而HLF和MM4SA方法输出的速度数据不被考虑使用,以避免因速度偏差而引起的模型精度问题。
根据受试者P的数据集,分别在云服务器上运行GA和LM算法可确定式(1)中参数a1~a5的值,进而建立P的健身跑运动模型。当已知P的第i分钟速度值,可用该模型估算对应的心率值。每个受试者在健身跑过程中心率的平均绝对误差IΔh被作为度量指标以定量地回答RQ2。IΔh的定义如式(8)所示,算法对应的IΔh越小说明越优。
| $ {I_{\Delta h}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\hat H}_i}-{H_i}} \right|} $ | (8) |
式中:N为观测周期,对应数据集中行数;Hi表示第i分钟的心率测量值;
本文采用Wilcoxon秩和检验对实验数据进行统计分析,并将置信水平α的值设置为0.05。Wilcoxon秩和检验能够给出对比数据在统计学上显著的差异性(大小用p-value表示)。为了进一步直观观测差异程度的大小(effect size),本文采用Vargha-Delaney[28]的
1)RQ1的结果
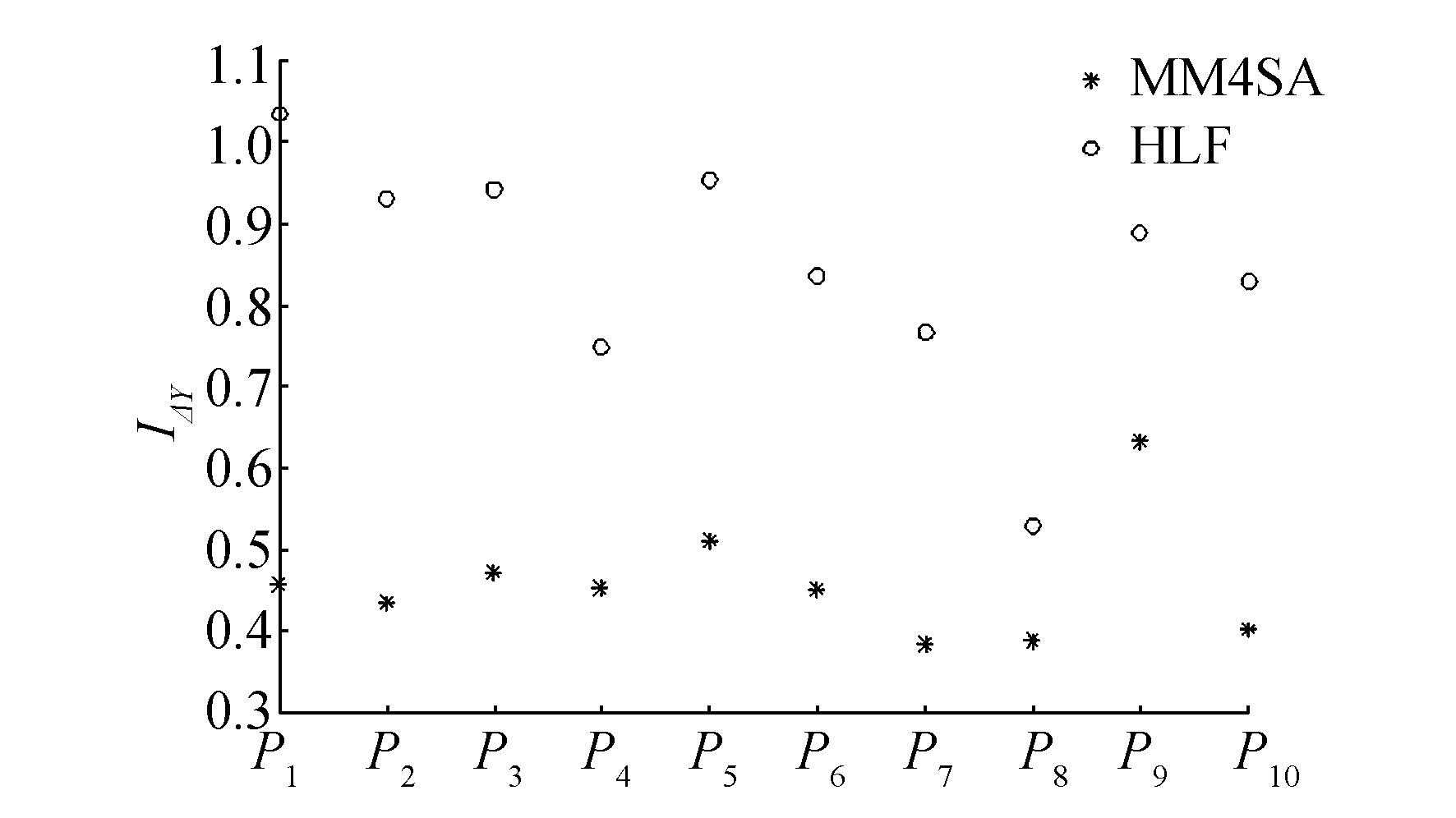
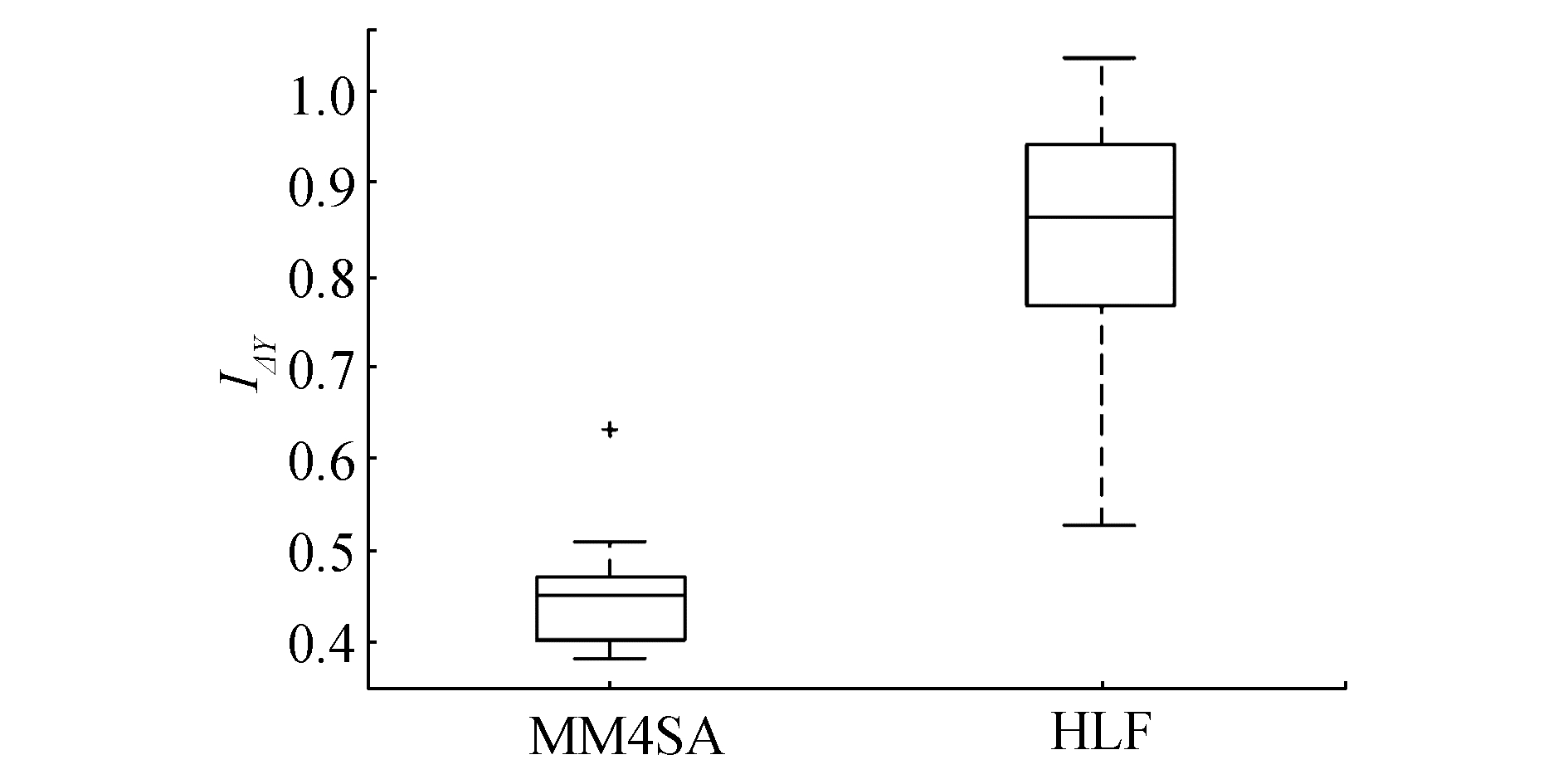
图 6和图 7分别给出了MM4SA和HLF方法对应的10名受试者健身跑IΔv(速度的平均绝对误差)指标值的散点图和统计盒图。从图 6和图 7可以直观看出,MM4SA方法明显优于HLF方法。对IΔv的统计实验得出:p-value和effect size分别为2.461 3×10-4和0.9,也表明MM4SA显著优于HLF。这说明与HLF方法相比,MM4SA方法考虑了健身跑中绑缚于腰部的手机在发生间歇性姿态变化时产生的脉冲噪声对三轴加速度信号本身的干扰及对重力分量滤除的影响,进而可以获取更加接近于人体实际运动的速度。
|
图 6 MM4SA和HLF方法对应的10名受试者健身跑IΔv(速度的平均绝对误差)指标值的散点图 Fig.6 Scatter plot using the quality indicator IΔv applied to MM4SA and HLF based on the datasets of 10 subjects |
|
图 7 MM4SA和HLF方法对应的10名受试者健身跑IΔv(速度的平均绝对误差)指标值的统计盒图 Fig.7 Boxplot using the quality indicator I Δv applied to MM4SA and HLF based on the dataset of 10 subjects |
2) RQ2的结果
考虑到GA算法随机性的特点,在每个数据集上运行20次,而对于确定性算法LM则只需运行1次。表 2显示了GA和LM算法分别运行20次和1次对应的10名受试者健身跑IΔh(心率的平均绝对误差)指标的平均、最好、最差和中位数等统计量的情况。表 3给出了GA和LM算法对应的IΔh秩和实验结果。从表 2可看出,除了受试者P1的最差IΔh外,其余情况GA均优于LM算法。从表 3的10组统计实验得出:对于所有受试者,p-vaule值均小于0.05,而effect size的值均为1,说明GA算法显著地优于LM算法。这表明GA算法可以搜索更大的模型空间,获取较LM算法更为精确的健身跑运动模型。
| 表 2 GA和LM算法分别运行20次和1次对应的10名受试者健身跑IΔh(心率的平均绝对误差)指标的统计量 Tab.2 Basic summary statistics for the quality indicator IΔh based on 20 runs of GA and single run of LM using the datasets generated by 10 subjects |
| 表 3 GA和LM算法分别运行20次和1次对应的10名受试者健身跑IΔh秩和实验的p-value及effect size Tab.3 p-value and effect size of the quality indicator IΔhobtained in Wilcoxon experiments based on 20 runs of GA and single run of LM using the datasets generated by 10 subjects |
本文提出了基于智能手机多传感器和中值滤波的速度数据采集方法。该方法利用中值滤波器滤除健身跑中手机间歇性的姿态变化对三轴加速度信号产生的脉冲噪声,结合方向传感器输出的方向信号对手机三轴加速度中包含的重力分量进行过滤。并设计了一种健身跑演化建模算法GA。GA算法可在Cheng和Scalzi等定义的庞大的模型空间中,搜索出较优的健身跑运动模型。
未来我们将受试对象扩展到不同年龄段并采集更多的数据,研究本文建模方法的稳定性。进一步开展个性化健身跑运动方案生成和健身跑运动过程监控等方面研发工作。
| [1] |
颜庆. 不同强度和时间有氧健身跑对体脂的影响[J]. 武汉体育学院学报, 2013, 47(10): 54-58. YAN Qing. Effect of different intensity and duration of aerobic fitness exercise on body fat[J]. Journal of wuhan institute of physical education, 2013, 47(10): 54-58. DOI:10.3969/j.issn.1000-520X.2013.10.011 (  0) 0)
|
| [2] |
ALLMAN K. Five fitness apps worth the download[J]. LSJ:law society of NSW journal, 2017(31): 57. ( 0) 0)
|
| [3] |
RENAUDIN V, SUSI M, LACHAPELLE G. Step length estimation using handheld inertial sensors[J]. Sensors, 2012, 12(7): 8507-8525. ( 0) 0)
|
| [4] |
HO N H, TRUONG P H, JEONG G M. Step-detection and adaptive step-length estimation for pedestrian dead-reckoning at various walking speeds using a smartphone[J]. Sensors, 2016, 16(9): 1423. DOI:10.3390/s16091423 ( 0) 0)
|
| [5] |
LI F, ZHAO C, DING G, et al. A reliable and accurate indoor localization method using phone inertial sensors[C]//Proceedings of the 2012 ACM Conference on Ubiquitous Computing. Pittsburgh, USA, 2012:421-430.
( 0) 0)
|
| [6] |
谢雨驼, 边耐政. Android手机端运动量检测的研究与应用[J]. 计算机应用与软件, 2012, 29(10): 227-229. XIE Yutuo, BIAN Naizheng. RESEARCH and application of physical activity consumption detection on android smart phone[J]. Computer applications and software, 2012, 29(10): 227-229. (  0) 0)
|
| [7] |
KWAPISZ J R, WEISS G M, MOORE S A. Activity recognition using cell phone accelerometers[J]. ACM sigkdd explorations newsletter, 2011, 12(2): 74-82. DOI:10.1145/1964897 ( 0) 0)
|
| [8] |
BAI Y W, YU C H, WU S C. Using a three-axis accelerometer and GPS module in a smart phone to measure walking steps and distance[C]//2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE). Toronto, Canada, 2014:1-6.
( 0) 0)
|
| [9] |
马松岩. 基于iOS平台的健身应用的设计与实现[D]. 北京: 北京邮电大学, 2013. MA Songyan. The design and implementation of a pedometer application based on ios platform[D]. Beijing:Beijing University of Posts and Telecommunications, 2013. (  0) 0)
|
| [10] |
FASEL B, DUC C, DADASHI F, et al. A wrist sensor and algorithm to determine instantaneous walking cadence and speed in daily life walking[J]. Med biol eng comput, 2017, 55: 1773-1785. DOI:10.1007/s11517-017-1621-2 ( 0) 0)
|
| [11] |
NEVILLE J G, ROWLANDS D D, LEE J B, et al. A Model for comparing over-ground running speed and accelerometer derived step rate in elite level athletes[J]. IEEE sensors journal, 2016, 16(1): 185-191. DOI:10.1109/JSEN.2015.2477497 ( 0) 0)
|
| [12] |
赵寅, 徐国华, 杨超, 等. 基于模糊卡尔曼滤波算法的速度估算方法[J]. 仪表技术与传感器, 2013(12): 80-83. ZHAO Yin, XU Guohua, YANG Chao, et al. Estimation of speed based on fuzzy-Kalman filter[J]. Instrument technique and sensor, 2013(12): 80-83. DOI:10.3969/j.issn.1002-1841.2013.12.027 (  0) 0)
|
| [13] |
KRANZ M, MÖLLER A, HAMMERLA N, et al. The mobile fitness coach:towards individualized skill assessment using personalized mobile devices[J]. Pervasive and mobile computing, 2013, 9(2): 203-215. DOI:10.1016/j.pmcj.2012.06.002 ( 0) 0)
|
| [14] |
周萍, 田磊. 有氧健身跑对大学生身体意象影响的研究[J]. 运动, 2016(21): 53-54. ZHOU Ping, TIAN Lei. The Research about effect of aerobic fitness running on body intention[J]. Sports, 2016(21): 53-54. DOI:10.3969/j.issn.1674-151x.2016.21.028 (  0) 0)
|
| [15] |
SORNANATHAN L, KHALIL I. Fitness monitoring system based on heart rate and SpO2 level[C]//201010th IEEE International Conference on Information Technology and Applications in Biomedicine (ITAB). Kuantan, Malaysia, 2010:1-5.
( 0) 0)
|
| [16] |
FUDGE B W, WILSON J, EASTON C, et al. Estimation of oxygen uptake during fast running using accelerometry and heart rate[J]. Medicine and science in sports and exercise, 2007, 39(1): 192-198. DOI:10.1249/01.mss.0000235884.71487.21 ( 0) 0)
|
| [17] |
孙泊, 刘宇, 庄涛, 等. 基于腰部加速度计的行走能耗建模实验研究[J]. 体育科学, 2013(4): 36-41. SUN Bo, LIU Yu, ZHUANG Tao, et al. The experimental research on modeling of walking energy expenditure based on the waist accelerometer[J]. China sport science, 2013(4): 36-41. (  0) 0)
|
| [18] |
GARCIA-GARCIA F, GARCIA-SÁEZ G, CHAUSA P, et al. Statistical machine learning for automatic assessment of physical activity intensity using multi-axial accelerometry and heart rate[J]. Lecture notes in computer science, 2011, 6747: 70-79. DOI:10.1007/978-3-642-22218-4 ( 0) 0)
|
| [19] |
CHENG T M, SAVKIN A V, CELLER B G, et al. Nonlinear modeling and control of human heart rate response during exercise with various work load intensities[J]. IEEE transactions on biomedical engineering, 2008, 55(11): 2499-2508. DOI:10.1109/TBME.2008.2001131 ( 0) 0)
|
| [20] |
SCALZI S, TOMEI P, VERRELLI C M. Nonlinear control techniques for the heart rate regulation in treadmill exercises[J]. IEEE transactions on biomedical engineering, 2012, 59(3): 599-603. DOI:10.1109/TBME.2011.2179300 ( 0) 0)
|
| [21] |
BRZOSTOWSKI K, DRAPAŁA J, GRZECH A, et al. Adaptive decision support system for automatic physical effort plan generation-data-driven approach[J]. Cybernetics and systems, 2013, 44(2/3): 204-221. ( 0) 0)
|
| [22] |
FUJIKI Y, TSIAMYRTZIS P, PAVLIDIS I. Making sense of accelerometer measurements in pervasive physical activity applications[C]//CHI'09 Extended Abstracts on Human Factors in Computing Systems. Boston, USA, 2009:3425-3430.
( 0) 0)
|
| [23] |
KUO Y S, PANNUTO P, HSIAO K J, et al. Luxapose:Indoor positioning with mobile phones and visible light[C]//Proceedings of the 20th Annual International Conference on Mobile Computing and Networking.Maui, USA, 2014:447-458.
( 0) 0)
|
| [24] |
SUN H, MCINTOSH S. Phone call detection based on smartphone sensor data[C]//International Conference on Cloud Computing and Security. Nanjing, China, 2016:284-295.
( 0) 0)
|
| [25] |
SHI D, WANG R, WU Y, et al. A novel orientation-and location-independent activity recognition method[J]. Personal and ubiquitous computing, 2017, 21(3): 1-15. ( 0) 0)
|
| [26] |
WANG Z, ZHANG D. Progressive switching median filter for the removal of impulse noise from highly corrupted images[J]. IEEE transactions on circuits and systems Ⅱ:analog and digital signal processing, 1999, 46(1): 78-80. DOI:10.1109/82.749102 ( 0) 0)
|
| [27] |
FORSYTHE G E, MOLER C B, MALCOLM M A. Computer methods for mathematical computations[M]. Upper Saddle River: Prentice-Hall, 1977.
( 0) 0)
|
| [28] |
Goulden K J. Effect sizes for research:a broad practical approach[J]. Lawrence erlbaum associates, 2005, 27(5): 419-420. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


