2. 苏州大学 计算机科学与技术学院,江苏 苏州 215006
2. School of Computer Science and Technology, Soochow University, Suzhou 215006, China
相比于浅层网络,由单层模块堆叠形成的深度网络具有更加有效的函数表征能力。通过预训练与微调过程,深度网络能够学习到高度非线性函数的一种更加紧凑的表示,并且同时具备优秀的泛化能力。无监督的预训练过程往往涉及某种特征检测模型,常用的有自编码器(auto-encoder, AE)[1-3]和受限玻尔兹曼机(restricted Boltzmann machine, RBM)[4-8]。堆叠自编码器得到的深度网络与堆叠受限玻尔兹曼机得到的深度网络具有相近的性能。相较而言,自编码器深度网络作为深度学习中更为简单的模型,拥有更易于理解的理论基础与实现过程。
近年来,自编码器及其改善的版本(如降噪自编码器[9-12]、收缩自编码器[13-14])在模式识别领域中展现出优异的性能。相对于手工设计的低层次特征,这些深度网络的成功归因于它们学习丰富的中间层特征表示的能力。然而为了估计上百万的参数,有监督的微调过程需要大量的带标签的样本。于是,在深度网络强有力的模型表达能力下,如果提供的有标签样本数量太少就非常容易造成过拟合的问题。这样的性质就阻止了堆叠的自编码器在有限训练数据下的施展应用。
为了解决这个问题,我们提取栈式自编码器在大数据集上学到的图像特征并迁移到只有有限训练数据的视觉识别任务中。设计的方法复用MNIST数据集上训练的隐藏层,为小型MNIST变体数据集来计算中间层的图像表示。实验结果表明,尽管源任务与目标任务中的两组数据存在差异,迁移的表示能够导致更加高效和更加准确的识别结果。
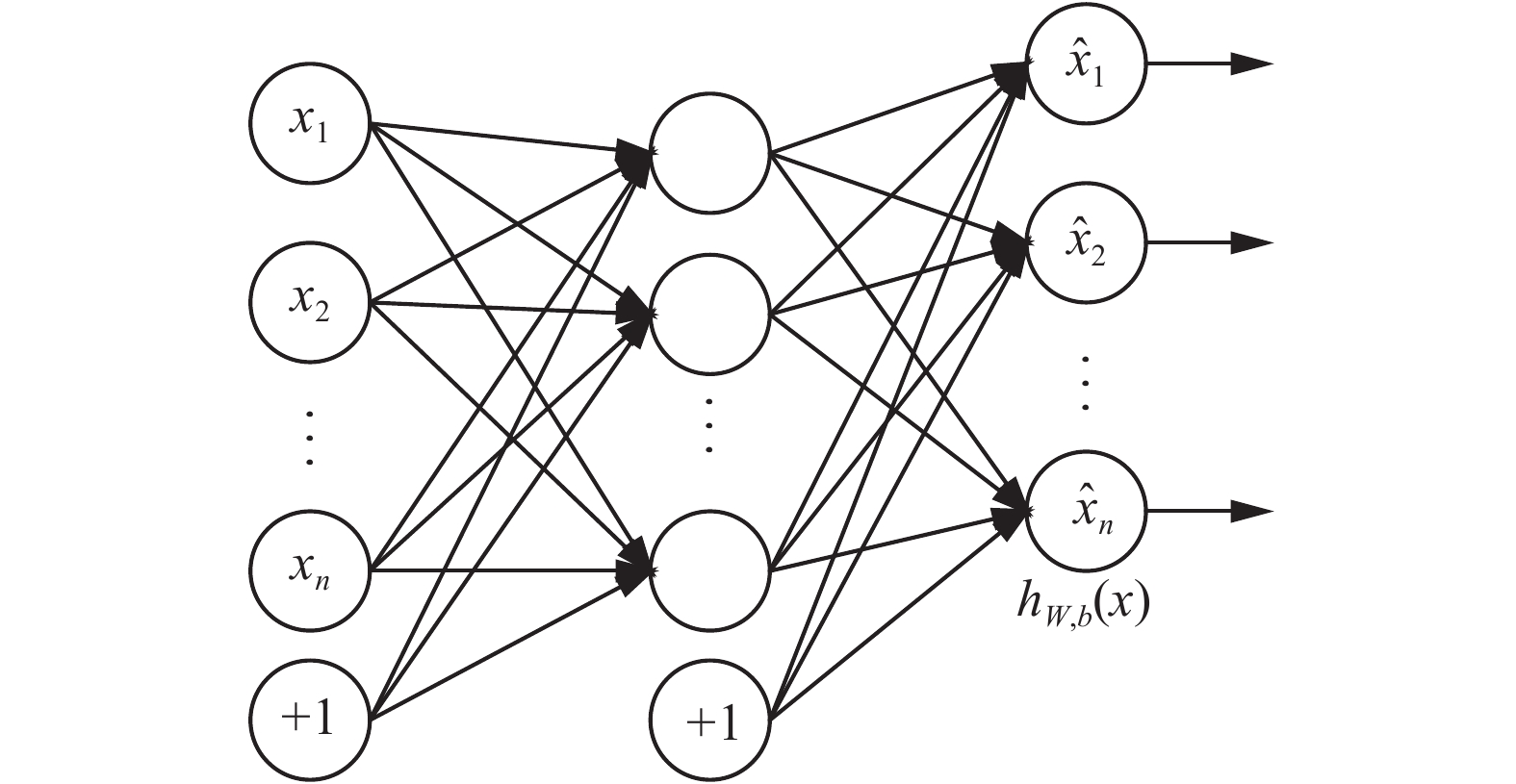
1 自编码器自编码器属于一种特殊的人工神经网络(artificial neural network, ANN),采用反向传播算法(back propagation, BP)进行优化。作为无监督的特征检测模型,自编码器能够学习到输入数据的另一种特征表示。典型的模型由输入层、隐藏层和输出层构成,并且输入层和输出层具有相同个数的神经元。自编码器的目标是尽可能地让输入等于输出,那么中间的隐藏层就必须捕捉能够代表输入的最重要因素,以此给出输入的另一种表示。图1给出了一个典型自编码器的示意图。
|
图 1 自编码器示意图 Fig.1 Auto-encoder diagram |
| ${h_{{\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{b}}}}}({\mathit{\boldsymbol{x}}}) = f({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}}) = f(\sum\nolimits_{i = 1}^n {{W_i}{x_i} + b}) $ |
常用的激活函数包括逻辑函数(logistic)以及双曲正切函数(tanh)[15]:
| $\begin{array}{l}{f_{\rm{\log istic}}}({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}}) = \displaystyle\frac{1}{{1 + {{\rm{e}}^{ - ({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}})}}}}\\[10pt]{f_{\tanh }}({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}}) = \displaystyle\frac{{{{\rm{e}}^{{{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}}}} - {{\rm{e}}^{ - ({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}})}}}}{{{{\rm{e}}^{{{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}}}} + {{\rm{e}}^{ - ({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{\mathit{\boldsymbol{x}}} + {\mathit{\boldsymbol{b}}})}}}}\end{array}$ |
在神经网络训练过程中,需要最小化网络输入输出差值。由于自编码器的无监督性,需要将损失函数(loss function)
| $J({\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{b}}}) = \frac{1}{m}\sum\nolimits_{i = 1}^m {\frac{1}{2}} \left\| {{h_{{\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{b}}}}}\left( {{{\mathit{\boldsymbol{x}}}^{(i)}}} \right) - {{\mathit{\boldsymbol{x}}}^{(i)}}} \right\|_2^2 + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{W}}} \right\|_2^2$ |
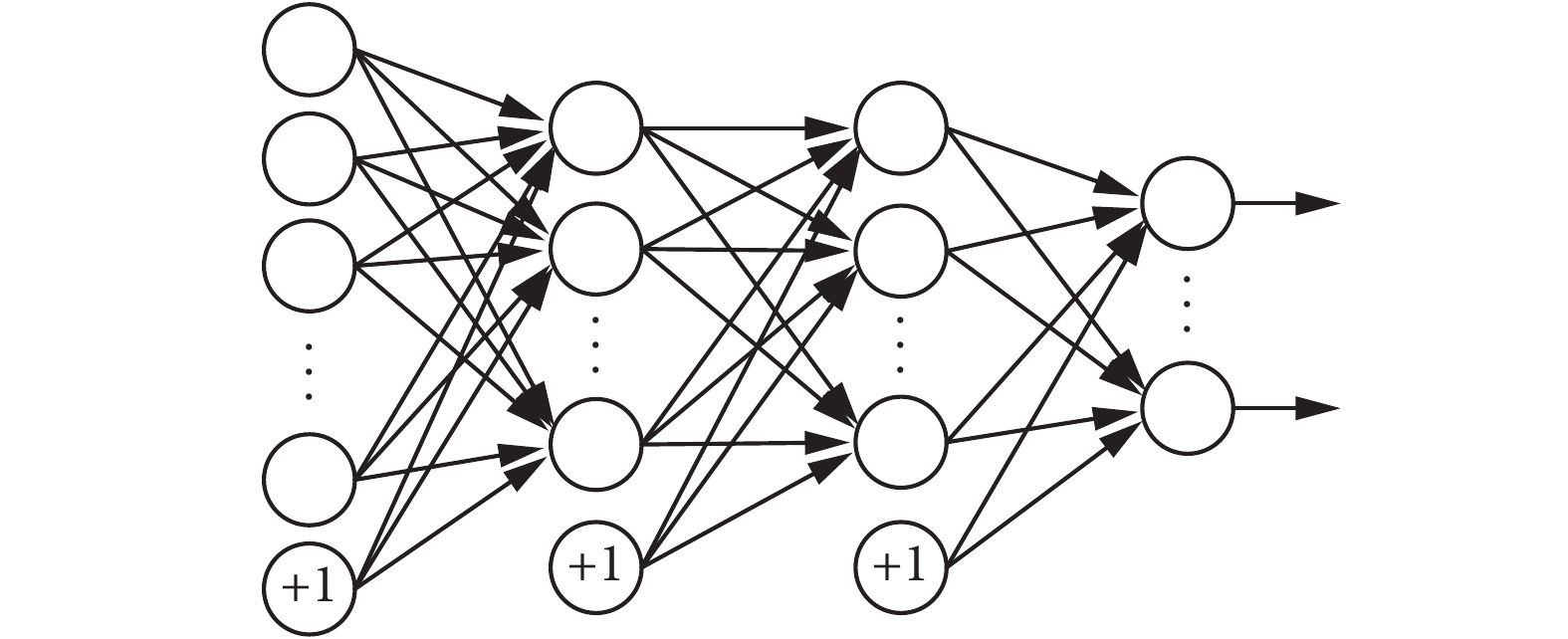
栈式自编码网络是将多个自编码器堆叠而成的深度网络,也是深度学习的一个典型模型。当将原始数据输入到首个训练好的自编码器后,它的隐藏层就学习到了一阶特征表示。然后这层隐藏层特征就作为另一个自编码器的输入,用来学习二阶特征表示。以此类推,原始数据的多阶特征表示便可以逐一得到。在构建深度网络的时候,各个自编码器需要去除输出层,只保留各阶学习到的特征表示。图2给出了包含两个隐藏层和一个最终分类器输出层的栈式自编码网络。
|
图 2 栈式自编码器示意图 Fig.2 Stacked auto-encoder diagram |
通常,含有多个隐藏层的栈式自编码网络包含数以百万个模型参数。要训练这样的深度网络,需要大量的带标签的训练数据集。然而,现实中这样规模庞大的有标签数据集并不多见,直接从几百个或者几千个训练图像中学习如此众多的参数是一件十分困难的事情。现有的解决方式包括手工标注数据集或者进行数据扩充,不仅需要繁复的工作,而且极大地增加了任务的执行时间。那么,需要每次都为新的识别任务寻找上万个有标签的数据集吗?
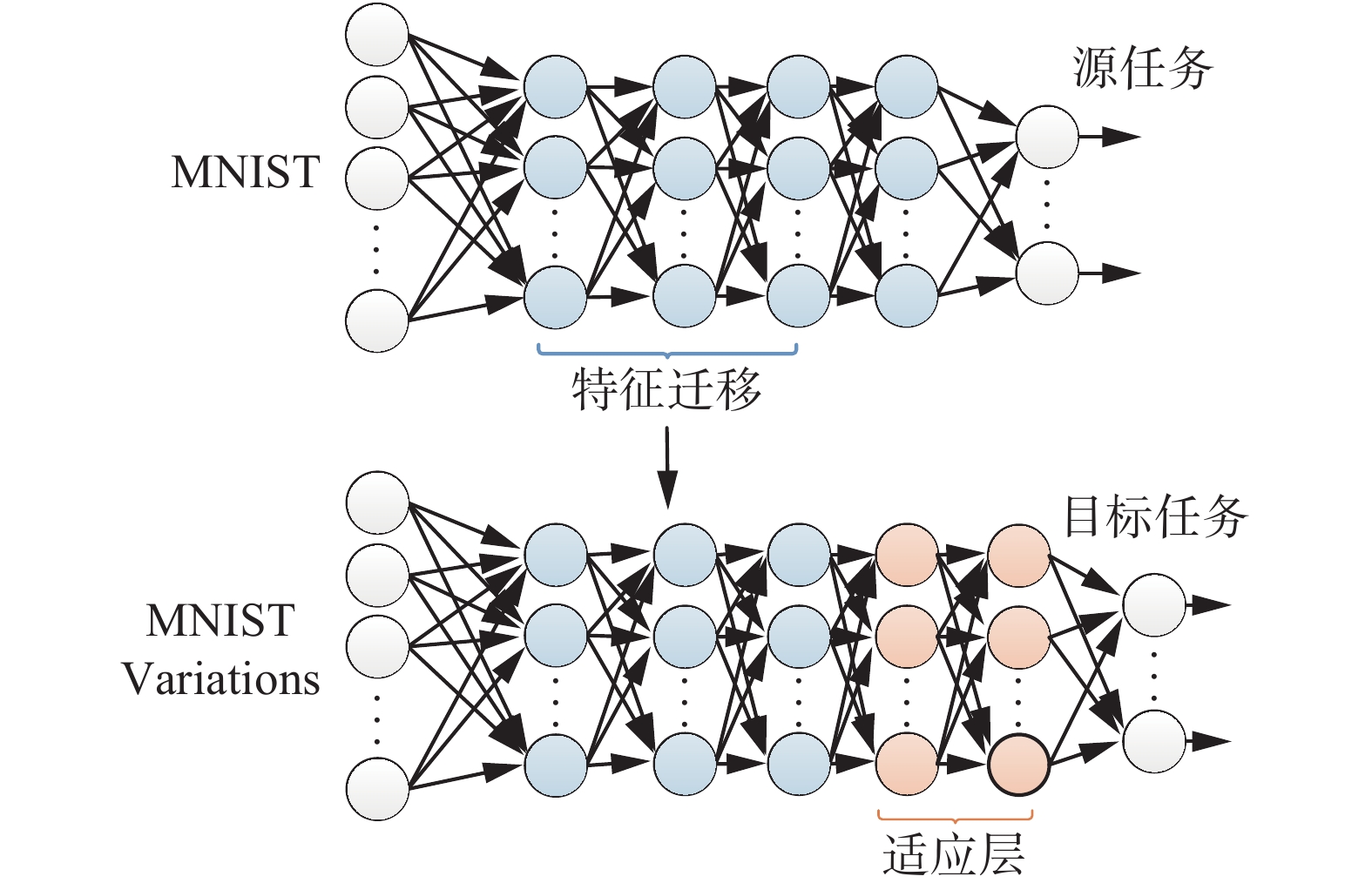
特征迁移模型的关键思想是将栈式自编码网络的内部隐藏层当作一个通用的中间级图像特征提取器。在源任务(source task)数据集(如MNIST)上预训练得到的图像特征能够被复用在其他的目标任务(target task)数据集(如MNIST variations)上。模型如图3所示,图中省略了偏置结点。
|
图 3 特征迁移模型示意图 Fig.3 Feature transfer model diagram |
对于源任务,我们采用含有4层隐藏层的栈式自编码网络。图3中第1个神经网络模型中最左层L1为网络的输入层(input layer),中间L2、L3、L4、L5是4个隐藏层(hidden layer),最后一层L6为输出层(output layer)。记
| ${{\mathit{\boldsymbol{z}}}^{(l + 1)}} = {{\mathit{\boldsymbol{W}}}^{(l)}}{{\mathit{\boldsymbol{a}}}^{(l)}} + {{\mathit{\boldsymbol{b}}}^{(l)}}$ |
| ${{\mathit{\boldsymbol{a}}}^{(l + 1)}} = f\left( {{\mathit{\boldsymbol{z}}}^{(l + 1)}} \right)$ |
利用式(1)~(2),可以依次计算出图3中第1个神经网络的L2、L3、L4、L5的输出值,从而可以以前向传播(forward propagation)的方式得到整个栈式自编码网络的输出
目标任务旨在为MNIST-variations数据集输出正确的数字标签。由于手工标注数据集费时费力,因此在一定程度上限制了MNIST-variations的规模。为了在小规模数据集上顺利地训练深度网络并获得正确的识别结果,特征迁移模型保留在大规模数据集上训练的网络模型参数,作为中间级特征迁移到新的识别任务中。在上述含有4层隐藏层的栈式自编码网络的基础上,保持前三层隐藏层的网络参数不变,移除最后一层隐藏层,并在靠近输出层增加两层随机初始化的隐藏层,以此获得目标任务的栈式自编码网络结构。通过这样的设置,模型既保留了MNIST数据集的中级图像特征,又为MNIST-variations上进行训练时留有调整的余地。
特征迁移模型具有能够通过实验证明的理论依据,即尽管不同图像的表现形式不同,但它们共享低中级层次的图像特征[16]。图像低级特征通常代表图像中特定的方向和位置上的边缘,通过发现边缘的特定排列来检测图形;中级特征能够集合这些图形到更大的组合,一般对应于熟悉的物体部件。而新网络模型所增加的两层隐藏层,作为适应层,能够检测到由部件组合而成的完整物体,在手写体数字的例子中即对应于完整的字符。
网络模型的输出层采用Softmax分类器来解决多分类问题,输出层的神经元个数k代表样本类标签的k个可取值。因此,对于m个训练样本
| ${h_{\mathit{\boldsymbol{\theta }}}}({\mathit{\boldsymbol{x}}}) = \left[ {\begin{array}{*{20}{c}}{p(y = 1|{\mathit{\boldsymbol{x}}};{\mathit{\boldsymbol{\theta }}})}\\ \vdots \\{p(y = k|{\mathit{\boldsymbol{x}}};{\mathit{\boldsymbol{\theta }}})}\end{array}} \right] = \frac{1}{{\sum\nolimits_{i = 1}^k {{{\rm{e}}^{{\mathit{\boldsymbol{\theta}}}_i^{\rm{T}}{\mathit{\boldsymbol{x}}}}}} }}\left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^{{\mathit{\boldsymbol{\theta}}}_1^{\rm{T}}{\mathit{\boldsymbol{x}}}}}}\\ \vdots \\{{{\rm{e}}^{{\mathit{\boldsymbol{\theta}}} _k^{\rm{T}}{\mathit{\boldsymbol{x}}}}}}\end{array}} \right]$ |
式中:
| $J({\mathit{\boldsymbol{\theta }}}) = - \frac{1}{m}\sum\nolimits_{i = 1}^m {\sum\nolimits_{j = 1}^k {1\left\{ {{y^{(i)}} = j} \right\}} } \log \frac{{{{\rm{e}}^{{\mathit{\boldsymbol{\theta}}} _l^{\rm{T}}{{\mathit{\boldsymbol{x}}}^{(i)}}}}}}{{\sum\nolimits_{l = 1}^k {{{\rm{e}}^{{\mathit{\boldsymbol{\theta}}} _l^{\rm{T}}{{\mathit{\boldsymbol{x}}}^{(i)}}}}} }}$ |
式中:指示函数(indicator function)1
| $1\left\{ {{y^{(i)}} = j} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}}{1,} &\quad {{y^{(i)}} = j}\\{0,} &\quad {{y^{(i)}} \ne j}\end{array}} \right.$ |
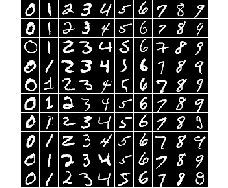
MNIST数据集由0~9的手写体数字组成,10种数字构成了10类数据。MNIST包含60 000张训练图像和10 000张测试图像。图4给出了MNIST数据集的一些示例样本。
|
图 4 MNIST示例样本 Fig.4 MNIST samples |
MNIST variations包含MNIST的4种变体数据集,包括:MNIST-rot,即在手写体数字上施加一些随机旋转;MNIST-back-rand,即在数字图像中插入随机的背景;MNIST-back-image,一小块黑白图像被用作数字图像的背景;MNIST-rot-back-image,即MNIST-rot与MNIST-back-image相结合。图5给出了MNIST-variations数据集的一些示例样本。

|
图 5 MNIST-variations示例样本 Fig.5 MNIST-variations samples |
特征迁移模型所使用的两个栈式自编码网络的网络结构中神经元结点的分布如下:第1个网络隐藏层结点数依次为[784, 200, 100, 50, 100, 10],第2个网络依次为[784, 200, 100, 50, 100, 200, 10]。在MNIST数据集上训练得到的中级图像特征如图6。

|
图 6 MNIST中级特征 Fig.6 MNIST mid-level features |
借助中级图像特征的迁移,在MNIST-variations数据集上同样获得了不错的中级图像特征,如图7所示。
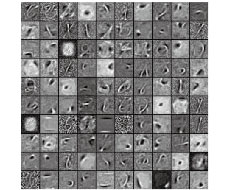
|
图 7 MNIST-variations中级特征 Fig.7 MNIST-variations mid-level features |
为了验证特征迁移模型的识别效果,输出层全部采用Softmax分类器进行分类,我们在MNIST-variations数据集上利用栈式自编码网络(stacked auto-encoder,SAE)、受限玻尔兹曼机(restricted Boltzmann machine, RBM)、降噪自编码器(denoising auto-encoder,DAE)、收缩自编码器(contracting auto-encoder,CAE)分别与特征迁移模型的分类错误率进行实验比较,比较结果如表1所示。
| 表 1 分类错误率 Tab.1 Classification error rate |
作为深度学习模型的一种,栈式自编码网络在模式识别领域已然卓有成效。相对于手工设计的低级特征而言,深度网络的成功主要归因于它们学习丰富的中间级特征的能力。然而在现实应用中,带有标签的大规模数据集通常是稀缺的。在深度神经网络强大的表征能力下,数据不充足往往会使模型陷入过拟合的尴尬情形。为了解决在小规模数据样本下训练深度神经网络的问题,我们提出一个特征迁移模型。我们展示了如何将学习到的中级图像特征有效地迁移到新的视觉识别任务中。实验结果表明,尽管源任务与目标任务采用的数据集之间存在差异,但是特征迁移模型仍然能够训练出目标数据集的图像特征,并且在目标任务的识别过程中能够达到优于经典深度学习模型的分类效果。
| [1] |
HINTON G E, ZEMEL R S. Autoencoder minimum description length and helmholtz free energy[C]//Conference on Neural Information Processing Systems(NIPS). Denver, USA, 1993: 3–10.
( 0) 0)
|
| [2] |
SOCHER R, HUANG E H, PENNINGTON J, et al. Dynamic pooling and unfolding recursive autoencoders for paraphrase detection[C]//Proc Neural Information and Processing Systems. Granada, Spain, 2011: 801–809.
( 0) 0)
|
| [3] |
SWERSKY K, RANZATO M, BUCHMAN D, et al. On score matching for energy based models: generalizing autoencoders and simplifying deep learning[C]//Proc Int’l Conf Machine Learning Bellevue. Washington, USA, 2011: 1201–1208.
( 0) 0)
|
| [4] |
FISCHER A, IGEL C. An introduction to restricted Boltzmann machines[C]//Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications. Guadalajara, Mexico, 2012: 14–36.
( 0) 0)
|
| [5] |
BREULEUX O, BENGIO Y, VINCENT P. Quickly generating representative samples from an RBM-derived process[J]. Neural computation, 2011, 23(8): 2053-2073. ( 0) 0)
|
| [6] |
COURVILLE A, BERGSTRA J, BENGIO Y. Unsupervised models of images by spike-and-slab RBMs[C]//Proc Int’l Conf Machine Learning. Bellevue, Washington, USA, 2011: 1145–1152.
( 0) 0)
|
| [7] |
SCHMAH T, HINTON G E, ZEMEL R, et al. Generative versus discriminative training of RBMs for classification of fMRI images[C]//Proc Neural Information and Processing Systems. Vancouver, Canada, 2008: 1409–1416.
( 0) 0)
|
| [8] |
ERHAN D, BENGIO Y, COURVILLE A, et al. Why does unsupervised pre-training help deep learning?[J]. Machine learning research, 2010, 11: 625-660. ( 0) 0)
|
| [9] |
VINCENT P. Extracting and composing robust features with denoising auto-encoders[C]//International Conference on Machine Learning(ICML). Helsinki, Finland, 2008: 1096–1103.
( 0) 0)
|
| [10] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Machine learning research, 2010, 11: 3371-3408. ( 0) 0)
|
| [11] |
CHEN M, XU Z, WINBERGER K Q, et al. Marginalized denoising autoencoders for domain adaptation[C]//International Conference on Machine Learning. Edinburgh, Scotland, 2012: 1206–1214.
( 0) 0)
|
| [12] |
VINCENT P. A connection between score matching and denoising autoencoders[J]. Neural computation, 2011, 23(7): 1661-1674. ( 0) 0)
|
| [13] |
RIFAI S. Contractive auto-encoders: explicit invariance during feature extraction[C]//Proceedings of the Twenty-eight International Conference on Machine Learning. Bellevue, USA, 2011: 833–840
( 0) 0)
|
| [14] |
RIFAI S, BENGIO Y, DAUPHIN Y, et al. A generative process for sampling contractive auto-encoders[C]//Proc Int’l Conf Machine Learning. Edinburgh, Scotland, UK, 2012: 1206–1214.
( 0) 0)
|
| [15] |
LECUN Y. Neural networks: tricks of the trade (2nd ed.) [M]. Germany: Springer, 2012: 9–48
( 0) 0)
|
| [16] |
ZEILER M D, TAYLOR G W, FERGUS R. Adaptive deconvolutional networks for mid and high level feature learning[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 2013–2025.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


