Generalized dominance-based multi-granularity intuitionistic fuzzy rough set and acquisition of decision rules
直觉模糊集是Atanassov[1-3]在系统研究Zadeh[4]模糊集理论的基础上于1986年提出的。与传统Zadeh模糊集相比,由于同时考虑了元素的隶属度、非隶属度和犹豫度3个方面的信息,因此在表达和处理模糊性、不确定性等问题的时候更具灵活性和实用性。近年来将直觉模糊集理论[5-6]与粗糙集理论结合研究受到了广泛关注。
经典的粗糙集理论[7-8]建立在一个等价关系之上,即处理单个粒空间上的目标近似逼近理论。考虑到多个属性之间的关系可能是相互独立的,文献[9-12]从多个角度、多个层次出发,提出了多粒度粗糙集的概念。此后,许多学者开始了多粒度粗糙集的相关研究[13-18]。实际问题中,经常需要考虑描述对象的属性具有顺序性,如距离远近、人口密度等,S. Greco[19-20]等提出了基于优势关系的粗糙集模型,并将该方法引入到模糊信息系统中。以往研究中要么是建立在经典关系或者模糊关系上[21]的多粒度优势关系粗糙集,要么是考虑在单个粒度上的优势直觉模糊粗糙集,并未考虑将二者结合起来研究。
本文主要考虑在直觉模糊语义下,通过引入三角模和三角余模,定义了强、弱、平均3种优势关系,得到了与之对应的3种优势类。在此基础上提出了广义优势关系多粒度直觉模糊粗糙集模型。通过讨论该模型的主要性质,进而获取决策规则。
1 预备知识
1.1 直觉模糊信息系统
定义1[1-3] 设U是非空集合,称
${{A}} \!=\! \left\{\! {\left\langle {{\mu _{{A}}}\left( x \right),{\nu _{{A}}}\left( x \right)} \right\rangle \! |} \right.$
$\left. {x \in U} \right\}$
为直觉模糊集,其中
${\mu _{{A}}}\left( x \right)$
,
${\nu _{{A}}}\left( x \right) \in \left[ {0,1} \right]$
分别为U中元素x属于A的隶属度和非隶属度,且对于
$\forall x \in U$
满足关系式
$0 \leqslant {\mu _{{A}}}\left( x \right) + {\nu _{{A}}}\left( x \right) \leqslant 1$
。称
$1 - {\mu _{{A}}}\left( x \right) - $
$ {\nu _{{A}}}\left( x \right)$
为x属于A的犹豫度或不确定度。用
${\rm{IFS}}\left( U \right)$
表示U上全体直觉模糊子集,
$P\left( U \right)$
表示U上全体经典子集。
定义2[1] 对于任意
${{A}},{{B}} \in {\rm{IFS}}\left( U \right)$
,即
${{A}} \!=\! \left\{ {\left\langle {{\mu _{{A}}}\left( x \right),} \right.} \right.$
$\left. {\left. {{\nu _{{A}}}\left( x \right)} \right\rangle \left| {x \in U} \right.} \right\},{{B}} = \left\{ {\left\langle {{\mu _{{B}}}\left( x \right),{\nu _{{B}}}\left( x \right)} \right\rangle \left| {x \in U} \right.} \right\}$
,有:
1)
${{A}} \subseteq {{B}} \Leftrightarrow \forall x \in U$
,
${\mu _{{A}}}\left( x \right) \leqslant {\mu _{{B}}}\left( x \right)$
且
${\nu _{{A}}}\left( x \right) \geqslant {\nu _{{B}}}\left( x \right)$
;
2)
${{A}} \!=\! {{B}} \Leftrightarrow \forall x \in U$
,
${\mu _{{A}}}\left( x \right) = {\mu _{{B}}}\left( x \right)$
,且
${\nu _{{A}}}\left( x \right) \! \geqslant \! {\nu _{{B}}}\left( x \right)$
;
3)
$\sim {{A}} = \left\{ {\left\langle {{\nu _{{A}}}\left( x \right),{\mu _{{A}}}\left( x \right)} \right\rangle \left| {x \in U} \right.} \right\}$
;
4)
${{A}} \cap {{B}} \Leftrightarrow \left\{ {\left\langle {{\mu _{{A}}}\left( x \right) \wedge {\mu _{{B}}}\left( x \right),{\nu _{{A}}}\left( x \right) \vee {\nu _{{B}}}\left( x \right)} \right\rangle \left| {x \in U} \right.} \right\}$
;
5)
${{A}} \cup { B} \Leftrightarrow \left\{ {\left\langle {{\mu _{{A}}}\left( x \right) \vee {\mu _{{{B}}}}\left( x \right),{\nu _{{A}}}\left( x \right) \wedge {\nu _{{{B}}}}\left( x \right)} \right\rangle \left| {x \in U} \right.} \right\}$
。
设
$\alpha = \left( {{u_\alpha },{v_\alpha }} \right)$
,其中
${\mu _\alpha }$
,
${\nu _\beta } \in \left[ {0,1} \right]$
,且
$0 \leqslant {\mu _\alpha } + {\nu _\alpha } \leqslant 1$
,则称α为一个直觉模糊数。全体直觉模糊数集合记为IFN。它的得分函数
$s\left( \alpha \right) = {u_\alpha } - {v_\alpha }$
,精确函数为
$h\left( \alpha \right) = {u_\alpha } + {v_\alpha }$
,利用得分函数和精确函数就可以给出比较两个直觉模糊数大小的方法。
定义3[22] 对于
$\forall {\alpha _1},\,{\alpha _2} \in {\rm{INF}}$
,如果
$\forall a,\,b,\,c \in $
[0,1],
$s\left( {{\alpha _1}} \right) < s\left( {{\alpha _2}} \right)$
,则
${\alpha _1} < {\alpha _2}$
;如果
$s\left( {{\alpha _1}} \right) = s\left( {{\alpha _2}} \right)$
,且若
$h\left( {{\alpha _1}} \right) < h\left( {{\alpha _2}} \right)$
,则
${\alpha _1} < {\alpha _2}$
;若
$h\left( {{\alpha _1}} \right) = h\left( {{\alpha _2}} \right)$
,则
${\alpha _1} = $
$ {\alpha _2}$
。
定义4[1-3] 称
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$
为对象集,
$A = \left\{ {{a_1},{a_2}, \cdots ,{a_m}} \right\}$
为条件属性集,R为U到A的直觉模糊二元关系,即
$R = \left\{ {\left\langle {\left( {x,a} \right),{\mu _a}\left( x \right),{\nu _a}\left( x \right)} \right\rangle \left| {\left( {x,a} \right) \in U \times A \cup \left\{ d \right\}} \right.} \right\}$
。其中
${\mu _a}:$
$U \times A \to \left[ {0,1} \right],{\nu _a}:U \times A \to \left[ {0,1} \right]$
,且满足
$\forall \left( {x,a} \right) \in U \times A$
,
$0 \leqslant {\mu _a}\left( x \right) + {\nu _a}\left( x \right) \leqslant 1$
。本文中记
$U \times A$
上的直觉模糊关系全体为
${\rm{IFR}}\left( {U \times A} \right)$
。
1.2 三角模算子
定义5[23] 若映射
$N:\left[ {0,1} \right] \to \left[ {0,1} \right]$
,
$\forall a,b \in \left[ {0,1} \right]$
若满足以下条件:
1)
$N\left( 0 \right) = 1$
,
$N\left( 1 \right) = 0$
(边界性);
2)
$a \leqslant b$
,则
$N\left( a \right) \geqslant N(b)$
(单调性);
称映射N为模糊补映射(或模糊负算子)。
若
$\forall a \in \left[ {0,1} \right]$
均有
$N\left( a \right) = 1 - a$
成立,称N为标准模糊补算子,记为Ns。
定义6[24] 若映射
$T : \left[ {0,1} \right] \, \times \, \left[ {0,1} \right] \, \to \, \left[ {0,1} \right]$
,若
$\forall a,b,c \in \left[ {0,1} \right]$
,满足以下条件:
1)
$T\left( {a,1} \right) = a$
(边界性);
2) 若
$b \leqslant c$
,则
$T\left( {a,b} \right) \leqslant T\left( {a,c} \right)$
(单调性);
3)
$T\left( {a,b} \right){\rm{ = }}T\left( {b,a} \right)$
(交换性);
4)
$T\left( {a,T\left( {b,c} \right)} \right){\rm{ = }}T\left( {T\left( {a,b} \right),c} \right)$
(结合性);
则称T为三角模(t-模)。
定义7[24] 若映射
$S:\left[ {0,1} \right] \, \times \, \left[ {0,1} \right] \, \to \, \left[ {0,1} \right]$
,若
$\forall a,b,c \in \left[ {0,1} \right]$
,满足以下条件:
1)
$S\left( {a,0} \right) = a$
(边界性);
2) 若
$b \leqslant c$
,则
$S\left( {a,b} \right) \leqslant S\left( {a,c} \right)$
(单调性);
3)
$S\left( {a,b} \right){\rm{ = }}S\left( {b,a} \right)$
(交换性);
4)
$S\left( {a,S\left( {b,c} \right)} \right){\rm{ = }}S\left( {S\left( {a,b} \right),c} \right)$
(结合性);
称S为三角模余模(t-余模)。
T和ST关于模糊补算子N满足是对偶的当且仅当
$\forall a,b \in \left[ {0,1} \right]$
,
$N\left( {T\left( {a,b} \right)} \right) = {S_T}\left( {N\left( a \right),N\left( b \right)} \right)$
或
$N\left( {{S_T}\left( {a,b} \right)} \right) = T\left( {N\left( a \right),N\left( b \right)} \right)$
,称
$\left( {T,{S_T},N} \right)$
为对偶三元组。常见的对偶三元组有:
•
$\min \text{-} \max :\left( {\min \left( {a,b} \right),\max \left( {a,b} \right),{N_S}} \right)$
;
•
${\rm{product \text{-} sum}}:\left( {ab,a + b - 1,{N_S}} \right)$
;
•
${\rm{Lukasiewicz}}:\left( {\max (0,a + b - 1),\min (1,a + b),{N_S}} \right)$
。
2 多粒度直觉模糊粗糙集
2.1 直觉模糊信息系统中的优势关系
定义8 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \subseteq A$
,
$\forall x,y \in U$
,称
$R_{f,B}^{\leqslant} = \left\{ {\left( {x,y} \right) \in U \times U:{f_a}\left( x \right) \leqslant {f_a}\left( y \right),} \right.$
$\left. {\forall a \in B} \right\}$
为直觉模糊信息系统中属性子集B的普通优势关系,其中
${f_a}\left( x \right) = \left\langle {{u_a}\left( x \right),{v_a}\left( x \right)} \right\rangle $
。
定义9 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \subseteq A$
,
$\forall x,y \in U$
,称
$R_{T,B}^{\leqslant } = \left\{ {\left( {x,y} \right) \in U \times U:{T_a}\left( x \right) \leqslant {T_a}\left( y \right),} \right.$
$\left. {\forall a \in B} \right\}$
为直觉模糊信息系统中属性子集B的强优势关系, 其中
${T_a}\left( x \right) = T\left( {{u_a}\left( x \right),N\left( {{v_a}\left( x \right)} \right)} \right)$
。
定义10 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \subseteq A$
,
$\forall x,y \in U$
,称
$R_{S,B}^ \leqslant = \left\{ {\left( {x,y} \right) \in U \times U:{S_a}\left( x \right) \leqslant {S_a}\left( y \right),} \right.$
$\left. {\forall a \in B} \right\}$
为直觉模糊信息系统中属性子集B的弱优势关系,其中
${S_a}\left( x \right) = S\left( {{u_a}\left( x \right),N\left( {{v_a}\left( x \right)} \right)} \right)$
。
定义11 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \! \subseteq \! A$
,
$\forall x,y \! \in \! U$
,称
$R_{AV,B}^{\leqslant} \!=\! \left\{ {\left( {x,y} \right) \! \in \! U \! \times \! U:A{V_a} \! \left( x \right) \! \leqslant \! A{V_a}\left( y \right),} \right.$
$\left. {\forall a \in B} \right\}$
为直觉模糊信息系统中属性子集B的平均优势关系,其中
$A{V_a}\left( x \right) = \displaystyle\frac{1}{2}\left( {T\left( {{u_a}\left( x \right),N\left( {{v_a}\left( x \right)} \right)} \right) + {S_T}\left( {{u_a}\left( x \right),} \right.} \right.$
$\left. {\left. {N\left( {{v_a}\left( x \right)} \right)} \right)} \right)$
。
根据以上定义的3种优势关系,我们可以得到相应的3种优势类。
定义12 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \subseteq A$
,
$\forall x,y \in U$
,称
$\left[ x \right]_{T,B}^ \leqslant $
为对象x的强优势类,其中
$\left[ x \right]_{T,B}^ \leqslant = \left\{ {y \in U:\left( {x,y} \right) \in R_{T,B}^ \leqslant } \right\}$
。
类似地,将
$R_{T,B}^ \leqslant $
替换成
$R_{f,B}^ \leqslant ,R_{S,B}^ \leqslant ,R_{AV,B}^ \leqslant $
可以得到对象x的普通优势类
$\left[ x \right]_{f,B}^ \leqslant $
、弱优势类
$\left[ x \right]_{S,B}^ \leqslant $
、平均优势类
$\left[ x \right]_{AV,B}^ \leqslant $
。
定理1 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$B \subseteq A$
,
$\forall x,y \in U$
,有
$\left[ x \right]_{AV,B}^{\leqslant} \subseteq \left[ x \right]_{T,B}^{\leqslant} \cup \left[ x \right]_{S,B}^{\leqslant} $
。
证明 假设
$y \notin \left[ x \right]_{T,B}^{\leqslant} \cup \left[ x \right]_{S,B}^{\leqslant} $
,有
$y \notin \left[ x \right]_{T,B}^{\leqslant} $
且
$y \notin \left[ x \right]_{S,B}^{\leqslant} $
即
${T_a}\left( x \right) > {T_a}\left( y \right)$
且
${S_a}\left( x \right) > {S_a}\left( y \right)$
。根据定义11可得
$A{V_a}\left( x \right) > A{V_a}\left( y \right)$
,由定义12可知
$y \notin \left[ x \right]_{AV,B}^{\leqslant} $
,从而证得
$\left[ x \right]_{AV,B}^{\leqslant} \subseteq \left[ x \right]_{T,B}^{\leqslant} \cup \left[ x \right]_{S,B}^{\leqslant} $
。
定理2 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$A{V^1},A{V^2},A{V^3}$
分别由常见的对偶三元组生成,对于
$\left( {U,A,R} \right)$
,
$U \!=\! \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$
有
$\left[ x \right]_{A{V^1},B}^{\leqslant} = \left[ x \right]_{A{V^2},B}^{\leqslant} = \left[ x \right]_{A{V^3},B}^{\leqslant} $
。
证明 只需要证明对于
$\forall \left( {x,a} \right) \in U \times A$
均有
$A{V_a}^1\left( x \right) = A{V_a}^3\left( x \right) = A{V_a}^3\left( x \right)$
即可。
|
$\begin{array}{c}AV_a^1\left( x \right) = \displaystyle\frac{1}{2}\left( {\min \left( {{u_a}\left( x \right),N\left( {{v_a}\left( x \right)} \right)} \right) + } \right.\\\left. {\max \left( {{u_a}\left( x \right),N\left( {{v_a}\left( x \right)} \right)} \right)} \right) = \\{\left( {{u_a}\left( x \right) + N\left( {{v_a}\left( x \right)} \right)} \right)/2}\end{array}$
|
|
$\begin{array}{c}AV_a^2\left( x \right) = \displaystyle\frac{1}{2}\left( {{u_a}\left( x \right) \cdot N\left( {{v_a}\left( x \right)} \right) + {u_a}\left( x \right) + } \right.\\\left. {N\left( {{v_a}\left( x \right)} \right) - {u_a}\left( x \right) \cdot N\left( {{v_a}\left( x \right)} \right)} \right) = \\\left( {{u_a}\left( x \right) + N\left( {{v_a}\left( x \right)} \right)} \right)/2\end{array}$
|
|
$\begin{array}{c}AV_a^3\left( x \right) = \displaystyle\frac{1}{2}\left( {\max \left( {0,{u_a}\left( x \right) + N\left( {{v_a}\left( x \right)} \right) - 1} \right) + } \right.\\\left. {\min \left( {1,{u_a}\left( x \right) + N\left( {{v_a}\left( x \right)} \right)} \right)} \right) = \\\displaystyle\frac{1}{2}\left( {\max \left( {0,{u_a}\left( x \right) - {v_a}\left( x \right)} \right) + } \right.\\\left. {\min \left( {1,{u_a}\left( x \right) + 1 - {v_a}\left( x \right)} \right)} \right)\end{array}$
|
分两种情况讨论
$AV_a^3\left( x \right)$
:
1) 若
${u_a}\left( x \right) - {v_a}\left( x \right) \geqslant 0$
,
$\min \left( {1,{u_a}\left( x \right) + 1 - {v_a}\left( x \right)} \right) = 1$
,
$\max \left( {0,{u_a}\left( x \right) - {v_a}\left( x \right)} \right) = {u_a}\left( x \right) - {v_a}\left( x \right)$
,则有
$AV_a^3 = {u_a}\left( x \right) + $
$ N\left( {{v_a}\left( x \right)} \right)$
;
2) 若
${u_a}\left( x \right) - {v_a}\left( x \right) < 0$
,有
$\min \left( {1,{u_a}\left( x \right) + 1 - {v_a}\left( x \right)} \right) = $
${u_a}\left( x \right) \!+\! 1 \!-\! {v_a}\left( x \right)$
,
$\max \left( {0,{u_a}\left( x \right) \!-\! {v_a}\left( x \right)} \right) \!=\! 0$
,则
$AV_a^3 \!=\! {u_a}\left( x \right) \!+ $
$ N\left( {{v_a}\left( x \right)} \right)$
,证毕。
例1 假设一场选举中有6个候选人
$\left\{ {{x_1},{x_2}, \cdots ,} \right.$
$\left. {{x_6}} \right\}$
,一名投票者A对6位候选人的支持意向表示为
$ \left\langle \right. $
0.8,0, 1
$ \left. \right\rangle $
,
$ \left\langle \right. $
0.4,0.2
$ \left. \right\rangle $
,
$ \left\langle \right. $
0.5,0.3
$ \left. \right\rangle $
,
$ \left\langle \right. $
0.5,0.4
$ \left. \right\rangle $
,
$ \left\langle \right. $
0.6,0.4
$ \left. \right\rangle $
,
$ \left\langle \right. $
0.4,0.1
$ \left. \right\rangle $
,利用定义9~定义12的优势关系,计算6位候选人优势关系如下:
1)
${x_4} \leqslant {x_2} \leqslant {x_3} \leqslant {x_5} \leqslant {x_6} \leqslant {x_1}$
;
2)
${x_2} = {x_6} \leqslant {x_4} = {x_3} \leqslant {x_5} \leqslant {x_1}$
;
3)
${x_4} = {x_5} \leqslant {x_3} \leqslant {x_2} \leqslant {x_6} = {x_1}$
;
4)
${x_4} \leqslant {x_2} = {x_3} = {x_5} \leqslant {x_6} \leqslant {x_1}$
。
结果显示,
$\left[ x \right]_{f,B}^{\leqslant} $
过多关注支持与反对的绝对差,
$\left[ x \right]_{T,B}^{\leqslant} $
侧重于表达相对于属性子集B支持程度绝对高于x的对象集合,
$\left[ x \right]_{S,B}^{\leqslant} $
侧重于表达相对于属性子集B支持程度可能高于x的对象集合,
$\left[ x \right]_{AV,B}^{\leqslant} $
则侧重于表达相对于属性子集B支持程度平均高于x的对象集合。若
$\forall \left( {x,a} \right) \in U \times A$
,都有
${\mu _a}\left( x \right) + {\nu _a}\left( x \right) = 1$
,则
$\left[ x \right]_{f,B}^{\leqslant} = \left[ x \right]_{T,B}^{\leqslant} = \left[ x \right]_{S,B}^{\leqslant} = \left[ x \right]_{AV,B}^{\leqslant} $
均为普通模糊信息系统中的优势类。
定理3 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$
。对于
$\forall B \subseteq A$
,
$\left[ x \right]_{ \cdot ,B}^{\leqslant} $
是由
$R_{ \cdot ,B}^{\leqslant} $
生成的优势类, ·表示T,S,AV 3种算子,则
1)
$R_{ \cdot ,B}^{\leqslant} $
满足自反性和传递性;
2)
${x_j} \in \left[ {{x_k}} \right]_{ \cdot ,B}^{\leqslant} \Leftrightarrow \left[ {{x_j}} \right]_{ \cdot ,B}^{\leqslant} \subseteq \left[ {{x_k}} \right]_{ \cdot ,B}^{\leqslant} $
;
3)
$\left[ {{x_i}} \right]_{ \cdot ,B}^{\leqslant} = \cup \left\{ {\left[ {{x_j}} \right]_{ \cdot ,B}^{\leqslant} :{x_j} \in \left[ {{x_i}} \right]_{ \cdot ,B}^{\leqslant} } \right\}$
;
4)
$U = \bigcup\nolimits_{i = 1}^m {\left[ {{x_i}} \right]_{ \cdot ,B}^{\leqslant} } $
;
5)
$\left[ {{x_i}} \right]_{ \cdot ,B}^{\leqslant} = \left[ {{x_j}} \right]_{ \cdot ,B}^{\leqslant} \Leftrightarrow {T_{{a_i}}}\left( {{x_i}} \right) = {T_{{a_i}}}\left( {{x_j}} \right)$
,
$\forall {a_i} \in B$
。
证明 我们以
$\left[ x \right]_{T,B}^{\leqslant} $
为例,只证明2),其余均可直接由定义14直接证明。
充分性:若
${x_l} \in \left[ {{x_j}} \right]_{T,B}^{\leqslant} $
,则对于
$\forall {a_i} \in B$
有
${T_{{a_i}}}\left( {{x_j}} \right){\leqslant} $
$ {T_{{a_i}}}\left( {{x_l}} \right)$
;由于
${x_j} \in \left[ {{x_k}} \right]_{T,B}^{\leqslant} $
,则对于
$\forall {a_i} \in B$
有
${T_{{a_i}}}\left( {{x_k}} \right) {\leqslant}$
$ {T_{{a_i}}}\left( {{x_j}} \right)$
,成立,从而
${x_l} \in \left[ {{x_k}} \right]_{T,B}^{\leqslant} $
,即
$\left[ {{x_j}} \right]_{T,B}^{\leqslant} \subseteq \left[ {{x_k}} \right]_{T,B}^{\leqslant} $
。
必要性:根据
$R_{T,B}^{\leqslant} $
满足自反性有
${x_j} \in \left[ {x{}_j} \right]_{T,B}^{\leqslant} $
,由于
$\left[ {{x_j}} \right]_{T,B}^{\leqslant} \subseteq \left[ {{x_k}} \right]_{T,B}^{\leqslant} $
成立,故有
${x_j} \in \left[ {x{}_k} \right]_{T,B}^{\leqslant} $
。
2.2 多粒度优势直觉模糊粗糙集
根据文献[6-9]所提出的多粒度粗糙集的思想,以下给出优势关系下直觉模糊多粒度粗糙集定义。
定义13 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$
。
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A$
,
$\forall X \in U$
,
$\left[ x \right]_{T,{A_i}}^{\leqslant} $
是由
$R_{T,{A_i}}^{\leqslant} $
诱导产生的强优势关系类,则X在强优势关系下乐观多粒度下上近似集合分别为
|
$\begin{array}{c}\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( X \right) = \left\{ {x \in U:\left[ x \right]_{T,{A_1}}^{\leqslant} \subseteq X \vee \left[ x \right]_{T,{A_2}}^{\leqslant} } \subseteq \right.\\\left. { X \vee \cdots \vee \left[ x \right]_{T,{A_n}}^{\leqslant} \subseteq X} \right\}\\[5pt]\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( X \right) = \sim \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( { \sim X} \right)\end{array}$
|
式中
$ \sim X$
表示集合X的补集。
序对
$\left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( X \right),\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( X \right)} \right)$
称为强优势关系下X的乐观直觉模糊粗糙集。
定义14 设
$\left( {U,A,R} \right)$
为一个直觉模糊信息系统,
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$
。
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A$
,
$\forall X \in U$
,
$\left[ x \right]_{T,{A_i}}^{\leqslant} $
是由
$R_{T,{A_i}}^{\leqslant} $
诱导产生的强优势关系类,则X在强优势关系下悲观多粒度下上近似集合分别为
|
$\begin{array}{c}\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( X \right) = \left\{ {x \in U:\left[ x \right]_{T,{A_1}}^{\leqslant} \subseteq X \wedge \left[ x \right]_{T,{A_2}}^{\leqslant} } \subseteq \right.\\\left. { X \wedge \cdots \wedge \left[ x \right]_{T,{A_n}}^{\leqslant} \subseteq X} \right\},\\\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( X \right) = \sim \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( { \sim X} \right),\end{array}$
|
式中
$ \sim X$
表示集合X的补集。
序对
$\left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( X \right),\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( X \right)} \right)$
称为强优势关系下的悲观直觉模糊粗糙集。
上述定义的乐观多粒度下近似要求至少有一个粒度满足优势关系,而悲观多粒度下近似则要求在所有粒度空间中满足一致的优势关系。多粒度上近似均由下近似的补集定义得到。
3 多粒度优势粗糙直觉模糊集及决策规则获取
在直觉模糊决策信息系统中,由于被近似的决策属性集合是直觉模糊集合,而不是由决策属性确定的等价类集合,因此需要将上述结论进行推广。
3.1 多粒度优势粗糙直觉模糊集
定义15 设
$\left( {U,A \cup \left\{ d \right\},R} \right)$
为一个直觉模糊决策信息系统,其中
$U = \left\{ {{x_1}, {x_2}, \cdots ,{x_m}} \right\}$
,
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A$
,决策属性d基于强优势关系
$R_{T,{A_i}}^{\leqslant} $
的多粒度乐观下上近似集分别为
|
$\begin{array}{l}\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( d \right)\left( x \right) = \vee _{i = 1}^n\left\{ { \wedge \left\{ {d\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\leqslant}} \right\}} \right\}\\[5pt]\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( d \right)\left( x \right) = \wedge _{i = 1}^n\left\{ { \vee \left\{ {d\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\geqslant} } \right\}} \right\}\end{array}$
|
序对
$\left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( {{f_d}} \right),\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} O}} } \left( {{f_d}} \right)} \right)$
称为强优势关系下fd的乐观直觉模糊粗糙集。
定义16 设
$\left( {U,A \cup \left\{ d \right\},R} \right)$
为一个直觉模糊决策信息系统,其中
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$
,
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A$
,决策属性d基于强优势关系
$R_{T,{A_i}}^{\leqslant} $
的多粒度悲观下上近似集分别为
|
$\begin{array}{c}\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right)\left( x \right) = \wedge _{i = 1}^n\left\{ { \wedge \left\{ {{f_d}\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\leqslant}} \right\}} \right\}\\[5pt]\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {{f_d}} \right)\left( x \right) = \vee _{i = 1}^n\left\{ { \vee \left\{ {{f_d}\left( y \right):y \in \left[ x \right]_{T,{A_i}}^ {\geqslant} } \right\}} \right\}\end{array}$
|
序对
$\left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( X \right),\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( X \right)} \right)$
称为强优势关系下fd的悲观直觉模糊粗糙集。
例2 表1为一个关于风险投资的直觉模糊决策信息系统实例。其中
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_8}} \right\}$
表示风险投资项目;
$A = \left\{ {{a_1},{a_2},{a_3},{a_4}} \right\}$
为条件属性,表示不同领域专家对投资项目所在位置、人口密度、交通状况和投资额度给出的评价,d为决策属性。
表 1(Tab. 1
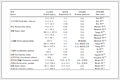
表 1 风险决策直觉模糊信息系统
Tab. 1 Intuitionistic fuzzy information system with risk decision
| U
|
a1 |
a2 |
a3 |
a4 |
d
|
| x1 |
$ \left\langle \right. $
0.90, 0.05
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.70, 0.20
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.20, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.70, 0.20
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.7, 0.2
$ \left. \right\rangle $
|
| x2 |
$ \left\langle \right. $
0.90, 0.05
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.20, 0.60
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.20, 0.50
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.8, 0.1
$ \left. \right\rangle $
|
| x3 |
$ \left\langle \right. $
0.10, 0.70
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.05
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.0, 1.0
$ \left. \right\rangle $
|
| x4 |
$ \left\langle \right. $
0.00, 0.90
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.10
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.10
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.80, 0.10
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.5, 0.4
$ \left. \right\rangle $
|
| x5 |
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.90
$ \left. \right\rangle $
|
$ \left\langle \right. $
1.00, 0.00
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.80, 0.05
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.4, 0.6
$ \left. \right\rangle $
|
| x6 |
$ \left\langle \right. $
0.30, 0.60
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.20, 0.70
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.00
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.15, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.3, 0.6
$ \left. \right\rangle $
|
| x7 |
$ \left\langle \right. $
0.00, 0.90
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.10
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.20, 0.60
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.0, 0.9
$ \left. \right\rangle $
|
| x8 |
$ \left\langle \right. $
0.90, 0.05
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.90, 0.10
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.10, 0.80
$ \left. \right\rangle $
|
$ \left\langle \right. $
1.00, 0.00
$ \left. \right\rangle $
|
$ \left\langle \right. $
0.6, 0.3
$ \left. \right\rangle $
|
|
表 1 风险决策直觉模糊信息系统
Tab.1 Intuitionistic fuzzy information system with risk decision |
若将例2中每个条件属性都看作一个独立的粒度空间,则根据定义15、定义16,决策属性d关于属性集合的多粒度乐观和悲观下、上近似集如下所示。
|
$\begin{array}{c}\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} O}} } \left( {{f_d}} \right) = \left\{ {\left\langle {0.6,0.3} \right\rangle ,\left\langle {0.6,0.3} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,} \right.\\[4.5pt]\left\langle {0.5,0.4} \right\rangle ,\left\langle {0.4,0.6} \right\rangle \left. {,\left\langle {0.3,0.6} \right\rangle ,\left\langle {0.0,0.9} \right\rangle ,\left\langle {0.6,0.3} \right\rangle } \right\}\\[4.5pt]\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( {{f_d}} \right) = \left\{ {\left\langle {0.7,0.2} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.4,0.6} \right\rangle ,} \right.\\[4.5pt]\left\langle {0.5,0.4} \right\rangle ,\left. {\left\langle {0.4,0.6} \right\rangle ,\left\langle {0.4,0.6} \right\rangle ,\left\langle {0.4,0.6} \right\rangle ,\left\langle {0.6,0.3} \right\rangle } \right\}\\[4.5pt]\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right) = \left\{ {\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,} \right.\\[4.5pt]\left. {\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle ,\left\langle {0.0,1.0} \right\rangle } \right\}\\[4.5pt]\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}P}} } \left( {{f_d}} \right) = \left\{ {\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle } \right.,\\[4.5pt]\left. {\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,\left\langle {0.8,0.1} \right\rangle ,} \right\}\end{array}$
|
定理4 设
$\left( {U,A \cup \left\{ d \right\},R} \right)$
为直觉模糊决策信息系统,其中
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A$
,则:
1)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) \subseteq {f_d} \subseteq \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)$
,
$\underline {{\mkern 1mu} \sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}P}} } \left( {{f_d}} \right) \subseteq $
${f_d} \subseteq \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}P}} } \left( {{f_d}} \right)$
;
2)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) = \cup _{i = 1}^n\underline {R_{T,{A_i}}^{{\leqslant} O}} \left( {{f_d}} \right)$
,
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} O}} } \left( {{f_d}} \right) =\cap _{i = 1}^n $
$ \overline {R_{T,{A_i}}^{ {\leqslant} O}} \left( {{f_d}} \right)$
;
3)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {{f_d}} \right) = \cap _{i = 1}^n\underline {R_{T,{A_i}}^{ {\leqslant} P}} \left( {{f_d}} \right)$
,
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right) =\cup _{i = 1}^n $
$ \overline {R_{T,{A_i}}^{ {\leqslant} P}} \left( {{f_d}} \right)$
;
4)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( {{f_d}} \right)} \right) = \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant}O}} } \left( {{f_d}} \right)$
,
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } $
$ \left( {\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( {{f_d}} \right)} \right) = \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)$
;
5)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right)} \right) = \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right)$
,
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } $
$\left( {\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {{f_d}} \right)} \right) = \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} P}} } \left( {{f_d}} \right)$
。
证明 这里只给出乐观多粒度情况下的证明,悲观多粒度的可类似得到。
1)
$\forall x \in U$
,根据定义15有
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( d \right)\left( x \right) = $
$ \vee _{i = 1}^n\left\{ { \wedge \left\{ {d\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\leqslant} } \right\}} \right\}$
。由近似关系的自反性知
$ \wedge \left\{ {d\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\leqslant} } \right\}{\leqslant} {f_d}\left( x \right)$
,从而
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( d \right)\left( x \right){\leqslant} \vee _{i = 1}^n $
$ \left( {{f_d}\left( x \right)} \right) = {f_d}\left( x \right)$
,即
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) \subseteq {f_d}$
成立。同理
${f_d} \subseteq $
$ \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} O}} } \left( {{f_d}} \right)$
。
2)
$\forall x \in U$
,由定义15有
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)\left( x \right) = \vee _{i = 1}^n $
$ \left\{ { \wedge \left\{ {d\left( y \right):y \in \left[ x \right]_{T,{A_i}}^{\leqslant}} \right\}} \right\} = \vee _{i = 1}^n\underline {R_{T,{A_i}}^{{\leqslant} O}} \left( {{f_d}} \right)\left( x \right)$
,即
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) = $
$ \cup _{i = 1}^n\underline {R_{T,{A_i}}^{{\leqslant} O}} \left( {{f_d}} \right)$
。
3) 同理
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{ {\leqslant} O}} } \left( {{f_d}} \right) = \cap _{i = 1}^n\overline {R_{T,{A_i}}^{ {\leqslant} O}} \left( {{f_d}} \right)$
。
4) 由1)可知
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)} \right) \subseteq $
$ \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } $
(fd),因此只要证明
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) \! \subseteq \! \underline {\sum\nolimits_{i = 1}^n \! {R_{T,{A_i}}^{{\leqslant} O}} } \! \left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)} \right)$
即可。由2)可知
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant}O}} } \left( {\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)} \right) = \cup _{i = 1}^n\underline {R_{T,{A_i}}^{{\leqslant} O}}$
$ \left( {\underline {\sum\nolimits_{i = 1}^n \, {R_{T,{A_i}}^{{\leqslant} O}} } \, \left( {{f_d}} \right)} \right) = \cup _{i = 1}^n \, \underline {R_{T,{A_i}}^{{\leqslant} O}} \, \left( { \cup _{i = 1}^n \, \underline {R_{T,{A_i}}^{{\leqslant} O}} \, \left( {{f_d}} \right)} \right) \supseteq \cup _{i = 1}^n \cup _{i = 1}^n\underline {R_{T,{A_i}}^{{\leqslant} O}} $
$\left( {\underline {R_{T,{A_i}}^{{\leqslant}O}} \left( {{f_d}} \right)} \right) = \cup _{i = 1}^n\underline {R_{T,{A_i}}^{ {\leqslant} O}} \left( {{f_d}} \right) = \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)$
。类似的,易证
$\left( {\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)} \right) = \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)$
。
定理5 设
$\left( {U,A \cup \left\{ d \right\},R} \right)$
为直觉模糊决策信息系统,其中
${A_1}, {A_2}, \cdots ,{A_n} \subseteq A,$
则:
1)
$\underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {{f_d}} \right) \subseteq \underline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right)$
;
2)
$\overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} O}} } \left( {{f_d}} \right) \subseteq \overline {\sum\nolimits_{i = 1}^n {R_{T,{A_i}}^{{\leqslant} P}} } \left( {{f_d}} \right)$
。
证明:根据定义15、定义16,此定义易证。
3.2 决策规则获取
经典粗糙集理论中,下近似中的元素对决策规则的支持是确定的,而边界域中的元素对决策规则的支持是不确定的。在此基础上Greco利用优势关系定义了两种由逻辑连词“且”构成的决策规则。根据多粒度思想,由上一小节构造的优势关系多粒度粗糙直觉模糊集可得到逻辑连接词为“或”的两种决策规则,具体形式如下:
“at least”决策规则:
|
$\begin{array}{c}{T_{{a_1}}}\left( y \right) \geqslant {T_{{a_1}}}\left( x \right) \vee {T_{{a_2}}}\left( x \right) \vee \cdots \vee {T_{{a_n}}}\left( y \right) \geqslant {T_{{a_n}}}\left( x \right) \to \\[5pt]{f_d}\left( y \right) \geqslant \underline {\sum\nolimits_{i = 1}^n {R_{T,{a_i}}^{ \leqslant O}} } \left( {{f_d}} \right)\left( x \right);\end{array}$
|
“at most”决策规则:
|
$\begin{array}{c}{T_{{a_1}}}\left( y \right) \leqslant {T_{{a_1}}}\left( x \right) \vee {T_{{a_2}}}\left( x \right) \vee \cdots \vee {T_{{a_n}}}\left( y \right) \leqslant {T_{{a_n}}}\left( x \right) \to \\[5pt]{f_d}\left( y \right) \leqslant \underline {\sum\nolimits_{i = 1}^n {R_{T,{a_i}}^{ \leqslant P}} } \left( {{f_d}} \right)\left( x \right).\end{array}$
|
例3 根据例2计算结果,可以生成两种“或”决策规则,这里只给出“at least”规则:
1)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.86 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.56 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.04 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.56 \to {f_d}\left( y \right) \geqslant \left( {0.6,0.3} \right) $
;
2)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.86 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.08 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.10 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.02 \to {f_d}\left( y \right) \geqslant \left( {0.6,0.3} \right) $
;
3)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.03 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.02 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.02 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.86 \to {f_d}\left( y \right) \geqslant \left( {0.0,1.0} \right) $
;
4)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.00 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.81 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.81 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.72 \to {f_d}\left( y \right) \geqslant \left( {0.5,0.4} \right) $
;
5)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.02 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.01 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 1.0 \,\, \vee $
${T_{{a_4}}}\left( y \right) \geqslant 0.76 \to {f_d}\left( y \right) \geqslant \left( {0.4,0.6} \right) $
;
6)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.12 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.06 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.90 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.02 \to {f_d}\left( y \right) \geqslant \left( {0.3,0.6} \right) $
;
7)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.00 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.02 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.81 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 0.08 \to {f_d}\left( y \right) \geqslant \left( {0.0,0.9} \right) $
;
8)
$ {T_{{a_1}}}\left( y \right) \,\geqslant\, 0.86 \vee {T_{{a_2}}}\left( y \right) \,\geqslant\, 0.81 \vee {T_{{a_3}}}\left( y \right) \,\geqslant\, 0.02 \,\, \vee $
$ {T_{{a_4}}}\left( y \right) \geqslant 1.0 \to {f_d}\left( y \right) \geqslant \left( {0.6,0.3} \right) $
。
4 结束语
本文将多粒度的基本思想引入到直觉模糊决策信息系统中,利用t-模及t-余模定义了3种新的优势关系。分析这3种优势关系所表达的不同语义,在此基础上提出了广义优势关系下多粒度直觉模糊粗糙集模型。通过该模型的主要性质进行讨论,这种模型使得多粒度方法能够有效处理直觉模糊决策信息系统中直觉模糊概念近似和规则提取等问题。最后结合实例,具体给出了在直觉模糊决策信息系统中,逻辑连接词为“或”的决策规则。
在本文基础上,将深入研究3种优势关系之间的内在联系,以及如何利用辨识矩阵和启发算法获得广义优势关系多粒度粗糙直觉模糊集模型的属性约简。
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2017, Vol. 12
2017, Vol. 12


