2. 重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065
2. Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
多标签学习在文本分类[1-2]、图像注释[3-4]和生物信息学[5]等多个应用领域得到了广泛关注,也具有越来越重要的应用价值。在多标签学习中,训练集的一个样本均对应一组标签集合。假设X表示样本空间, Y={1,2,…,q}表示所有可能的标签集合,其中标签的总数为q,T={(x1, Y1), (x2, Y2),…, (xm, Ym)}为具有m个样本的训练集,其中xi∈X且Yi⊆Y。则多标签分类的目标是输出一个多标签分类器h:x→2y,使得对每一个给定的实例x∈X,都能预测出合适的标签集合Y*⊆Y。
多标签学习的关键挑战在于分类器预测的标签空间数量为指数级(2q)。为了解决这个问题,有效地利用不同标签之间的相关性以促进学习过程已成为多标签学习的关键[6-7]。在过去几年,许多利用标签相关性的算法被提出,如校准标签排序(CLR)[8],随机k标签集(RAkEL)[9]和广义k标签集成(GLE)[10]均考虑了标签之间的相关性,然而这些算法的计算复杂度随标签数量的增加而显著增加。
同时,大部分现有的多标签学习方法没有充分考虑多标签数据的固有属性,即标签类别不平衡。对每一个标签yj∈Y,令Dj+={(xi, +1)yj∈Yi, 1≤i≤N}以及Dj-={(xi, -1)yj∉Yi, 1≤i≤N}作为正样本和负样本。一般来说,每个类别的正训练样本数远远低于其负训练样本数,这可能导致大多数多标签学习算法的性能降低[11]。文献[12-14]指出,不平衡问题普遍存在于多标签应用中,会损害分类性能。算法交叉耦合聚合学习方法(cross-coupling aggregation, COCOA)[14]同时考虑了标签相关性和不平衡问题,同样其算法复杂度很高,因此如何有效和高效地利用标签间的相关性并削弱不平衡问题的影响仍然是一个悬而未决的问题。
另一方面,目前现实应用中的多标签数据集的样本、特征和标签的数量远远超过常规大小,例如,视频共享网站Youtube中有数百万个视频,而每个视频可以被数百万个候选类别标记。然而,大多数多标签学习算法不能很好地适应数据集规模很大的应用。对近3年出现的多标签学习方法[15-23]使用的训练集的规模进行统计,可以看出训练样本数在50 000~100 000之间的数据集仅有5个,样本数大于100 000的数据集仅有1个,大多数现有的多标签学习算法仅适用于处理中小规模数据集。其次,文献[19]虽然利用大规模数据集进行了实验,但是它的计算复杂度高。
多标签超网络MLHN与协同演化多标签超网络Co-MLHN[24]可以挖掘标签间的高阶关系,它将传统的超网络转为多标签超网络,用超边和超边的权重来表示特征子集与标签之间的高阶关系,利用了任意标签间的相关性,且计算复杂度随标签数量的增加呈线性增长,但是其算法时间复杂度与样本数量呈平方级关系,不能很好地处理规模较大的数据集, 同时算法也未考虑到标签不平衡对性能的影响。
针对目前多标签超网络存在的问题,本文基于MLHN的思想,提出了Spark平台下的改进多标签超网络集成算法SEI-MLHN,有效且高效地解决了多标签学习问题。首先对多标签数据集进行划分;然后对划分后的数据分别用基于Spark平台的改进超网络算法SI-MLHN进行训练,形成多个局部超网络;最后对多个局部超网络进行选择性集成完成对测试样本的预测。其中,SI-MLHN利用MLHN的思想并在Spark平台下进行改进,首先计算每个样本的k近邻,然后利用k近邻对超网络进行演化学习,得到演化超网络。
为了评估本文算法的性能以及对大规模数据集的适应性,选用不同规模数据集来进行对比实验,验证了本文算法具有良好性能以及具备处理大规模数据集的能力。本文的主要贡献如下:
1) 引入了代价敏感,使其能良好地适应多标签不平衡数据,提升算法性能;
2) 改良了超网络演化学习过程,大幅度降低MLHN算法的计算复杂度;
3) 利用选择性集成,降低了时间复杂度,并提高分类性能;
4) 基于Spark计算框架实现算法,使算法实现并行,提高算法运行效率。
1 相关工作虽然多标签学习已经成功应用于生物信息学、音频分类[25]以及web挖掘[26]等多个领域,但是由于多标签分类器的输出空间为指数级,以及现在大部分应用的数据集规模日益增加,对多标签学习造成了很大的挑战。
为了应对分类器输出空间数量巨大这个问题,现有的方法是利用标签相关性来促进学习过程。基于标签关联性,张敏灵和周志华[27-28]将现有的学习算法分为3类,分别为一阶策略、二阶策略以及高阶策略。一阶策略是简单地将多标签学习转为多个独立的二分类问题来解决多标签学习问题,例如ML-KNN[29]、BR[30]等;二阶策略通过利用标签之间的成对关系解决多标签学习问题,例如CLR[31]、BP-MLL[32]等;高阶策略通过探索标签之间的高阶关系来解决多标签学习问题,例如CC[33]、CNMF[34]等。对这3种策略进行比较分析,一阶策略的效率高且概念易理解,但忽略了标签相关性。二阶策略在一定程度上解决了标签相关性,但忽略了现实世界中相关性超过二阶的情况。高阶策略具有比一阶和二阶更强的建模能力,但是其计算复杂度更高,可扩展性更低。
为了应对多标签数据的不平衡性造成算法性能下降这个问题,常规解决方案是为每一个标签训练一个二分类器,并通过随机或合成欠采样/过采样来处理这个二分类器[35-36],但这些方法没有很好地利用标签间的关联性。也有其他的解决方案,如张敏灵等[14]提出交叉耦合聚合算法COCOA,但是这种算法时间复杂度高,不适合处理大规模数据集。
为了应对数据集规模大这个问题,现有的解决方案是利用分布式存储系统,提供一个基础架构,从而实现高效和可扩展的大数据挖掘与分析。目前,为大数据分析开发了大量的计算框架[37-41],其中,最经典的是MapReduce[37]。MapReduce简单、通用且成熟,被广泛使用,但是它只能进行Map和Reduce计算,不适合描述复杂数据处理过程,数据需要写到磁盘,不能有效地执行迭代算法。为了克服MapReduce的缺点,大量的计算框架被设计出来,如Haloop [38]、Apache Mahout [39]、i2MapReduce [40]和Apache Spark[41]等。Haloop是Hadoop MapReduce框架的修改版本,它继承了Hadoop的基本分布式计算模型和架构。Apache Mahout是一个开源项目,主要用于创建可扩展的机器学习算法。i2MapReduce是MapReduce的一个增量处理扩展,并广泛用于大数据挖掘。Apache Spark是一个开源的集群计算框架,用于大规模的交互计算。在上述框架中,Apache Spark利用内存计算,并保留MapReduce的可扩展性和容错能力,对迭代算法非常有效。Spark执行速度比Hadoop MapReduce快100倍[41],并且显著快于其他计算框架。
综上所述,为了解决上述问题,本文使用Spark计算框架作为平台来实现多标签算法。
2 Spark下改进多标签超网络集成算法MLHN可以高效地挖掘标签间的关联性且学习复杂度与标签维度呈线性关系,因此本文基于MLHN算法提出了Spark平台下的改进多标签超网络集成算法SEI-MLHN,高效地解决了多标签问题。首先,对多标签数据集进行划分,然后对划分后的数据分别用SI-MLHN算法进行训练,形成多个局部超网络,最后对多个局部超网络进行选择性集成完成对测试样本的预测。其中,算法SI-MLHN利用MLHN的思想,在Spark平台下进行改进,首先计算每个样本的k近邻,然后利用k近邻对超网络进行演化学习,得到超网络。本节中,将对算法MLHN,MLHN的改进算法SI-MLHN,以及以SI-MLHN为基学习器进行选择性集成的算法SEI-MLHN依次进行介绍。
2.1 多标签演化超网络(MLHN)多标签演化超网络利用超边集合以及超边权重来表示样本特征子集与多标签类别之间的高阶关联。通过演化学习,可以近似地表示训练样本X和其标签Y之间的概率分布P(X, Y),在MLHN中可以按式(1)进行表示:
| $ \begin{array}{*{20}{c}} {P\left( {{y_i} = 1\left| \mathit{\boldsymbol{x}} \right.} \right) = \frac{{P\left( {\mathit{\boldsymbol{x}},{y_i} = 1} \right)}}{{P\left( \mathit{\boldsymbol{x}} \right)}} = }\\ {\frac{{\sum\nolimits_{j = 1}^{\left| E \right|} {{w_{ji}}I\left( {\mathit{\boldsymbol{x}},{y_i} = 1;{e_j}} \right)} }}{{\sum\nolimits_{j = 1}^{\left| E \right|} {{w_{ji}}I\left( {\mathit{\boldsymbol{x}},{y_i} = 1;{e_j}} \right)} + \sum\nolimits_{j = 1}^{\left| E \right|} {{w_{ji}}I\left( {\mathit{\boldsymbol{x}},{y_i} = 0;{e_j}} \right)} }}} \end{array} $ | (1) |
式中:yi为样本x的第i个标签;wji为超边集合|E|中ej的第i个权重向量的值;I(x, yi; ej)为超边与样本匹配函数,若匹配则取值为1,反之则为0,如式(2)所示:
| $ I\left( {{\mathit{\boldsymbol{x}}_n},{y_{ni}};{e_j}} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;{\rm{dis}}\left( {{\mathit{\boldsymbol{x}}_n};{e_j}} \right) \le \delta \;且\;{y_{ij}} = {y_{ni}}\\ 0,\;\;\;\;\;其他 \end{array} \right. $ | (2) |
式中:yji是超边ej的第i个标签,dis(xn; ej)为超边ej与样本x的欧氏距离,δ为匹配阈值。δ的计算方法如式(3):
| $ \delta = \frac{{\dim \left( {{e_j}} \right)}}{{\left| {{G_x}} \right| \times \dim \left( \mathit{\boldsymbol{x}} \right)}}\sum\limits_{\mathit{\boldsymbol{x'}} \in {\mathit{\boldsymbol{G}}_\mathit{\boldsymbol{x}}}} {\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{x'}}} \right\|} $ | (3) |
式中:其中Gx为x的近邻样本集合,dim(x)为样本x的特征维度。
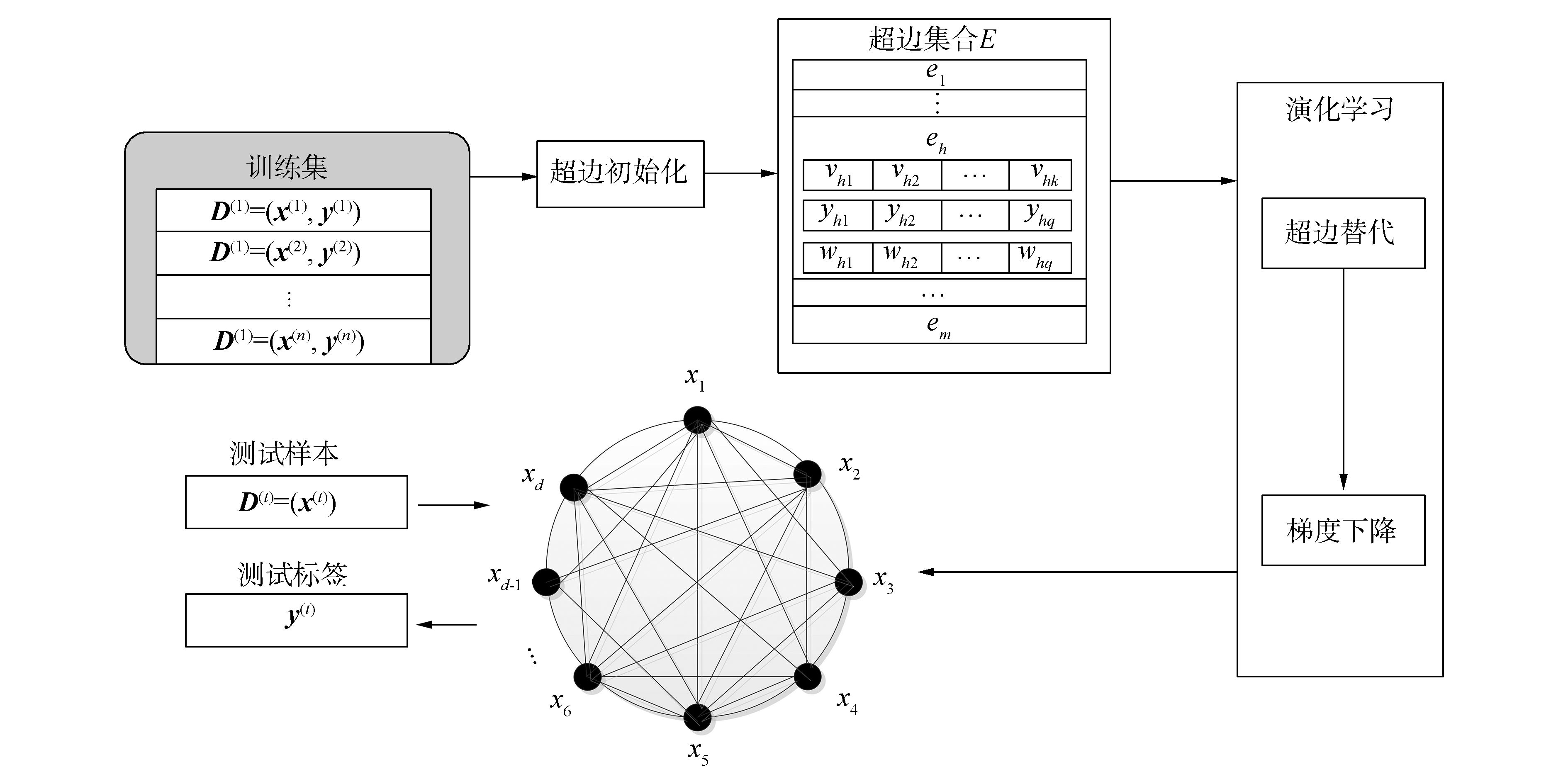
为了对未知样本进行预测,MLHN通常把标签预测误差和相关标签不一致性最小化作为演化学习目标。通过超边初始化、超边替代和梯度下降演化学习来对训练集进行学习,使超边权重wji进行更新,流程如图 1所示。图 1中,超边eh=(vh, yh, wh),vh是超边的顶点,为x的部分特征;yh为x的标签;wh是xh对应yh的权重向量。
|
图 1 MLHN算法流程图 Fig.1 Basic flow chart of MLHN |
MLHN是一种有效的多标签学习算法,但是目前的MLHN算法计算复杂度高,且对多标签数据的不平衡特性没有关注。本文一方面改进了MLHN的训练过程,引入了代价敏感;另一方面通过并行计算来降低运算时间,设计了Spark下改进多标签超网络,记作SI-MLHN。在本小节,将分别介绍SI-MLHN的多标签分类学习过程和演化学习过程。
2.2.1 SI-MLHN分类学习过程SI-MLHN算法关注了多标签样本中普遍存在的标签类别不平衡现象。对于一个未知样本xn,SI-MLHN将返回每个标签的概率P(yni=1|xn),如式(4):
| $ P\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right) = \frac{1}{{1 + {{\rm{e}}^{ - \left( {W_{ni}^1 - W_{ni}^0} \right)}}}} $ | (4) |
式中:Wni1为将样本xn的标签i分类为1的权重和,Wni0则为分类为0的权重和,计算方法如式(5)、(6):
| $ \mathit{\boldsymbol{W}}_{ni}^1 = \sum\nolimits_{j = 1}^{\left| E \right|} {{w_{ji}}I\left( {{\mathit{\boldsymbol{x}}_n},{y_{ni}} = 1;{e_j}} \right)} \times \cos {t_i} $ | (5) |
| $ \mathit{\boldsymbol{W}}_{ni}^0 = \sum\nolimits_{j = 1}^{\left| E \right|} {{w_{ji}}I\left( {{\mathit{\boldsymbol{x}}_n},{y_{ni}} = 0;{e_j}} \right)} $ | (6) |
式中:yni为样本x的第i个标签; wji为超边集合|E|中ej的第i个权重向量的值; I(xn, yni; ej)的计算方法如式(2);cos ti为第i个标签的代价值,计算方式如式(7):
| $ \cos {t_i} = 1 + \lg \sum\limits_{\left( {{x_n},{y_n}} \right) \in T} {\frac{{\left| {\left\{ {\left( {{x_n},{y_n}} \right)\left| {{y_{ni}} = 0} \right.} \right\}} \right|}}{{\left| {\left\{ {\left( {{x_n},{y_n}} \right)\left| {{y_{ni}} = 1} \right.} \right\}} \right|}}} $ | (7) |
式中T为有m个样本的训练集。
由于SI-MLHN采用sigmoid函数返回了每个标签与样本相关的概率P(yni=1|xn),故将相关标签阈值ti设定为0.5,从而获得每个样本的标签集合,如式(8):
| $ y_{ni}^ * = \left\{ \begin{array}{l} 1,\;\;\;\;P\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right) \ge {t_i}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (8) |
在多标签学习中,一个样本只包含标签空间中的部分标签。如果可以排除一些不可能的标签,可以减少标签预测的不确定性。因此,SI-MLHN借鉴了Co-MLHN算法的思想, 将KNN引入算法,减少算法预测的不确定标签,提高算法的性能。算法1为SI-MLHN分类学习过程的伪代码。
算法 1 SI-MLHN分类学习过程
输入 训练集T, 测试样本xn, 标签数q,近邻数量k, SI-MLHN模型H, 标签阈值ti;
输出 标签概率p, 预测标签y*。
1) 在训练集T中计算xn的k近邻
2) 将模型H中是xn的近邻且与xn匹配的超边加入集合U中
3) 从U中提取标签yi=1的超边到集合U1中
4) for i=1 to q do
5) W1[i]←0
6) for each ej∈U1
7) W1[i]=W1[i]+wji×cos ti
8) end for
9) end for
10) 从U中提取标签yi=0的超边到集U0中
11) for i=1 to q do
12) W0[i]←0
13) for each ej∈U0
14) W0[i]=W0[i]+wji
15) end for
16) end for
17) for i=1 to q do
18)
19) p[i]=P(yi= 1|xn)
20) if P(yni=1| xn)≥ti
21) y*[i]=1
22) else y*[i]=0
23) end if
24) end for
25) return p, y*
2.2.2 SI-MLHN演化学习过程SI-MLHN利用超边的顶点和权重向量来代表多标签数据标签间的高阶关联,其权重向量由超边从训练集中演化学习而来,首先进行了超边初始化,然后进行了超边替代与梯度下降演化学习,并利用Spark进行分布式并行计算,通过多个操作技巧,如cache、broadst,将变量缓存于内存中,大量减少了网络交换数据量和磁盘I/O操作,使算法更高效。
在超边初始化的过程中,利用样本(x, y)生成超边
由于超边顶点向量v为随机的,为了更好地拟合训练样本,需要通过超边替代来选择适应度高的超边。如果新生成的超边适应值高于现有超边,则替换该超边。适应值的计算方法如式(9)所示:
| $ {\rm{fitness}}\left( {{e_j}} \right) = \frac{1}{{\left| G \right|}}\sum\limits_{\left( {{\mathit{\boldsymbol{x}}_n},{\mathit{\boldsymbol{y}}_n}} \right)} {\frac{1}{q}\sum\limits_{i = 1}^q {\left| {\left\{ {i\left| {{y_{ni}} = {{y'}_i}} \right.} \right\}} \right|} } $ | (9) |
式中:超边ej的近邻样本个数为k,G为与超边ej匹配的抽样训练集TS样本集合,则将TS中样本的数量设置为10倍的k,其中k个是超边ej的近邻样本,其余的样本则为训练集样本的随机抽样;q为标签数量;yni为样本(xn, yn)的第i个标签;yi′为超边ej的第i个标签。由式(9)可以看出适应值代表了超边标签与匹配样本标签的相似度的平均值,相似度越高,则适应值越高。同时,式(4)也展示出,样本与匹配超边的标签相似度越高,被正确分类的概率越大。
本文将预测误差作为学习目标。损失函数如式(10)所示,P*(yni=1|xn)为SI-MLHN分类器对样本(xn, yn)的第i个标签的预测值,利用梯度下降调整超边的权重,降低损失值。超边权重更新为式(11),并通过式(12)~(14),计算Δwki,其中wki为第k条超边第i个标签的权重,η为学习速率。
| $ {\rm{Er}}{{\rm{r}}_n}\left( W \right) = \frac{1}{2}\sum\limits_{i = 1}^q {{{\left[ {{P^ * }\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right) - P\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right)} \right]}^2}} $ | (10) |
| $ {w_{ki}} = {w_{ki}} + \Delta {w_{ki}} $ | (11) |
| $ \Delta {w_{ki}} = - \eta \frac{{\partial {\rm{Er}}{{\rm{r}}_n}\left( W \right)}}{{\partial {w_{ki}}}} $ | (12) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial {\rm{Er}}{{\rm{r}}_n}\left( W \right)}}{{\partial {w_{ki}}}} = \left( {P\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right) - } \right.}\\ {\left. {{P^ * }\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_n}} \right.} \right)} \right)\frac{{\partial {P^ * }\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{n}}}} \right.} \right)}}{{\partial {w_{ki}}}}} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial {P^ * }\left( {{y_{ni}} = 1\left| {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{n}}}} \right.} \right)}}{{\partial {w_{ki}}}} = \frac{{\partial \frac{1}{{1 + {{\rm{e}}^{ - \left( {W_{ni}^1 - W_{ni}^0} \right)}}}}}}{{\partial {w_{ki}}}} = }\\ {\frac{{1 - \frac{1}{{1 + {{\rm{e}}^{ - \left( {W_{ni}^1 - W_{ni}^0} \right)}}}}}}{{1 + {{\rm{e}}^{ - \left( {W_{ni}^1 - W_{ni}^0} \right)}}}}} \end{array} $ | (14) |
算法2 为SI-MLHN的演化学习流程伪代码。由于本文采用欧氏距离作为距离度量,故需要先进行归一化处理。
算法 2 SI-MLHN演化学习算法
输入 训练集T={(xn, yn)}(1≤n≤N),标签数q,每个样本生成的超边数e,超边替代迭代次数tr,随机梯度下降迭代次数td,样本的近邻数量k;
输出 SI-MLHN:H。
1) Tnor =T.map
2) 每条样本进行归一化
3) end map.cache
4) TnorBro= broadcast (Tnor)
5) Tkv=Tnor.map
6) 每条样本计算与TnorBro中样本的欧式距离
7) end map.map
8) 获取距离最近的k个样本
9) end map
10) TkvBro= broadcast (Tkv)
11) Hini=Tkv.flatmap
12) 每条样本生成e条超边
13) end flatmap.cache
14) Hre0=Hini.map
15) 对超边进行tr次替代
16) end map.cache
17) for t←1 to td do
18) Hret-1Bro= broadcast(Hret-1)
19) Htmp=Tkv.map
20) 对样本利用Hret-1Bro中超边集合预测
21) end map.flatmap
22) 对超边进行梯度计算
23) end flatmap.reduceByKey(合并梯度值)
24) Hret=Hret-1.leftjoin (Htmp)
25) .map
26) 利用合并后梯度值更新超边权重
27) end map
28) end for
29) H=Hret
30) return H
Tnor为训练集经过分布式并行归一化处理后的结果;broadcast操作可以保存只读变量,并保在每个节点内存中;TnorBro为归一化后样本广播变量;TkvBro为样本与其k近邻的键值对Tkv的广播变量;Hini为超边初始化集合;Hre0为超边替代后集合;Hret为超边演化学习后集合。
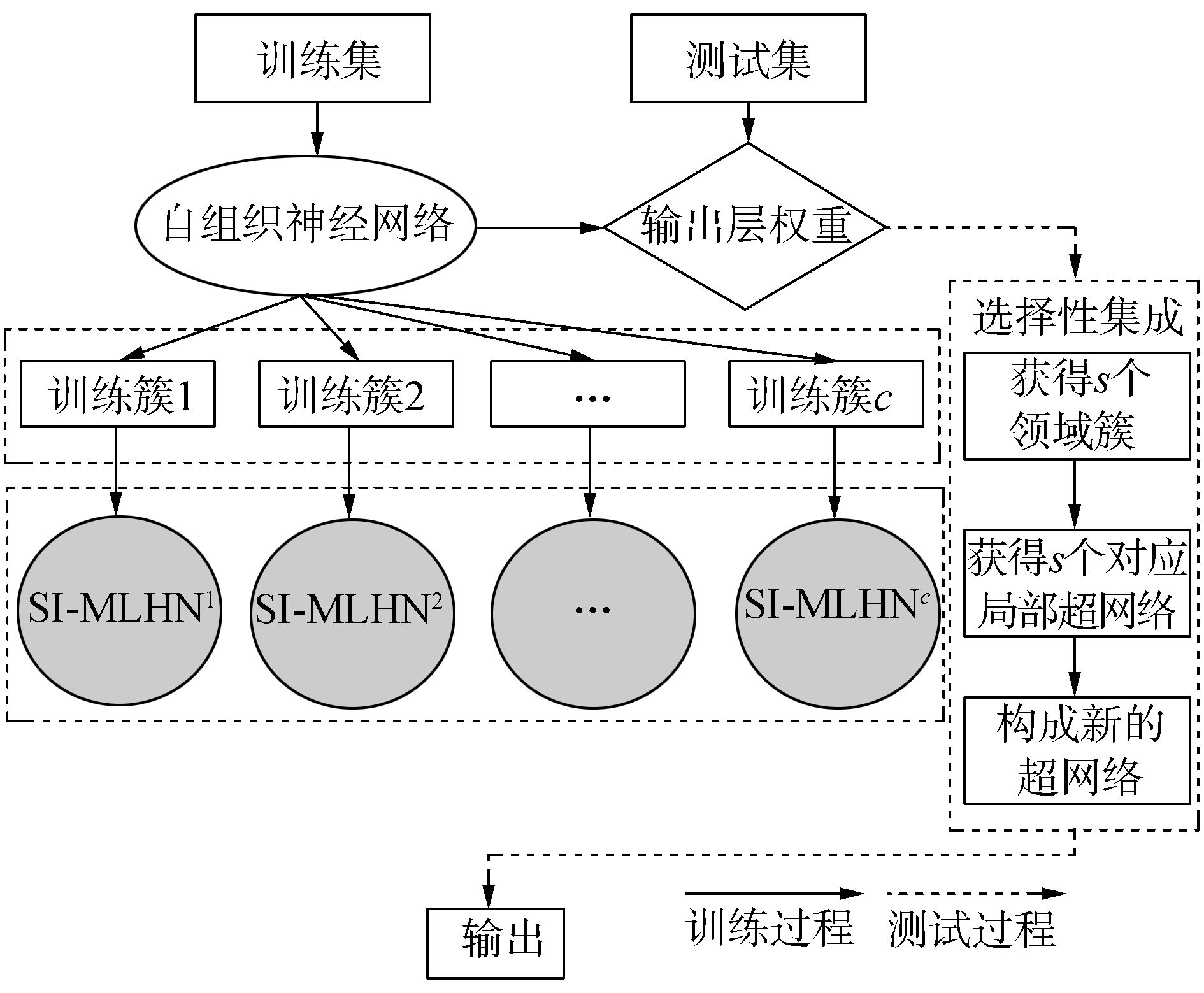
2.3 Spark下集成多标签超网络(SEI-MLHN)SI-MLHN为MLHN的Spark平台下分布式并行改进方法,大幅缩短了训练时间,但是其时间复杂度仍然随着样本数量的增加呈平方级增长,仍然无法很好适应大样本数据。故本文利用选择性集成,一方面降低时间复杂度,另一方面提高算法性能,提出了Spark下集成多标签超网络,记作SEI-MLHN。SEI-MLHN首先将训练集进行分簇,并分别用SI-MLHN算法演化学习多个局部多标签超网络。对于未知样本,首先获得近邻簇,然后利用局部超网络选择性集成对测试样本进行预测,SEI-MLHN的流程见图 2。
|
图 2 SEI-MLHN流程图 Fig.2 Flow chart of SEI-MLHN |
为了对训练样本进行分簇,本文选择了基于神经网络的无监督聚类方法自组织神经网络(SOM)[42]。SOM对类簇初始化不敏感,并且可以很好地发现数据之间的结构关系,为了让其适应大规模数据处理将其进行了Spark下并行化扩展,记为S-SOM。算法3为算法伪代码,首先利用每个分区计算获胜节点,并更新优胜邻域中的输出单元,然后将各个分区的值利用reduce算子进行合并, 并更新优胜邻域,达到终止条件得到最终输出层。其中,计算邻域函数选取高斯函数,距离仍然选取欧氏距离,WBro为SOM初始化输出层W的广播变量在6)~12)中完成了一次迭代计算,Wct为每次迭代利用每个分区样本更新后输出层,Wrt为分区合并的输出层。
算法 3 S-SOM
输入 训练集T={(xn, yn)}(1≤n≤N),类簇个数c,学习率η,迭代次数ti;
输出 类簇T1′, T2′, …, Ts′。
1) Tnor =T.map
2) 每条样本进行归一化
3) end map.cache
4) W=初始化输出层(随机抽取c个样本)
5) WBro =broadcast(W)
6) for t←1 to ti
7) for each Tnor的分区do
8) for each分区内样本do
9) 利用输出层计算获胜节点
10) 更新优胜邻域中的值为Wct
11) end for
12) end for
13) 更新优胜邻域
14) Wrt=利用reduce合并各分区Wct
15) end for
16) T1′, T2′, …, Tp′ =Tnor,计算获胜节点(Wrt)
17) return T1′, T2′, …, Ts′
完成训练集分簇后,利用算法2对簇构建SI-MLHN超网络。对于测试集,SEI-MLHN将进行选择性集成,伪代码见算法4。
算法 4 SEI-MLHN分类算法
输入 测试集E={ xn}(1≤n≤M),样本数量为M, 样本近邻数量k , SEI-MLHN:H={H1′, H2′, …, H3′},簇数为c,邻域簇数为s,S-SOM输出为T1′, T2′, …, Tc′;
输出 E*={(xn, pn, yn*)}(1≤n≤M),其中p为测试集标签概率,y*为测试集预测标签。
1) E在T1′, T2′, …, Tc′中计算s个最近邻簇, 并将其加入Us,簇对应的超网络为H1′, H2′, …, Hs′
2) for each Ti′∈Us do
3) Ekvi=寻找E中样本在Ti′在中的k近邻
4) Ekhi=Ekvi.flatmap
5) 组成测试样本与近邻样本对
6) end flatmap.leftjoin (Hi′).reduceByKey
7) end for
8) 将s个Ekhi合并为集合F
9) E*= F.reduceByKey()
10) .map
11) 从s*k近邻中选取最近k,利用算法1进行预测
12) end map
13) return E*
算法4中,对测试样本选取了s个最近类簇产生的局部超网络并把局部组合起来,然后进行预测,得到分类结果。其中,Ekvi为测试样本与其在第i个簇中的k近邻组成的键值对,Ekhi为测试样本与其在第i个簇中的k近邻以及超边组成的键值对。
2.4 时间复杂度分析SEI-MLHN利用SI-MLHN进行选择性集成来提高学习器的稳定性和泛化能力。对于含有N个训练样本,样本特征纬度为d,标签数量为q的训练集,SI-MLHN的训练复杂度为O(N2d+enkN+kqN),记为FSI(N, k, e, n, d, q),其中e为每个训练样本产生的超边数量,k为近邻数量,n为训练样本的抽样,在大规模数据集中n≪N。对于未知样本进行预测时,SI-MLHN首先在训练集中寻找k个近邻样本,然后利用与之匹配的近邻样本产生的超边进行预测。因此对有M个样本的测试集,SI-MLHN的预测时间复杂度为O(MNd+eMN+kqM), 记为FSI′(M, k, e, N, d, q)。SEI-MLHN对训练集进行了分簇,并在预测时删除了冗余学习器,因此其训练时间复杂度为O(c·FSI(N′, k, e, n, d, q)), 测试时间复杂度为O(s·FSI′(M, k, e, N′, d, q)),其中c为训练集聚类簇数,s为邻域簇的数量,N′为最大类簇中样本的数量,N′的数量取决于c以及训练数据的分布,一般接近于N/c。
3 实验 3.1 数据集为了对算法性能进行全面的评估,本文选择了11个公开的常用多标签数据集进行实验,其中训练样本数小于5 000的数据集有6个,大于100 000的数据集有2个,如表 1所示,表中的标签基数是指每个样本关联标签的平均数量。由于文本数据具有高维稀疏的特性,故在表 1中对所有的文本数据集均使用Lee和Jiang[43]提出的模糊相关度量进行了变换,在模糊变换之后,每个文档由模糊相关性向量表示,且维度与标签维度相同。
| 表 1 实验使用的多标签数据集 Tab.1 Multilabel data sets used in experiments |
假设X表示样本空间,Y={1, 2, …, q}表示所有可能的标签集合,E={(xi, Yi)1≤i≤M}为具有M个样本的多标签测试集,h为输出的多标签分类器,则测试样本xi的预测结果为h(xi)。f(xi, y)是标签y在样本xi上排名质量的实值函数,例如对于任意y1∈Y以及y2∈Y而言,f(xi, y1)>f(xi, y2)成立。实值函数f(·, ·)也可以转为排序函数rankf(·, ·),即将所有的实值输出f(xi, y)映射到集合Y上,使得f(xi, y1)>f(xi, y2)时,ran kf(xi, y1)>rankf(xi, y2)也成立。基于上述描述,本文采用的多标签性能评价指标如下。
1) Hamming Loss:用于考察样本在单个标签上的误分类情况。
| $ {\rm{hloss}}\left( h \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\frac{1}{Q}\left| {h\left( {{x_i}} \right)\Delta {Y_i}} \right|} $ |
式中Δ表示两个集合的对称差。
2) One-error:用于考察样本测标签排序集合中最前端的标签误分类的情况。
| $ {\rm{one - erro}}{{\rm{r}}_s}\left( f \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\left[ {\left( {\arg \mathop {\max }\limits_{y \in Y} f\left( {{x_i},y} \right)} \right) \notin {Y_i}} \right]} $ |
3) Ranking Loss:用于考察样本的预测标签排序集合中的错排情况。
| $ {\rm{rlos}}{{\rm{s}}_s}\left( f \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\frac{L}{{\left| {{Y_i}} \right|\left| {{{\bar Y}_i}} \right|}}} $ |
式中Yi是Yi的补集。
4) Average Precision:用于考察样本的预测标签集合中排在该样本标签之前的标签分类正确的情况。
| $ \begin{array}{*{20}{c}} {{\rm{avgpre}}{{\rm{c}}_s}\left( f \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\frac{1}{{\left| {{Y_i}} \right|}}} \cdot }\\ {\sum\limits_{y \in {Y_i}} {\frac{{\left| {\left\{ {y'\left| {{\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y'} \right)} \right. \le {\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y} \right),y' \in {Y_i}} \right\}} \right|}}{{{\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y} \right)}}} } \end{array} $ |
5) Example Based F1:
| $ {F_1} = \frac{1}{M}\sum\limits_{i = 1}^M {\frac{{2\left| {{Y_i} \cap h\left( {{x_i}} \right)} \right|}}{{\left| {{Y_i}} \right| + \left| {h\left( {{x_i}} \right)} \right|}}} $ |
在本文中,将SEI-MLHN与两种系列的算法进行比较实验,第1种系列是常用的多标签学习算法,如表 2的前8种算法所示,它们均在表 3所示的单节点环境中实现。第二种系列是在Spark平台下实现的超网络多标签学习算法,如S-CoMLHN以及SEI-MLHN的基学习器SI-MLHN,Spark集群环境如表 4所示,其中S-CoMLHN是Co-MLHN在Spark平台下的实现。
| 表 2 实验中的比较算法 Tab.2 Comparison of algorithms used in experiments |
| 表 3 实验单节点环境 Tab.3 Experimental environment |
| 表 4 集群环境配置 Tab.4 Configuration in clustered environment |
在实验过程中比较算法的参数设置取自文献[8-9, 14, 24, 30, 39, 44],详细设置见表 3,其中算法SI-MLHN中每个样本生成超边的数量e为10,超边替代迭代次数tr为5,随机梯度下降迭代次数td为5。
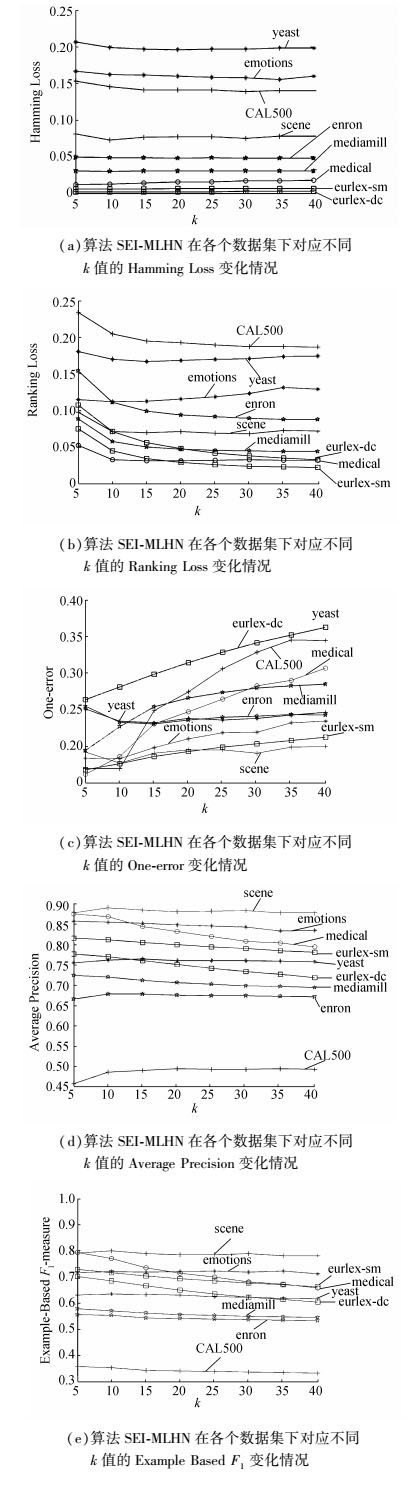
3.4 实验结果 3.4.1 参数分析对于算法SEI-MLHN,近邻个数k是关键参数之一,为了测试算法对k参数的敏感度,本节将k以5为步长,在5~40范围内测试算法SI-MLHN的性能。如图 3所示,(c)、(e)随k的增大波动较大,部分数据集k>10后趋于稳定,多数数据集随k增大性能变差;(a)中对k值不敏感,几乎没有变化;(b)随k值增大性能变好,且在k > 10后趋于平稳;在(d)中不同的数据集随着k值的变化,性能既有增加的,也有降低的,但总体上在k=10时,能有较好的性能。这是由于k值直接关系着预测样本的匹配超边数量,当k太小时与之匹配的超边数量太小,会漏掉一些相关标签,k值太大则会引入噪声标签且会影响算法运行效率,故本文将k取为10。
|
图 3 算法SEI-MLHN在各个数据集下对应不同k值的分类性能比较 Fig.3 Performance comparison of SEI-MLHN under different values of k on Data Sets |
对于SEI-MLHN簇数c,由于本文采用自组织神经网络进行分簇,将训练数据映射到二维空间,故本文将c设置为完全平方数,且将选择分类器个数s设为

|
图 4 算法SEI-MLHN在各个数据集下对应不同c值的分类性能比较 Fig.4 Performance comparison of SEI-MLHN under different values of c on Data Sets |
图 4中,(a)、(c)、(d)、(e)中算法SEI-MLHN在各个数据集中的性能几乎不变或变化幅度非常小,说明Hamming Loss、One-error、Average Precision和Example Based F1对c和s的变化不敏感,(b)中SEI-MLHN的性能在数据集nuswide-cVLADplus中随c和s的增大有小幅度的优化,(f)中可以看出较小规模数据随簇数c和s的增加训练时间小幅增加,而对于大规模数据集,算法训练时间大幅减少。故本文对样本数量小于10 000的训练集,c和s分别选取4和2;样本数量在10 000到100 000之间的训练集,c和s分别选取9和3;样本数量大于100 000的训练集,c和s分别选取25和5。
3.4.2 分类性能比较在实验中,所有的多标签学习算法均采用相同的数据划分,用50%的数据进行训练,其余50%的数据进行测试。在计算评价指标时,评价指标取重复10次实验的平均值。由于比较的部分算法无法在一周内对数据集nuswide-cVLADplus、nuswide-bow完成训练预测,故在对算法性能进行比较与分析时只取其余9个数据集进行实验,如表 5所示。在表 6中列出了本文算法在nuswide-bow、nuswide-cVLADplus数据集上的评价指标值。
| 表 5 比较算法在5个评价指标上的实验结果(均值、排名) Tab.5 Experimental results of each comparing algorithm(mean rank) on five evaluation metrics |
| 表 6 SI-MLHN和SEI-MLHN在数据集nus-wide-full-cVLADplus和nuswide-bow上的性能指标(均值±方差) Tab.6 Classification performance (mean±std.) of SI-MLHN and SEI-MLHN on nus-wide-full-cVLADplus and nuswide-bow |
表 5为5个不同评价指标下各个多标签学习算法在常规规模的数据集上的学习性能,表 5中评价指标后的“↓”表示指标取值越小性能越佳,符号“↑”表示指标取值越大性能越佳, 其中AveR表示该算法的平均排名。此外,表 7对每个学习算法进行编号,例如BRSVM(A1)表示用A1代表算法BRSVM,再进一步给出了各多标签学习算法之间的相对性能,具体为,给定算法A1和A2,A1>A2表示在给定的评价指标上,基于显著度0.05的威尔科克森符号秩检验(Wilcoxon signed rank test),算法A1的性能显著优于A2。本文通过打分的方式对各学习算法的性能进行总体评价,若A1>A2,则A1的分数加1,A2的分数减1,通过比较每个算法的最终分数,可以对算法进行排序,其中A1分数高于A2,表示算法A1的总体性能优于A2。
| 表 7 各多标签学习算法在不同数据集上的相对性能比较 Tab.7 Relative performance comparison of multi-label algorithms on data sets |
从表 7中可以发现,算法SEI-MLHN在除Ranking loss外的各项指标以及总分均显著高于其余算法,表明它的分类性能在总体上优于其余算法。其次, 算法SI-MLHN在Example based F1上明显优于S-CoMLHN,说明SI-MLHN在一定程度上削弱了标签不平衡的影响,虽然算法SI-MLHN在Hanmming Loss和Ranking loss上稍劣于S-CoMLHN,但从整体性能上进行比较,算法SI-MLHN仍优于S-CoMLHN。再次,算法COCOA考虑了标签间的高阶关系且削弱了不平衡性的影响,但在Hanmming Loss上的性能较差,导致总分稍低于S-CoMLHN,也说明其总体性能稍低于S-CoMLHN。最后,可以从表 7中得出结论,本文所提出的算法SEI-MLHN具有很好的处理多标签分类问题的能力。
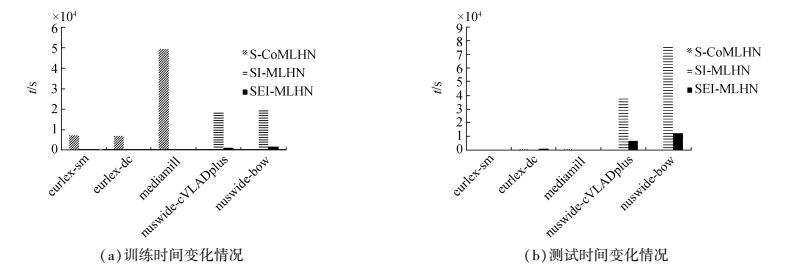
3.4.3 运行效率比较为了对算法S-CoMLHN、SI-MLHN以及SEI-MLHN的运行时间进行比较,本文用3个较大规模数据集(eurlex-sm、eurlex-dc、mediamill)和2个大规模数据集(nuswide-bow、nuswide-cVLADplus)进行实验,且令所有实验的SparkTask为32。由于S-CoMLHN在24小时内无法完成2个大规模数据集的训练和预测,故图 5中无对比结果。
|
图 5 算法对不同规模数据集训练与测试时间 Fig.5 Training and testing time of each comparing algorithm on multilabel data sets |
从图 5(a)中观察到,算法S-CoMLHN的训练时间显著高于SI-MLHN和SEI-MLHN,且在数据集nuswide-bow和nuswide-cVLADplus上没有得到有效结果,说明该算法不能很好地适应大规模数据。在数据集eurlex-sm、eurlex-dc-leaves、mediamill上,算法SEI-MLHN与SI-MLHN的训练时间没有较大的区别,但是当数据集规模增大时,算法SEI-MLHN的训练时间明显低于SI-MLHN,表明算法SEI-MLHN比SI-MLHN大大缩短了训练时间。从图 5(b)中观察到,在数据集eurlex-sm、eurlex-dc、mediamill上,S-CoMLHN、SI-MLHN以及SEI-MLHN的测试时间没有较大的区别,但是当数据集规模增大后,S-CoMLHN无法得到有效结果,且算法SEI-MLHN的测试时间也明显低于SI-MLHN,说明算法SEI-MLHN也缩短了算法的测试时间。从图 5中可以得到结论,算法SEI-MLHN具有较高的算法运行效率,且对大规模数据集具有良好的适应能力。
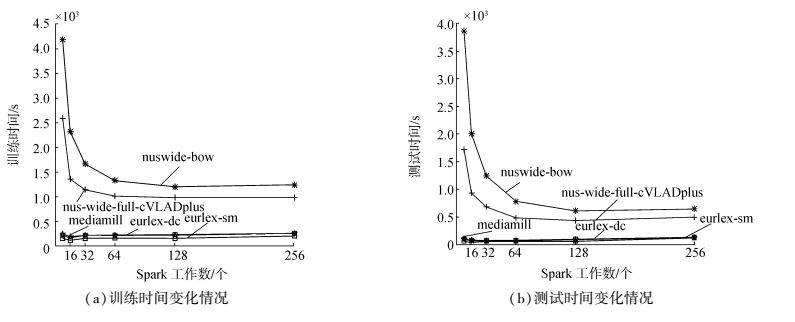
由于不同的SparkTask数值会对算法的运行时间产生影响,因此,为了测试SparkTask对算法SEI-MLHN运行效率的影响,选择了不同大小规模的数据集进行实验。图 6给出了随不同的任务数,算法SEI-MLHN在各个数据集下的训练与测试时间的变化情况,时间以秒为单位。从图 6中观察得到,对规模较小的多标签数据集,如emontions、yeast,不同的SparkTask数值对算法的运行时间没有较大的影响。而对于较大规模数据集mediamil,随着SparkTask数值的增加,算法的训练时间与测试时间急速下降,最后趋于平稳,但是当SparkTask增加到一定数量时训练测试时间均增大,这是因为当数据集规模不够大,SparkTask达到某个饱和点时,集群上各个节点的通信时间远远大于计算时间,算法的性能趋于平缓甚至变弱。
|
图 6 SEI-MLHN在不同SparkTask下不同数据集的训练与测试时间的变化 Fig.6 Training and testing time of SEI-MLHN under different values of SparkTask |
本文基于MLHN提出了一种能有效利用标签相关性处理大数据集Spark平台下的改进多标签超网络集成算法SEI-MLHN。该算法首先引入代价敏感,使其适应不平衡数据集并提升算法性能。然后,在超网络演化学习过程中利用抽样信息,以及修改损失函数,降低算法时间复杂度。最后,进行选择性集成,提高算法性能。在11个不同规模的数据集上进行实验,结果表明,该算法具有良好的分类性能、较低的时间复杂度以及良好的处理大规模数据集的能力。
在SEI-MLHN中,我们只考虑标签之间的相关性,即标签的同现。然而,标签之间的排他关系对于多标签分类也很重要。在未来,我们将研究如何利用超网络标签之间的包含性和排他性。
| [1] |
GAO S, WU W, LEE C H, et al. A MFoM learning approach to robust multiclass multi-label text categorization[C]//Proceedings of the 21st International Conference on Machine Learning. Canada:ACM Press, 2004:42.
( 0) 0)
|
| [2] |
JIANG J Y, TSAI S C, LEE S J. FSKNN:multi-label text categorization based on fuzzy similarity and k nearest neighbors[J]. Expert systems with applications, 2012, 39(3): 2813-2821. DOI:10.1016/j.eswa.2011.08.141 ( 0) 0)
|
| [3] |
BOUTELL M R, LUO J, SHEN X, et al. Learning multi-label scene classification ☆[J]. Pattern recognition, 2004, 37(9): 1757-1771. DOI:10.1016/j.patcog.2004.03.009 ( 0) 0)
|
| [4] |
QI G J, HUA X S, RUI Y, et al. Correlative multi-label video annotation[C]//In Proceedings of the 15th ACM International Conference on Multimedia. Germany:ACM Press, 2007:17-26.
( 0) 0)
|
| [5] |
CESA-BIANCHI N, RE M, VALENTINI G. Synergy of multi-label hierarchical ensembles, data fusion, and cost-sensitive methods for gene functional inference[J]. Machine learning, 2012, 88(1): 209-241. ( 0) 0)
|
| [6] |
ZHANG M L, ZHANG K. Multi-label learning by exploiting label dependency[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. USA:ACM Press, 2010:999-1008.
( 0) 0)
|
| [7] |
TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Mining multi-label data[M]. New York: Springer US, 2009: 667-685.
( 0) 0)
|
| [8] |
FüRNKRANZ J, HüLLERMEIER E, MENCíA E L, et al. Multilabel classification via calibrated label ranking[J]. Machine Learning, 2008, 73(2): 133-153. DOI:10.1007/s10994-008-5064-8 ( 0) 0)
|
| [9] |
TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Random k-Labelsets for Multilabel Classification[J]. IEEE transactions on knowledge & data engineering, 2010, 23(7): 1079-1089. ( 0) 0)
|
| [10] |
LO H Y, LIN S D, WANG H M. Generalized k-labelsets ensemble for multi-label and cost-sensitive classification[J]. Knowledge & data engineering IEEE transactions on, 2014, 26(7): 1679-1691. ( 0) 0)
|
| [11] |
HE H, GARCIA E A. Learning from imbalanced data[J]. IEEE transactions on knowledge and data engineering, 2009, 21(9): 1263-1284. DOI:10.1109/TKDE.2008.239 ( 0) 0)
|
| [12] |
XIOUFIS E S, SPILIOPOULOU M, TSOUMAKAS G, et al. Dealing with concept drift and class imbalance in multi-label stream classification[C]//IJCAI 2011 Proceedings of the International Joint Conference on Artificial Intelligence. Barcelona, Spain, 2011:1583-1588.
( 0) 0)
|
| [13] |
CHARTE F, RIVERA A, del JESUS M J, et al. A first approach to deal with imbalance in multi-label datasets[C]//In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems. Springer Berlin Heidelberg, USA, 2013:150-160.
( 0) 0)
|
| [14] |
ZHANG M L, LI Y K, LIU X Y. Towards class-imbalance aware multi-label learning[C]//Proceedings of the 24th International Joint Conference on Artificial Intelligence. Argentina:AAAI Press, 2015:4041-4047.
( 0) 0)
|
| [15] |
LIU H, LI X, ZHANG S. Learning instance correlation functions for multilabel classification[J]. IEEE transactions on cybernetics, 2017, 47(2): 499-510. DOI:10.1109/TCYB.2016.2519683 ( 0) 0)
|
| [16] |
ZHANG M L, WU L. Lift:multi-label learning with label[J]. Pattern analysis & machine intelligence IEEE transactions on, 2015, 37(1): 107-20. ( 0) 0)
|
| [17] |
ALALI A, KUBAT M. PruDent:A pruned and confident stacking approach for multi-label classification[J]. IEEE transactions on knowledge & data engineering, 2015, 27(9): 1-1. ( 0) 0)
|
| [18] |
WU Q, TAN M, Song H, et al. ML-forest:a multi-label tree ensemble method for multi-label classification[J]. IEEE transactions on knowledge and data engineering, 2016, 28(10): 1-1. ( 0) 0)
|
| [19] |
HUANG J, LI G, HUANG Q, et al. Learning label-specific features and class-dependent labels for multi-label classification[J]. IEEE transactions on knowledge and data engineering, 2016, 28(12): 3309-3323. DOI:10.1109/TKDE.2016.2608339 ( 0) 0)
|
| [20] |
WU Q, YE Y, ZHANG H, et al. ML-Tree:a tree-structure-based approach to multilabel learning[J]. IEEE trans neural netw learn syst, 2014, 26(3): 430-443. ( 0) 0)
|
| [21] |
CHARTE F. LI-MLC:A Label Inference Methodology for Addressing High Dimensionality in the Label Space for Multilabel Classification[J]. IEEE trans. neural networks and learning systems, 2014, 25(10): 1842-1854. DOI:10.1109/TNNLS.2013.2296501 ( 0) 0)
|
| [22] |
MONTAñES E, SENGE R, BARRANQUERO J, et al. Dependent binary relevance models for multi-label classification[J]. Pattern recognition, 2014, 47(3): 1494-1508. DOI:10.1016/j.patcog.2013.09.029 ( 0) 0)
|
| [23] |
LO H Y, LIN S D, WANG H M. Generalized k-labelsets ensemble for multi-label and cost-sensitive classification[J]. Knowledge and data engineering IEEE transactions on, 2014, 26(7): 1679-1691. DOI:10.1109/TKDE.2013.112 ( 0) 0)
|
| [24] |
SUN K W, LEE C H, WANG J. Multilabel classification via co-evolutionary multilabel hypernetwork[J]. IEEE transactions on knowledge and data engineering, 2016, 28(9): 1-1. ( 0) 0)
|
| [25] |
LO H Y, WANG J C, WANG H M, et al. Cost-sensitive multi-label learning for audio tag annotation and retrieval[J]. IEEE transactions on multimedia, 2011, 13(3): 518-529. DOI:10.1109/TMM.2011.2129498 ( 0) 0)
|
| [26] |
OZONAT K, YOUNG D. Towards a universal marketplace over the web:statistical multi-label classification of service provider forms with simulated annealing[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2009:1295-1304.
( 0) 0)
|
| [27] |
ZHANG M L, ZHOU Z H. A review on multi-label learning algorithms[J]. IEEE transactions on knowledge and dada engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 ( 0) 0)
|
| [28] |
ZHANG M L, ZHANG K. Multi-label learning by exploiting label dependency[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. USA:ACM Press, 2010:999-1008.
( 0) 0)
|
| [29] |
ZHANG M L, ZHOU Z H. ML-KNN:A lazy learning approach to multi-label learning[J]. Pattern recognition, 2007, 40(7): 2038-2048. DOI:10.1016/j.patcog.2006.12.019 ( 0) 0)
|
| [30] |
BOUTELL M R, LUO J, SHEN X, et al. Learning multi-label scene classification[J]. Pattern recognition, 2004, 37(9): 1757-1771. DOI:10.1016/j.patcog.2004.03.009 ( 0) 0)
|
| [31] |
ELISSEEFF A, WESTON J. A kernel method for multi-labelled classification[C]//In NIPS'01 Proceedings of the 14th International Conference on Neural Information Processing Systems:Natural and Synthetic. Vancouver, British Columbia, Canada:MIT Press, 2001:681-687.
( 0) 0)
|
| [32] |
ZHANG M L, ZHOU Z H. Multilabel neural networks with applications to functional genomics and text categorization[J]. IEEE transactions on knowledge and data engineering, 2006, 18(10): 1338-1351. DOI:10.1109/TKDE.2006.162 ( 0) 0)
|
| [33] |
READ J, PFAHRINGER B, HOLMES G, et al. Classifier chains for multi-label classification[J]. Machine learning, 2011, 85(3): 254-269. ( 0) 0)
|
| [34] |
YI L, RONG J, LIU Y. Semi-supervised Multi-label Learning by Constrained Non-negative Matrix Factorization.[C]//In AAAI'06 Proceedings of the 21st national conference on Artificial intelligence. Boston:AAAI Press, 2006:421-426.
( 0) 0)
|
| [35] |
LIU X Y, LI Q Q, ZHOU Z H. Learning imbalanced multi-class data with optimal dichotomy weights[C]//Proceedings of the 2013 IEEE 13th International Conference on Data Mining. USA:IEEE Press, 2013:478-487.
( 0) 0)
|
| [36] |
TAHIR M A, KITTLER J, MIKOLAJCZYK K, et al. Improving multilabel classification performance by using ensemble of multi-label classifiers[C]//Proceedings of the International Workshop on Multiple Classifier Systems. Egypt:Springer Berlin Heidelberg, 2010:11-21.
( 0) 0)
|
| [37] |
DEAN J, GHEMAWAT S. MapReduce:Simplified data processing on large clusters[C]//In OSDI'04 Proceedings of the 6th conference on Symposium on Opearting Systems Design & Implementation. Berkeley, USA, 2004:10-10.
( 0) 0)
|
| [38] |
ZAHARIA M, CHOWDHURY M, FRANKLIN M J, et al. Spark:cluster computing with working sets[C]//In HotCloud'10 Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing. Berkeley, USA, 2010:10-10.
( 0) 0)
|
| [39] |
MIKA P. Flink:semantic web technology for the extraction and analysis of social networks[J]. Web semantics science services and agents on the world Wide Web, 2005, 3(2/3): 211-223. ( 0) 0)
|
| [40] |
BU Y, HOWE B, BALAZINSKA M, et al. HaLoop:efficient iterative data processing on large clusters[J]. Proceedings of the Vldb endowment, 2010, 3(1/2): 285-296. ( 0) 0)
|
| [41] |
ZAHARIA M, CHOWDHURY M, DAS T, et al. Resilient distributed datasets:a fault-tolerant abstraction for in-memory cluster computing[C]//In Proceedings of the 9th USENIX Conference on Networked Systems Design and Implementation. San Jose:USENIX Association, 2012:2.
( 0) 0)
|
| [42] |
VESANTO J, ALHONIEMI E. Clustering of the self-organizing map[J]. IEEE transactions on neural networks, 2000, 11(3): 586-600. DOI:10.1109/72.846731 ( 0) 0)
|
| [43] |
LEE S J, JIANG J Y. Multilabel text categorization based on fuzzy relevance clustering[J]. IEEE transactions on fuzzy systems, 2014, 22(6): 1457-1471. DOI:10.1109/TFUZZ.2013.2294355 ( 0) 0)
|
| [44] |
CHENG W, HüLLERMEIER E. Combining instance-based learning and logistic regression for multilabel classification[J]. Machine learning, 2009, 76(2): 211-225. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


