强化学习要研究的问题是智能体(agents)如何在一个环境(environment)中学到一定的策略(policy),使得长期的奖赏(reward)最大。但是传统的强化学习方法面临着维度灾难,即当环境较为复杂或者任务较为困难时,agent的状态(state)空间过大,会导致需要学习的参数以及所需的存储空间急速增长,强化学习难以取得理想的效果。为了解决维度灾难,研究者提出了分层强化学习(hierarchical reinforcement learning,HRL)。HRL的主要目标是将复杂的问题分解成多个小问题,分别解决小问题从而达到解决原问题的目的[1]。近些年来,人们认为分层强化学习基本可以解决强化学习的维度灾难问题[2-3],转而将研究方向转向如何将复杂的问题抽象成不同的层级,从而更好地解决这些问题[4]。
现在已有的一些分层学习大致可以分为4大类,分别是基于选项(option)的强化学习、基于分层抽象机(hierarchical of abstract machines)的分层强化学习、基于MaxQ值函数分解(MaxQ value function decomposition)的分层强化学习,以及端到端的(end to end)分层强化学习。
1 背景知识在本节中,我们主要介绍强化学习、马尔可夫决策过程(Markov decision process)和半马尔克夫决策过程(Semi-Markov decision process)的定义以及相关的背景知识。
1.1 强化学习与马尔可夫决策过程强化学习是机器学习和人工智能中一个重要的领域,主要研究的问题是agent如何通过直接与环境交互来学习策略,使得长期的奖赏最大。强化学习有一些特点,比如无监督学习,奖赏的反馈有延迟,agent选择的动作会影响之后接收的数据等。
大多数关于强化学习的研究都是建立在马尔可夫决策过程(MDP)的基础上,MDP可以表示为一个五元组〈S, A, P, R, γ〉。其中,S为状态(state)的有限集合,集合中某个状态表示为s∈S;A为动作(action)的有限集合,集合中某个动作表示为a∈ A,A为状态s下可执行的动作集合;P为状态转移方程,P(s′|s, a)表示在状态s执行动作a后将以P(s′|s, a)的概率跳转到状态s′;R为奖赏函数(reward function);γ为折损系数(discount factor),0≤γ≤1。假设一个agent观察到自己的状态s,此时它选择一个动作a,它会得到一个即时的奖赏rsa=R(s, a),然后以P(s′|s, a)的概率达到下一个状态s′。马尔可夫决策过程有马尔可夫性,即系统的下个状态只与当前状态有关,与之前的状态无关。当马尔可夫决策过程中作出决策时,只需要考虑当前的状态,而不需要历史数据,这样大大降低了问题的复杂度。
强化学习需要agent学习到一个策略π:S×A→[0, 1],通过π(s, a)的值来指导agent进行动作的选择。给定一个策略π和一个状态s,Vsπ表示从s开始按照策略π进行选择可以得到的期望累积奖赏。我们将V称作值函数(value function),其具体的数学定义为Vπ(s)=E{rt+γrt+1+γ2rt+2+…+rnrt+n| s=st, π}。强化学习的目标是学到一个最优的策略π*,最大化每一个状态下的V值,此时的最优值函数记作V*。
除了值函数,动作-值函数(action-value function)也在强化学习中扮演着重要的角色,记作Qπ(s, a),表示给定一个策略π,在状态s上执行动作a可以得到的期望累积奖赏。我们也将Qπ(s, a)叫作Q函数,其具体的数学定义表示为
| ${Q^\pi }\left( {s,a} \right) = E\{ {r_t} + \gamma {r_{t + 1}} + {\gamma ^2}{r_{t + 2}} + \cdots {\rm{ |}}{s_t} = s,{a_t} = a,\pi \} $ |
同样的,我们也希望通过学习到一个最优的Q函数Q*,使agent可以直接通过Q函数来选择当前状态下应该执行的动作。
经过多年的研究,已经出现一些算法,致力于解决传统的强化学习问题,比如Q-Learning、蒙特卡洛方法(Monte-Carlo learning)、时序差分方法(temporal-difference learning)等。其中Q-Learning方法常常在分层强化学习中被使用。Q-Learning通过不断迭代更新Q函数的值来逼近最优的Q*。其迭代式如下
| $\begin{array}{l} {Q_{k + 1}}\left( {s,a} \right) = (1 - {\alpha _k}){Q_k}\left( {s,a} \right) + \\ \quad \quad \quad \quad \quad {\alpha _k}(r + \gamma {\rm{ma}}{{\rm{x}}_{a\prime \in {A_{s\prime }}}}{Q_k}\left( {s\prime ,a\prime } \right)) \end{array}$ |
其中s′表示下一个状态。
1.2 半马尔可夫决策过程马尔可夫决策过程中,选择一个动作后,agent会立刻根据状态转移方程P跳转到下一个状态,而在半马尔可夫决策过程(SMDP)中,当前状态到下一个状态的步数是个随机变量τ,即在某个状态s下选择一个动作a后,经过τ步才会以一个概率转移到下一个状态s′。此时的状态转移概率是s和τ的联合概率P(s′, τ|s, a)。根据τ的定义域不同,SMDP所定义的系统也有所不同。当τ的取值为实数值,则SMDP构建了一个连续时间-离散事件系统(continuous-time discrete-event system)[5];而当τ的取值为正整数,则是一个离散时间SMDP(discrete-time SMDP)[6]。出于简单考虑,绝大部分分层强化学习都是在离散时间SMDP上进行讨论。
2 分层强化学习方法分层强化学习是将复杂的强化学习问题分解成一些容易解决的子问题(sub-problem),通过分别解决这些子问题,最终解决原本的强化学习问题[7-9]。常见的分层强化学习方法可以大致分为四大类,分别为基于选项(option)的强化学习、基于分层抽象机(hierarchical of abstract machines)的分层强化学习、基于MaxQ函数分解(MaxQ value function decomposition)的分层强化学习,以及端到端的(end to end)的分层强化学习。本节将对它们逐一进行探讨。
2.1 基于选项的分层强化学习“选项”(option)的概念在1999年由Sutton等人提出[10],是一种对动作的抽象。一般的,option可表示为一个三元组〈I, π, β〉。其中,π:S×A→[0, 1]表示此option中的策略;β:S→[0, 1]表示终止条件,β(s)表示状态s有β(s)的概率终止并退出此option;I⊆S表示option的初始状态集合。option〈I, π, β〉在状态s上可用,当且仅当s∈I。当option开始执行时,agent通过该option的π进行动作选择直到终止。值得注意的是,一个单独的动作a也可以是一个option,通常被称作one-step option,I={s:a∈As},并且对任意的状态s都有β(s)=1。
基于option的分层强化学习的过程如下:假设agent当前在某个状态,选择一个option,通过这个option的策略,agent选择了一个动作或者另一个option。若选择了一个动作,则直接执行转移到下一个状态;若选择了另一个option,则用选择的新option继续选择,直到最后得出一个动作。
为了使用option来解决分层强化学习问题,我们还需要定义一个更高层级的策略μ:S×Os→[0, 1]。其中,O表示所有option的集合,而Os表示状态s下可用的option的集合;μ(s, o)表示在状态s时以μ(s, o)的概率选择o作为当前的option。此时的Q函数定义为
| ${Q^\mu }\left( {s,o} \right) = E\{ {r_t} + \gamma {r_{t + 1}} + {\gamma ^2}{r_{t + 2}} + \cdots {\rm{ }}\left| {{o_r}} \right. = o,{s_t} = s\} $ |
此时的Q-Learning的更新公式为
| $\begin{array}{l} {Q_{k + 1}}({s_t},{o_t}) = (1 - {\alpha _k}){Q_k}({s_t},{o_t}) + {\alpha _k}({r_t} + \gamma {r_{t + 1}} + \cdots + \\ \quad \quad \quad \quad \quad {\gamma ^{\tau - 1}}{r_{t + \tau }} + {\gamma ^\tau }{\rm{ma}}{{\rm{x}}_{o\prime \in {O_{s\prime }}}}{Q_k}({s_{t + \tau }},o\prime )) \end{array}$ |
其中,αk为第k轮迭代时的学习率,τ表示option o在执行τ步之后在状态st+τ停止,而o′为在o执行结束后的下一个option。可以注意到,当所有的option均为one-step option时,这个Q-Learning就退化为普通的Q-Learning过程。
2.2 基于分层抽象机的分层强化分层抽象机(hierarchies of abstract machines,HAMs,)是Parr和Russell提出的方法[11]。和option的方法类似,HAMs的方法也是建立在SMDP的理论基础之上的。HAMs的主要思想是将当前所在状态以及有限状态机的状态结合考虑,从而选择不同的策略。
令M为一个有限MDP,S为状态集合,A为动作集合。{Hi}为一个有限状态机的集合,其中每个有限状态机Hi都有一个状态集合Si、一个概率转移方程δi以及一个随机函数fi:S→Si。每个状态机都有4种类型的状态,即动作(action)、调用(call)、选择(choice)以及停止(stop)。action类型的状态会根据状态机的具体状态执行一个MDP中的动作。在call类型的状态时,当前状态机Hi将被挂起,开始初始化下一个状态机Hj,即把Hj的状态设置为fj(st),其中j的值根据mti得出,mti表示第i个状态机在时刻t时的状态。choice类型的状态则是非确定性地选择当前状态机的下一个状态。stop状态则是停止当前状态机的活动,恢复调用它的状态机的活动,同时agent根据之前选择的动作进行状态转移并得到奖赏。如果在这个过程中没有选择出动作,例如某个状态机Hi刚被调用就被随机函数fi初始化到了一个stop状态以至于返回时并没有选出要执行的动作,则M保持当前的状态。
HAMs也可以通过改进Q-Learning算法进行学习。对于一个马尔可夫决策过程M和任意一个状态机H,HºM是一个MDP[11],其中状态集合为S×SH,动作集合为A×AH。只有当H的状态是choice类型的状态时,HºM才需要进行决策,其他状态下都可以根据状态机的状态自动进行状态转移,所以实际上HºM是个SMDP。因此我们需要维护的Q函数为Q([sc, mc], ac),其中,c表示HºM中需要作出选择的状态的下标,[sc, mc]被称作选择点(choice point)。此时Q-Learning的更新公式为
| $\begin{array}{l} \;{Q_{k + 1}}([{s_c},{m_c}],{a_c}) = (1 - {\alpha _k}){Q_k}([{s_c},{m_c}],{a_c}) + \alpha [{r_t} + \\ \gamma {r_{t + 1}} + \cdots + {\gamma ^{\tau - 1}}{r_{t + \tau - 1}} + {\gamma ^\tau }{\rm{ma}}{{\rm{x}}_{a\prime }}{Q_k}(s{\prime _c},m{\prime _c}],a\prime )] \end{array}$ |
其中,τ为由sc到sc′所经过的步数。
2.3 基于MaxQ值函数分解的分层强化学习MaxQ值函数分解(MaxQ value function decomposition),是由Dietterich提出的另外一种分层强化学习的方法[12]。首先将一个马尔可夫决策过程M分解成多个子任务{M0, M1, …, Mn},M0为根子任务,解决了M0就意味着解决了原问题M。对于每一个子任务Mi,都有一个终止断言(termination predicate) Ti和一个动作集合Ai。这个动作集合中的元素既可以是其他的子任务,也可以是一个MDP中的action。一个子任务的目标是转移到一个状态,可以满足终止断言,使得此子任务完成并终止。我们需要学到一个高层次的策略π={π0, …, πn},其中πi为子任务Mi的策略。
令V(i, s)表示子任务i在状态s的值函数,即该子问题从状态s开始一直按照某个策略执行最终达到终止状态的期望累计奖赏。类似的,令Q(i, s, j)为子任务i在状态s执行动作j之后按照某个策略执行直到达到终止状态的期望累计奖赏,可以表示为
| $Q\left( {i,s,j} \right) = E({r_t} + \gamma {r_{t + 1}} + {\gamma ^2}{r_{t + 2}} + \cdots |{\rm{ }}{s_t} = s,\pi )$ |
假设选择的动作j一共执行了τ步才返回,那么我们可以把Q函数写成
| $Q\left( {i,s,j} \right) = E\{ \sum\limits_{u = 0}^{\tau - 1} {{\gamma ^u}{r_{t + u}}} + \sum\limits_{u = \tau }^\infty {{\gamma ^u}{r_{t + u}}|} {s_{t = s}},\pi \} $ |
其中右边的第1项实际上是V(j, s),第2项叫作完成函数(completion function),记作C(i, s, j)。则Q函数的贝尔曼方程可以写为
| $\begin{array}{l} \quad Q\left( {i,s,j} \right) = \sum\limits_{s\prime ,\tau } P \left( {s\prime ,\tau |s,j} \right)(V\left( {j,s} \right) + \\ {\gamma ^\tau }{\rm{ma}}{{\rm{x}}_{j\prime }}Q\left( {i,s\prime ,{\rm{ }}j\prime } \right)) = V\left( {j,s} \right) + C\left( {i,s,j} \right) \end{array}$ |
当选择的动作j完成后,得到下一个状态s′以及做完这个动作经过的时间τ,则可更新完成函数
| $\begin{array}{l} {C_{t + 1}}\left( {i,s,j} \right) = (1 - {\alpha _t}){C_t}\left( {i,s,j} \right) + \\ {\alpha _t}{\gamma ^\tau }[{\rm{ma}}{{\rm{x}}_{a\prime }}V\left( {a\prime ,s\prime } \right) + {C_t}\left( {i,s\prime ,a\prime } \right)] \end{array}$ |
这样也就更新了Q函数。
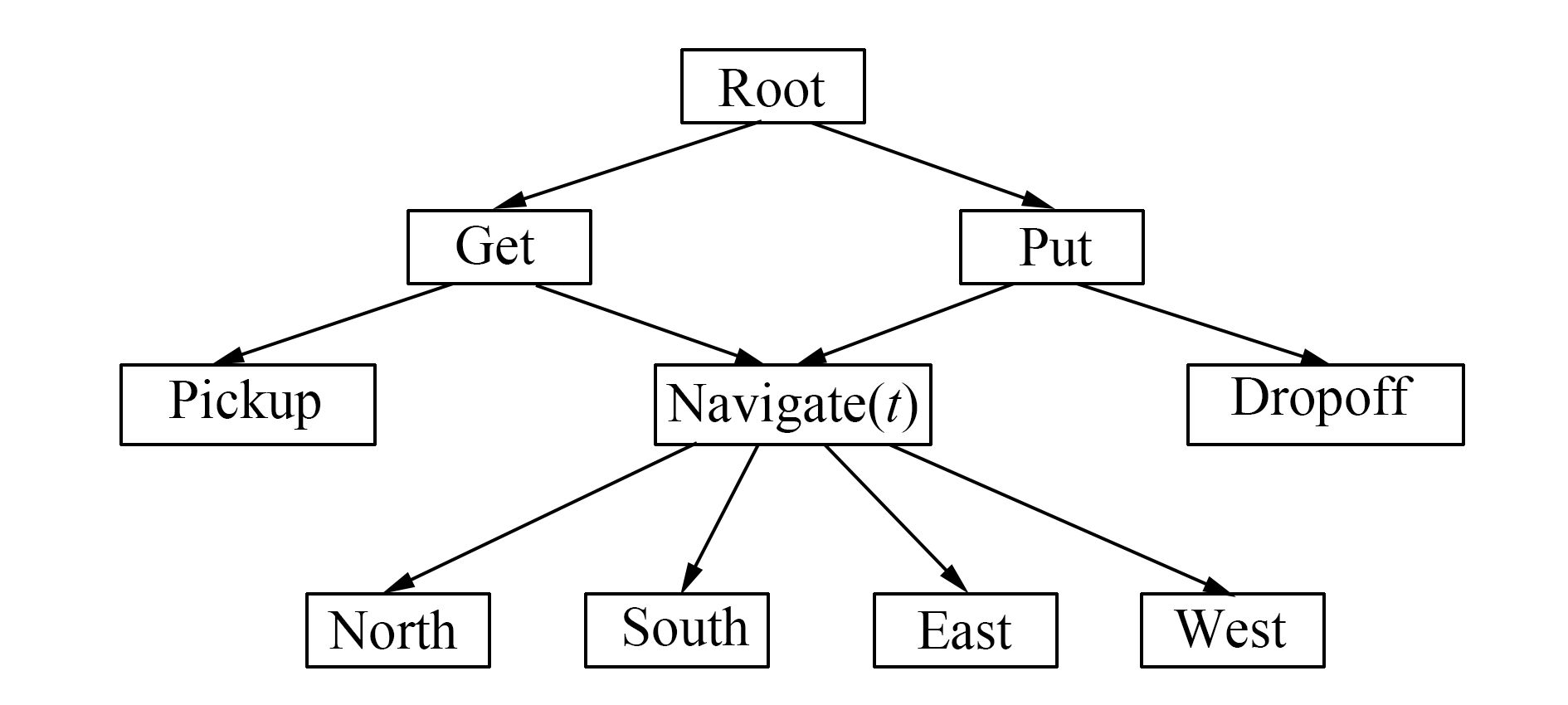
图 1为利用MaxQ方法解决taxi problem的任务划分示意图[12]。
|
图 1 出租车问题的任务图 Fig.1 Task graph for the taxi problem |
出租车问题是指一个出租车agent需要到特定位置接一位乘客并且把他送到特定的位置让其下车。一共有6个动作,分别是上车(pick up)、下车(drop off),以及向东南西北四个方向开车的动作。这里使用MaxQ方法,将原问题分解成了get和put两个子任务,这两个子任务又进行分解,get分解成一个基本动作pick up和一个子任务navigate,而put也分解成了一个基本动作drop off和一个子任务navigate。子任务navigate(t)表示t时刻应该开车的方向。对于这个强化学习问题,agent首先选择get,然后get子问题navigate,直到到达乘客所在地,然后get选择pick up动作,乘客上车。之后agent选择put子任务,put子任务选择navigate,直到到达乘客目的地,之后put子任务选择drop off动作,乘客下车,任务完成。
2.4 端到端的的分层强化学习上述的几种方法,都需要人工来做很多工作,比如人工进行option的选取,人工进行HAMs的构建,人工划分子任务等。人工设计不仅耗时耗力,并且会直接影响最终强化学习结果的好坏。近些年来人们关注如何让agent自己学到合理的分层抽象,而非人为进行划分和指定。
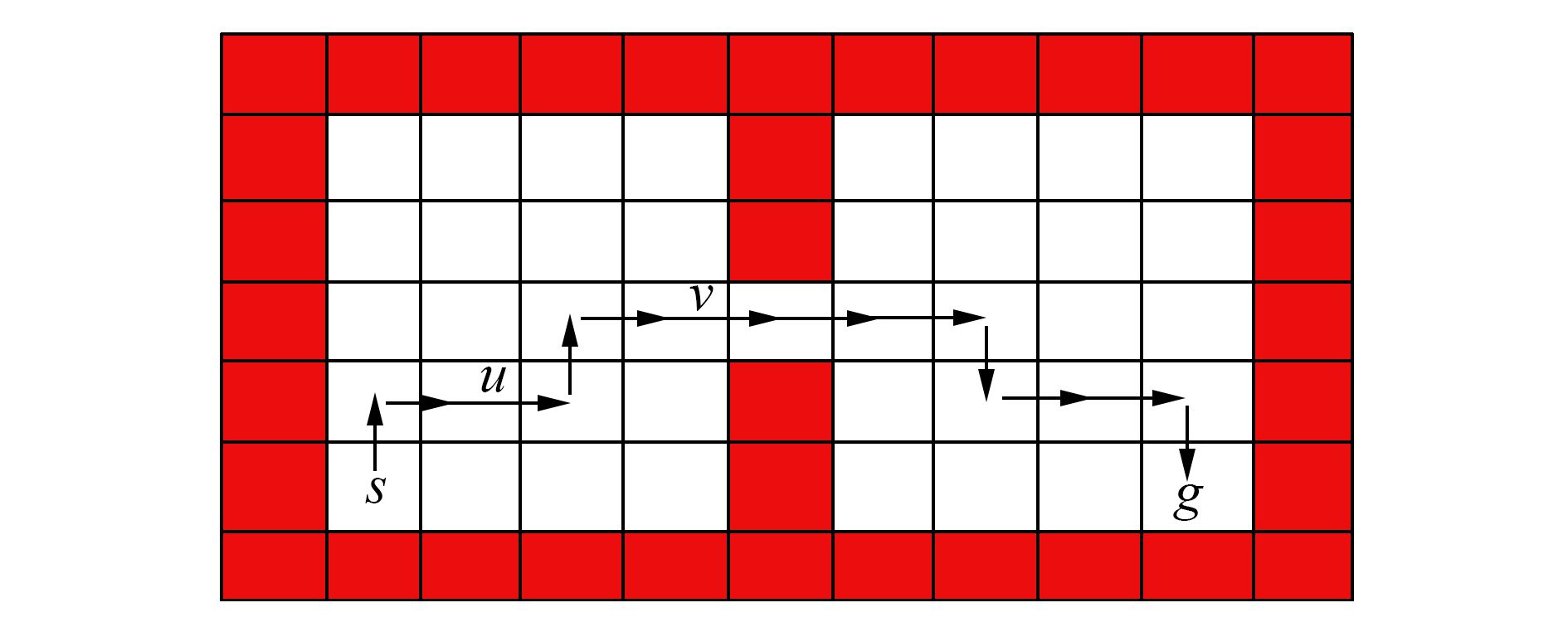
有人提出利用蚁群算法启发式地寻找合理的划分点[13]。作者利用蚁群算法根据信息素的变化程度寻找“瓶颈”(bottle neck),瓶颈像一座桥梁一样连接着问题空间中不同的连续区域。图 2为一个Grid Word问题,agent需要从状态s出发到达状态g。通过蚁群算法分析信息素的变化程度找出瓶颈在两个房间的窄门处,即图 2中的状态v附近。
|
图 2 通过蚁群算法找到从s到g的最短路径 Fig.2 Shortest path between s and g found by ant system |
通过多次探索留下的信息素密集程度来找到瓶颈即可将问题空间划分,再使用基于option的分层强化学习即可解决。
除了启发式的抽象方法,有人还提出使用神经网络结构来自动进行问题的分层抽象和学习[14-20]。近些年来神经网络快速发展,尤其是在图像识别领域,更是取得了很多成果。因此有人尝试通过结合神经网络和强化学习来设计电子游戏的AI,输入为游戏画面,通过神经网络和强化学习学习到游戏策略。有些游戏复杂度较高,需要使用分层强化学习。文献[14]中提出了Option-Critic架构,旨在通过神经网络强大的学习能力,模糊发现option和学习option之间的界限,直接通过神经网络一起训练。在一些游戏上取得了比不使用分层强化学习的Deep Q Network更好的结果。文献[15]中提出了Manager-Worker架构,Manager负责给Worker一个子目标,而Worker根据子目标和当前所处的状态给出具体执行的动作。在这个方法中,Manager和Worker分别是两个不同的神经网络,并且用各自的梯度分别进行优化,在实验中也取得了很好的效果。
人工进行分层和抽象,不仅费时费力,而且容易忽视问题中不易发现的内在联系。因此使用端到端的分层强化学习,从分层抽象到训练学习,都通过机器学习的方法自动进行必然是今后人们不断研究的方向。
3 总束语本文对于分层强化学习进行了回顾。首先介绍了强化学习、马尔科夫决策过程以及半马尔科夫决策过程的定义和基本概念,规定了本文的符号使用。然后,在第2节分4个方面,阐述了Sutton等提出的option方法,Parr和Russell提出的HAMs方法以及Dierrerich等提出的MaxQ方法,阐述了这些方法具体的计算方法。分析了近两年来的研究方向,介绍了一些端到端的、自动抽象的分层强化学习。分层强化学习是解决大规模强化学习的潜在途径,然而其受到的关注不足。希望本篇综述能够引起更多人关注分层强化学习。
| [1] |
BARTO A G, MAHADEVAN S. Recent advances in hierarchical reinforcement learning[J]. Discrete event dynamic systems, 2013, 13(4): 341-379. ( 0) 0)
|
| [2] |
YAN Q, LIU Q, HU D. A hierarchical reinforcement learning algorithm based on heuristic reward function[C]//In Proceedings of 2nd International Conference on Advanced Computer Control. Shenyang, China, 2010, 3:371-376.
( 0) 0)
|
| [3] |
DETHLEFS N, CUAYÁHUITL H. Combining hierarchical reinforcement learning and Bayesian networks for natural language generation in situated dialogue[C]//European Workshop on Natural Language Generation. Nancy, France, 2011:110-120.
( 0) 0)
|
| [4] |
AL-EMRAN M. Hierarchical reinforcement learning:a survey[J]. International journal of computing and digital systems, 2015, 4(2): 137-143. DOI:10.12785/ijcds/040207 ( 0) 0)
|
| [5] |
MAHADEVAN S, MARCHALLECK N. Self-improving factory simulation using continuous-time average-reward reinforcement learning[C]. In Proceedings of the Machine Learning International Workshop. Nashville, USA, 1997:202-210.
( 0) 0)
|
| [6] |
HOWARD R A. Semi-Markov and decision processes[M]. New York: DOVER Publications, 2007.
( 0) 0)
|
| [7] |
GIL P, NUNES L. Hierarchical reinforcement learning using path clustering[C]//In Proceedings of 8th Iberian Conference on Information Systems and Technologies. Lisboa, Portugal, 2013:1-6.
( 0) 0)
|
| [8] |
STULP F, SCHAAL S. Hierarchical reinforcement learning with movement primitives[C]//In Proceedings of 11th IEEE-RAS International Conference on Humanoid Robots. Bled, Slovenia, 2011:231-238.
( 0) 0)
|
| [9] |
DU X, LI Q, HAN J. Applying hierarchical reinforcement learning to computer games[C]//In Proceedings of IEEE International Conference on Automation and Logistics. Xi'an, China, 2009:929-932.
( 0) 0)
|
| [10] |
SUTTON R S, PRECUP D, SINGH S. Between MDPs and semi-MDPs:a framework for temporal abstraction in reinforcement learning[J]. Artificial intelligence, 1999, 112(1/2): 181-211. ( 0) 0)
|
| [11] |
PARR R, RUSSELL S. Reinforcement learning with hierarchies of machines[C]//Advances in Neural Information Processing Systems. Colorado, USA, 1998:1043-1049.
( 0) 0)
|
| [12] |
DIETTERICH T G. Hierarchical reinforcement learning with the MAXQ value function decomposition[J]. Journal of artificial intelligence research, 2000, 13: 227-303. ( 0) 0)
|
| [13] |
MOHSEN G, TAGHIZADEH N, et al. Automatic abstraction in reinforcement learning using ant system algorithm[C]//In Proceedings of AAAI Spring Symposium:Lifelong Machine Learning. Stanford, USA, 2013:114-122.
( 0) 0)
|
| [14] |
PIERRE-LUC BACON, JEAN HARB. The option-critic architecture[C]//In Proceeding of 31th AAAI Conference on Artificial Intelligence. San Francisco, USA, 2017:1726-1734.
( 0) 0)
|
| [15] |
VEZHNEVETS A S, OSINDERO S, SCHAUL T, et al. FeUdal networks for hierarchical reinforcement learning[C]//In Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia, 2017:3540-3549.
( 0) 0)
|
| [16] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(2): 529-533. ( 0) 0)
|
| [17] |
TEJAS D. K, KARTHNIK N, ARDAVAN S, et al. Hierarchical deep reinforcement learning:integrating temporal abstraction and intrinsic motivation[C]//Annual Conference on Neural Information Processing Systems. Barcelona, Spain, 2016:3675-3683.
( 0) 0)
|
| [18] |
CARLOS FLORENSA, YAN D, PIETER A. Stochastic neural networks for hierarchical reinforcement learning[EB/OL]. Berkeley, USA, arXiv. 2017, https://arxiv.org/pdf/1704.03012.pdf.
( 0) 0)
|
| [19] |
LAKSHMINARAYANAN A S, KRISHNAMURTHY R, KUMAR P, et al. Option discovery in hierarchical reinforcement learning using spatio-temporal clustering[EB/OL]. Madras, India, arXiv, 2016, https://arxiv.org/pdf/1605.05359.pdf.
( 0) 0)
|
| [20] |
XUE B, GLEN B. DeepLoco:dynamic locomotion skills using hierarchical deep reinforcement learning[J]. ACM transactions on graphics, 2017, 36(4): 1-13. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


