线性回归模型因为其较好的泛化性能及相对简单快速的求解方法而受到广泛关注，并已成为统计机器学习中一类最基本的方法^[1]。虽然上述线性模型在现实中有广泛应用。但只有当问题的输入呈线性关系时，它才会有较好的效果。另一方面，线性模型本身缺乏对输入变量间关系的探索机制。由此自然地转向考虑含有二阶交叉项的线性模型(此处线性相对参数而言)。含有二阶交叉项的线性模型考虑了输入特征间的相互关系。因此，当输入数据的特征间呈非线性关系，特别是二次关系时，其性能优于一般的线性模型。

推荐系统近年来广受关注^[2]，广义上的推荐系统就是给用户推荐物品的系统，它还可具体到一些特定领域，如音乐、书籍等。推荐系统的主要任务是根据用户的历史行为记录去预测用户未来可能会购买的物品。从本质上说就是探索用户与用户间以及用户与物品间的关系，也就是变量与变量间的关系。针对推荐系统，最近S. Rendle等^[3]提出了一个新的二阶交叉项模型：因子分解机(FM)。在FM中，每个变量x_i都对应着一个在隐空间的k维的向量v_i, x_i和x_j的交叉项系数等于x_i和x_j的内积，当输入数据非常稀疏时，一般的二阶交叉模型无法学习到有效的交叉项系数。而FM分解了交叉项系数，这个特性使得FM能学习到数据中隐藏的变量间相互关系^[3-4]。因此，FM特别适用于稀疏数据。

虽然对交叉项系数进行分解能显著提升模型性能，但当k(因子分解维度)较大时，FM模型包含大量参数，为了避免过拟合，常常需要对目标函数添加正则化项。一种常用的正则化方法是添加 ${\ell _2}$ 范数。但是，对于高维数据，我们希望选出那些最具判别性的特征。通常的做法是向目标损失函数添加能够诱导稀疏解的正则化项，通过优化正则化的目标函数来获得稀疏解。比如在线性回归中，向目标函数添加 ${\ell _1}$ 范数的正则项^[5]，不仅能防止过拟合，还能起到特征选择的作用。虽然， ${\ell _1}$ 范数能获得稀疏解，但是，这种稀疏并不包含结构信息。在FM中，其特征应当满足这样一种性质，即涉及同一个特征的线性项和二阶项要么同时被选要么同时不被选，当该特征是噪音时，应当同时不被选，而当该特征是重要变量时，应当同时被选。而 ${\ell _1}$ 范数不能利用此先验结构信息。

Group Lasso(GL) 是M.Yuan等^[6]基于Lasso提出的用于对组变量进行特征选择的方法，与Lasso不同的是，GL能同时选择或者不选组内的所有变量。首先根据先验知识将变量按照相关性划分为不同组，从聚类角度看就是将同类变量划分为同组，不同类变量划分为不同组。在FM中，将关于特征x_i的线性项系数ω_i和其在隐空间的特征表示向量v_i分在同组中，这样，GL就能保证当x_i是噪音时，ω_i和v_i同时不选，反之，则同时选择。虽然GL能实现这种结构稀疏，但是，对于选中的组，并不是所有特征都是有用的。因此，GL的使用有非常大限制，有必要继续选择组内重要的特征。

Simon等^[7]在GL的基础上提出了基于Sparse Group Lasso（SGL）的线性回归模型。与GL相同的是它们都对变量进行分组，与GL不同的是, SGL在GL的基础上，继续选择组内重要特征。因此，SGL能同时实现组间稀疏和组内稀疏, 而GL只实现了组间稀疏。SGL结合了Lasso和GL的优点，当待求变量存在结构稀疏信息时，仅使用Lasso会丢失结构信息，而仅使用GL又会导致求得冗余的解。基于上述事实，SGL既保留了GL的结构信息，又具有Lasso的高效特征选择的能力。

从另一角度看，当输入的数据非常稀疏而k选择较大值时，FM容易过拟合。此时，SGL的组内稀疏能通过特征选择控制k的大小。而且，不同的特征由于重要程度的不同，其对应的分解向量v的维度也应当不同，所以，组内稀疏在一定程度上通过特征选择对不同维度特征自适应了最优的k值。

当前虽然已有一些关于FM的研究，如Mathieu等^[8]在FM的基础上进一步提出了高阶因子分解机(阶数≥3)，M. Li等^[9]提出了分布式的FM以及W-S CHIN等^[10]提出了针对二类分类问题的FM的优化算法并将其并行化。但是，它们并没有探索FM的稀疏化机制。本文首次针对FM的二阶特征结构提出了SGL-FM，而且，本文的方法也可以直接推广到高阶的FM中以探索高阶FM的稀疏化机制。

1 因子分解机 1.1 目标函数

FM的基本模型如下：

$\hat y({\mathit{\boldsymbol{x}}}) = {\omega _0} + {\mathop \sum \limits_{i = 1}^p} {{\mathit{\boldsymbol{\omega }}}_i}{{\mathit{\boldsymbol{x}}}_i} +{\mathop \sum \limits_{i = 1}^p} {\mathop \sum \limits_{j = i + 1}^p} < {{\mathit{\boldsymbol{v}}}_i},{{\mathit{\boldsymbol{v}}}_j} > {{\mathit{\boldsymbol{x}}}_i}{{\mathit{\boldsymbol{x}}}_j}$

(1)

式(1)也可变形为

$\hat y({\mathit{\boldsymbol{x}}}) = {\omega _0} +{\mathop \sum \limits_{i = 1}^p} {{\mathit{\boldsymbol{\omega }}}_i}{{\mathit{\boldsymbol{x}}}_i} + \frac{1}{2}{\mathop \sum \limits_{f = 1}^k} ({({\mathop \sum \limits_{i = 1}^p} {{\mathit{\boldsymbol{v}}}_{i,f}}{{\mathit{\boldsymbol{x}}}_i})^2} - {\mathop \sum \limits_{i = 1}^p} {{\mathit{\boldsymbol{v}}}_{i,f}}^2{{\mathit{\boldsymbol{x}}}_{\mathit{\boldsymbol{i}}}}^2)$

(2)

FM的目标函数如下：

$\mathop {{\mathop{\rm argmin}\nolimits} }\limits_{\omega ,V} {\mathop \sum \limits_{i = 1}^n} \ell ({\hat y_i},{y_i}) + {\lambda _1}||{\mathit{\boldsymbol{\omega }}}|{|_2}^2 + {\lambda _2}||{\mathit{\boldsymbol{V}}}|{|_F}^2$

(3)

式中： $\ell ({\hat y_i},{y_i})$ 表示第i个样本的损失， ${\hat y_i}$ 是预测的标号值，y_i是样本的真实标记， ${\lambda _1}$ 和 ${\lambda _2}$ 均为控制模型复杂度的超参数。FM用于回归问题时通常采用最小平方损失函数，因此有

$\ell ({\hat y_i},{y_i}) = {({\hat y_i} - {y_i})^2}$

(4)

1.2 优化方法

目前已经有多种基于迭代的优化算法被提出用于优化FM，如MCMC, ALS^[12]等。其中最常用的是随机梯度下降法（SGD），即每次随机选取一个样本计算损失函数关于变量的梯度，之后用梯度更新待求变量，如此迭代便可优化目标函数。

假设 $\Theta $ 为所有待求参数的集合，而θ表示 $\Theta $ 的分量，θ可以是ω₀、ω_i或者V_ij，则在第t+1时刻的更新公式为

${\theta ^{t + 1}} = {\theta ^t} - \eta (\frac{\partial }{{\partial {\theta ^t}}}\ell (\hat y({\mathit{\boldsymbol{x}}_i}|{\Theta ^t}),{y_i}) + 2\lambda {\theta ^t})$

(5)

式中：η是学习率，表示每次梯度更新的步长。对于最小平方损失函数有:

$\frac{{\partial \ell (\hat y({\mathit{\boldsymbol{x}}_i}|\Theta ),{y_i})}}{{\partial \theta }} = 2(\hat y({\mathit{\boldsymbol{x}}_i}|\Theta ) - {y_i})\frac{{\partial \hat y({\mathit{\boldsymbol{x}}_i}|\Theta )}}{{\partial \theta }}$

(6)

将式(2)对各个参数求导可得^[12]：

$\displaystyle\frac{\rm{\partial} }{{\rm{\partial} \theta }}\hat y(\mathit{\boldsymbol{x}}) = \left\{ \begin{array}{l}1,\quad \theta = {\omega _0}\\{\mathit{\boldsymbol{x}}_i},\quad \theta = {\mathit{\boldsymbol{\omega }}_i}\quad \\{\mathit{\boldsymbol{x}}_i}({\sum _{j = 1}}{\mathit{\boldsymbol{x}}_j}{\mathit{\boldsymbol{v}}_{j,f}} - {\mathit{\boldsymbol{x}}_i}{\mathit{\boldsymbol{v}}_{i,f}}){\rm{, }}\quad \theta = {\mathit{\boldsymbol{v}}_{i,f}}\end{array} \right.$

(7)

基于式(5)~(7), 即可根据给定的样本计算损失函数关于变量的梯度。

2 基于SGL的因子分解机 2.1 目标函数

本文通过对损失函数添加SGL的正则项以期望得到含有结构稀疏性质的解向量, SGL-FM的目标函数如下:

$\mathop {{\mathop{\rm argmin}\nolimits} }\limits_{{\mathit{\boldsymbol{\omega}}}, \, {\mathit{\boldsymbol{V}}}} {\mathop \sum \limits_{i = 1}^n} \ell ({\hat y_i},{y_i}) + {\lambda _1}{\mathop \sum \limits_{i = 1}^p} {\left\| {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{\omega }}_i}}\\{{\mathit{\boldsymbol{v}}_i}}\end{array}} \right\|_2} + {\lambda _2}{\mathop \sum \limits_{i = 1}^p} {\left\| {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{\omega }}_i}}\\{{\mathit{\boldsymbol{v}}_i}}\end{array}} \right\|_1}$

(8)

式中：将ω_i和 ${{\mathit{\boldsymbol{v}}}_i}(1 \leqslant i \leqslant p)$ 分为一组，共分为p组，其中 ${\left\| {{{[{{\mathit{\boldsymbol{\omega }}}_i} \,\,{{\mathit{\boldsymbol{v}}}_i}]}^{\rm{T}}}} \right\|_2}$ 表示同时选择或同时不选ω_i和v_i，实现了组间稀疏。 ${\left\| {{{[{{\mathit{\boldsymbol{\omega }}}_i} \,\,{{\mathit{\boldsymbol{v}}}_i}]}^{\rm{T}}}} \right\|_1}$ 表示对选中的ω_i和v_i进一步进行特征选择，实现了组内稀疏，而组内稀疏也相当于对各个维度自适应选择最优k值。值得注意的是， ${\ell _2}\text{、}{\ell _1}$ 范数均非光滑，且损失函数非凸。因此，目标函数非凸非光滑，而FM的目标函数非凸但光滑，因此，优化式(8)具有更大的挑战, 不能照搬FM的优化方法。在下一节中，我们给出优化该目标函数的有效算法。实验结果也表明，该算法能有效收敛。

式(8)还包括了另外两个稀疏化模型，当 ${\lambda _1} = 0$ 时，目标函数只有 ${\ell _1}$ 项，简记该模型为L1-FM。当 ${\lambda _2} = 0$ 时，目标函数仅有Group Lasso项，简记该模型为GL-FM。

2.2 优化方法

因为L1-FM和GL-FM均为SGL-FM的特例，给出SGL-FM的优化方法后，L1-FM和GL-FM的优化方法可以直接得到，因此本文仅关注SGL-FM的优化。FM可以使用SGD算法优化，但是在SGL-FM中，由于 ${\ell _2}$ 范数和 ${\ell _1}$ 范数在零点不可微，虽然也可利用次梯度的方法迭代。但是，直接利用次梯度迭代很少能使变量达到不可微点^[11]，也即很少会得到含有零元素的解向量，而在很多情况下零点才是目标函数的局部最小点。从另一个角度看，稀疏解能够体现目标变量的结构信息。使用次梯度优化方法得到的结果相悖于我们期望的稀疏结果。所以，本文引入了前向后向切分算法(forward backward splitting, FOBOS)^[11]来优化该问题。

2.2.1 FOBOS算法

FOBOS是一种基于迭代优化的算法框架，主要用来求解含有正则项的目标函数的优化问题，特别是一些不可微的正则项如: ${\ell _1}$ 、 ${\ell _2\text{、}1}$ （Group Lasso）、 ${\ell _\infty }$ 等^[11]，相比于直接用次梯度计算，使用FOBOS算法得到的模型具有更好的预测性能和更符合问题先验的稀疏结构^[11]。

假设待求目标函数由两部分组成： $f(\mathit{\boldsymbol{\omega }}) + r(\mathit{\boldsymbol{\omega }})$ , 其中 $f(\mathit{\boldsymbol{\omega }})$ 一般为损失函数，本文中损失函数为最小平方损失，第2项 $r(\mathit{\boldsymbol{\omega }})$ 是关于目标变量ω的正则项。其每次迭代过程分2步:

${\mathit{\boldsymbol{\omega}}}^{t + \frac{1}{2}} = {\mathit{\boldsymbol{\omega }}}^t - {\eta _t}g_f^t$

(9)

${\mathit{\boldsymbol{\omega }}^t} = {{\mathop{\rm argmin}\nolimits} _\omega }\left\{ {\frac{1}{2}{{\left\| {\mathit{\boldsymbol{\omega }} - {\mathit{\boldsymbol{\omega }}^{t + \frac{1}{2}}}} \right\|}^2} + {\eta _{t + \frac{1}{2}}}r(\mathit{\boldsymbol{\omega }})} \right\}$

(10)

式中：g_f^t为在t时刻损失函数 $f(\mathit{\boldsymbol{\omega }})$ 关于权重的梯度, ${\eta _t}$ 为t时刻的学习率， ${\eta _{t + \frac{1}{2}}}$ 是在式(10)迭代中正则项前的系数，在具体算法实现中，通常设置 ${\eta _{t + \frac{1}{2}}} = {\eta _t}$ 。步骤1）等价于标准的无正则项梯度下降过程，式(10)中结果是在第一步结果 ${\mathit{\boldsymbol{\omega }}^{t + \frac{1}{2}}}$ 基础上进行了微调，一方面希望新的结果尽可能靠近第一步的结果，另一方面还需要尽可能最小化 $r(\mathit{\boldsymbol{\omega }})$ 。

2.2.2 利用FOBOS算法求解SGL-FM

根据FOBOS算法，首先将SGL-FM的目标函数分为两部分:

$f({\omega _0},{\mathit{\boldsymbol{\omega }}},{\mathit{\boldsymbol{V}}}) + r({\mathit{\boldsymbol{\omega }}} + {\mathit{\boldsymbol{V}}})$

(11)

式中： $\displaystyle f({\omega _0},{\mathit{\boldsymbol{\omega }}},{\mathit{\boldsymbol{V}}}) = {\mathop \sum \limits_{i = 1}^n} \ell ({\hat y_i},{y_i})$ 且 $\displaystyle r({\mathit{\boldsymbol{\omega }}} + {\mathit{\boldsymbol{V}}}) = {\lambda _1}{\mathop \sum \limits_{i = 1}^p} {\left\| {\begin{array}{*{20}{c}}\! {{{\mathit{\boldsymbol{\omega }}}_i}} \! \\\! {{{\mathit{\boldsymbol{v}}}_i}} \!\end{array}} \right\|_2} + $ ${\lambda _2}{\mathop \sum \limits_{i = 1}^p} {\left\| {\begin{array}{*{20}{c}}{{{\mathit{\boldsymbol{\omega }}}_i}}\\{{{\mathit{\boldsymbol{v}}_i}}}\end{array}} \right\|_1}$ 。假设输入一个新的样本 $(x,y)$ ，根据式(5)~(7)、式(9)可知FOBOS算法的第1步更新公式为

$ \left\{\begin{array}{l}\!\!\!\! \omega _0^{t + \frac{1}{2}} = \omega _0^t - {\eta _t} \cdot 2(\hat y(\mathit{\boldsymbol{x}}|\Theta ) - y)\\[5pt]\!\!\!\! {\mathit{\boldsymbol{\omega }}_i}^{t + \frac{1}{2}} = {\mathit{\boldsymbol{\omega }}_i}^t - {\eta _t} \cdot 2(\hat y(\mathit{\boldsymbol{x}}|\Theta ) - y) \cdot {\mathit{\boldsymbol{x}}_i}\\[5pt]\!\!\!\! \mathit{\boldsymbol{v}}_{i,f}^{t + \frac{1}{2}} = \mathit{\boldsymbol{v}}_{i,j}^t - {\eta _t} \cdot 2(\hat y(\mathit{\boldsymbol{x}}|\Theta ) - y) \cdot {\mathit{\boldsymbol{x}}_i}({\sum _{j = 1}}{\mathit{\boldsymbol{x}}_j}{\mathit{\boldsymbol{v}}_{j,f}} - {\mathit{\boldsymbol{x}}_i}{\mathit{\boldsymbol{v}}_{i,f}})\end{array}\right.$

(12)

式中 $\, 1 \leqslant i \leqslant p$ 且 $1 \leqslant f \leqslant k$ 。

设 ${\lambda _1}^\prime = {\eta _t}{\lambda _1}$ , ${\lambda _2}^\prime = {\eta _t}{\lambda _2}$ , ${\mathit{\boldsymbol{\theta }}}_{\,i}^t = {[{\mathit{\boldsymbol{\omega }}}_i^t \,\,{\mathit{\boldsymbol{v}}}_i^t]^{\rm{T}}} \in {R^{k + 1}}$ , 则FOBOS算法的第2步等价于优化以下问题：

$\mathit{\boldsymbol{\theta }}_{\, i}^t = \arg {\min _{{\theta _i}}}\{ \frac{1}{2}{\left\| {{\mathit{\boldsymbol{\theta }}_i} - \mathit{\boldsymbol{\theta }}_i^{t + \frac{1}{2}}} \right\|^2} + {\lambda '_1}{\left\| {{\mathit{\boldsymbol{\theta }}_i}} \right\|_2} + {\lambda _2}^\prime {\left\| {{\mathit{\boldsymbol{\theta }}_i}} \right\|_1}\} $

(13)

式中： $1 \leqslant i \leqslant p$ 。文献[11]中给出了当正则项分别为 ${\ell _{1}}$ 、 ${\ell _{2,1}}$ 、 ${\ell _\infty }$ 时相应的求解算法，但是当正则项为SGL时，文献[11]并没有给出其求解算法，而且直接将 ${\ell _{1}}$ , ${\ell _{2,1}}$ 的解法推广到SGL是非平凡的。

Liu等在文献[13]中提出了一种有效算法用于求解含有树结构信息的正则化问题。本文中的SGL是其中一种特例。如图1所示，SGL的结构可以表示成p棵树，每棵树的根节点包含了第i维特征的一阶系数ω_i和其在隐空间的特征表示向量v_i，子节点分别是其各个分量，SGL相当于对树的每个节点都添加了 ${\ell _2}$ 范数的约束。

由文献[13]，我们在算法1中直接给出了优化式(13)的具体流程。并在算法2中给出了利用FOBOS算法优化SGL-FM的完整流程。

算法1　树结构正则项的优化算法

输入　Step 1的输出 $\mathit{\boldsymbol{\theta }}_i^{t + \frac{1}{2}},(1 \leqslant i \leqslant p)$ ， ${\lambda _1}^\prime ,{\lambda _2}^\prime $ ；

输出　更新后的参数 $\mathit{\boldsymbol{\theta }}_i^t = {[\mathit{\boldsymbol{\omega }}_i^t,\mathit{\boldsymbol{v}}_i^t]^{\rm{T}}}(1 \leqslant i \leqslant p)$ 。

1) for i = 1: p do

2) ${\mathit{\boldsymbol{\theta }}_i} = \mathit{\boldsymbol{\theta }}_i^{t + \frac{1}{2}}$

3) for j = 1: k+1

4) if ( $\left| {{\mathit{\boldsymbol{\theta }}_i}[j]} \right| \leqslant {\lambda _2}^\prime $ ) then ${\mathit{\boldsymbol{\theta }}_i}[j] = 0$

5) else $\displaystyle{\mathit{\boldsymbol{\theta }}_i}[j] = \left( {\left. {\frac{{|{\mathit{\boldsymbol{\theta }}_i}[j]| - {\lambda _2}^\prime }}{{|{\mathit{\boldsymbol{\theta }}_i}[j]|}}} \right)} \right. \cdot {\mathit{\boldsymbol{\theta }}_i}[j]$

6) end if

7) end for

8) if ${\left\| {{\mathit{\boldsymbol{\theta }}_i}} \right\|_2} \leqslant {\lambda _1}^\prime $ then ${\mathit{\boldsymbol{\theta }}_i} = 0$

9) else $\displaystyle{\mathit{\boldsymbol{\theta }}_i} = \left( {\frac{{||{\mathit{\boldsymbol{\theta }}_i}|{|_2} - {\lambda _1}^\prime }}{{||{\mathit{\boldsymbol{\theta }}_i}|{|_2}}}} \right) \cdot {\mathit{\boldsymbol{\theta }}_i}$

10) end if

11) end for

算法2　用于求解SGL-FM的FOBOS算法

输入　训练数据，正则项参数 ${\lambda _1},{\lambda _2}$ ；

输出　 ω₀, $\mathit{\boldsymbol{\omega }} \in {R^p}$ 及 $\mathit{\boldsymbol{V}} \in {R^{p \times k}}$ 。

1) for k=1:num_epoch %迭代次数

2) 随机排列所有训练样本

3) for i = 1:num_samples %遍历所有样本

4) 取出样本x_i

5) 根据式(12)执行随机梯度下降

6) 根据算法1优化式(13)

7) end for

8) end for

3 实验与分析 3.1 实验设置与实验数据

为了验证算法的性能，在3个推荐系统数据集上进行了实验，数据的基本信息如表1所示，其中Movielens的两个数据均为电影评分数据, Last.fm为音乐推荐数据，所有数据均采用One-Hot-Encoding编码方式。本文将所有数据均划分70%作为训练集，30%作为测试集。

实验不仅对比了SGL-FM、FM、L1-FM和GL-FM等方法。还加入了线性模型Lasso和一般的二阶回归模型（SEC-REG）作为基准对比方法。

所有方法的超参数均采用3折交叉验证选取。FM、Lasso以及SEC-REG的所有正则化参数均从{0.000 01, 0.000 1, 0.001, 0.01, 0.1, 1}中选取，而SGL-FM、L1-FM和GL-FM的超参数均从{10^-6, 10^-5, 10^-4, 10^-3}中选取。

实验以均方根误差（RMSE）作为评价准则，其计算公式为

$\normalsize{\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} } $

式中：n为测试样本数， \normalsize${\hat y_i},{y_i}$ 分别为第i个样本的预测标号和真实标号。实验也比较了各个模型所得系数的稀疏度，稀疏度的计算方式为

${\rm{sparsity}} = \frac{{{n_z}}}{{{n_a}}}$

式中：n_a表示线性项系数 ${\mathit{\boldsymbol{\omega }}} \in {R^p}$ 和二阶项系数矩阵 ${\mathit{\boldsymbol{V}}} \in {R^{p \times k}}$ 中所有分量的个数，即 ${n_a} = p(k + 1)$ ；n_z表示这些分量中零元素个数。

3.2 性能与稀疏度分析

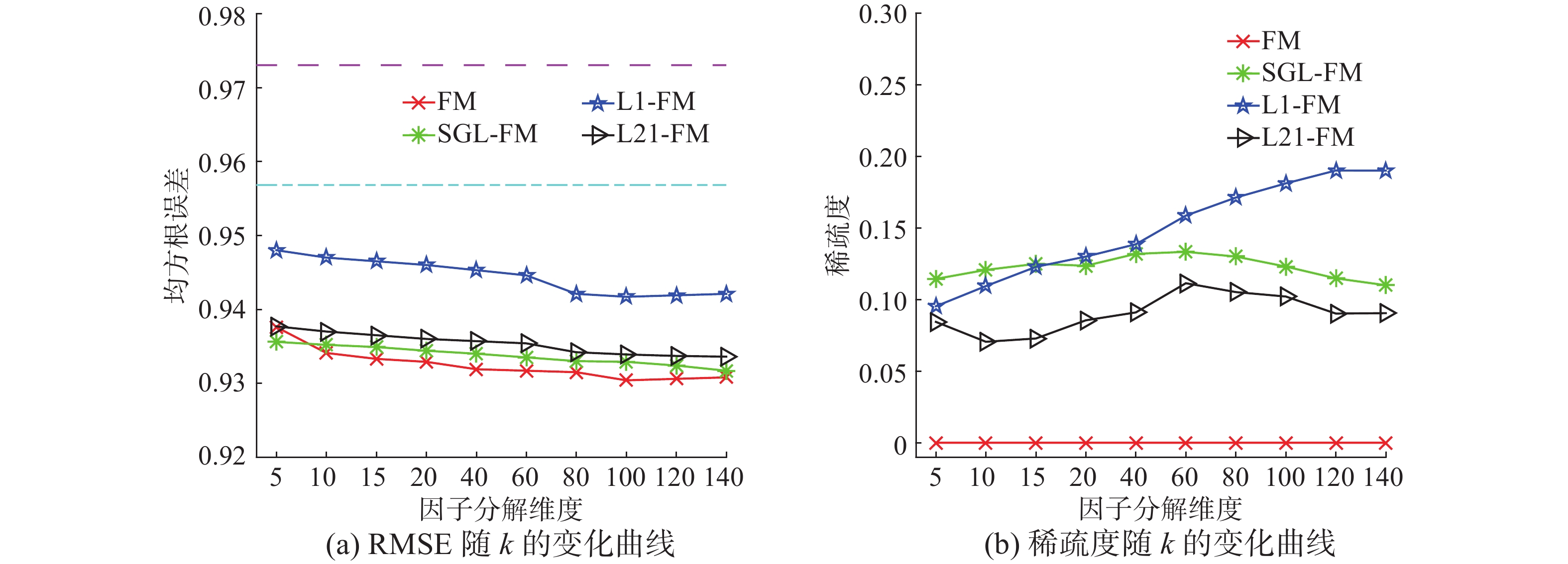
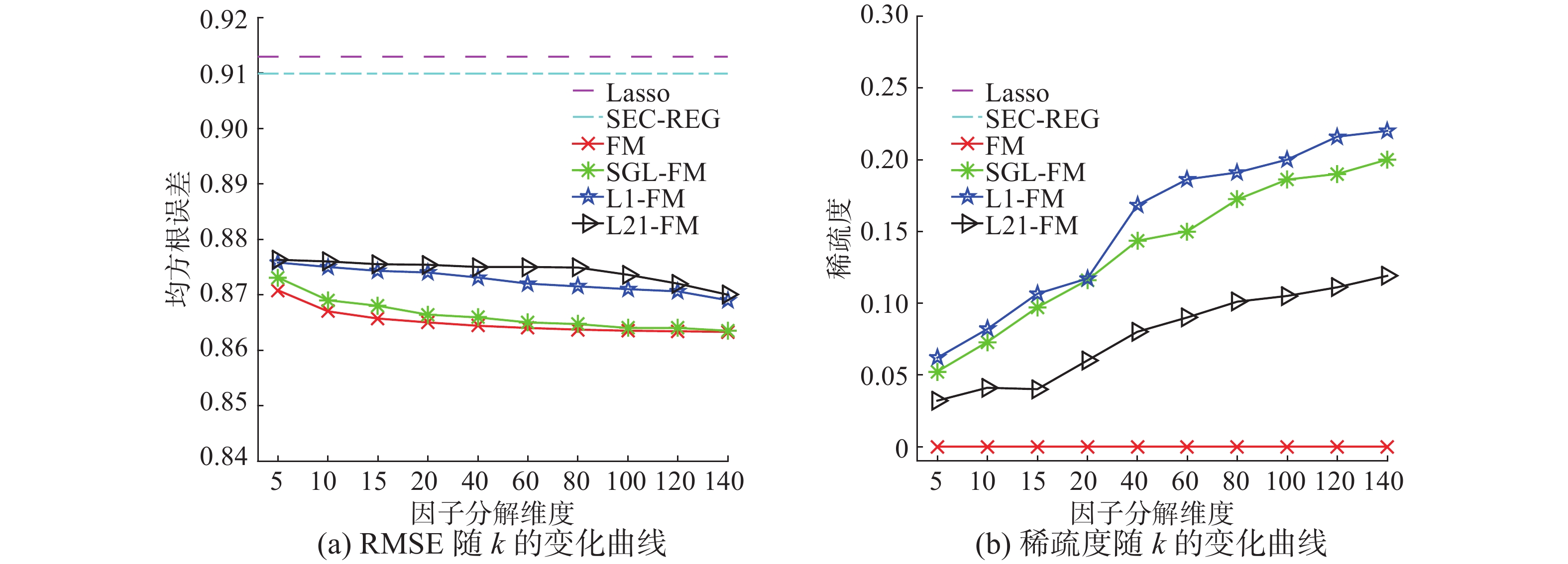
图2~4 分别比较了各个算法在3个数据集上的RMSE和稀疏度随着k的变化趋势，可以看出，线性模型Lasso由于未探索变量间的关系，因此效果较差。而由于数据过于稀疏，二阶模型SEC-REG的精度也差于因子分解机类算法。

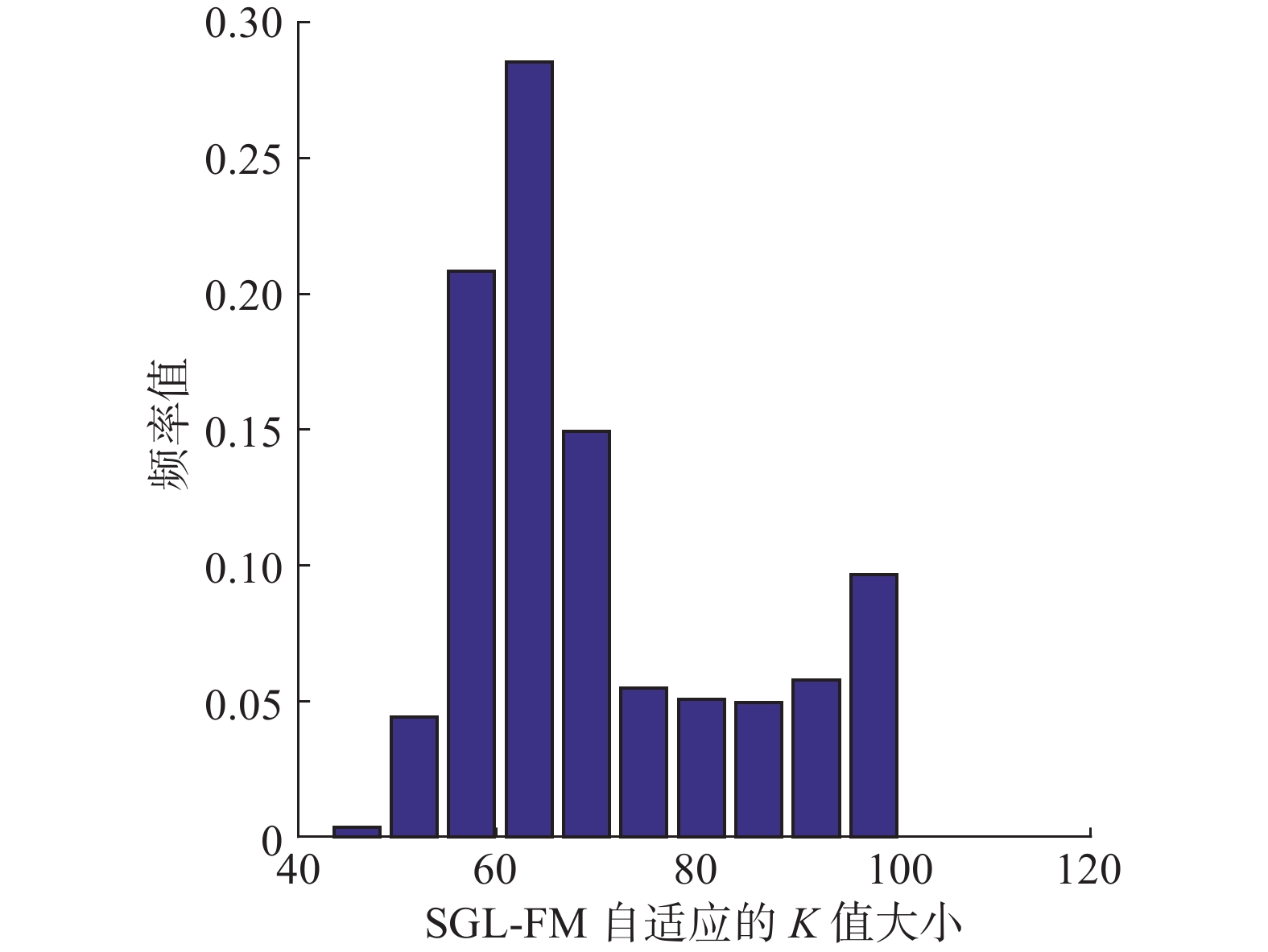
比较SGL-FM与FM，可以看出在Movie-lens数据集上SGL-FM的稀疏度最高达到了20%，虽然FM有更多的参数，但是SGL-FM的性能与FM的性能非常接近，说明SGL-FM能进行有效的特征选择。在Last.fm数据上，当k>100时, SGL-FM的稀疏度达到了25%~30%, 虽然SGL-FM的参数更少，但是其性能要优于稀疏度等于0的FM，说明由于数据各个特征的分布不同，不同特征有各自最优的k值，SGL-FM通过特征选择为各个维度自适应了最佳的k值，去除了冗余的组内特征。图5 给出了在Last.fm数据集上，当k=100时，SGL-FM求出的特征表示向量 ${{\mathit{\boldsymbol{v}}}_i}(1 \leqslant i \leqslant p)$ 所自适应的k值分布，从图中可以看出，对于Last.fm数据，大部分特征的k值分布在50~70之间，从图5中也可以看出，当k=60时，FM的效果最好，大于60时，FM的效果开始变差，这是因为参数过多，FM发生了过拟合。比较SGL-FM与GL-FM，SGL-FM由于既实现了组内稀疏又实现了组间稀疏，因此其性能优于只实现了组间稀疏的GL-FM。从稀疏度变化中也可以看出，相比于GL包含了太多的冗余组内特征，SGL能进一步地对组内特征做特征选择，从而不仅提高稀疏度，更能提高模型的性能。比较SGL-FM与L1-FM，由于L1-FM不包含结构信息且对所有特征无差别选择，因此，虽然L1-FM有更高的稀疏度，但是其性能比SGL-FM差。

3.3 收敛性分析

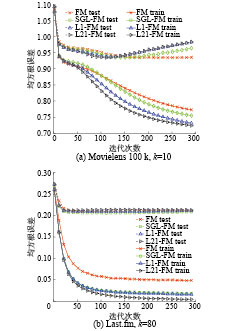
当采用随机梯度优化这种算法时，算法的收敛性是常常需要考虑的问题，由于FM的特殊性，其目标函数关于待求参数非凸^[3]，原始文献[3]中并没有给出收敛性证明，但是实验结果表明，FM是收敛的，图6给出了本文提出的算法和FM在两个数据集上的迭代过程，可以看出，所有算法均稳定收敛。而且本文提出的SGL-FM，L1-FM以及GL-FM具有更快的收敛速率，这是由于SGL-FM等去除了噪音的干扰，因而收敛更快。

4 结束语

考虑到因子分解机特殊的二阶特征结构，本文结合了GL和Lasso的优点，提出了基于Sparse Group Lasso的因子分解机。同时，作为SGL-FM的特例，我们还导出了L1-FM和GL-FM。不同于一般的二阶模型和一般的FM，SGL-FM的目标函数非凸且非光滑，本文引入了FOBOS算法来优化该问题。SGL-FM不仅获得了比FM更稀疏的解，节省了内存空间，更能通过去除噪音特征，从而提升性能，实验结果也证明了这一点。