根据世界卫生组织2016年公布的数据,肺癌在全球的发病率和死亡率均为最高[1]。肺癌的早期发现及治疗对于挽救患者的生命具有重要意义[2]。肺癌早期通常表现为肺结节[3-4]。在临床上,医生通常结合肺部医学影像来对肺部结节进行分析与诊断。CT是一种常用的辅助检查肺结节医学成像模态的手段。然而,由于医生个人经验等主观因素的影响,不同的医生可能对于同一个患者的CT图像产生不同的诊断结果。因此,使用计算机辅助诊断系统(computer-aided diagnosis, CAD)[5]对肺部CT图像进行自动分析,提供一个客观的肺结节诊断结果具有重要的意义。
一般情况下,肺部CT图像的数据标注较少,大量的数据是未标记的。受限于临床专业知识,人工对所有的数据进行标注将耗费大量的人力。半监督学习思想是利用少量的标记样本和大量的未标记样本训练分类器,通过未标记数据的信息辅助提升分类器的性能。因此,本文使用半监督学习方法对肺结节进行分类。
半监督聚类是一种常用的半监督学习方法[6],通过利用少量标记样本辅助提高聚类的准确率。半监督FCM算法是半监督聚类算法的经典算法之一。Bensaid等[7]针对传统FCM中簇数的选择以及训练样本数量较少等问题提出了一种部分监督聚类FCM算法;张慧哲等[8]针对传统FCM算法聚类结果受初始聚类中心的影响,提出了一种简洁快速的初始聚类中心选取规则,并根据聚类中心的分离特性改进了目标函数,从而使聚类结果达到最优;李春芳等[9]针对传统的半监督FCM算法的目标函数在α=1, 0时退化为经典的FCM算法,提出了一种基于改进目标函数的半监督模糊聚类算法SS-FCM,提高了聚类的准确性和收敛速度;K.L. Wu[10]针对传统半监督FCM的模糊因子参数m的选择进行了详细的分析,提出在数据集包含噪声和离群值的情况下m=4有更强的健壮性和聚类效果;侯薇等[11]针对计算FCM隶属度导致算法执行率低这一问题, 提出了一种抽样初始化产生较好的初始聚类中心, 对较大隶属度的数据点, 通过k-means操作更新模糊聚类中心, 同时仅更新小隶属度来达到提高FCM算法聚类的效率;李斌等[12]针对传统的核模糊C均值中只考虑类内关系忽略了类间关系,从而使边界对噪声敏感等问题,提出了一种改进核FCM类间极大化聚类算法MKFCM,使边界处样本得到很好的划分。
现有的半监督FCM虽然能够在一定程度上取得了较好的聚类效果, 但标记样本与未标记样本的分布不平衡问题将会影响半监督聚类的性能[13]。传统半监督FCM算法的思想是基于类内加权平方误差最小化准则,聚类中心是通过标记样本的隶属度来控制的[14],样本通常归属于最近的聚类中心所代表的类。当标记样本与未标记样本数量差异较大时,将会弱化标记样本的监督信息在聚类中的作用,导致聚类结果产生错误,进而影响肺结节分类的准确率。本文针对这一问题,提出了一种基于先验分布的半监督FCM算法,通过引入标记样本的先验分布信息,赋予标记样本更大的权重,并将其融入到FCM聚类过程中,使得监督信息在最后聚类中发挥更重要的作用,从而更好地指导聚类。在LIDC数据库进行了实验,实验结果证明了本文提出的算法能够取得更高的分类准确率。
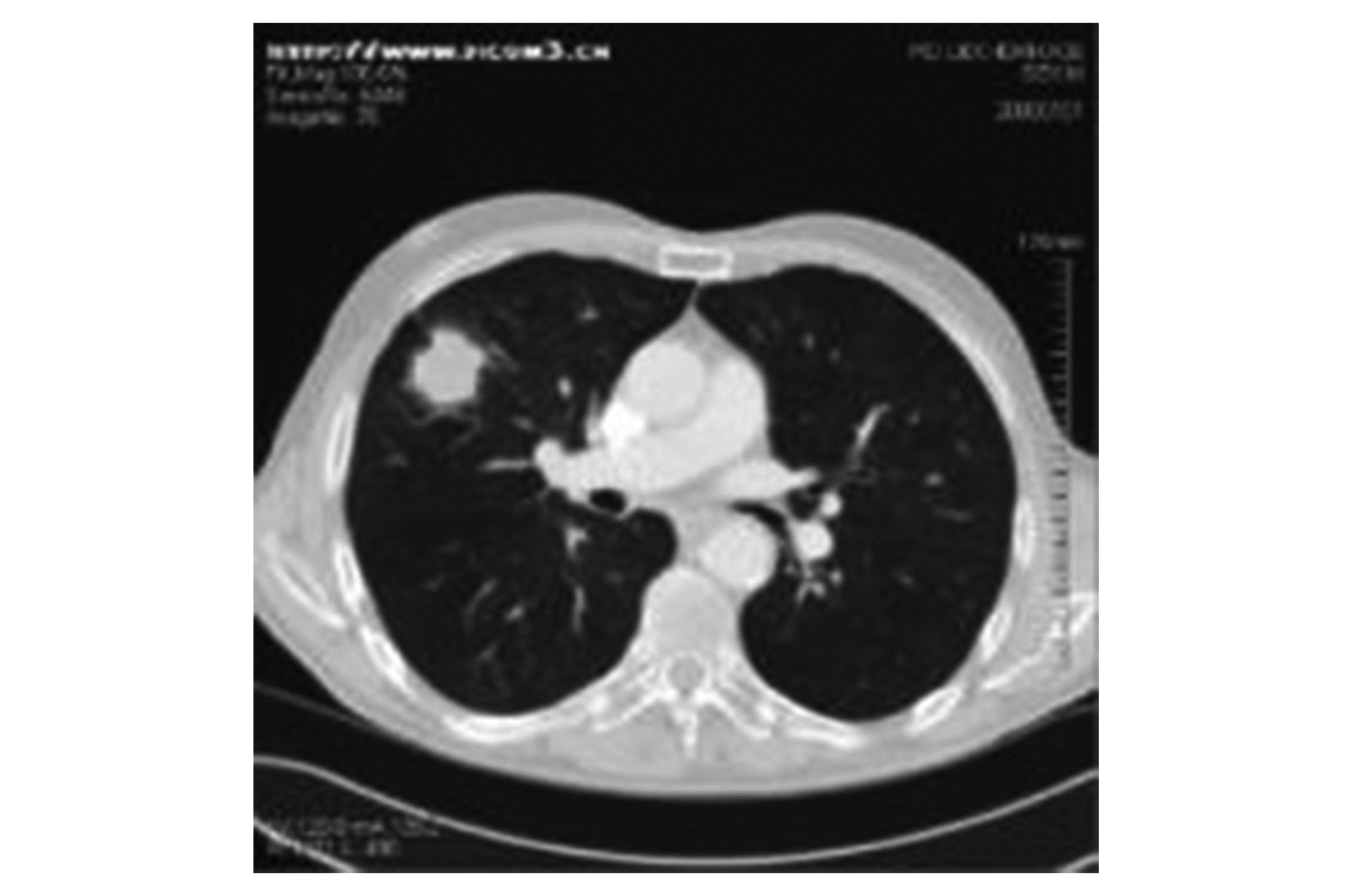
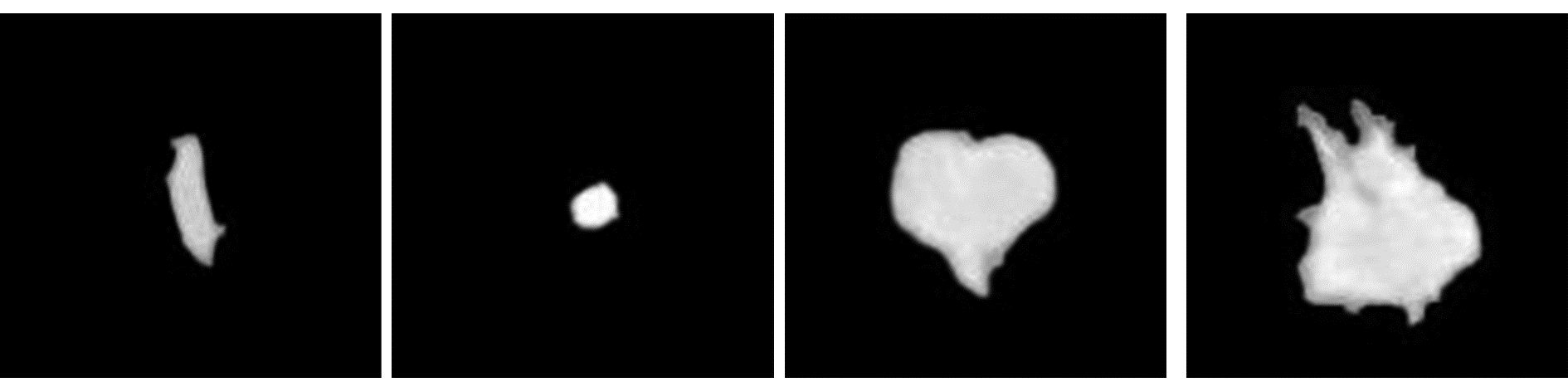
1 特征提取肺结节的诊断过程主要分为肺结节的分割、特征提取、肺结节良恶性分类。图 1为一幅肺部CT图像,图 2为分割出的肺结节。基于分割的肺结节,进行特征提取。在临床上,肺结节的形状及边缘的粗糙程度等信息是判断良恶性的重要依据,为了获取这些重要信息,本文主要提取以下特征[15]:灰度特征[16](灰度方差、灰度直方图熵),形态特征[17](似圆度、紧凑度、径向均值、径向方差,边界粗糙度、形状不变矩H0,H1,H2,H3)等11维特征,并对每一维特征进行归一化。
|
图 1 LIDC中肺部CT图像 Fig.1 Lung CT image in LIDC |
|
图 2 肺结节分割 Fig.2 Segmentation of pulmonary nodules |
FCM算法[18]主要思想是在每个样本进行聚类时,引入一个类簇的隶属度计算样本属于某个类簇的可能性。聚类的过程可形式化为目标函数的优化过程,如式(1)所示。其中k的取值为式(2)所示。FCM算法通过不断迭代求解模糊隶属度函数uk和聚类中心vi,使得目标函数最小化,迭代停止,即完成聚类。
| $ {J_m}\left( {u,v} \right) = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {u_{ik}^p{{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right\|}^2}} } $ | (1) |
| $ k = 1,2, \cdots ,N $ | (2) |
| $ {u_{ik}} = \frac{1}{{\sum\limits_{j = 1}^n {{{\left( {\frac{{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right\|}}{{\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_j}} \right\|}}} \right)}^{\frac{2}{{p - 1}}}}} }} $ | (3) |
| $ {v_i} = \frac{{\sum\limits_{k = 1}^N {u_{ik}^p{\mathit{\boldsymbol{x}}_k}} }}{{\sum\limits_{k = 1}^N {u_{ik}^p} }} $ | (4) |
式中:C为聚类个数;N为样本个数;uik为FCM中的模糊隶属度,表示第k个样本点属于第i个聚类中心的隶属度,其取值范围为[0, 1];vi表示第i类的聚类中心;‖ xk-vi‖2表示第k个样本点相对于第i个聚类中心的欧式距离;P为模糊因子,它决定样本在不同类中的模糊程度。
通过不断地更新迭代公式(3)、(4),直到式(1)中目标函数的值小于特定的值ε时或者相对于上次的目标函数值的改变量小于特定的值时,停止迭代。
2.2 部分监督的FCM算法Bensaid在经典的FCM算法的基础上,提出了一种部分监督聚类算法。他提出的算法加强了标记信息在聚类过程中的指导作用。通过给标记样本赋予较大的权重,使标记样本在聚类中心的形成过程中发挥更重要的作用,提高了聚类的精度。其目标函数为
| $ {J_m}\left( {u,v:x} \right) = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {u_{ik}^p\left\| {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right\|_A^2} } $ | (5) |
其聚类中心为
| $ {v_{i,t}} = \frac{{\left( {\sum\limits_{k = 1}^n {{w_k}{{\left( {u_{ik,t}^d} \right)}^m}x_k^d} + \sum\limits_{k = 1}^n {{{\left( {u_{ik,t}^u} \right)}^m}x_k^u} } \right)}}{{\sum\limits_{k = 1}^n {{w_k}{{\left( {u_{ik,t}^d} \right)}^m}} + \sum\limits_{k = 1}^n {{{\left( {u_{ik,t}^u} \right)}^m}} }} $ | (6) |
模糊隶属度为
| $ u_{ik,t}^d = {f_{ik}} $ | (7) |
| $ u_{ik,t}^u = \frac{1}{{\sum\limits_{j = 1}^n {{{\left( {\frac{{{{\left\| {\mathit{\boldsymbol{x}}_k^u - {\mathit{\boldsymbol{v}}_{i,t - 1}}} \right\|}_\mathit{\boldsymbol{A}}}}}{{{{\left\| {\mathit{\boldsymbol{x}}_k^u - {\mathit{\boldsymbol{v}}_{j,t - 1}}} \right\|}_\mathit{\boldsymbol{A}}}}}} \right)}^{\frac{2}{{m - 1}}}}} }} $ | (8) |
式中:聚类中心中的wk为权重因子,w=[w1 w2 … wnd]T, 文中使wk=w,其中w为具体的数值,表示标记样本的数量,通过对少量的标记样本进行增加权重,可以更好地加强标记样本的作用;模糊隶属度为uik,表示第k个样本点相对于第i个聚类中心的模糊隶属度,其取值范围为[0, 1];uik, td=fik表示部分监督样本的模糊隶属度;uik, tu表示无监督样本的模糊隶属度;其中
| $ \left\| {{\mathit{\boldsymbol{x}}_K} - {\mathit{\boldsymbol{v}}_i}} \right\|_\mathit{\boldsymbol{A}}^2 = {\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right)^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{v}}_i}} \right) $ | (9) |
A是任何的正定矩阵。
2.3 基于样本分布先验的半监督FCM算法基于样本分布先验的半监督FCM的目标函数[19]如下:
| $ J = \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^N {u_{ik}^pd_{ik}^2} } + \alpha \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^N {\left( {{u_{ik}} - {f_{ik}}{b_k}} \right)d_{ik}^2} } $ | (10) |
式中:标记样本的隶属度F=[fik],i=1, 2,…,C;N=1, 2,…,n;dik表示第k个样本点相对于第i个聚类中心间的欧式距离;通常情况下模糊因子取经验值p=2;α是使监督和无监督样本之间保持相对平衡的因子,其中α本文选取的是传统的半监督FCM算法中α的取值,即总样本和标记样本数量之比。为区分标记样本和未标记样本,引入了二值向量b=bk, 其中k=1, 2,…,n,标记样本时bk=1,相反未标记样本时bk=0。
为了增强标记样本的监督作用,在计算模糊隶属度和聚类中心时分别引入了样本的分布信息。本文通过在式(15)、(16)、(17)中引入两个权重θ和β,其中θ表示标记样本的权重,β表示未标记样本的权重。通过θ和β来指导实现聚类的过程。
| $ q = M/N $ | (11) |
| $ r = \left( {N - M} \right)/N $ | (12) |
| $ \theta = 1 - q $ | (13) |
| $ \beta = 1 - r $ | (14) |
式中:q表示标记样本的先验概率;M表示标记样本的数量;N表示总样本的数量;r表示未标记样本的先验概率;(N-M)表示未标记样本的数量。通过优化目标函数,标记样本的模糊隶属度为
| $ u_{ik}^L = \theta \times \left( {\frac{1}{{1 + \alpha }}\left( {\frac{1}{{\sum\limits_{j = 1}^c {\frac{{d_{ik}^2}}{{d_{jk}^2}}} }} + \alpha {f_{ik}}} \right)} \right) $ | (15) |
未标记样本的模糊隶属度为
| $ u_{ik}^u = \beta \times \left( {\frac{1}{{\sum\limits_{j = 1}^c {\frac{{d_{ik}^2}}{{d_{jk}^2}}} }}} \right) $ | (16) |
聚类中心为
| $ {v_{ik}} = \frac{{\sum\limits_{{x_k} \in {x^d}} {{{\left( {\theta u_{ik}^L} \right)}^2}{x_k}} + \sum\limits_{{x_k} \in {x^u}} {{{\left( {\beta u_{ik}^u} \right)}^2}{x_k}} }}{{\sum\limits_{{x_k} \in {x^d}} {{{\left( {\theta u_{ik}^L} \right)}^2}} + \sum\limits_{{x_k} \in {x^u}} {{{\left( {\beta u_{ik}^u} \right)}^2}} }} $ | (17) |
由于未标记样本数量会远远大于标记样本的数量,基于上述公式,权重θ的值一般要大于β。通过在聚类中心中引入权重θ和β,聚类中心以及样本的聚类结果可以根据样本的先验分布进行自动的调整,θ可以强化标记信息对聚类的指导。
综上所述,基于先验分布的半监督FCM算法的流程大致如下所示。
输入 肺结节图像。
输出 肺结节的分类结果和肺结节分类准确率。
算法流程:
1) 计算输入图像中肺结节的特征,并组成一个矩阵;
2) 确定样本个数C,平衡因子α,阈值ε,标记样本的先验概率q,未标记样本的先验概率r,以及标记样本的个数M;
3) 初始化聚类中心vik以及模糊隶属度uik(包括标记样本的隶属度uikd以及未标记样本隶属度uiku);
4) 按照式(15)、(16)更新模糊隶属度uik;
5) 按照式(17)更新聚类中心;
6) 重复循环步骤3),当两次迭代矩阵模糊隶属度的差小于ε阈值时停止迭代;
7) 根据计算得到的模糊隶属度uik结果进行分类。
3 实验结果及分析本文的实验图像来自美国的LIDC[20](美国癌症研究),本文选择了188个病例,一共451个结节,其中包括了147个恶性结点,155个假阳性结点,149个良性结点。同时,本文实验中选取144例监督样本,即47个恶性、42个良性及55个假阳性结点,剩余的样本作为测试样本。实验中,采用肺结节分类识别准确率作为评估算法性能准则。图 3为部分分类后的结节,大部分样本都能分类正确,只有少量样本存在分类错误,这是因为在特征提取方面这些肺结节的灰度特征不够明显,导致分类错误。本实验为了证明提出算法的有效性,在不同未标记样本和标记样本之间的比例下(分别为7倍、6倍、5倍、4倍、3倍、2倍),对比提出的算法与其他算法的分类正确率。未标记样本和标记样本比例为7倍、6倍、5倍时分类结果准确率变化不是十分明显,所以本文只给出了比例为7倍的分类准确率。表 1给出了传统FCM部分监督FCM算法、SS-FCM、改进的半监督FCM算法[21]以及本文提出的基于样本先验概率的半监督聚类算法准确率的比较结果。

|
图 3 部分结节分类后的结果 Fig.3 Nodules classification results |
| 表 1 不同方法的准确率对比 Tab.1 Comparison of the accuracy of different methods |
由表 1可知,随着标记样本数量的增加,半监督FCM框架下的肺结节分类的准确率大致是逐渐提高的。与其他的半监督FCM方法相比较,本文提出的算法效果更好。因为本文引入了样本的先验分布信息,能够强化标记信息对聚类的指导作用,从而能够提高分类效果。但是根据表 1中数据我们可以看出,标记样本为90时的分类准确率要比标记样本为144时的分类准确率高,这是因为随着标记样本的增加,当标记样本和未标记样本的数量越来越接近时,公式中引入的标记样本和未标记样本的权重也就越来越相近,那么式(17)中的系数就可以约掉,本文的算法退化为传统的半监督模糊C均值算法,从而使得准确率降低。这也是下一步工作的重点。
4 结束语为了解决半监督聚类算法中标记样本数量少导致标记信息在聚类过程中作用弱化的问题,本文提出了一种基于先验分布的半监督FCM算法。引入样本的分布先验信息,自适应调节样本的权重,强化标记样本在聚类过程中的指导作用,提高半监督FCM算法在少量标记样本情况下的性能。在本文的实验中,通过与传统的半监督聚类算法对比,证明提出的方法能够取得更高的聚类正确率。
但是当标记样本数量非常小的时候,给其赋以过大的权重会出现分类结果偏离实际的情况。这也是在未来的工作中进一步研究的问题。
| [1] |
MCGUIRE S. World Cancer Report 2014. Geneva, Switzerland:World Health Organization, International Agency for Research on Cancer, WHO Press, 2015[R]. Advances in nutrition, 2016, 7(2):418-419.
( 0) 0)
|
| [2] |
伍长荣, 接标, 叶明全. CT图像肺结节计算机辅助检测与诊断技术研究综述[J]. 数据采集与处理, 2016, 31(5): 868-881. WU Changrong, JIE Biao, YE Mingquan. Reviews on computer-aided detection and diagnosis of pulmonary nodules in CT images[J]. Journal of data acquisition and processing, 2016, 31(5): 868-881. (  0) 0)
|
| [3] |
LEE S L A, KOUZANI A Z, HU E J. Automated detection of lung nodules in computed tomography images:a review[J]. Machine vision and applications, 2012, 23(1): 151-163. DOI:10.1007/s00138-010-0271-2 ( 0) 0)
|
| [4] |
VALENTE I R S, CORTEZ P C, NETO E C, et al. Automatic 3D pulmonary nodule detection in CT images:A survey[J]. Computer methods and programs in biomedicine, 2016, 124(C): 91-107. ( 0) 0)
|
| [5] |
HAN F, WANG H, ZHANG G, et al. Texture feature analysis for computer-aided diagnosis on pulmonary nodules[J]. Journal of digital imaging, 2015, 28(1): 99. DOI:10.1007/s10278-014-9718-8 ( 0) 0)
|
| [6] |
HADY M F A, SCHWENKER F. Semi-supervised learning[J]. Intelligent systems reference library, 2010, 49(2): 215-239. ( 0) 0)
|
| [7] |
BENSAID A M, HALL L O, BEZDEK J C, et al. Partially supervised clustering for image segmentation[J]. Pattern recognition, 1996, 29(5): 859-871. DOI:10.1016/0031-3203(95)00120-4 ( 0) 0)
|
| [8] |
张慧哲, 王坚. 基于初始聚类中心选取的改进FCM聚类算法[J]. 计算机科学, 2009, 36(6): 206-209. ZHANG Huizhe, WANG Jian. Improved fuzzy C means clustering algorithm based on selecting initial clustering centers[J]. Computer science, 2009, 36(6): 206-209. (  0) 0)
|
| [9] |
李春芳, 庞雅静, 钱丽璞, 等. 半监督FCM聚类算法目标函数研究[J]. 计算机工程与应用, 2009, 45(14): 128-132. LI Chunfang, PANG Yajing, QIAN Lipu, et al. Objective function of semi-supervised FCM clustering algorithm[J]. Computer engineering and application, 2009, 45(14): 128-132. DOI:10.3778/j.issn.1002-8331.2009.14.039 (  0) 0)
|
| [10] |
WU K L. Analysis of parameter selections for fuzzy C-means[J]. Pattern recognition, 2012, 45(1): 407-415. DOI:10.1016/j.patcog.2011.07.012 ( 0) 0)
|
| [11] |
侯薇, 董红斌, 印桂生. 一种基于隶属度优化的演化聚类算法[J]. 计算机研究与发展, 2013, 50(3): 548-558. HOU Wei, DONG Hongbin, YIN Guisheng. A membership degree refinement-based evolutionary clustering algorithm[J]. Journal of computer research and development, 2013, 50(3): 548-558. DOI:10.7544/issn1000-1239.2013.20111346 (  0) 0)
|
| [12] |
李斌, 狄岚, 王少华, 等. 基于改进核模糊C均值类间极大化聚类算法[J]. 计算机应用, 2016, 36(7): 1981-1987. LI Bin, DI Lan, WANG Shaohua, et al. Clustering algorithm with maximum distance between clusters based on improved kernel fuzzy C-means[J]. Journal of computer applications, 2016, 36(7): 1981-1987. DOI:10.11772/j.issn.1001-9081.2016.07.1981 (  0) 0)
|
| [13] |
文传军, 汪庆淼, 詹永照. 均衡模糊C均值聚类算法[J]. 计算机科学, 2014, 41(8): 250-253. WEN Chuanjun, WANG Qingmiao, ZHAN Yongzhao, et al. Equalization fuzzy C-means clustering algorithm[J]. Computer science, 2014, 41(8): 250-253. DOI:10.11896/j.issn.1002-137X.2014.08.053 (  0) 0)
|
| [14] |
蔡加欣, 杨丰, 冯国灿. 改进退化的半监督模糊聚类应用于MR图像分割[J]. 中国图象图形学报, 2011, 16(5): 784-791. CAI Jiaxin, YANG Feng, FENG Guocan, et al. Degeneracy-improved semi-supervised fuzzy clustering with application in MR image segmentation[J]. Journal of image and graphics, 2011, 16(5): 784-791. DOI:10.11834/jig.20110521 (  0) 0)
|
| [15] |
苏志远, 刘慧, 尹义龙. 基于弱监督ECOC算法的肺结节辅助检测[J]. 数据采集与处理, 2015, 30(5): 1003-1010. SU Zhiyuan, LIU Hui, YIN Yilong, et al. Pulmonary nodule aided detection based on weakly-supervised ECOC algorithm[J]. Jornal of data acqusition and processing, 2015, 30(5): 1003-1010. (  0) 0)
|
| [16] |
MURRAY P, MARSHALL S. A new design tool for feature extraction in noisy images based on grayscale hit-or-miss transforms[J]. IEEE transactions on image processing a publication of the ieee signal processing society, 2011, 20(7): 1938-48. DOI:10.1109/TIP.2010.2103952 ( 0) 0)
|
| [17] |
BAE H J, KANG E Y, YONG H S, et al. Paratracheal air cysts on thoracic multidetector CT:incidence, morphological characteristics and relevance to pulmonary emphysema[J]. British journal of radiology, 2013, 86(1021): 20120218. DOI:10.1259/bjr.20120218 ( 0) 0)
|
| [18] |
BEZDEK J C, EHRLICH R, FULL W. FCM:the fuzzy C-means clustering algorithm[J]. Computers and geosciences, 1984, 10(2/3): 191-203. ( 0) 0)
|
| [19] |
PEDRYCZ W, WEMBER J, WALETZKY J. Fuzzy clusteringwith partial supervision[J]. IEEE transaction on system, man, and cybernetics, part B:cybernetics, 1997, 27(5): 787-795. DOI:10.1109/3477.623232 ( 0) 0)
|
| [20] |
MCNITT-GRAY M F, MEYER C R, REEVES A P, et al. The lung image database consortium (LIDC) data collection process for nodule detection and annotation[J]. Academic radiology, 2008, 14(12): 1464-1474. ( 0) 0)
|
| [21] |
李秋萍, 刘慧, 苏志远. 基于改进的半监督FCM聚类算法的肺结节分类与识别[J]. 图学学报, 2015, 36(2): 244-250. LI Qiuping, LIU Hui, SU Zhiyuan. Modified fuzzy clustering with partial supervision algorithm in classification and recognition of pulmonary nodules[J]. Journal of graphics, 2015, 36(2): 244-250. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


