对地观测卫星(earth observing satellite, EOS)利用卫星遥感器对地球表面进行探测,以获取有关信息,具有覆盖区域广、不受空域国界限制、不涉及人员安全等特点,在大地测绘、自然灾害检测、海洋搜救、军事应用等领域产生了巨大效益[1]。
为了更好地利用宝贵的卫星资源,最大化地满足用户需求,卫星任务规划得到了全世界学者的广泛关注。当前,卫星任务规划的对象是整个卫星集合,规划的目的是安排整个卫星集合的动作,使得在满足卫星所有约束的前提下,能够最大化满足用户需求。主要的研究工作可以分为集中式规划和分布式规划两个类别。
集中式的任务规划方法[2]通常采用约束满足问题模型[3]、图模型[4]等对多星任务调度问题进行统一建模,然后采用贪婪算法、启发式算法[5]以及各种智能优化算法[6-7]进行求解,处理的卫星均为同种类型。
而分布式任务规划研究则主要是将卫星建模为具有自主性、协同性、社会性的Agent,多颗卫星通过自主协商完成任务优化分配,目前多采用基于拍卖的协商协议[8]。例如,采用基于方案融合的合同网方法[9],采用聚类降载与演化计算相结合的协同方法[10],基于协同进化与迁移学习的协同方法[11]等。分布式卫星任务规划较集中式卫星任务规划而言,有更大的灵活性,可以将不同类型的卫星建模为异构的卫星规划Agent,从而能处理不同种类卫星的任务规划问题,且可采用Agent并行协同方式提升规划效率。但随着卫星规模的增加,任务协同计算代价增长明显。
传统卫星任务规划问题中,卫星数量通常在几颗到十几颗左右,当问题规模上升为数十颗乃至上百颗卫星时,集中式规划方法会因为问题规模巨大很难给出用户满意解,分布式规划方法也会因为协同耗时太长很难在有效时间内给出问题可行解。
随着航天科技的飞速发展,逐渐出现了由多种异构卫星组成的卫星集群[12],如用于木星大气层探测的SMARA微型卫星群[13]、用于小行星探测的ANTS群卫星系统[14]、用于天文观测的OLFAR卫星集群[15]等,这些卫星集群的规模都在几十颗到上百颗之间。与传统的卫星系统相比,卫星集群的规模更大,能力更多,通常只需从集群中挑选一个子集(称为面向任务的卫星团队,简称卫星团队),即可完成一组对地观测任务。
可见,卫星群任务规划在规划场景、规划目的、问题规模上均与传统的卫星任务规划方法存在较大差别,传统的任务规划方法难以直接应用。
基于上述分析,对卫星集群的任务规划可分解为两个子问题:子问题1,根据任务集特点从整个卫星集群中筛选出一个能够胜任该任务集的卫星团队;子问题2,针对筛选出的卫星团队采用传统任务规划方法优化安排每一颗卫星的观测动作,从而达到缩减任务规划中卫星资源规模,降低时间复杂度的目的。
我们拟对子问题1展开研究。但由于卫星异构的特性,不同团队执行同一组对地观测任务的代价通常不同。如何构建能够完成多组观测任务的最小卫星团队(团队中不存在冗余观测能力),且执行代价最小,已经成为卫星任务规划领域出现的新而亟待解决的问题。
T. Okimoto等[16]处理巴黎火灾救援问题时,将救援设备建模为Agent,根据火势大小,向各个火灾点组织消防车团队进行救援,是一种面向任务的Agent团队构建思想。受此启发,我们拟对观测任务集合、卫星集群能力[17]进行建模,研究面向任务的卫星Agent团队构建方法。设定卫星集群中的每颗卫星在执行每一个对地观测任务时,可以获得对应的收益和代价,执行不同的任务,代价不同。因此在胜任集合中所有任务的前提下,合理挑选卫星,使卫星团队执行所有任务的总代价最小[18]。
1 问题描述面向任务的对地观测卫星团队构建问题就是在已知系统的初始状态、可用资源、每颗卫星的负载情况的前提下,针对对地观测任务集合,基于卫星在执行任务时产生的代价从卫星集群中挑选出一组能胜任所有观测任务的卫星,组成卫星团队,使得执行所有任务的总代价最小。
1.1 符号定义为了方便描述,首先给出相关符号定义,如表 1所示。
1.2 目标函数面向任务的对地观测卫星团队构建问题的目标是从卫星集群中找到一个能够胜任这些任务的卫星团队,并使团队的总代价最小,即当team∈TEAMM时:
| ${\rm{team}}.{\rm{Cost}} = \sum {_{i = 1}^M} {C_{{\rm{ST}}}}\left( {{\rm{Sa}}{{\rm{t}}_j},{\rm{tas}}{{\rm{k}}_i}} \right) \to {\rm{MIN}}$ |
团队的总代价是团队中所有卫星执行任务的代价之和。
卫星Sati执行任务taskj的代价CST(Sati, taskj)可由SCi和TCj计算得到:
| ${C_{{\rm{ST}}}}\left( {{\rm{Sa}}{{\rm{t}}_j},{\rm{tas}}{{\rm{k}}_i}} \right) = {\rm{S}}{{\rm{C}}_i} \times {\rm{T}}{{\rm{C}}_j}$ |
SCi由卫星Sati当前时刻执行任务情况决定。卫星的使用代价SCi与执行的任务数、被占用的时间窗数正相关:
| ${\rm{S}}{{\rm{C}}_i} = \alpha \left( {\left| {{\rm{Btask}}{{\rm{s}}_{\rm{i}}}} \right| + \left| {{\rm{TW}}\_{\rm{use}}{{\rm{d}}_i}} \right|} \right)$ |
在团队构建过程中,卫星使用代价随着承担任务数增多,而不断增长。
| 表 1 符号定义 Tab.1 Symbol definitions |
卫星Sati能够执行任务taskj的条件:在卫星拥有的时间资源TWi中,找到一组观测时间窗TWtasks,胜任Btasksi和taskj,且与卫星上已经被占用的时间窗集合TW_usedi不产生冲突。考虑卫星在执行任务时,受星上电源容量、载荷硬件特性、轨道参数等限制,将一个时间窗看作一次观测活动,对TWtasks和TW_usedi组成的时间窗集合TWdet进行以下约束检测,TWdet中的TW按照ts排序。
1) 两次观测活动不能同时进行。卫星一次只能进行一个观测活动,即
| $\forall \;{\rm{t}}{{\rm{w}}_m} \in {\rm{T}}{{\rm{W}}_{\det }},T_s^{{\rm{t}}{{\rm{w}}_{m + 1}}} - T_e^{{\rm{t}}{{\rm{w}}_m}} \ge 0$ |
2) 两次观测活动最短时间间隔。卫星关机后需要一段时间才能重新开机,即
| $\forall \;{\rm{t}}{{\rm{w}}_m} \in {\rm{T}}{{\rm{W}}_{\det }},T_s^{{\rm{t}}{{\rm{w}}_{m + 1}}} - T_e^{{\rm{t}}{{\rm{w}}_m}} \ge \Delta T_{{\rm{sd}}}^i$ |
3) 单圈最长观测时间约束。卫星单圈累计观测时间要小于单圈最长开机时间,即
| $\forall \;{\rm{t}}{{\rm{w}}_m} \in {\rm{T}}{{\rm{W}}_{{\rm{cir}}P}},\sum {\left( {T_e^{{\rm{t}}{{\rm{w}}_m}} - T_s^{{\rm{t}}{{\rm{w}}_m}}} \right)} \ge T_{{\rm{cir}}}^i$ |
式中TWcirP表示TWdet中所有圈号为P的时间窗。
4) 单天最长观测时间约束。卫星单天累计观测时间限制要小于单天最长观测时间,即
| $\forall \;{\rm{t}}{{\rm{w}}_m} \in {\rm{T}}{{\rm{W}}_{{\rm{day}}Q}},\sum {\left( {T_e^{{\rm{t}}{{\rm{w}}_m}} - T_s^{{\rm{t}}{{\rm{w}}_m}}} \right)} \ge \Delta T_{{\rm{day}}}^i$ |
式中TWdayQ表示TWdet中所有时间窗起始时间在第Q天内的时间窗集合。
2 基于分枝限界的卫星任务团队构建算法由上述模型可知,该问题是一个典型的组合优化问题,我们拟采用树构建与搜索方法,以初始的空团队team0作为根节点,以完成任务为条件向下分支,形成新的团队,遍历完所有任务,可建构一颗广义的搜索树。
算法 1 TFCA
功能 基于分枝限界思想的团队构建算法的主算法;
输入 TaskSet, SatSet, 初始的空团队team0;
输出 最优团队teamMbest。
1) Begin
2) set teamMbest=∅, team=team0
3) TFOfEachTask (1, team, teamMbest)
4) Return teamMbest
5) End
我们采用深度优先策略进行树搜索,以当前搜索到的能够胜任任务集合中所有任务的最优团队teamMbest的代价作为上界,根据分支限界法对树进行剪枝,即对于当前正在构建的卫星任务团队Curteam,如果:
| ${\rm{Curteam}}.{\rm{Cost}} \ge {\rm{team}}_M^{{\rm{best}}} \cdot {\rm{Cost}}$ |
则减去Curteam这个节点向下的所有分枝。
基于这种搜索剪枝策略,提出了基于分枝限界思想的团队构建算法(team formation complete algorithm based-on a branch and bound techniques,TFCA),伪代码如算法1、2、3所示。
算法 2 TFOfEachTask
功能 从第m个任务开始搜索构建团队的迭代算法。
输入 m, team, teamMbest;
输出 目标找到的最优团队teamMbest。
1) Begin
2) if (m>M)
3) if (team.Cost<teamMbest.Cost||teamMbest=∅
4) teamMbest=team
5) Return
6) else if (team. Cost>teamMbest.Cost&&teamMbest=∅)
7) Return
8) end if
9) solve (1, team, teamSet, m)
10) for each team in teamSet
11) TFOfEachTask (m+1, team, teamMbest)
12) end for
13) End
算法 3 solve
功能 寻找team向下能完成taskm的团队的迭代算法;
输入 n, team, teamSet, m;
输出 当前team下能完成taskm的团队集合teamSet。
1) Begin
2) if (n>N)
3) Return
4) else if (Satn能完成taskm)
5) team1=Update (team)
6) teamSet=teamSet∪{team1}
7) solve (n+1, team, teamSet, m)
8) end if
9) End
算法1是基于分枝限界思想的团队构建算法的主算法,采用深度优先的搜索方式遍历所有的团队,首先将最优团队teamMbest置为空,语句3)是以初始团队team0为根节点的迭代搜索。
算法2从第m个任务开始搜索构建团队的迭代算法,语句2)~5)表示该分支的team构建完成,如果team的代价小于teamMbest的代价或者teamMbest为空,则更新team为最佳团队并结束该分支搜索。语句7)~8)为基于分枝限界思想的剪枝过程,当team还不能胜任所有的任务,而其代价已经大于等于teamMbest的代价,则结束该分支搜索。语句9)表示在当前team的情况下,完成taskm产生的所有方案存入teamSet。语句10)~12)对teamSet中的每个team进入下一任务的搜索。
算法3寻找在当前team下,能完成taskm的所有团队的迭代算法。在当前team的情况,依次判断每颗卫星Satn能否完成taskm,如果能完成,则生成新团队team1,并将该team1加入teamSet。
由算法的迭代过程可以看出,如果针对M个任务,在N个卫星中构建团队,在最坏的情况下即每颗卫星都有能力执行所有的任务,而且没有任何剪枝操作发生,于是有TEAMi=Ni,那么迭代过程中形成的方案总数为
由上述分析可知,在最坏的情况下,算法时间复杂度将呈指数增长,该问题组合爆炸特征明显。为了降低基于分枝限界思想的团队构建算法的时间复杂度,提出了一种基于剪枝策略的启发式算法。
3 基于剪枝策略的启发式算法通过TFCA算法进行树搜索,首先要找到一个胜任所有任务的团队,以这个团队的代价作为上界才可以进行剪枝操作,运行时间较长,剪掉的分支有限,效率较低,为了提高树搜索效率,需要寻找一种新的剪枝策略。
我们将深度优先的搜索方式改成广度优先,对每一层的团队集合TEAM进行剪枝操作,从而达到减少树分枝,降低时间复杂度的目的。
首先,给出剪枝策略。设team1, team2∈TEAMi,如果
| ${\rm{tea}}{{\rm{m}}_1}.{\rm{Cost}} \ge \left( {1 + \frac{\varepsilon }{i}} \right){\rm{tea}}{{\rm{m}}_2}.{\rm{Cost}}$ |
0<ε<1记为team1<team2,则剪去team1这个团队所在的结点。其中,i是TEAMi中的每个团队完成的任务个数,ε根据卫星初始状态调整,尽量为团队挑选承担任务数少的卫星。
基于这种剪枝策略,提出了启发式团队构建算法(heuristic team formation algorithm based-on a pruning strategy, HTFA),算法伪码如算法4所示。
算法4是基于剪枝策略的启发式算法,以team0作为根节点,从第1个任务开始搜索,TEAM1是所有完成task1的team集合,对TEAM1中每个team,搜索task2,以此类推直到搜索到TEAMM。语句8)~22)是根据剪枝策略对TEAMM进行的剪枝操作。
算法 4 HTFA
功能 基于剪枝策略的启发式算法;
输入 TaskSet, SatSet, team0;
输出 teamMbest。
1) Begin
2) set TEAMi=∅, i∈(0, M)
3) TEAM0=TEAM0∪team0
4) for(i=1; i≤M; i++)
5) for each teaminTEAMi-1
6) set TEAMi=∅
7) solve (1, team, teamSet, i)
8) for each team1 in teamSet
9) if (TEAMi=∅)
10) TEAMi=TEAMi∪team1
11) else
12) for each team2in TEAMi
13) if (team1>team2)
14) TEAMi=TEAMi/team2
15) TEAMi=TEAMi∪team1
16) else
17) if (team2>team1)
18) break
19) else
20) TEAMi=TEAMi∪team1
21) end for
22) end for
23) end for
24) end for
25) for each team in TEAMM
26) if (team.Cost<teamMbest.Cost)
27) teamMbest=team
28) end for
29) return teamMbest
30) End
由于HTFA算法的这种剪枝策略,TaskSet的输入顺序可能会影响算法最终输出结果。如果在随机的任务集合中,代价小的任务排在前面,HTFA将会优先挑选代价小的卫星执行该任务,代价大的任务只能选择代价大的卫星,会使最终构建出的卫星
团队的代价偏大。为此,对输入任务集合TaskSet进行排序:
1) 记无序的任务集合为TaskSet-S,以TaskSet-S作为输入的HTFA算法为HTFA-S;
2) 根据任务代价由高到低排序的任务集合为TaskSet-C,以TaskSet-C作为输入的HTFA算法为HTFA-C;
3) 根据任务性价比由高到低排序的任务集合为TaskSet-RC,以TaskSet-RC作为输入的HTFA算法为HTFA-RC。
4 实验与分析为了验证TFCA算法、HTFA-S算法、HTFA-C算法、HTFA-RC算法的性能,设计了4组实验。
计算平台:Intel(R) Core(TM) i5-6400 CPU @ 2.70 GHz (4 CPUs),内存8192 MB RAM,操作系统Win7,采用Microsoft Visual Studio 2010 C#编码。
实验 数据 在STK卫星数据库中选取50颗低轨卫星数据模拟卫星集群的运行,以全球100个重要城市作为观测目标,从中随机挑选。设定每颗卫星上携带可见光、红外、电磁探测、多光谱、超光谱5种载荷。根据卫星硬件情况,设置卫星使用代价SCi=α(|Btasksi|+|TW_usedi|)中的参数α,随机挑选1~5个时间窗作为卫星上已经被占用的时间窗集合TW_used。采用随机生成一组任务的方式,模拟真实环境下一段时间内卫星系统接收到的待规划任务集合。
卫星集群按照卫星成员的数量可以分为小规模卫星集群(small-scale satellite cluster, SSC)和大规模卫星集群(large-scale satellite cluster, LSC)。小规模卫星集群中成员数量在10颗以下,大规模卫星集群的成员数量大于10颗。
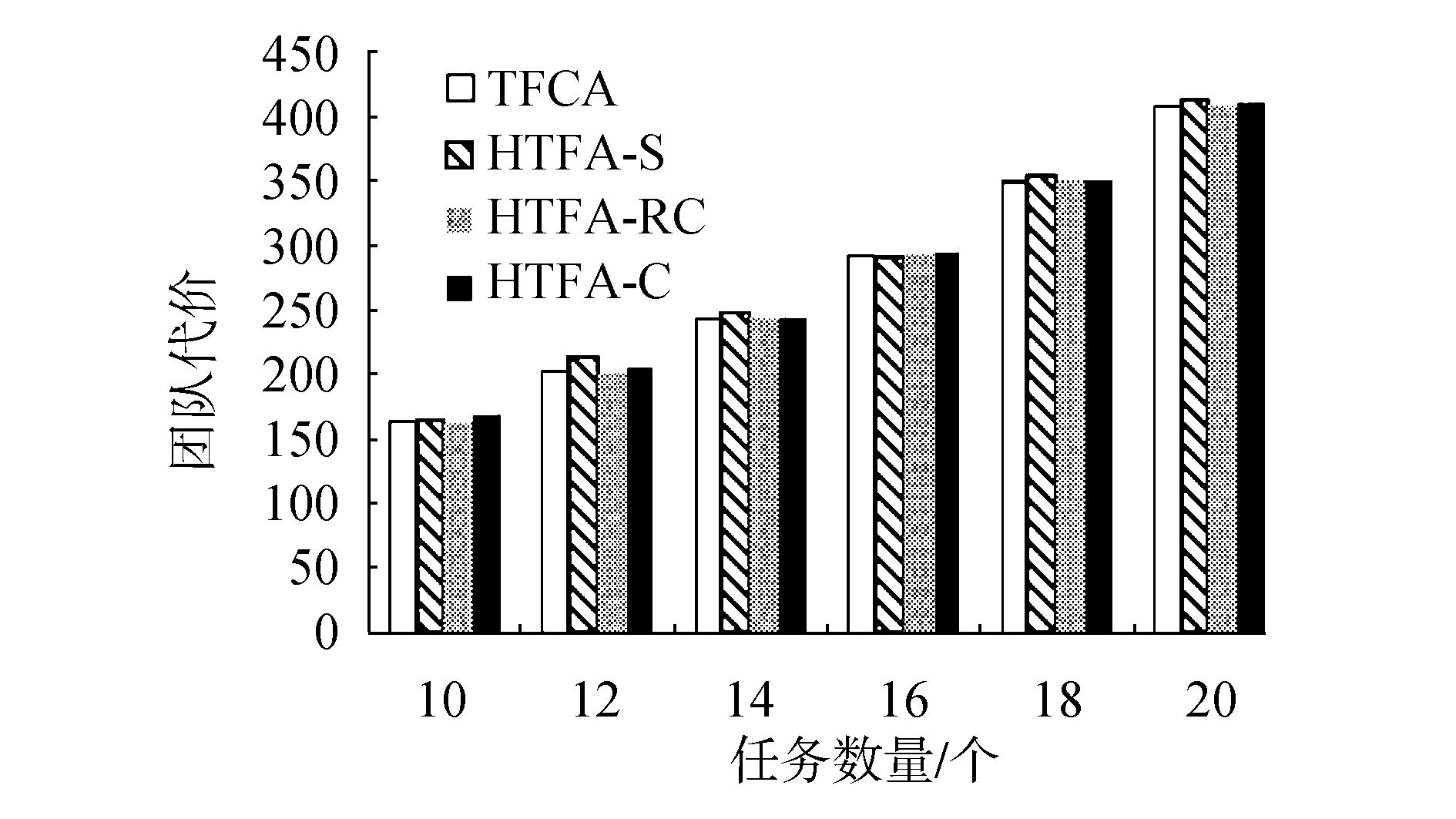
实验 1 随机生成6组任务,在10颗卫星构成的小规模集群上采用TFCA、HTFA-S、HTFA-C、HTFA-RC构建团队,比较4种算法的性能。实验结果如图 1和表 2。
|
图 1 4种算法在小规模卫星集群上的性能对比 Fig.1 Performances of four algorithms in SSC |
| 表 2 4种算法在小规模卫星集群上的运行时间对比 Tab.2 Running time of four algorithms in SSC |
从图 1可以看出,在小规模卫星集群中,HTFA-S、HTFA-RC、HTFA-C算法构建的团队效果接近TFCA算法。HTFA-S算法由于任务输入的无序性,在大部分情况下构建团队的效果比HTFA-RC、HTFA-C算法差。表 2展示了4种算法的时间特性,TFCA算法的运行时间随着任务的增多,呈现指数增长趋势,HTFA-S、HTFA-RC、HTFA-C算法的运行时间增长缓慢。
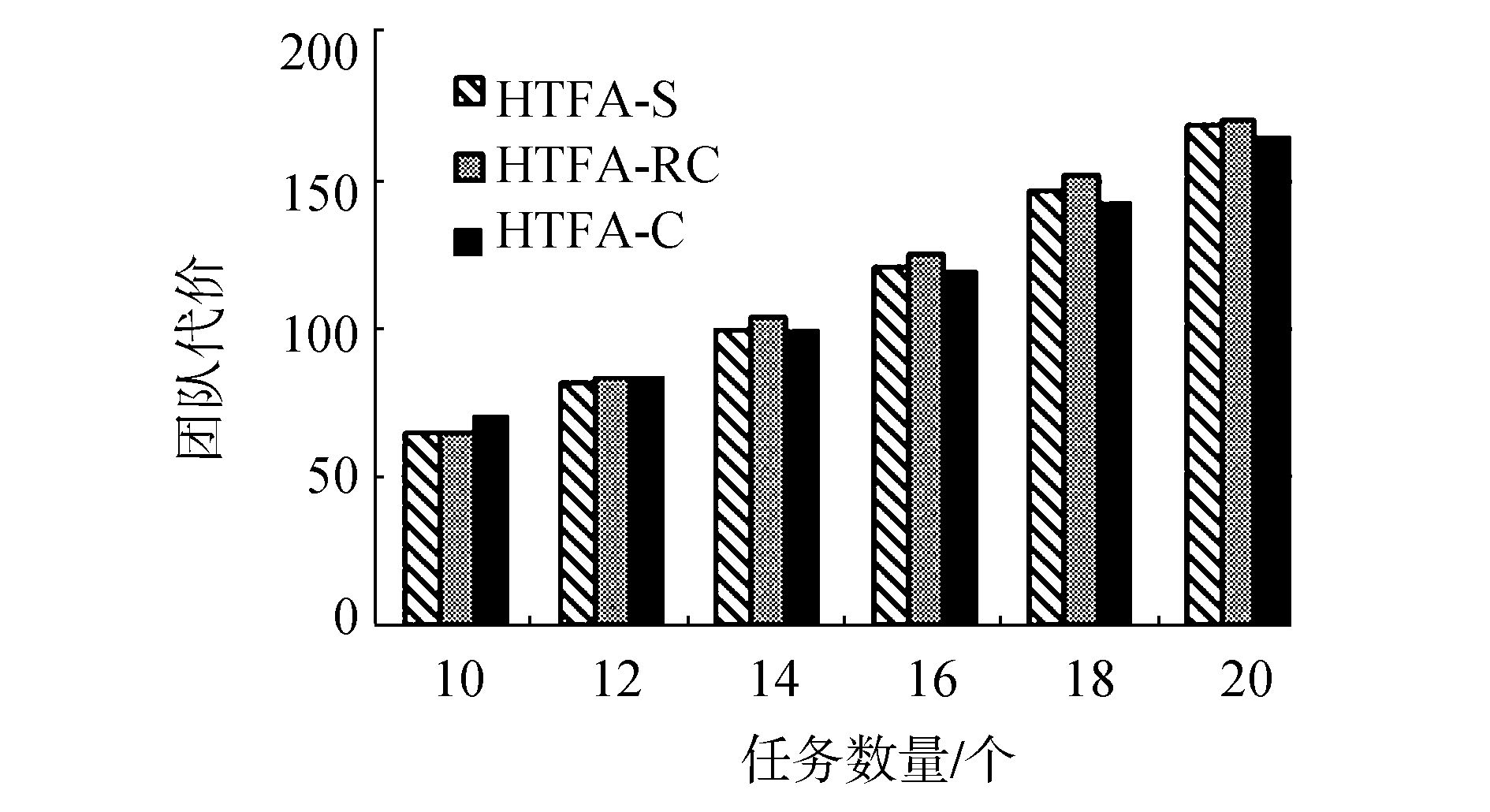
实验 2 为了进一步验证我们提出的算法在大规模卫星集群上的性能,在50颗卫星组成的卫星集群上重新测试实验1中的6组任务数据。但由于TFCA算法运行时间太长(在50颗卫星组成的集群上,对12个任务构建团队时,运行超过12 h仍然不能给出有效结果)我们仅对比HTFA-S、HTFA-RC和HTFA-C的实验结果,如图 2、3所示。
|
图 2 3种启发式算法在LSC上的性能对比 Fig.2 Performances of three algorithms in LSC |
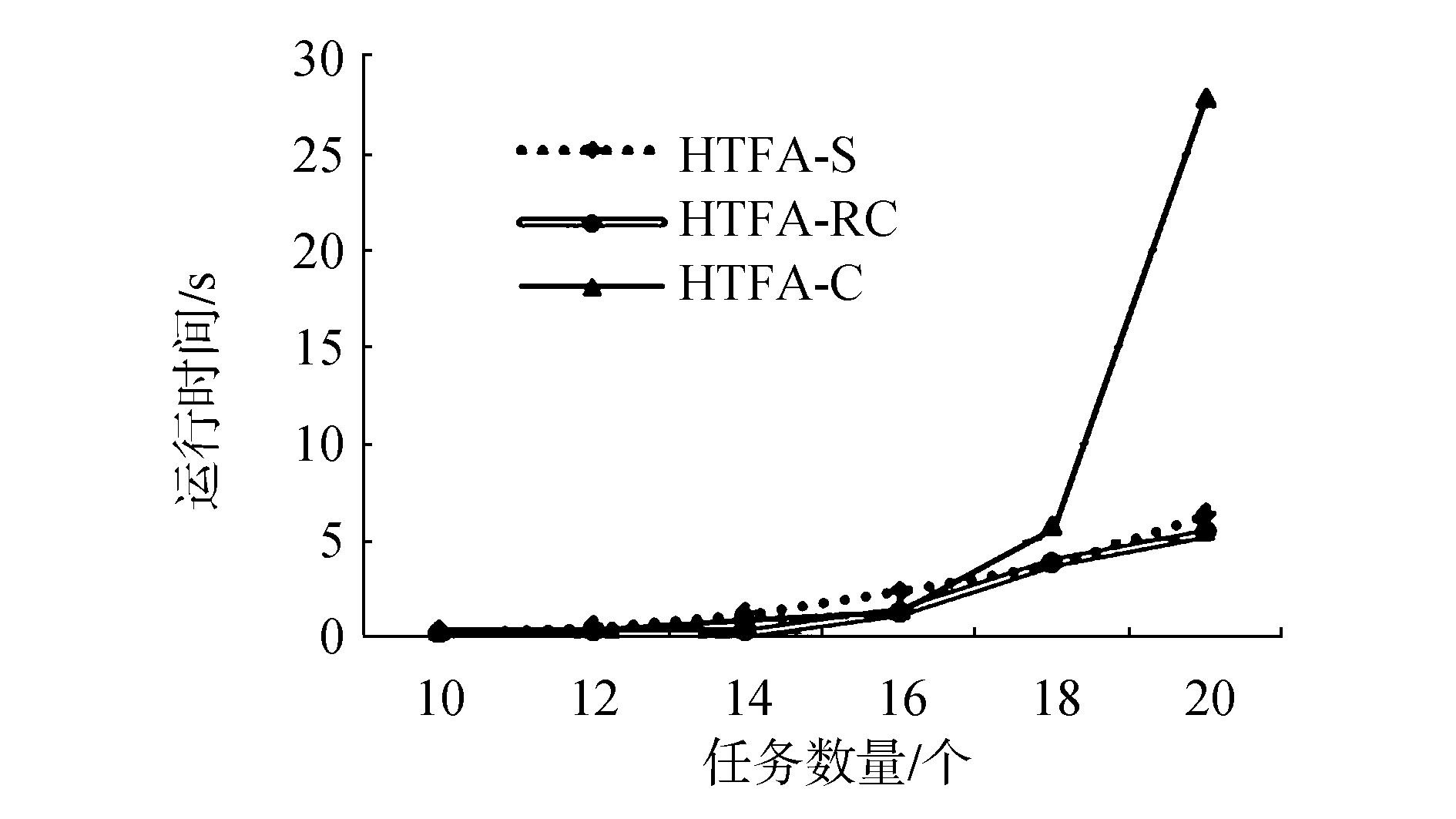
|
图 3 3种启发式算法在LSC上的运行时间对比 Fig.3 Time comparison of three algorithms in LSC |
图 2展现了在大规模卫星集群上HTFA-S、HTFA-RC、HTFA-C算法的性能差异。HTFA-RC、HTFA-C算法构建团队的效果普遍优于HTFA-S算法。从图 3中可以看出,随着任务增多,HTFA-S、HTFA-RC、HTFA-C算法构建团队时间都在逐渐增加,而HTFA-C构建团队时间的增长速度明显高于HTFA-S和HTFA-RC,这是因为HTFA-C任务的有序性在相同的剪枝策略下相比于其他两种算法,HTFA-C在每一层会更多地保留效果好的分枝,因此整个团队构建过程中,搜索的分枝更多。
实验 3 随机生成一组由10个任务构成的任务集合,在不同规模的卫星集群上构建团队,比较TFCA、HTFA-S、HTFA-C、HTFA-RC算法性能,实验结果如表 3、图 4所示。
| 表 3 4种算法的运行时间对比 Tab.3 Running time of four algorithms |

|
图 4 4种算法在不同规模卫星集群上的性能对比 Fig.4 Performances of four algorithms in different scales of SC |
图 4是在中小规模的多个卫星集群上对同一组任务数据构建团队对比4种算法的性能。随着卫星规模的逐步增大,团队的代价越来越小。多数情况下,HTFA-C、HTFA-RC算法的性能优于HTFA-S算法。从表 3中可以看出,TFCA算法的运行时间随着集群规模增大爆发式增长。而HTFA-S、HTFA-RC、HTFA-C算法的运行时间增长不明显。
实验 4 为了进一步比较3种启发式算法在大规模卫星集群上的性能,随机生成一组由20个任务组成的任务集合,在10、20、30、40、50颗卫星组成的卫星集群上进行实验。由于TFCA算法运行时间太长(在20颗卫星组成的集群上,对20个任务构建团队时,运行超过12 h仍然不能给出有效结果),我们仅对比HTFA-S、HTFA-RC和HTFA-C的实验结果,如图 5、6所示。

|
图 5 3种启发式算法在不同规模卫星集群上的性能对比 Fig.5 Performances of three algorithms in different scales of SC |

|
图 6 3种启发式算法在不同规模的卫星集群上运行时间 Fig.6 Time comparison of three algorithms in different scales of SC |
图 6中随着卫星规模的增大,对同一组任务构建的团队代价逐渐减少,而构建团队的时间逐渐增大。这是因为规模增大,可以挑选多个卫星承担任务,无需一个卫星承担多个任务,团队代价随之降低。
整体上来看,3种启发式算法HTFA-S、HTFA-RC和HTFA-C构建团队所需的时间成本远小于TFCA算法,而其性能与TFCA相差不大,对任务集合根据任务代价排序的HTFA-C构建的团队的代价最接近TFCA算法构建的团队的代价,也就是最接近全局最优解,HTFA-RC次之。
5 结束语面向任务的对地观测卫星团队构建问题,是卫星任务规划领域出现的新而亟待解决的问题。在对问题进行分析的基础上,建立了数学模型,提出了基于分枝限界的卫星团队构建精确搜索算法(TFCA)。针对TFCA算法时间复杂度高的缺点,引入了启发式剪枝策略,并根据算法输入中任务集合的次序不同,提出了3种启发式卫星团队构建算法:HTFA-S、HTFA-RC和HTFA-C算法。实验结果表明:3种启发式算法HTFA-S、HTFA-RC和HTFA-C,构建团队所需的时间成本远小于TFCA算法,而其性能与TFCA算法相差不大,对任务集合根据任务代价排序的HTFA-C构建的团队的代价最接近TFCA算法构建的团队的代价。
在下一步的工作中,我们将从理论上分析HTFA-S、HTFA-RC和HTFA-C算法近似程度,并给出算法性能上界。
| [1] |
LIN Zhenhai. Mission planning for electromagnetic environment monitors satellite based on simulated annealing algorithm[C]//2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE). Halifax, Canada, 2015:530-535.
( 0) 0)
|
| [2] |
姜维, 郝会成, 李一军. 对地观测卫星任务规划问题研究述评[J]. 系统工程与电子技术, 2013, 35(9): 1878-1885. JIANG Wei, HAO Huicheng, LI Yijun. Review of task scheduling research for the earth observing satellites[J]. Systems engineering and electronics, 2013, 35(9): 1878-1885. (  0) 0)
|
| [3] |
WANG Jun, JING Ning, LI Jun, et al. A multi-objective imaging scheduling approach for earth observing satellites[C]//Proceedings of the 9th annual conference on Genetic and evolutionary computation. London, England, 2007:2211-2218.
( 0) 0)
|
| [4] |
CHEN Hao, LI Jun, JING Ning. User-oriented data acquisition chain task planning algorithm for operationally responsive space satellite[J]. Journal of systems engineering and electronics, 2016, 27(5): 1028-1039. DOI:10.21629/JSEE.2016.05.11 ( 0) 0)
|
| [5] |
WANG P, REINELT G, GAO P, et al. A model, a heuristic and a decision support system to solve the scheduling problem of an earth observing satellite constellation[J]. Computers & industrial engineering, 2011, 61(2): 322-335. ( 0) 0)
|
| [6] |
郭玉华. 多类型对地观测卫星联合任务规划关键技术研究[D]. 长沙: 国防科技大学, 2009: 19-57. GUO Yuhua. The study on key technologies of multiple types of earth observing satellites united scheduling[D]. Changsha:national university of defense technology, 2009:19-57. http://cdmd.cnki.com.cn/Article/CDMD-90002-2010165395.htm (  0) 0)
|
| [7] |
BIANCHESSI N, RIGHINI G. Planning and scheduling algorithms for the COSMO-SkyMed constellation[J]. Aerospace science & technology, 2008, 12(7): 535-544. ( 0) 0)
|
| [8] |
BOTELHO S C, Alami R. M+:a scheme for multi-robot cooperation through negotiated task allocation and achievement[C]//1999 IEEE International Conference on Robotics and Automation. Detroit, USA, 1999, 2:1234-1239.
( 0) 0)
|
| [9] |
PENG Shuang, CHEN Hao, LIN Jun, et al. Multi-agent collaborative planning method of emergency mission based on scheme fusion strategy[C]//2014 IEEE Symposium on Computer Applications and Communications(SCAC). Weihai, China, 2014:87-92.
( 0) 0)
|
| [10] |
FENG Peng, CHEN Hao, PENG Shuang, et al. A method of distributed multi-satellite mission scheduling based on improved contract net protocol[C]//201511th International Conference on Natural Computation (ICNC). Zhangjiajie, China, 2015:1062-1068.
( 0) 0)
|
| [11] |
WANG Chong, JING Ning, et al. A distributed cooperative dynamic task planning algorithm for multiple satellites based on multi-agent hybrid learning[J]. Chinese journal of aeronautics, 2011, 24(4): 493-505. DOI:10.1016/S1000-9361(11)60057-5 ( 0) 0)
|
| [12] |
董云峰, 王兴龙. 卫星集群概念研究[J]. 航天器工程, 2012, 21(4): 83-88. DONG Yunfeng, WANG Xinglong. Research on conception of satellite cluster[J]. Spacecraft engineering, 2012, 21(4): 83-88. (  0) 0)
|
| [13] |
MOORES J E, CARROLL K A, DESOUZE I, et al. The small reconnaissance of atmospheres mission platform concept, part 2:design of carrier spacecraft and atmospheric entry probes[J]. International journal of space science & engineering, 2014, 2(4): 345-364. ( 0) 0)
|
| [14] |
HINCHEY M G, STERRITT R, ROUFF C. Swarms and swarm intelligence[J]. Computer, 2007, 40(4): 111-113. DOI:10.1109/MC.2007.144 ( 0) 0)
|
| [15] |
DEKENS E, ENGELEN S, NOOMEN R. A satellite swarm for radio astronomy[J]. Acta astronautica, 2014, 102: 321-331. DOI:10.1016/j.actaastro.2013.11.033 ( 0) 0)
|
| [16] |
OKIMOTO T, SCHWIND N, CLEMENT M, et al. How to form a task-oriented robust team[C]//Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. International Foundation for Autonomous Agents and Multiagent Systems. Istanbul, Turkey, 2015:395-403.
( 0) 0)
|
| [17] |
HE L, IOERGER T R. A quantitative model of capabilities in multi-agent systems[C]//Proceeding of the International Conference on Artificial Intelligence(IC-AI) Las Vegas, USA, 2003:730-736.
( 0) 0)
|
| [18] |
CRAWFORD C, RAHAMAN Z, Sen S. Evaluating the efficiency of robust team formation algorithms[C]//International Conference on Autonomous Agents and Multiagent Systems. Tulsa, USA, 2016:14-29.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


