2. 国家海洋局 北海预报中心, 山东 青岛 266000
2. Beihai Forecast Center of State Oceanic Administration, Qingdao 266000, China
风暴潮(storm surge)是一种由于强烈大气扰动,如热带气旋(台风、飓风)、温带气旋等,引起的海面异常升高现象。它具有数小时至数天的周期,通常叠加在正常潮位之上,而风浪、涌浪(具有数秒的周期)则叠加在风暴潮和正常潮位之上。它们的结合所引起的沿岸海水暴涨常常酿成巨大潮灾[1]。风暴潮灾害的及时预报能极大地减少其对沿海地区带来的人员伤害和经济损失,具有很强的实用价值。
传统的风暴潮预报方法主要分为两大类:经验预报方法和数值预报方法。经验预报方法通常是指预报员的主观经验和经验统计预报方法,而数值预报方法主要包括诺模图方法和数值预报方法[2]。曾德美[3]研究了青岛港的风暴潮概况,提出了青岛港极值增减水的经验公式。谢亚力和黄世昌[4]将风暴潮经验预报与动力线性模型相结合,建立了经验预报方程,并在钱塘江风暴潮预报中取得了不错的效果。高清清等[2]通过研究位于长江入海口的南通单站历史水文气象资料,分析该站的风暴增水特征,提出了针对该站台风风暴潮经验预报公式。
从20世纪80年代以来,基于数值模拟方法的风暴潮预报技术取得了较大的发展和进步。朱建荣和朱首贤[5]将原正交的ECOM模式改进为非正交曲线坐标系下模式,以更好地拟合河岸线的形状,应用于长江河口、杭州湾及邻近海区,取得了不错的效果。黄世昌等[6]基于河口海岸水动力二维数值模型,建立起了风暴潮与天文潮相互耦合的数值模式,可用于浙江沿海增水预测。王培涛等[7]提出了一种基于高级环流模型(ADCIRC)适合台湾海峡及福建沿海区域的精细化台风风暴潮数值预报模式。
然而,基于经验和数值的传统风暴潮预报通常需要研究员对风暴潮的动力学规律具有非常深入的研究,操作复杂难懂,并且很难建立起相对准确的模型。后来,随着计算机技术的发展和大数据时代的到来,许多学者将基于海量数据的机器学习方法用于风暴潮预报中。T. L. Lee[8]将风速、风向、压强等要素作为输入训练前馈神经网络(feedforward neural network, FNN),用来进行风暴潮的预测。S. Rajasekaran等[9]则使用支持向量回归(support vector regression, SVR)来对风暴潮进行预报。
现存的基于机器学习的风暴潮预测方法虽不需要引入风暴潮动力学先验,直接通过数据本身进行预测,但大都只提取出风暴潮数据间的静态关系,并没有充分挖掘其背后的时序关联特性。递归神经网络[10-12](recurrent neural network, RNN)中隐藏层神经元间相互连接构成有向图,网络状态随时间变化,耦合了时间参数,非常适合分析具有时序特征的数据。受此启发,本文基于递归神经网络来进行风暴潮增水预测。风暴潮是随时间变化发展的,得到的风暴潮数据明显具有时序特性。相比于传统的机器学习方法,递归神经网络更加适用于风暴潮预报问题。本文采用递归神经网络进行风暴潮增水过程预测,并在真实数据上进行了实验验证。
1 原理说明 1.1 前馈神经网络人工神经网络(artificial neural network, ANN)是一种常用的进行预报的方法。它是一种应用类似于大脑神经连接的结构进行信号处理的数学模型,广泛应用于语音识别、自然语言处理、图像处理等领域[13-15]。目前,在大数据分析中主要采用前馈神经网络来提取静态数据之间的关系。
前馈神经网络[16]是一种具有前向结构的人工神经网络,一般是多层结构,包含输入层、隐含层以及输出层,隐含层可以有多层。每一层神经元的输入是上一层的输出,并通过全连接将其输出传递给下一层,且整个网络中没有反馈。每一个神经元可以是多输入的,但是只有一个输出。多层前馈神经网络是感知器的推广,只要有一层包含足够多神经元的隐含层就能够以任意精度逼近任意复杂度的连续函数[17]。以3层前馈神经网络为例,结构如图 1所示。

|
图 1 多层感知器 Fig.1 Multi-layer perceptron |
图 1中,Lin表示输入层,x=[x1 x2x3]T是多层感知器输入;Lhidden表示隐含层,包含4个神经元,表示为h=[h1 h2h3 h4]T;Lout是输出层,输出维数为3(y=[y1 y2y3]T)。前向传播是指数据从输入到输出这个传播过程,可以用式(1)表示:
| $\begin{array}{l} \mathit{\boldsymbol{h}} = f\left( {\mathit{\boldsymbol{W}}_1^{\rm{T}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_1}} \right)\\ \mathit{\boldsymbol{y}} = f\left( {\mathit{\boldsymbol{W}}_2^{\rm{T}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_2}} \right) \end{array}$ | (1) |
式中:W1∈
虽然多层前馈神经网络能够一定程度上解决非线性问题,但其仍然属于静态网络,网络当前时刻的输出与上一时刻的输入无关,因此对于具有时序特征的数据无能为力。为了解决输入之间前后关联的问题,多层前馈神经网络的隐含层不仅需要接收当前的输入,也要接收上一时刻的输出,由此产生了递归神经网络。
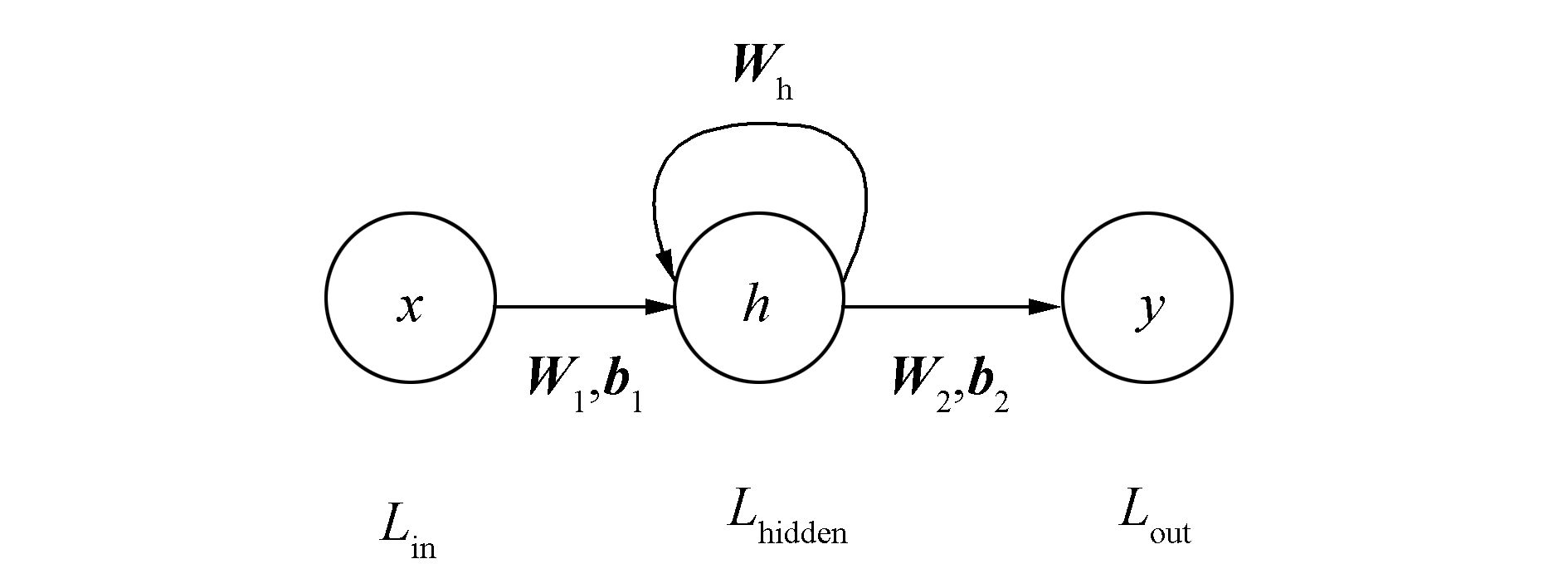
1.2 递归神经网络为了克服前馈神经网络无法处理序列数据的问题,递归神经网络将隐含层之间的节点相互连接,使得隐含层的输入不仅仅是当前时刻输入层的输出还包括了上一时刻隐含层的输出。通过这种方式,递归神经网络可以将当前时刻以前的信息记忆在网络之中[19]。如图 2所示,递归神经网络与前馈神经网络的结构大致相同,不同之处在于隐含层之间的连接关系,即增加了隐含层间的权重Wh。
|
图 2 递归神经网络 Fig.2 Recurrent neural networks |
若Lhidden隐含层包含m个神经元,则Wh为m×m维的权重矩阵。递归神经网络的传播过程可以用式(2)表示:
| $\begin{array}{l} {\mathit{\boldsymbol{h}}_t} = f\left( {\mathit{\boldsymbol{W}}_1^{\rm{T}}\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{W}}_{\rm{h}}^{\rm{T}}{\mathit{\boldsymbol{h}}_{t - 1}} + {\mathit{\boldsymbol{b}}_1}} \right)\\ \quad \quad \mathit{\boldsymbol{y}} = f\left( {\mathit{\boldsymbol{W}}_2^{\rm{T}}{\mathit{\boldsymbol{h}}_t} + {\mathit{\boldsymbol{b}}_2}} \right) \end{array}$ | (2) |
式中:W1表示输入层和隐含层之间的连接权重;W2表示隐含层和输出层之间的连接权重;b1和b2分别表示隐含层和输出层的偏置;xt、ht和yt分别表示第t时刻网络的输入、隐含层输出和网络的输出;ht-1表示第t-1时刻隐含层的输出。激活函数一般是双曲正切函数或者Relu函数。
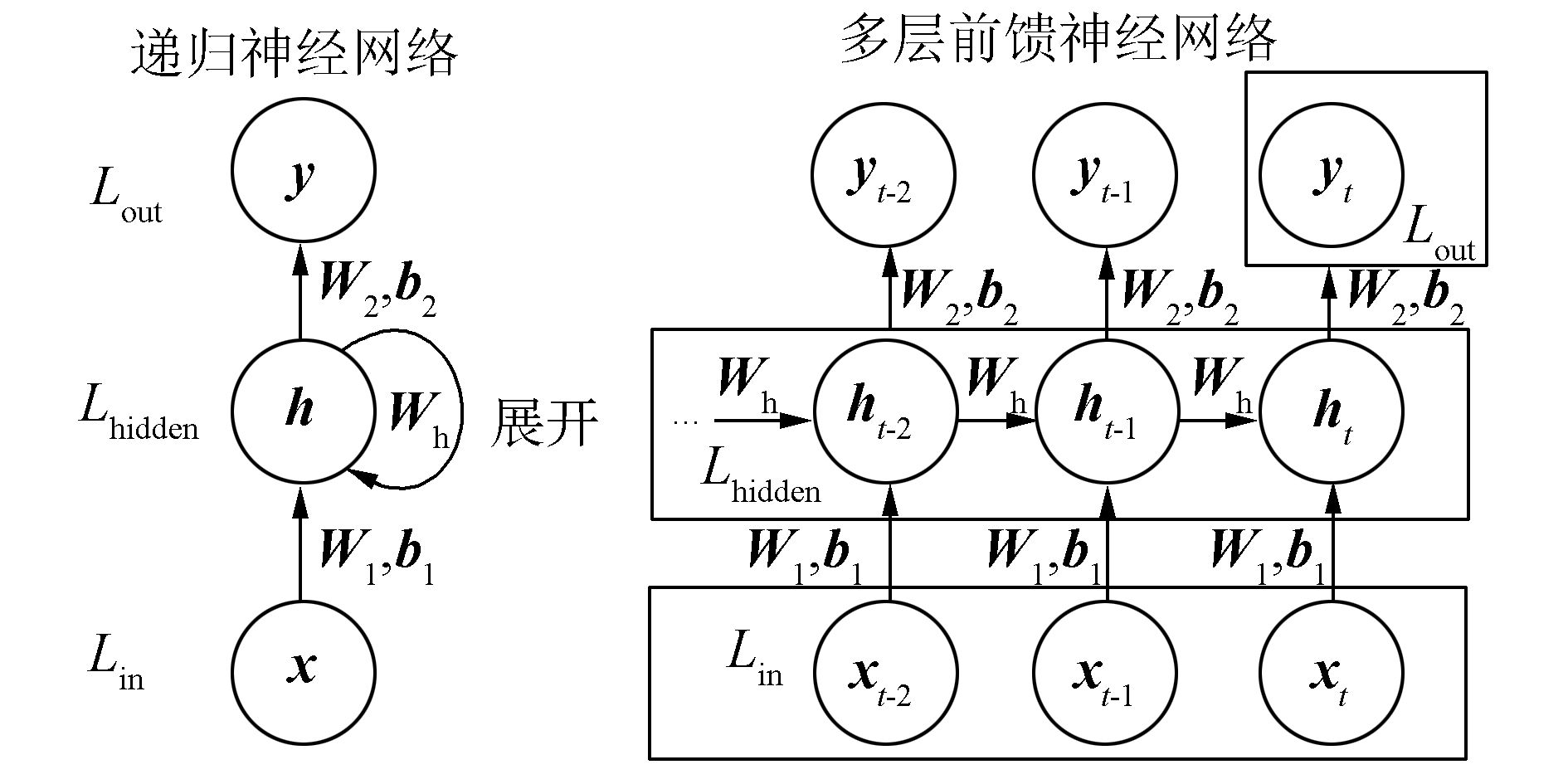
此外,递归神经网络还可以展开成相对应的多层前馈神经网络,从而可以使用BPTT(back-propagation through time)算法[20]进行训练,展开过程如图 3所示。
|
图 3 递归神经网络展开过程 Fig.3 The unfolding of recurrent neural networks |
若训练样本中包含T个时刻的数据,则递归神经网络将展开成一个包含T个隐含层的前馈神经网络。理论上来说,递归神经网络可以处理任意长度的序列数据,但是当处理无限长的序列数据时,展开的多层前馈神经网络也是无限层的。因此,在实际应用中通常只假设当前状态与之前有限个状态相关,以降低复杂度。与传统的前馈神经网络不同的是,展开的递归神经网络有如下特点。
1) 每个隐含层的输入都由两部分组成,即对应时刻输入层的输出和上一时刻隐含层的输出。而传统前馈神经网络的输入只能是上一层(隐含层或输入层)的输出。
2) 如图 3所示,展开的递归神经网络相同位置的参数W1、b1、W2、b2、Wh是共享的,而传统前馈神经网络则是非共享的,这也大大地降低了网络所要学习的参数。
3) 对于递归神经网络,每一个时刻都会给出一个输出,但是并不是必要的,只有t时刻的输出yt才是模型的预测结果,其余的输出结果都保存在了隐含层中。
1.3 递归神经网络用于风暴潮增水预测风暴潮增水数据是一维的时间序列,基于递归神经网络进行预报的具体做法如下。
假设样本数据为d={d1, d2, …, dT},利用前k个数据作为特征预测下一个数据,则可以组成训练样本X和标签y:
| $\begin{align} & \quad \quad \quad \quad \quad \quad \mathit{\boldsymbol{X}}=\left( {{\mathit{\boldsymbol{x}}}_{1}},{{\mathit{\boldsymbol{x}}}_{2}},\cdots ,{{\mathit{\boldsymbol{x}}}_{T-k}} \right)= \\ & \left\{ \left\{ {{d}_{1}},{{d}_{2}},\cdots ,{{d}_{~}}_{k} \right\},\left\{ {{d}_{2}},{{d}_{3}},\cdots ,{{d}_{~}}_{k+1} \right\},\cdots ,\left\{ {{d}_{T-k}},\cdots ,{{d}_{T-k+1}},\cdots ,{{d}_{T-1}} \right\} \right\} \\ & \quad \quad \mathit{\boldsymbol{y}}=\left\{ {{\mathit{\boldsymbol{y}}}_{1}},{{\mathit{\boldsymbol{y}}}_{2}},\cdots ,{{\mathit{\boldsymbol{y}}}_{T-k}} \right\}=\left\{ {{d}_{k+1}},{{d}_{k+2}},\cdots ,{{d}_{T}} \right\} \\ \end{align}$ |
一般假设当前状态只和前l个状态有关,因此再将X和y进一步按照状态数目分割,制作最终的训练样本
| $\begin{array}{l} \mathit{\boldsymbol{\hat X}} = \{ \left\{ {{\rm{ }}{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}, \ldots ,{\mathit{\boldsymbol{x}}_l}} \right\},\left\{ {{\mathit{\boldsymbol{x}}_2},{\mathit{\boldsymbol{x}}_3}, \ldots ,{\mathit{\boldsymbol{x}}_{l + 1}}} \right\}, \ldots ,\\ \quad \quad \quad \{ {\mathit{\boldsymbol{x}}_{T - k - l + 1}},{\mathit{\boldsymbol{x}}_{T - k - l + 2}}, \ldots ,{\mathit{\boldsymbol{x}}_{T - k}}\} \} \\ \mathit{\boldsymbol{\hat y}} = \{ \left\{ {{\mathit{\boldsymbol{y}}_1},{\mathit{\boldsymbol{y}}_2}, \ldots ,{\mathit{\boldsymbol{y}}_l}} \right\},\left\{ {{\mathit{\boldsymbol{y}}_2},{\mathit{\boldsymbol{y}}_3}, \ldots ,{\mathit{\boldsymbol{y}}_{l + 1}}} \right\}, \ldots ,\\ \quad \quad \quad \left\{ {{\mathit{\boldsymbol{y}}_{T - k - l + 1}},{\mathit{\boldsymbol{y}}_{T - k - l + 2}}, \ldots ,{\mathit{\boldsymbol{y}}_{T - k}}} \right\}\} \end{array}$ |
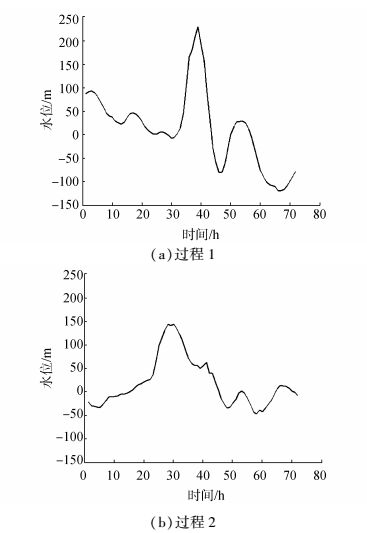
本文的实验数据集是潍坊水站从2008~2014年记录的风暴潮增水过程数据。每个增水过程共历时3天,每隔1 h记录1个水位数据,总计72个数据。图 4展示了2008年里的2个增水过程。
|
图 4 风暴潮增水过程 Fig.4 The process of storm surge |
使用递归神经网络进行预测时,时间延迟选3,即输入层的神经单元数目为3,隐含层的神经单元数目为15。训练时,为了避免因为数据的数量级差别而造成递归神经网络预测误差较大,首先对输入数据进行归一化处理,将它们归一化到区间[0, 1]之中,采用的归一化公式如下:
| $\hat x = \frac{{x - {x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}}$ |
式中:
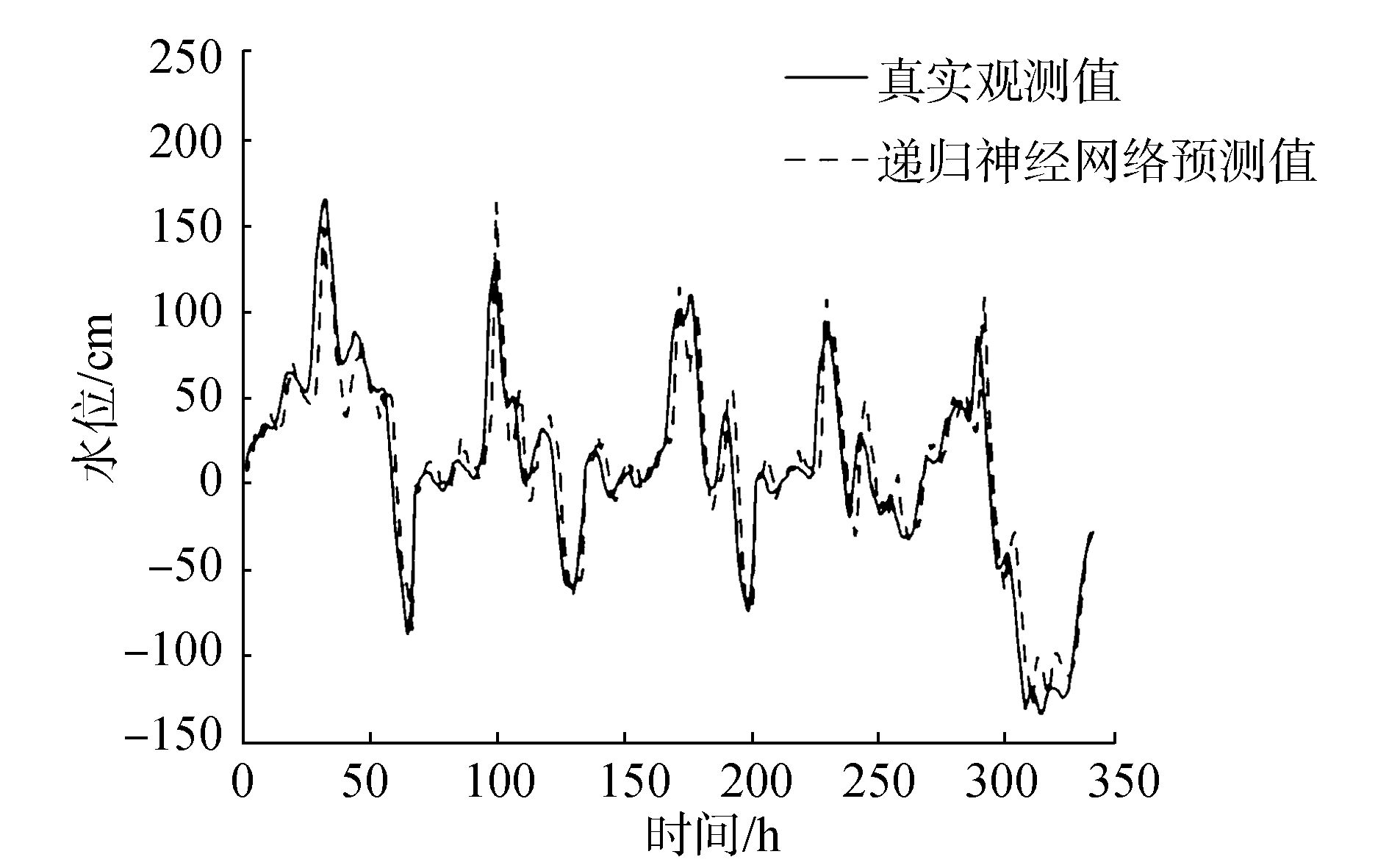
本文选取了2008~2013年记录到的31个增水过程当作训练数据,训练得到递归神经网络的参数,并将2014年记录的5个增水过程当作测试数据,对3 h后的水位进行预测。如图 5所示,实线表示真实的观测值,虚线表示用训练好的递归神经网络预测出的结果。为了便于分析实验结果,将测试数据中的5个增水过程串联在一起进行显示。为了更好地验证递归神经网络对风暴潮增水预测的效果,图 6展示了使用BP神经网络进行预测的结果。BP神经网络采用与递归神经网络一样的结构,也是3个输入层单元,15个隐含层单元。
|
图 5 递归神经网络3 h预测结果 Fig.5 The prediction of recurrent neural network for 3 hour later |

|
图 6 BP神经网络3 h预测结果 Fig.6 The prediction of back propagation network (multilayer perceptron) for 3 hour later |
从图 5和图 6可以看出,相比于BP神经网络,递归神经网络的3 h预测结果更加接近真实的观测值。对于增水过程中的峰值预报,递归神经网络的预测结果较BP神经网络偏离得更小。整体而言,BP神经网络的预测结果波动很大,而递归神经网络的预测结果则相对平滑。
本文采用平均绝对误差(mean absolute error, MAE)来定量地评价预测误差,如下式所示:
| ${\rm{MAE = }}\frac{1}{N}\sum\limits_i^N {\left| {{y_i} - {{\hat y}_i}} \right|} $ |
式中yi和
从表 1中可以看出,随着预测时间的延长,递归神经网络和BP神经网络的预测误差是逐渐升高的。但不管预测时间是多少,递归神经网络的预测精度都优于BP神经网络的预测精度。从中可以看出,相当于BP神经网络,递归神经网络更加适合于对风暴潮增水进行预测。
| 表 1 2014年增水过程预测的平均绝对误差 Tab.1 The mean absolute error of the prediction of storm surge in 2014 |
本文采用递归神经网络对风暴潮增水进行预测。传统的BP神经网络只能用来提取静态数据之间的关系,而由于增添了反馈连接,递归神经网络就更加适合用于时序数据的处理。本文在真实的数据集上进行了验证,结果表明,相对于BP神经网络,递归神经网络能更好地对风暴潮增水进行预测,误差精度更低。
在实验中发现,随着预测时间的增加,递归神经网络预测误差会逐步加大,并且预测结果与真实测量值的相位差会越来越大。如何采取有效的措施对这一现象进行缓解,是作者下一步需要研究的工作。
| [1] |
王喜年. 风暴潮预报知识讲座[J]. 海洋预报, 2001, 18(1): 73-78. DOI:10.11737/j.issn.1003-0239.2001.01.010 ( 0) 0)
|
| [2] |
高清清, 曹兵, 高鑫鑫, 等. 南通沿海台风风暴潮分析及其经验预报初探[J]. 海洋预报, 2014, 31(1): 29-35. GAO Qingqing, CAO Bing, GAO Xinxin, et al. Analysis of the typhoon storm surge in the Nantong coastal zone and the forecasting formulas[J]. Marine forecasts, 2014, 31(1): 29-35. (  0) 0)
|
| [3] |
曾德美. 青岛港风暴潮经验统计预报[J]. 海洋预报, 1992, 9(3): 66-73. ZENG Demei. A statistical forecasting of storm surge in qingdao harbor[J]. Marine forecasts, 1992, 9(3): 66-73. DOI:10.11737/j.issn.1003-0239.1992.03.009 (  0) 0)
|
| [4] |
谢亚力, 黄世昌. 钱塘江河口风暴潮经验预报[J]. 海洋预报, 2006, 23(1): 54-58. XIE Yali, HUANG Shichang. Effects on watercourse and hydrological factor in downstrean nanxi river due to water diversion[J]. Marine forecasts, 2006, 23(1): 54-58. DOI:10.11737/j.issn.1003-0239.2006.01.009 (  0) 0)
|
| [5] |
朱建荣, 朱首贤. ECOM模式的改进及在长江河口、杭州湾及邻近海区的应用[J]. 海洋与湖沼, 2003, 34(4): 364-373. ZHU Jianrong, ZHU Shouxian. Improvement of the ECOM with application to the changjiang river estuary, Hangzhou bay and adjacent waters[J]. Oceanologia Et limnologia sinica, 2003, 34(4): 364-373. DOI:10.11693/hyhz200304003003 (  0) 0)
|
| [6] |
黄世昌, 李玉成, 赵鑫, 等. 浙江沿海超强台风作用下风暴潮增水数值分析[J]. 海洋工程, 2008, 26(3): 58-64. HUANG Shichang, LI Yucheng, ZHAO Xin, et al. Numerical analysis of storm surge due to a super typhoon in coastal region of Zhejiang province[J]. The ocean engineering, 2008, 26(3): 58-64. (  0) 0)
|
| [7] |
王培涛, 于福江, 刘秋兴, 等. 福建沿海精细化台风风暴潮集合数值预报技术研究及应用[J]. 海洋预报, 2010, 27(5): 7-15. DOI:10.11737/j.issn.1003-0239.2010.05.002 ( 0) 0)
|
| [8] |
LEE T L. Neural network prediction of a storm surge[J]. Ocean engineering, 2006, 33(3): 483-494. ( 0) 0)
|
| [9] |
RAJASEKARAN S, GAYATHRI S, LEE T L, et al. Support vector regression methodology for storm surge predictions[J]. Ocean engineering, 2008, 35(16): 1578-1587. DOI:10.1016/j.oceaneng.2008.08.004 ( 0) 0)
|
| [10] |
WILLIAMS R J, ZIPSER D. A learning algorithm for continually running fully recurrent neural networks[J]. Neural computation, 1989, 1(2): 270-280. DOI:10.1162/neco.1989.1.2.270 ( 0) 0)
|
| [11] |
ELMAN J L. Finding structure in time[J]. Cognitive science, 1990, 14(2): 179-211. DOI:10.1207/s15516709cog1402_1 ( 0) 0)
|
| [12] |
BOTVINICK M M, PLAUT D C. Short-term memory for serial order:a recurrent neural network model[J]. Psychological review, 2006, 113(2): 201-233. DOI:10.1037/0033-295X.113.2.201 ( 0) 0)
|
| [13] |
SAINATH T N, KINGSBURY B, SAON G, et al. Deep convolutional neural networks for large-scale speech tasks[J]. Neural networks, 2015, 64: 39-48. DOI:10.1016/j.neunet.2014.08.005 ( 0) 0)
|
| [14] |
SARIKAYA R, HINTON G E, DEORAS A, et al. Application of deep belief networks for natural language understanding[J]. IEEE transactions on audio, speech, and language processing, 2014, 22(4): 778-784. DOI:10.1109/TASLP.2014.2303296 ( 0) 0)
|
| [15] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E, et al. ImageNet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems. Nevada, America, 2012:1097-1105.
( 0) 0)
|
| [16] |
SVOZIL D, KVASNICKA V, POSPICHAL J, et al. Introduction to multi-layer feed-forward neural networks[J]. Chemometrics and intelligent laboratory systems, 1997, 39(1): 43-62. DOI:10.1016/S0169-7439(97)00061-0 ( 0) 0)
|
| [17] |
HORNIK K, STINCHCOMBE M B, WHITE H, et al. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366. DOI:10.1016/0893-6080(89)90020-8 ( 0) 0)
|
| [18] |
RUMELHART D E, HINTON G E, WILLIAMS R J, et al. Learning representations by back-propagating errors[J]. Nature, 1988, 323(6088): 533-536. ( 0) 0)
|
| [19] |
KOSMATOPOULOS E B, POLYCARPOU M M, CHRISTODOULOU M A, et al. High-order neural network structures for identification of dynamical systems[J]. IEEE transactions on neural networks, 1995, 6(2): 422-431. DOI:10.1109/72.363477 ( 0) 0)
|
| [20] |
WERBOS P J. Backpropagation through time:what it does and how to do it[J]. Proceedings of the IEEE, 1990, 78(10): 1550-1560. DOI:10.1109/5.58337 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


