萤火虫算法(firefly algorithm,FA)是受自然界中萤火虫发光特性的启发, 由剑桥学者Yang于2008年提出的一种群体智能随机优化算法[1-5]。在多个科学与工程领域中,萤火虫算法已得到成功的应用[6-9],虽然FA表现出了良好的性能,但在一些问题的优化上,萤火虫算法依然存在收敛速度慢、解的精度不高、容易陷入局部最优等不足。近年来,很多学者已经进行了多角度的改进。文献[10]为了解决萤火虫算法过早地收敛和陷入局部最优的不足,利用广义反向学习策略来优化萤火虫算法。文献[11]采用正交学习策略改进FA算法, 利用精英萤火虫来构造指导向量, 通过指导向量引导群体向全局最优区域移动。文献[12]提出基于蛙跳的萤火虫算法, 在原始的FA算法中引入蛙跳算法中的分群。同时,为了加强算法的局部开发能力,引入了模拟退火的思想。该算法对于高维多模态函数的优化问题,表现得还不够理想。文献[13]提出了一种基于多种群学习机制的萤火虫优化算法,把萤火虫分为不同的子群,同时,子群建立学习机制,实现不同子群间的信息交流,完成局部和全局的寻优。文献[14]引入模式搜索思想,把FA算法与模式搜索相结合,FA算法具有较强的全局搜索能力,模式搜索具有较好的局部搜索能力,利用两者的优势来提高FA算法的性能。文献[15]针对高维问题,提出了多维反向学习的萤火虫算法,用反向学习策略初始化萤火虫种群。同时,用基于多维的方法更新不同维度上萤火虫的位置。算法在收敛速度和精度上比原始萤火虫算法更优。
以上文献虽然对FA算法做了很好的改进,但是在收敛速度和精度上还不够理想,为了更好地提高FA算法的收敛速度和收敛精度,本文基于文献[16]利用精英反向学习策略来改进差分演化算法的思想,提出了一种精英反向学习的萤火虫算法,在文献[16]中,通过设置一个参数来选取精英个体,而本文根据原解和反向解适应度值的大小选取精英个体,这样能更充分地利用精英群体的良好信息,提高算法的收敛速度。同时,本文采用了差分演化策略(differential evolutionary mutation)来增强算法的局部搜索能力。最后,为了增强和平衡算法的开发能力,本文提出了一种线性递减的自适应步长。在5个标准测试函数上进行实验,并和多个改进的FA算法进行实验对比。结果表明,本文算法在收敛速度和收敛精度上更好。
1 萤火虫算法(FA)FA是受自然界中萤火虫个体通过发光来吸引同伴求偶或觅食行为的启发而提出的一种元启发式算法[1-2],萤火虫之间相互吸引以及位置迭代更新的过程是搜索和优化的过程。寻找最亮萤火虫的问题是求解最优值的问题,不断用最好的位置替换较差的位置来完成整个搜索过程。在一定的搜索区域内所有发光弱的萤火虫向发光强的萤火虫移动,从而实现位置寻优[17]。每个萤火虫被看作一个个体,个体主要有“位置、亮度、吸引度”等属性,有两个重要的影响因子,即亮度I和吸引度β。亮度高说明其所处位置好,并吸引亮度低的个体向其靠近。吸引度高则萤火虫移动的距离大。从FA开始, 萤火虫的个体随机地分布在指定的局域内,个体的亮度由目标函数决定。
设I0表示萤火虫个体的固有亮度,γ为介质的光亮度吸收系数,rij为任意两个个体i和j的相对距离(一般使用欧氏距离),β0为萤火虫个体固有吸引度,随距离r变化的个体光强度I表示为
| $ I = {I_0}{{\rm{e}}^{ - \gamma {r^2}}} $ | (1) |
则萤火虫i与萤火虫j之间的相互吸引力计算公式为
| $ \beta = {\beta _0} \times {{\rm{e}}^{ - \gamma {r_{ij}}}} $ | (2) |
设xi(t)和xj(t)分别表示萤火虫i和j在t时刻的位置,则两者之间的距离计算公式为
| $ {r_{ij}} = {\left\| {{\mathit{\boldsymbol{x}}_i}\left( t \right) - {\mathit{\boldsymbol{x}}_j}\left( t \right)} \right\|_2} = \sqrt {\sum\limits_{m = 1}^d {{{\left( {{x_{im}} - {x_{jm}}} \right)}^2}} } $ | (3) |
萤火虫i向萤火虫j移动,其位置更新方程为
| $ {x_{i + 1}}\left( {t + 1} \right) = {x_i}\left( t \right) + \beta \left( {{x_j}\left( t \right) - {x_i}\left( t \right)} \right) + \alpha \left( {{\rm{rand}} - \frac{1}{2}} \right) $ | (4) |
式中:xi+1(t+1)表示萤火虫i在t+1时刻的位置;α∈[0, 1],表示步长因子。
2 精英反向学习的萤火虫算法 2.1 反向学习策略反向学习策略是近年来计算智能领域出现的新概念[18-19],其主要思想是对一个问题的可行解,求其反向解,并对原解和反向解进行评估,从中选出较优的解作为下一代个体。其中反向点和反向解的定义如下。
定义1 反向点(opposite point,OP)[18]。设x=(x1, x2, …, xD)是D维空间中的一个点,且x1, x2, …, xD∈R,xj∈[aj, bj],则x对应的反向点x*=(x1*, x2*, …, xD*)定义为
| $ x_j^ * = {a_j} + {b_j} - {x_j} $ | (5) |
定义2 动态反向学习策略(dynamic opposition based learning,DOBL)。[18]设xi(t)=(xi1(t), xi2(t), …, xiD(t))为问题第t代的一个可行解,xij(t)是其j维上的分量,xij*(t)是xij(t)对应的反向解,则xi*(t)是xi(t)对应的反向解, 其中
| $ x_{ij}^ * \left( t \right) = k\left( {{a_j}\left( t \right) + {b_j}\left( t \right)} \right) - {x_{ij}}\left( t \right) $ | (6) |
式中:a(t)=min(xij(t)),b(t)=max(xij(t))为当前搜索区域的最小值和最大值,其随着迭代的改变,而发生变化;i∈[1, n],j∈[1, D];n是种群大小;D是解空间的维数;k是介于0~1的随机数。
2.2 精英反向学习反向解的引入,可以扩大算法的搜索区域,但对那些原解适应度值大于反向解适应度值的个体,对其进行反向区域的搜索,浪费时间,则应加强其领域搜索。而对原解适应度值小于反向解适应度值的个体,对其进行反向区域的搜素价值要高于其领域的开发价值。因此,本文将原解适应度值小于反向解适应度值的个体作为研究对象,求其反向解,既可以扩大搜素区域,也能有效避免盲目搜索带来的时间浪费。
同时,本文为了提高算法的收敛速度,首先在当前解所构造的空间中,求所有当前解的反向解;然后,通过比较适应度值,选出那些原解适应度值大于反向解适应度值的个体组成精英群体;最后,在精英群体构造的新的搜索空间上,再求原解适应度值小于反向解适应度值的个体的反向解。如果算法能收敛到全局最优解,则精英群体所形成的搜索区间必将收敛到最优解所在的区域[16],这样充分利用了精英群体的有效信息,在精英群体所构成的动态定义区间上生成反向解,引导搜索向最优解靠近。
定义3 精英(elite)。设xi(t)=(xi1, xi2, …, xiD)是第t次迭代的一个解,其反向解为xi*(t),f(x)为目标函数。当f(xi(t))≥f(xi*(t))时,称xi(t)为第t次迭代的精英个体,记为Ni(t);当f(xi(t)) < f(xi*(t))时,称xt(t)为第t次迭代的普通个体,记为Qi(t)。若精英群体的规模为p(1 < p≤n, n为解的总个数)时,则p个精英个体可表示为{N1(t), N2(t), …, Np(t)}⊆{x1(t), x2(t), …, xn(t)}。
定义4 精英反向解(elite opposite solution)[18]。设xij为普通个体xi在j维上的值,则其反向解可定义为
| $ x_{ij}^ * \left( t \right) = k\left( {{a_j}\left( t \right) + {b_j}\left( t \right)} \right) - {x_{ij}}\left( t \right) $ | (7) |
式中:k是介于0~1的随机数;aj(t)= min(N1j(t), N2j(t), …, Npj(t));bj(t)=max(N1j(t), N2j(t), …, Npj(t))。[aj(t), bj(t)]为精英群体所构造的区间,当反向解越过边界[aj(t), bj(t)]时,可以用下列方式进行重置:
| $ \left\{ \begin{array}{l} x_{ij}^ * = {a_j}\left( t \right),\;\;\;\;\;x_{ij}^ * < {a_j}\left( t \right)\\ x_{ij}^ * = {b_j}\left( t \right),\;\;\;\;\;x_{ij}^ * > {b_j}\left( t \right) \end{array} \right. $ | (8) |
在FA中,群体中的最优个体xbest引导群体向最优方向移动,如果xbest陷入局部最优,群体的移动终止,即收敛到局部最优,则群体无法到达全局最优。因此,本文为了求得全局最优解,引入差分变异策略,对xbest进行变异操作,使其陷入局部最优的概率减小。
本文要对最优个体进行变异操作,使其跳出局部最优的概率增大,因此选择“DE/best/1”作为变异操作,公式为
| $ {c_{ij}} = {x_{{\rm{best}},j}} + F \cdot \left( {{x_{{n_1},j}} - {x_{{n_2},j}}} \right) $ | (9) |
式中:xbest, j为最优个体的第j维;F是缩放系数;n1、n2是[1, n]上两个互不相同的随机整数,代表不同个体的下标;j是维度;cij是变异后的值。
将变异后的个体和父代个体进行如下交叉操作:
| $ {{\bar x}_{{\rm{best}},j}} = \left\{ \begin{array}{l} {c_{ij}},\;\;\;\;\;\;{\rm{rand}}\left[ {0,1} \right] \le {\rm{CR}}\;或者\;j = {\rm{rand}}\left( {1,{\rm{D}}} \right)\\ {x_{{\rm{best}},j}},\;\;\;\;其他 \end{array} \right. $ | (10) |
式中:xbest, j为新生成个体的第j维;rand[0, 1]是[0, 1]的随机数;CR是交叉概率;rand(1, D)是[1, D]的一个随机整数;参数F、CR分别设为1和0.1。
2.4 自适应步长在原始萤火虫算法FA中,步长因子α在每次迭代时保持不变。但是当α取较大的值时,增强了算法的全局搜索能力,降低了算法的收敛速度和搜索的精度;当α取较小的值时,有利于算法的局部搜索,提高了搜索精度和算法的收敛速度。在算法迭代前期,较大的α有利于算法的全局搜索;在后期,较小的α显得更有利。因此本文对α采用动态递减的方式,计算公式为
| $ {\alpha _{t + 1}} = {\alpha _t} \cdot \left( {\frac{{T - \frac{t}{{10}}}}{T}} \right),t = 1,2, \cdots ,T $ | (11) |
式中t为迭代次数。
2.5 EOFA算法描述EOFA算法流程如下。
输入 目标函数和搜索空间;
输出 全局最优解和最优位置。
1) 初始化参数m, n, T, α, β, γ,在[m, n]上生成初始种群xi(i=1, 2, …, n)。
2) 执行EOFA算法搜索。
3) 把xi(t)(i=1, 2, …, n)带入目标函数,计算函数值,把目标函数的值作为每个个体的亮度值Ii(t)。
4) 在[m, n]生成xi(t)的反向解xi*(t),并计算亮度Ii*(t)。对Ii(t)和Ii*(t)进行比较,if Ii(t)>Ii*(t),则xi(t)为精英个体Ni(t),记精英群体大小为p(p>1, i=1,2,…,p)。设精英个体的区间范围为[aj(t), bj(t)](若精英群体的规模小于2, 则在xi(t)(i=1, 2, …, n)构成的区间上求xi(i=1, 2, …, n)的反向解)。elsexi(t)是普通个体,普通群体大小为n-p。
5) 用式(7)在精英个体构成的区间[aj(t), bj(t)]上计算普通群体的反向解xi′(t)(i=1, …, n-p)。
6) 精英群体和普通群体的反向解群体构成当前新种群,计算新种群的亮度,并进行排序,选出最优的个体xbest(t)。
7) 用式(3)计算每个个体i和最优个体xbest(t)之间的距离Rij(t)。
8) 用式(2)计算吸引力βij(t)。个体i向最优个体xbest(t)移动,用公式(6)更新位置xinew(t)。
9) 用式(11)计算α(t),并用式(9)、(10)对最优个体进行位置扰动。
10)算法搜索结束,输出全局最优解和最优位置。
若种群的规模为n,空间维度为D, 则种群初始化的时间复杂度为O(nD);从迭代开始到结束的整个过程中,迭代的次数为t, 其中3)是计算种群的亮度,复杂度为O(nDt);4)~9)是建立新的种群,并进行位置的更新,复杂度为O((6n-p)·Dt),p(p≤n)是精英群体的规模。因此本文算法的时间复杂度为O(nDt)。
3 实验仿真及分析 3.1 测试函数在仿真实验中,本文采用下列5个常用的标准测试函数对算法进行测试。
1) Sphere函数
| $ {f_1}\left( x \right) = \sum\limits_{i = 1}^d {x_i^2,{x_i} \in \left( { - 5.12,5.12} \right)} $ |
Sphere函数为多维单峰值函数,在点x=(0, 0, …, 0)处取得极小值0。
2) Rosenbrock函数
| $ \begin{array}{*{20}{c}} {{f_2}\left( x \right) = \sum\limits_{i = 1}^d {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right],} }\\ {{x_i} \in \left( { - 2.048,2.048} \right)} \end{array} $ |
Rosenbrock函数为多维病态二次函数,在点x=(1, 1, …, 1)处取得全局极小值0。
3) Ackley函数
| $ \begin{array}{*{20}{c}} {{f_3}\left( x \right) = - 20{\rm{e}}\sqrt[{ - 0.2}]{{\frac{1}{d}\sum\limits_{i = 1}^d {x_i^2} }} - {\rm{e}}\frac{1}{d}\sum\limits_{i = 1}^d {\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} + 22.7128,}\\ {{x_i} \in \left( { - 32.7,32.7} \right)} \end{array} $ |
Ackley函数为多维多峰值函数,在点x=(0, 0, …, 0)处取得全局极小值0。
4) Griewank函数
| $ \begin{array}{*{20}{c}} {{f_4}\left( x \right) = \sum\limits_{i = 1}^d {\frac{{x_i^2}}{{4000}}} - \prod\limits_{i = 1}^d {\cos \left( {\frac{{{x^i}}}{{\sqrt i }}} \right) + 1} ,}\\ {{x_i} \in \left( { - 600,600} \right)} \end{array} $ |
Griewank函数为多维多峰值函数,在点x=(0, 0, …, 0)处取得全局极小值0。
5) Rastrigin函数
| $ \begin{array}{*{20}{c}} {{f_5}\left( x \right) = 10d + \sum\limits_{i = 1}^d {\left[ {x_i^2 - 10\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} \right]} ,}\\ {{x_i} \in \left( { - 5.12,5.12} \right)} \end{array} $ |
Rastrigin函数为多维多峰值函数,在点x=(0, 0, …, 0)处取得全局极小值0。
3.2 EOFA算法的测试结果实验环境为:Inter Core(TM) i5-2450M CPU@2.50 GHz,内存4 GB,Window7操作系统,MATLAB 7.8.0版本。分别选取标准的FA算法[1],LFA算法[20],MFA算法[21]与本文提出的EOFA算法在5种标准的测试函数上进行实验比较,种群规模n取40,初始α取值为0.98。维度D取10和30,γ=1,MFA算法中方向向量的个数m取30,其他参数分别取T=1 000, β=1。分别记录4种算法迭代1 000次并在测试函数上独立运行40次的最优值、最差值和平均值,结果如表 1所示。
| 表 1 4种算法的实验结果 Tab.1 Experimental results of four algorithms |
FA是原始的萤火虫算法。LFA是根据Levy分布来设置一种随机步长对传统萤火虫算法进行改进,其主要优点是算法收敛到局部最优的概率降低。MFA算法是从随机生成的方向向量中选择使种群进化到最优的方向向量,方向向量的个数对算法的性能有很大的影响,数量越大,算法收敛性越好。由表 1可知,EOFA、LFA和MFA算法在10维和30维函数上都优于FA算法。本文提出的EOFA算法在5种测试函数上的函数值都小于FA、LFA、MFA算法在测试函数上的值,即EOFA算法的收敛性更好,在每个测试函数上EOFA算法的求解精度比其他3种算法都高。
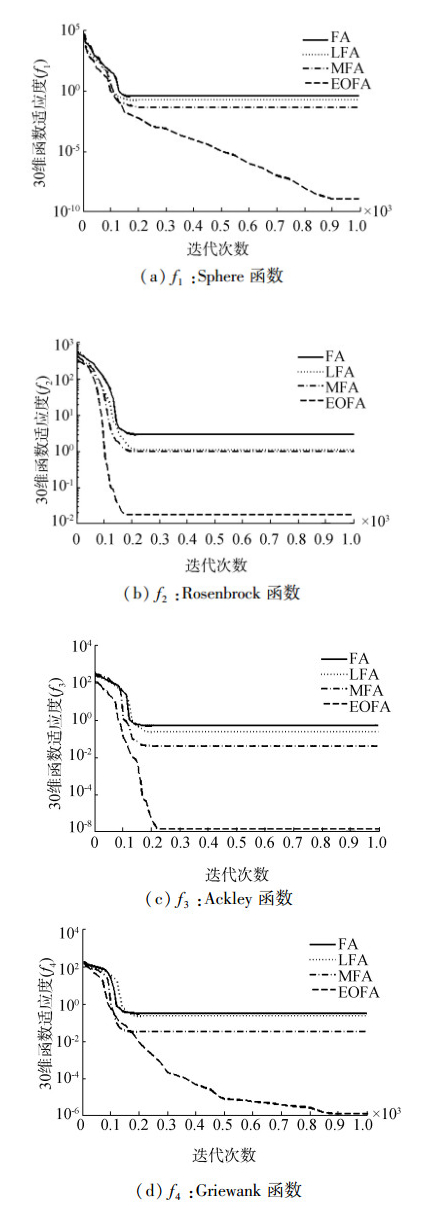
为了更好地验证EOFA算法的有效性,本文用图描述4种算法的收敛性,由于受篇幅的限制,仅给出4个代表性的函数收敛曲线图,结果如图 1、2所示。

|
图 1 维度为10时算法收敛曲线对比 Fig.1 Comparison of convergent graphs for a dimensionality of 10 |
|
图 2 维度为30时算法收敛曲线对比 Fig.2 Comparison of convergent graphs for a dimensionality of 30 |
由图 1、2可以看出,对于每一个测试函数,EOFA算法总比其他3种算法表现出更好的收敛性,因为它构建了动态的精英反向解区间,同时,精英群体的规模自适应的改变,使普通个体向最优个体移动的速度加快。对于函数f1、f4,当函数维度为10和30时,FA、LFA、MFA这3种算法出现了早熟,而EOFA算法继续收敛,且收敛速度比其他3种算法都快。对于函数f2、f3虽然4种算法都出现了早熟,但EOFA算法解的精确度比其他算法更好。当维数从10增加到30时,4种算法的性能都有所下降,但EOFA算法的性能优于其他3种算法。EOFA算法具有较优性能的原因是:首先EOFA算法采用反向学习策略,构造精英群体和普通群体,扩大了搜索范围,通过生成每个个体的反向解,增加解的多样性来提高种群多样性。同时加入了差分演化变异策略,使其跳出局部最优的概率增大。最后,为了增强算法开发能力,采用递减的自适应步长。
4 结束语本文提出的精英反向学习萤火虫算法(EOFA),通过精英反向学习策略生成当前解的反向解,评估当前解和反向解,构建精英群体和普通群体,增加了群体的多样性;在动态的精英区间上求普通群体的反向解,提高算法的收敛速度。差分演化变异策略对最优个体进行变异操作,对其领域空间进行搜索,增强了EOFA的局部开采能力。同时,采用自适应步长,提高和平衡算法的开发能力。通过实验结果得出,EOFA算法在解的精度和收敛速度上都表现出更好的性能。本文只考虑了最优个体对每个个体的影响,下一步工作是将个体邻域的信息加入,进一步提高算法性能。
| [1] |
YANG X S. Firefly algorithms for multimodal optimiz-ation[C]//Stochastic Algorithms:Foundations and Applic-ations. Sapporo, Japan, 2009, 5792:169-178.
( 0) 0)
|
| [2] |
朱书伟, 周治平, 张道文. 融合并行混沌萤火虫算法的K-调和均值聚类[J]. 智能系统学报, 2015, 37(6): 342-347. ZHU Shuxin, ZHOU Zhiping, ZHANG Daowen. Kharm-onic means clustering merged with parallel chaotic firefly algorithm[J]. CAAI transactions on intelligent systems, 2015, 37(2): 342-347. (  0) 0)
|
| [3] |
赵杰, 雷秀娟, 吴振强. 基于最优类中心扰动的萤火虫聚类算法[J]. 计算机工程与科学, 2015, 37(2): 342-347. ZHAO Jie, LEI Xiujuan, WU Zhenqiang. A clustering al-gorithm for Fireflies based on optimal class center pert-urbation[J]. Computer engineering & science, 2015, 37(2): 342-347. (  0) 0)
|
| [4] |
莫愿斌, 马彦追, 郑巧燕. 单纯形法的改进萤火虫算法及其在非线性方程组求解中的应用[J]. 智能系统学报, 2014, 9(6): 747-755. MO Yuanbin, MA Yanzhui, ZHENG Qiaoyan. Improved firefly algorithm based on simplex method and its appli-cation in solving non-near equation groups[J]. CAAI tr-ansactions on intelligent systems, 2014, 9(6): 747-755. (  0) 0)
|
| [5] |
HORNG M H. Vector quantization using the firefly al-gorithm for image compression[J]. Expert systems with applications, 2012, 39(1): 1078-1091. DOI:10.1016/j.eswa.2011.07.108 ( 0) 0)
|
| [6] |
MARICHELVAM M K, PRABAHARAN T, YANG XS. A discrete firefly algorithm for the multi-objective hy-brid flow shop scheduling problems[J]. IEEE transactio-ns on evolutionary computation, 2014, 18(2): 301-305. DOI:10.1109/TEVC.2013.2240304 ( 0) 0)
|
| [7] |
YANG X S, HOSSEINI S S S, GANDOMI A. Firefly algorithm for solving non-convex economic dispatch pr-oblems with valve loading effect[J]. Applied soft com-puting, 2012, 12(3): 1180-1186. DOI:10.1016/j.asoc.2011.09.017 ( 0) 0)
|
| [8] |
SENTHILNATH J, OMKAR S, MANI V. Clustering using firefly algorithm:performance study[J]. Swarm and evolutionary computation, 2011, 1(3): 164-171. DOI:10.1016/j.swevo.2011.06.003 ( 0) 0)
|
| [9] |
FALCON R, ALMEID M, NAYAK A. Fault identification with binary adaptive fireflies in parallel and distrib-uted systems[C]//2011 IEEE Congress on Evolutionary Computation(CEC).New Orleans, USA, 2011:1359-1366.
( 0) 0)
|
| [10] |
YU S, ZHU S, MA Y, et al. Enhancing firefly algorit-hmusing generalized opposition based learning[J]. Com-puting, 2015, 97(7): 741-754. ( 0) 0)
|
| [11] |
周凌云, 丁立新, 何进荣. 精英正交学习萤火虫算法[J]. 计算机科学, 2015, 42(10): 211-216. ZHOU Lingyun, DING Lixin, HE Jinrong. Elite-orth-ogonal learning firefly algorithm[J]. Computer science, 2015, 42(10): 211-216. (  0) 0)
|
| [12] |
李洋. 蛙跳萤火虫算法及其在含风电场的电力系统调度中的应用[D]. 上海: 华东理工大学, 2013. LI Yang. Leapfrog firefly algorithm and application in di-spatch of power system containing wind farm[D]. Shanghai:East China University of Science and Technol ogy, 2013. (  0) 0)
|
| [13] |
符强, 童楠, 赵一鸣. 一种基于多种群学习机制的萤火虫优化算法[J]. 计算机应用研究, 2013, 30(12): 3600-3603. FU Qiang, TONG Nan, ZHAO Yiming. Firefly algorithm based on multi-grouplearning mechanism[J]. Application research of computers, 2013, 30(12): 3600-3603. DOI:10.3969/j.issn.1001-3695.2013.12.021 (  0) 0)
|
| [14] |
FISTER I, JR F, YANG X S, et al. A comprehensivereview of firefly algorithms[J]. Swarm and evolutionary computation, 2013, 13(1): 34-46. ( 0) 0)
|
| [15] |
VERMA O P, AGGARWAL D, PATODI T. Opposition and dimensional based modified firefly algorithm[J]. Ex-pert-systems with applications an international journal, 2016, 44(C): 168-176. ( 0) 0)
|
| [16] |
汪慎文, 丁立新, 谢大同. 应用精英反向学习策略的混合差分演化算法[J]. 武汉大学学报:理学版, 2013, 59(3): 111-116. WANG Shenwen, DING Lixin, XIE Datong. A hybrid differential evolution with elite opposition-based learning[J]. Journal of Wuhan university:natural science edition, 2013, 59(3): 111-116. (  0) 0)
|
| [17] |
程美英, 倪志伟, 朱旭辉. 萤火虫优化算法理论研究综述[J]. 计算机科学, 2015, 42(4): 19-24. CHENG Meiying, NI Zhiwei, ZHU Xuhui. Over-view on glow-worm swarm optimization or firefly algorithm[J]. Computer science, 2015, 42(4): 19-24. DOI:10.11896/j.issn.1002-137X.2015.04.002 (  0) 0)
|
| [18] |
汪慎文, 丁立新, 谢大同. 应用反向学习策略的群搜索优化算法[J]. 计算机科学, 2012, 39(9): 183-187. WANG Shenwen, DING Lixin, XIE Datong. Group search optimizer applying opposition-based learning[J]. Computer science, 2012, 39(9): 183-187. (  0) 0)
|
| [19] |
周新宇, 吴志健, 王晖, 等. 一种精英反向学习的粒子群优化算法[J]. 电子学报, 2013, 41(8): 1647-1652. ZHOU Xinyu, WU Zhijian, WANG Hui, et al. A particle swarm optimization algorithm based on elite reverse learning[J]. Sinica Acta electronica, 2013, 41(8): 1647-1652. (  0) 0)
|
| [20] |
YANG XS. Firefly Algorithm Lévy flights and global optimization[C]//Research and Development in Intelligent Systems XXVI. London, Springer, 2010:209-218.
( 0) 0)
|
| [21] |
TILAHUN S L, HONG C O. Modified firefly algorithm[J]. Journal of applied mathematics, 2012, 2012(12): 2428-2439. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


