在实际生活以及各种工业领域中都会遇到各种多个目标彼此冲突,且在一定条件约束下,但又要求得优化结果的问题,这一类问题被称为多目标优化问题。为了解决这个问题,近年来一些国内外学者提出了许多基于智能进化计算的求解算法,取得了显著的成果,并将其应用在了科学研究和工程方面。第1代的多目标优化算法是以Fonseca等[1]于1993年提出的多目标遗传算法MOGA(multi-objective genetic algorithm)、Srinivas等[2]提出的非支配排序遗传算法NSGA(non-dominated sorting genetic algorithm)、Horn等[3]提出的小生境Pareto多目标标优化遗传算法NPGA (niched pareto genetic algorithm)为主。第2代多目标优化算法主要以精英保留机制为特征,在20世纪末和21世纪初相继被提出:Zitzler等[4]于1999年提出加强Pareto进化算法(strength pareto evolutionary algorithm,SPEA),3年之后, 他们提出了SPEA改进版本SPEA2;Erichson等[5]于2001年提出了NPGA的改进版本NPGA2;经典且效率极高的NSGA-Ⅱ算法于2002年由Deb等[6]通过对NSGA进行改进而提出。
膜计算(membrane computing)是自然计算的新分支,旨在从生命细胞的结构与功能以及组织和器官等细胞群的协作中抽象出计算模型[7]。膜计算又被称为膜系统或P系统,膜计算由欧洲科学院院士Paun于1998年提出,由于其具有分布式和并行计算的能力,目前在将膜计算理论应用于多目标优化问题上获得了一些研究成果。Zaharie等[8]于2009年通过对比分布式演化算法和膜算法的异同,受膜算法的启发提出了运用于求解连续优化问题的分布式演化算法;Liu等[9]提出将遗传算法引入到膜算法,利用遗传算法的交叉与变异机制,该算法求解ZDT系列优化问题表现出了较好的求解能力;Zhang等[10]提出了将差分演化与P系统相结合的算法,并将其运用于多目标优化问题上。
受到膜计算理论启发,本文提出了一种结合膜系统理论的多目标优化算法,即基于P系统的遗传算法(P-genetic algorithm,P-GA)。本文采用的膜系统只具有表层膜和基本膜,将一定数量的种群放入表层膜中,然后经过非支配排序后分配到基本膜中。并在基本膜中运用遗传机制来求解多目标优化问题的非支配解集,在表层膜中引入NSGA-Ⅱ算法,以此来维持非支配解集的多样性,采用KUR和ZDT系列多目标测试函数来进行仿真实验,得出的非支配解集能够较好地逼近真实的Pareto前沿。本文参考了文献[11]的设计思路,不同点在于,基本膜中利用通信规则并将交叉与变异的操作进行了改变。
1 多目标优化问题和膜计算理论 1.1 多目标优化问题的数学描述多目标优化问题有很多种表示方式,用数学方式描述比较直观,便于理解。不失一般性的描述为
| $ \left\{ \begin{array}{l} F\left( x \right) = {\rm{min}}\{ {f_1}\left( x \right), {f_2}\left( x \right), \cdots, {f_m}\left( x \right)\} \\ {\rm{s}}{\rm{.t}}\;{g_i}\left( x \right) = 0, {\rm{ }}i = 1, 2, \cdots, q\\ {h_j}\left( x \right) \ge 0, {\rm{ }}j = 1, 2, \cdots, p \end{array} \right. $ | (1) |
式(1)中有n个决策变量,x={x1, x2, …xn}∈Rn,Rn为n维决策空间;F(x)∈Rm,Rm为m维的目标空间;目标函数F(x)定义了m个由决策空间向目标空间映射的关系;gi(x)=0, i=(1, 2, …, q)描述了q个等式约束条件;hj(x)≥0, j=(1, 2, …, p)定义了p个不等式约束条件。在以上的描述基础上,给出以下几个定义。
定义1 (可行解)对于任意一个x∈Rm,且满足式(1)中所给出的约束条件,则称x为可行解
定义2 (Pareto占优)对所有满足定义1的可行解组成的集合称为可行解集合,用X表示,则X⊆Rn;假设有两个可行解xa, xb∈X,若xa与xb相比较,xa是Pareto占优的,则条件当且仅当满足:
| $ \left\{ \begin{array}{l} \forall i = 1, 2, \cdots, m, \;\;{\rm{ }}{f_i}({x_a}) \le {f_i}({x_b}) \wedge \\ \exists j = 1, 2, \cdots, m, \;\;{f_j}({x_a}) < j\left( {{x_b}} \right) \end{array} \right. $ | (2) |
记作xa < xb,也称为xa支配xb。若xa和xb之间不存在相互支配关系,则称它们之间非支配。
定义3 (Pareto最优解X*)如果存在一个X*满足¬∃x∈Rn, x < x*,则X*为Pareto最优解,也叫作非支配解;Pareto最优解集定义为所有Pareto最优解组成的集合,记作P。
定义4 (Pareto前沿)最优解集P在目标函数空间上的映射,记作PF,表示为
| $ {\rm{PF}} = \{ F({x^*}) = {\rm{min}}\{ {f_1}({x^*}), {\rm{ }}{f_2}({x^*}), \cdots, {\rm{ }}{f_m}({x^*})\} \left| {{x^*} \in P} \right.\} $ | (3) |
目前,对膜的研究主要包括细胞型、组织型和神经型3种模型[12]。本文所提出的算法是建立在细胞型膜系统上,下面介绍细胞型膜系统理论的主要内容:
| $ \prod = \{ V, T, \mu, {w_1}, {w_2}, \cdots, {w_m}, R\} $ | (4) |
根据式(4)的多元组,其中:V是字母表,V中的元素称为字符对象;T⊆V,T为输出的字母表;μ是包含m个膜的膜结构,其中m表示∏的度;wi∈V*,且i=1, 2, …, m,表示膜结构μ中第i个膜所包含的字符多重集,V*表示由V中的字符对象组成的任意多重集;R是进化规则的有限集合,进化规则是二元组;Ri(i=1, 2, …, m)对应的是膜结构μ中的区域i的进化规则集合。
细胞型膜结构如图 1所示,最外层把细胞膜结构与外界环境隔开的膜称为表层膜;每一个膜都确定一个区域,区域中包含了反应规则和多重集;对任意一个膜,若该膜区域内不包含其他的膜,即膜中无膜,则称为基本膜。
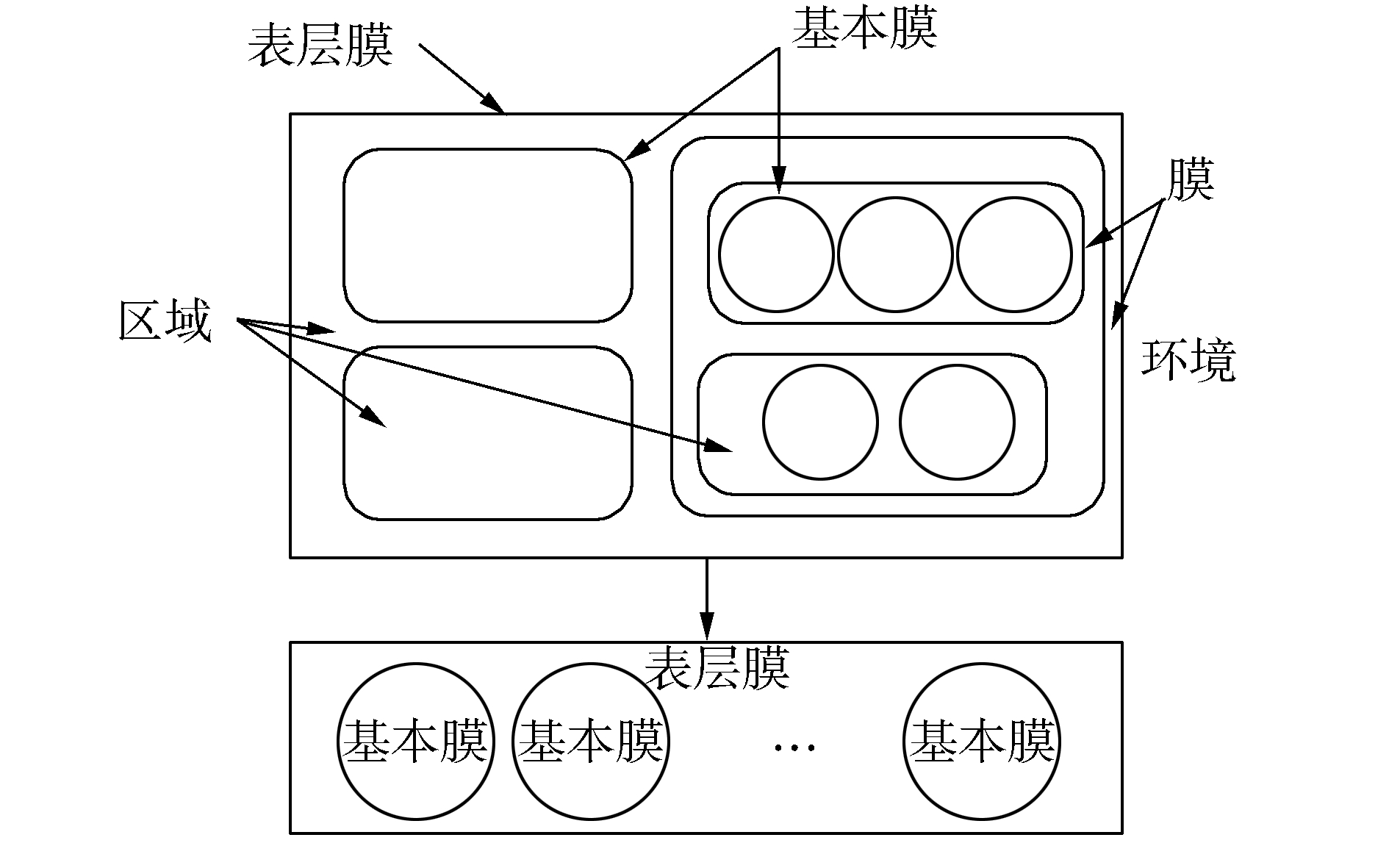
|
图 1 膜系统与其简化结构 Fig.1 Membrane system with its simplified structure |
P系统由字符对象多重集、反应规则和膜结构三部分组成[13]。在P系统中,字符对象与多重集分别对应所求多目标优化问题的解和解集,且每一个字符对象都会通过适应度函数得到一个适应度值;反应规则既是算法具体的执行,也有对细胞膜的操作,比如分裂、溶解等;膜结构的运用使算法具有了分布式和并行计算的能力[14]。在每一次的迭代,将随机产生的字符对象放入表层膜区域中,利用表层膜区域中的反应规则和通信规则进行操作;最后通过膜的溶解将多重集释放到表层膜区域中交流信息。为了降低仿真实验难度,所提算法采用的细胞型膜结构只有表层膜与基本膜,这种二层结构相较于原结构复杂度较低。
为了使算法得出的多重集有较好的多样性,故引入SGA-Ⅱ算法,利用其非支配排序和拥挤距离两种机制来获得。
遗传算法(genetic algorithm,GA)是模拟达尔文进化论(适者生存、优胜劣汰遗传机制),借鉴生物界的进化规律演化而来的随机化搜索方法。该方法具有并行性和更好的全局寻优能力[15-16]。
P-GA算法基于膜计算理论,包含了遗传机制,利用NSGA-Ⅱ算法的非支配排序和拥挤距离两种机制来设计算法,详细步骤如下。
1) 根据优化问题的约束条件,在表层膜的区域内随机生成N个字符对象(N≥i≥1),所有字符对象均为十进制编码,具体形式为
| $ {s_{i, j}} = ({s_{{\rm{max}}, j}}-{s_{{\rm{min}}, j}}) \times {\rm{rand}}() + {s_{{\rm{max}}, j}} $ | (5) |
式中:si, j表示第i个字符对象的第j维;j的范围为D≥j≥1,D表示维数;smin, j表示第j维的最小值,smax, j表示第j维的最大值;rand()为随机数函数,产生从0~1的随机数。
2) 根据所要优化问题的目标函数计算出每个字符对象的适应度值,从而完成对所有字符对象的评价。
3) 在初始化完成以后,利用表层膜的分裂规则,在表层膜内部区域分裂出m+1个基本膜,且分裂出的基本膜具有求解多目标优化问题的能力。首先,将初始化完成的m个多重集复制一份发送到第m+1个基本膜的区域中;然后,将m个多重集发送到前m个基本膜的区域中,逐一对应。具体表层膜分裂规则如式(6):
| $ {[\;]_0} \to \left[{{{[\;]}_1}, {{[\;]}_2}, \cdots, {{[\;]}_m}, {{[\;]}_{m + 1}}} \right] $ | (6) |
式中:[]0表示表层膜,[]i表示第i个基本膜。
为了使每个基本膜的内部区域都有对应的多重集,利用NSGA-Ⅱ的非支配排序机制对表层膜区域中的所有字符对象进行排序,排序标准参照2)完成适应值大小,排序结束以后再将其按照等数量划分为多个子字符多重集。具体划分的形式化表述如式(7)所示:
| $ \left\{ \begin{array}{l} \dot w = {\rm{sort}}\left( w \right)\\ \dot w = \{ {w_1}, {w_2}, \cdots, {w_m}\} \\ n = {\rm{sizeof}}\left( w \right)/m \end{array} \right. $ | (7) |
式中:w表示字符多重集;sort(w)表示对表层膜区域中的多重集进行非支配排序;wi表示第i个子字符多重集;sizeof(w)表示多重集中字符对象个数;m表示基本膜的个数;n表示每个基本膜取得字符对象个数,具体放入规则对n进行取模。
4) 对前m个基本膜用GA算法中的交叉规则进行多线程并行计算,以获得新的字符对象,而并行计算可以极大地加快求解速度,具体交叉操作为
| $ \left\{ \begin{array}{l} {S_{t + 1}}^1 = \alpha \cdot{S_t}^1 + \left( {1-\alpha } \right)\cdot{S_t}^2\\ {S_{t + 1}}^2 = \alpha \cdot{S_t}^2 + \left( {1-\alpha } \right)\cdot{S_t}^1 \end{array} \right. $ | (8) |
式中:St1表示字符对象S1第t代的值;St2表示字符对象S2第t代的值;St+11表示字符对像S1第t+1代的值;St+12表示字符对象S2第t+1代的值;α表示交叉系数,经过多次实验测试,当选取α=0.5~0.7时能获得最好的结果,故本文提出P-GA算法采用这一数值。
5) 利用通信规则将前m个基本膜中产生的交叉结果复制一份发送到第m+1个基本膜中,对第m+1个基本膜中的多重集进行变异操作。由于自然进化中种群变异率往往比较低,因此在一次迭代中,只有利用足够多的字符对象进行变异操作才能产生更多的新个体,具体变异操作如式(9)所示:
| $ {S_{(t + 1, j)}} = {S_{(t, j)}} + 0.1 \times ({S_{({\rm{max}}, j)}}{S_{({\rm{min}}, j)}}) \times {\rm{rand}}(\;\;) $ | (9) |
式中:S(t, j)表示字符对象S的第t代j维的值;S(min, j)表示第j维的最小值;S(max, j)表示第j维的最大值;rand()为随机数函数,产生从0~1的随机数。
6) 当每个基本膜中的规则和操作都结束以后,调用基本膜区域内的溶解规则,当m+1个基本膜全部溶解后,表层膜区域中就会有来自于不同基本膜中的字符对象;本文引入外部档案集,将从基本膜中溶解出的字符对象插入到外部档案集中,而后将表层膜区域中的字符对象与归入外部档案的字符对象进行非支配排序操作。外部档案的执行流程为:①对所有字符对象执行NSGA-Ⅱ算法中的两种机制;②根据执行结果选取支配等级较低的字符对象,若两者支配等级相等,则比较拥挤距离大小,选取拥挤距离较大的字符对象;③通过②的选取后,将获得的所有字符对象归入外部档案集,然后删除档案中受支配的字符对象,剩余存在于外部档案集中的字符对象将作为下一代的非支配多重集。
这个操作发挥了膜计算的优势,即在基本膜之间共享和交换信息,从而提高算法对全局未知解的探索,当然也提高了解的多样性[11, 17]。
7) 如果算法不满足条件,则重复2)~6)的步骤;若算法满足条件,则终止迭代,此时将表层膜区域中的多重集输出即可。
具体流程如图 2所示。

|
图 2 P-GA算法流程图 Fig.2 P-GA algorithm implementation flow chart |
为了检验所提出的算法是否能够较好地逼近真实的Pareto前沿,采用了KUR、ZDT1、ZDT2、和ZDT3多目标问题测试函数。这些测试函数可以较好地测试算法在多目标优化问题的表现。
3.2 实验环境仿真实验硬件环境:CPU Intel酷睿i5-4200H,主频为3.4 GHz,辅以8 GB内存,操作系统为Windows 10,使用MATLAB R2015B进行编程仿真。本文选用了PESA2算法和SPEA2算法与所提出的P-GA算法进行比较,这两个算法的具体参数如表 1所示。
| 表 1 算法参数设置 Tab.1 Algorithm parameter setting |
表 1中,D表示决策变量的维度,本文所提出的P-GA算法群体大小设置为200,表层膜中分裂出11个基本膜,交叉与变异概率均与PESA2算法和SPEA2算法相同。
3.3 仿真结果KUR测试维度为3,ZDT系列的维度均为30,迭代次数均为100次,测得结果如图 3~6所示。

|
图 3 基于KUR测试函数分布图 Fig.3 KUR test function distribution |
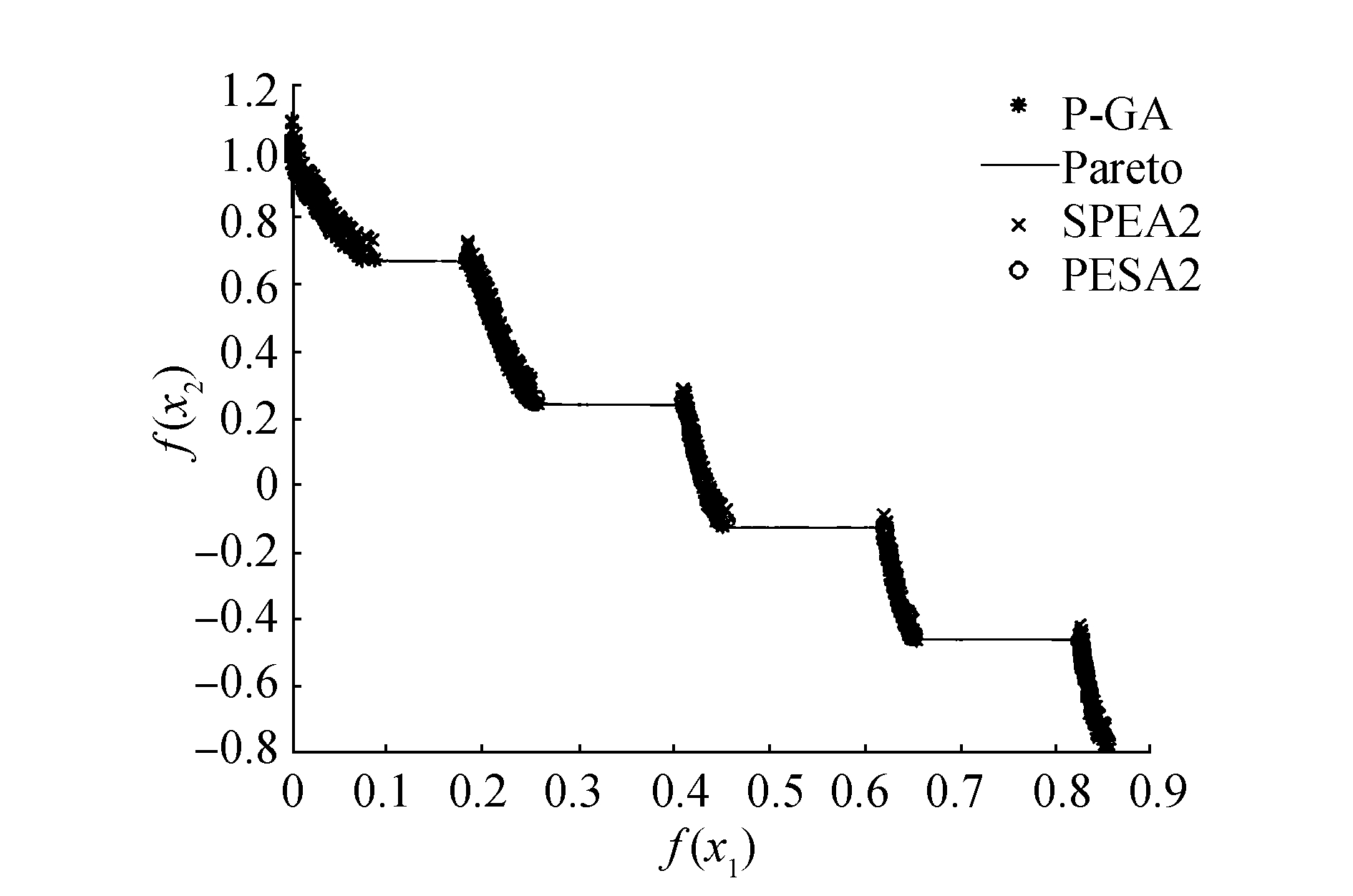
|
图 6 基于ZDT3测试函数分布 Fig.6 ZDT3 test function distribution |
从图 3可以看出,PESA2算法与P-GA算法都取得了较好的结果,但P-GA算法较其他两种算法分散程度较低,而SPEA2效果显得比较差;通过图 4和图 5可以很直观地看出P-GA算法能够较好地逼近真实的Pareto前沿,逼近程度相较于另外两种算法更高,说明G-PA算法能够较快地收敛,且分布程度也与另外两种算法相当,整体上取得的非支配解好于PESA2算法和SPEA2算法;在图 6中可以看出,整体3种算法都取得了较好的效果,都能够逼近真实的Pareto前沿,且分布离散程度也比较接近。
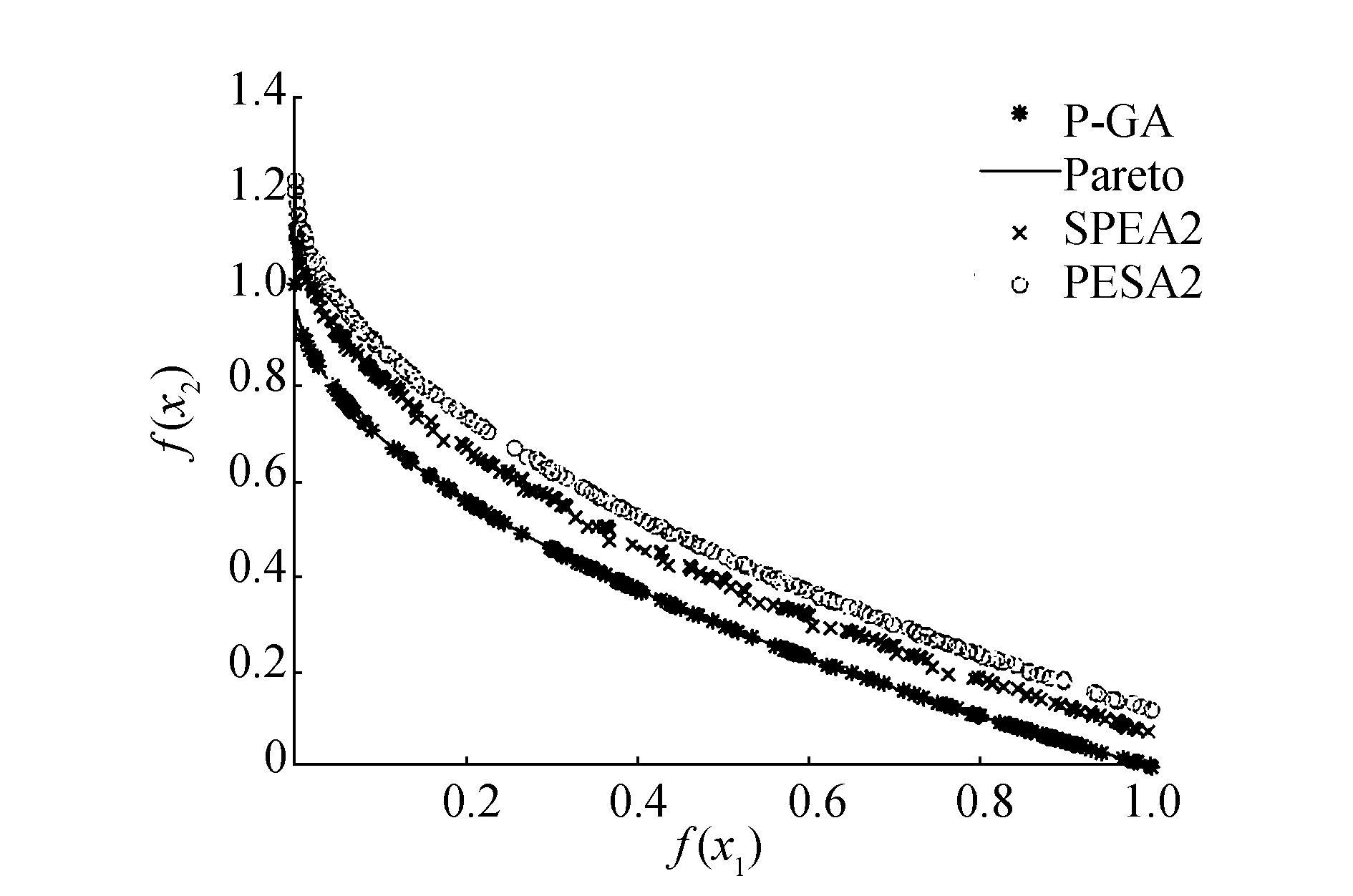
|
图 4 基于ZDT1测试函数分布图 Fig.4 ZDT1 test function distribution |
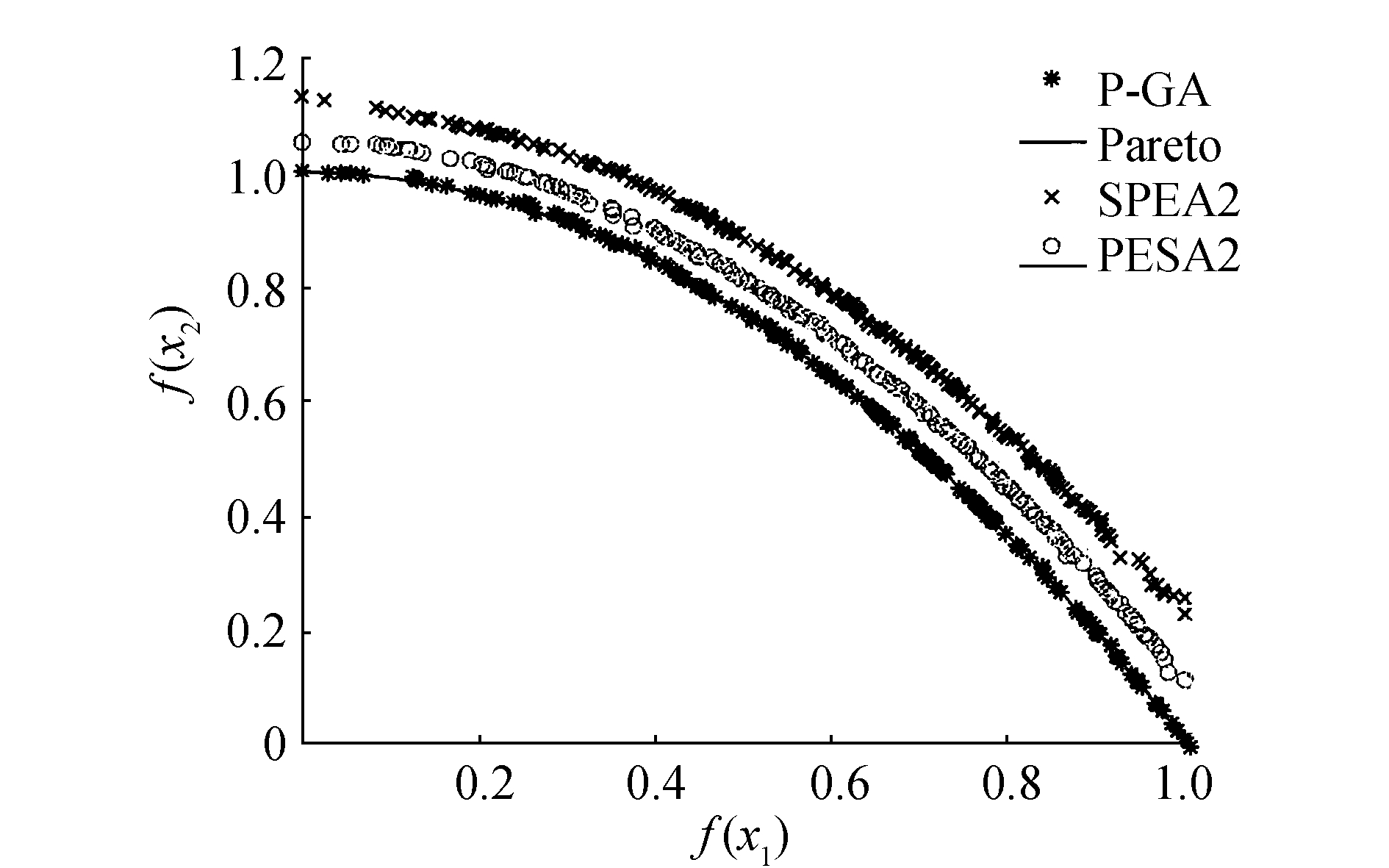
|
图 5 基于ZDT2测试函数分布 Fig.5 ZDT2 test function distribution |
本文采用反转时代距离(inverted generational distant, IGD)作为评价指标[18-19]。IGD是度量算法得到的Pareto前沿到真实的Pareto前沿的距离指标,该指标值的大小与算法Pareto前沿收敛性及多样性呈负相关[20]。通过仿真,得到这3个多目标优化算法在4个测试函数上的数据,其中Mean表示均值,Std.表示标准差,每个算法均在所有测试函数上独立测试100并进行了统计,表 2列出了详细的统计数据。
| 表 2 3个算法在4个测试函数上的IGD性能统计 Tab.2 Comparison of IGD performance of three algorithms on four test functions |
从表 2中可以看出,在KUR测试函数上,PESA2算法取得了最好的效果,但P-GA算法获得统计结果与其相差无几,SPEA2算法表现最差;P-GA在ZDT1和ZDT2测试函数上获得的统计数据明显好于其他两个算法;3种算法在ZDT3测试函数上IGD均值和标准差结果相近。最后需要强调的是,仿真实验表明在算法流程迭代次数超过2 000次以后,3种算法在测试函数上取得的IGD指标基本一致,在此就不去列举了。
4 结束语本文提出了一种基于膜系统下的一种多目标优化算法—P -GA算法,该算法将膜计算相关理论引入,并采用了遗传算法中的交叉与变异机制来增加算法适应能力。仿真实验表明,该算法有精度高、收敛速度快、分布较为均匀等优点。此外,膜优化算法的本质具有分布式和并行计算的执行逻辑,但目前的研究仍局限于串行的工作方式,这也是不足之处。因此,如何实现算法的并行优化计算,也是下一步研究的重点内容和方向。
| [1] |
FONSECA C M, FLEMING P J. Genetic algorithms for multi-objective optimization:formulation, discussion and generalization[C]//The 5th International Conference on Genetic Algorithms. San Mateo, CA, USA, 1993:416-423.
( 0) 0)
|
| [2] |
SRINIVAS N, DEB K. Multi-objective optimization using non-dominated sorting in genetic algorithms[J]. Evolutionary computation, 1994, 2(3): 221-248. DOI:10.1162/evco.1994.2.3.221 ( 0) 0)
|
| [3] |
HORN J, NAFPLIOTIS N, GOLDBERG D E. A niched pareto genetic algorithm for multi-objective optimization[C]//Proceedings of the first IEEE Conference on Evolutionary Computation. Orlando, FL, USA, 1994:82-87.
( 0) 0)
|
| [4] |
ZITZLER E, THIELE L. Multi-objective evolutionary algorithms:a comparative case study and the strength Pareto approach[J]. IEEE trans. on evolutionary computation, 199, 3(4): 257-271. ( 0) 0)
|
| [5] |
MARK ERICKSON A M, HORN J. The niched pareto genetic algorithm 2 applied to the design of groundwater remediation systems[J]. Lecture notes in computer science, 2001, 1993: 681-695. DOI:10.1007/3-540-44719-9 ( 0) 0)
|
| [6] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE trans. on evolutionary computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 ( 0) 0)
|
| [7] |
PAUN G, ROZENBERG G. A guide to membrane computing[J]. Theoretical computer science, 2002, 287(1): 73-100. DOI:10.1016/S0304-3975(02)00136-6 ( 0) 0)
|
| [8] |
ZAHARIE D, CIOBANU G. Distributed evolutionary algorithms inspired by membranes in solving continuous optimization problems[J]. Lecture notes in computer science, 2009, 4361: 536-553. ( 0) 0)
|
| [9] |
LIU C, HAN M, WANG X Z. A multi-objective evolutionary algorithm based on membrane systems[C]//Fourth International Workshop on Advanced Computational Intelligence. Wuhan, China, 2011:103-109.
( 0) 0)
|
| [10] |
ZHANG G, CHENG J, GHEORGHE M, et al. A hybrid approach based on differential evolution and tissue membrane systems for solving constrained manufacturing parameter optimization problems[J]. Applied soft computing, 2013, 13(3): 1528-1542. DOI:10.1016/j.asoc.2012.05.032 ( 0) 0)
|
| [11] |
韩敏, 刘闯, 邢军. 一种基于膜系统理论的多目标演算法[J]. 自动化学报, 2014, 40(3): 431-438. HAN Min, LIU Chuang, XING Jun. A multi-objective evolutionary algorithm based on membrane system theory[J]. Acta automatica sinica, 2014, 40(3): 431-438. (  0) 0)
|
| [12] |
PAUN G, ROZENBERG G, SALOMAA A. The Oxford handbook of membrane computing[M]. Oxford: Oxford University Press, 2010.
( 0) 0)
|
| [13] |
张葛祥, 潘林强. 自然计算的新分支——膜计算[J]. 计算机学报, 2010, 33(2): 208-214. ZHANG Gexiang, PAN Linqiang. A survey of membrane computing as a new branch of natural computing[J]. Chinese journal of computers, 2010, 33(2): 208-214. (  0) 0)
|
| [14] |
张葛祥, 程吉祥, 王涛, 等. 膜计算:理论与应用[M]. 北京: 科学出版社, 2015.
( 0) 0)
|
| [15] |
张玉良. 改进粒子群优化算法在图像矢量量化中的应用研究[D]. 天津: 天津工业大学, 2013. ZHANG Yuliang. Application of improved particle swarm optimization algorithm in image vector quantization[D]. Tianjin:Tianjin Polytechnic University, 2013. (  0) 0)
|
| [16] |
周明. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999.
( 0) 0)
|
| [17] |
李俊. 基于膜计算模型的多目标优化算法研究[D]. 合肥: 安徽大学, 2016. LI Jun. Study on Multi-objective Optimization Algorithm Based on Membrane Computing Model[D]. Hefei:Anhui University, 2016. (  0) 0)
|
| [18] |
黄席越, 张著洪, 何传江, 等. 现代智能算法理论及应用[M]. 北京: 科学出版社, 2005.
( 0) 0)
|
| [19] |
JU Y, ZHANG S, DING N, et al. Complex network clustering by a multi-objective evolutionary algorithm based on decomposition and membrane structure[J]. Scientific reports, 2016, 6: 33870. DOI:10.1038/srep33870 ( 0) 0)
|
| [20] |
ZHANG G, LI Y, GHEORGHE M. A multi-objective membrane algorithm for knapsack problems[C]//IEEE Fifth International Conference on Bio-Inspired Computing:Theories and Applications. Gwalior, India, 2012:604-609.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


