词向量是单词在实数空间所表示的一个低维连续向量,它能够同时捕获单词的语义信息和语法信息。近年来,词向量已被广泛地应用于各种各样的自然语言处理任务中[1-5],如命名实体识别、情感分析、机器翻译等。在处理上述任务的过程中通常需要用到更大单位级别(如短语、句子、段落、篇章)的向量表示, 这些向量则可以由词向量组合获得。因此学习优质的词向量非常重要。
现有的词向量学习方法是利用单词的上下文信息预测该单词含义,并且使上下文信息相似的单词含义也相似,因此对应的词向量在空间距离上更靠近。现有的词向量学习方法大致可以分为基于神经网络学习词向量和基于矩阵分解学习词向量。基于神经网络学习词向量是根据上下文与目标单词之间的关系建立语言模型,通过训练语言模型获得词向量[6-12]。但有效词向量的获取是建立在训练大规模文本语料库的基础上,这无疑使计算成本很高。近年来提出的CBOW和skip-gram模型[11]去除了神经网络结构中非线性隐层,使算法复杂度大大降低,并且也获得了高效的词向量。CBOW根据上下文预测目标单词,skip-gram根据目标单词预测上下文单词。基于矩阵分解的词向量学习模型[13-15]是通过分解从文本语料库中提取的矩阵(如共现矩阵或由共现矩阵生成的PMI矩阵)得到低维连续的词向量,并且文献[13]和文献[14]证明了矩阵分解的词向量学习模型与skip-gram完全等价。
上述模型学习的词向量已被有效地应用于自然语言处理任务中,然而这些模型在学习词向量的过程中仅使用了文本语料库信息,却忽略了单词间的语义信息。一旦遇到下列情形很难保证所得词向量的质量:1)含义不同甚至完全相反的单词(good/bad)往往出现在相似的上下文中,那么它们的词向量必然十分相似,这明显与现实世界相悖;2)对于两个含义相似的单词,其中一个出现在语料库中的次数极少,另外一个却频繁出现,或者它们出现在不同的上下文中,那么最终它们学得的词向量会有很大差别;3)大量上下文噪音的存在使学得的词向量不能准确反映出单词间的真实关系,甚至会误导整个词向量的训练过程。
为解决上述问题,本文考虑从领域知识库提取语义信息并融入到词向量学习的过程中。这会给词向量的学习带来下列优势。
首先,知识库明确定义了单词的语义关系(knife/fork都属于餐具,animal/dog具有范畴包含关系等),引入这些语义关系约束词向量的学习,使学到的词向量具有更准确的关系。另外,相似单词出现在不同的上下文中或者出现频次存在较大差异带来的词向量偏差问题,都可以通过知识库丰富的语义信息予以修正。再者,知识库是各领域的权威专家构建的,具有更高的可靠性。因此,引入语义信息约束词向量的学习是很有必要的。
目前融合语义信息学习词向量已有一些研究成果。Bian等[16]利用单词结构信息、语法信息及语义信息学习词向量,并取得了良好的效果。Xu等[17]分别给取自于知识库的两类知识信息(R-NET和C-NET)建立正则约束函数,并将它们与skip-gram模型联合学习词向量,提出了RC-NET模型。Yu等[18]将单词间的语义相似信息融入到CBOW的学习过程中,提出了高质量的词向量联合学习模型RCM。Liu等[19]通过在训练skip-gram模型过程中加入单词相似性排序信息约束词向量学习,提出了SWE模型,该模型通过单词间的3种语义关系,即近反义关系、上下位关系及类别关系获取单词相似性排序信息。Faruqui等[20]采用后处理的方式调整已经预先训练好的词向量,提出了Retro模型,该模型可以利用任意知识库信息调整由任意词向量模型训练好的词向量,而无需重新训练词向量。
以上研究都是通过拓展神经网络词向量学习模型构建的。与之不同,本文提出的KbEMF模型是基于矩阵分解学习词向量。该模型以Li等[13]提出的EMF模型为框架加入领域知识约束项,使具有较强语义关系的词对学习到的词向量在实数空间中的距离更近,也就是更加近似。与Faruqui等采用后处理方式调整训练好的词向量方式不同,KbEMF是一个同时利用语料库和知识库学习词向量的联合模型,并且在单词类比推理和单词相似度量两个实验任务中展示了它的优越性。
1 矩阵分解词向量学习模型相关背景KbEMF模型是通过扩展矩阵分解词向量学习模型构建的,本节介绍有关矩阵分解学习词向量涉及的背景知识。
矩阵分解 给定一个矩阵X,矩阵分解的目标在于找到两个低秩的矩阵Y和Z,使得X≈YZ,因此矩阵分解的目标函数可以用
共现矩阵 对于一个特定的训练语料库T,V是从该语料库中提取的全部单词生成的词汇表,当上下文窗口设定为L时,对任意的wi∈V,它的上下文单词为wi-L, …, wi-1, wi+1, …,wi+L,则共现矩阵X的每个元素值#(w, c)表示w和c的共现次数,即上下文单词c出现在目标单词w上下文中的次数,
EMF模型 skip-gram模型学得的词向量在多项自然语言处理任务中都取得了良好的表现,却没有清晰的理论原理解释。由此,EMF从表示学习的角度出发,重新定义了skip-gram模型的目标函数,将其精确地解释为矩阵分解模型,把词向量解释为softmax损失下显示词向量dw关于表示字典C的一个隐表示,并直接显式地证明了skip-gram就是分解词共现矩阵学习词向量的模型。这一证明为进一步推广及拓展skip-gram提供了坚实理论基础。EMF目标函数用(1)式表示:
| ${\min _{\mathit{\boldsymbol{W, C}}}}\zeta \left( {\mathit{\boldsymbol{X, WC}}} \right) = - {\rm{tr}}\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}} \right) + \sum\nolimits_{w \in V} {\ln \left( {\sum\limits_{X_{w \in {S_w}}^\prime } {{{\rm{e}}^{X_w^{\prime {\rm{T}}}{C^{\rm{T}}}\mathit{\boldsymbol{w}}}}} } \right)} $ | (1) |
式中:X为共现矩阵;W为单词矩阵;C为上下文矩阵,V中单词w、上下文单词c对应的词向量构成W和C的列向量,dw为单词w所在X列的列向量。Sw=Sw, 1×Sw, 2×…×Sw, c×…×Sw, |V|, 表示Sw, c的笛卡尔乘积,Sw, c={0, 1, …, k
本文选择WordNet做先验知识库。WordNet是一个覆盖范围较广的英语词汇语义网,它把含义相同的单词组织在同义词集合中,每个同义词集合都代表一个基本的语义概念,并且这些集合之间也由各种关系(例如整体部分关系、上下文关系)连接。
本文基于同义词集合及集合间的关系词构建一个语义关系矩阵S∈ℝV×V, 它的每一个元素Sij=S(wi, wj)表示词汇表V中第i个单词wi与第j个单词wj之间的语义相关性。如果Sij=0表示单词wi与wj没有语义相关性,反之Sij≠0则表示单词wi与wj具有相关性。简单起见,本文将语义关系矩阵S构建成0-1矩阵,如果单词wi与wj具有上述语义关系则令Sij=1,否则Sij=0。
2.2 构建语义约束模型本文构建语义约束模型的前提是具有语义相关性的词对wi、wj学到的词向量更相似,在实数空间中有更近的距离,本文采用向量的欧氏距离作为度量词对相似程度的标尺,即d(wi, wj)=||wi-wj||2。因此,语义约束模型可以表示为
| $\begin{matrix} R=\sum\limits_{{{w}_{i}},{{w}_{j}}\in V}{{}}{{S}_{ij}}{{\left\| {{\mathit{\boldsymbol{w}}}_{i}}-{{\mathit{\boldsymbol{w}}}_{j}} \right\|}^{2}}= \\ \sum\limits_{i, j=1}^{\left| V \right|}{{}}{{S}_{ij}}({{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{i}}+{{\mathit{\boldsymbol{w}}}_{j}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}}-2{{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}})= \\ \sum\limits_{i=1}^{\left| V \right|}{{}}(\sum\limits_{j=1}^{\left| V \right|}{{}}{{S}_{ij}}){{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{i}}+\sum\limits_{j=1}^{\left| V \right|}{{}}(\sum\limits_{i=1}^{\left| V \right|}{{}}{{S}_{ij}}){{\mathit{\boldsymbol{w}}}_{j}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}}-2\sum\limits_{i, j=1}^{\left| V \right|}{{}}{{S}_{ij}}{{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}}= \\ \sum\limits_{i=1}^{\left| V \right|}{{}}{{S}_{i}}{{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{i}}+\sum\limits_{j=1}^{\left| V \right|}{{}}{{S}_{j}}{{\mathit{\boldsymbol{w}}}_{j}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}}-2\sum\limits_{i, j=1}^{\left| V \right|}{{}}{{S}_{ij}}{{\mathit{\boldsymbol{w}}}_{i}}^{\rm{T}}{{\mathit{\boldsymbol{w}}}_{j}}= \\ \rm{tr}({{\mathit{\boldsymbol{W}}}^{T}}{{\mathit{\boldsymbol{S}}}_{\rm{row}}}\mathit{\boldsymbol{W}})+tr({{\mathit{\boldsymbol{W}}}^{\rm{T}}}{{\mathit{\boldsymbol{S}}}_{\rm{col}}}\mathit{\boldsymbol{W}})-2\rm{tr}({{\mathit{\boldsymbol{W}}}^{\rm{T}}}\mathit{\boldsymbol{SW}})= \\ \rm{tr}({{\mathit{\boldsymbol{W}}}^{\rm{T}}}({{\mathit{\boldsymbol{S}}}_{\rm{row}}}+{{\mathit{\boldsymbol{S}}}_{\rm{col}}}-2\mathit{\boldsymbol{S}})\mathit{\boldsymbol{W}}) \\ \end{matrix}$ |
最终所得语义约束模型为
| $R=\rm{tr}({{\mathit{\boldsymbol{W}}}^{\rm{T}}}({{\mathit{\boldsymbol{S}}}_{\rm{row}}}+{{\mathit{\boldsymbol{S}}}_{\rm{col}}}-2\mathit{\boldsymbol{S}})\mathit{\boldsymbol{W}})$ | (2) |
式中:tr(·)表示矩阵的迹;Si表示语义矩阵S第i行全部元素值的加和,即S的第i行和;Sj表示语义矩阵S第j列全部元素值的加和,即S的第j列和;Srow表示以Si为对角元素值的对角矩阵,Scol表示以Sj为对角元素值的对角矩阵。
2.3 模型融合将语义约束模型R与EMF相结合,得到融合语义信息的矩阵分解词向量学习模型KbEMF:
| $\begin{array}{c} \mathit{\boldsymbol{O}} = - {\rm{tr}}\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}} \right) + \sum\limits_{w \in V} {} \ln (\sum\limits_{\mathit{\boldsymbol{X}}{\prime _w} \in \mathit{\boldsymbol{S}}{_w}} {} {\rm{ }}{{\rm{e}}^{\mathit{\boldsymbol{X}}\prime _\mathit{\boldsymbol{w}}^{\bf{T}}}}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{w}}) + \\ {\rm{ }}\gamma {\rm{tr}}\left( {{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {{\rm{ }}{\mathit{\boldsymbol{S}}_{{\rm{row}}}} + {\mathit{\boldsymbol{S}}_{{\rm{col}}}} - 2\mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{W}}} \right) \end{array}$ | (3) |
式中γ是语义组合权重,表示语义约束模型在联合模型中所占的比重大小。γ在词向量学习过程中扮演相当重要的角色,该参数设置值过小时会弱化先验知识对词向量学习的影响,若过大则会破坏词向量学习的通用性,无论哪种情况都不利于词向量的学习。该模型目标在于最小化目标函数O,采用变量交替迭代策略求取最优解。当γ=0时表示没有融合语义信息,即为EMF模型。
2.4 模型求解目标函数,即式(3)不是关于C和W的联合凸函数,但却是关于C或W的凸函数,因此本文采用被广泛应用于矩阵分解的变量交替迭代优化策略求取模型的最优解。分别对C、W求偏导数,得到
| $\frac{{\partial \mathit{\boldsymbol{O}}}}{{\partial \mathit{\boldsymbol{C}}}} = \left( {{E_{\mathit{\boldsymbol{X}}|{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{X - X}}} \right){\mathit{\boldsymbol{W}}^{\rm{T}}}$ | (4) |
| $\frac{{\partial \mathit{\boldsymbol{O}}}}{{\partial \mathit{\boldsymbol{W}}}} = \mathit{\boldsymbol{C}}\left( {{E_{\mathit{\boldsymbol{X}}|{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{X - X}}} \right) + \gamma (\mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{L}}^{\rm{T}}})\mathit{\boldsymbol{W}}$ | (5) |
式中:L=Srow+Scol-2S;
| $\mathit{\boldsymbol{W}} \leftarrow \mathit{\boldsymbol{W}} + \eta \left[ {\mathit{\boldsymbol{C}}\left( {{E_{\mathit{\boldsymbol{X}}|{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{X - X}}} \right) + \gamma (\mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{L}}^{\rm{T}}})\mathit{\boldsymbol{W}}} \right]$ | (6) |
| $\mathit{\boldsymbol{C}} \leftarrow \mathit{\boldsymbol{C}} + \eta [\left( {{E_{\mathit{\boldsymbol{X}}|{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{X - X}}} \right){\mathit{\boldsymbol{W}}^{\rm{T}}}]$ | (7) |
在一次循环中先对W迭代更新,直到目标函数O对W收敛为止,然后对C迭代更新,再次使目标函数O对C收敛,至此一次循环结束,依此循环下去直到最终目标函数关于C和W都收敛为止。
算法 KbEMF算法的伪代码
输入 共现矩阵X,语义关系矩阵S,学习率η,最大迭代次数K,k;
输出 WK, CK。
1) 随机初始化:W0, C0
2) for i = 1 to K,执行
3) Wi=Wi-1
4) for j = 1 to k, 执行
5)
6) j=j+1
7) Ci=Ci-1
8) for j=1 to k, 执行
9) Ci=Ci+η
10) j=j+1
11) i=i+1
3 实验与结果本节主要展示融合语义信息后获取的词向量在单词类比推理和单词相似度量任务上的性能表现。首先介绍实验数据集及实验设置,然后分别描述每个实验的任务和结果,并分析实验结果。
3.1 数据集本实验选择Enwik91作为训练语料库,经过去除原始语料库中HTML元数据、超链接等预处理操作后,得到一个词汇量将近13亿的训练数据集。然后通过设置单词过滤词频限制词汇表的大小,把低于设定过滤词频的单词剔除词汇表,因此,不同过滤词频产生不同大小的词汇表。
本实验选用WordNet2作为知识库,WordNet2有120 000同义词集合,其中包含150 000单词。本文借助JWI3从WordNet2中抽取单词间的语义关系:同一个同义词集合内单词对的同义关系,以及不同集合间单词对的上下位关系。
不同的实验任务所用的测试数据集也不相同。
在单词类比推理任务中,本文使用的测试集为谷歌查询数据集(Google query dataset4),该数据集包含19 544个问题,共14种关系类型,其中5种语义关系,9种语法关系。在单词相似度量任务中,本文使用下列3个数据集:Luong等[24]使用的稀有单词,Finkelstein等[25]使用的Wordsim-353 (WS353)数据集(RW),Huang等[6]发布的上下文单词相似数据集(SCWS)。它们分别包含2003、2034、353个单词对及相应的人工标注的相似度分值。
3.2 实验设置下列实验展示了由KbEMF获取的词向量在不同任务中的性能表现。为保持实验效果的一致性,所有模型设置相同的参数。词向量维数统一设置为200,学习率设置为6×10-7,上下文窗口为5,迭代次数设置为300。
另外,语义组合权重的大小也对实验有重要影响。对于单词类比推理和单词相似度量任务本文均采取相同的实验策略寻找最佳语义组合权重,下面以单词类比推理任务为例详细说明最佳语义组合权重找寻的实验过程。设定γ∈[0.01, 100],首先实验γ=0.01,0.1,1,10,100的单词推理正确率,如图 1 (b)所示,γ=0.01,0.1,1时KbEMF没有提升实验效果,因为语义信息所起作用太小;在γ=100时KbEMF实验效果反而更差,这是过分强调语义信息破坏了词向量的通用性;只有在γ=10时KbEMF效果较好,则最佳语义组合权重在γ=10附近的可能性最大。然后在γ∈[1, 10]和γ∈[10, 100]采取同样的策略继续寻找下去,最终会得到最佳组合权重。实验结果表明,不同任务在不同词频下的最优语义组合权重也不同。
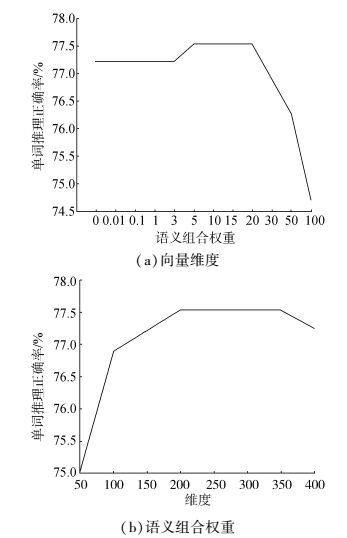
|
图 1 KbEMF在不同向量维度和语义组合权重的正确率 Fig.1 Performance when incorporating semantic knowledge related to word analogical reasoning for different vector sizes and semantic combination weights |
给出一个问题a:b::c:d,a、b、c、d各表示一个单词其中d是未知的,类比推理任务的目标在于找到一个最合适的d使得a, b, c, d的词向量满足vec(d)与vec(b)-vec(a)+vec(c)的余弦距离最近。例如,语义推理Germary:Berlin::France:d, 则需要找出一个向量vec(d),使它与vec(Berlin)-vec(Germary)+vec(France)最近似, 如果vec(d)对应的d是Paris则推理正确。同理,又如语法推理quick:quickly::slow:d, 如果找到d是slowly则推理正确。该实验任务的评价指标是推理出单词d的正确率,正确率越高,则KbEMF学得的词向量越好。
本实验评估了不同参数设置对KbEMF模型影响,图 1是词频为6 000次时,分别改变模型中词向量维度及语义组合权重所绘制的。
从图 1 (a)可以看出,词向量维度小于200时,随着词向量维度增加单词推理正确率在提升,词向量维度在200~350之间实验效果趋向于稳定,因此在同时兼顾实验速度与效果的情况下,本文选择学习200维度的词向量。
图 1 (b)中随着语义组合权重增大,单词推理正确率在提升,继续增大正确率反而减小,说明过大或过小的语义组合权重都不利于学习词向量。从该实验还可以看出,语义组合权重在[5, 20]之间单词推理正确率最高,词向量在该任务中表现最优。
图 2展示了在不同过滤词频下,KbEMF的单词推理正确率均在不同程度上高于EMF,尤其在词频为3 500时效果最佳。对于不同词频,该实验均设置语义组合权重γ=10,尽管该参数值在某些词频下不是最优的,却在一定程度上说明本文模型的普遍适用性。

|
图 2 不同过滤词频下EMF与KbEMF的正确率对比 Fig.2 Performance of KbEMF compared to EMF for different word frequencies |
下面通过将KbEMF与EMF、Retro(CBOW)、Retro(Skip-gram)5、SWE进行比较来说明KbEMF的优越性。Retro根据知识库信息对预先训练好的词向量进行微调,该模型的缺点在于无法在语料库学习词向量阶段利用丰富的语义信息。虽然SWE同时利用了语义信息和语料库信息学习词向量,但该模型的基础框架skip-gram只考虑了语料库的局部共现信息。本文提出的KbEMF则克服了上述模型的弱点,同时利用语料信息和语义信息学习词向量,并且它所分解的共现矩阵覆盖了语料库的全局共现信息。表 1展示了词频为3 500时KbEMF与EMF、Retro(CBOW)、Retro(Skip-gram)5、SWE的单词推理正确率。
| 表 1 KbEMF与其他方法的单词推理正确率 Tab.1 Performance of KbEMF compared to other approaches |
表 1中KbEMF对应的单词推理正确率最高,这说明该模型所获取的词向量质量最优。
3.4 单词相似度量单词相似度量是评估词向量优劣的又一经典实验。该实验把人工标注的词对相似度作为词对相似度的标准值,把计算得到的词对向量余弦值作为词对相似度的估计值,然后计算词对相似度的标准值与估计值之间的斯皮尔曼相关系数(spearman correlation coefficient),并将它作为词向量优劣的评价指标。斯皮尔曼相关系数的值越高表明单词对相似度的估计值与标准值越一致,学习的词向量越好。
由于单词相似度量希望相似度高或相关度高的词对间彼此更靠近,语义信息的融入使具有强语义关系的词对获得更相似的词向量。那么计算所得的关系词对向量的余弦值越大,词对相似度的标准值与估计值之间的斯皮尔曼相关系数就越高。
与单词类比推理实验过程类似,通过调整KbEMF模型参数(词向量维度、语义组合权重以及单词过滤词频),获得单词相似度量实验中表现优异的词向量。
本实验比较了KbEMF与SWE、Retro在单词相似度量任务中的性能表现,结果展示在表 2中。由于不同数据集下最佳语义组合权重不同,该实验针对数据集WS353/SCWS/RW分别设置语义组合权重为γ=1,γ=1,γ=15。
| 表 2 不同数据集下KbEMF与其他方法的斯皮尔曼相关系数 Tab.2 Spearman correlation coefficients of KbEMF compared to other approaches on different datasets |
表 2中KbEMF在上述3个数据集的斯皮尔曼相关系数均有所提升,因为KbEMF相比较Retro在语料库学习词向量阶段就融入了语义知识库信息,相较于SWE则运用了语料库全局的共现信息,因此表现最好。尤其KbEMF在RW上的斯皮尔曼相关系数提升显著,这说明语义知识库信息的融入有助于改善学习稀有单词的词向量。
4 结束语学习高效的词向量对自然语言处理至关重要。仅依赖语料库学习词向量无法很好地体现单词本身的含义及单词间复杂的关系,因此本文通过从丰富的知识库提取有价值的语义信息作为对单一依赖语料库信息的约束监督,提出了融合语义信息的矩阵分解词向量学习模型,该模型大大改善了词向量的质量。在实验中将Enwik9作为训练文本语料库并且将WordNet作为先验知识库,将学到的词向量用于单词相似度量和单词类比推理两项任务中,充分展示了本文模型的优越性。
在后续的研究工作中,我们将继续探索结合其他知识库(如PPDB、WAN等),从中抽取更多类型的语义信息(如部分整体关系、多义词等),进而定义不同更有针对性的语义约束模型,进一步改善词向量。并将它们用于文本挖掘和自然语言处理任务中。
| [1] |
TURIAN J, RATINOV L, BENGIO Y. Word representations:a simple and general method for semi-supervised learning[C]//Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics. Uppsala, Sweden, 2010:384-394.
( 0) 0)
|
| [2] |
LIU Y, LIU Z, CHUA T S, et al. Topical word embeddings[C]//Association for the Advancement of Artificial Intelligence. Austin Texas, USA, 2015:2418-2424.
( 0) 0)
|
| [3] |
MAAS A L, DALY R E, PHAM P T, et al. Learning word vectors for sentiment analysis[C]//Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics. Portland Oregon, USA, 2011:142-150.
( 0) 0)
|
| [4] |
DHILLON P, FOSTER D P, UNGAR L H. Multi-view learning of word embeddings via cca[C]//Advances in Neural Information Processing Systems. Granada, Spain, 2011:199-207.
( 0) 0)
|
| [5] |
BANSAL M, GIMPEL K, LIVESCU K. Tailoring continuous word representations for dependency parsing[C]//Meeting of the Association for Computational Linguistics. Baltimore Maryland, USA, 2014:809-815.
( 0) 0)
|
| [6] |
HUANG E H, SOCHER R, MANNING C D, et al. Improving word representations via global context and multiple word prototypes[C]//Meeting of the Association for Computational Linguistics. Jeju Island, Korea, 2012:873-882.
( 0) 0)
|
| [7] |
MNIH A, HINTON G. Three new graphical models for statistical language modelling[C]//Proceedings of the 24th International Conference on Machine Learning. New York, USA, 2007:641-648.
( 0) 0)
|
| [8] |
MNIH A, HINTON G. A scalable hierarchical distributed language model[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2008:1081-1088.
( 0) 0)
|
| [9] |
BENGIO Y, DUCHARME R, VINCENT P, et al. A neural probabilistic language model[J]. Journal of machine learning research, 2003, 3(02): 1137-1155. ( 0) 0)
|
| [10] |
COLLOBERT R, WESTON J, BOTTOU L, et al. Natural language processing (almost) from scratch[J]. Journal of machine learning research, 2011, 12(8): 2493-2537. ( 0) 0)
|
| [11] |
MIKOLOV T, CHEN K, CORRADO G, ET AL. Efficient estimation of word representations in vector space[C]//International Conference on Learning Representations. Scottsdale, USA, 2013.
( 0) 0)
|
| [12] |
BAIN J, Gao B, Liu T Y. Knowledge-powered deep learning for word embedding[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, Berlin, Heidelberg, 2014:132-148.
( 0) 0)
|
| [13] |
LI Y, XU L, TIAN F, ET AL. Word embedding revisited:a new representation learning and explicit matrix factorization perspective[C]//International Conference on Artificial Intelligence. Buenos Aires, Argentina, 2015:3650-3656.
( 0) 0)
|
| [14] |
LEVY O, GOLDBERG Y. Neural word embedding as implicit matrix factorization[C]//Advances in Neural Information Processing Systems. Montreal Quebec, Canada, 2014:2177-2185.
( 0) 0)
|
| [15] |
PENNINGTON J, SOCHER R, MANNING C. Glove:global vectors for word representation[C]//Conference on Empirical Methods in Natural Language Processing. Doha, Qatar, 2014:1532-1543.
( 0) 0)
|
| [16] |
BIAN J, GAO B, LIU T Y. Knowledge-powered deep learning for word embedding[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany, 2014:132-148.
( 0) 0)
|
| [17] |
XU C, BAI Y, BIAN J, et al. Rc-net:a general framework for incorporating knowledge into word representations[C]//Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management. Shanghai, China, 2014:1219-1228.
( 0) 0)
|
| [18] |
YU M, DREDZE M. Improving lexical embeddings with semantic knowledge[C]//Meeting of the Association for Computational Linguistics. Baltimore Maryland, USA, 2014:545-550.
( 0) 0)
|
| [19] |
LIU Q, JIANG H, WEI S, et al. Learning semantic word embeddings based on ordinal knowledge constraints[C]//The 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference of the Asian Federation of Natural Language Processing. Beijing, China, 2015:1501-1511.
( 0) 0)
|
| [20] |
FARUQUI M, DODGE J, JAUHAR S K, et al. Retrofitting word vectors to semantic lexicons[C]//The 2015 Conference of the North American Chapter of the Association for Computational Linguistics. Colorado, USA, 2015:1606-1615.
( 0) 0)
|
| [21] |
LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization[C]//Advances in Neural Information Processing Systems.Vancouver, Canada, 2001:556-562.
( 0) 0)
|
| [22] |
MNIH A, SALAKHUTDINOV R. Probabilistic matrix factorization[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2008:1257-1264.
( 0) 0)
|
| [23] |
SREBRO N, RENNIE J D M, JAAKKOLA T. Maximum-margin matrix factorization[J]. Advances in neural information processing systems, 2004, 37(2): 1329-1336. ( 0) 0)
|
| [24] |
LUONG T, SOCHER R, MANNING C D. Better word representations with recursive neural networks for morphology[C]//Seventeenth Conference on Computational Natural Language Learning. Sofia, Bulgaria, 2013:104-113.
( 0) 0)
|
| [25] |
FINKELSTEIN R L. Placing search in context:the concept revisited[J]. ACM transactions on information systems, 2002, 20(1): 116-131. DOI:10.1145/503104.503110 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


