2. 国网浙江省电力公司信息通信分公司,浙江 杭州 310073;
3. 浙江工业大学 计算机科学与技术学院,浙江 杭州 310023
2. State Network Zhejiang Electric Power Corporation Information Communications Branch, Hangzhou 3100073, China;
3. School of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China
家庭用电系统作为需求侧的重要组成部分,其规律性明显,用户数目众多,用电总量庞大,也是电网负荷管理的重要部分。因此,需求侧响应概念被越来越多地引入到平衡电网负载中[1]。现阶段需求响应操作主要可划分为基于价格的方式和基于激励的方式[2]。基于价格的需求响应主要依靠分时电价策略,依靠需求侧的主观调节方式来减少电网高峰负荷。基于激励的需求响应是指供电侧制定响应,策略,激励需求侧在电网负荷较大时及时响应,如削减一定的负荷[3]。然而,现有需求响应尚存在诸多问题:1)由于电量计量方式的误差,数据传输滞后,需求侧与供电侧所统计结果存在差异;2)缺乏合理的激励机制,进一步导致需求侧主观积极性下降;3)缺乏有效的响应交互机制,不利于供电侧对电能资源进行再分配[4-6]。故将智能电网引入需求响应有重要实际意义。
随着物联网的快速发展,智能电网作为智能化的电能服务网络,提高了供电侧与用电侧的交互性,有利于整体电能的资源合理优化和高效利用,进一步有利于稳定电网负荷。智能电网在传统供电侧到需求侧的传输基础上,集合了传感测量技术、网络通信技术、智能计算技术和自动控制技术[7]。引入智能电网可以有效地提高计量方式的准确性,提高电能资源的分配效率。通过引入智能电网的实时交互策略,调动需求侧参与响应或通过提前签订协议,对需求侧直接进行远程的需求响应,可以有效地实现电网负荷的柔性化管理[8]。
随着分时电价、峰值电价等策略的提出,需求侧管理更需要保证实时性。针对需求侧大规模的家庭用电,单一的优化算法已不能满足电网实时性的需求。现有针对需求响应的算法大多应用于处理单个目标优化问题,或简单地将多目标加权之后转化为单目标来进行优化[9]。这种算法在增加了需求侧用电器数量之后,算法延时时间也会相应地增加。本文提出采用多目标进化算法,以最小化电能消耗和最小化延时时间为目标,应用于需求响应控制。供电侧可以通过提前与用户签订协议,在家庭中布置智能控制器,对家用电器进行实时控制,以便在电网高峰时期减小电网负荷。
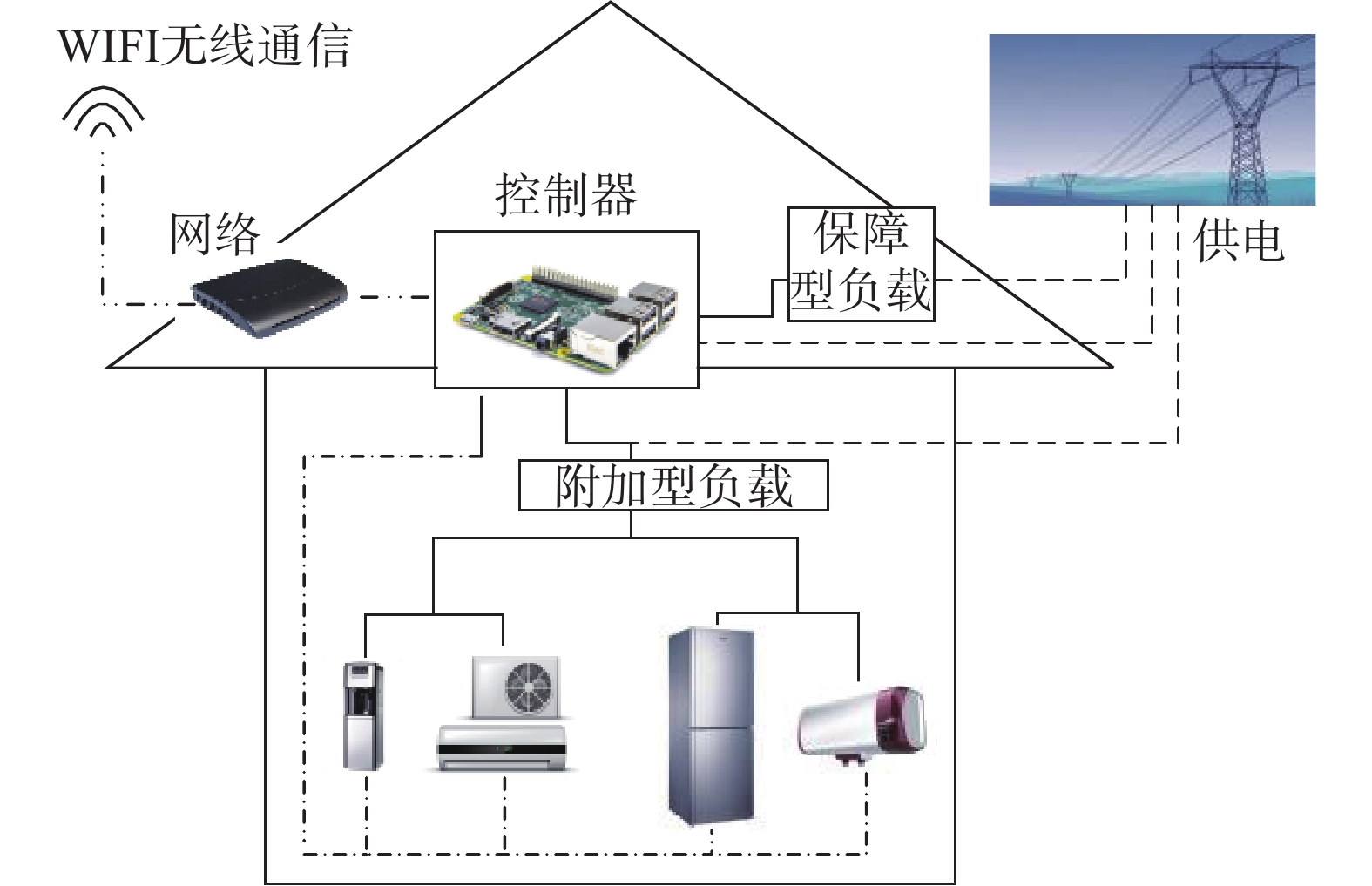
1 智能电网环境下家电系统运行方式智能电网领域有各种通信架构,而在互联网等公共领域,合适架构的选择问题是至关重要的。适合的架构可以使用户便捷地参与到需求响应的过程中,并且保证了系统的实时性[10]。针对家庭常用电器,如冰箱、空调、热水器、饮水机、电视机、电脑、洗衣机及照明电路等,这些负载可分为保障型负载和附加型负载。保障型负载(如照明电路等)作为居民生活条件的基本保障,且由于其功率相对较低,因此不作为家庭用电优化控制的对象。图1所示的智能电网下的家庭用电管理系统,只显示出附加型负载,而不包括对保障型负载的控制,以实现在需求侧管理过程中,对需求侧居民生活所造成的影响降到最小。智能电网下的家庭用电管理系统结构图如图1所示。智能家庭用电管理系统中,多项附加型负载均通过控制器再接入电路中。供电侧可从控制器中获取用户家庭耗电量,如某一家电的单位时间电能消耗情况,并对统计信息进行优化计算,将计算结果返回控制器,进一步对家庭中的附加型负载进行控制,以减弱高峰时刻的电网负荷。
|
Download:
|
| 图 1 智能家庭用电管理系统 Fig. 1 Diagram of home energy management system | |
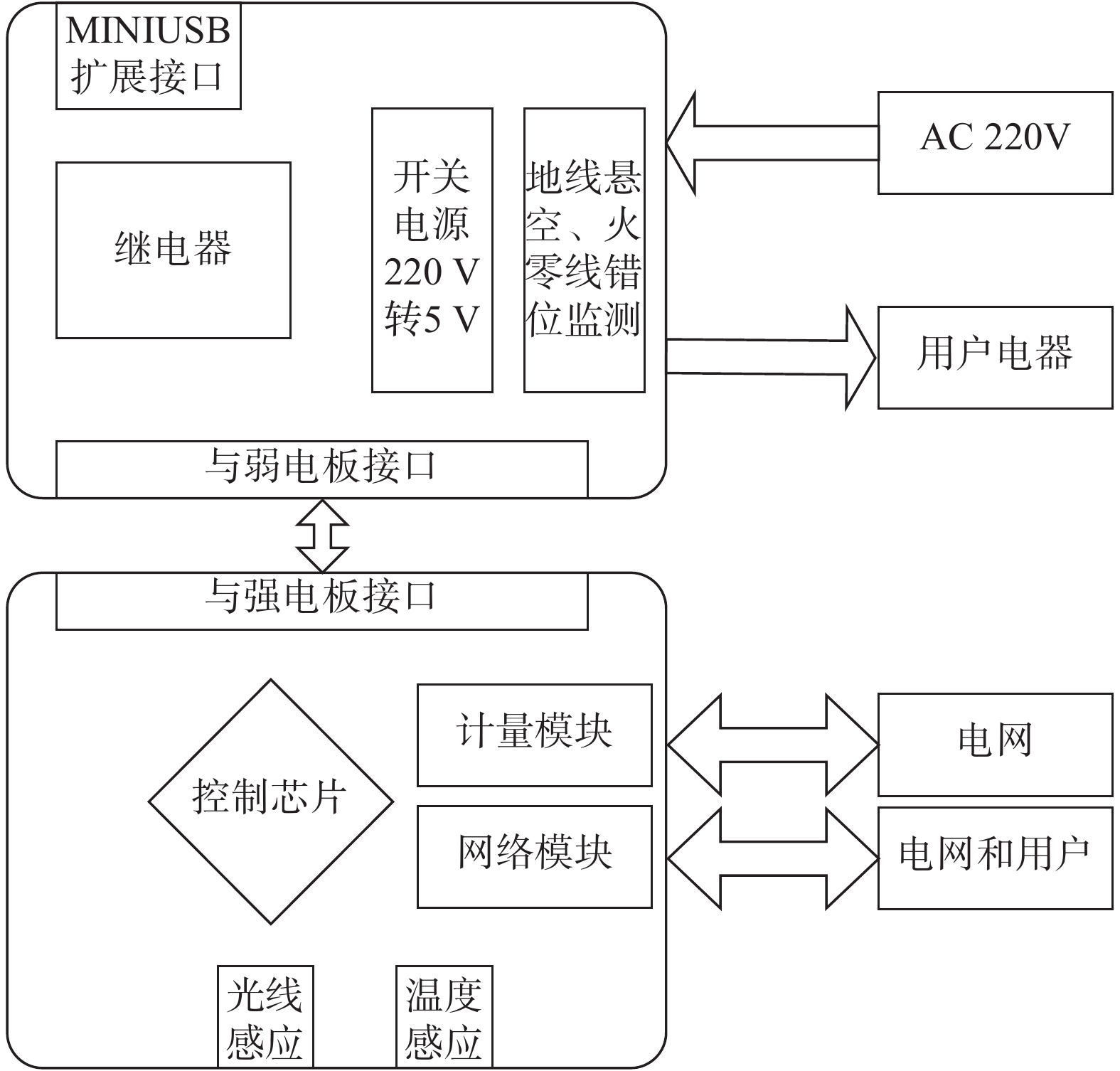
图1中所示控制器采用交互式通信平台,集成用电量计量技术,除获取电网负荷数据并对管理家庭用电量进行管理的功能之外,其还可以对用户提供电价的分时段计量,减少用户的用电费用。并通过控制器内置的光线传感器和温度传感器,获取家庭内的环境信息以进一步对家庭中电器做出多级调整,在尽可能保证用户舒适度的同时实现电网平衡。控制器系统结构图如图2所示。
|
Download:
|
| 图 2 控制器系统结构 Fig. 2 Chart of control system structure | |
需求侧管理下的家庭用电响应模式是指家庭用户依据自己的经济和舒适型要求采取的负荷响应方式,为了使供电侧(如电力公司等)具有即时管理能力,需要用户与供电侧签订合同,使供电侧可以通过智能控制器,直接控制用户家中的部分附加型负载。并且用户可以根据本家庭负载情况,自主对家庭中多种大功率附加型负载进行权值设置[11],权值大的优先级高,在用电高峰时期到来之前,供电侧可以对权值较小的负载进行优先降负荷处理。
2.1 附加型负载系统模型根据家庭用电负载的特点,选取空调、热水器等附加型负载作为优化控制对象,设置空调权重为αk,热水器权重为αr。
| ${Q_t} = (\sum\nolimits_i {{\beta _d}{P_k}} + \sum\nolimits_j {{\beta _e}{P_r}} ) \cdot {q_t}$ | (1) |
式中:Pk为空调功率,Pr为热水器功率,i为空调数量,j为热水器数量,qt为时隙t内电价,βd和βe均为负载的工作指数,Qt为时隙t内附加型负载的耗电所产生的用电费用。该模型同样可以应用到电网系统集中控制中,对多个家庭的用电负荷进行计量与优化,同时也便于扩展其他类型的家用电器进行优化运算。其中,用户家庭中当前用电功率为
| ${W_t} = {\beta _d}{P_k} + {\beta _e}{P_r}$ | (2) |
式中Wt为时隙t内用户的附加型负载总功率。
由于需求侧管理机制直接操作了用户家庭电器情况,在一定程度上影响了用户体验,引入最小操作量函数Z:
| $Z = \Delta W \cdot T$ | (3) |
| $\Delta W = {W_t} - {W_x}$ | (4) |
式中:Wt为控制器监测到时隙t内,电网负荷逼近高峰时刻需要进行需求管理时的家庭内负荷总功率,Wx为用户端响应后,对附加型负载进行调节后的家庭内负荷总功率;T为响应总时间,即在响应过程中对用户造成的总影响的时间;Z为响应过程中,供电侧为了削峰保护而对需求侧做出的管理后所节约的电能总量,单位是kW·h。
2.2 多目标蜻蜓算法目前,在家庭用电优化控制[15]中主要采用的方法有粒子群算法[16]和遗传算法[17]等,主要思想均是明确目标函数与约束条件信息,在全局范围内寻求概率最大的解,适合解决复杂的非线性寻优问题。但是考虑到需求响应的即时性,即为了防止电网负荷达到峰顶,需要在负荷增长的过程中就开始对协议用户进行一定量的响应控制。而粒子群算法和遗传算法均需要较长时间的初始化和迭代过程,很难达到所要求分钟级别的响应时间,因此需要计算时间更短、反应速度更快的多目标优化算法。
多目标蜻蜓算法是近年来新提出的一种进化算法,其主要灵感来自于蜻蜓在哺食与避敌过程中通过对路径的规划与探索来完成预定目标的特性,在两者均需要达到最佳的时候选取最近的路径,在此将捕食与避敌过程分别看成用户总耗电量和所受影响时间两个目标。在算法中,将一系列过程抽象化为3个特征,即分散、同步、汇聚,并以数学方式建模。
将上述算法引入系统优化控制模型中,将附加型负载的数量视为蜻蜓的数量,耗电量和响应延时时间视为捕食与避敌过程,设定优化个体数量为m,m表示为家庭总数。针对系统负载影响最大的空调和热水器等附加型负载进行试验,目标为耗电量最小和高峰时段需求响应时间最短。根据某用电监管平台数据,对全天多户家庭负载功率数的平均值进行了统计。为了清晰描述出优化控制过程中的最小化负载数和最小化响应延时时间这两个目标参数,本文将用式(5)~(11)来对其进行模拟,其表达式如下[18-19]。
1) 分散行为:
| ${S_i} = - \sum\limits_{j = 1}^n {X - {X_j}} $ | (5) |
式中:X表示当前个体的位置, Xj表示第j个相邻个体的位置,n为相邻个体的总数。在本控制过程中,Xj为j时隙过程中系统的耗电量。
2) 同步行为:
| ${A_i} = \frac{{\sum\nolimits_{j = 1}^n {{V_j}} }}{N}$ | (6) |
式中:Vj表示第j个相邻个体的速度, n为相邻个体的总数,N为个体总数。在本控制过程中,将其视为响应时的速度,即智能控制器调节负载过程的行为。
3) 汇聚行为:
| ${C_i} = \frac{{\sum\nolimits_{j = 1}^n {{X_j}} }}{N} - X$ | (7) |
式中:X表示当前个体的位置,Xj表示第j个相邻个体的位置,n为相邻个体的总数,N为个体总数。汇聚行为即表示优化过程中算法的收敛过程。
4) 优化过程:
蜻蜓在捕食过程中,趋向于食物的定义为
| ${F_i} = \overline X - X$ | (8) |
式中:X表示当前个体的位置,
5) 避敌行为:
另一方面,蜻蜓规避天敌的定义为
| ${E_i} = \widetilde X + X$ | (9) |
式中:X为当前个体的位置,
| $\Delta {X_{t + 1}} = (s{S_i} + a{A_i} + c{C_i} + f{F_i} + e{E_i}) + w\Delta {X_i}$ | (10) |
式中:s表示分散行为的权重,Si表示第i个个体行进分散行为,a表示同步行为的权重,Ai表示第i个个体行进同步行为,c表示汇聚行为的权重,Ci表示第i个个体行进汇聚行为,f表示食物特征系数,Fi表示第i个个体的食物源,e表示天敌特征系数,Ei表示第i个个体天敌的位置,w为迭代权重,t为迭代计数。此外,位置向量定义为
| ${{\mathit{\boldsymbol{X}}}_{t + 1}} = {{\mathit{\boldsymbol{X}}}_t} + \Delta {{\mathit{\boldsymbol{X}}}_{t + 1}}$ | (11) |
综上,该算法可同时以两个目标为收敛条件,比传统优化算法收敛速度快,可以达到及时响应的效果。
具体算法步骤:
1) 算法读取当前系统耗电量,Si=Qt;
2) 读取当前系统响应时间,Ei=Z;
3) 输入待优化数目,初始设为m,设置空调和热水器权值相等,αk=αr;
4) 根据式(10)(位置和加速度)对系统的耗电量和响应时间进行迭代计算,初始化迭代步数为30;
5) 进行响应管理时刻,优先对权值较小的负载进行处理;
6) 选取收敛标准,当系统整体耗电量降为历史数据的80%时,即认为算法运行有效,选取所受影响时间最短的值作为输出结果。
3 仿真实验结果分析通过对某小区内500余户家庭的家电负荷进行实地调查,排除照明设施等保障性负载,仅考虑空调和热水器两种负荷较大的家电。现有参数信息如表1,表1展示了某小区主要家电负荷信息统计,从中可以看出,虽然空调热水器作为附加型负载,但是居民的日常使用频率依然很高,且电器数量也超过了家庭总数。表2展示了该小区的分时电价信息。
| 表 1 某小区主要家电负荷信息统计 Tab.1 Home appliance load information |
| 表 2 分时电价信息 Tab.2 Time-sharing electricity price |
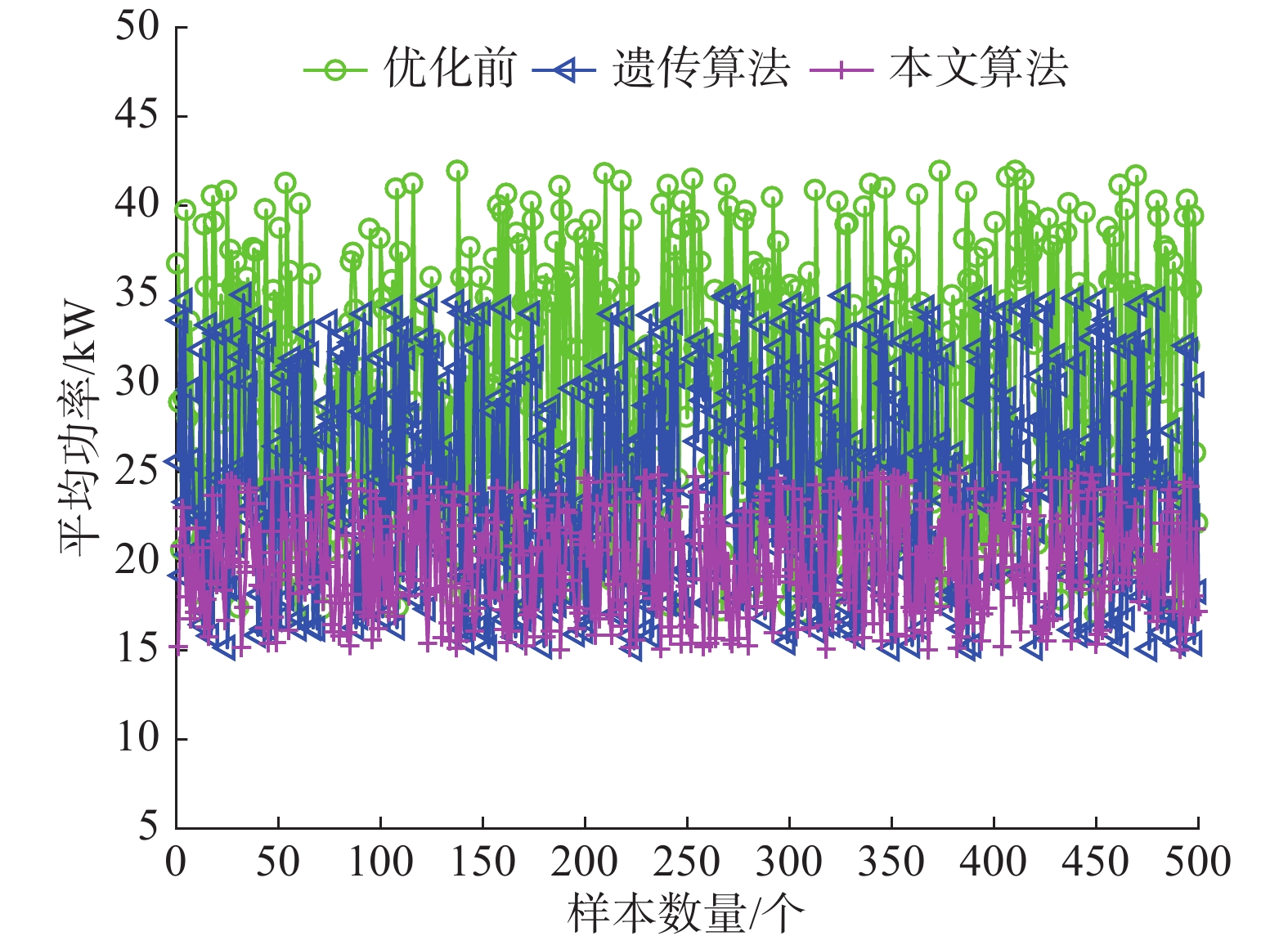
针对电网运行高峰时段,展示出对比响应前后的家庭附加型负载总功率数,如图3所示。从图3可明显看出,应用了本算法之后,相较于优化前和遗传算法情况,用户用电量的平均功率数有了明显下降。图3中“o”型曲线所显示的为优化前的500户用户的平均功率数,其分布较散,且均值较大。应用了遗传算法进行优化之后,用户的平均功率数下降了20.6%,如图中“*”型曲线所示,而本算法则有较好的处理效果,如图3中“+”型曲线所示。同时从用户角度出发,本文计算了高峰时刻用户用电所花费的情况,其对比结果如图4所示,图4展示了多目标优化后的用户平均花费情况。类似于图3,图4中“o”型曲线为优化前高峰时段用户用电平均花费,“Δ”型曲线为应用遗传算法之后的效果,“+”型曲线为本算法的应用效果,结果显示本算法也帮助用户节约了一定费用。为了展示本算法的运算过程,本文对遗传算法与本算法的延时时间进行了实验并统计了结果,平均延时时间如图5所示。
|
Download:
|
| 图 3 优化前后平均功率数对比 Fig. 3 Comparison of average power | |

|
Download:
|
| 图 4 优化前后用户用电花费对比 Fig. 4 Comparison of user electricity consumption | |
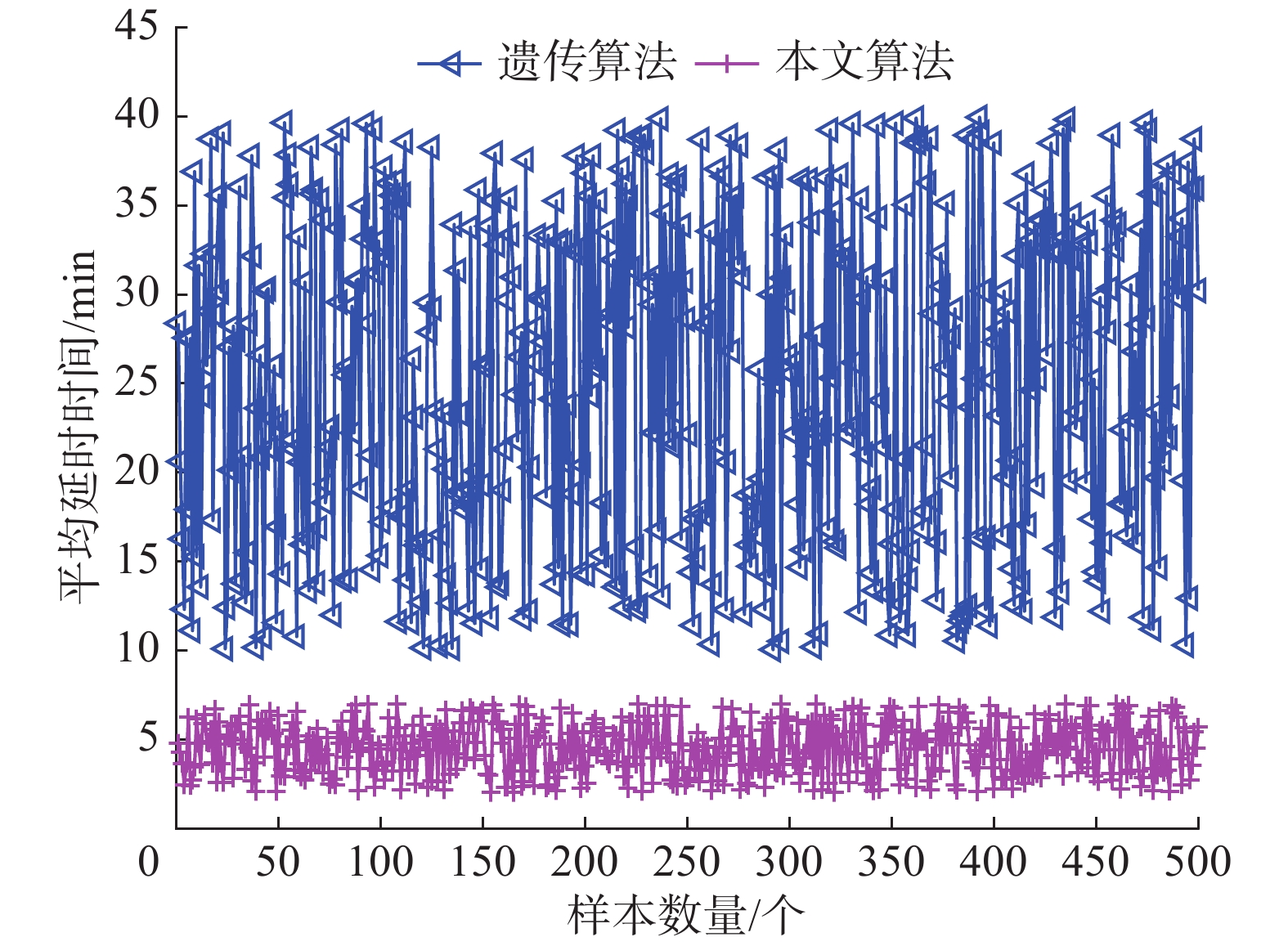
从响应的延时时间角度可明显看出,传统遗传算法其响应时间长且波动较大,上下浮动在10~40 min ,而实施本文算法之后,由于算法收敛速度快,计算结果迅速,其整体的响应时间在4.5 min上下波动,可以达到及时响应的效果。
|
Download:
|
| 图 5 平均延时时间对比 Fig. 5 Comparison of average delay times | |
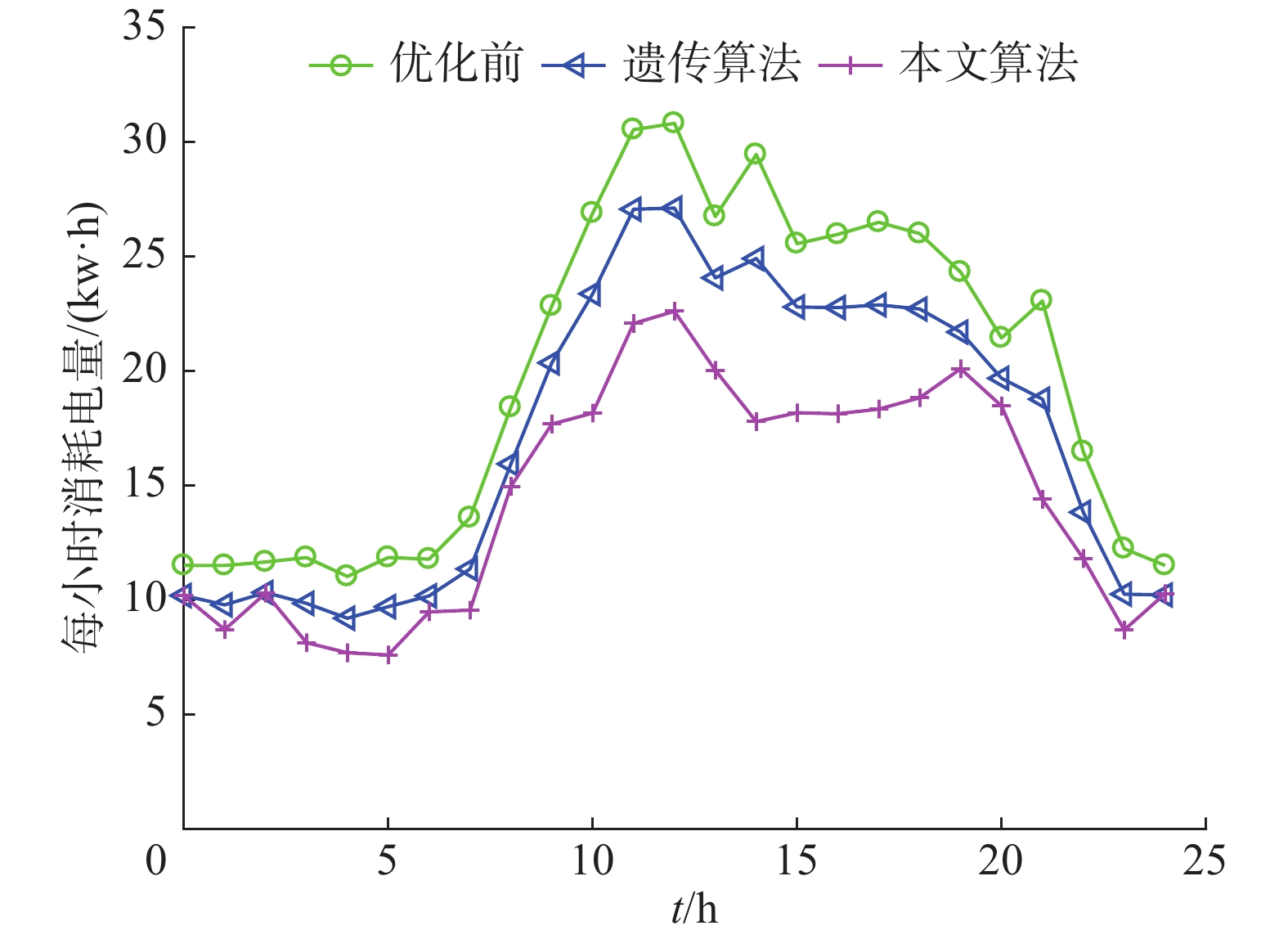
针对一天内的高峰时刻电量消耗变化量,本文进行了500户家庭一天内各个时间段的电量消耗量的统计,结果如图6所示。图6显示了500户家庭在一天内各个时刻的平均电能消耗量与应用了遗传算法和本算法之后的效果对比。从图6中优化前的数据可以看出,每小时的平均电能消耗量(kW·h)在6:00之后有了明显的上升趋势,并且在12:00~13:00维持了较高的消耗量,一直持续到晚上21:00开始有了下降趋势。本算法的结果如图6中“+”形曲线所示,可以看出本算法在高峰时期的每小时耗电量较为平稳,且相较于遗传算法优化结果和未优化前结果,本算法在高峰时期有较好的降负载效果。
|
Download:
|
| 图 6 一天内电量消耗情况 Fig. 6 Power consumption during one day | |
需求侧管理作为一种缓解电网高峰负荷的有效手段,一直以来面对着需求侧用户数量众多、单一耗电量低、应用困难的问题。在智能电网的环境下,在对需求侧众多用户应用了多目标优化算法之后,可以在较短的时间内得出计算结果并通过智能控制器对家庭用电器进行需求侧管理。实验结果显示,对小规模群体用户施行需求侧管理操作可以有效地降低其功率平均数,同时降低了用户的用电费用,进一步可以降低电网负荷,保障电网的稳定性。优化控制过程中引入多目标蜻蜓算法,在约束了系统耗电量降低的最低标准后,实验中算法收敛速度快,可以达到分钟级别的响应效果,适合在实际生活中应用。本实验尚存在一些不足,如尚未对多数小区同时进行需求响应的集中控制,下一阶段的主要目标是针对中大规模的家庭群进行需求响应优化控制。
| [1] |
中国电力企业联合会规划发展部. 2016年电力供需形势分析预测与建议[J]. 中国电力企业管理, 2016(4): 27-29. China federation of electric power enterprise planning and development. 2016 Analysis and forecast of electricity supply demand and the suggestion[J]. China electric power enterprise management, 2016(4): 27-29. (  0) 0)
|
| [2] |
SIANO P. Demand response and smart grids—a survey[J]. Renewable and sustainable energy reviews, 2014, 30: 461-478. DOI:10.1016/j.rser.2013.10.022 ( 0) 0)
|
| [3] |
薛晨, 黎灿兵, 曹一家, 等. 智能电网中的电网友好技术概述及展望[J]. 电力系统自动化, 2011, 35(15): 102-107. XUE Chen, LI Canbing, CAO Yijia, et al. An overview and prospects of grid friendly technology in smart grid[J]. Automation of electric power systems, 2011, 35(15): 102-107. (  0) 0)
|
| [4] |
GUNGOR V C, SAHIN D, KOCAK T, et al. Smart grid technologies: communication technologies and standards[J]. IEEE transactions on industrial informatics, 2011, 7(4): 529-539. DOI:10.1109/TII.2011.2166794 ( 0) 0)
|
| [5] |
GKATZIKIS L, KOUTSOPOULOS I, SALONIDIS T. The role of aggregators in smart grid demand response markets[J]. IEEE journal on selected areas in communications, 2013, 31(7): 1247-1257. DOI:10.1109/JSAC.2013.130708 ( 0) 0)
|
| [6] |
IWAYEMI A, YI Peizhong, DONG Xihua, et al. Knowing when to act: an optimal stopping method for smart grid demand response[J]. IEEE network, 2011, 25(5): 44-49. DOI:10.1109/MNET.2011.6033035 ( 0) 0)
|
| [7] |
刘壮志, 许柏婷, 牛东晓. 智能电网需求响应与均衡分析发展趋势[J]. 电网技术, 2013, 37(6): 1555-1561. LIU Zhuangzhi, XU Baiting, NIU Dongxiao. Development tendency of equilibrium analysis and demand response for smart grid[J]. Power system technology, 2013, 37(6): 1555-1561. (  0) 0)
|
| [8] |
王丹, 范孟华, 贾宏杰. 考虑用户舒适约束的家居温控负荷需求响应和能效电厂建模[J]. 中国电机工程学报, 2014, 34(13): 2071-2077. WANG Dan, FAN Menghua, JIA Hongjie. User comfort constraint demand response for residential thermostatically-controlled loads and efficient power plant modeling[J]. Proceedings of the CSEE, 2014, 34(13): 2071-2077. (  0) 0)
|
| [9] |
SAELE H, GRANDE O S. Demand response from household customers: experiences from a pilot study in norway[J]. IEEE transactions on smart grid, 2011, 2(1): 102-109. DOI:10.1109/TSG.2010.2104165 ( 0) 0)
|
| [10] |
陆苏青, 唐楠, 王蓓蓓, 等. 美国需求响应技术和思考(下)[J]. 电力需求侧管理, 2016(1): 60-64. LU Suqing, TANG Nan, WANG Beibei, et al. Demand response technology and thinking in America[J]. Power demand side management, 2016(1): 60-64. (  0) 0)
|
| [11] |
NORRIS S, PENDAKUR K. Imputing rent in consumption measures, with an application to consumption poverty in Canada, 1997–2009[J]. Canadian journal of economics/revue canadienne d'économique, 2013, 46(4): 1537-1570. DOI:10.1111/caje.12054 ( 0) 0)
|
| [12] |
CONSTANTOPOULOS P, SCHWEPPE F C, LARSON R C. Estia: a real-time consumer control scheme for space conditioning usage under spot electricity pricing[J]. Computers and operations research, 1991, 18(8): 751-765. DOI:10.1016/0305-0548(91)90013-H ( 0) 0)
|
| [13] |
LEE J, PARK G L, KIM S W, et al. Power consumption scheduling for peak load reduction in smart grid homes[C]//Proceedings of 2011 ACM Symposium on Applied Computing. TaiChung, China, 2011: 584–588.
( 0) 0)
|
| [14] |
NASIRAGHDAM H, JADID S. Load model effect assessment on optimal distributed generation (DG) sizing and allocation using improved harmony search algorithm[C]//Proceedings of 2013 Smart Grid Conference. Tehran, Iran, 2013: 210–218.
( 0) 0)
|
| [15] |
张延宇, 曾鹏, 李忠文, 等. 智能电网环境下空调系统多目标优化控制算法[J]. 电网技术, 2014, 38(7): 1819-1826. ZHANG Yanyu, ZENG Peng, LI Zhongwen, et al. A multi-objective optimal control algorithm for air Conditioning system in smart grid[J]. Power system technology, 2014, 38(7): 1819-1826. (  0) 0)
|
| [16] |
XIONG Gang, CHEN Chen, KISHORE S, et al. Smart (in-home) power scheduling for demand response on the smart grid[C]//Proceedings of 2011 IEEE PES Innovative Smart Grid Technologies. Anaheim, CA, USA, 2011: 1–7.
( 0) 0)
|
| [17] |
MOHSENIAN-RAD A H, WONG V W S, JATSKEVICH J, et al. Optimal and autonomous incentive-based energy consumption scheduling algorithm for smart grid[C]//Proceedings of 2010 Innovative Smart Grid Technologies. Gaithersburg, MD, USA, 2010: 1–6.
( 0) 0)
|
| [18] |
BASU B, MAHANTI G K. Thinning of concentric two-ring circular array antenna using fire fly algorithm[J]. Scientia iranica, 2012, 19(6): 1802-1809. DOI:10.1016/j.scient.2012.06.030 ( 0) 0)
|
| [19] |
REYNOLDS C W. Flocks, herds and schools: a distributed behavioral model[C]//Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA, 1987: 25–34.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


