2. 安徽大学 计算机智能与信号处理教育部重点实验室, 安徽 合肥 230601;
3. 安徽大学 国际商学院, 安徽 合肥 230601
2. Key Laboratory of Intelligent Computing and Signal Processing of Ministry of Education, Anhui University, Hefei 230601, China;
3. School of Business, Anhui University, Hefei 230601, China
在现实世界中,很多事物的联系都是以网络的形式存在的。例如,互联网中的社交网络,社会系统中的人际关系网,生态系统中的神经元网和蛋白质交互网。大量的研究表明,许多实际网络中都存在着社团结构[1-2]。社团将网络中具有紧密联系的事物划分在一起,每个社团内部的节点之间连接相对紧密而社团之间的连接比较稀疏[3]。研究网络中的社团结构具有重要意义。如何有效地进行社团划分,成为了社团研究者们一直致力于研究的一个重要方向之一。近年来,许多学者分别从不同角度对社团进行划分研究,其中著名的算法有Kernighan-Lin算法[4]、谱平分法[5-6]和GN算法[7]等。随着研究的深入,人们发现在进行社团划分时经常会出现重叠部分,即一个节点被多个社团包含。因实际需要将重叠节点划分到单个社团中,更有助于发现社团内存在的规律,并预测网络的行为和功能[8]。因此,对于非重叠社团划分的研究,也是十分必要的。
对于非重叠社团划分的研究也引起了很多学者的关注和研究。Newman快速算法(newman fast algorithm, NFA)[9]依靠模块度获得最优社团结构;Radicchi等[10]提出了自包含GN算法(self-contained GN algorithm),给出了强社团和弱社团结构两种量的定义,为如何确定社团结构提供了一种衡量标准;赵姝等[11]将粒计算思想引入到网络的社团划分中,通过对网络结构的聚类粒化实现社团划分,其时间复杂度低、收敛速度快、精确度高,实现了时间复杂度与精确度之间的平衡。这些现有的非重叠社团划分算法从不同的角度和应用层面对非重叠社团的划分进行了研究,并取得了丰硕的研究成果。但这些算法对重叠部分处理时都只应用了传统的二支决策[12-13]方法,即根据已有的信息只做出接受或拒绝决策。但重叠部分的节点往往因为信息量不够无法决定其归属,才会出现在重叠部分,如果强制做出决策,可能影响最终非重叠社团划分的结果。三支决策对于处理那些不确定信息具有一定的实用性[14-19]。当信息不足时,三支决策理论对不确定性问题首先做三分类,即正域、负域、边界域;再通过进一步观察,获得足够的信息,将边界域的对象进行二次划分,实现最终的二支决策。本文在文献[11]的基础上,引入三支决策思想[20],改进了对于重叠部分的处理方法,提出了一种基于三支决策的非重叠划分算法(three-way decision based on non-overlapping community division,N-TWD),以划分出更合理的非重叠社团。以划分出更合理的非重叠社团。该算法首先将两个存在重叠部分的社团的左边社团非重叠部分定义为正域,右边社团的非重叠部分定义为负域,而两个社团的重叠部分定义为边界域,分别计算边界域中的节点与正域和负域的社团归属度BP、BN, 依据两者的差值进行二次划分。对于二次划分后仍然留在边界域中的节点将利用投票的方法决定其最终归属,最终获得非重叠的社团结构。
N-TWD算法对于社团重叠部分(边界域)获取了节点,与已明确划分的社团(正域/负域)之间的紧密关系依次进行划分,而不仅仅只根据邻居数目进行投票,更好地体现了节点的真实归属。本文采用4个真实的社交网络数据集和1个真实数据集对N-TWD算法进行了验证,实验结果证明了三支决策方法对部分重叠节点处理的可行性和有效性。
1 相关工作 1.1 三支决策理论三支决策理论对于现实世界中的不确定信息决策问题的解决具有高效性,尤其对那些信息缺失、证据不充分或者不完整的情况。这时,由于信息不精确、不一致、不完整等原因,无法立即做出接受或拒绝的决策。于是,可以采用一种延迟决策或边界决策,即不做任何承诺的决策。正常情况下,当证据变得足够或者完备时,就有可能进一步做出正决策或负决策。
三支决策的主要思想是将整体分为3个独立的部分:正域、负域、边界域。对不同的部分采取不同的处理方法,为求解复杂问题提供了一种有效的策略与方法[15]。
当前,三支决策的研究主要基于决策粗糙集,整个论域被划分成3个部分,即正域(POS)、负域(NEG)和边界域(BND),分别代表着接受、拒绝和不承诺3种决策结果。决策粗糙集模型理论(decision-theoretic rough set model, DTRS),是由姚一豫等在1990年提出[21-23]。它将概率粗糙集和最小风险贝叶斯决策结合起来,通过计算各类分类决策风险损失值,对正域(POS)、负域(NEG)和边界域(BND)进行划分。假设有两种状态的集合Ω={X, ¬X}, X和¬X是互补关系的两种状态,即对象属于X或者属于¬X。由于分类结果有3个域,给定决策集A=(P, B, N),其中P、B、N分别表示将对象划分到正域、负域、边界域的决策行为。由于采取不同决策行为会产生不同的损失,λPP、λBP、λNP分别代表当x属于X时,x被划分到正域、负域、边界域的损失;λPN、λBN、λNN则分别代表当x不属于X时,x被划分到正域、负域、边界域的损失。表 1为对应的决策损失矩阵。
| 表 1 3种决策的损失矩阵 Tab.1 Loss function matrix of three-way decisions |
根据Bayes决策过程的推导,通过引入参数α、β可得到基于决策粗糙集的三支决策规则。
| $ 若P\left( {X\left| {{{\left[X \right]}_R}} \right.} \right) \ge \alpha, 则x \in {\rm{POS}}\left( X \right) $ | (1) |
| $ 若\beta < P\left( {X\left| {{{\left[X \right]}_R}} \right.} \right) < \alpha, 则x \in {\rm{BND}}\left( X \right) $ | (2) |
| $ 若P\left( {X\left| {{{\left[X \right]}_R}} \right.} \right) \le \beta, 则x \in {\rm{NEG}}\left( X \right) $ | (3) |
其中
| $ \alpha = \frac{{{\lambda _{PN}}-{\lambda _{BN}}}}{{\left( {{\lambda _{PN}}-{\lambda _{BN}}} \right) + \left( {{\lambda _{BP}}-{\lambda _{PP}}} \right)}} $ | (4) |
| $ \beta = \frac{{{\lambda _{PN}}-{\lambda _{NN}}}}{{\left( {{\lambda _{BN}}-{\lambda _{NN}}} \right) + \left( {{\lambda _{NP}}-{\lambda _{BP}}} \right)}} $ | (5) |
本文基于三支决策的思想,实现对网络的非重叠社团结构划分。对于初始聚类粒化后获得重叠的社团结构定义如下。
1) 正域(POS):左边社团的非重叠节点。
2) 负域(NEG):右边社团的非重叠节点。
3) 边界域(BND):重叠部分的节点。
其中,正域与负域仅仅为相对的概念,也可将边界域的左边定义为负域,右边定义为正域。本文为叙述方便,只将左边称为正域,右边称为负域。
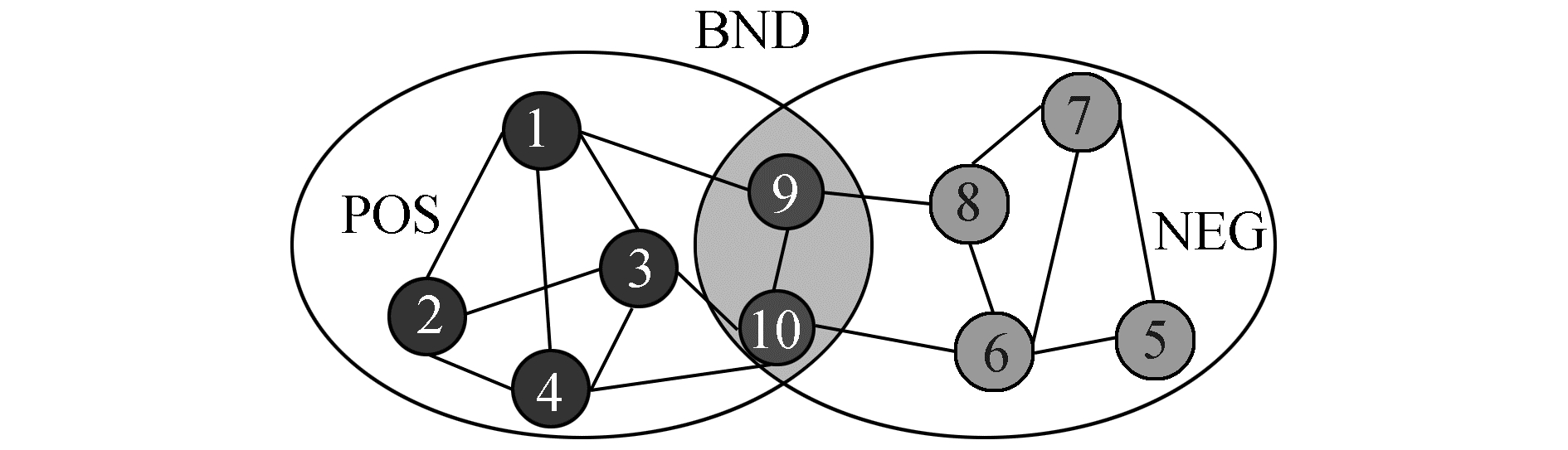
如图 1所示,左右两个椭圆分别代表两个社团结构,从图中可以看出两个社团存在一定的重叠部分,如图中阴影部分,节点9和节点10。依据三支决策思想,可以将重叠部分定义为边界域,重叠部分左边社团定义为正域(POS(X)),即节点集合{1,2,3,4},重叠部分右边社团定义为负域(NEG(X)),即节点集合{5,6,7,8}。图 1中的阴影部分为边界域(BND(X)),即节点集合{9,10}。
|
图 1 重叠社团3个域的划分 Fig.1 The division of three domains in overlapping community |
本文采用与文献[11]相同的聚类粒化思想进行初始社团划分,形成重叠的社团结构。算法中以粒化系数为阈值控制合成过程,并选取模块度函数Q对划分结果进行评价,现将粒化系数和模块度概念介绍如下。
粒化系数f(C) 是判断是否对社团进行聚类粒化的一个标准,其公式如下:
| $ 粒化系数\;f\left( C \right) = \frac{{\left\lfloor {{\text{BND}}} \right\rfloor }}{{\left\lfloor {{\text{POS + NEG + BND}}} \right\rfloor }} $ | (6) |
式中:Ci, Cj⊆C, BND=Ci∩Cj, POS=Ci-BND, NEG=Cj-BND; C是粒化到当前的粒集合;
给出一个参数λ∈[0, 1],当粒集合中存在任意两个粒的粒化系数f(Gr)≥λ时,对这两个粒进行邻接粒化操作,否则,就不对该粒集合进行邻接粒化操作。
模块度函数Q[24] 模块度函数Q是由Newman和Girvan提出的,在社交网络中,它是衡量一个非重叠社团划分好坏的量化指标。目前,模块度函数Q作为社团划分评价标准已经被广泛使用。其定义如下:
| $ Q = \sum\limits_i {\left( {{e_{ii}} - a_i^2} \right)} = {\rm{Tre}} - \left\| {{\mathit{\boldsymbol{e}}^2}} \right\| $ | (7) |
式中:‖e2‖表示矩阵e2中所有元素之和。先定义一个k×k的对称矩阵e=(eij),eij表示网络中连接两个不同社团的节点的边在所有边中所占的比例,这两个节点分别位于第i个社团和第j个社团。设矩阵中对角线上的元素之和为
三支决策模型根据正域、负域和边界域获取决策规则,在处理模糊性、不完整性数据时,可以给出不承诺规则,能够降低误判[25], 提高决策正确性。对于社团划分,边界域的存在是暂时的,随着获取信息的增多,对边界域中对象的认识更加细化,最终的划分必须是明确的,即正域和负域。为了划分边界域中节点的归属问题,本文基于三支决策理论,计算边界域节点的社团归属度,增加新的信息进行二次决策,提出一种基于三支决策的非重叠社团划分算法。
2.1 节点相似度与社团归属度为了评价边界域中的节点与正域、负域间的归属关系,给出如下定义。
定义1 节点相似度SVV[26]。给定一个无向无权网络G=(V, E), 其中V={vi, i=1, 2, …, n}代表网络中节点的集合,E={(u, v)∣u, v∈V}代表边的集合。邻居节点的相似度可以表示为
| $ {\rm{SVV}}\left( {{v_i}, {v_j}} \right) = \frac{{\left| {\mathit{\Gamma }\left( {{v_i}} \right) \cap \mathit{\Gamma }\left( {{v_j}} \right)} \right|}}{{k\left( {{v_i}} \right) \times k\left( {{v_j}} \right)}} $ | (8) |
式中:对于边界域中的节点v,定义它的邻居为Γ(v),k(v)=∣Γ(v)∣是节点v的度; Γ(vi)、Γ(vj)表示节点vi、vj的邻居数目; ∣Γ(vi)∩Γ(vj)∣表示共同邻居数目; k(vi)、k(vj)分别表示节点vi、vj的度。
定义2 边界域中节点v与正域、负域间的归属度。由于边界域节点与正域(负域)间的归属度反映了该域节点与正域(负域)连接的紧密程度,归属度越大,说明它们之间连接越紧密,更有可能被划分到正域(负域)中。边界域中节点与正域、负域之间的归属度分别表示为
| $ \begin{array}{*{20}{c}} {{B_P} = {\rm{Belongness\_POS}}\left( {v, {\rm{POS}}} \right) = }\\ {\frac{{\sum\limits_i^{{N_P}} {{\rm{SVV}}\left( {{v_i}, {v_j}} \right)} }}{{{N_P}}}} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {{B_N} = {\rm{Belongness\_NEG}}\left( {v, {\rm{NEG}}} \right) = }\\ {\frac{{\sum\limits_i^{{N_N}} {{\rm{SVV}}\left( {{v_i}, {v_j}} \right)} }}{{{N_N}}}} \end{array} $ | (10) |
式中:vi∈BND; vj∈POS (NEG); NP是正域中节点数目总和, NP=POS; NN是负域中节点数目总和, NN=NEG; BP表示边界域中的节点与正域的归属度;BN表示边界域中的节点与负域的归属度。
定义3 边界域参数γ。BP、BN表示通过式(9)、式(10) 计算得到的归属度值,即BP表示边界域中节点v与正域计算得到的归属度,BN表示边界域中节点v与负域计算得到的边界域的归属度,∣BP-BN∣max表示归属度差值绝对值的最大值。可依据边界域参数γ进行如下划分:
| $ 若\frac{{{B_P} - {B_N}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} > \gamma, 则\;v \in {\rm{POS}}\left( X \right) $ | (11) |
| $ 若\frac{{{B_N} - {B_P}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} > \gamma, 则\;v \in {\rm{NEG}}\left( X \right) $ | (12) |
| $ 若\frac{{{\left| {{B_P} - {B_N}} \right|}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} < \gamma, 则\;v \in {\rm{BND}}\left( X \right) $ | (13) |
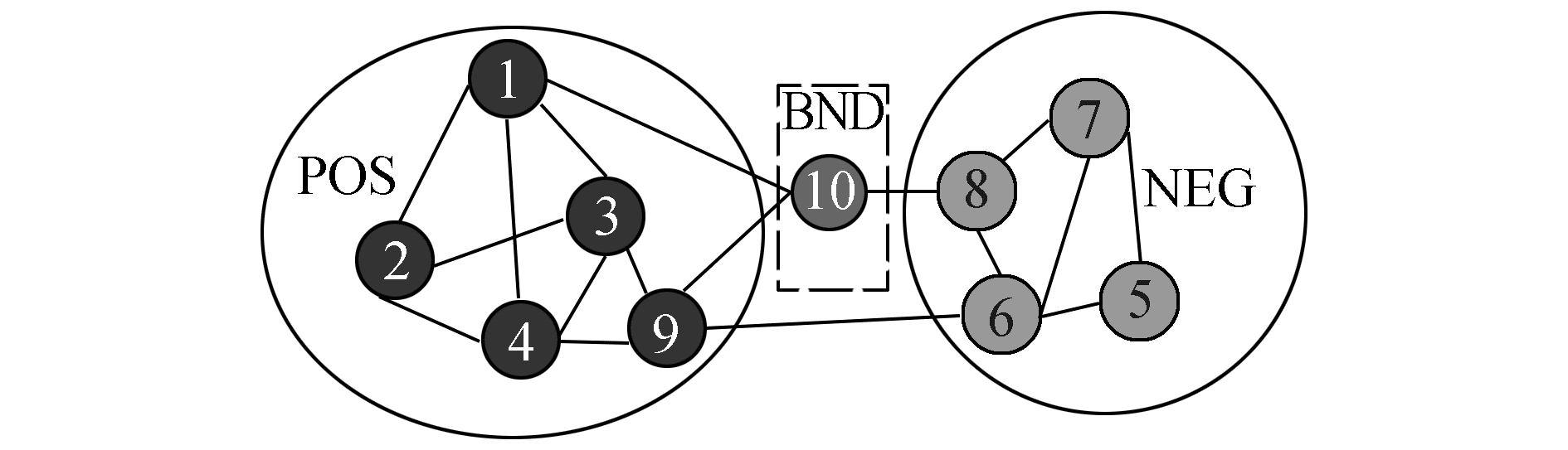
根据式(11)~(13) 可将边界域参数映射到[0, 1]区间。将边界域中的节点进一步划分到正域或负域中。如图 2所示,通过分别计算边界域中节点9、10与正域(负域)的归属度及其差值,即
|
图 2 计算归属度后3个域的划分 Fig.2 The division of three domains after calculation of belonging degree |
| $ \begin{array}{*{20}{c}} {{B_{P9}} = 0.11, {B_{N9}} = 0.05;}\\ {{B_{P9}} - {B_{N9}} = 0.11 - 0.05 = 0.06;}\\ {{B_{N9}} - {B_{P9}} = 0.05 - 0.11 = - 0.06;} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{B_{P10}} = 0.12, {B_{N10}} = 0.09;}\\ {{B_{P10}} - {B_{N10}} = 0.12 - 0.09 = 0.03;}\\ {{B_{N10}} - {B_{P10}} = 0.09 - 0.12 = - 0.03;} \end{array} $ |
则∣BP-BN∣max=0.11-0.05=0.06,此时当γ=0.6时,对于节点9,
在N-TWD算法中引入三支决策的思想,算法流程具体描述如算法1所示。算法1中针对归属度处理后依然留在边界域中的节点按照邻居节点投票法进行处理,假设归属度处理后仍留在边界域中的节点v∈BND(X),令与节点v直接相连的k个节点的集合为{v1, v2, …, vk};如果v∈BND(X)与POS(X)中的节点vi有直接连边,则标记lpi;反之与NEG(X)中的节点vj有直接连边,则标记lni。其中pi表示节点vi属于正域的编号,ni表示节点vj属于负域的编号。因此,可得归属度处理后仍留在边界域中的节点v对应的编号集合为L=Label(v)={l(p1, p2, …, pk), l(n1, n2, …, nk)},N(L)函数返回编号集合L中出现频率最高的社团编号。最终可获得非重叠的社团结构划分结果。
算法1 N-TWD算法。
输入 一个无向无权网络G:(V, E)。
输出 无重叠的网络社团结构POS(X)、NEG(X)。
1) 初始化网络,根据公式(6) 计算粒化系数POS(X)、NEG(X)、BND(X)。
2) 计算边界域中节点与正域、负域中的社团的归属度BP和BN:
| $ \begin{array}{*{20}{c}} {{\rm{while}}\;\exists v \in {\rm{BND}}\left( X \right)、\frac{{{\left| {{B_P} - {B_N}} \right|}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} > \gamma \;{\rm{do}}}\\ {{\rm{if}}\frac{{{B_P} - {B_N}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} > \gamma }\\ {{\rm{then}}\;v \in {\rm{POS}}\left( X \right), {\rm{POS}}\left( X \right) = {\rm{POS}}\left( X \right) + \left\{ v \right\}}\\ {{\rm{else}}\;v \in {\rm{NEG}}\left( X \right), {\rm{NEG}}\left( X \right) = {\rm{NEG}}\left( X \right) + \left\{ v \right\}}\\ {{\rm{end}}\;{\rm{while}}} \end{array} $ |
3) 在2) 完成后,对于仍然留在边界域中的节点进行投票处理:
| $ \begin{array}{*{20}{c}} {{\rm{while}}\;\exists v \in {\rm{BND}}\left( X \right), \frac{{{\left| {{B_P} - {B_N}} \right|}}}{{{{\left| {{B_P} - {B_N}} \right|}_{\max }}}} < \gamma \;{\rm{do}}}\\ {L = {\rm{Label}}\left( v \right)}\\ {{\rm{if}}\;N\left( L \right) \in {\rm{POS}}\left( X \right)}\\ {{\rm{then}}\;v \in {\rm{POS}}\left( X \right), {\rm{POS}}\left( X \right) = {\rm{POS}}\left( X \right) + \left\{ v \right\}}\\ {{\rm{else}},\;v \in {\rm{NEG}}\left( X \right), {\rm{NEG}}\left( X \right) = {\rm{NEG}}\left( X \right) + \left\{ v \right\}}\\ {{\rm{end}}\;{\rm{while}}} \end{array} $ |
4) 输出POS(X)和NEG(X)。
3 实验分析 3.1 基准数据实验为了验证N-TWD算法的有效性和可行性,本文采用了4个典型社交网络数据集作为测试数据集,分别是著名的空手道俱乐部网络(Zachary's karate club)、足球联盟网络(American college football)、海豚网络(dolphin social network)和悲惨世界网络(lesmis)。实验数据集的基本信息如表 2。
| 表 2 实验数据集的基本信息 Tab.2 Benchmark datasets information |
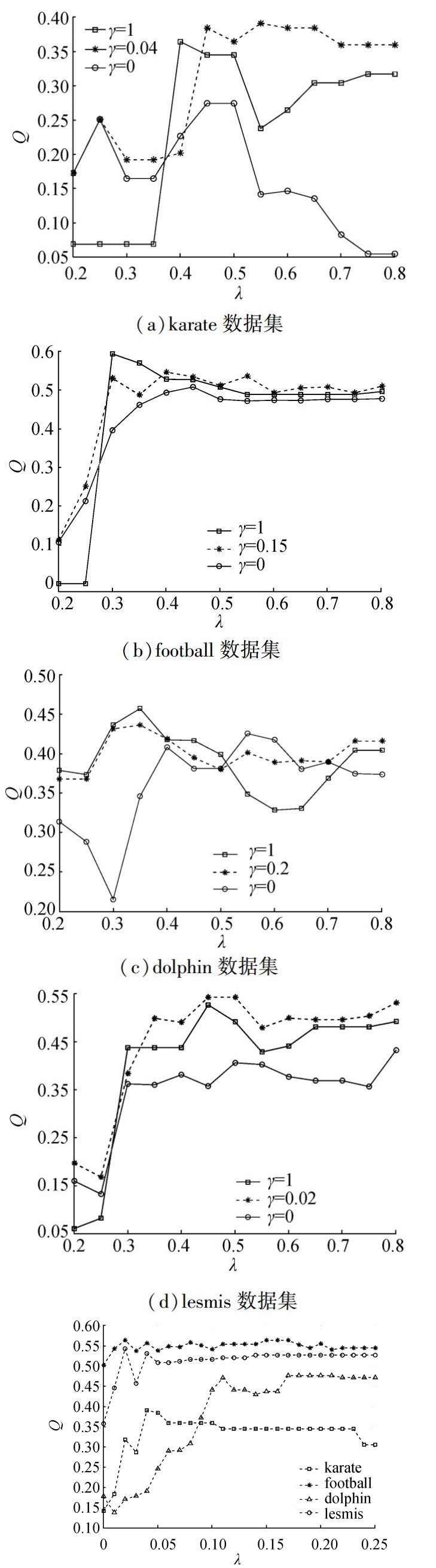
在N-TWD算法中,粒化参数λ、边界域参数γ的取值对算法的最终结果有一定的影响。参数λ作为粒化系数,控制着初始社团粒度,对于最终的社团划分好坏有一定的影响。若λ为1,则任意两粒子都不满足粒化条件,算法无法进行粒化操作迭代,直接按投票法获得最终的社团结构;若λ为0,则任意两粒子之间均可进行粒化操作,迭代后所得到的粒子包含了所有网络的节点,即该网络可视为一个社团。参数γ作为边界域参数,它的大小决定投票和归属度这两种方法对边界域中节点处理的多少。γ为1时,则边界域中的节点采用全投票法,等同于文献[11]所提算法;γ为0时,则边界域中的节点采用全归属度方法处理。图 3给出了在不同数据集上γ取得最优值时Q值随参数λ值变化的关系图。其中,γ=1表示完全采用投票处理边界域中的节点;γ=0表示完全使用归属度处理边界域中的节点;γ≠0表示对边界域中的节点先采用归属度处理后,对于仍留在边界域中的节点采用投票法处理。从图 3中(a)、(b)、(d)明显可以看出,随着λ的增大, 折线λ≠0基本都在折线λ=0和γ=1上方。图 3中(c)图, 由于dolphin数据集自身网络特别稀疏,在层次聚类粒化的过程中获得的重叠部分较少,所以使用本算法划分后效果不明显。总体上,即当γ≠0时,在4个数据集上社团划分评价指标Q的值都基本优于γ=0和γ=1时的值,此时划分后的社团内部联系比较紧密,说明采用三支决策的方法对边界域中重叠节点进行二步决策对社团划分有明显的作用,使社团划分更加合理。
|
图 3 Q值与λ值关系图 Fig.3 The connection between λ and Q |
从图 3的分析可知,边界域参数γ的引入可以使延迟决策划分到边界域中的重叠节点做出二次决策,决策结果对非重叠社团划分的好坏有较为显著的影响。图 4给出了在4个不同数据集上,当λ取上述最优值时,Q值随着边界域参数γ的变化情况。由于各个数据集自身网络结构不同,需要从不同的侧面来了解网络结构,从而获得更充分的信息做出二次决策。在二次决策时,我们引入归属度计算和邻居节点投票处理。归属度反映了节点与社团间联系的紧密程度;投票法根据节点的邻居数目多少决定其归属。这两者从不同的侧面对边界域中的对象有了更细化的认识,而γ取值的大小决定两种方法对重叠部分处理的多少。根据不同数据集的自身特性选择合适的值作为边界域参数γ的值。由图 4可以看出,随着γ的增大,数据集karate、football、lesmis的模块度Q值在0~0.05范围先增后减,在γ=0.05~0.25之间波动范围不大。而dolphin数据集在γ=0.1~0.15之间先增后减,在γ=0.15~0.2之间虽有增大趋势但未超过最高值,在γ=0.2以后基本趋于平稳。其中karate、football、dolphin、lesmis这4个数据集中γ取值分别为0.04、0.15、0.2、0.02时,Q值最大,说明γ∈[0, 0.2]时,边界域中节点划分效果最好。

|
图 4 γ值与Q值关系图 Fig.4 The connection between γ and Q |
作者将本文算法与其他相关社团划分算法(GN、NFA、LPA、CACDA)在4个真实的网络数据集上的模块度Q值进行了对比,实验结果如表 3所示。其中,GN[7]为经典的分裂式层次社团挖掘算法, NFA[9]为Newman快速算法,是基于模块度优化的凝聚式社团挖掘算法, LPA[27]为快速标签传播算法, CACDA[11]为基于邻接粒化的社团发现算法。
| 表 3 数据集中不同算法Q值的比较 Tab.3 Comparison of Q by different algorithm in datasets |
表 3给出了N-TWD算法与其他相关算法划分后最优的模块度值的对比实验结果。从表 3中可以看出,本文提出的算法N-TWD在karate和lesmis、football上都获得了最高的模块度值,在dolphin上也获得了较高的模块度值。CACDA在football上获得了最高的模块度值,但没能在其他网络上获取较高的模块度值。由于本文算法和CACDA算法的主要开销在于进行粒化,需要遍历邻接矩阵的每行(每列),其时间复杂度均为O(n2)。GN虽然在数据集dolphin上取得最高的Q值,但是它的时间复杂度是这5种算法中最高的,为O(n3)。NFA虽然在dolphin获得了第2高模块度值,但由于NFA本身是贪婪寻优算法,所以可以获得很高的模块度算法,且NFA需要非常多的时间进行迭代,其时间复杂度为O((m+n)n)。LPA的线性复杂度为O(m+n)。从表 3中可以看出,本文提出的算法相比其他4个算法,时间复杂度较低,获取的社团模块度值总体上更高,总体性能更优。
3.2 应用数据实验为了进一步验证本文所提出的N-TWD算法的有效性,本文以某市移动通信的实际应用数据为例进行实验。实验数据根据通信基站间是否有信号切换确定两基站节点间是否存在边来构建网络模型。构建的无权无向网络如图 5所示,其中包含3 644个顶点,6 976条边。

|
图 5 无权无向网络 Fig.5 A unweighted and undirected network |
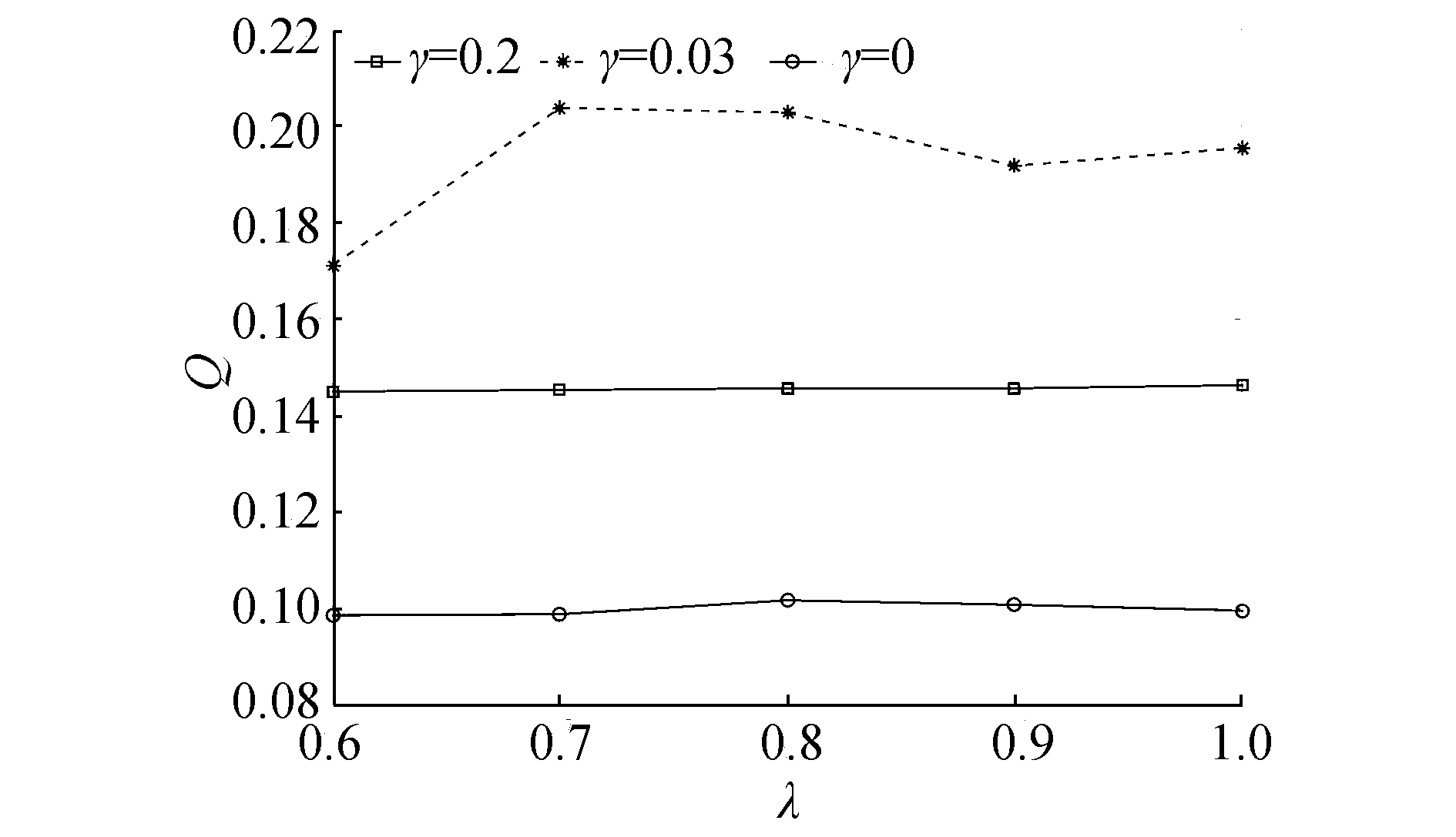
将图 5所示的网络采用本文N-TWD算法进行社团划分,图 6给出了在真实数据集上Q值与λ值的关系图。从图 6可以看出,在真实数据集网络中,对于划分到边界域中的重叠节点,采用本算法进行社团划分依然具有有效性。图 6中虚折线表示N-TWD算法处理后社团模块度的变化趋势,正方形实折线和圆形实折线分别表示仅采用投票和仅采用归属度处理情况下的模块度变化趋势。图 6中随着λ的变化,γ取得最优值时(γ=0.03) 能比投票(γ=0.2) 和归属度方法(γ=0) 直接决策取得更高Q值,采用和文献[11]相同的干扰模型评价可以得到更优的频点干扰值。表明在N-TWD算法划分下可以更真实地体现应用数据集中的网络结构特征。
|
图 6 真实数据集中Q值与λ值关系图 Fig.6 The connection between λ and Q of true dataset |
本文将三支决策的思想应用于非重叠社团划分,提出了一种基于三支决策的非重叠社团划分算法(N-TWD),旨在解决社团划分过程中出现的节点重叠部分。本文算法基于三支决策的思想,对于社团重叠部分(边界域)通过计算节点与明确社团(正域/负域)间的归属度,再对重叠节点的具体归属进行二次决策,从而进行三分类,即正域、负域、待处理(仍留在边界域),对于待处理部分采取邻居节点投票法进行再一次决策,最终将其准确划分到正域或负域中。与其他算法相比,本文算法随着决策步骤的增加,对边界域中样本的归属认知更加细化,时间复杂度总体较低,且获取了更高的Q值,划分后的社团结构联系比较紧密,说明边界域中的重叠节点得到了更为稳定的划分。下一步将会基于网络的局部信息,进一步改进初始重叠社团的获取方法。
| [1] |
SHEN H, CHENG X, CAI K, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica a: statistical mechanics and its applications, 2009, 388(8): 1706-1712. DOI:10.1016/j.physa.2008.12.021 ( 0) 0)
|
| [2] |
LIU Y, PAN L, JIA X, et al. Three-way decision based overlapping community detection[C]//Rough Sets and Knowledge Technology. Springer, Berlin, 2013: 279-290. http://link.springer.com/chapter/10.1007/978-3-642-41299-8_27
( 0) 0)
|
| [3] |
柯望. 基于层次粒化的社团发现方法研究[D]. 合肥: 安徽大学, 2016. KE Wang. Reach on community detection algorithm based on Hierarchical Granulation[D]. Hefei: Anhui University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10357-1016128267.htm (  0) 0)
|
| [4] |
KERNIGHAN B W, LIN S. An efficient heuristic procedure for partitioning graphs[J]. The bell system technical journal, 1970, 49(2): 291-307. DOI:10.1002/bltj.1970.49.issue-2 ( 0) 0)
|
| [5] |
ZHANG Y P, WANG Y. Detecting communities using spectral bisection method based on normal matrix[J]. Computer engineering and applications, 2006, 46(27): 43-45. ( 0) 0)
|
| [6] |
POTHEN A, SIMON H D, LIOU K P. Partitioning sparse matrices with eigenvectors of graphs[J]. SIAM journal on matrix analysis and applications, 1990, 11(3): 430-452. DOI:10.1137/0611030 ( 0) 0)
|
| [7] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the national academy of sciences, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 ( 0) 0)
|
| [8] |
金弟, 杨博, 刘杰, 等. 复杂网络簇结构探测——基于随机游走的蚁群算法[J]. 软件学报, 2012, 23(3): 451-464. JIN Di, YANG Bo, LIU Jie, et al. Ant colony optimization based on random walk for community detection in complex networks[J]. Journal of software, 2012, 23(3): 451-464. (  0) 0)
|
| [9] |
NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical review E, 2004, 69(6): 066133. DOI:10.1103/PhysRevE.69.066133 ( 0) 0)
|
| [10] |
RADICCHI F, CASTELLANO C, CECCONI F, et al. Defining and identifying communities in networks[J]. Proceedings of the national academy of sciences of the United States of America, 2004, 101(9): 2658-2663. DOI:10.1073/pnas.0400054101 ( 0) 0)
|
| [11] |
赵姝, 柯望, 陈洁, 等. 基于聚类粒化的社团发现算法[J]. 计算机应用, 2014, 34(10): 2812-2815. ZHAO Shu, KE Wang, CHEN Jie, et al. Community detection algorithm based on clustering granulation[J]. Journal of computer applications, 2014, 34(10): 2812-2815. DOI:10.11772/j.issn.1001-9081.2014.10.2812 (  0) 0)
|
| [12] |
YAO Y Y. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341-353. DOI:10.1016/j.ins.2009.09.021 ( 0) 0)
|
| [13] |
YAO Y. Two semantic issues in a probabilistic rough set model[J]. Fundamental informaticae, 2011, 108(3/4): 249-265. ( 0) 0)
|
| [14] |
贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M]. 南京: 南京大学出版社, 2012.
( 0) 0)
|
| [15] |
于洪, 王国胤, 李天瑞, 等. 三支决策:复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015.
( 0) 0)
|
| [16] |
YU H, ZHANG C, WANG G. A tree-based incremental overlapping clustering method using the three-way decision theory[J]. Knowledge-based systems, 2016, 91: 189-203. DOI:10.1016/j.knosys.2015.05.028 ( 0) 0)
|
| [17] |
YU H, WANG Y, JIAO P. A three-way decisions approach to density-based overlapping clustering[M]. Berlin Heidelberg: Springer, 2014: 92-109.
( 0) 0)
|
| [18] |
YU H, ZHANG C, HU F. An Incremental Clustering Approach Based on Three-Way Decisions[C]//Rough Sets and Current Trends in Computing.Springer, Berlin Heidelberg, 2014, 8536: 152-159. https://link.springer.com/chapter/10.1007/978-3-319-08644-6_16
( 0) 0)
|
| [19] |
LIU Y, PAN L, JIA X, et al. Three-way decision based overlapping community detection[C]//Rough Sets and Knowledge Technology, 2013, 8171: 279-290. https://link.springer.com/chapter/10.1007/978-3-642-41299-8_27
( 0) 0)
|
| [20] |
YAO Y. An Outline of a theory of three-way decisions[C]//Rough Sets and Currnet Trends in Computing. Berlin Heidelberg:Springer, 2012: 1-17. https://link.springer.com/chapter/10.1007/978-3-642-32115-3_1
( 0) 0)
|
| [21] |
YAO Y Y, WONG S K M. A decision theoretic framework for approximating concepts[J]. International journal of man-machine studies, 1992, 37(6): 793-809. DOI:10.1016/0020-7373(92)90069-W ( 0) 0)
|
| [22] |
JIA X, TANG Z, LIAO W, et al. On an optimization representation of decision-theoretic rough set model[J]. International journal of approximate reasoning, 2014, 55(1): 156-166. DOI:10.1016/j.ijar.2013.02.010 ( 0) 0)
|
| [23] |
QIAN Y, ZHANG H, SANG Y, et al. Multi-granulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 225-237. DOI:10.1016/j.ijar.2013.03.004 ( 0) 0)
|
| [24] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 ( 0) 0)
|
| [25] |
贾修一, 李伟湋, 商琳, 等. 一种自适应求三枝决策中决策阈值的算法[J]. 电子学报, 2011, 39(11): 2520-2525. JIA Xiuyi, LI Weiwei, SHANG Lin, et al. An adaptive learning parameters algorithm in three-way decision-throretic rough set model[J]. Chinese journal of electronics, 2011, 39(11): 2520-2525. (  0) 0)
|
| [26] |
LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks[J]. Physical review E, 2006, 73(2): 026120. DOI:10.1103/PhysRevE.73.026120 ( 0) 0)
|
| [27] |
RAGHAVAN U N, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical reviewe, 2007, 76(3): 036106. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


