2. 江南大学 数字媒体学院,江苏 无锡 214122
2. School of Digital Media, Jiangnan University, Wuxi 214122, China
与传统媒介相比较,互联网为大众媒体提供了更加广泛、快捷和实时的信息传播平台。网络舆情的传播总是伴随着媒体的参与,没有媒体参与的传播模型和实际情况相去甚远[1]。近年来,媒体作用下的网络舆情传播引起了学者们的广泛关注,但大部分研究均局限于通过加入媒体节点,对经典复杂网络传播模型进行改进,关注于媒体节点本身在模型上的体现[2]。
近几年,互联网舆情传播研究工作借鉴传染病模型,如利用SIR、SIS等模型来模拟互联网舆情传播[3-7]。自Sudbury[8]首次将传染病SIR模型用于解释谣言传播以来,不断有学者提出改进的模型来描述网络舆情传播。顾亦然[9]提出了基于在线社交网络的谣言传播SEIR模型,并给出了抑制谣言传播的免疫策略;钱颖等[10]基于SIR模型对微博上的舆情传播进行了研究,建立了微博舆情传播模型;Xu等[11]通过将信息价值与用户行为引入社交网络信息传播模型中,改进和修改了SEIR模型,构建了基于社交网络的S-SEIR模型;李林等[12]利用网络传播的SIR模型,考虑两种冲突信息在社会网络上的同时传播,传播过程中引入个体处理冲突信息的3种行为方式,建立了信息的传播演化模型;夏承遗等[13]从复杂网络的拓扑结构和流行病的感染机制方面综述了当前国内外传播动力学研究的现状;文献[14-15]提到了新媒体中网络舆论对社会的影响,以及在线网络在网络舆论中的地位和发展[16-17]。
借鉴Bonzani等 [18]多车道的车辆动力学交通流量模型,本文认为舆情传播过程中的未知人群和传播人群均可以划分为3个层次,分别为消极、中立、积极,从消极到积极或从积极到消极的转换一般是要有个过程,即存在一个中立的过程。中立型人群的存在是有一定的合理性,也可以解释成潜在舆情传播的网民,这些网民表现为关注事态的发展,但不轻易表露自己的观点。中立型人群的存在对舆情传播具有非常重要的作用,媒体的导向作用真正起作用的往往就是这个群体。由此,我们试图通过构建带媒体作用下的舆情传播模型,把舆情群体划分为消极、中立、积极3个层次, 构建新的模型:(SI)3R模型。本文主要针对如何定义3种群体、构建(SI)3R模型,通过数值模拟仿真考察(SI)3R模型的参数选择及其媒体作用。
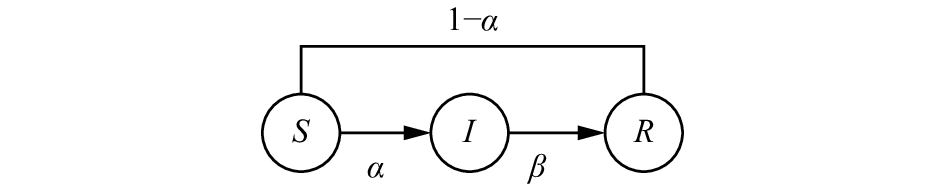
1 相关工作 1.1 SIR模型假设研究的信息系统是一个连接的无向有限网络,它有N个节点,如图1所示。
|
Download:
|
| 图 1 SIR模型 Fig. 1 SIR model | |
该系统由3类节点组成,分别为未知者(S)、传播者(I)、移除者(R)。在该模型中,如果一个未知者个体获得了谣言,它将作为一个传播者在每个时间步长以概率α传播给它的邻居,这在疾病传播模型中称为疾病传播率。另一方面,如果它遇到了一个传播者或移除者,传播者以β的概率变为移除者或者未知者以1–α的概率变为移除者。这就是所谓的传播者自发传播谣言机制。用S(t)、I(t)、R(t)分别表示未知者、传播者和移除者的数量,借鉴疾病模型,相应的密度分别为i(t)=I(t)/N,s(t)=S(t)/N,r(t)= R(t)/N,满足i(t)+s(t)+r(t)=1。
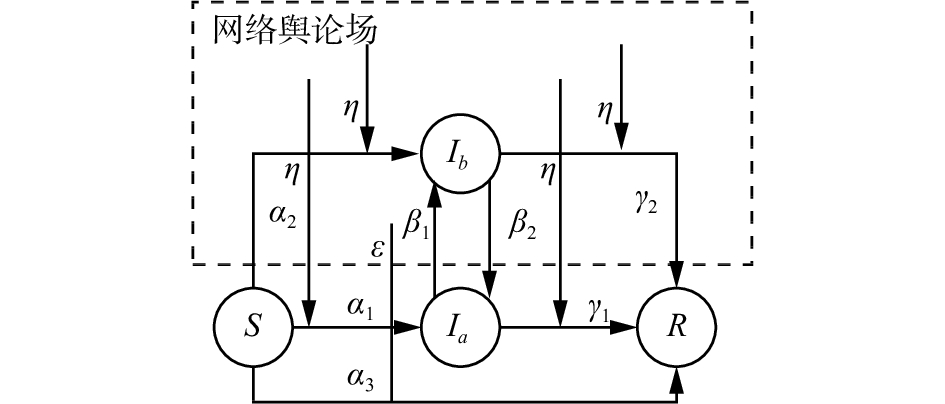
1.2 SIaIbR模型张立凡[2]考虑了媒体干预下带有讨论机制的网络舆情传播模型,如图2所示。
|
Download:
|
| 图 2 SIaIbR模型 Fig. 2 SIaIbR model | |
该模型中网民处于4中状态:未知状态S、传播状态Ia、传播状态Ib、移除状态R。Ia、Ib表示对于话题的两种不同观点,Ia是网民中靠近媒体一方的观点,而Ib表示在没有媒体刻意干预下网民自发形成的观点。
对应于SIaIbR模型的动力学方程为
| $\left\{ \begin{aligned} & \frac{{{\rm{d}}S}}{{{\rm{d}}t}} = A - {\alpha _1}S{I_a} - {\alpha _2}S{I_b} - {\alpha _3}S \\ & \frac{{{\rm{d}}{I_a}}}{{{\rm{d}}t}} = {\alpha _1}S{I_a} + {\beta _2}{I_a}{I_b} - {\beta _1}{I_a}{I_b} - {\gamma _1}{I_a} \\ & \frac{{{\rm{d}}{I_b}}}{{{\rm{d}}t}} = {\alpha _2}S{I_b} + {\beta _1}{I_a}{I_b} - {\beta _2}{I_a}{I_b} - {\gamma _2}{I_b} \\ & \frac{{{\rm{d}}R}}{{{\rm{d}}t}} = {\alpha _3}S + {\gamma _1}{I_a} + {\gamma _2}{I_b}\end{aligned} \right.$ | (1) |
在借鉴Bonzani [18]的多车道车辆动力学交通流量模型的同时,考虑到网络媒体传播的实际情况,本文提出了带有媒体作用的具有分层演化的网络舆情传播新模型。该模型主要探讨了在网络群体中,持3种不同观点的人群相互作用的转换机制,以及该机制对舆情传播过程的影响。该模型中网络群体处于3种状态:未知态(S)、传播态(I)、移除态(R)。用S(t)、I(t)、R(t)分别表示t时刻处于3种状态的网民占网民总量的比率。
2.1 两个定义定义1 媒体干预度η。在话题出现的时候,媒体的导向会使得未感染人群加入话题行列,表现为中立人群往积极人群状态转变的概率增大,并完整叠加到各层之间的转换概率。
定义2 层内渗透度ω+、ω–。表示处于同一个群体内活跃度不同的个体在交互过程中,因受到他方的影响而改变之前对事态的看法,进而转变到他方的层次中。这里假设每个群体有3层:消极层、中立层、积极层。这种因接触而发生状态转移的概率定义为渗透度,这里假设积极层与消极层之间的转换必须经过中立层,即不能直接转换。转入渗透率用ω+表示,转出渗透率用ω–表示,两者为对称关系,即ω–ij=ω+ji(i, j={1, 2, 3})。
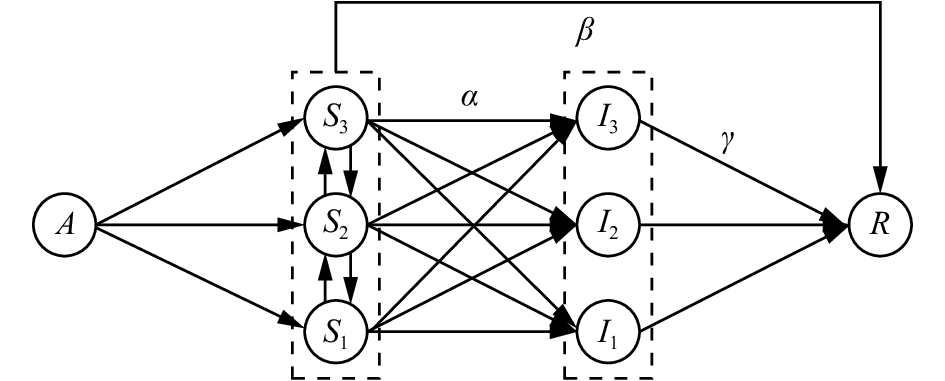
2.2 (SI)3R模型示意图具有分层演化趋向行为的网络舆情传播模型(SI)3R如图3所示。与之对应的带有媒体干预的具有分层演化趋向行为的网络舆情传播模型如图4所示。
|
Download:
|
| 图 3 分层演化趋向行为的网络舆情传播模型(SI)3R Fig. 3 Internet public opinion dissemination (SI)3R model of hierarchical evolutionary behavior | |

|
Download:
|
| 图 4 媒体作用讨论机制的网络舆情话题传播模型 Fig. 4 Internet public opinion dissemination model with discussion under the influence of media | |
图3给出了分层演化趋向行为的网络舆情传播模型,与图2比较,图3中未知群体(S)分成了3种情况,即消极、中立和积极,传播群体(I)也对应地分成了3种情况,即消极、中立和积极,对模型的描述更加细化。图4则给出了具有媒体干预下的图3表达形式,其中只给出了一个层面的媒体干预传播模型,其中i=1, 2, 3分别对应于消极、中立和积极。
2.3 动力学模型(SI)3R模型对应的动力学方程为式(2),其中i={1, 2, 3}对应于每个种群中的3个层次之一,分别对应消极层、中立层、积极层。
| $\left\{ \begin{aligned} & \frac{{{\rm{d}}{S_i}}}{{{\rm{d}}t}} = A - {S_i}\sum\limits_{j = 1}^3 {(\omega _{ij}^ - S{}_j - \omega _{ij}^ + S{}_j + {\alpha _{ij}}I{}_j)} - \beta {}_i{S_i} \\ & \frac{{{\rm{d}}{I_i}}}{{{\rm{d}}t}} = {S_i}\sum\limits_{j = 1}^3 {{\alpha _{ij}}I{}_j} - \gamma {}_i{I_i} \\ & \frac{{{\rm{d}}R}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^3 {({\beta _j}{S_j} + \gamma {}_j{I_j})} \end{aligned} \right.$ | (2) |
表1给出了式(2)中出现的各个参数说明,其中i, j={1, 2, 3}。
| 表 1 参数说明 Tab.1 Parameter description |
媒体干预是一个对网民演化影响很大的重要因素;媒体干预程度在概率密度中作为一个现象参数ηi (i=1, 2, 3),ηi∈[0, 1]。ηi值越小表示媒体干预程度越低,越大表示媒体干预程度越高。
对于未知人群所处的层次j和传播人群所处层次k,考虑两种情况:j≤k,j>k。对于每种情况,可推导出未知人群转化为传播人群或保持群体不变的概率。
2.4.1 未知人群等级低于或等于传播人群等级(j≤k)当j≤k 时,候选网民在未知人群中受到传播人群中等级较高的网民影响。发生作用后,候选网民可能留在原来的未知人群中或者变换到传播人群中。
1) j≠3时
| $\omega _{jk}^ - = \left\{\! {\begin{array}{*{20}{l}}{0, \quad j = j - 1}\\{(1 - {\eta _j})[1 - {I_k}(1 - {S_j})], \quad j = j}\\{{\eta _j}[1 - {I_k}(1 - {S_j})], \quad j = j + 1}\end{array}} \right.$ | (3) |
| ${\alpha _{jk}} = \left\{\! {\begin{array}{*{20}{l}}{(1 - {\eta _j}){I_k}(1 - {S_j}), \quad j = k - 1}\\{{\eta _j}{I_k}(1 - {S_j}), \quad j = k}\\{0, \quad j = k + 1}\end{array}} \right.$ | (4) |
式(3)给出了候选网民保持在当前未知人群种类的概率。人群种类中网民参与的密度越低,当前人群种类的密度越高,则保持在当前人群种类的概率就越高。实际上,当媒体干预度η=0时,网民会保持原有的传播速度,在任何情况下都不会转移;当η=1时则转移。式(4)给出了候选网民从未知人群变换到传播人群中的概率。这个概率的大小取决于媒体干预度和j类人群、j-1类人群的网民参与密度,消极人群的密度越小,这个概率就越小。
2) j=3时
| $\omega _{jk}^ - = \left\{\! {\begin{array}{*{20}{l}}\!\!\!{0, \quad j = j - 1}\\\!\!\!{(1 - {\eta _j}), \quad j = j}\\\!\!\!{{\rm{0}}, \quad j = j + 1}\end{array}} \right.$ | (5) |
| ${\alpha _{jk}} = \left\{\! {\begin{array}{*{20}{l}}\!\!\!{{\rm{0}}, \quad j = k - 1}\\\!\!\!{{\eta _j}, \quad j = k}\\\!\!\!{0, \quad j = k + 1}\end{array}} \right.$ | (6) |
当 j>k 时,候选网民在未知人群中受到传播人群中等级较低的网民影响。发生作用后,候选网民可能留在原来的人群中或者变换到传播人群中,则对应的转移概率规则如下:
| $\omega _{jk}^ - = \left\{\! {\begin{array}{*{20}{l}}\!\!\!{(1 - {\eta _j})[1 - {I_k}(1 - {S_j})], \quad j = j - 1}\\\!\!\!{{\eta _j}[1 - {I_k}(1 - {S_j})], \quad j = j}\\\!\!\!{{\rm{0}}, \quad j = j + 1}\end{array}} \right.$ | (7) |
| ${\alpha _{jk}} = \left\{\! {\begin{array}{*{20}{l}}\!\!\!{{\rm{0}}, \quad j = k - 1}\\\!\!\!{(1 - {\eta _j}){I_k}(1 - {S_j}), \quad j = k}\\\!\!\!{{\eta _j}{I_k}(1 - {S_j}), \quad j = k + 1}\end{array}} \right.$ | (8) |
这一节我们考察传播模型的数值模拟。为便于考察模型的动力学特性,这里我们分3种情况讨论参数对传播过程的影响。1)未知群体初始化对传播过程的影响,即3个分量分配不同的比例对传播过程的影响;2)总体密度变化对传播过程的影响;3)媒体干预度对传播过程的影响。
正常情况下,媒体干预度η≤0.4[2],因此,3.1、3.2节的实验中,均设η=0.3。
3.1 不同初始化S分量对传播过程的影响为了检验不同的初始化S分量对传播过程的影响,我们做了4组实验,表2给出了初始化S分量的不同百分比的设置(满足S1+S2+S3=1)。设未知人群总体密度S=0.9,媒体干预度η=0.3。
| 表 2 初始化S分量的不同设置 Tab.2 Different settings of S component initialization |
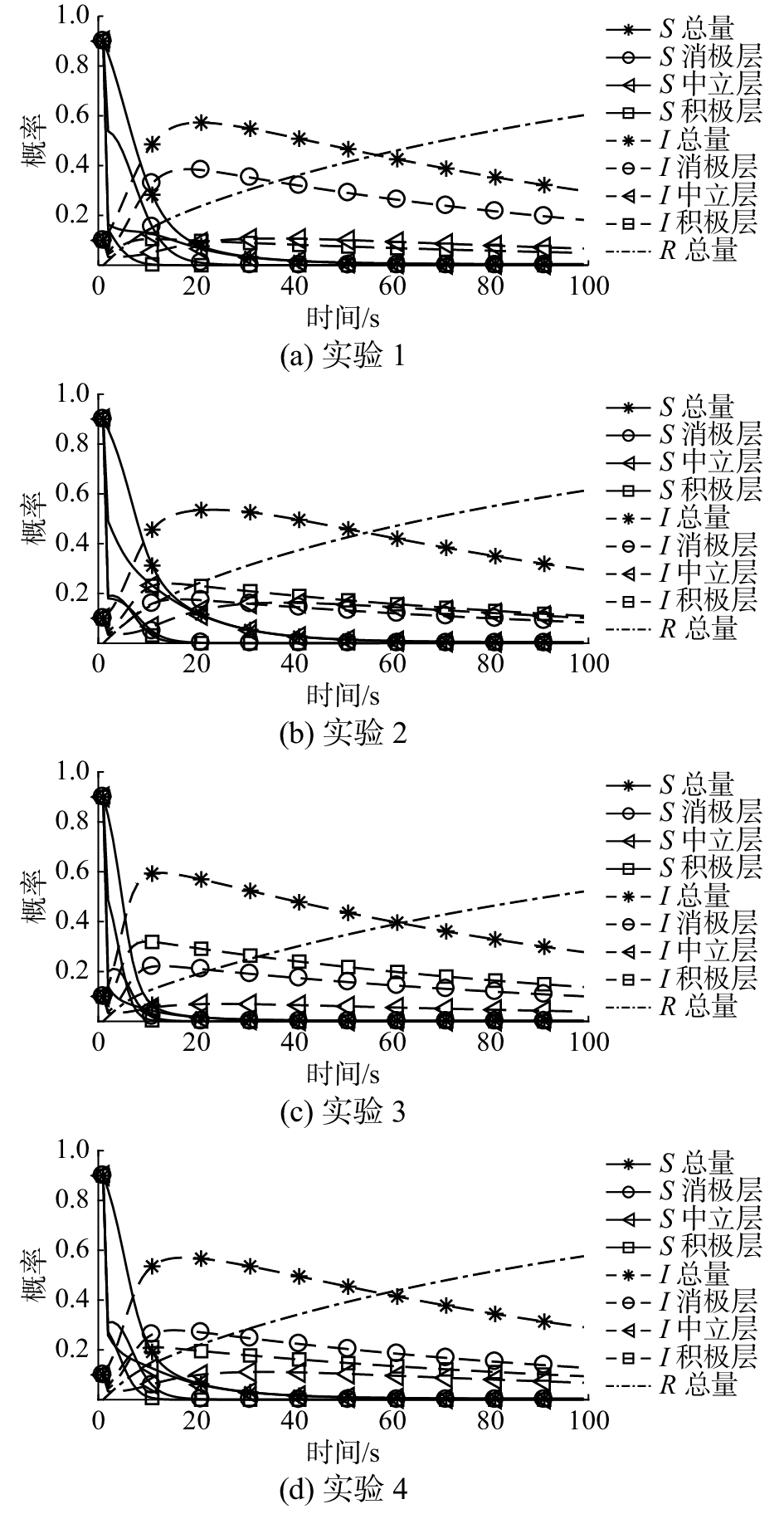
仿真实验中,未知人群(实线)、传播人群(虚线)、移除人群(中心线),第一分量消极层(圆形标记)、第二分量中立层(三角形标记)、第三分量积极层(正方形标记)、总量(星号标记)随时间的变化曲线关系如图5~8所示。
|
Download:
|
| 图 5 初始化S分量的不同设置对比 Fig. 5 Comparison of different settings of S component initialization | |
|
Download:
|
| 图 6 不同的总体密度设置 Fig. 6 Settings of different total densities | |
|
Download:
|
| 图 7 不同媒体干预度设置 Fig. 7 Settings of different media intervention degrees | |

|
Download:
|
| 图 8 (SI)3R模型 Fig. 8 (SI)3R model | |
从图5可以看到,传播人群的I1、I3对未知人群密度初值的设置比较敏感,I2没有多少变化。这说明,处于中立层的传播群体相对比较稳定,不会因初始值大小而发生较大的波动,即在一定时间段内,进入中立层的人数与离开中立层的人数基本保持平衡。中立层人群的平衡对传播过程所起到的作用比较重要,因此媒体作用的主要对象应该是中立层人群。
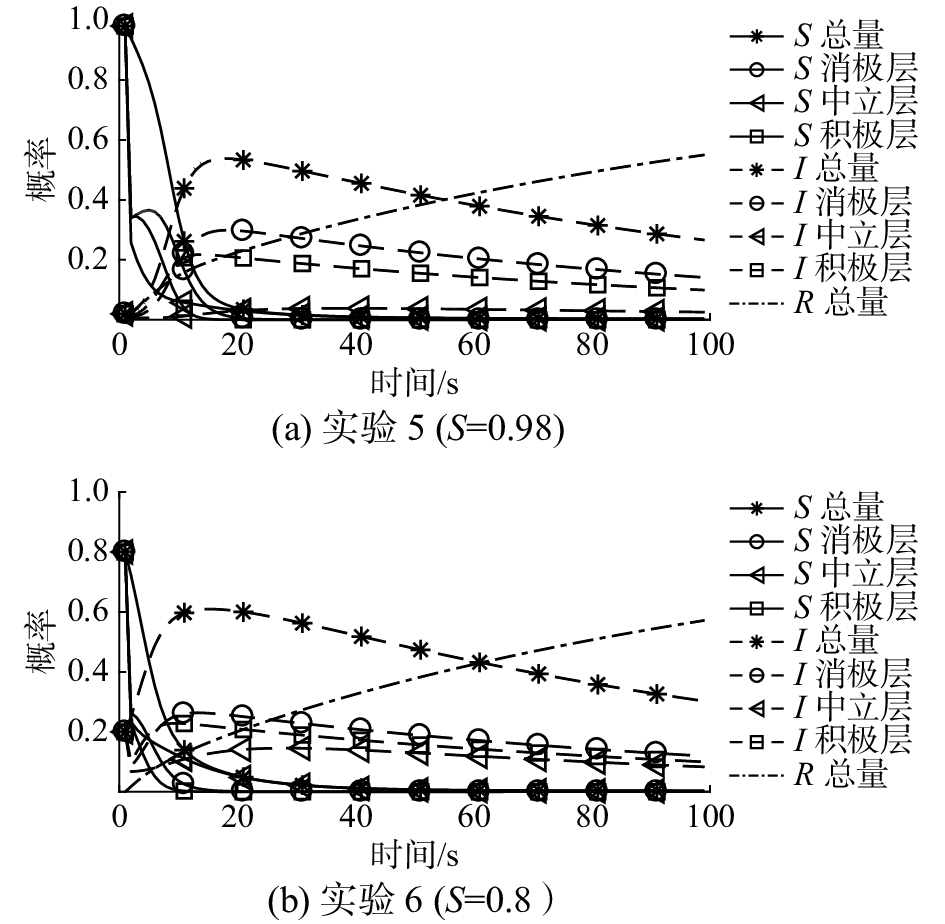
3.2 总体密度变化对传播过程的影响为了进一步验证未知人群密度较高时,总体密度的变化对传播过程的影响,将总体密度S分别取0.98和0.8,给出相应的2组实验结果(实验5、实验6)。假设初始S各分量权重相同(S1=S2=S3=1/3),媒体干预度η=0.3。
观察图6,再借鉴前面的图5(d)的实验4 (S=0.9),可以看到,S较大时,未知人群中的第一分量的第2、3时刻的两个值存在较大的波动,这说明处于消极层的未知群体不是稳定的,受到整体趋势的影响在随后的过程中会进入下降的稳态。另外,S较大时,传播人群中的第一分量占主导地位,随着S的逐步减少,传播人群中的3个分量趋于一致。
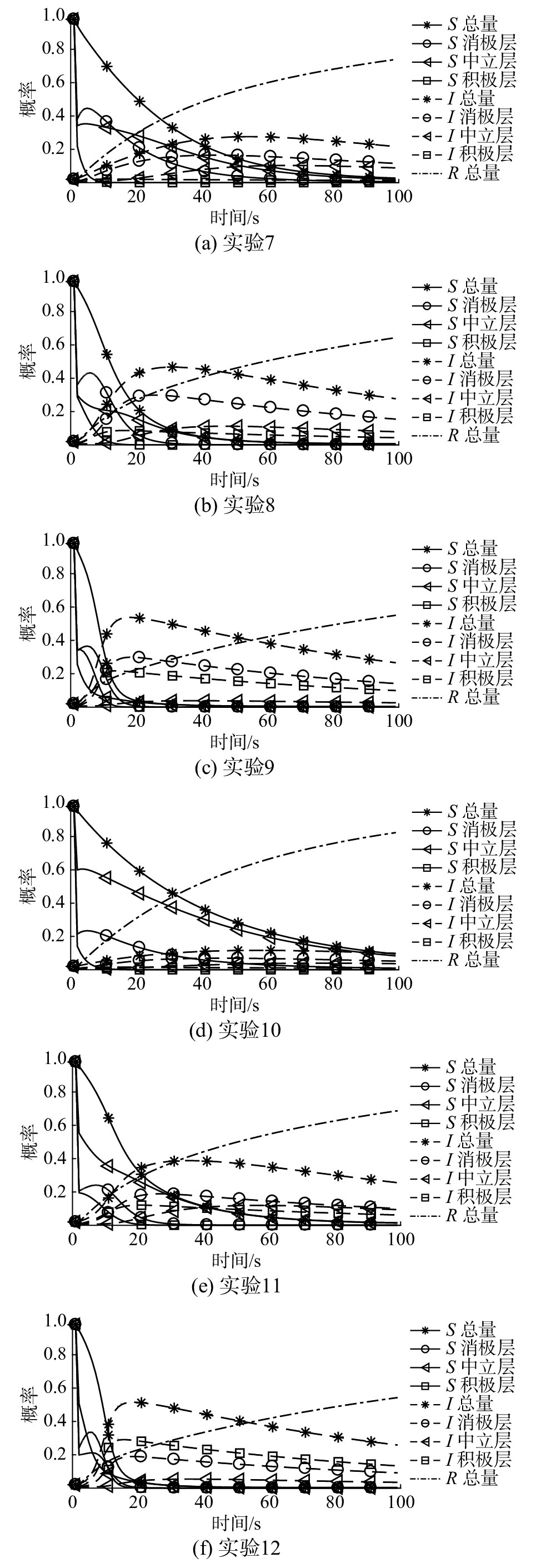
3.3 媒体干预参数对传播过程的影响这里我们考虑两种情况,即初始S各分量权重相同和权重不同时, 不同媒体干预度η对传播过程的影响。权重相同时取S1=S2=S3=1/3,权重不同时取中立分量权重较大的情况:S1=0.2,S2=0.6,S3=0.2。在未知人群总体密度S=0.98的情况下,媒体干预度参数设置与对应的实验编号见表3。
| 表 3 不同媒体干预度参数设置 Tab.3 Parameter settings of different media intervention degrees |
从图7(a)~(c)可以看到,在初始S各分量权重相同(S1=S2=S3=1/3)的情况下,当媒体干预度η>0.4时,传播人群受到严重抑制,70%以上的未知人群没有进入传播态,而是直接进入移除态。当媒体干预度η≤0.4时,传播态人群的数量会达到一定的规模(50%左右),且传播模型在受控状态下运行。未知人群和传播人群中首先是消极层占主导地位,然后是积极层逐渐占主导地位。
从图7(d)~(f)可以看到,在初始S各分量权重不相同(S1=0.2,S2=0.6,S3=0.2) 的情况下,当媒体干预度η>0.4时,传播人群受到严重抑制,90%以上的未知人群没有进入传播态,而是直接进入移除态。未知人群内部中立层始终占主导地位。当媒体干预度η≤0.4时,传播态人群的数量会达到一定的规模(50%左右),且传播模型在受控状态下运行。传播人群首先是消极层占主导地位,随后被积极层替代,积极层在传播过程中占据优势;未知群体中中立层首先占主导地位,同样被积极层替代主导地位。
由此可见,过多的媒体干预影响了传播的速度,即很长时间之后,才有较少量的人转化到传播人群,大量的人群直接进入了移除人群,这种情况对应中立分量权重较大(S1=0.2,S2=0.6,S3=0.2)时更加明显。适当的媒体干预(η≤0.4)会使得一定量的人群进入传播人群,这种情况对应中立分量权重较大时,未知人群中立层优势被积极层替代,传播人群消极层优势被积极层替代。
3.4 (SI)3R模型与SIaIbR模型的对比实验针对两个模型,均假设未知人群总体密度S=0.9,媒体干预度η=0.3。(SI)3R的初始S分量为:S1=S2=0.2,S3=0.6。算式(1)中SIaIbR的不同渗透率的参数取值为:β1=0.15,β2=0.2,对比结果如图8~9。
图8和图9给出了有媒体作用下,(SI)3R模型与SIaIbR两种模型的对比实验。实验结果表明,由于中立层次的存在,(SI)3R模型支持群体的变化更容易受到媒体作用的影响,即在有媒体作用下,(SI)3R模型与SIaIbR模型相比,具有更好的可控性。

|
Download:
|
| 图 9 SIaIbR模型 Fig. 9 SIaIbR model | |
与传统的SIR、SIaIbR模型对比,(SI)3R模型能够反映传播群体内部的层次结构,即积极层、中立层、消极层,符合实际中网络谣言传播系统的特点。3个层次在传播过程中所起到的作用不同,整个系统是在3者相互作用的情况下运行的。媒体对三者的影响有较大的区别,根据实际情况,对中立者的影响最大,经过媒体干预,每个层次的传播者生存的周期受到一定的影响,并且存在一定的波动或交替主导作用。
| [1] |
朱恒民, 刘凯, 卢子芳. 媒体作用下互联网舆情话题传播模型研究[J]. 现代图书情报技术, 2013(3): 45-50. ZHU Hengmin, LIU Kai, LU Zifang. Study on topic propagation model of Internet public opinion under the influence of the media[J]. New technology of library and information service, 2013(3): 45-50. (  0) 0)
|
| [2] |
张立凡, 赵凯. 媒体干预下带有讨论机制的网络舆情传播模型研究[J]. 现代图书情报技术, 2015(11): 60-67. ZHANG Lifan, ZHAO Kai. Study on the Internet public opinion dissemination model with discussion under the effect of media[J]. New technology of library and information service, 2015(11): 60-67. DOI:10.11925/infotech.1003-3513.2015.11.09 (  0) 0)
|
| [3] |
GRUHL D, GUHA R, LIBEN-NOWELL D, et al. Information diffusion through blogspace[C]// Proceedings of the 13th International Conference on World Wide Web. New York, USA, 2004: 491–501.
( 0) 0)
|
| [4] |
LESKOVEC J, MCGLOHON M, FALOUTSOS C, et al. Patterns of cascading behavior in large blog graphs[C]// Proceedings of the 2007 SIAM International Conference on Data Mining. Minneapolis, Minnesota, New York, USA, 2007: 551–556.
( 0) 0)
|
| [5] |
ARTALEJO J R, ECONOMOU A, LOPEZ-HERRERO M J. The stochastic SEIR model before extinction: computational approaches[J]. Applied mathematics and computation, 2015, 265: 1026-1043. DOI:10.1016/j.amc.2015.05.141 ( 0) 0)
|
| [6] |
CAI Yongli, KANG Yun, BANERJEE M, et al. A stochastic SIRS epidemic model with infectious force under intervention strategies[J]. Journal of differential equations, 2015, 259(12): 7463-7502. DOI:10.1016/j.jde.2015.08.024 ( 0) 0)
|
| [7] |
LI Weihua, TANG Shaoting, FANG Wenyi, et al. How multiple social networks affect user awareness: the information diffusion process in multiplex networks[J]. Physical review E, statistical, nonlinear, and soft matter physics, 2015, 92(4): 042810. DOI:10.1103/PhysRevE.92.042810 ( 0) 0)
|
| [8] |
SUDBURY A. The proportion of the population never hearing a Rumour[J]. Journal of applied probability, 1985, 22(2): 443-446. DOI:10.2307/3213787 ( 0) 0)
|
| [9] |
顾亦然, 夏玲玲. 在线社交网络中谣言的传播与抑制[J]. 物理学报, 2012, 61(23): 544-550. GU Yiran, XIA Lingling. The propagation and inhibition of rumors in online social network[J]. Acta physica sinica, 2012, 61(23): 544-550. (  0) 0)
|
| [10] |
钱颖, 张楠, 赵来军, 等. 微博舆情传播规律研究[J]. 情报学报, 2012, 31(12): 1299-1304. QIAN Ying, ZHANG Nan, ZHAO Laijun, et al. The spread of public sentiment on micro-blogging under emergencies[J]. Journal of the China society for scientific and technical information, 2012, 31(12): 1299-1304. DOI:10.3772/j.issn.1000-0135.2012.12.010 (  0) 0)
|
| [11] |
XU Ruzhi, LI Heli, Xing Changming. Research on information dissemination model for social networking services[J]. International journal of computer science and application, 2013, 2(1): 1-6. ( 0) 0)
|
| [12] |
李林, 孙军华. 基于社会网络冲突信息传播的群体特征[J]. 系统工程理论与实践, 2014, 34(1): 207-214. LI Lin, SUN Junhua. Population characteristics based on conflict information spreading on social network[J]. System engineering-theory & practice, 2014, 34(1): 207-214. (  0) 0)
|
| [13] |
夏承遗, 刘忠信, 陈增强. 复杂网络上的传播动力学及其新进展[J]. 智能系统学报, 2009, 4(5): 392-397. XIA Chengyi, LIU Zhongxin, CHEN Zengqiang. Transmission dynamics in complex networks[J]. CAAI transactions on intelligent systems, 2009, 4(5): 392-397. (  0) 0)
|
| [14] |
蒋乐进. 论网络舆论形成与作用[J]. 北京理工大学学报: 社会科学版, 2006, 8(4): 10-14. JIANG Lejin. How network public opinion formation and its effect[J]. Journal of Beijing institute of technology: social sciences edition, 2006, 8(4): 10-14. (  0) 0)
|
| [15] |
陈波, 于泠, 刘君亭, 等. 泛在媒体环境下的网络舆情传播控制模型[J]. 系统工程理论与实践, 2011, 31(11): 2140-2150. CHEN Bo, YU Ling, LIU Junting, et al. Dissemination and control model of Internet public opinion in the ubiquitous media environments[J]. Systems engineering -theory and practice, 2011, 31(11): 2140-2150. DOI:10.12011/1000-6788(2011)11-2140 (  0) 0)
|
| [16] |
CROKIDAKIS N. Effects of mass media on opinion spreading in the Sznajd sociophysics model[J]. Physica A: statistical mechanics and its applications, 2012, 391(4): 1729-1734. DOI:10.1016/j.physa.2011.11.038 ( 0) 0)
|
| [17] |
LI Dandan, MA Jing. How the government’s punishment and individual’s sensitivity affect the rumor spreading in online social networks[J]. Physica A: statistical mechanics and its applications, 2017, 469: 284-292. DOI:10.1016/j.physa.2016.11.033 ( 0) 0)
|
| [18] |
BONZANI I, CUMIN L M G. Modelling and simulations of multilane traffic flow by kinetic theory methods[J]. Computers and mathematics with applications, 2008, 56(9): 2418-2428. DOI:10.1016/j.camwa.2008.05.033 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


