能源与环境问题的日益突出,严重威胁人类社会的可持续发展。电力环境经济调度是现今能源可持续发展的重要研究内容,主要目标是尽可能地降低煤耗成本与污染气体的排放。如何在发电中实现经济、环保、安全的机组负荷调度,对于电力环境经济调度具有重要意义[1-2]。
电力环境经济调度是一个非线性的多目标优化问题。有关模拟退火[3],粒子群与万有引力搜索相结合的混合算法[4],差分进化[5-7]等基于群体智能的算法在电力环境经济调度问题中取得了一定的成果;文献[8]采用评价函数与改进的粒子群算法在该问题的求解上得到了较好的解,但在兼顾系统有功损耗上需要进一步研究;文献[9]将花授粉算法应用于电力环境经济调度问题的求解到了较好的效果。同时,基于数值计算的序列二次规划SQP在求解非线性优化问题上具有较好的优势[10-11]。将群体智能算法与SQP相混合的方法应用于电力环境经济调度问题上具有一定的有效性[12-13]。文献[14]将差分进化算法DE和粒子群算法PSO作为求解该问题的全局最优解,利用SQP将最优解进行局部微调,在该问题求解上提供了新的思路。
智能水滴算法(IWD)是Shah Hosseini根据自然界水的流动而提出的群智能算法,该算法被应用于求解旅行商问题(traveling salesman problem,TSP)、组合优化、路径规划等复杂问题[15-18]。本文将水滴所产生的解作为SQP的初始点用于求解电力环境经济调度问题,从而得到较好质量的解。本文使用一个10机组的测试系统对算法进行仿真实验,与其他方法求解该环境经济调度问题相比,所提出的混合算法具有可行性和有效性。
1 电力环境经济调度问题模型电力环境经济调度主要兼顾发电煤耗成本与污染气体排放,在满足发电负荷需求以及各项约束条件下,确定各机组的较优出力。通常,考虑阀点效应的煤耗成本与排放量可表示为式(1)、(2)关于机组有功功率的二次函数。
| ${\text{Cost}} = \sum\limits_{i = 1}^{i = N} {{a_i} + {b_i}{P_i} + {c_i}{{({P_i})}^2} + \left| {{e_i}\sin ({f_i}({P_i}^{{\text{min}}} - {P_i}))} \right|} $ | (1) |
| ${\text{Emission}} = \sum\limits_{i = 1}^{i = N} {{\alpha _i} + {\beta _i}{P_i} + {\gamma _i}{{({P_i})}^2} + {\eta _i}\exp ({\delta _i}{P_i})} $ | (2) |
式中:Cost、Emission分别为N台机组的煤耗成本与排放量;N为机组的台数;
| $\sum\limits_{i = 1}^{\text{N}} {{P_i}} = {P_D}{\text{ + }}{P_L}$ | (3) |
| ${P_i^{\min}} \leqslant P_i \leqslant {P_i^{\max}}$ | (4) |
式中:
| ${P_L}{\text{ = }}\sum\limits_{i{\text{ = }}1}^N {\sum\limits_{j{\text{ = }}1}^N {{P_i}{B_{ij}}{P_j}} }$ | (5) |
本文通过引入权重因子w将煤耗成本与排放量两目标转化为单目标,同时使用较大惩罚因子
| $T = w \cdot {\text{Cost}} + (1 - w){\text{Emission}} + \lambda \left| {\sum\limits_{i = 1}^N {{P_i} - ({P_D} + {P_L})} } \right|$ | (6) |
智能水滴算法主要思想是自然界中水滴由于重力作用,根据环境以及自身属性选择一条较优的路径从而受到启发形成的一种优化算法。智能水滴算法最初被用于解决离散优化问题,现将其应用于求解连续优化问题。算法主要包括初始化、水滴选择、局部信息更新、参数确定和全局更新5个过程。
2.1.1 算法初始化根据参数取值范围确定参数的精度,将每个参数转换为由n个有效位组成,每个有效位取[0,9]之间整数,由此形成n×10的二维节点优化空间。将水滴随机分布在优化空间中,作为水滴流动的起点。根据水滴当前的位置,水滴访问过的城市集合为
移动过程中水滴偏向于选择泥土含量较少的路径,水滴iwd在城市i时选择j作为下一节点的概率为
| $P_i^{{\text{iwd}}}(j) = \left\{ {\begin{array}{*{20}{l}} {\displaystyle\frac{{f({\text{soil}}(i,j))}}{{\sum {f({\text{soil}}(i,k))} }}}, \quad k \in {J_{{\text{iwd}}}}(i) {0}, \quad {\text{其他}} \end{array}} \right.$ | (7) |
式中:
| ${J_{{\text{iwd}}}}(i) \in {C_{x,y}},\;\;\;\;x \notin {\text{VCX}}({\text{iwd}})$ | (8) |
式中:x、y表示城市的坐标;
水滴在从城市i移动到城市j时,水滴携带的泥土量、水滴速度、路径中的泥土量以及流动过程中泥土量的改变量分别按式(9)~(12)更新。
| ${\text{soil}}({\text{idw}}) = {\text{soil}}({\text{idw}}) + \Delta {\text{soil}}(i,j)$ | (9) |
| ${\text{velocity}}(j) = {\text{velocity}}(i) + \frac{{a_v}}{{b_v + c_v \cdot {\text{soil}}(i,j)}}$ | (10) |
| ${\text{soil}}(i,j) = (1 - \rho n) \cdot {\text{soil}}(i,j) - {\rho _n} \cdot \Delta {\text{soil}}(i,j)$ | (11) |
| $\Delta {\text{soil}}(i,j) = \frac{{a_s}}{{b_s + c_s \cdot {\text{time}}(i,j)}}$ | (12) |
式中:
每个水滴确定n个有效位的取值,根据小数点的位置计算出参数的取值,最优路径对应的参数取值即为最优参数,参数按式(13)计算:
| ${{\text{x}}_i} = \sum\limits_{j = 1 + (i - 1){P_i}}^{i \cdot {P_i}} {{y_j} \cdot {{10}^{{m_i} - \left[ {j - \left( {i - 1} \right)P} \right]}}}$ | (13) |
式中:
| ${P_i}{\text{ = }}{P_{i,{\text{min}}}}{\text{ + (}}{P_{i,{\text{max}}}} - {P_{i,{\text{min}}}}{\text{)}} \cdot {{{x_i}}/{{x_{i,{\text{max}}}}}}$ | (14) |
为了使得本次迭代的较优路径
| ${\text{soil}}(i,j) = 1.1 \times {\text{soil}}(i,j) - 0.01 \times \frac{{{\text{soil}}_{{\text{IB}}}^{{\text{iwd}}}}}{n}, \,\, \forall (i,j) \in T_{\text{IB}}$ | (15) |
式中:
序列二次规划SQP被广泛地应用于实际优化问题的求解,SQP在收敛速度、精度和可靠性方面具有较好的优势。SQP的主要思想是通过一系列的二次规划QP子问题来求解非线性问题[19]。QP子问题[13]可描述为
| $\begin{array}{c}{\rm{min }}\nabla F{({{{P}}_k})^{\rm{T}}}{{{d}}_k} + \displaystyle\frac{1}{2}{{d}}_k^{\rm{T}}{{{H}}_k}{{{d}}_k}\\[5pt]{\rm{s.t.}}\;{g_i}({{{P}}_k}) + \left| {\nabla g{{({{{P}}_k})}^{\rm{T}}}} \right|{d_k} = 0, \,\, {{ i}} = 1,2,\cdots,{m_e}\\[5pt]\;\;\;{g_i}({{{P}}_k}) + \left| {\nabla g{{({{{P}}_k})}^{\rm{T}}}} \right|{d_k} \leqslant 0, \,\, {{i}} = 1,2,\cdots,m\end{array}$ | (16) |
式中:
采用将智能水滴算法与SQP相混合的算法,其主要原理是将水滴所产生的解作为SQP的初始点进行求解。SQP对水滴所产生的所有解进行微调,最终得到较好的解。智能水滴算法与SQP相混合的IWD-SQP算法流程如图1所示。综上,智能水滴算法与SQP相混合的IWD-SQP算法步骤为:
1)初始化静态参数。确定智能水滴数目
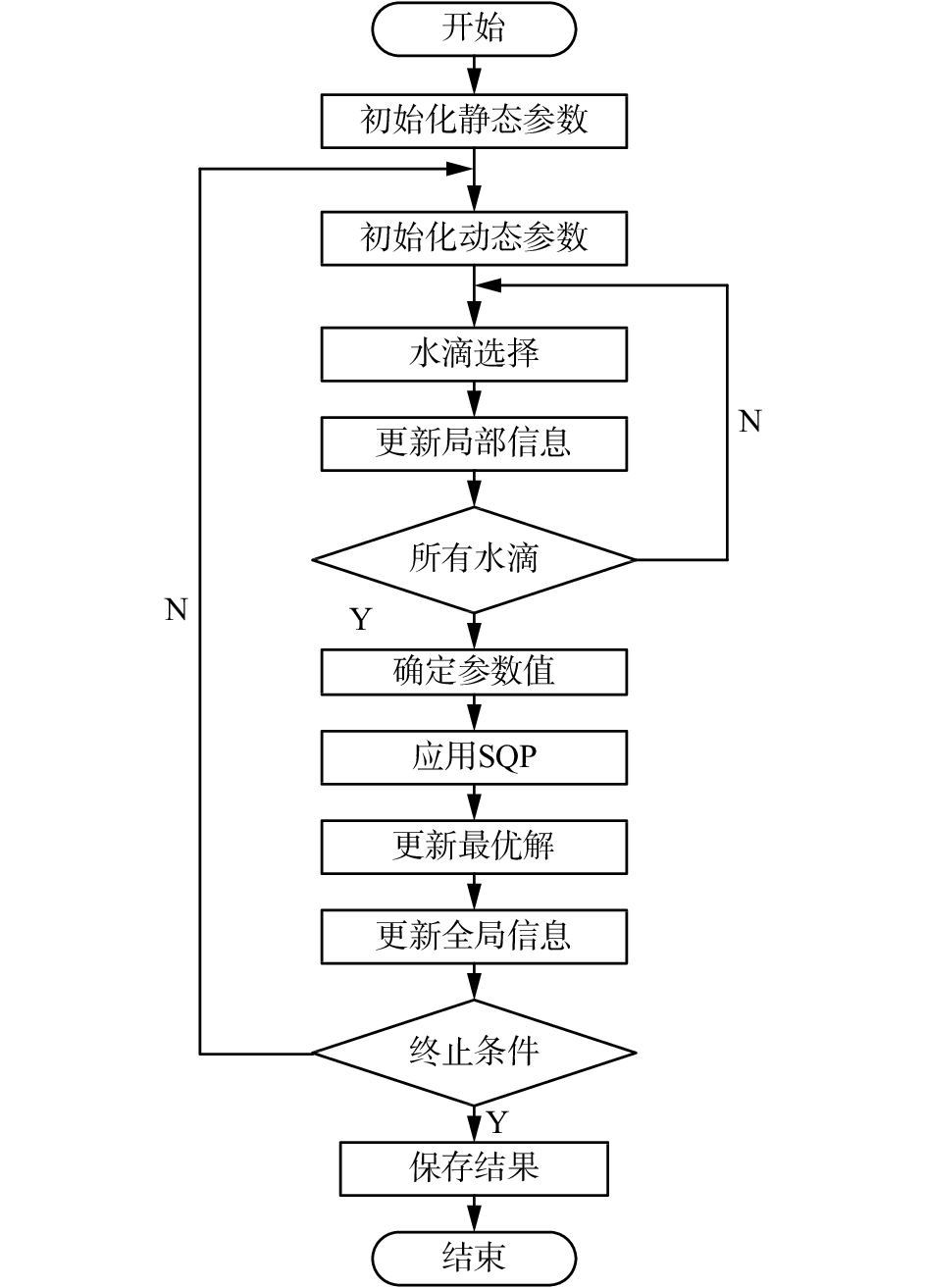
|
Download:
|
| 图 1 IWD-SQP算法流程图 Fig. 1 Flow chart of the IWD-SQP algorithm | |
2)初始化动态参数和水滴初始位置。设置水滴的初始速度以及携带的初始泥土量,水滴访问过的节点集。对每个水滴的初始位置进行随机初始化。
3)水滴选择并更新局部信息。水滴根据路径中的泥土量大小,按照式(7)概率大小选择下一个节点;水滴根据被选择的节点更新局部信息,按式(9)~(12)局部更新水滴的信息。
4)重复3),直到所有的水滴都完成流动,即所有的水滴都有一条路径形成完整的解。
5)确定参数的值。根据各水滴所形成的流动路径,将其分别按式(13)、(14)计算出各个参数的值,得到本次迭代水滴的解。
6)应用SQP微调各参数值。将5)中本次迭代水滴所产生的解作为SQP的初始点进行计算,得到本次迭代的解与目标值。
7)确定本次迭代的最优解,更新全局量。确定本次迭代最优解并根据本次迭代最优解更新全局最优解,同时根据式(15)更新全局泥土量。
8)判断是否满足终止条件。当所有的水滴都收敛到同一路径上或者算法达到设定的最大迭代次数时转到9),否则转到2)。
9)保存结果。将最优解与目标值保存,算法结束。
3 实验分析 3.1 实验对象与环境为了验证本文所提算法的有效性,将一个10机组的测试系统作为实验对象,机组的煤耗成本系数、排放系数、出力上下限以及机组损耗系数见文献[20]。分别采用本文提出的混合算法IWD-SQP、遗传算法GA、差分进化算法DE、粒子群算法PSO和序列二次规划SQP,以及文献[14]中的DE-SQP、PSO-SQP算法求解该电力环境经济调度问题。同时,将IWD和IWD-SQP用于两个标准测试函数进行求解分析混合的IWD-SQP算法的优势。实验环境为主频2.40 GHz、4 GB RAM配置的个人计算机,算法仿真软件为MATLAB R2014a。
3.2 算法参数设置在实验中,IWD-SQP的设置参数水滴数量为20,迭代次数Iter=100,水滴的初始速度InitVel=100,水滴初始携带的泥土量Soil=0,路径中初始泥土量InitSoil=1 000,智能水滴数为
为了更好地分析混合的IWD-SQP算法与IWD相比的优势,将2维的Ackley和Beale标准测试函数作为目标函数在MATLAB环境中进行实验求解对比。表1给出了IWD和IWD-SQP算法求解两个2维标准测试函数的最优值和算法收敛时迭代次数。由表1可知,IWD与IWD-SQP算法都能得到较好的最优值,相比之下IWD-SQP算法所求解得到的值更接近理论最优值;同时算法IWD-SQP求解到最优值时算法迭代次数也较IWD低。由此可以看出,IWD-SQP算法在收敛速度上的优势,同时具有较好的寻优能力。
| 表 1 算法IWD与IWD-SQP求解标准测试函数实验结果 Tab.1 The experiment results of the IWD and IWD-SQP algorithm to solve the standard test function |
采用不同的方法,在负荷LOAD=1 036 MW,w分别为0.5和1时,重复25次实验,取目标最优值作为实验结果,得到各机组的调度方案如表2、表3所示,调度方案的煤耗成本值、排放量以及总的目标值如表4所示。
由表4可知,在同一负荷需求目标值满足实际要求的情况下,权重因子w分别为0.5和1时,与其他几种方法相比本文提出的IWD-SQP算法求解该电力环境经济调度问题的总目标值最好,采用本文提出的算法能得到较优解,说明IWD-SQP算法在求解该问题上是可行的、有效的。在w=0.5时,本文提出的IWD-SQP算法总目标值T为32 596,比DE-SQP算法总目标值32 643低47,并且IWD-SQP算法污染物排放量在几种方法中也是最低的。在w=1时,本文提出的IWD-SQP算法总目标值T为60 798,较DE-SQP算法总目标值61 107低309;同时由表3可知,在w=1时,本文提出的IWD-SQP算法调度方案的网络损耗为19.57 MW,在几种方法中最低。由此可以看出,本文提出的IWD-SQP算法在求解该电力环境经济调度问题上具有优势。
| 表 2 LOAD =1 036 MW,w=0.5时各机组调度方案 Tab.2 Scheduling scheme (MW) for LOAD =1 036 MW, w=0.5 |
| 表 3 LOAD=1 036 MW,w=1时各机组调度方案 Tab.3 Scheduling scheme (MW) for LOAD =1 036 MW, w=1 |
| 表 4 LOAD=1 036 MW时燃料费用、排放量以及总目标值 Tab.4 Cost, Emission and total object for LOAD=1 036 MW |
本文针对电力环境经济调度问题,提出了将智能水滴算法与序列二次规划SQP相混合的算法应用于该问题求解。通过智能水滴算法产生的解作为SQP的初始点进行求解,将两个标准测试函数和一个10机组的测试系统进行实验,与其他几种方法相比本文提出的算法在求解该问题上具有一定的优势,验证了该算法的可行性与有效性,为电力环境经济调度问题求解提供了一种新的方法。
| [1] |
马钊, 周孝信, 尚宇炜, 等. 未来配电系统形态及发展趋势[J]. 中国电机工程学报, 2015, 35(6): 1289-1298. MA Zhao, ZHOU Xiaoxin, SHANG Yuwei, et al. Form and development trend of future distribution system[J]. Proceedings of the CSEE, 2015, 35(6): 1289-1298. (  0) 0)
|
| [2] |
付鹏, 王宁玲, 李晓恩, 等. 基于信息物理融合的火电机组节能环保负荷优化分配[J]. 中国电机工程学报, 2015, 35(14): 3685-3692. FU Peng, WANG Ningling, LI Xiaoen, et al. CPS-based load dispatching model for the energy conversation and emission reduction of thermal power units[J]. Proceedings of the CSEE, 2015, 35(14): 3685-3692. (  0) 0)
|
| [3] |
ZIANE I, BENHAMIDA F, GRAA A, et al. Combined economic emission dispatch with new price penalty factors[C]//Proceedings of the 4th International Conference on Electrical Engineering. Boumerdes, Algeria, 2015: 1–5.
( 0) 0)
|
| [4] |
RADOSAVLJEVIĆ J. A solution to the combined economic and emission dispatch using hybrid PSOGSA algorithm[J]. Applied artificial intelligence, 2016, 30(5): 445-474. DOI:10.1080/08839514.2016.1185860 ( 0) 0)
|
| [5] |
吴亮红, 王耀南, 袁小芳, 等. 基于快速自适应差分进化算法的电力系统经济负荷分配[J]. 控制与决策, 2013, 28(4): 557-562. WU Lianghong, WANG Yaonan, YUAN Xiaofang, et al. Fast self-adaptive differential evolution algorithm for power economic load dispatch[J]. Control and decision, 2013, 28(4): 557-562. (  0) 0)
|
| [6] |
刘自发, 张建华. 一种求解电力经济负荷分配问题的改进微分进化算法[J]. 中国电机工程学报, 2008, 28(10): 100-105. LIU Zifa, ZHANG Jianhua. An improved differential evolution algorithm for economic dispatch of power systems[J]. Proceedings of the CSEE, 2008, 28(10): 100-105. DOI:10.3321/j.issn:0258-8013.2008.10.017 (  0) 0)
|
| [7] |
黄伟, 黄婷, 周欢, 等. 基于改进微分进化算法的微电网动态经济优化调度[J]. 电力系统自动化, 2014, 38(9): 211-217. HUANG Wei, HUANG Ting, ZHOU Huan, et al. Dynamic economical dispatch for microgrid based on improved differential evolution algorithm[J]. Automation of electric power systems, 2014, 38(9): 211-217. DOI:10.7500/AEPS20130520003 (  0) 0)
|
| [8] |
龙军, 郑斌, 郭小璇, 等. 一种求解环境经济发电调度的交互式多目标优化方法[J]. 电力自动化设备, 2013, 33(5): 83-88. LONG Jun, ZHENG Bin, GUO Xiaoxuan, et al. Interactive multi-objective optimization of environmental and economic power generation scheduling[J]. Electric power automation equipment, 2013, 33(5): 83-88. (  0) 0)
|
| [9] |
ABDELAZIZ A Y, ALI E S, ELAZIM S M A. Implementation of flower pollination algorithm for solving economic load dispatch and combined economic emission dispatch problems in power systems[J]. Energy, 2016, 101: 506-518. DOI:10.1016/j.energy.2016.02.041 ( 0) 0)
|
| [10] |
徐丈星, 耿志强, 朱群雄, 等. 基于SQP局部搜索的混沌粒子群优化算法[J]. 控制与决策, 2012, 27(4): 557-561. XU Zhangxing, GENG Zhiqiang, ZHU Qunxiong, et al. Chaos particle swarm optimization algorithm integrated with sequential quadratic programming local search[J]. Control and decision, 2012, 27(4): 557-561. (  0) 0)
|
| [11] |
陈伟, 贾立. 间歇过程PSO-SQP混合优化算法研究[J]. 仪器仪表学报, 2016, 37(2): 339-347. CHEN Wei, JIA Li. PSO-SQP hybrid optimization algorithm for batch processes[J]. Chinese journal of scientific instrument, 2016, 37(2): 339-347. (  0) 0)
|
| [12] |
ELAIW A M, XIA X, SHEHATA A M. Solving dynamic economic emission dispatch problem with valve-point effects using hybrid DE-SQP[C]//Proceedings of Power Engineering Society Conference and Exposition in Africa. Johannesburg, South Africa, 2012: 1–6.
( 0) 0)
|
| [13] |
BASU M. Hybridization of bee colony optimization and sequential quadratic programming for dynamic economic dispatch[J]. International journal of electrical power & energy systems, 2013, 44(1): 591-596. ( 0) 0)
|
| [14] |
ELAIW A M, XIA X, SHEHATA A M. Hybrid DE-SQP and hybrid PSO-SQP methods for solving dynamic economic emission dispatch problem with valve-point effects[J]. Electric power systems research, 2013, 103: 192-200. DOI:10.1016/j.epsr.2013.05.015 ( 0) 0)
|
| [15] |
TEYMOURIAN E, KAYVANFAR V, KOMAKI G M, et al. Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem[J]. Information sciences, 2016, 334-335: 354-378. ( 0) 0)
|
| [16] |
SHAH-HOSSEINI H. The intelligent water drops algorithm: a nature-inspired swarm-based optimization algorithm[J]. International journal of bio-inspired computation, 2009, 1(1/2): 71-79. DOI:10.1504/IJBIC.2009.022775 ( 0) 0)
|
| [17] |
DUAN Haibin, LIU Senqi, WU Jiang. Novel intelligent water drops optimization approach to single UCAV smooth trajectory planning[J]. Aerospace science and technology, 2009, 13(8): 442-449. DOI:10.1016/j.ast.2009.07.002 ( 0) 0)
|
| [18] |
BASEM O A, WONG L P, LIM C P, et al. A modified intelligent water drops algorithm and its application to optimization problems[J]. Expert systems with applications, 2014, 41(15): 6555-6569. DOI:10.1016/j.eswa.2014.05.010 ( 0) 0)
|
| [19] |
张鼎逆, 刘毅. 基于改进遗传算法和序列二次规划的再入轨迹优化[J]. 浙江大学学报: 工学版, 2014, 48(1): 161-167. ZHANG Dingni, LIU Yi. Reentry trajectory optimization based on improved genetic algorithm and sequential quadratic programming[J]. Journal of Zhejiang university: engineering science, 2014, 48(1): 161-167. (  0) 0)
|
| [20] |
BASU M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-Ⅱ[J]. International journal of electrical power & energy systems, 2008, 30(2): 140-149. ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


