2. 渤海大学 数理学院, 辽宁 锦州 121000
2. College of Mathematics and Physics, Bohai University, Jinzhou 121000, China
粗糙集理论是由波兰数学家Z.Pawlak[1]于1982年提出的,它是一种处理不确定性知识的数据分析理论。目前粗糙集理论已被广泛应用于人工智能、过程控制、数据挖掘、决策支持以及知识发现等领域。属性约简是粗糙集理论的研究内容之一,它是利用粗糙集进行数据挖掘、规则抽取的理论基础。其主要思想是在确保信息表的分类能力不变的情况下,删除掉不必要属性,保留必要属性,从而导出问题的分类规则。属性约简无疑是在获取规则的过程中最重要的核心问题,历来受到大家的关注。
传统的粗糙集理论[1-3]是基于等价关系来描述的, 由等价关系粒化样本空间形成信息粒子, 构造论域上的上、下近似算子, 进而研究知识约简与知识获取问题。但是经典粗糙集只适用于离散型的数据,对于连续型数据,必须通过离散化才能处理。然而,数据的离散化会导致大量信息丢失,从而使计算的结果不能准确地反映分类信息。为此,经典粗糙集理论被进行了多角度的推广,其中包括邻域粗糙集模型[4-11]、优势粗糙集模型[12-13]、覆盖粗糙集模型[14-16]、模糊粗糙集模型[17-22]等。邻域粗糙集模型是重要的推广模型之一,基于此模型,许多学者研究了不同的依赖度函数,并设计了相应的属性约简算法[4-11]。例如,Hu[5]利用邻域的概念定义了样本空间的决策正域,构造了邻域依赖度函数来刻画属性的分类能力,用于处理混合数据的属性约简;Zhao[7]根据数据精度设计了一个自适应性的邻域粗糙集模型,并给出了基于该模型的代价敏感属性约简算法; Chen[8]利用邻域粗糙集模型和信息测度为肿瘤分类进行特征选择;Zhu[9]对邻域粗糙集模型的边界进行分布优化,从而为粒度的选取和组合提供了新方法。然而,邻域粗糙集模型中的决策正域只考虑了一致性样本与其他样本的可辨识性,忽略了边界样本的可分性。因此,基于正域的依赖度函数不能正确地刻画一个属性子集的分类能力。为了克服基于正域算法的缺点,本文提出了基于辨识矩阵的属性约简算法。该算法克服了依赖度算法的局限性。
1 邻域关系决策表的属性约简设(U, A, F)为信息表,其中,U={x1, x2, …, xn}为样本集合,A={a1, a2, …,am}是属性集合,F={fj:j≤m}为U和A的关系集,fj:U→Vj,j≤m,Vj为属性aj的值域。
定义1 设U={x1, x2, …, xn}为样本集,B⊆ A,令
| $ {{M}_{B}}=\{({{x}_{i}}, {{x}_{j}})\in U\times U:\text{ }\left| {{f}_{a}}({{x}_{i}})-{{f}_{a}}({{x}_{j}}) \right|\le \varepsilon, \forall a\in B\} $ |
则称MB为U上的邻域关系,称(U, A, F)为基于邻域关系的信息系统,简称邻域信息表,ε表示相似度阈值。对于任意xi∈U,令
| $ {{\delta }_{B}}({{x}_{i}})=\{{{x}_{j}}\in U:({{x}_{i}}, {{x}_{j}})\in {{M}_{B}}\} $ |
则称δB(xi)为xi关于MB的邻域。
邻域关系可以用一个关系矩阵来表示。设属性al∈A,对于任意xi, xj∈U,如果xj∈δal(xi),那么记Nl(i, j)=1,否则记Nl(i, j)=0。因此,一个属性al唯一地对应一个关系矩阵Nl。而属性集合A的关系矩阵可以由公式NA=∩al∈ANl计算。
定义2 设(U, A, F, D={d})为决策表,其中(U, A, F)为信息表,A={a1, a2, …am},D为决策属性。对于任意x∈U,令
| $ \begin{matrix} {{M}_{D}}=\left\{ ({{x}_{i}}, {{x}_{j}})\in U\times U\left| d({{x}_{i}})=d({{x}_{j}}) \right. \right\} \\ {{[{{x}_{i}}]}_{D}}=\{{{x}_{j}}\in U\left| d({{x}_{i}})=d({{x}_{j}}) \right.\} \\ \end{matrix} $ |
则称MD为U上的决策等价关系,[xi]D为xi的关于MD的决策等价类。称(U, A, F, D)为基于邻域关系的决策信息表,简称邻域决策表。若MA⊆ MD,则称(U, A, F, D)是协调的,否则,称它是不协调的。U上的所有决策等价类构成了U的一个划分,记为U/D={[xi]Dxi∈U}。
同理,决策等价关系MD可以用关系矩阵ND来表示。即对于任意xi, xj∈U,如果xj∈[xi]D,那么记ND(i, j)=1,否则记ND(i, j)=0。
设(U, A, F, D)为决策表,U/D={X1, X2, …, Xr}为决策划分,B⊆ A,对于任意Xk∈U/D,定义Xk的下近似为B(Xk)={xi∈U:δB(xi)⊆ X},D关于B的正域定义为POSB(D)=
设ai∈B⊆ A,如果POSB(D)=POSB-{ai}(D),则称ai相对于D是B中不必要的属性;否则,称ai是B中必要的属性。如果POSB(D)=POSA(D)且B中每一个属性相对于D都是B中必要的,则称B是A的一个属性约简。
定理1 设(U, A, F, D={d})为决策表, B⊆ A,则POSB(D)=POSA(D)的充要条件是:对于任意xi, xj∈U,如果满足以下条件之一,即
1)xi∈POSA(D), xj∉POSA(D)∧d(xi)≠d(xj);
2)xi, xj∈POSA(D)∧[xi]D∩[xj]D=Ø;则有xj∉δA(xi)⇒xj∉δB(xi)。
证明 充分性证明。设∀xi, xj∈U,如果xi∈POSA(D)和xj∉POSA(D)且d(xi)≠d(xj),则∃X0∈U/D使得xi∈A(X0)以及xj∉X0,于是δA(xi)⊆ X0,从而xj∉δA(xi)。由于POSB(D)=POSA(D),所以对于任意Xk∈U/D,都有B(Xk)=A(Xk),当然也有A(X0)=B(X0)。由xi∈A(X0),可得xi∈B(X0),于是δB(xi)⊆ X0,因此xj∉δB(xi)。
如果xi, xj∈POSA(D)且[xi]D∩[xj]D=Ø, 则存在X0和X1∈U/D使得X0≠X1且满足xi∈A(X0)以及xj∉X0。由xi∈A(X0)可得δA(xi)⊆ X0,从而xj∉δA(xi)。类似地,由于POSB(D)=POSA(D),所以A(X0)=B(X0)。由xi∈A(X0),可得xi∈B(X0)。从而δB(xi)⇒X0,因此xj∉δB(xi)。
必要性证明。设xi∈POSA(D),所以存在X0∈U/D使得δA(xi)⊆ X0。对于满足xj∉POSA(D)且d(xi)≠d(xj)的任意xj∈U,有xj∉X0,因此xj∉δA(xi)。由于xj∉δA(xi)⇒xj∉δB(xi),所以δB(xi)⇒X0,从而xi∈POSB(D)。于是POSA(D)⇒POSB(D), 而POSB(D)⇒POSA(D)显然成立, 因此POSB(D)=POSA(D)。
另设xi, xj∈POSA(D)且[xi]D∩[xj]D=Ø,则存在X0, X1∈U/D(X0≠X1)使得δA(xi)⊆ X0=[xi]D和δA(xj)⊆ X1=[xj]D。由于xj∉δA(xi)⇒xj∉δB(xi),所以δB(xi)⊆ X0,从而xi∈POSB(D)。于是POSA(D)⊆ POSB(D), 而POSB(D)⊆ POSA(D)是显然成立的,因此POSB(D)=POSA(D)。综上所述,结论成立。
根据定理1可以定义如下的辨识矩阵。
定义3 设(U, A, F, D={d})为决策表,U={x1, x2, …, xn},A={a1, a2, …am},令
| $ \begin{matrix} \text{DIS}=\{({{x}_{i}}, {{x}_{j}})\left| {{x}_{i}} \right.\in \text{PO}{{\text{S}}_{A}}\left( D \right), {{x}_{j}}\notin ~\text{PO}{{\text{S}}_{A}}\left( D \right)\wedge \\ d({{x}_{i}})\ne d({{x}_{j}})\}\cup \{({{x}_{i}}, {{x}_{j}})\text{ }\left| {{x}_{i}}, {{x}_{j}} \right.\in \\ \text{PO}{{\text{S}}_{A}}\left( D \right)\wedge \text{ }{{[{{x}_{i}}]}_{D}}\cap {{[{{x}_{j}}]}_{D}}=\varnothing \} \\ \end{matrix} $ |
则称DIS为决策表(U, A, F, D)的可辨识域。对于任意的样本对(xi, xj)∈DIS,记
| $ \boldsymbol{\text{DM}}\left( i,\text{ }j \right)=\left\{ \begin{align} & \{{{a}_{l}}\in A:{{x}_{j}}\notin {{\delta }_{{{a}_{l}}}}({{x}_{i}})\},\text{ }({{x}_{i}},{{x}_{j}})\in \text{DIS} \\ & A,\text{ }({{x}_{i}},{{x}_{j}})\notin \text{DIS} \\ \end{align} \right. $ |
则称DM(i, j)为xi, xj的辩识集合,称DM为基于邻域关系的辨识矩阵。
定理2 设DM为决策表(U, A, F, D={d})的辨识矩阵,B⊆ A,则B是决策表的一个约简的充要条件是:B满足B∩DM(i, j)≠Ø,∀xi, xj∈U的最小子集。
定理2说明通过辨识矩阵可以等价地刻画决策表的属性约简。下面给出决策表的属性约简的辨识公式。通过析取和合取运算可以获得决策表的全部约简。
定义4 设DM为决策表(U, A, F, D)的辨识矩阵,U={x1, x2, …, xn},辨识函数定义为
| $ f\left( U, A, F, D \right)=\underset{i, j=1}{\overset{n}{\mathop{\wedge }}}\, \left( \vee \boldsymbol{\text{DM}}\left( i, j \right) \right) $ |
定理3 设f(U, A, F, D)为决策表(U, A, F, D)的辨识函数,如果通过析取和合取运算,有
| $ f\left( U, A, F, D \right)=\underset{k=1}{\overset{L}{\mathop{\vee }}}\, (\wedge {{B}_{k}}) $ |
式中:Bk⊆ A,且Bk中每个属性只能出现一次。则称{Bk:k≤l}是A的所有约简组成的集类。
A的所有约简组成的集类记为REDD(A)={Bk:k≤l}。
下面通过一个具体的实例来说明应用辨识矩阵方法如何求解邻域决策表的属性约简。
例1 表 1是具有4种症状a1、a2、a3、a4的某些病例信息,具体描述如表 1所示。
| 表 1 病例决策信息表 Tab.1 Decision information for cases |
取ε=0.25,根据定义1和定义2,计算关系矩阵Nl(i≤4)、NA以及决策关系矩阵ND分别为
| $ {{\boldsymbol{N}}_{1}}=\left[\begin{matrix} 110000 \\ 110110 \\ 001001 \\ 010110 \\ 010110 \\ 001001 \\ \end{matrix} \right], {{\boldsymbol{N}}_{2}}=\left[\begin{matrix} 110110 \\ 110110 \\ 001001 \\ 110100 \\ 110010 \\ 001001 \\ \end{matrix} \right], {{\boldsymbol{N}}_{3}}=\left[\begin{matrix} 111111 \\ 110111 \\ 101011 \\ 110111 \\ 111111 \\ 111111 \\ \end{matrix} \right] $ |
| $ {{\boldsymbol{N}}_{4}}=\left[\begin{matrix} 110010 \\ 110110 \\ 001001 \\ 010110 \\ 110110 \\ 001001 \\ \end{matrix} \right], {{\boldsymbol{N}}_{A}}=\left[\begin{matrix} 110000 \\ 110110 \\ 001001 \\ 010100 \\ 010010 \\ 001001 \\ \end{matrix} \right], {{\boldsymbol{N}}_{D}}=\left[\begin{matrix} 110010 \\ 110010 \\ 001101 \\ 001101 \\ 110010 \\ 001101 \\ \end{matrix} \right] $ |
说明NA⊄ND。由以上计算知,POSA(D)= {x1, x3, x5, x6}。根据定义3,得到辨识矩阵如表 2所示。
| 表 2 病例决策信息表的辨识矩阵 Tab.2 Discernibility matrix of case decisions |
所以,可得决策表的辨识函数为
| $ \begin{matrix} f=({{a}_{1}}\vee {{a}_{4}})\wedge ({{a}_{1}}\vee {{a}_{2}}\vee {{a}_{4}})\wedge {{a}_{2}}= \\ ({{a}_{1}}\wedge {{a}_{2}})\vee ({{a}_{2}}\wedge {{a}_{4}}) \\ \end{matrix} $ |
因此{a1, a2}和{a2, a4}是病例决策表的两个约简。
2 属性约简算法经典粗糙集算法是以等价关系作为聚类标准的。对于数值型数据集,首先进行离散化并构造等价关系。若两个样本在所有属性上取值一样,那么这两个样本就为一类,否则不是一类。而在离散化过程中,避免不了信息流失,而这恰恰是当今研究的热点。本算法通过定义一个距离参数,考虑某两个样本在属性上的相似程度。如果两个样本之间距离小于阈值,则这两个样本就可以聚为一类,这比经典粗糙集的理论显然更多地考虑了样本之间的联系,避免大量信息的流失,从而提高了属性约简的精度。由于利用定理3去搜索决策表的全部约简是一个NP问题,因此利用本文提出的辨识矩阵的概念来构造一个启发式算法。
算法 辨识矩阵属性约简算法(DISRS)。
输入 (U, A, D={d}),阈值θ //θ是用于算法停止搜索的阈值。
输出 约简RED。
1) 计算正域POSA(D)。
2) 计算出关系矩阵ND,即对于任意的样本xi, xj∈U, 若d(xi)≠d(xj), 令ND(i, j)=0, 否则,令ND(i, j)=1。
3)∀al∈A, 计算可辨识矩阵Nl,对于任意xi∈POSA(D)和任意xj∈U, 当ND(i, j)=0时,若|fl(xi)-fl(xj)|>ε,令Nl(i, j)=1,否则令Nl(i, j)=0;当ND(i, j)=1,令Nl(i, j)=0。
4) 计算NA=∪Nl,RED←A。
5)∀al∈A,计算N{red-al}和sum(N{red-al}),其中sum(N{ red-al})表示对矩阵N{ red-al}的行列求和。
6) 选择满足sum(N{red-ak})=
7) 如果(sum(NA)-sum(Nred))/|U| < θ,输出约简RED。否则,转到5)。
了更好地理解所提出的算法,下面给出该算法的流程图,如图 1。
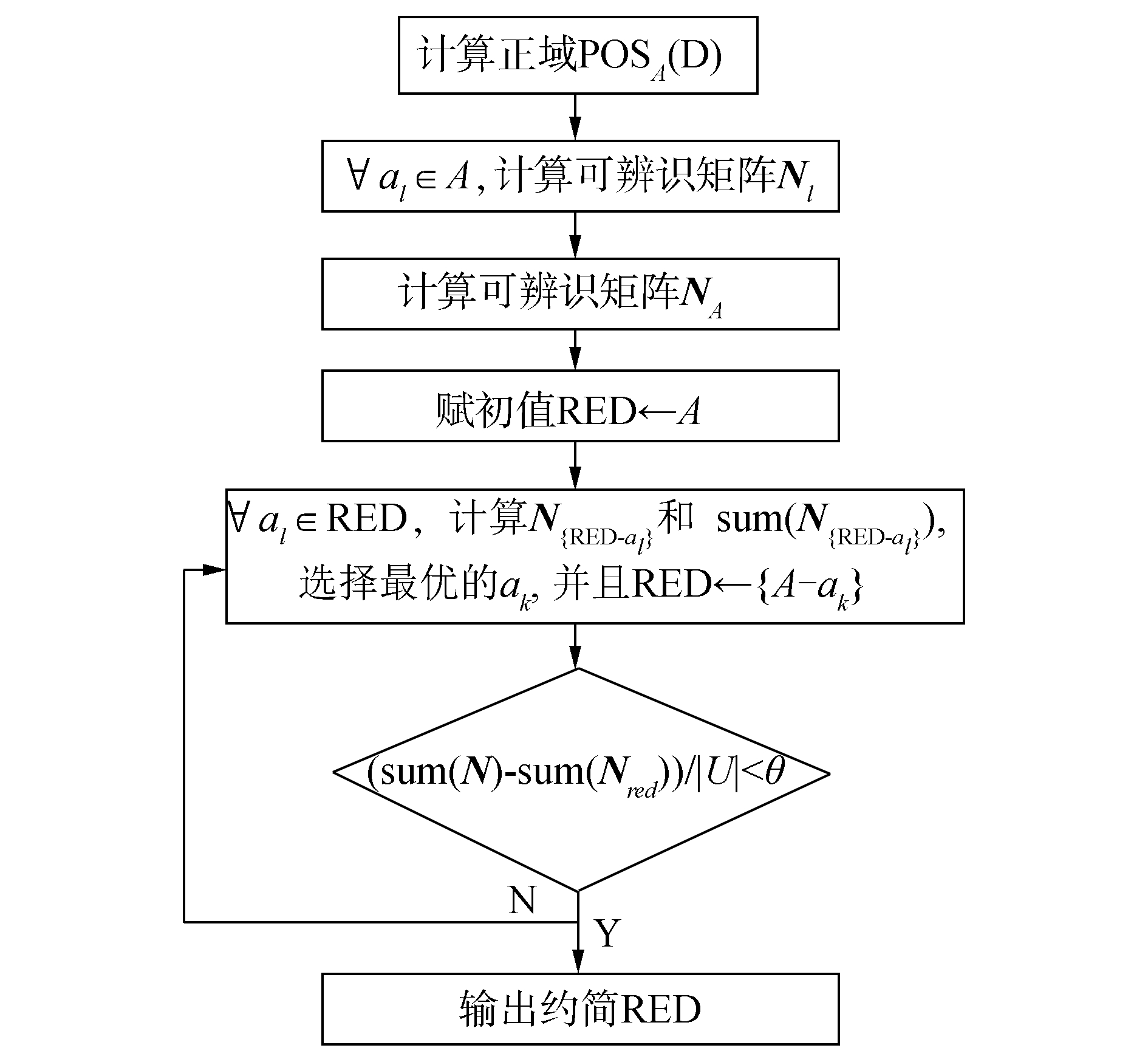
|
图 1 属性约简算法流程图 Fig.1 Flow chart of attribute reduction |
为了验证算法的有效性,从一些文献中选出4个相关的属性约简方法与本文所提的算法作比较。这4个算法分别是经典粗糙集算法(FCMRS)[1]、邻域粗糙集算法(NBRS) [5]、邻域粗糙信息测度算法(NBIM) [8]以及自适应邻域粗糙集模型(APTNB)[7]。本实验主要从算法选择的属性数目和相应的分类精度两个方面进行比较。计算机运行的环境参数为:奔腾双核,CPU E5200 1.90 GHz,RAM 4.0 GB,软件为MATLAB 2007。
本实验采用K近邻(KNN, K=3) 和支持向量机(RBF-SVM)分类器来评估这些属性约简算法的优劣,RBF-SVM分类器中参数采用默认值。数据的分类精度是基于十折交叉验证方法计算的。从UCI数据集中选择了5个数值型的数据集,其属性和分类信息描述如表 3所示。在本文所提的算法(DISRS)中,停止搜索的阈值θ设置为θ=0.005。为了说明该算法的有效性和可行性,首先对各个数据集进行了属性约简,选取约简数据的最高分类精度所对应的属性数目进行比较,具体结果如表 4所示,其中ε列表示对应数据约简后所取得的最高分类精度的相似度阈值的取值。表 5和表 6分别给出了各个数据集属性约简前后的分类精度。
| 表 3 数据描述 Tab.3 Data information |
| 表 4 属性约简的结果 Tab.4 Result of attribute reduction |
| 表 5 约简数据的SVM后的分类精度 Tab.5 Classification accuracy of reduced data with SVM |
| 表 6 约简数据的3NN分类精度 Tab.6 Classification accuracy of reduced data with 3NN |
从表 4中可以看出,这5种属性约简方法都能够有效地对数据集进行属性约简。FCMRS算法选取的属性数目最少,DISRS算法次之。表 5和表 6表明,DISRS算法的分类精度最高,FCMRS算法的分类精度最低。同时,DISRS算法所对应的分类精度明显好于其他方法。10次分类任务,DISRS算法获得了8次最高分类精度,APTNB获得了2次,NBIM获得了1次,而FCMRS和NBRS算法没有获得最高分类精度。但是NBRS算法的性能要比FCMRS方法好很多。这说明邻域粗糙集模型在处理连续型数据时比经典粗糙集方法具有更大的优势。造成FCMRS算法选择的属性数目少、分类精度低的原因,可能是由于FCMRS算法固有的离散化步骤破坏了原有数据的分类信息。而NBRS、NBIM和APTNB算法避免了离散化步骤,直接利用相似关系粒化数据空间,构造分类目标的依赖度函数用于分类,因此属性约简后的数据分类精度明显高于FCMRS算法。然而,NBRS、NBIM和APTNB算法只考虑一致样本和其他样本的可辨识性,忽略了边界样本点间可区分性,因此这3种算法的分类精度低于DISRS算法精度。而DISRS算法克服了NBRS、NBIM和APTNB算法的缺点,因此,在数据实验分析中取得了较好的性能,即DISRS算法的分类精度不仅高于其他算法,而且有效地删减了属性。根据数据实验分析表明,本文提出的算法是行之有效的,达到了理论预期的效果。
4 结束语邻域粗糙集中基于正域的贪心算法只考虑了区分一致性样本和异类样本,忽略了边界样本间的区分性。事实上,一个属性子集的分类能力不仅与一致样本有关,也与边界样本有关。而辨识矩阵的概念正好反映了一组特征的区分能力。本文研究了基于邻域辨识矩阵的属性约简方法,设计了启发式属性约简的算法,并通过UCI数据集验证了该算法的有效性。未来的工作将讨论该方法在分类决策中的应用。
| [1] |
PAWLAK Z. Rough sets[J]. International journal of computer and information sciences, 1982, 11(5): 341-356. DOI:10.1007/BF01001956 ( 0) 0)
|
| [2] |
SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[C]//Slowinski R. (Ed.), Intelligent Decision Support. Dordrecht, Kluwer Academic Publishers, 1992: 331-362.
( 0) 0)
|
| [3] |
MI J S, WU W Z, ZHANG W X. Approaches to knowledge reduction based on variable precision rough sets model[J]. Information sciences, 2004, 159(3/4): 255-272. ( 0) 0)
|
| [4] |
WU W Z, ZHANG W X. Neighborhood operator systems and approximations[J]. Information sciences, 2002, 144(1/4): 201-217. ( 0) 0)
|
| [5] |
HU Q H, YU D, LIU J F, et al. Neighborhood-rough-set based heterogeneous feature subset selection[J]. Information sciences, 2008, 178(18): 3577-3594. DOI:10.1016/j.ins.2008.05.024 ( 0) 0)
|
| [6] |
KIM D. Data classification based on tolerant rough set[J]. Pattern recognition, 2001, 34(8): 1613-1624. DOI:10.1016/S0031-3203(00)00057-1 ( 0) 0)
|
| [7] |
ZHAO H, WANG P, HU Q H. Cost-sensitive feature selection based on adaptive neighborhood granularity with multi-level confidence[J]. Information sciences, 2016, 366: 134-149. DOI:10.1016/j.ins.2016.05.025 ( 0) 0)
|
| [8] |
CHEN Y, ZHANG Z, ZHENG J, et al. Gene selection for tumor classification using neighborhood rough sets and entropy measures[J]. Journal of biomedical informatics, 2017, 67: 59-68. DOI:10.1016/j.jbi.2017.02.007 ( 0) 0)
|
| [9] |
ZHU P, HU Q H. Adaptive neighborhood granularity selection and combination based on margin distribution optimation[J]. Information sciences, 2013, 249: 1-12. DOI:10.1016/j.ins.2013.06.012 ( 0) 0)
|
| [10] |
鲍丽娜, 丁世飞, 许新征, 等. 基于邻域粗糙集的极速学习机算法[J]. 济南大学学报, 2015, 29(5): 367-371. BAO Lina, DING Shifei, XU Xinzheng, et al. Extreme learning machine algorithm based on neighborhood rough sets[J]. Journal of jinan university, 2015, 29(5): 367-371. (  0) 0)
|
| [11] |
谢娟英, 李楠, 乔子芮. 基于邻域粗糙集的不完整决策系统特征选择算法[J]. 南京大学学报, 2016, 47: 384-390. XIE Juanying, LI Nan, QIAO Zirui. A feature selection algorithm based on neighborhood rough sets for incomplete information systems[J]. Journal of Nanjing university, 2016, 47: 384-390. (  0) 0)
|
| [12] |
徐伟华. 序信息系统与粗糙集[M]. 北京: 科学出版社, 2013.
( 0) 0)
|
| [13] |
GRECO S, MATARAZZO B, SLOWINSKI R. Rough sets methodology for sorting problems in presence of multiple attributes and criteria[J]. European journal of operational research, 2002, 38: 247-259. ( 0) 0)
|
| [14] |
WANG C, HE Q, CHEN D G, et al. A novel method for attribute reduction of covering decision tables[J]. Information sciences, 2014, 254: 181-196. DOI:10.1016/j.ins.2013.08.057 ( 0) 0)
|
| [15] |
WANG C, SHAO M, SUN B, et al. An improved attribute reduction scheme with covering based rough sets[J]. Applied soft computing, 2015, 26(1): 235-243. ( 0) 0)
|
| [16] |
ZHU W, WANG F Y. Reduction and maximization of covering generalized rough sets[J]. Information sciences, 2003, 152: 217-230. DOI:10.1016/S0020-0255(03)00056-2 ( 0) 0)
|
| [17] |
DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International journal of general systems, 1990, 17: 191-208. DOI:10.1080/03081079008935107 ( 0) 0)
|
| [18] |
WANG C, QI Y, HU Q, et al. A fitting model for feature selection with fuzzy rough sets[J]. IEEE transaction on fuzzy systems, 2016, 99: 1-1. ( 0) 0)
|
| [19] |
WANG C, SHAO M, QIAN Y. Feature subset selection based on fuzzy neighborhood rough sets[J]. Knowledge-based systems, 2016, 111(1): 173-179. ( 0) 0)
|
| [20] |
CHEN D G, ZHANG L, ZHAO S Y, et al. A novel algorithm for finding reducts with fuzzy rough sets[J]. IEEE transaction on fuzzy systems, 2013, 20(2): 385-389. ( 0) 0)
|
| [21] |
WANG X Z, ZHAI J H, LU S X. Induction of multiple fuzzy decision trees based on rough set technique[J]. Information sciences, 2008, 178(16): 3188-3202. DOI:10.1016/j.ins.2008.03.021 ( 0) 0)
|
| [22] |
ZHAO S Y, TSANG C C, CHEN D. Building a rule-based classifier by using fuzzy rough set technique[J]. IEEE transaction on knowledge and data engineering, 2010, 22(5): 624-638. DOI:10.1109/TKDE.2009.118 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


